ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА Поверхностью второго порядка называют поверхность, определяемую уравнением второй степени относительно текущих декартовых координат х и у: где хотя бы один из коэффициентов
Поверхности второго порядка вырожденные невырожденные 1. пустое множество 2. точка 3. плоскость 4. пара параллельных или пересекающихся плоскостей 1. сфера 3. однополостный гиперболоид 4. двухполостный гиперболоид 5. эллиптический параболоид 6. гиперболический параболоид 7. эллиптический конус 8. эллиптический цилиндр 9. гиперболический цилиндр 10. параболический цилиндр 2. эллипсоид ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
Исследуем каждую из невырожденных поверхностей второго порядка методом параллельных сечений, то есть рассмотрим линии пересечения данной поверхности с плоскостями, параллельными координатным плоскостям. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
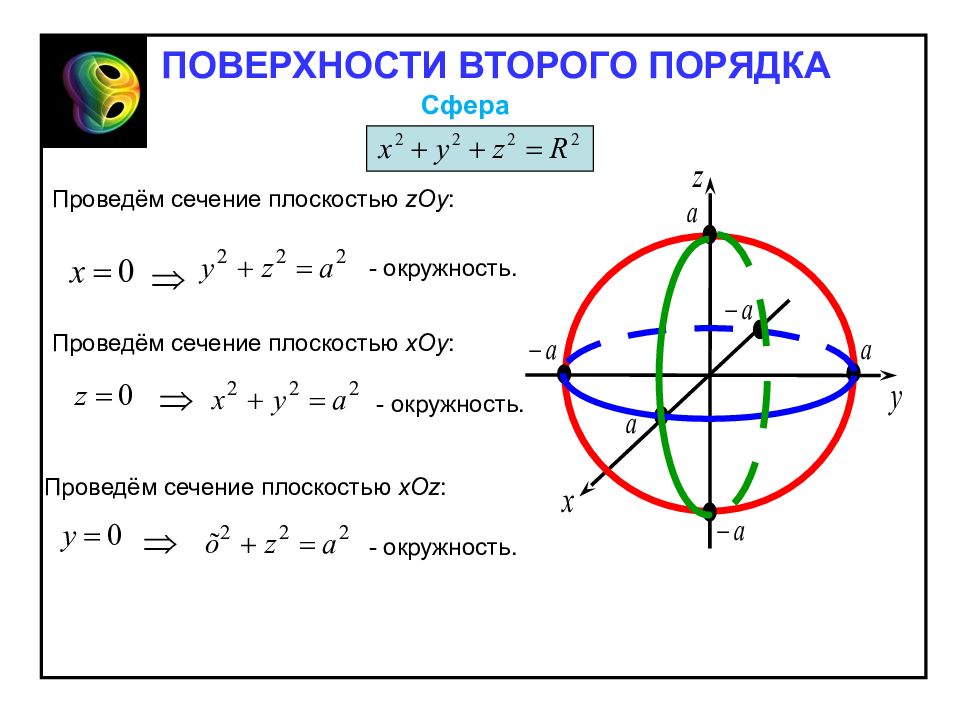
Сфера Сферой называется геометрическое место точек пространства, равноудаленных от фиксированной точки, называемой центром. Каноническое уравнение сферы имеет вид: Отметим свойства сферы, вытекающие из определения. Сфера – ограниченная поверхность, поскольку из его канонического уравнения следует, что Таким образом, эллипсоид расположен внутри куба с центром в точке O и сторонами, равными a. Сфера обладает: – центральной симметрией относительно начала координат; – осевой симметрией относительно координатных осей; – плоскостной симметрией относительно координатных плоскостей ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
Проведём сечение плоскостью zOy : - окружность. Проведём сечение плоскостью х Oy : - окружность. Проведём сечение плоскостью х Oz : - окружность. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА Сфера
О R R R R R R R R R R R R R R R R R ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА Сфера
ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА Сфера
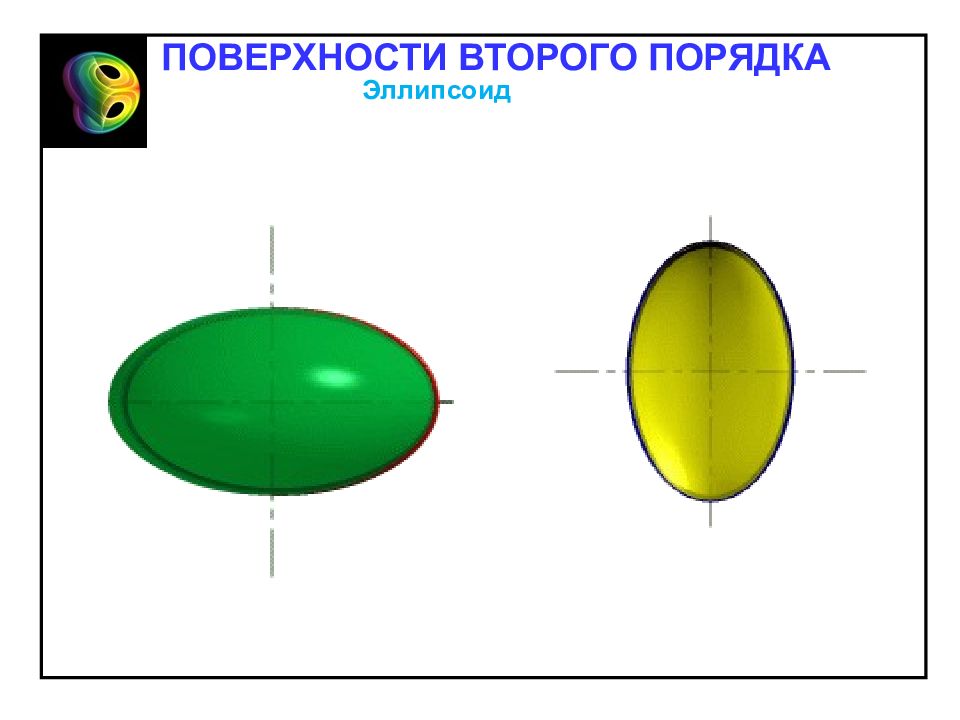
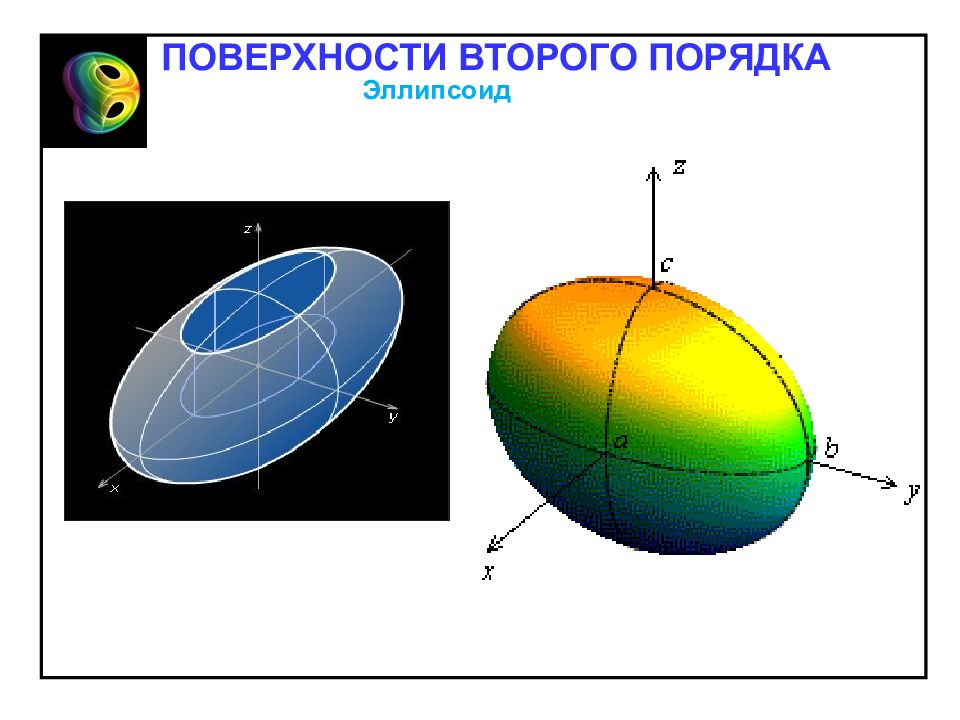
Числа a, b, c называются полуосям эллипсоида. Эллипсоид Эллипсоидом называется поверхность, каноническое уравнение которой в декартовой системе координат имеет вид Отметим свойства эллипсоида, вытекающие из определения. 1. Эллипсоид – ограниченная поверхность, поскольку из его канонического уравнения следует, что Таким образом, эллипсоид расположен внутри параллелепипеда с центром в точке O и сторонами, равными 2 a,2 b,2 c. 2. Эллипсоид обладает: – центральной симметрией относительно начала координат; – осевой симметрией относительно координатных осей; – плоскостной симметрией относительно координатных плоскостей 3. Точки пересечения с осями: точки и – вершины эллипсоида. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
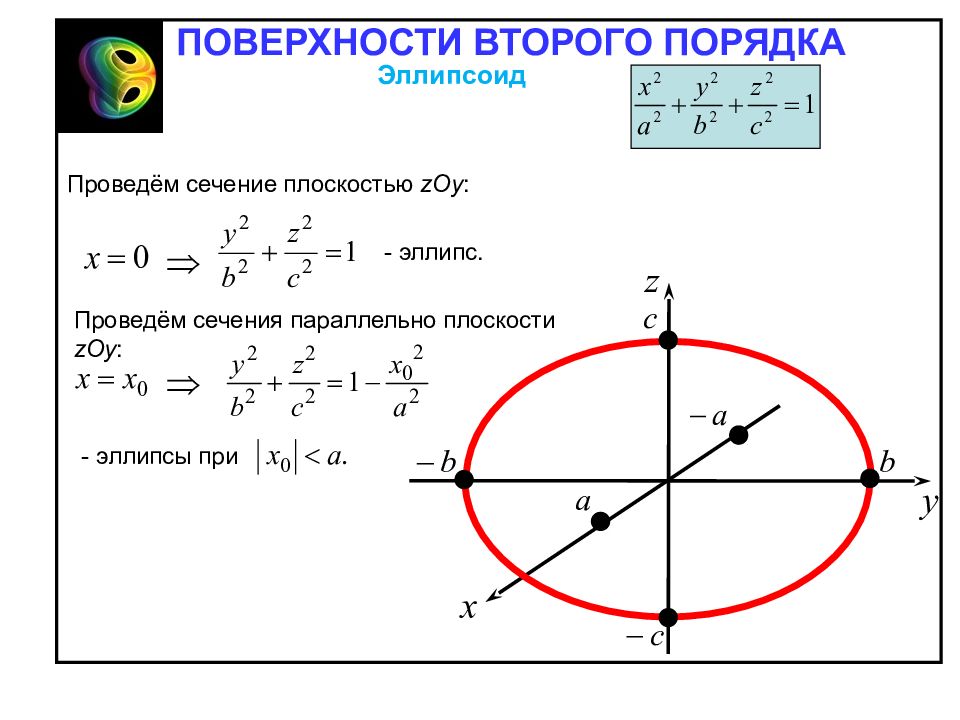
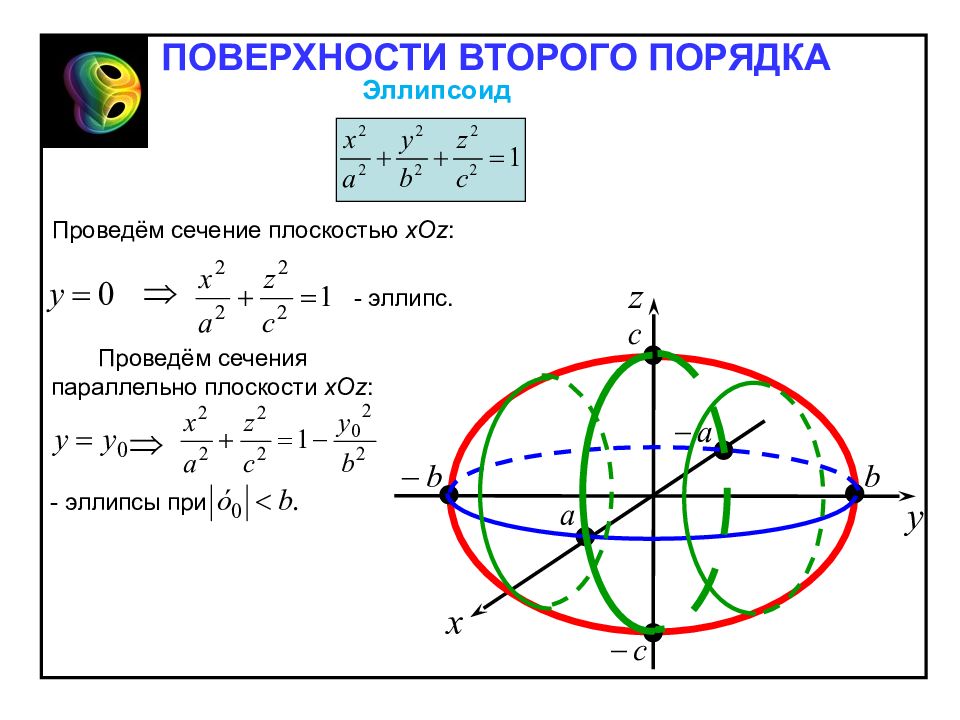
Проведём сечение плоскостью zOy : Проведём сечения параллельно плоскости zOy : - эллипсы при - эллипс. Эллипсоид ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
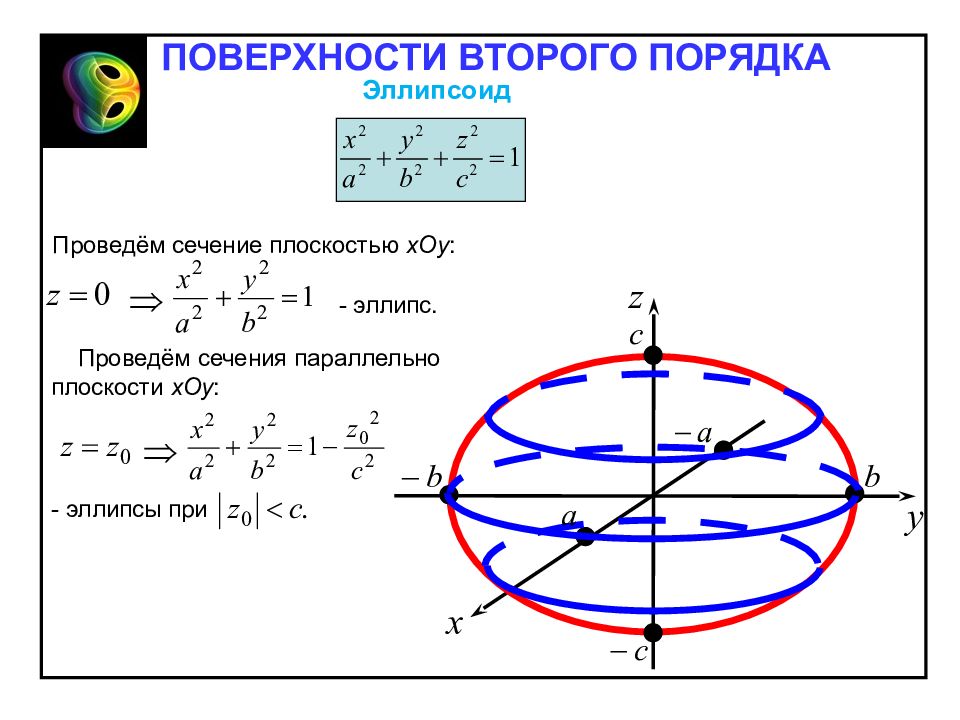
Проведём сечение плоскостью х Oy : Проведём сечения параллельно плоскости х Oy : - эллипсы при - эллипс. Эллипсоид ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
Проведём сечение плоскостью х Oz : Проведём сечения параллельно плоскости х Oz : - эллипсы при - эллипс. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА Эллипсоид
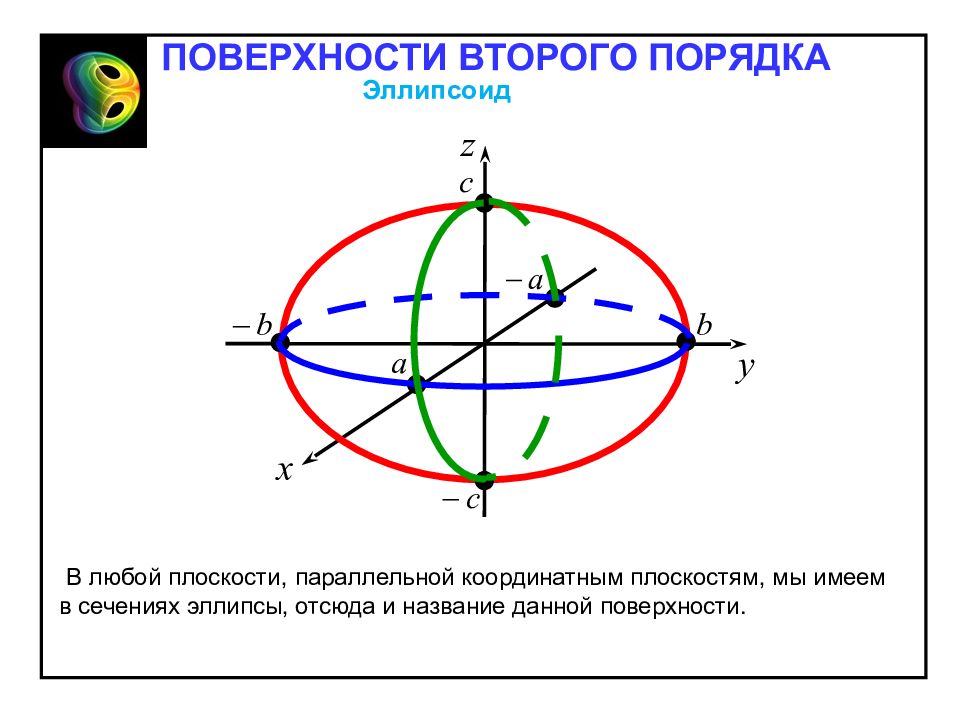
В любой плоскости, параллельной координатным плоскостям, мы имеем в сечениях эллипсы, отсюда и название данной поверхности. Эллипсоид ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
Эллипсоид ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
Эллипсоид ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
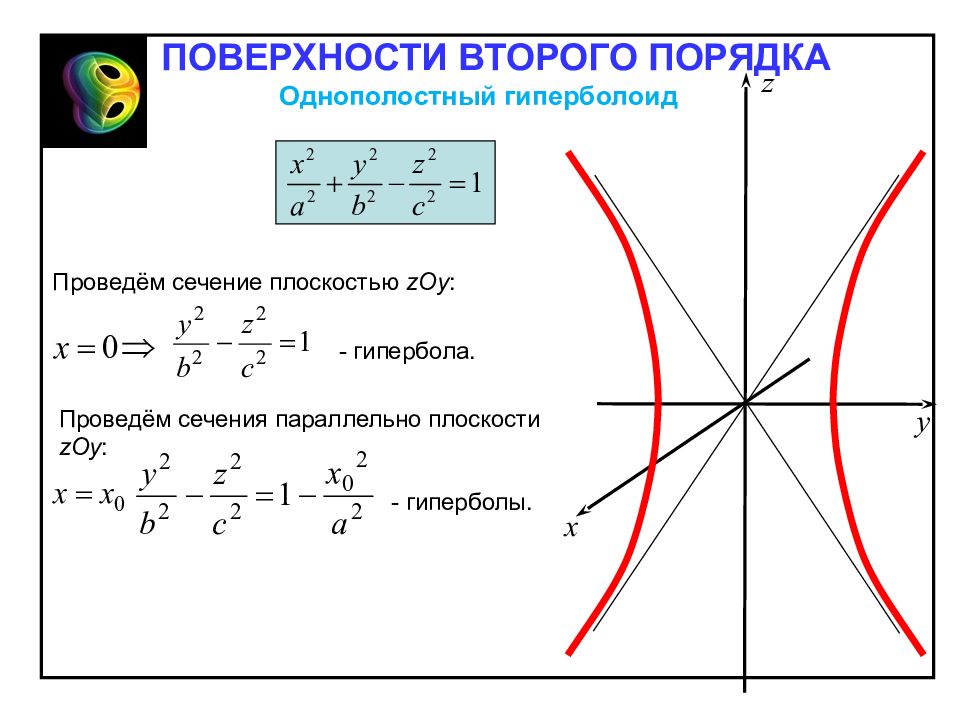
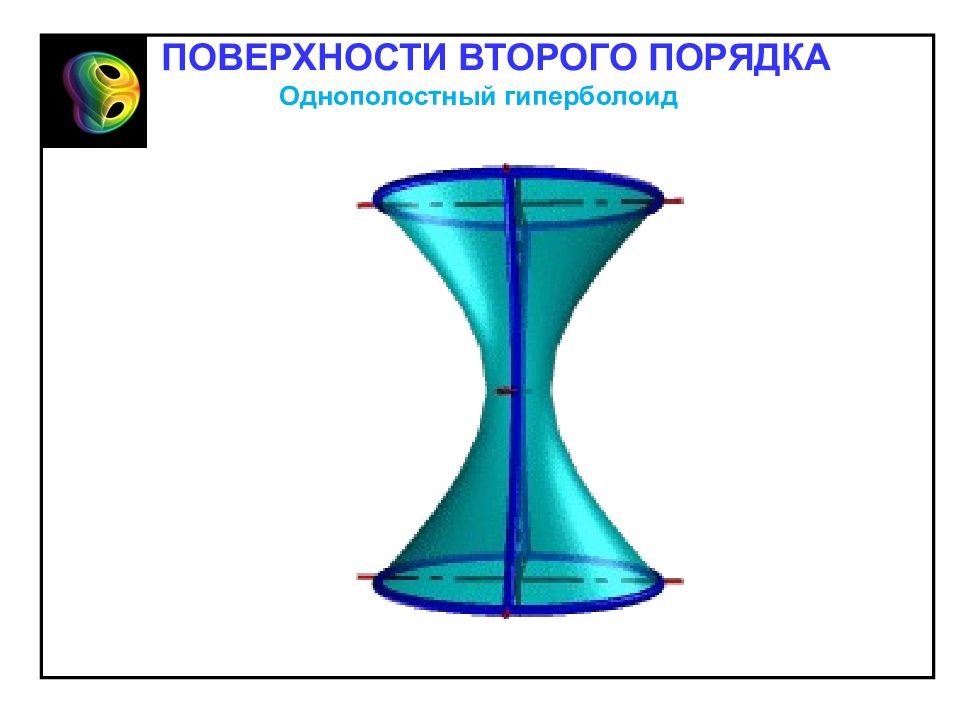
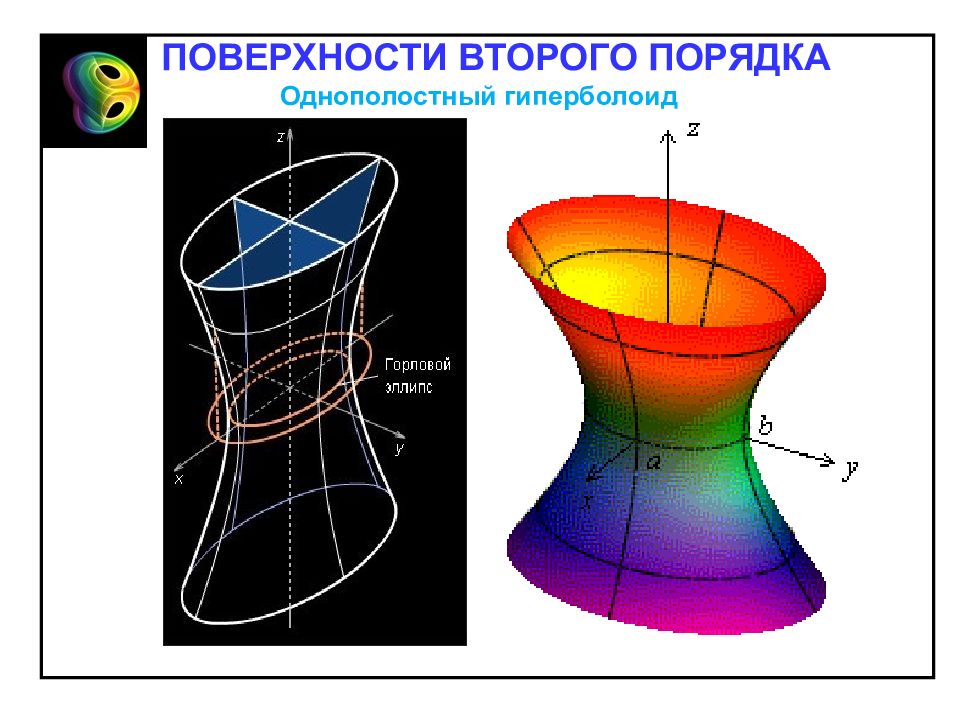
1. Однополостный гиперболоид – неограниченная поверхность, поскольку из его канонического уравнения следует, что Однополостный гиперболоид Однополостным гиперболоидом называется поверхность, каноническое уравнение которой имеет вид Отметим свойства однополостного гиперболоида, вытекающие из определения: 2. Однополостный гиперболоид обладает: – центральной симметрией относительно начала координат; – осевой симметрией относительно всех координатных осей; – плоскостной симметрией относительно всех координатных плоскостей. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
Проведём сечение плоскостью zOy : Проведём сечения параллельно плоскости zOy : - гиперболы. - гипербола. Однополостный гиперболоид ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
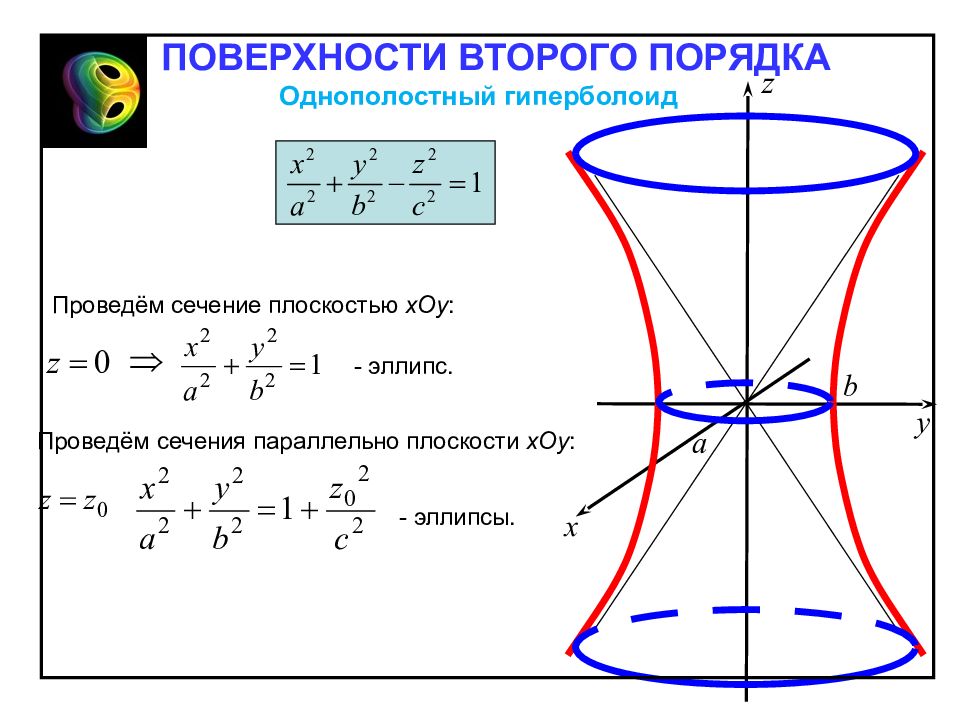
Проведём сечение плоскостью х Oy : Проведём сечения параллельно плоскости х Oy : - эллипсы. - эллипс. Однополостный гиперболоид ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
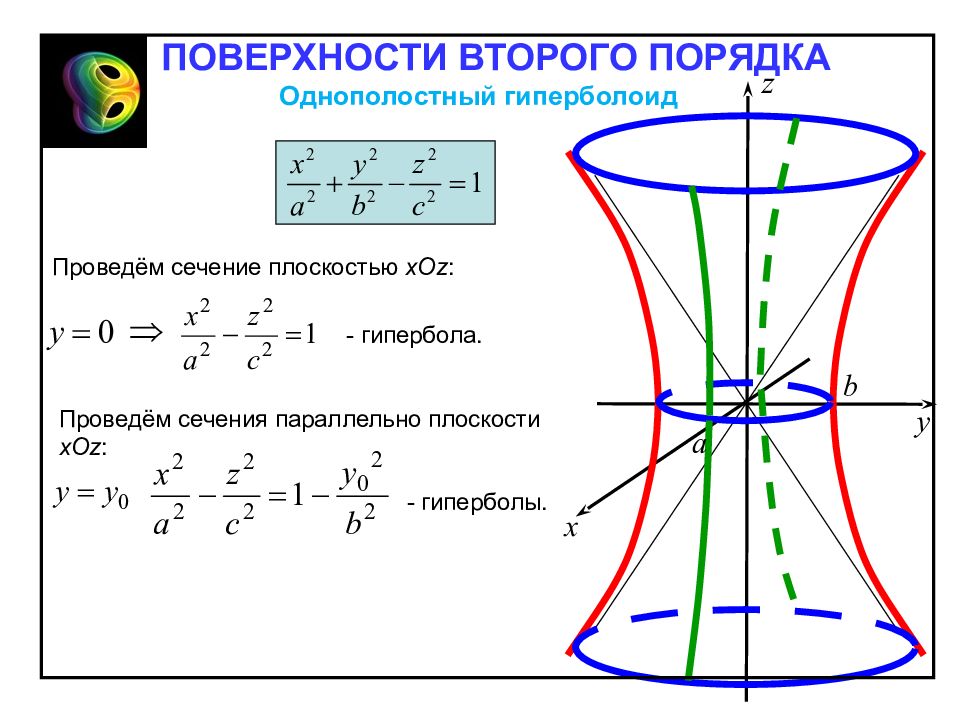
Проведём сечение плоскостью х Oz : Проведём сечения параллельно плоскости х Oz : - гиперболы. - гипербола. Однополостный гиперболоид ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА Однополостный гиперболоид
ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА Однополостный гиперболоид
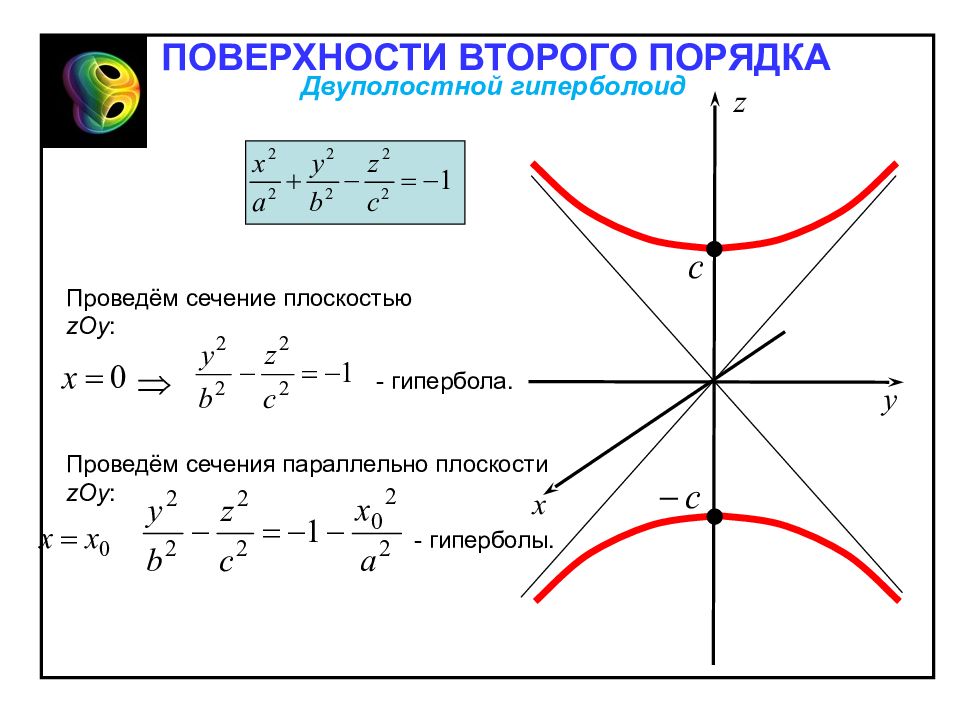
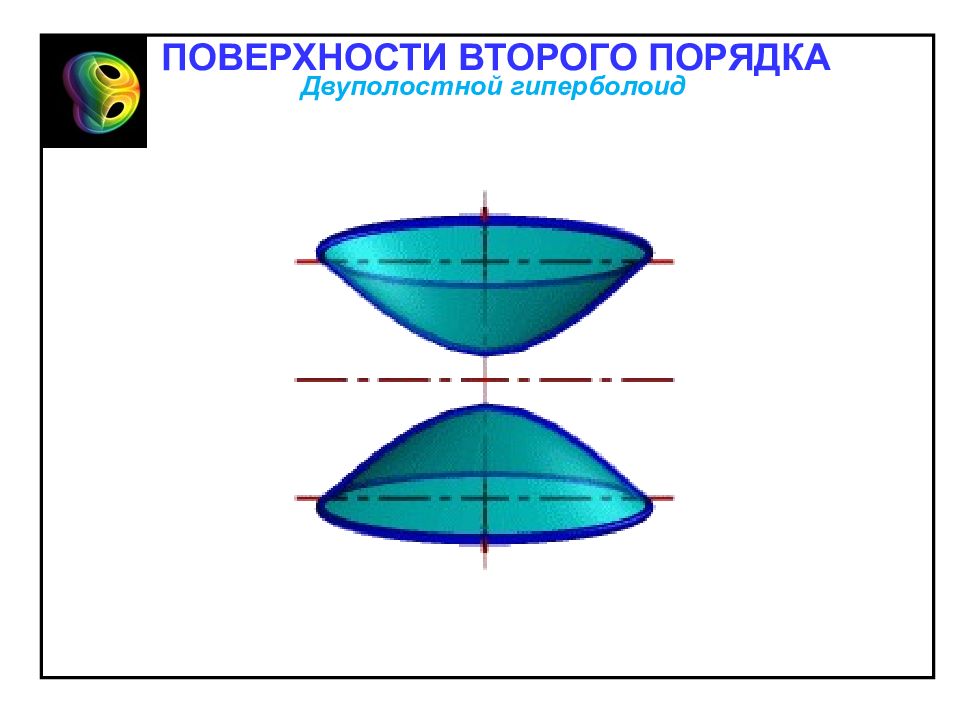
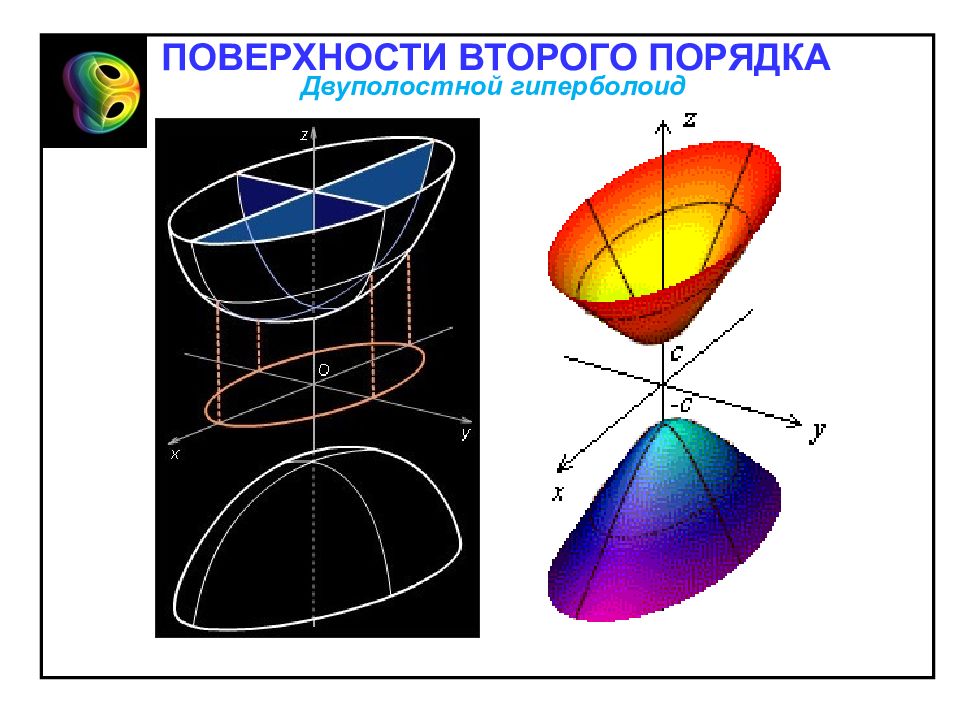
Двуполостным гиперболоидом называется поверхность, каноническое уравнение которой имеет следующий вид: 1. Двуполостной гиперболоид – неограниченная поверхность, поскольку из его канонического уравнения следует, что и не ограничен сверху. Двуполостной гиперболоид Отметим свойства двуполостного гиперболоида, вытекающие из определения. 2. Двуполостной гиперболоид обладает: – центральной симметрией относительно начала координат; – осевой симметрией относительно всех координатных осей; – симметрией относительно всех координатных плоскостей. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
Проведём сечение плоскостью zOy : - гипербола. Проведём сечения параллельно плоскости zOy : - гиперболы. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА Двуполостной гиперболоид
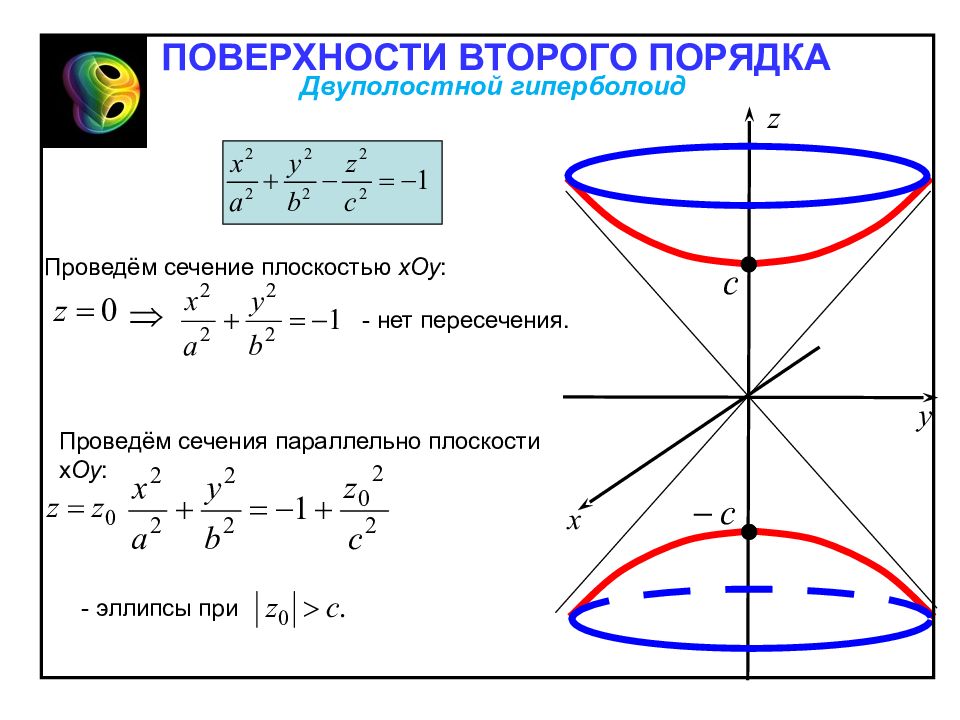
Проведём сечение плоскостью х Oy : Проведём сечения параллельно плоскости х Oy : - нет пересечения. - эллипсы при ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА Двуполостной гиперболоид
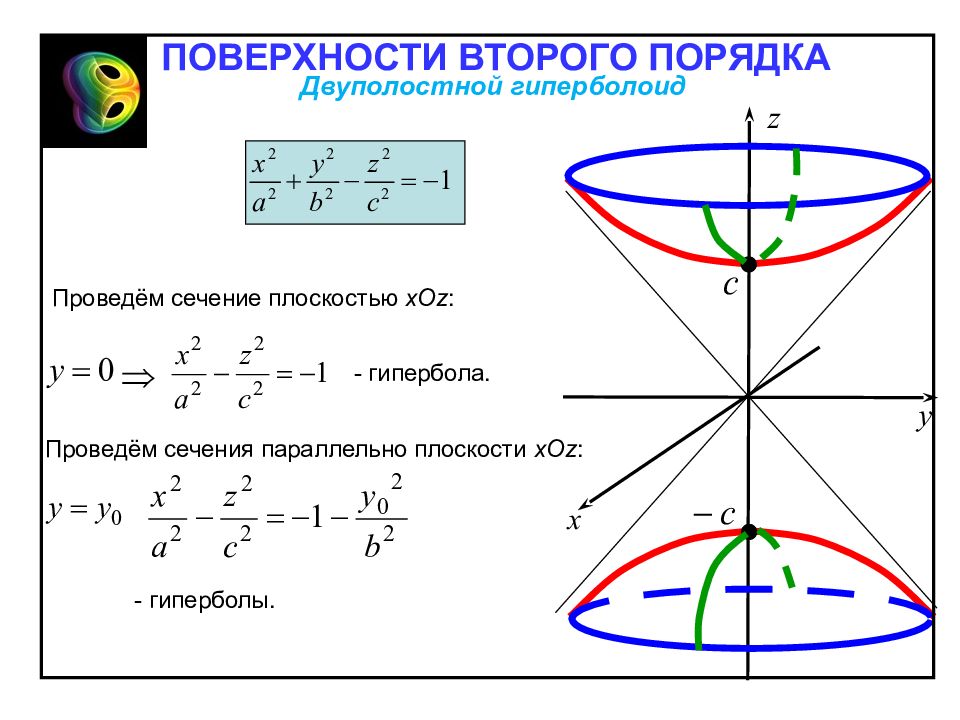
- гипербола. Проведём сечения параллельно плоскости х Oz : ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА Проведём сечение плоскостью х Oz : - гиперболы. Двуполостной гиперболоид
ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА Двуполостной гиперболоид
ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА Двуполостной гиперболоид
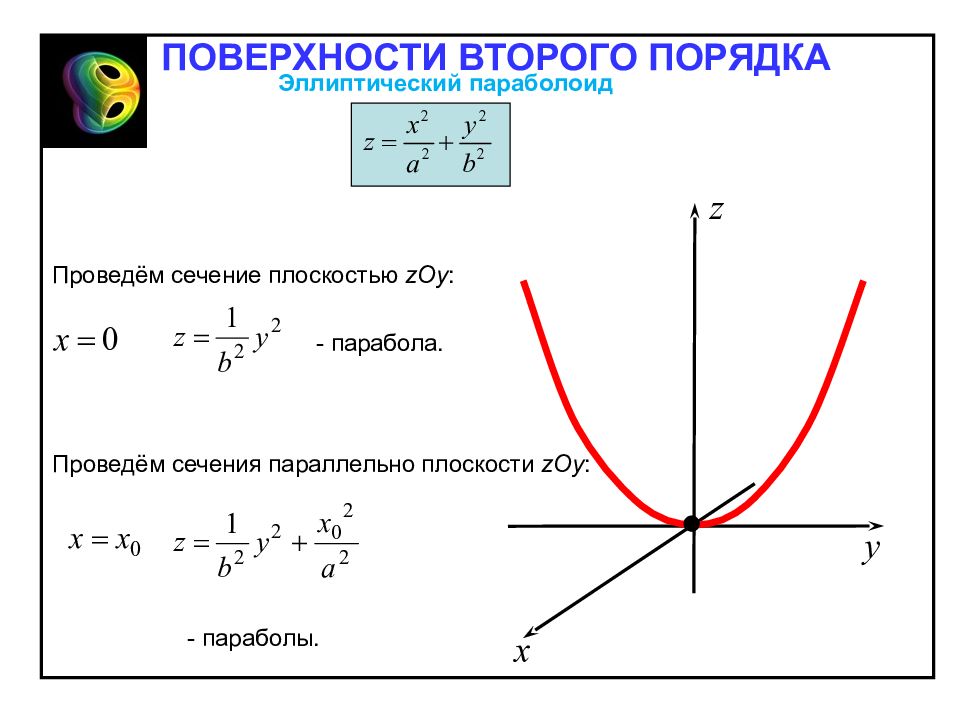
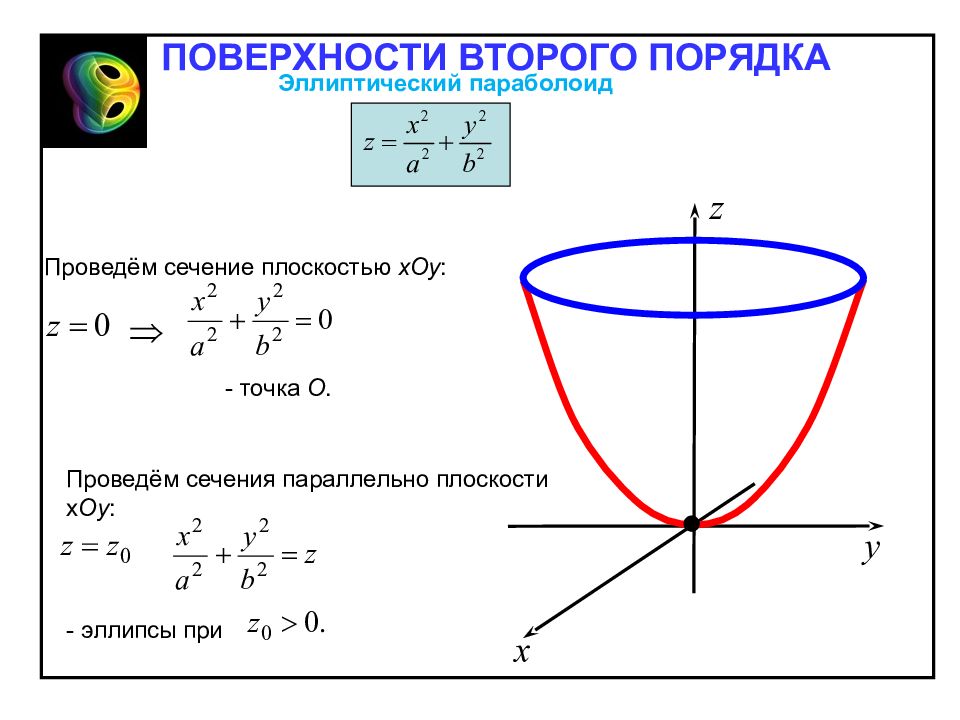
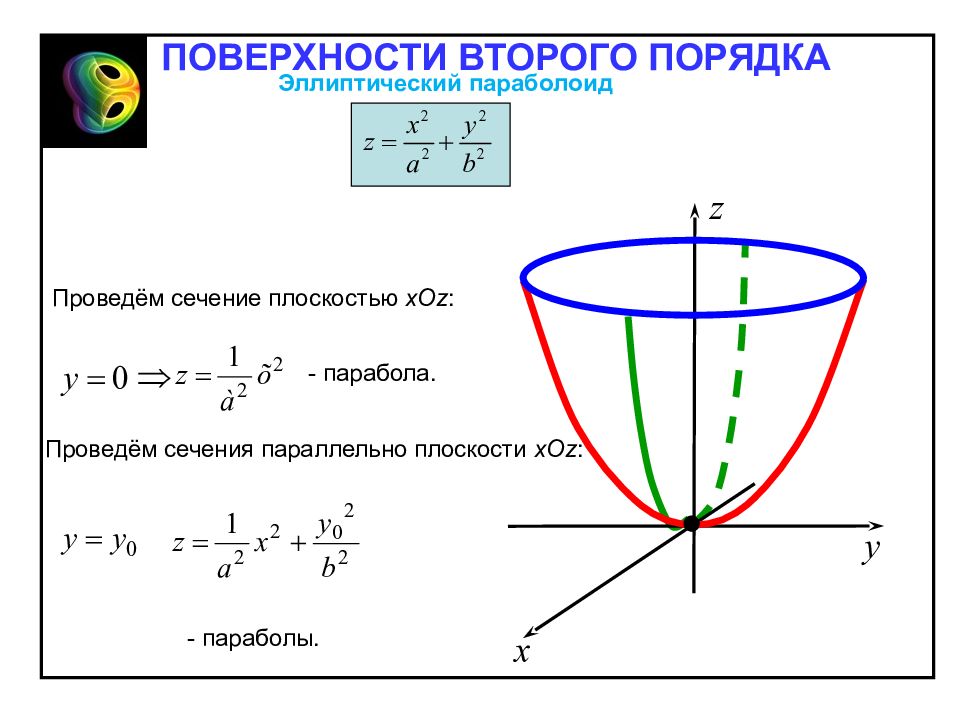
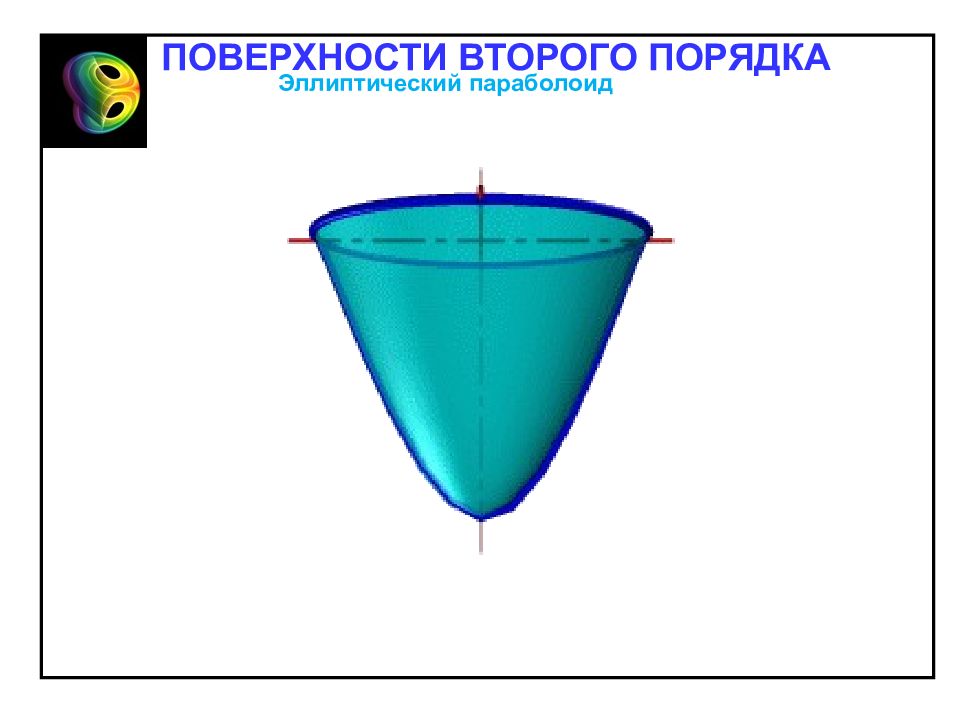
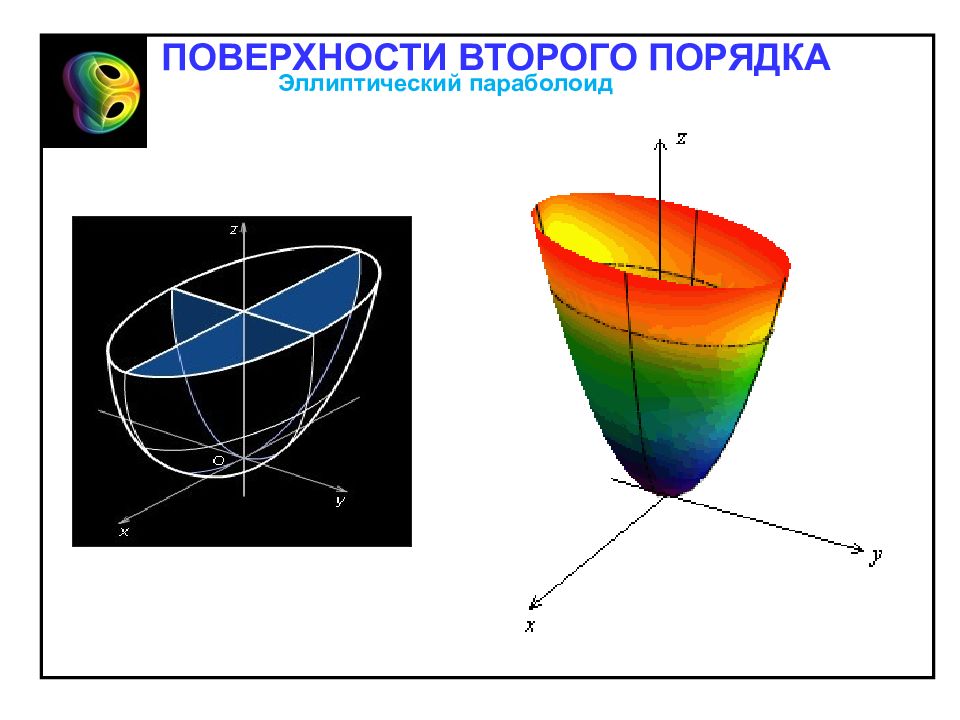
1. Эллиптический параболоид – неограниченная поверхность, поскольку из его канонического уравнения следует, что и принимает сколько угодно большие значения. Эллиптический параболоид Эллиптическим параболоидом называется поверхность, каноническое уравнения которой имеет вид Отметим свойства эллиптического параболоида, вытекающие из определения: 2. Эллиптический параболоид обладает: – осевой симметрией относительно оси Oz ; – плоскостной симметрией относительно координатных плоскостей Oxz и Oyz. 3. При z =0 уравнению удовлетворяют x = y = 0. Значит, точка O (0;0;0) – вершина параболоида. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
Проведём сечение плоскостью zOy : - парабола. Проведём сечения параллельно плоскости zOy : - параболы. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА Эллиптический параболоид
Проведём сечение плоскостью х Oy : - точка О. Проведём сечения параллельно плоскости х Oy : - эллипсы при ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА Эллиптический параболоид
Проведём сечение плоскостью х Oz : - парабола. Проведём сечения параллельно плоскости х Oz : - параболы. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА Эллиптический параболоид
ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА Эллиптический параболоид
ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА Эллиптический параболоид
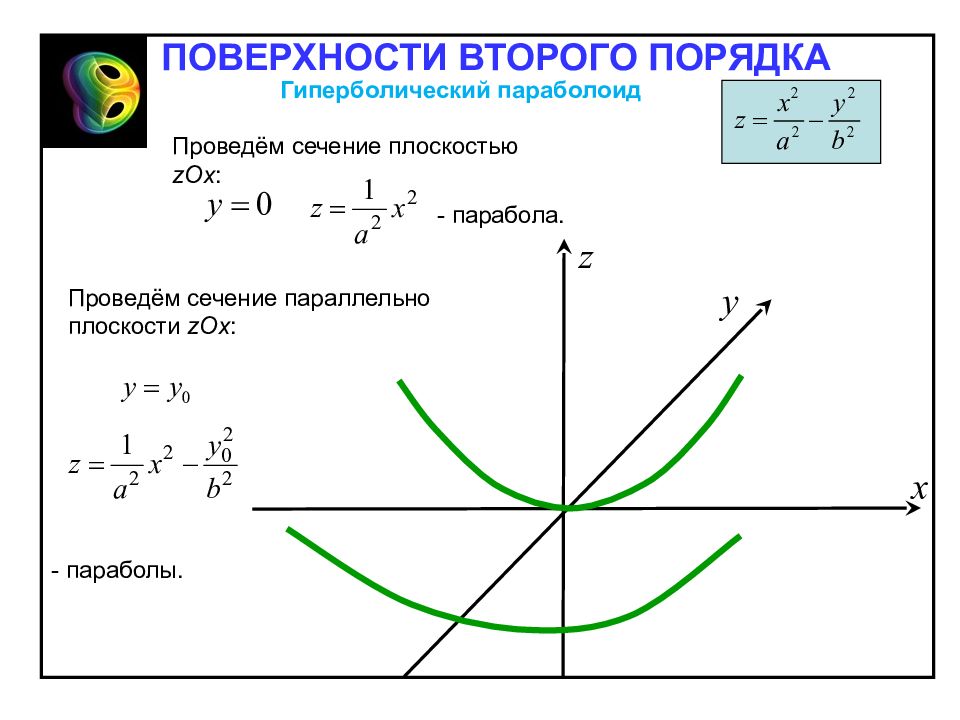
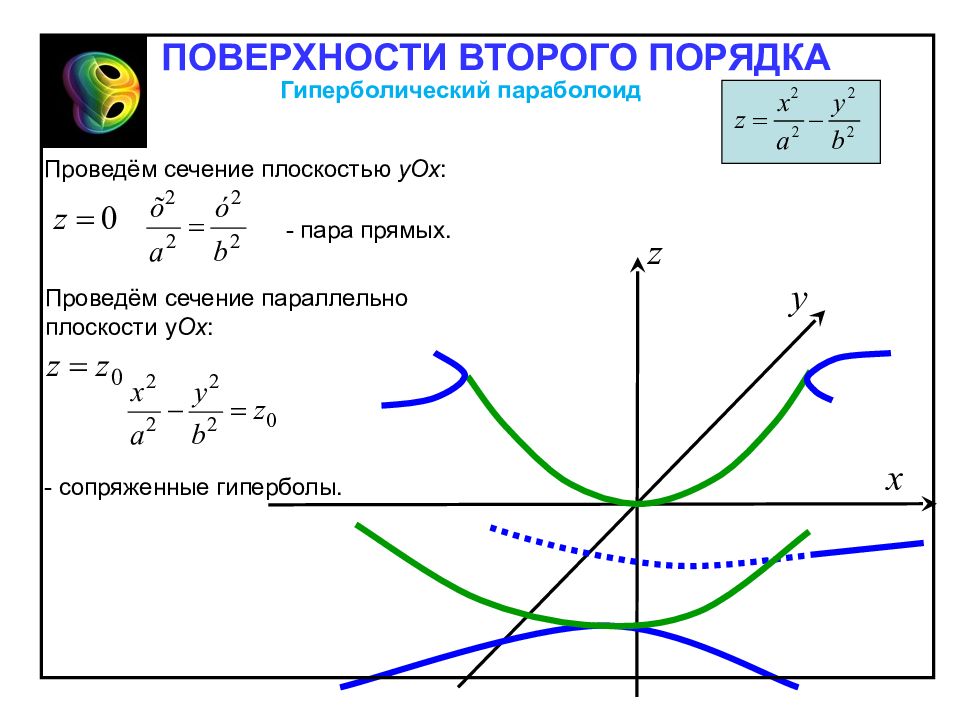
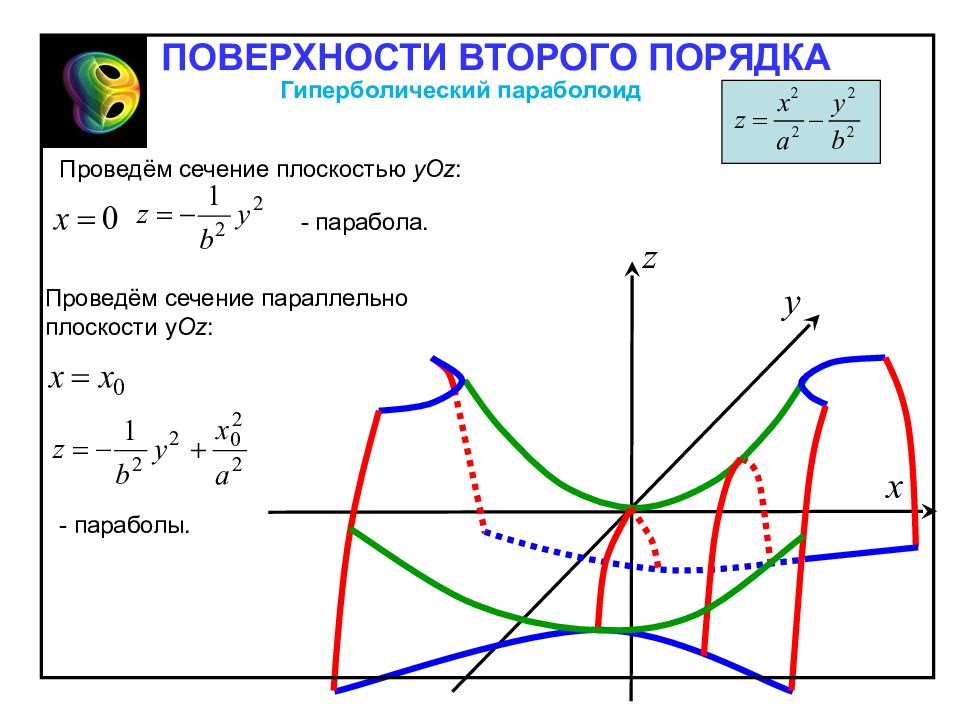
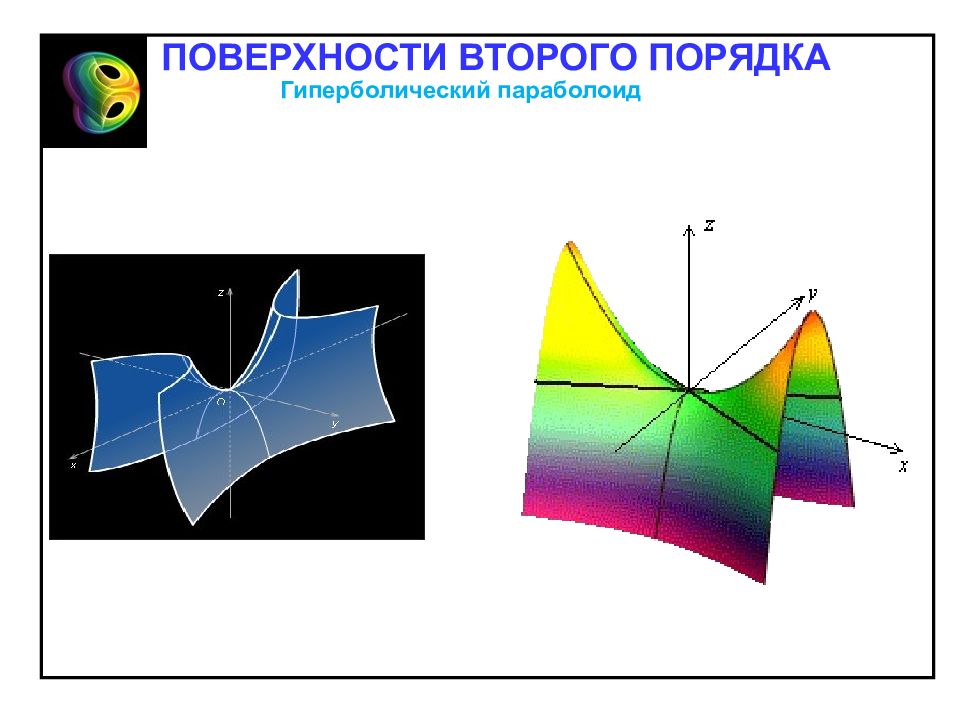
Гиперболическим параболоидом называется поверхность, каноническое уравнения которой имеет следующий вид: Гиперболический параболоид Отметим свойства гиперболического параболоида, вытекающие из определения: 1. Гиперболический параболоид – неограниченная поверхность, поскольку из его канонического уравнения следует, что z – любое. 2. Гиперболический параболоид обладает: – осевой симметрией относительно оси Oz ; – плоскостной симметрией относительно координатных плоскостей Oxz и Oyz. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
Проведём сечение плоскостью zO х : - парабола. Проведём сечение параллельно плоскости zO х : - параболы. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА Гиперболический параболоид
Проведём сечение плоскостью у O х : - пара прямых. Проведём сечение параллельно плоскости у O х : - сопряженные гиперболы. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА Гиперболический параболоид
Проведём сечение параллельно плоскости у Oz : - параболы. Проведём сечение плоскостью у Oz : - парабола. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА Гиперболический параболоид
ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА Гиперболический параболоид
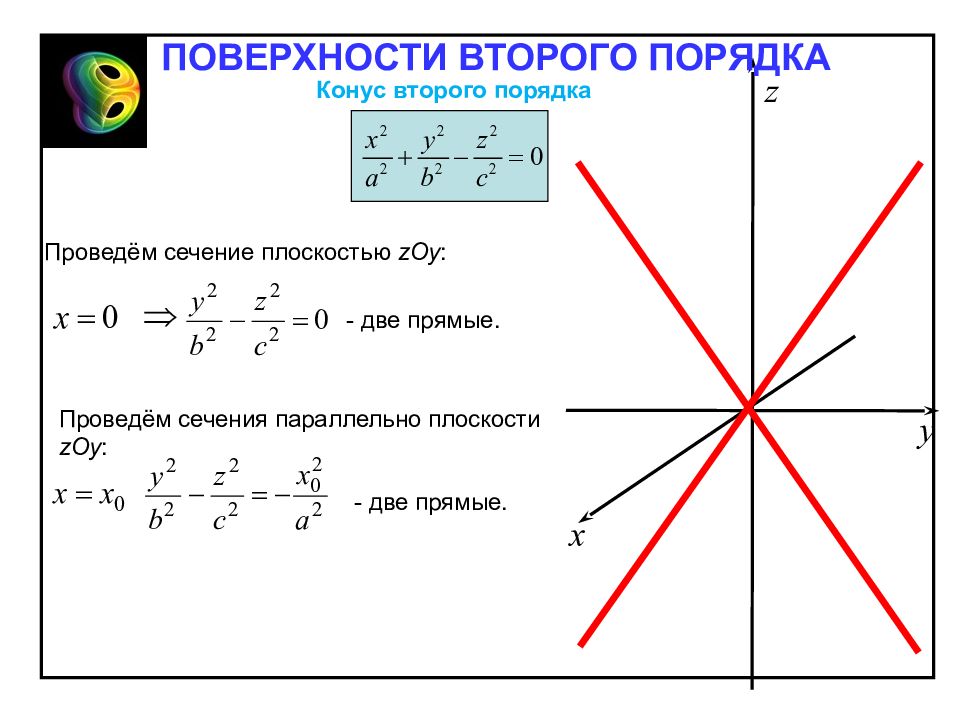
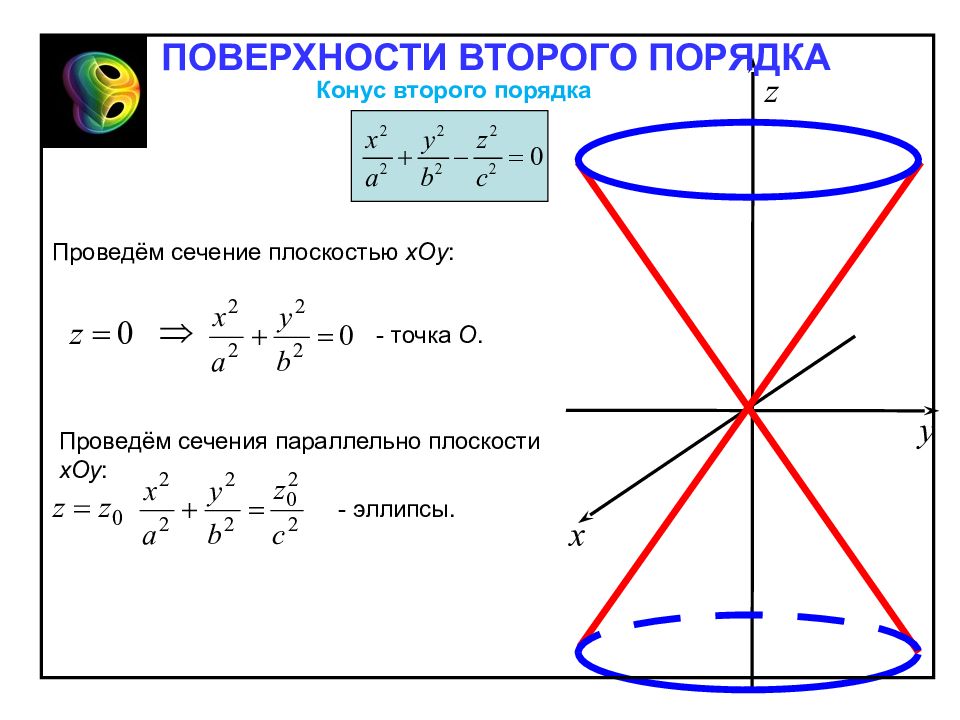
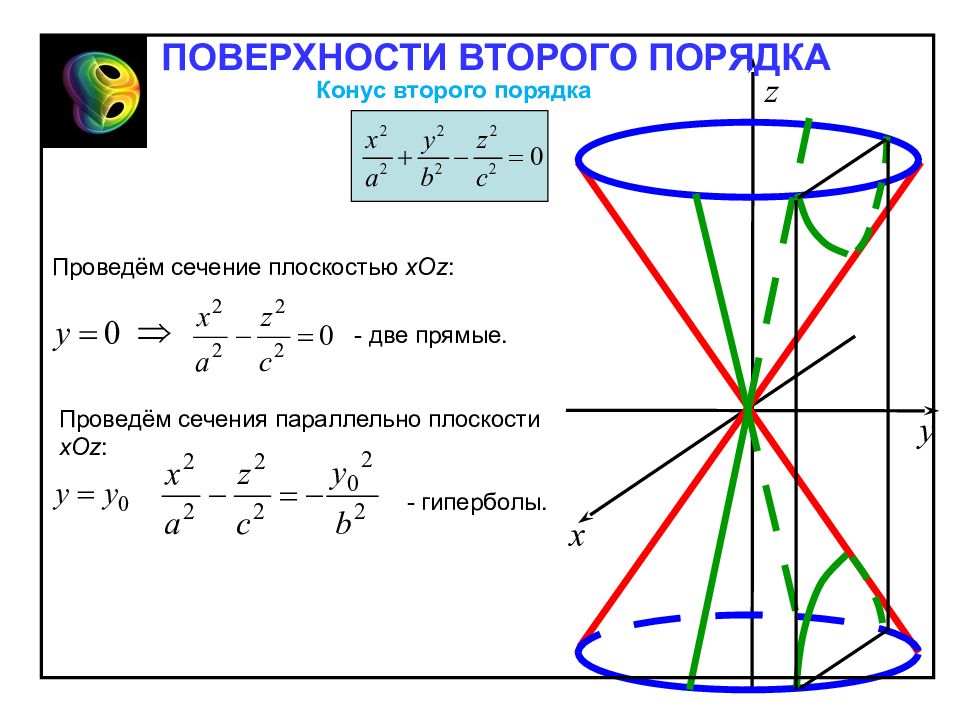
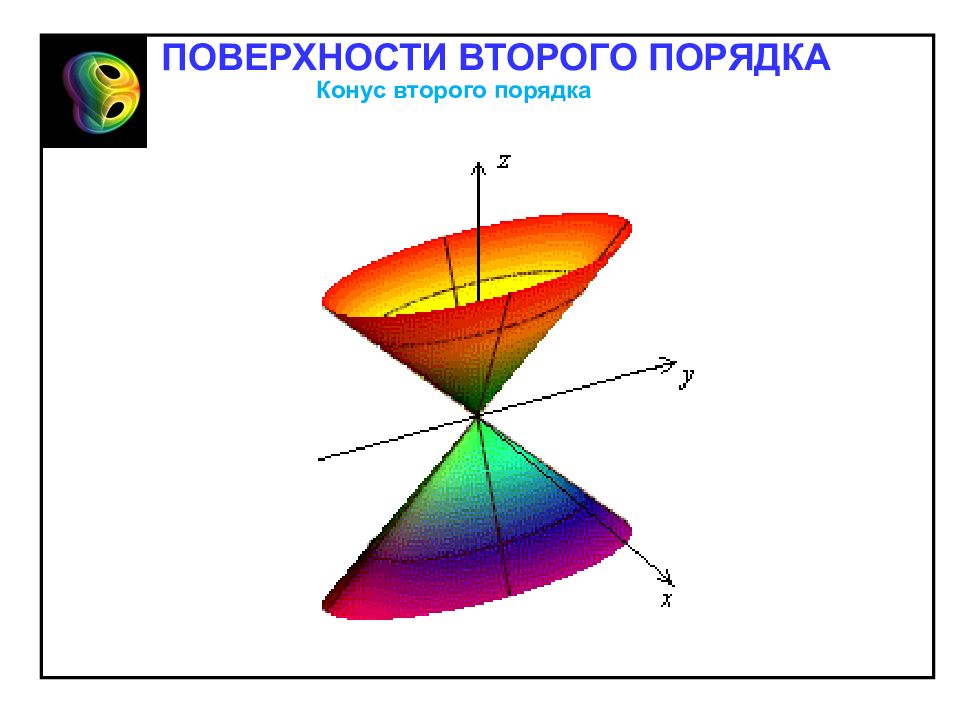
Конус второго порядка Конической поверхностью (конусом) второго порядка называют поверхность, определяемую в декартовой прямоугольной системе координат уравнением Отметим свойства конуса, вытекающие из определения: 1. Точка O – центр симметрии – вершина конуса. 2. Поверхность симметрична относительно координатных плоскостей. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
Проведём сечение плоскостью zOy : - две прямые. Проведём сечения параллельно плоскости zOy : - две прямые. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА Конус второго порядка
Проведём сечение плоскостью х Oy : - точка О. Проведём сечения параллельно плоскости х Oy : - эллипсы. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА Конус второго порядка
Проведём сечение плоскостью х Oz : - две прямые. Проведём сечения параллельно плоскости х Oz : - гиперболы. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА Конус второго порядка
ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА Конус второго порядка
Цилиндрические поверхности Цилиндрической поверхностью называется такая поверхность, каноническое уравнение которой не содержит одной из координат, например, z: . На плоскости Оху это уравнение определяет некоторую линию L. х y z L Пусть, т. е. координаты точки M удовлетворяют уравнению Но этому уравнению будут удовлетворять координаты любой точки Следовательно, уравнение F ( x ; y )=0 описывает поверхность, проектирующуюся на плоскость Оху в кривую L. В зависимости от типа направляющей L цилиндрические поверхности делятся на эллиптические, гиперболические и параболические. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
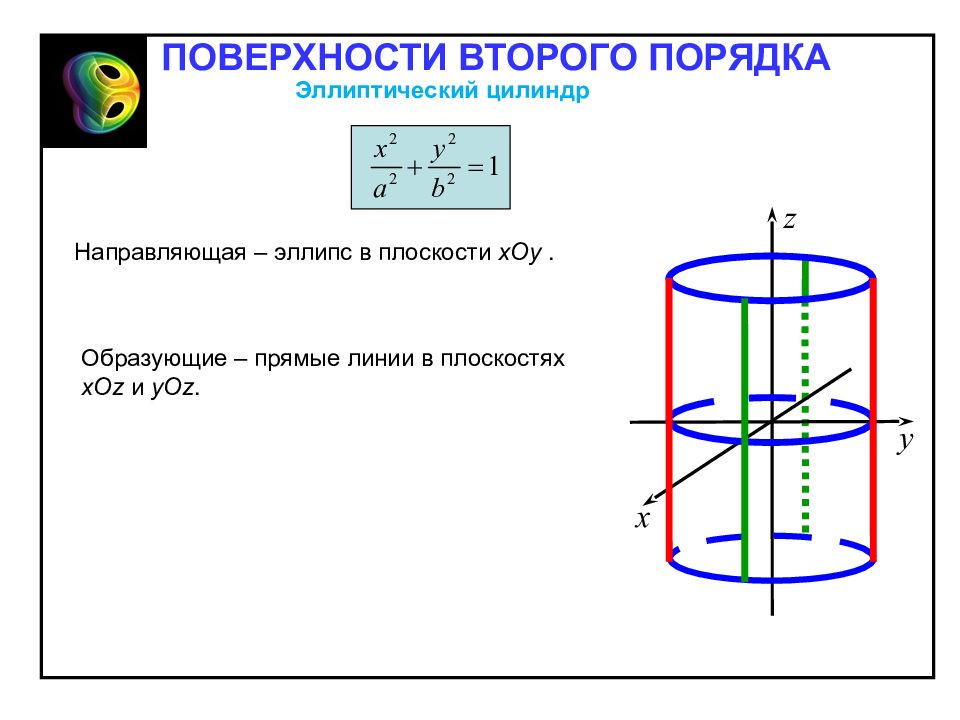
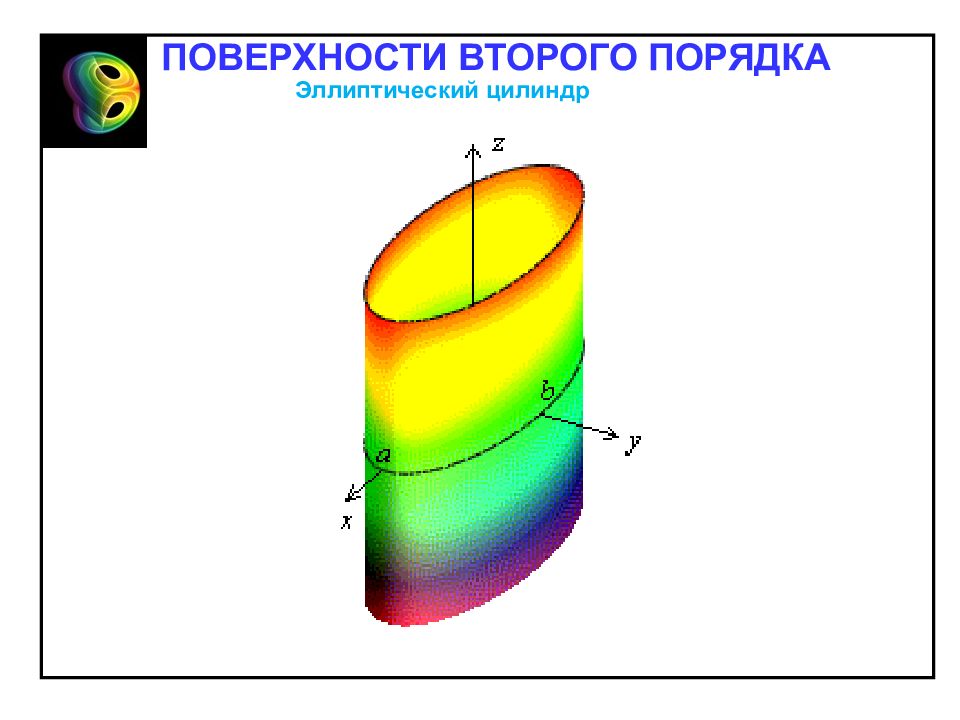
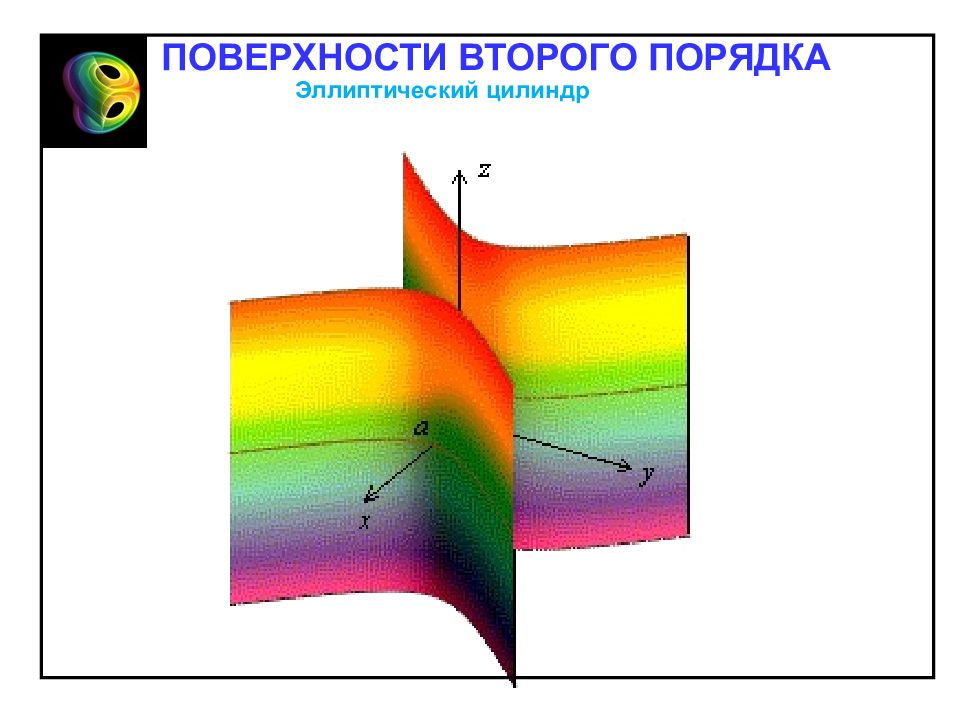
Направляющая – эллипс в плоскости хОу. Образующие – прямые линии в плоскостях хО z и уО z. Эллиптический цилиндр ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА Эллиптический цилиндр
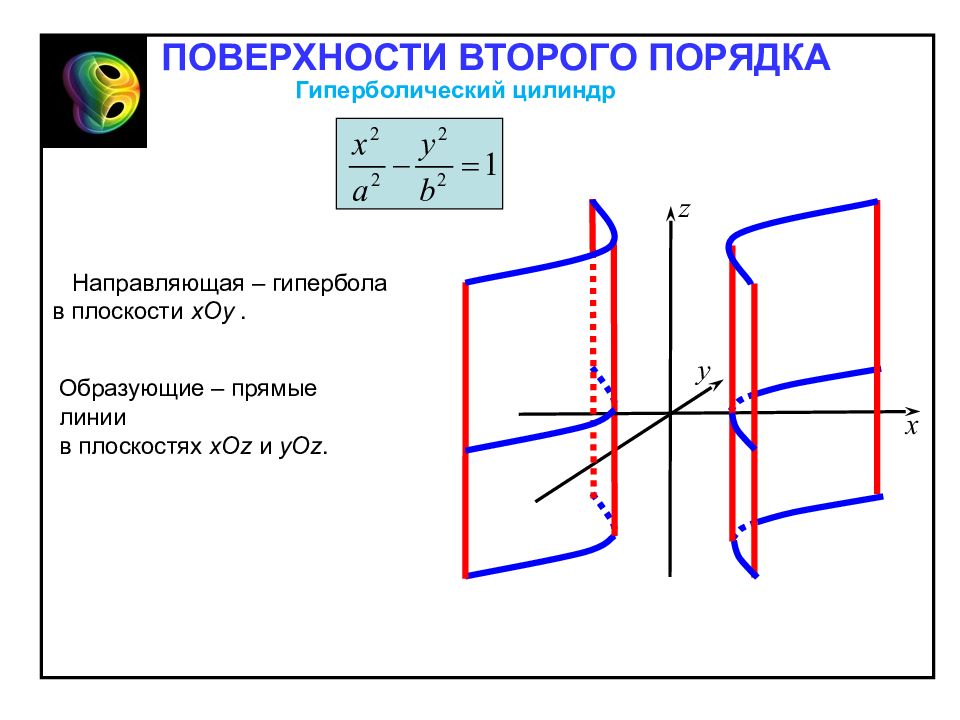
Направляющая – гипербола в плоскости хОу. Образующие – прямые линии в плоскостях хО z и уО z. Гиперболический цилиндр ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА Эллиптический цилиндр
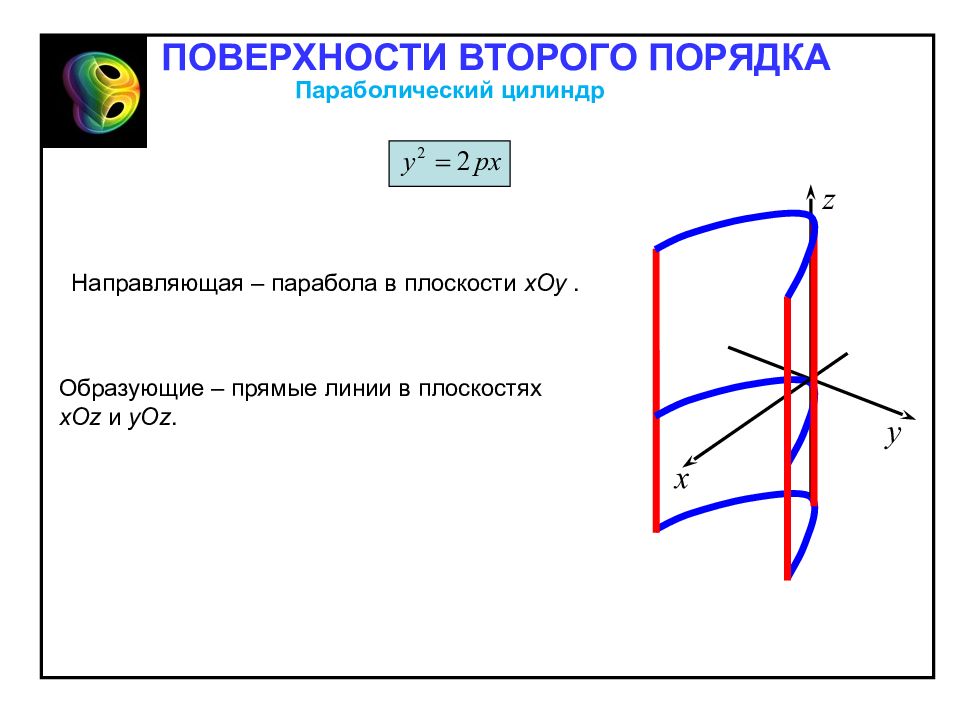
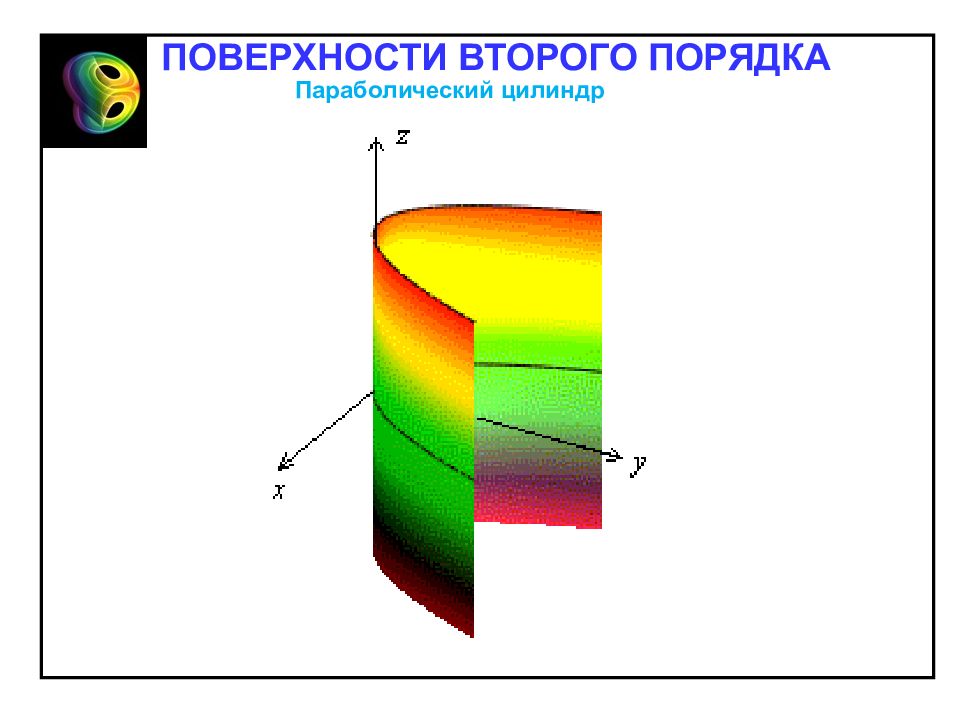
Направляющая – парабола в плоскости хОу. Образующие – прямые линии в плоскостях хО z и уО z. Параболический цилиндр ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА Параболический цилиндр
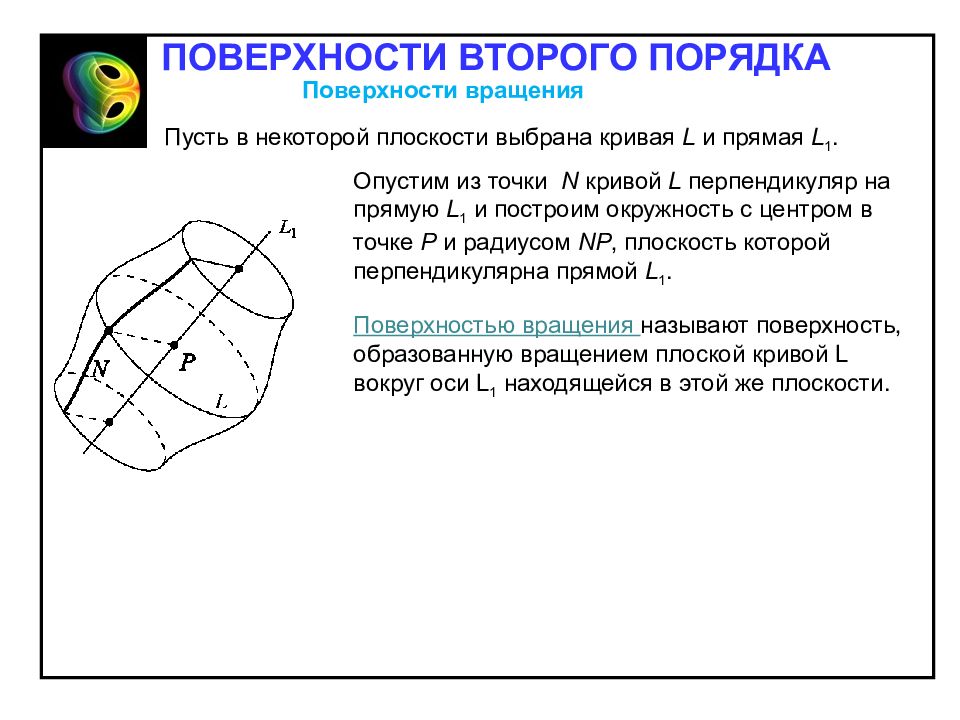
Поверхности вращения Пусть в некоторой плоскости выбрана кривая L и прямая L 1. Опустим из точки N кривой L перпендикуляр на прямую L 1 и построим окружность с центром в точке P и радиусом NP, плоскость которой перпендикулярна прямой L 1. Поверхностью вращения называют поверхность, образованную вращением плоской кривой L вокруг оси L 1 находящейся в этой же плоскости. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
Таким образом, мы показали, что если точка M 1 ( x, y, z ) принадлежит поверхности вращения, то ее координаты удовлетворяют уравнению Пусть L Оу z и О y – ось вращения, т. е. Выведем уравнение поверхности вращения. Вращая кривую L вокруг оси Oy, получим некоторую поверхность. Пусть т. М (0, х 0, у 0 ) лежит на L плоскости zOy. Пусть M 1 ( x, y, z ) – произвольная точка получившейся поверхности. Тогда Поэтому выполняется одно из соотношений: если то если то ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА Поверхности вращения
Полученное уравнение является уравнением поверхности вращения линии L вокруг оси Oy. Применимо следующее правило : чтобы получить уравнение поверхности, образованной вращением линии L, лежащей в плоскости yOz, вокруг оси Oy, нужно в уравнении этой линии заменить z на При выборе знака перед радикалом следует придерживаться следующего правила: знак должен совпадать в соответствующих точках со знаком координаты z на исходной кривой. Совершенно аналогичные правила будут для получения уравнений поверхностей вращения, получающихся вращением плоских линий вокруг других координатных осей. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА Поверхности вращения
К поверхностям вращения, например, относятся: 2. Эллипсоид вращения 4. Конус вращения 3. Цилиндр вращения 1. Сфера вращения ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА Поверхности вращения
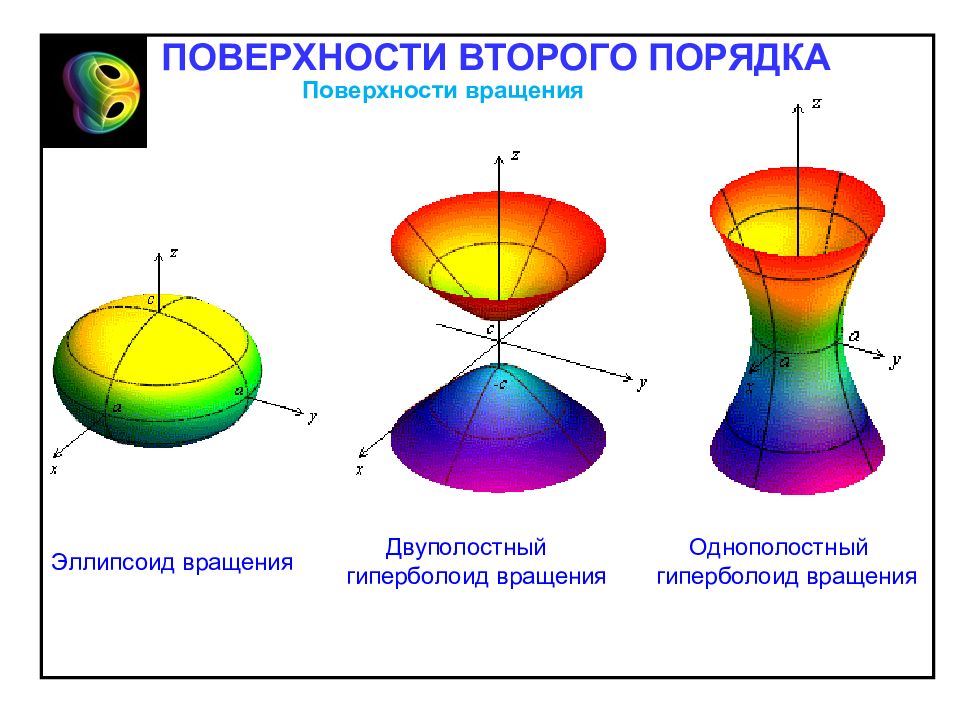
Однополостный гиперболоид вращения Эллипсоид вращения Двуполостный гиперболоид вращения ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА Поверхности вращения
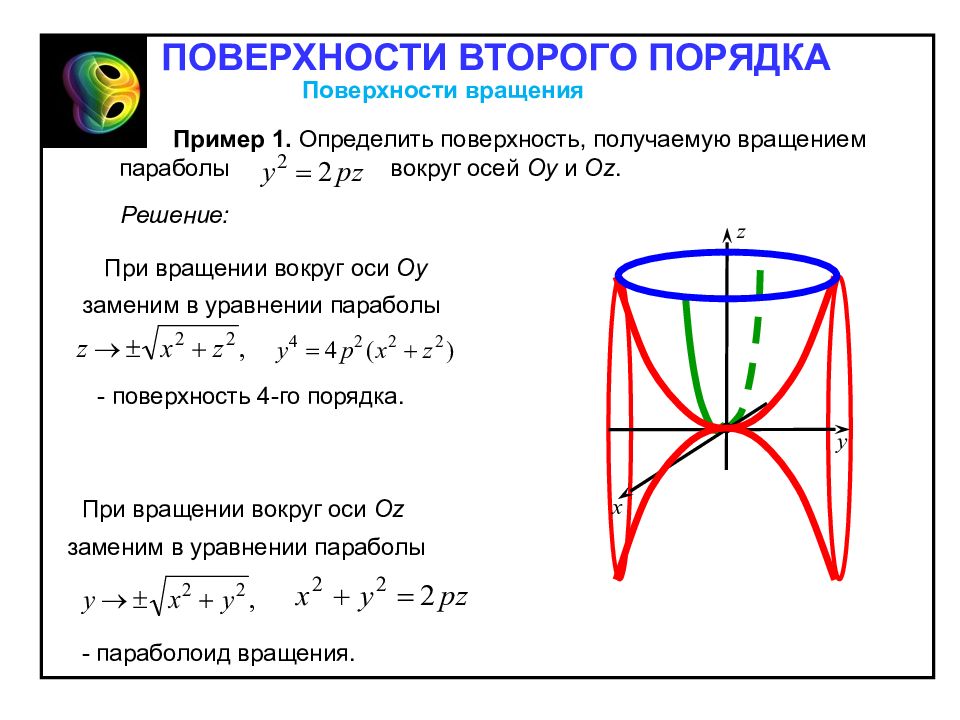
Пример 1. Определить поверхность, получаемую вращением параболы вокруг осей O у и Oz. Решение: При вращении вокруг оси O у заменим в уравнении параболы - поверхность 4-го порядка. При вращении вокруг оси Oz заменим в уравнении параболы - параболоид вращения. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА Поверхности вращения
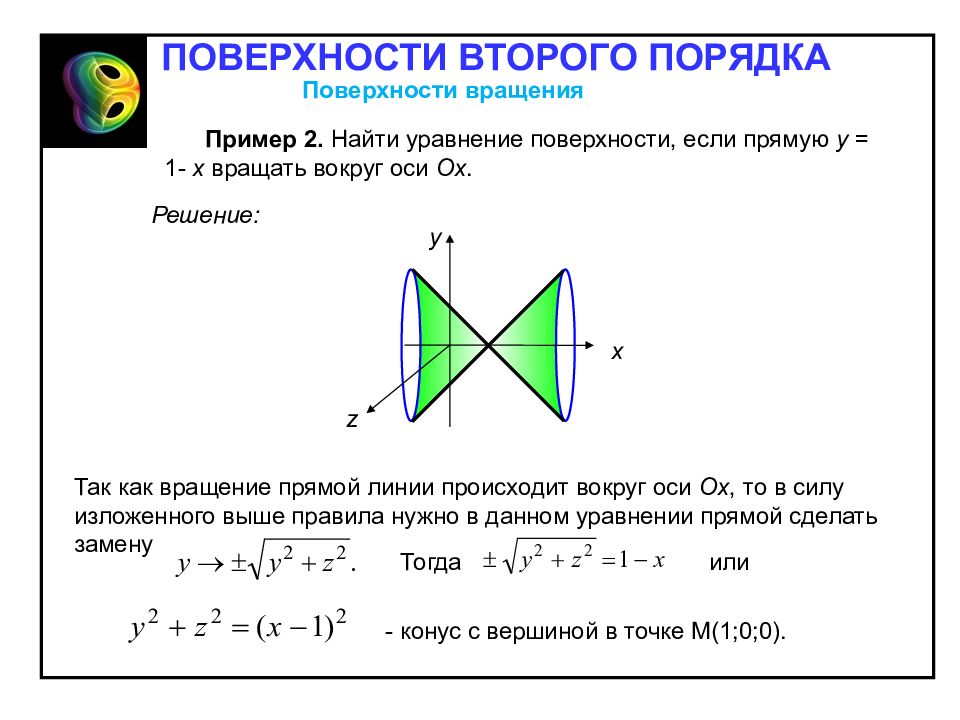
Пример 2. Найти уравнение поверхности, если прямую y = 1- x вращать вокруг оси Ox. Решение: x y z Так как вращение прямой линии происходит вокруг оси Ox, то в силу изложенного выше правила нужно в данном уравнении прямой сделать замену - конус с вершиной в точке М(1;0;0). Тогда или ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА Поверхности вращения
