Тема : Основные методы оценки риска инвестиционных проектов Занятие по дисциплине «Технологии оценки рисков инвестиционных проектов» к.э.н., доц. Болотников С.В.
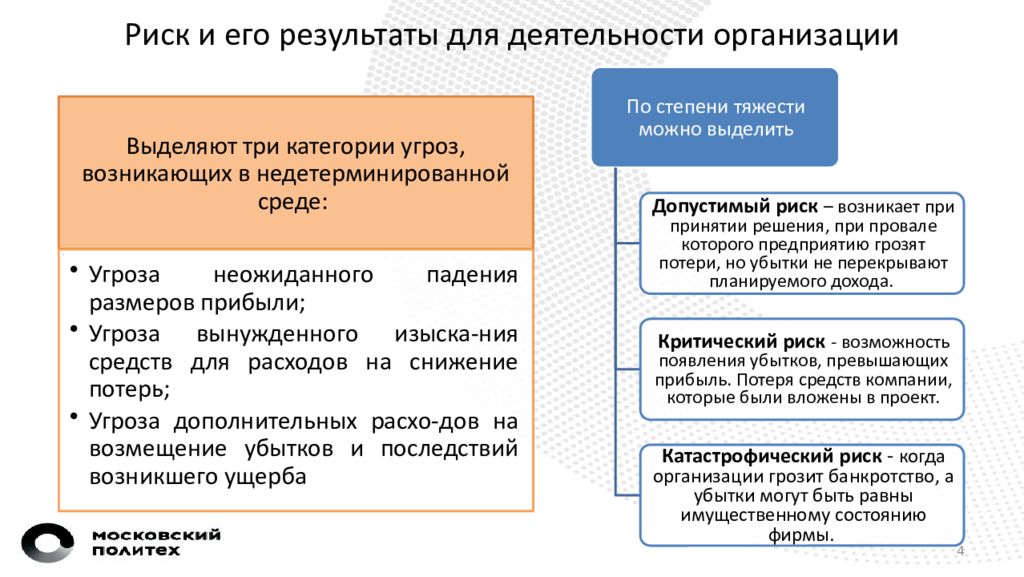
Бизнес-риск – состояние, когда лицо, принимающее решение, обладает объективным знанием среды действий и способно прогнозировать результат каждого из возможных решений. Степень риска — это вероятность наступления случая потерь, а также размер возможного ущерба от него. Инвестиционные решения в недетерминированной среде п орождают понятие «инвестиционный бизнес-риск» Идентификация рисков инвестиционной деятельности осуществляется на основе выявления наиболее существенных признаков {критериев риска), характеризующих неблагоприятность ситуации и ее последствий: оценка прибыли; оценка выручки; прогноз изменения стоимости имущества.
Неопределенность – это такое состояние знания, когда одна или более альтернатив решения имеют ряд возможных исходов, вероятность которых неизвестна. Случайность — это событие, в сходных условиях происходящее по разному. Риск имеет математически выраженную вероятность наступления потери. Вероятность — это возможность получения определенного результата принятого инвестиционного решения. Термины управления инвестиционными рисками
4 Риск и его результаты для деятельности организации .
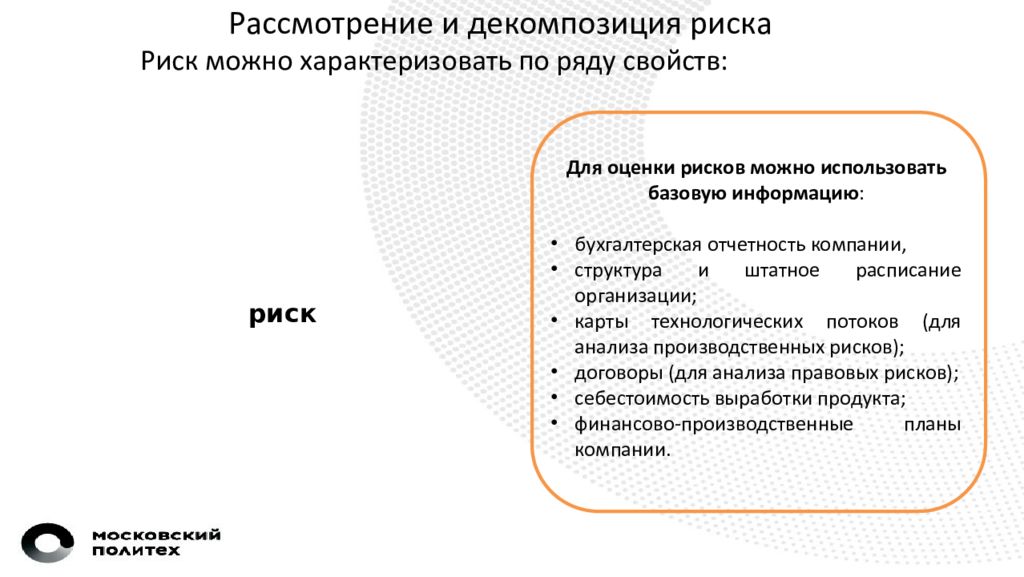
Рассмотрение и декомпозиция риска Для оценки рисков можно использовать базовую информацию : бухгалтерская отчетность компании, структура и штатное расписание организации; карты технологических потоков (для анализа производственных рисков ); договоры (для анализа правовых рисков ); себестоимость выработки продукта ; финансово-производственные планы компании. Риск можно характеризовать по ряду свойств: риск
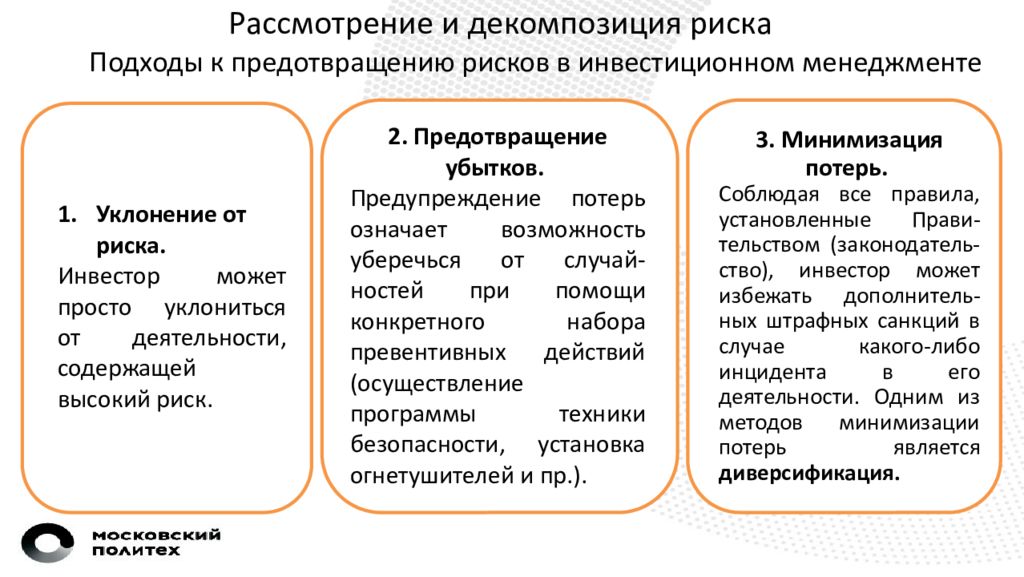
Рассмотрение и декомпозиция риска Подходы к предотвращению рисков в инвестиционном менеджменте 3. Минимизация потерь. Соблюдая все правила, установленные Прави-тельством ( законодатель- ство ), инвестор может избежать дополнитель-ных штрафных санкций в случае какого-либо инцидента в его деятельности. Одним из методов минимизации потерь является диверсификация. Уклонение от риска. Инвестор может просто уклониться от деятельности, содержащей высокий риск. 2. Предотвращение убытков. Предупреждение потерь означает возможность уберечься от случай- ностей при помощи конкретного набора превентивных действий (осуществление программы техники безопасности, установка огнетушителей и пр.).
Рассмотрение и декомпозиция риска Подходы к предотвращению рисков в инвестиционном менеджменте
Рассмотрение и декомпозиция риска Риск можно характеризовать по ряду параметров: доход, прибыль, убытки, ущерб. Формула функции для оценки динамики исследуемого параметра учитывает вероятность рискового события и уровень его последствий.
Методы оценки бизнес-рисков в недетерминированной среде Субъективный подход – предполагает широкое использование формально-логических и экспертных методов для оценки. Особенности: в качественном подходе значения присваиваются на уровне много/мало, больше/меньше, сильнее/слабее и т.д. Можно использовать разные по количеству делений шкалы. Типовыми шкалами являются 3х3 и 5х5. Вероятность Ущерб 3х3 Низкая/ Средняя/ Высокая Незначительный/ Средний/ Значительный 5х5 Очень низкая/ Низкая/ Средняя/ Высокая/ Очень высокая Незначительный/ Приемлемый/ Средний/ Большой/ Очень большой.
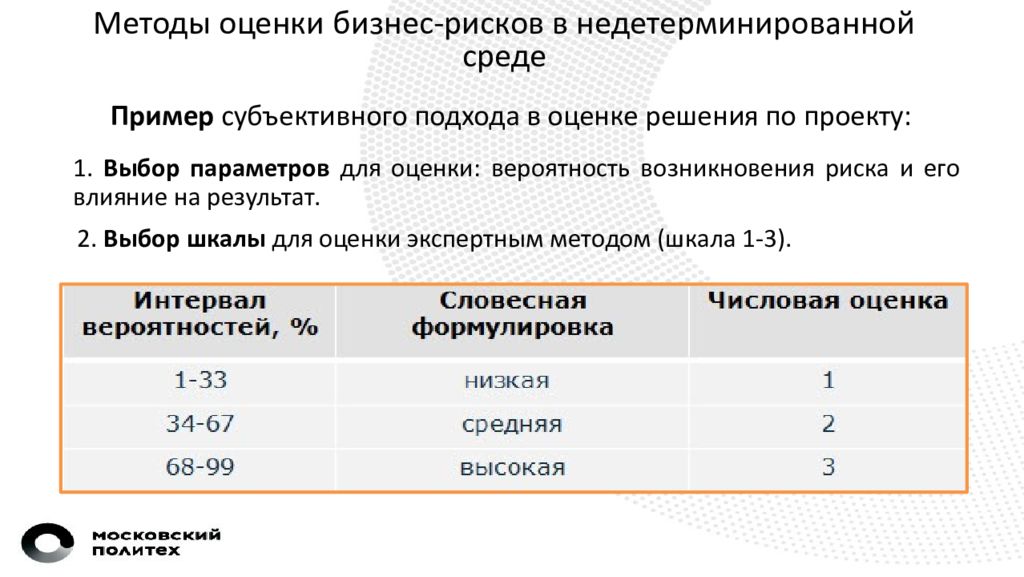
Методы оценки бизнес-рисков в недетерминированной среде Пример субъективного подхода в оценке решения по проекту: 1. Выбор параметров для оценки: вероятность возникновения риска и его влияние на результат. 2. Выбор шкалы для оценки экспертным методом (шкала 1-3).
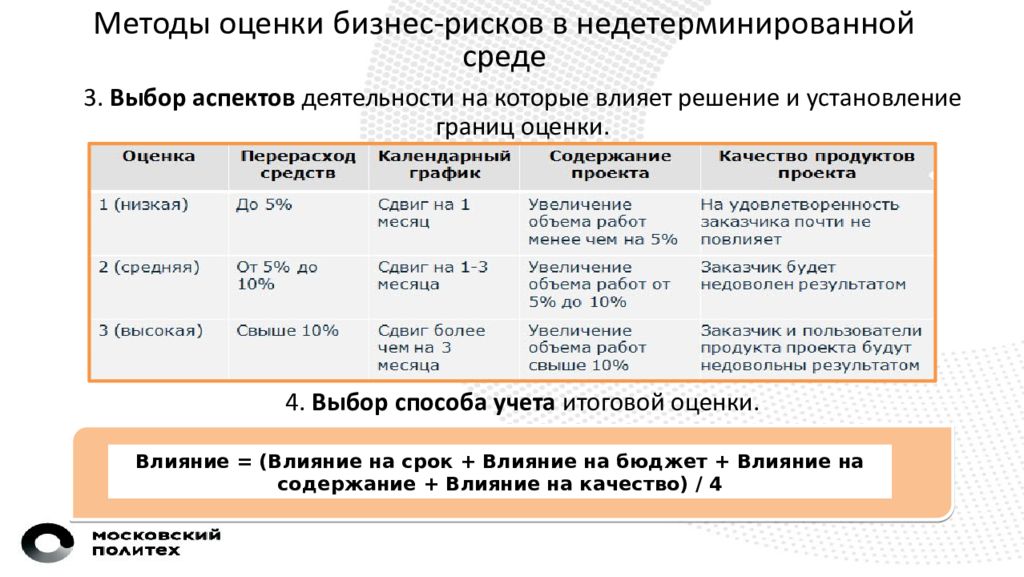
Методы оценки бизнес-рисков в недетерминированной среде 3. Выбор аспектов деятельности на которые влияет решение и установление границ оценки. 4. Выбор способа учета итоговой оценки. Влияние = (Влияние на срок + Влияние на бюджет + Влияние на содержание + Влияние на качество) / 4
Методы оценки бизнес-рисков в недетерминированной среде Результаты оценки могут быть использованы для сравнения нескольких вариантов решения проблемы. Расчет риска: Влияние = (3+2+3+0) / 4 = 2 Значение 2 – средний уровень риска для данного решения. Основные потери при негативно сценарии: средства организации и необходимость дополнительных работ. 5. Выставление оценки в баллах по каждому параметру:
Методы оценки бизнес-рисков в недетерминированной среде Количественный подход. Результат количественного подхода: расчет математического ожидания события – конкретного числового значения за пределами которого начинает область повышенного риска,
Математическое ожидание события - абсолютная величина этого события, умноженное на вероятность его наступления. Оценка вероятности события: Математическое ожидание события:
Объективный метод. Суть: основан на вычислении частоты, с которой происходит данное событие. Источник : ретроспективная информация. Пример: известно, что за период 10 лет количество объем прибыли в этом виде деятельности в отрасли регионе составило 25 тыс. на 1 шт. в 12 случаях из 20. Вероятность получения такого результата в будущем составляет: 12 : 20 = 0,6 Способы определения вероятности наступления события. Субъективный метод, основанный на использовании субъективных критериев: суждение оценивающего, его личный опыт, оценка эксперта
Расчет величины риска на основе среднего ожидаемого значения. Среднее ожидаемое значение — это средневзвешенное для всех возможных результатов, где вероятность каждого результата используется в качестве частоты или веса соответствующего значения.
Пример расчета среднего ожидаемого значения. Модальная величина (мода). Расчет среднего ожидаемого значения производится на основе определения модальной величины Мода (модальная величина) – это значение изучаемого признака, повторяющегося с наибольшей частотой. Пример: девять фирм продают товар по ценам (тыс. руб.): 4,4; 4,3; 4,4; 4,5; 4,3; 4,3:4,6; 4,2; 4,6. Чаше всего встречается цена 4.3. (три раза). Это - модальная величина.
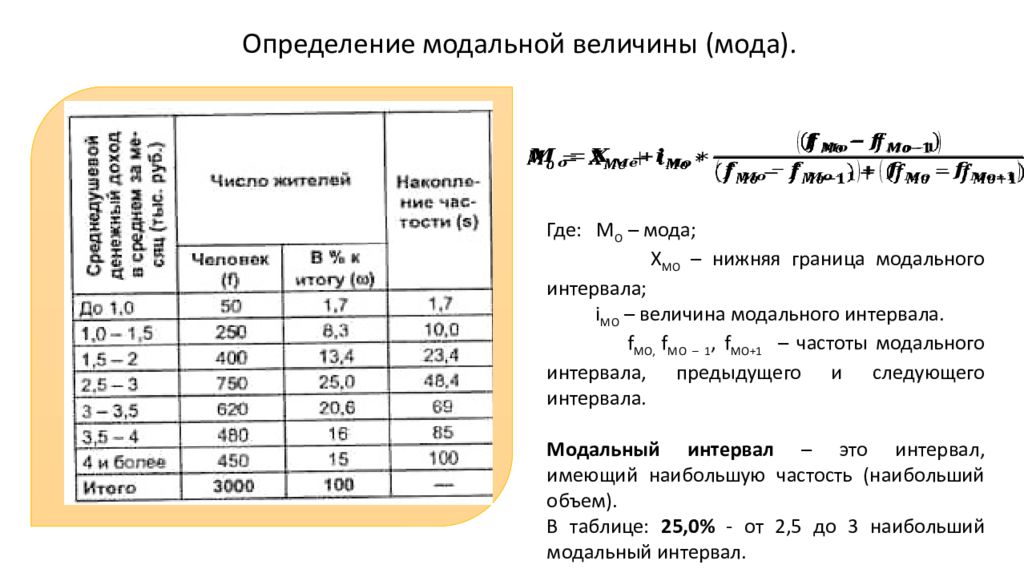
Определение модальной величины (мода). Где: М O – мода; X MO – нижняя граница модального интервала; i MO – величина модального интервала. f MO, f MO – 1, f MO +1 – частоты модального интервала, предыдущего и следующего интервала. Модальный интервал – это интервал, имеющий наибольшую частость (наибольший объем). В таблице: 25,0% - от 2,5 до 3 наибольший модальный интервал.
Определение модальной величины (мода). Расчет. = 2,5 * 0,365 = 2 904
Пример расчета среднего ожидаемого значения. Вариант А. З а 10 месячный период было рассмотрено 120 случаев инвестиций в объект А (аналоги). Из них: в 48 случаях было была получена прибыль 27 тыс. руб. / мес. ( вероятность: 48 / 120 = 0,4 ); в 36 случаях была получена прибыль 20 тыс. руб./мес. ( вероятность 36 / 120 = 0,3 ); в 36 случаях была получена прибыль 30 тыс. руб./мес. ( вероятность 36 / 120 = 0,3 ) Среднее ожидаемое значение: 27 х 0,4 + 20x0,3 + 30 x 0,3 = 26 тыс.руб. Вариант Б. З а 10 месячный период было рассмотрено 120 случаев инвестиций в объект Б (аналоги). Из них: в 36 случаях была получена прибыль – 40 тыс. руб./мес. (вероятность 0,3); в 23 случаях была получена прибыль – 15 тыс. руб./мес. (вероятность 0,2); в 62 случаях была получена прибыль – 30 тыс. руб./мес. (вероятность 0,5) Среднее ожидаемое значение: 40 х 0,3 + 30 х 0,5 + 15 х 0,2 = 30 тыс.руб.
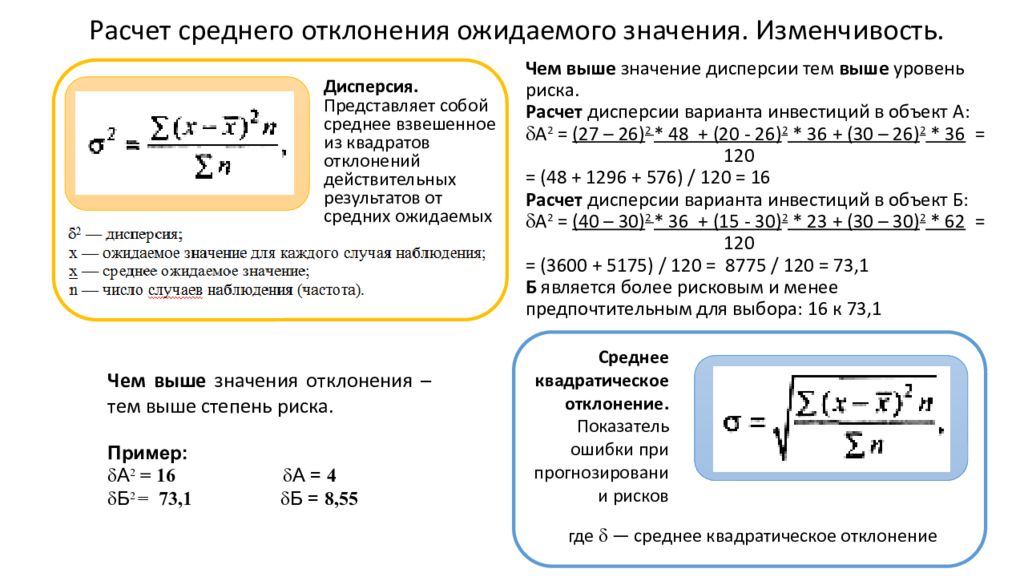
Среднее квадратическое отклонение. Показатель ошибки при прогнозировании рисков Расчет среднего отклонения ожидаемого значения. Изменчивость. Чем выше значение дисперсии тем выше уровень риска. Расчет дисперсии варианта инвестиций в объект А: А 2 = (27 – 26) 2 * 48 + (20 - 26) 2 * 36 + (30 – 26) 2 * 36 = 120 = (48 + 1296 + 576) / 120 = 16 Расчет дисперсии варианта инвестиций в объект Б: А 2 = (40 – 30) 2 * 36 + (15 - 30) 2 * 23 + (30 – 30) 2 * 62 = 120 = (3600 + 5175) / 120 = 8775 / 120 = 73,1 Б является более рисковым и менее предпочтительным для выбора: 16 к 73,1 где — среднее квадратическое отклонение Чем выше значения отклонения – тем выше степень риска. Пример: А 2 = 16 А = 4 Б 2 = 73,1 Б = 8,55 Дисперсия. Представляет собой среднее взвешенное из квадратов отклонений действительных результатов от средних ожидаемых
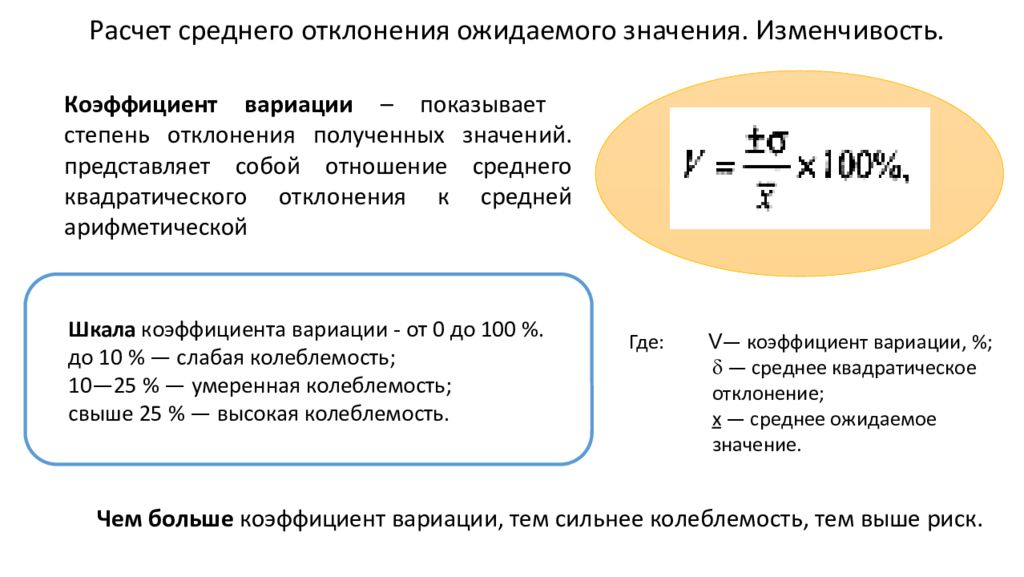
Расчет среднего отклонения ожидаемого значения. Изменчивость. Коэффициент вариации – показывает степень отклонения полученных значений. представляет собой отношение среднего квадратического отклонения к средней арифметической Где: V — коэффициент вариации, %; — среднее квадратическое отклонение; х — среднее ожидаемое значение. Шкала коэффициента вариации - от 0 до 100 %. до 10 % — слабая колеблемость ; 10—25 % — умеренная колеблемость ; свыше 25 % — высокая колеблемость. Чем больше коэффициент вариации, тем сильнее колеблемость, тем выше риск.
Расчет коэффициента вариации Пример : V (А) = 4 / 26 * 100 = 15,4% (норматив 10-25%) – умеренная колеблемость. V (Б) = 8,55 / 30 * 100 = 28,5% (свыше 25%) - высокая колеблемость. Вывод : Вариант с объектом Б является значительно более рисковым, нежели вариант с А. Предпочтителен вариант А: А 2 = 16; А = 4; V (А) = 15,4
Расчет величины риска на основе экстремумов Экстре́мум (лат. extremum — крайний) в математике — максимальное или минимальное значение функции на заданном множестве. Локальный экстремум (соответственно минимум или максимум) Суть метода: риск определяется оценкой вероятной величины максимального и минимального результата стратегии. Где: δ 2 — дисперсия; Pmax — вероятность получения максимального результата; Хmах — максимальная величина результата; Pm in — вероятность получения минимального результата; Хm in — минимальная величина результата; Х — средняя ожидаемая величина результата; δ — среднее квадратическое отклонение; V — коэффициент вариации. +
Вывод: Стратегия инвестирования Б – является более рисковой. Стратегия инвестирования А – предпочтительна. Расчет величины риска на основе экстремумов. Пример. Для решения А: Хmах – 30 тыс. руб.; Pmax - 0,3; x – 26 штук. Хm in - 20 тыс. руб.; Pm in - 0,3. Для решения Б: Хmах – 40 тыс. руб.; Pmax - 0,3; x – 30 штук. Хm in - 15 тыс. руб.; Pm in - 0,2. Расчет ( A ): δ 2 = 0,3 * (30 – 26) 2 + 0,3 * (20 – 26) 2 = 4,8 + 10,8 = 15,6 δ = √15,6 = 3,95 V = 3,95 / 26 * 100 = 15,2% - умеренная колеблемость. Расчет (Б): δ 2 = 0,3 * (40 – 30) 2 + 0,2 * (30 – 15) 2 = 30 + 45 = 75 δ = √ 75 = 8,7 V = 8,7 / 30 * 100 = 29% норматив свыше 25%) - высокая колеблемость.
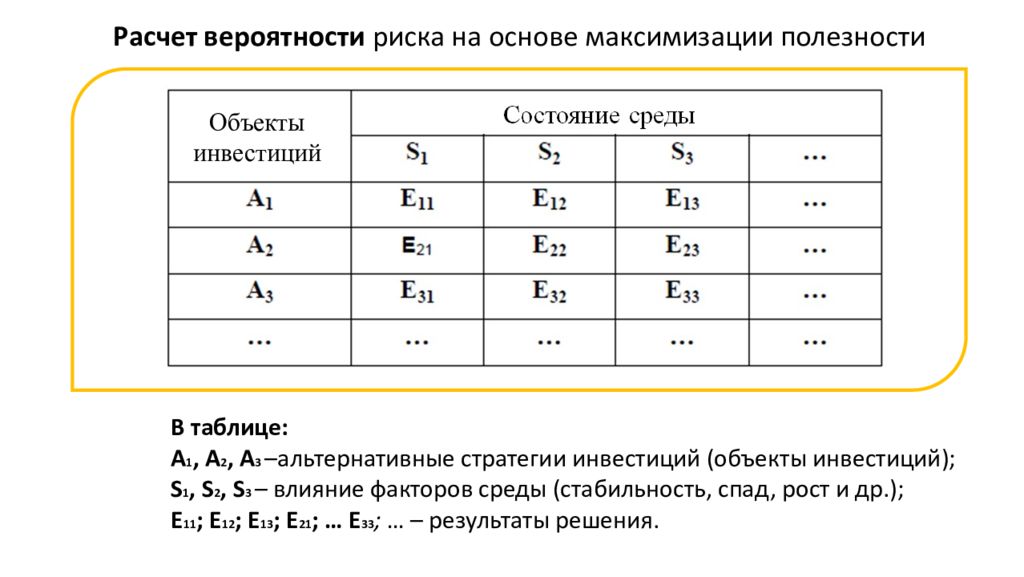
Расчет вероятности риска на основе максимизации полезности В таблице: A 1, A 2, A 3 –альтернативные стратегии инвестиций (объекты инвестиций); S 1, S 2, S 3 – влияние факторов среды (стабильность, спад, рост и др.); E 11 ; E 12 ; E 13 ; E 21 ; … E 33 ; … – результаты решения. Объекты инвестиций
Расчет вероятности риска на основе максимизации полезности Числа в ячейках матрицы представляют собой результаты реализации E ij решения A i в условиях S j. При этом в условиях риска вероятность наступления S j известна – w j ( S j ). Выбирается A i из совокупности { A i }, которая максимизирует ожидаемую стоимость его функции полезности E,j. В условиях риска основным моментом является определение вероятности наступления состояния среды S j, т. е. степени риска. После определения вероятности wj ( Sj ) наступления состояния среды Sj, определяют ожидаемую стоимость реализации каждой стратегии - средневзвешенную стоимость E( Ai ): Где: E( Ai ) – результат реализации Ai ; w j ( Sj ) – вероятность наступления Sj.
Расчет вероятности риска на основе максимизации полезности
ФГАОУ ВО «Московский политехнический университет» СПАСИБО ЗА ВНИМАНИЕ!
