Слайд 2: Содержание лекции
Методы и приборы для исследования свойств дисперсных систем Методы и приборы для исследования дисперсных систем, основанные на молекулярно-кинетических свойствах. Методы и приборы для исследования дисперсных систем, основанные на оптических свойствах. Методы и приборы для исследования дисперсных систем, основанные на реологических свойствах.
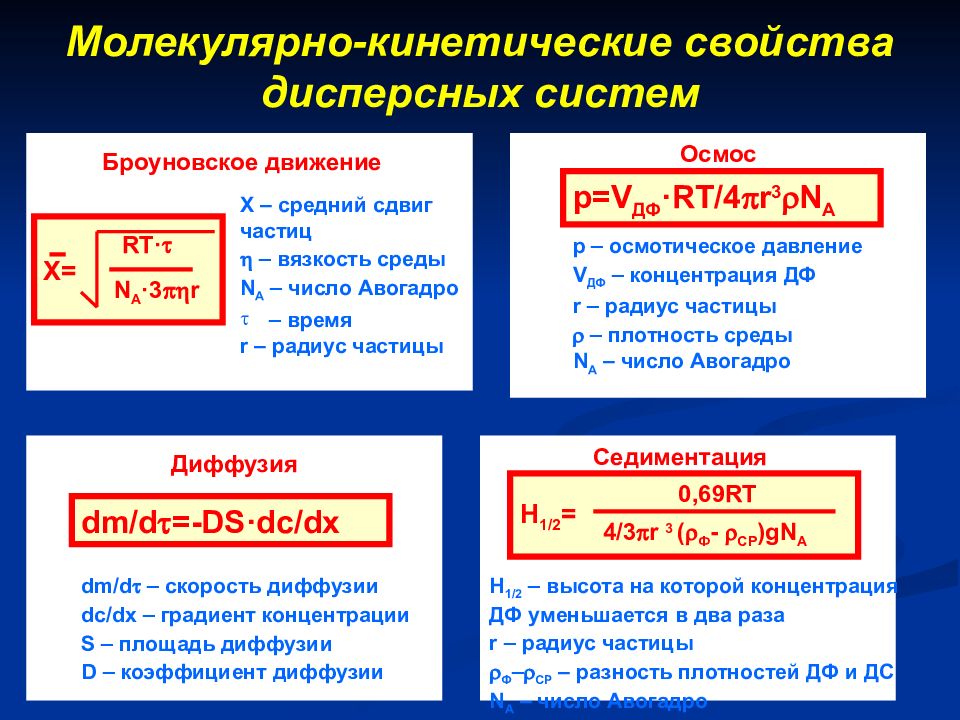
Броуновское движение X= RT· N A ·3 r X – средний сдвиг частиц – вязкость среды N A – число Авогадро – время r – радиус частицы Осмос p=V ДФ ·RT/4 r 3 N A p – осмотическое давление V ДФ – концентрация ДФ r – радиус частицы – плотность среды N A – число Авогадро Диффузия dm/d =-DS · dc/dx dm/d – скорость диффузии dc/dx – градиент концентрации S – площадь диффузии D – коэффициент диффузии Седиментация 0,69 RT 4/3 r 3 ( Ф - СР )g N A H 1/2 – высота на которой концентрация ДФ уменьшается в два раза r – радиус частицы Ф – СР – разность плотностей ДФ и ДС N A – число Авогадро H 1/2 = 0,69 RT 4/3 r 3 ( Ф - СР )g N A
Слайд 4: Седиментационный анализ
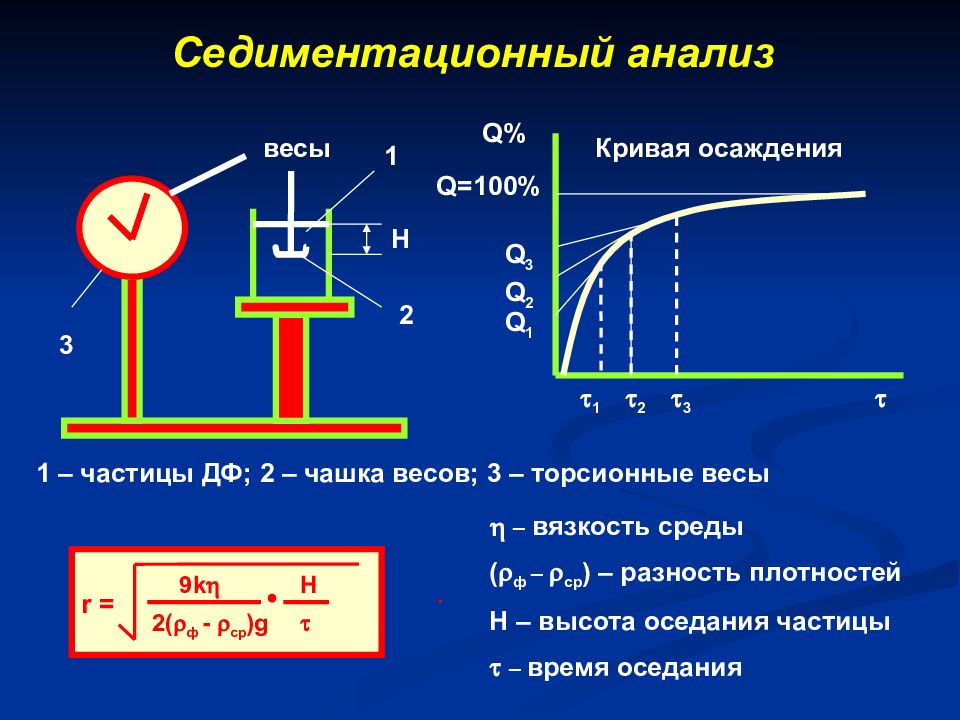
весы 1 H 2 3 1 – частицы ДФ; 2 – чашка весов; 3 – торсионные весы Q% Q 1 Q 2 Q 3 Q=100% 3 2 1 Кривая осаждения · r = 9k ( ф - ср )g H – вязкость среды ( ф – ср ) – разность плотностей Н – высота оседания частицы – время оседания r = 9k 2 ( ф - ср )g H
Слайд 5: Кривые распределения частиц по размерам
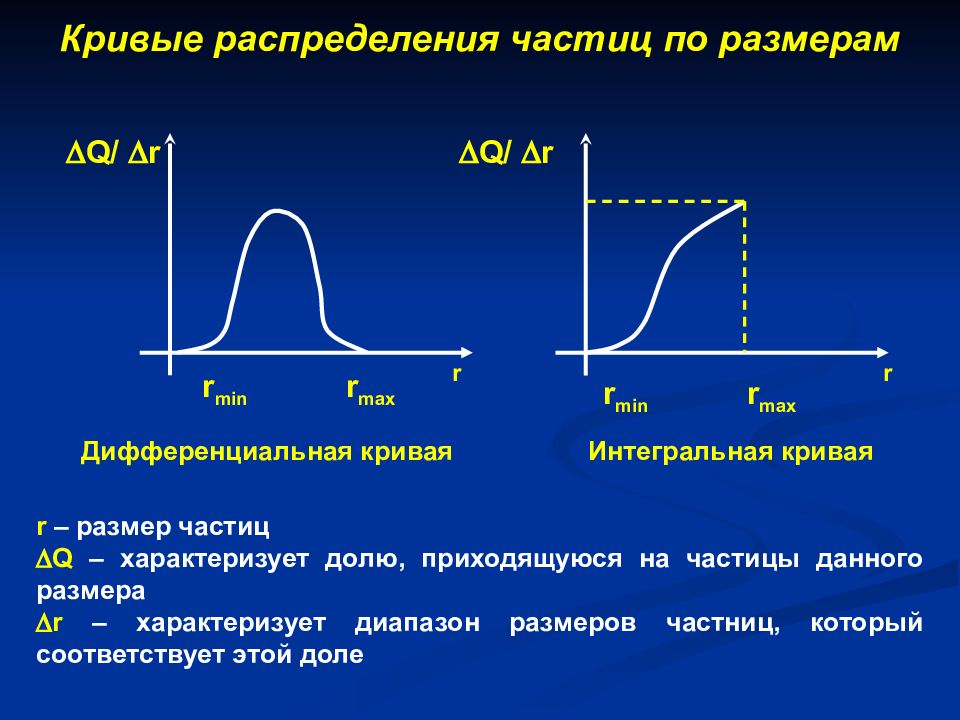
Дифференциальная кривая Интегральная кривая r – размер частиц Q – характеризует долю, приходящуюся на частицы данного размера r – характеризует диапазон размеров частниц, который соответствует этой доле Q/ r Q/ r r r r min r max r min r max
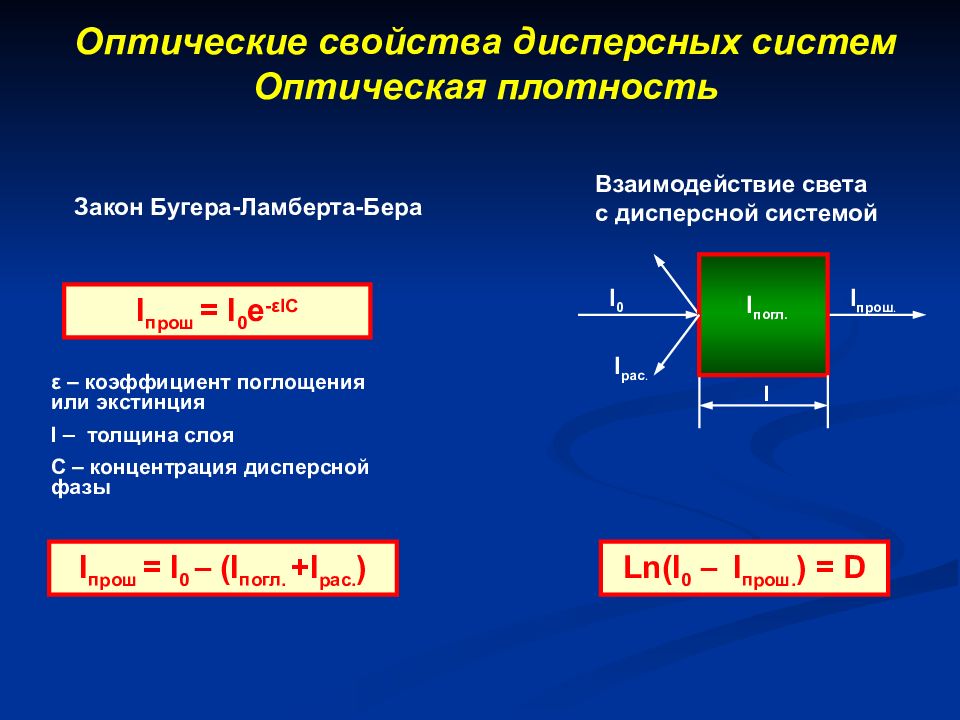
I прош = I 0 e - ε l С ε – коэффициент поглощения или экстинция l – толщина слоя С – концентрация дисперсной фазы I прош = I 0 – ( I погл. + I рас. ) I 0 I погл. I рас. l I прош. Ln(I 0 – I прош. ) = D Взаимодействие света с дисперсной системой Закон Бугера-Ламберта-Бера
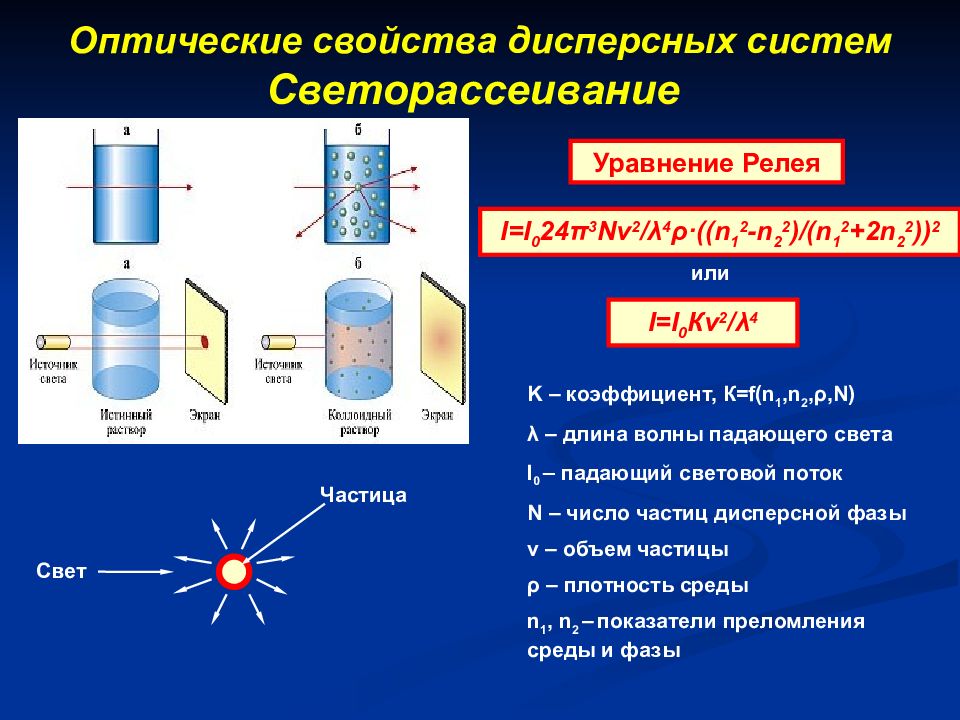
Слайд 7: Оптические свойства дисперсных систем Светорассеивание
Свет Частица I=I 0 24 π 3 Nv 2 / λ 4 ρ ·((n 1 2 -n 2 2 )/(n 1 2 +2n 2 2 )) 2 или I=I 0 К v 2 / λ 4 K – коэффициент, К= f(n 1,n 2, ρ, N) λ – длина волны падающего света I 0 – падающий световой поток N – число частиц дисперсной фазы ν – объем частицы ρ – плотность среды n 1, n 2 – показатели преломления среды и фазы Уравнение Релея
Слайд 8: Оптические методы анализа дисперсных систем
Нефелометрия – аналитический метод определения размеров и концентрации частиц, основанный на измерении интенсивности рассеянного света, падающего перпендикулярно к положению исследуемой системы. r X = r Э H Э H Х r X – радиус измеряемых частиц r Э – радиус эталонных частиц Н – высота освещенной части кюветы с эталонным и исследуемым раствором Турбидиметрия – аналитический метод определения размеров частиц, основанный на определении оптической плотности эталонного ( D Э ) и исследуемого ( D X ) образцов. Рассчитывается концентрация дисперсной фазы в исследуемой системе С Х : С Х = D X ·C Э D Э При одной и той же концентрации сравниваемых систем размеры исследуемой определяются по формуле: r X = r Э D Э 3 D Х
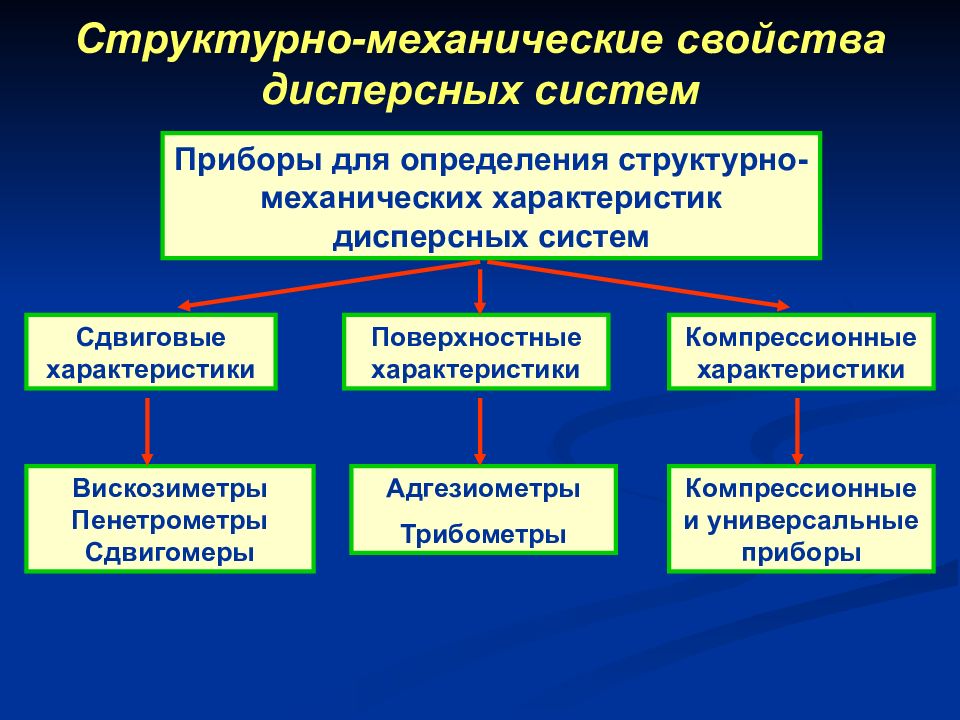
Слайд 9: Структурно-механические свойства дисперсных систем
Приборы для определения структурно-механических характеристик дисперсных систем Сдвиговые характеристики Компрессионные характеристики Поверхностные характеристики Вискозиметры Пенетрометры Сдвигомеры Адгезиометры Трибометры Компрессионные и универсальные приборы Структурно-механические свойства дисперсных систем
Слайд 10
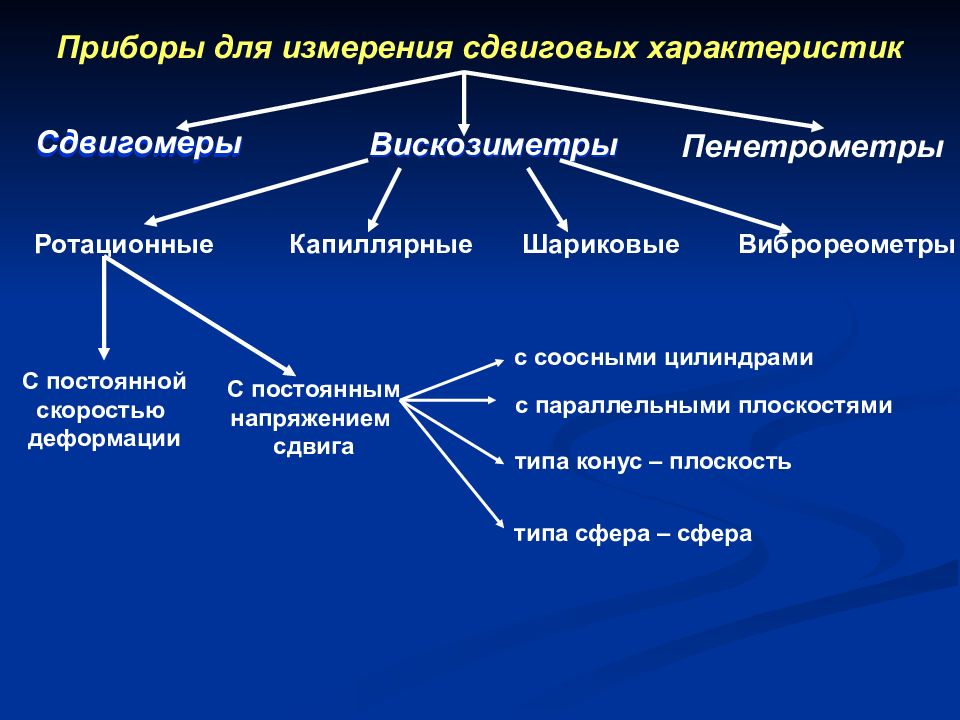
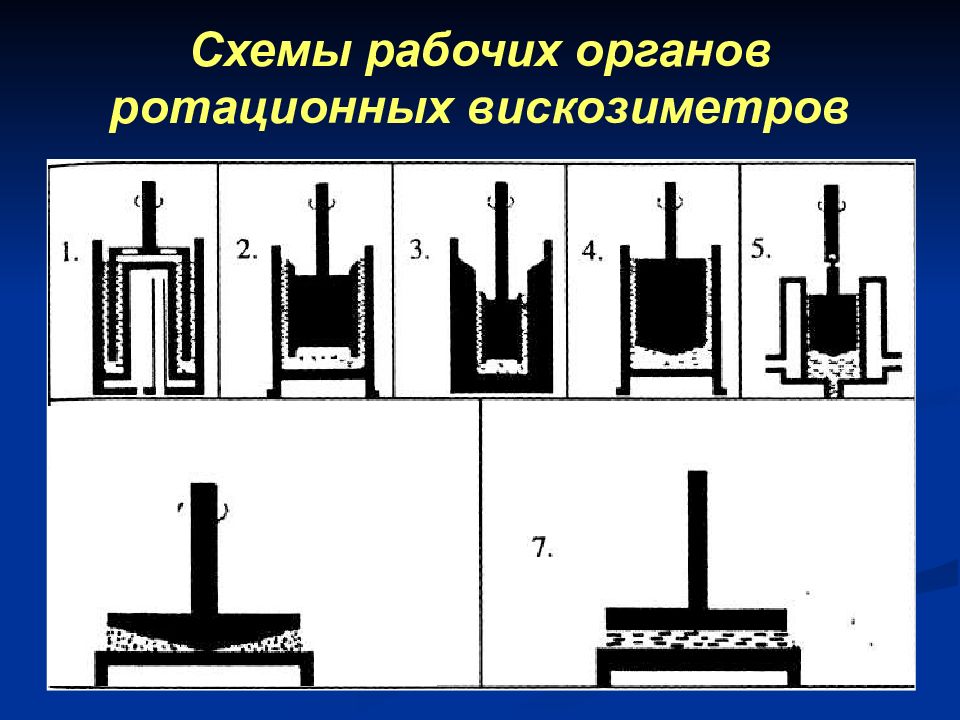
Приборы для измерения сдвиговых характеристик Сдвигомеры Вискозиметры Пенетрометры Ротационные Капиллярные Шариковые Виброреометры С постоянной скоростью деформации С постоянным напряжением сдвига с соосными цилиндрами с параллельными плоскостями типа конус – плоскость типа сфера – сфера Сдвигомеры Вискозиметры Сдвигомеры
Слайд 11
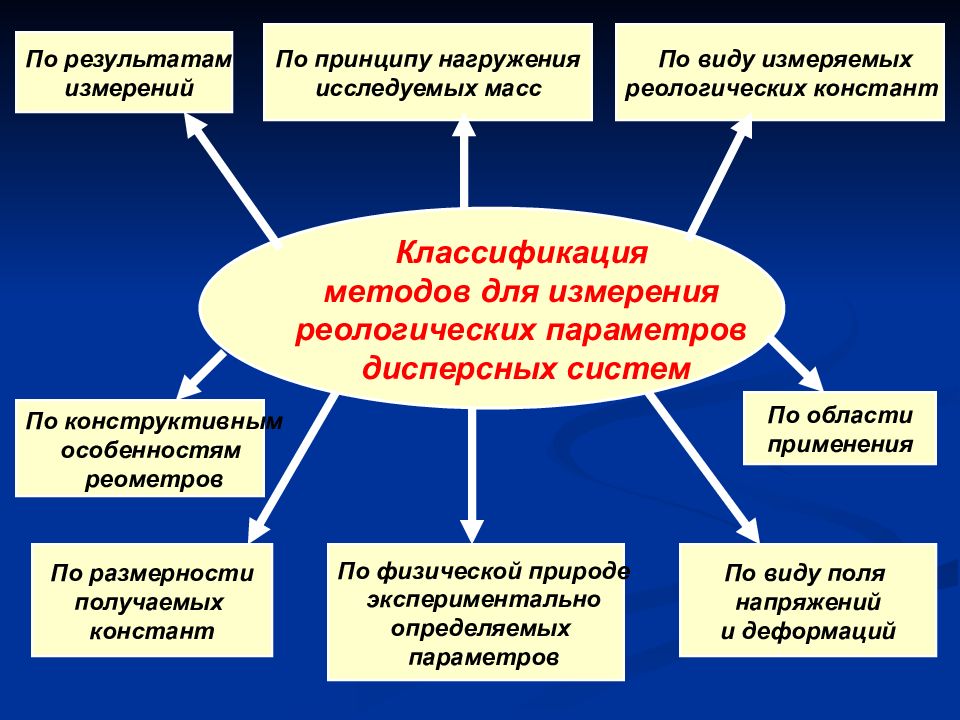
Классификация методов для измерения реологических параметров дисперсных систем По результатам измерений По области применения По виду измеряемых реологических констант По конструктивным особенностям реометров По размерности получаемых констант По физической природе экспериментально определяемых параметров По виду поля напряжений и деформаций По принципу нагружения исследуемых масс
Слайд 12: Метод капиллярной вискозиметрии
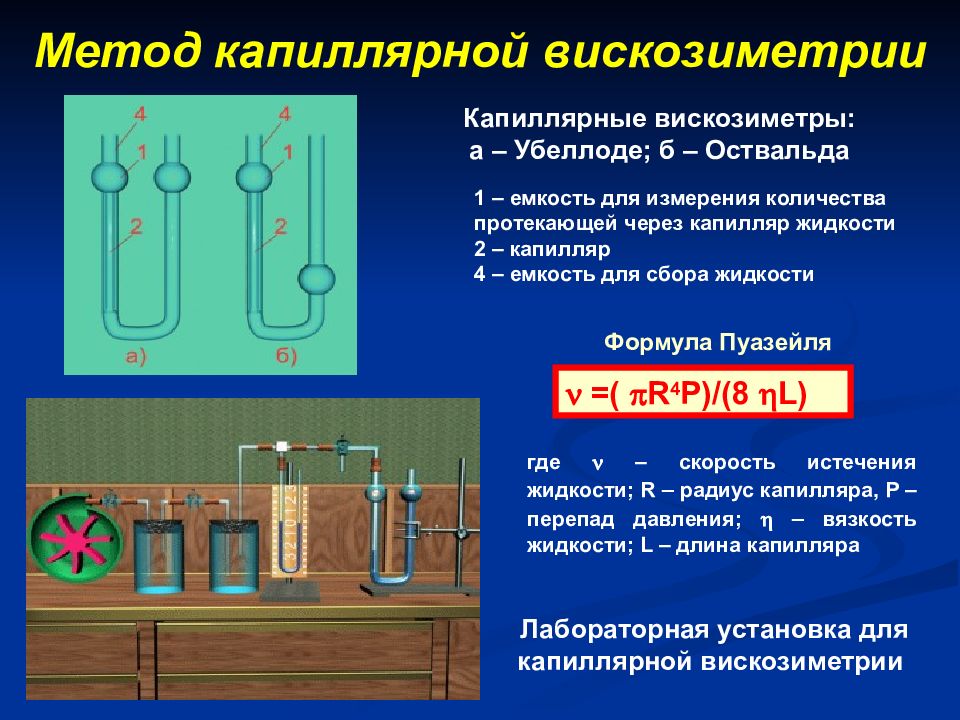
Капиллярные вискозиметры: а – Убеллоде; б – Оствальда Лабораторная установка для капиллярной вискозиметрии 1 – емкость для измерения количества протекающей через капилляр жидкости 2 – капилляр 4 – емкость для сбора жидкости =( R 4 P )/(8 L ) Формула Пуазейля где – скорость истечения жидкости; R – радиус капилляра, P – перепад давления; – вязкость жидкости; L – длина капилляра
Слайд 13: Метод шариковой вискозиметрии
=k( ш - ж )t где k – константа прибора Ш и Ж – плотность шарика и исследуемой жидкости t – время
Слайд 14: Ротационная реометрия
Сущность метода состоит в установлении связи между крутящим моментом и угловой частотой вращения одной из измерительных поверхностей. Основные режимы работы: постоянная скорость деформации ( ω ‘ = const ) и постоянное напряжение сдвига ( = const ). Использование ротационных приборов для исследования физико-механических свойств материалов имеет следующие преимущества: Возможность создания однородного по объему образца режима деформации со строго контролируемыми кинематическими и динамическими характеристиками. Возможность поддержания заданного режима в течение неограниченно долгого времени.
Слайд 15: Схема вискозиметра Воларовича
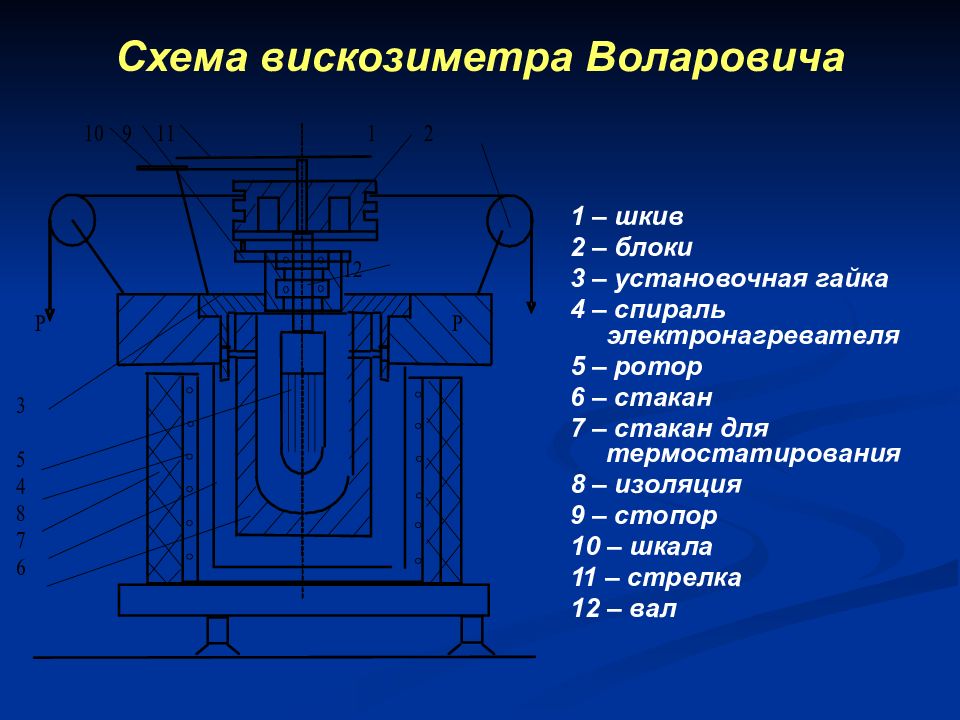
1 – шкив 2 – блоки 3 – установочная гайка 4 – спираль электронагревателя 5 – ротор 6 – стакан 7 – стакан для термостатирования 8 – изоляция 9 – стопор 10 – шкала 11 – стрелка 12 – вал
Слайд 17: Метод Ребиндера-Вейлера
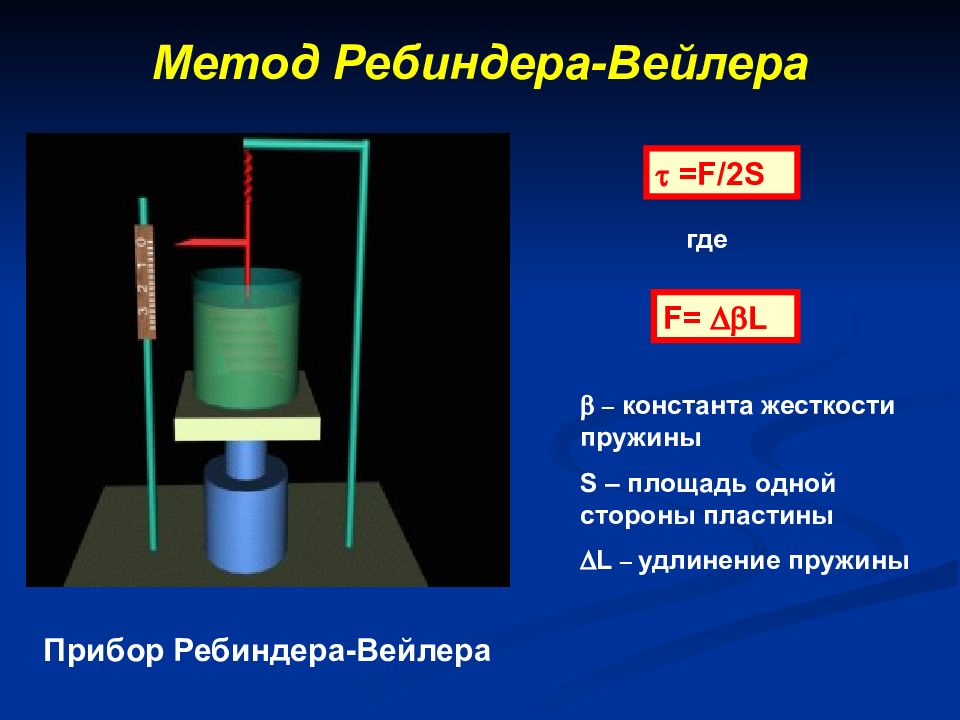
= F /2 S F = L где – константа жесткости пружины S – площадь одной стороны пластины L – удлинение пружины Прибор Ребиндера-Вейлера
Слайд 18
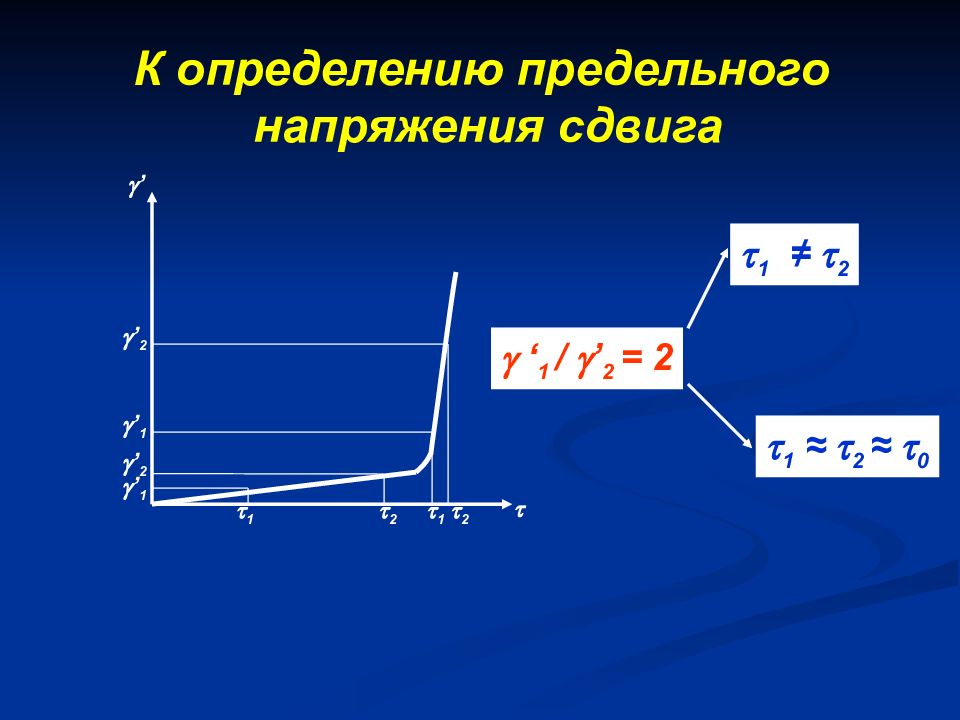
1 2 1 2 ’ 1 ’ 2 ’ 1 ’ 2 ’ ‘ 1 / ’ 2 = 2 1 ≠ 2 1 ≈ 2 ≈ 0 К определению предельного напряжения сдвига
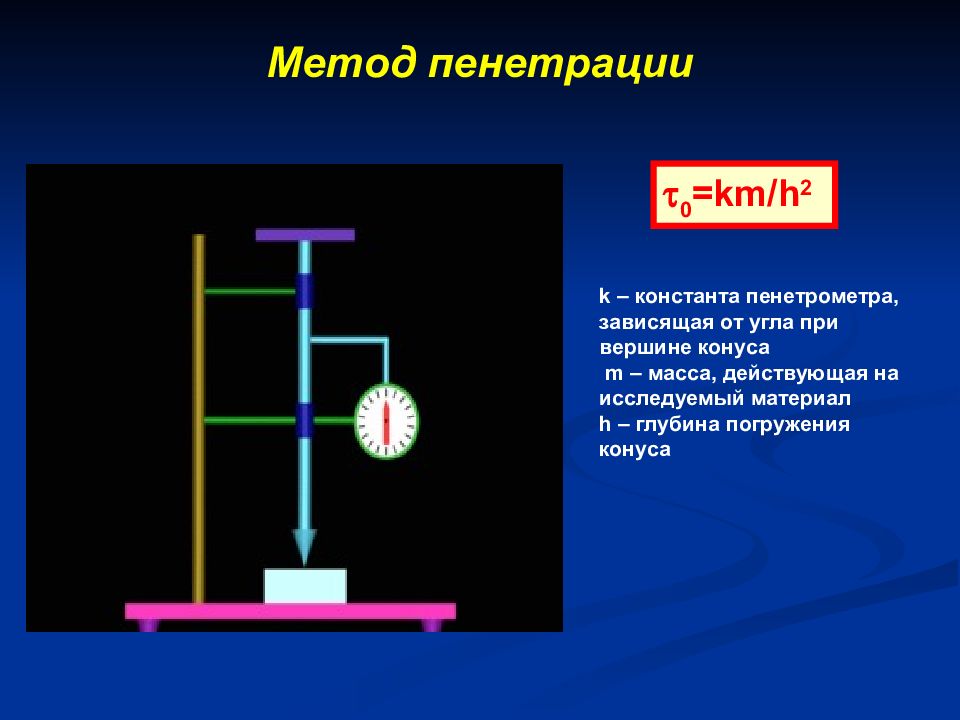
Слайд 19: Метод пенетрации
0 =km/h 2 k – константа пенетрометра, зависящая от угла при вершине конуса m – масса, действующая на исследуемый материал h – глубина погружения конуса
Слайд 20: Методы и приборы для определения поверхностных характеристик
Способы измерения адгезионной прочности
Слайд 21
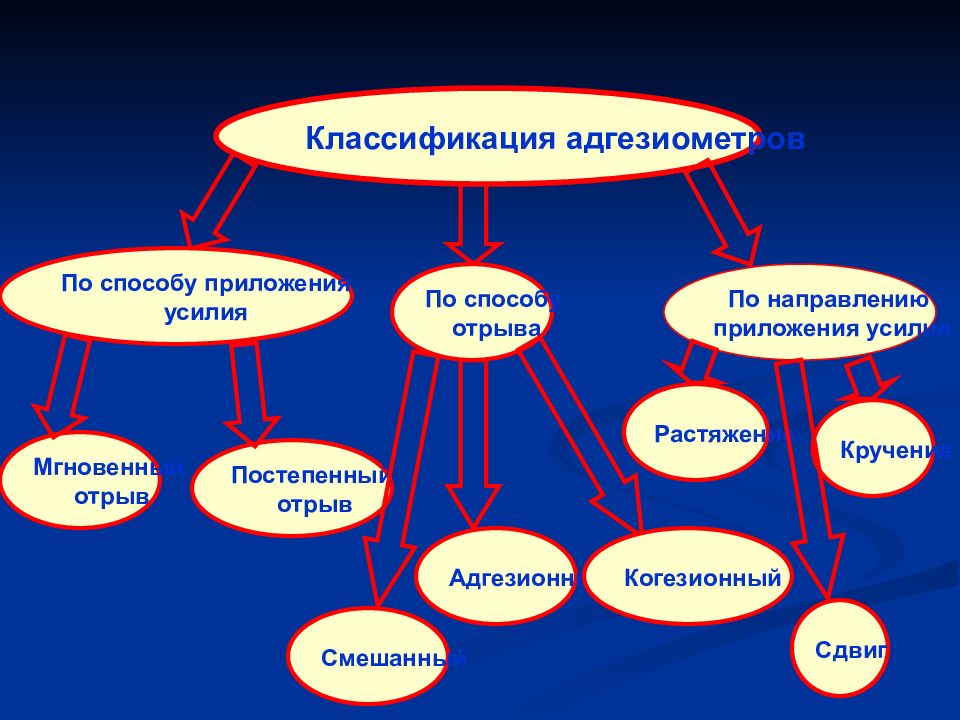
Классификация адгезиометров По способу приложения усилия По способу отрыва По направлению приложения усилия Мгновенный отрыв Постепенный отрыв Адгезионный Когезионный Смешанный Растяжение Кручение Сдвиг
Слайд 23: Примеры растяжения и сжатия при переработке пищевых масс
Вид нагружения Примеры Одноосное сжатие Штампование печенья, пряников, ириса, резание вафельных пластов Одноосное растяжения Формирование макарон, калибрование карамельного жгута Объёмные (компрессионное) сжатие Прессование порошков брикетированием, таблетированием, формование сыра
Слайд 24: Приборы для определения прочностных и компрессионных характеристик пищевых продуктов
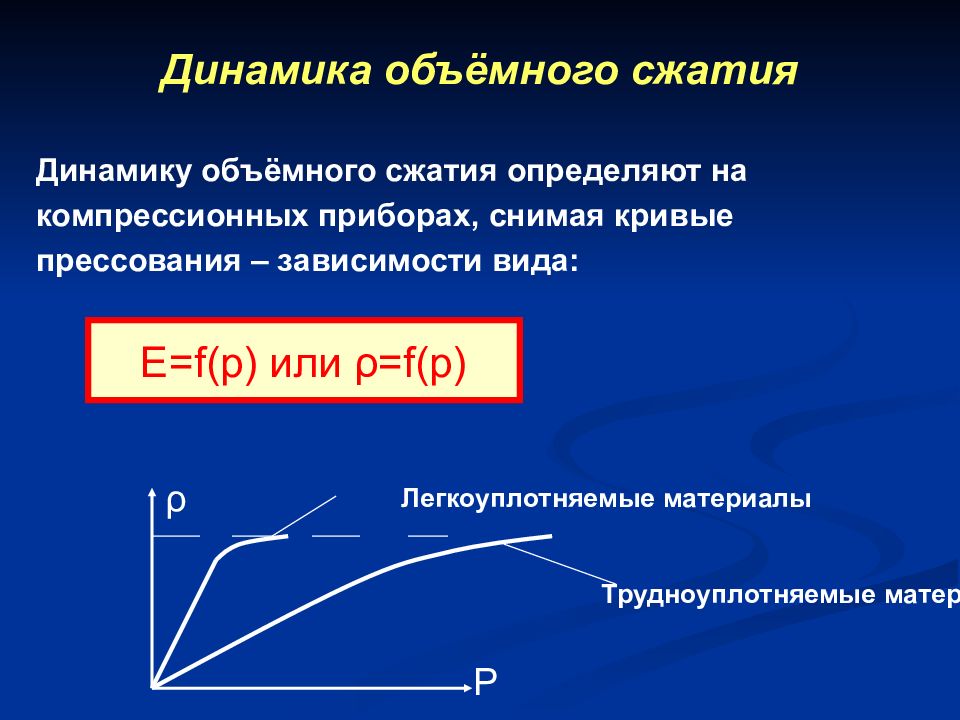
Слайд 25: Динамика объёмного сжатия
Динамику объёмного сжатия определяют на компрессионных приборах, снимая кривые прессования – зависимости вида: Ε =f(p) или ρ = f ( p ) ρ Р Легкоуплотняемые материалы Трудноуплотняемые материалы
Слайд 26: Формулы для расчёта компрессионных характеристик
Коэффициент бокового давления K б =P б /P п Кажущийся объёмный модуль E v =-P п /( Δ V/V 0 ) Коэффициент сжимаемости K с =1/E v
Слайд 27
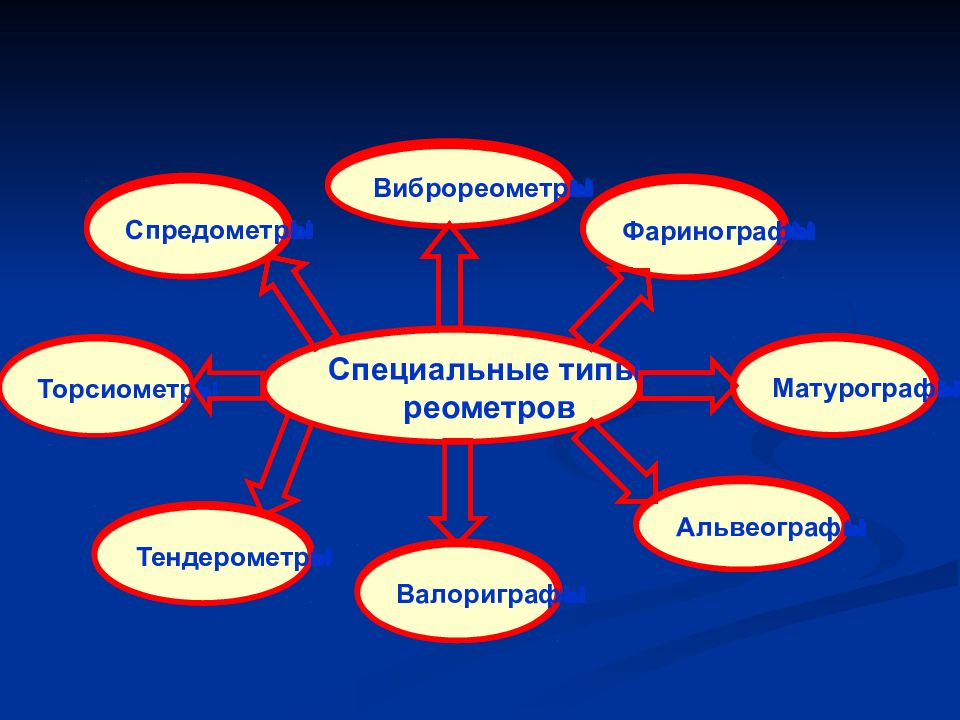
Специальные типы реометров Виброреометры Фаринографы Матурографы Альвеографы Валориграфы Тендерометры Торсиометры Спредометры Спредометры Виброреометры Спредометры Фаринографы Виброреометры Спредометры Матурографы Фаринографы Виброреометры Спредометры Альвеографы Матурографы Фаринографы Виброреометры Спредометры Валориграфы Альвеографы Матурографы Фаринографы Виброреометры Спредометры Тендерометры Валориграфы Альвеографы Матурографы Фаринографы Виброреометры Спредометры Торсиометры Тендерометры Валориграфы Альвеографы Матурографы Фаринографы Виброреометры Спредометры Специальные типы реометров Торсиометры Тендерометры Валориграфы Альвеографы Матурографы Фаринографы Виброреометры Спредометры Специальные типы реометров Торсиометры Тендерометры Валориграфы Альвеографы Матурографы Фаринографы Виброреометры Спредометры
Слайд 28: Вопросы к лекции 15
Для определения каких свойств дисперсных систем используют метод седиментационного анализа? Как можно на основании анализа интегральных и дифференциальных кривых распределения частиц по размерам сделать вывод о монодисперсности или полидисперсности? Какими специфическими оптическими свойствами обладают дисперсные системы? В чем заключается сущность методов нефелометрии и турбидиметрии? Какие методы используют для изучения структурно-механических характеристик дисперсных систем? В чем заключается сущность методов капиллярной, шариковой и ротационной вискозиметрии, пенетрации? Какие приборы используют для определения поверхностных характеристик? Какие реологические константы пищевых масс можно определить с помощью перечисленных методов?