Признаки равенства Прямоугольных треугольников
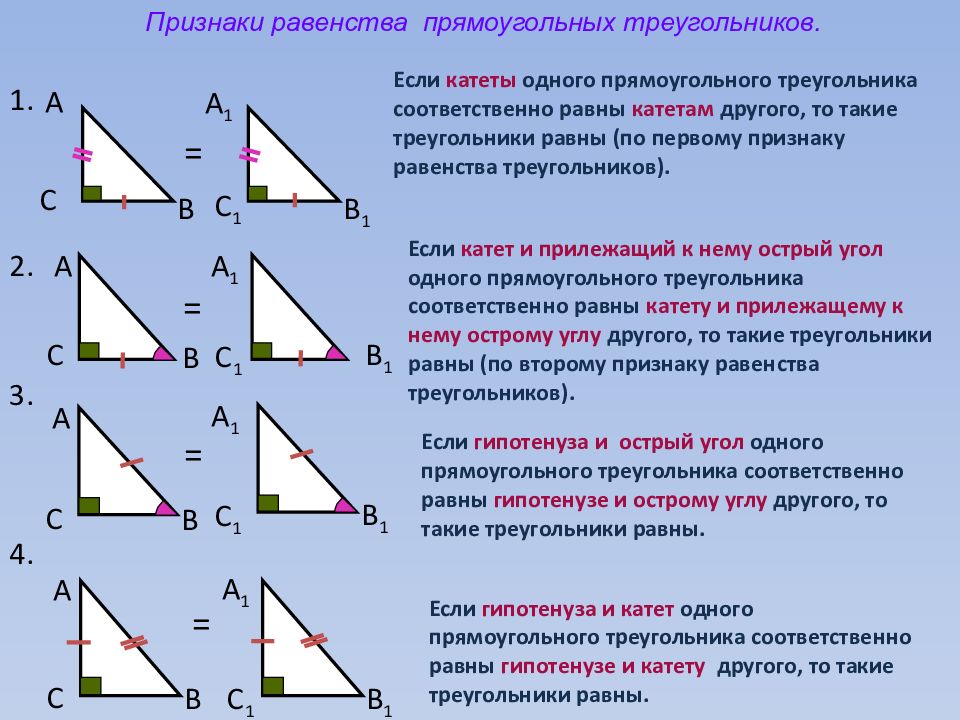
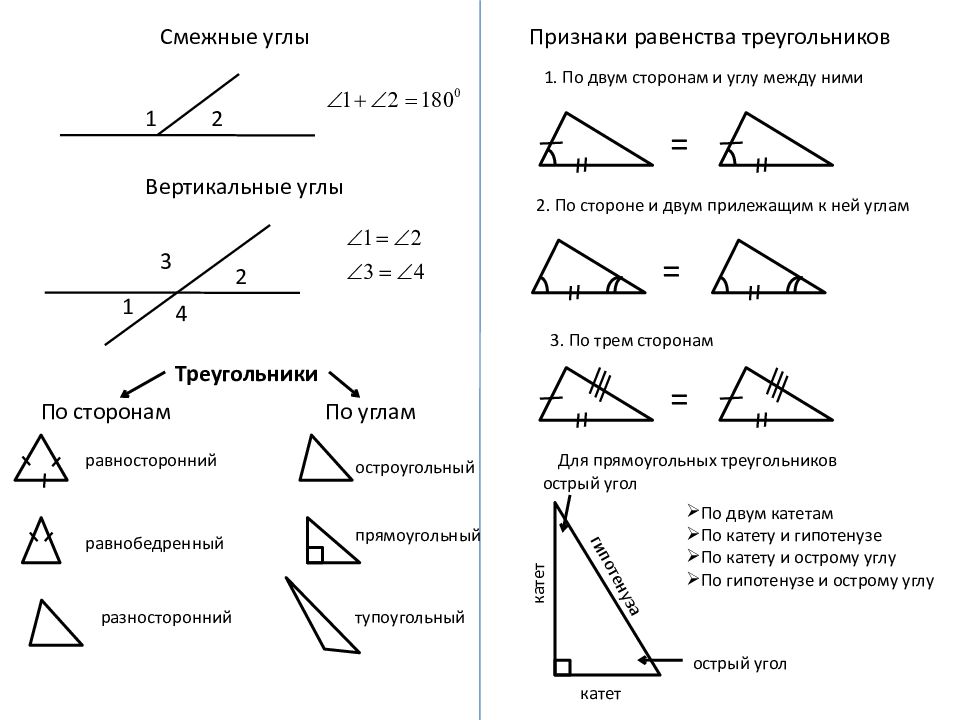
Признаки равенства прямоугольных треугольников. А C B А 1 C 1 B 1 1. = 2. А C B А 1 C 1 = B 1 Если катеты одного прямоугольного треугольника соответственно равны катетам другого, то такие треугольники равны (по первому признаку равенства треугольников). Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого, то такие треугольники равны (по второму признаку равенства треугольников). А C B Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого, то такие треугольники равны. А C B А 1 C 1 B 1 4. 3. А 1 C 1 B 1 = = Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого, то такие треугольники равны.
Задача 1 А В С D Доказать: Δ АВ D = Δ АС D ПО ГИПОТЕНУЗЕ И ОСТРОМУ УГЛУ
А В С D Доказать: Δ АВС= Δ А D С Задача 2 ПО КАТЕТУ И ГИПОТЕНУЗЕ
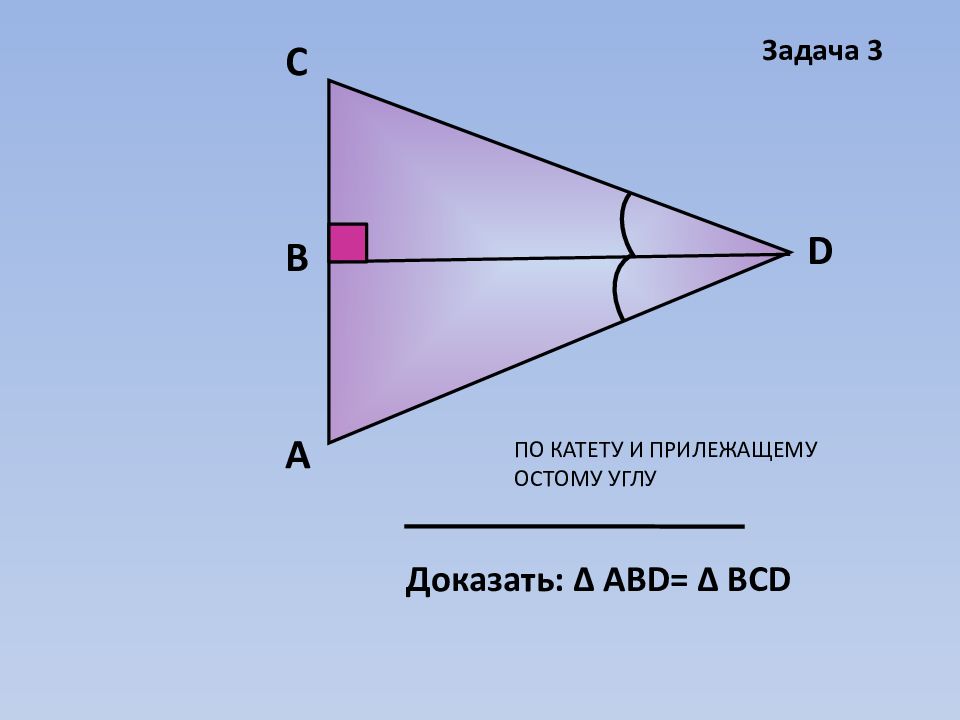
А D В C Доказать: Δ АВ D = Δ ВС D Задача 3 ПО КАТЕТУ И ПРИЛЕЖАЩЕМУ ОСТОМУ УГЛУ
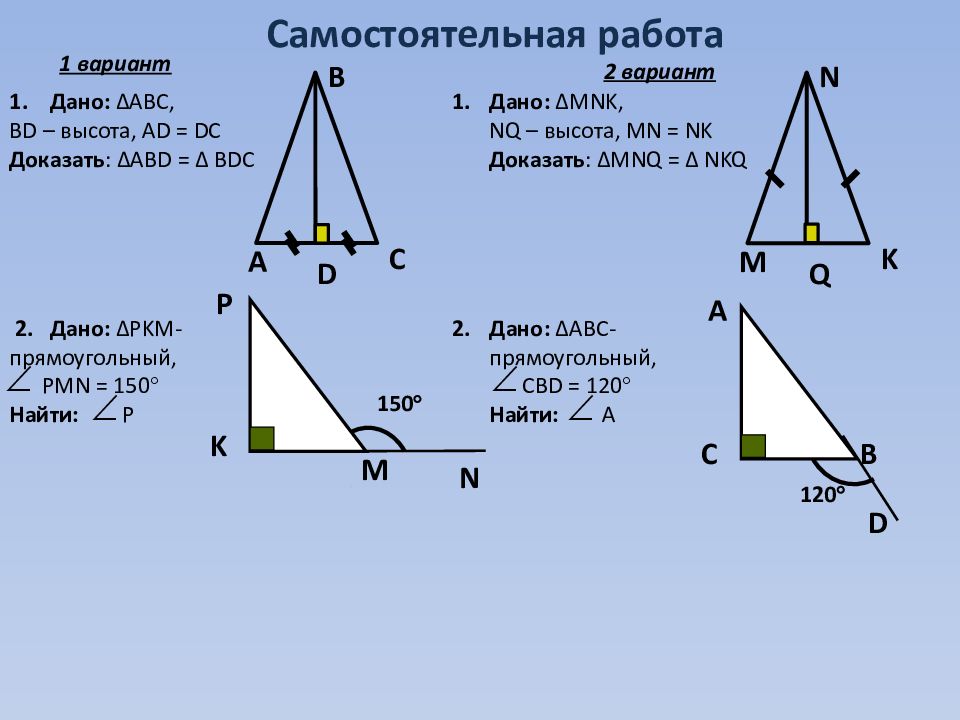
Самостоятельная работа А В С D M N K Q N P K M 150 D А C B 120 1. Дано: ∆ ABC, BD – высота, А D = DC Доказать : ∆ АВ D = ∆ BDC Дано: ∆ MNK, NQ – высота, MN = NK Доказать : ∆MNQ = ∆ NKQ 2. Дано: ∆ PKM- прямоугольный, PMN = 150 Найти: Р Дано: ∆АВС - прямоугольный, СВ D = 120 Найти: A 1 вариант 2 вариант 1. 2.
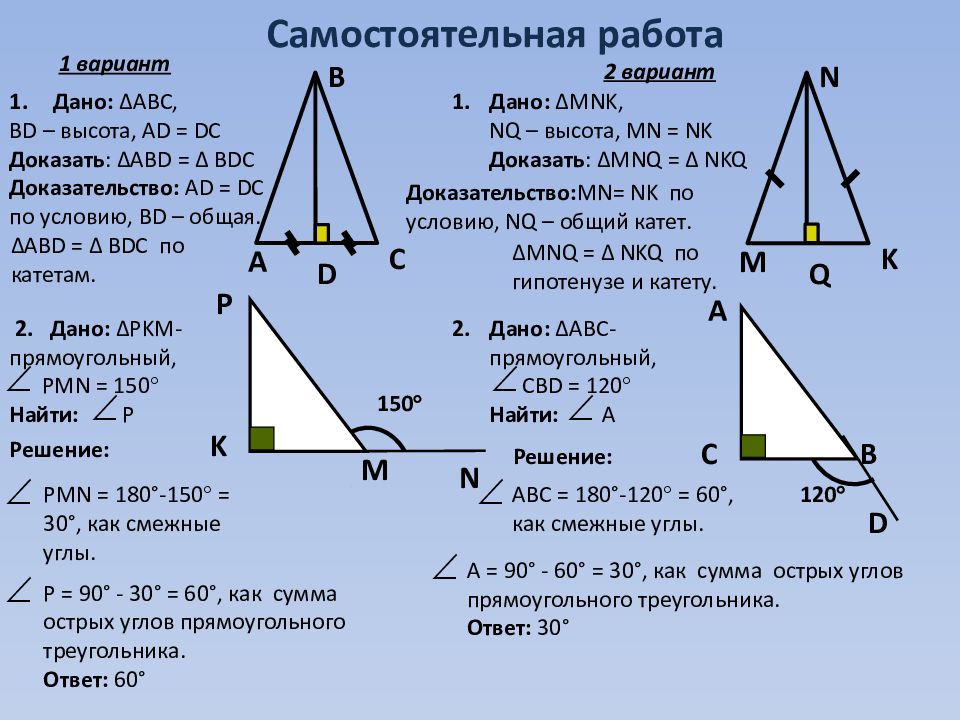
Самостоятельная работа А В С D M N K Q N P K M 150 D А C B 120 Дано: ∆ ABC, BD – высота, А D = DC Доказать : ∆ АВ D = ∆ BDC Доказательство: А D = DC по условию, BD – общая. Дано: ∆ MNK, NQ – высота, MN = NK Доказать : ∆MNQ = ∆ NKQ 2. Дано: ∆ PKM- прямоугольный, PMN = 150 Найти: Р Дано: ∆АВС - прямоугольный, СВ D = 120 Найти: A ∆ АВ D = ∆ BDC по катетам. 1. 1. 2. 1 вариант 2 вариант Доказательство: MN= NK по условию, NQ – общий катет. ∆MNQ = ∆ NKQ по гипотенузе и катету. PMN = 180°- 150 = 30°, как смежные углы. Р = 90° - 30° = 60°, как сумма острых углов прямоугольного треугольника. Ответ: 60° Решение: Решение: АВС = 180°- 1 2 0 = 60°, как смежные углы. А = 90° - 60° = 30°, как сумма острых углов прямоугольного треугольника. Ответ: 30°
