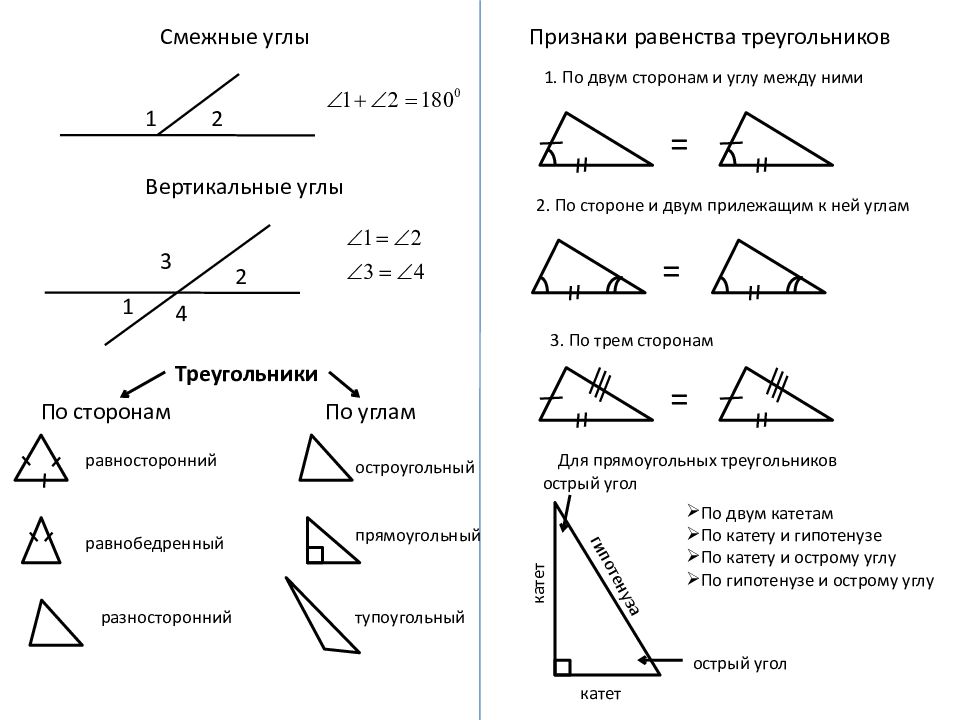
Смежные углы 1 2 Вертикальные углы 1 2 3 4 Признаки равенства треугольников 1. По двум сторонам и углу между ними = = 2. По стороне и двум прилежащим к ней углам 3. По трем сторонам = гипотенуза катет катет Для прямоугольных треугольников По двум катетам По катету и гипотенузе По катету и острому углу По гипотенузе и острому углу острый угол острый угол Треугольники По сторонам По углам равносторонний равнобедренный разносторонний остроугольный прямоугольный тупоугольный
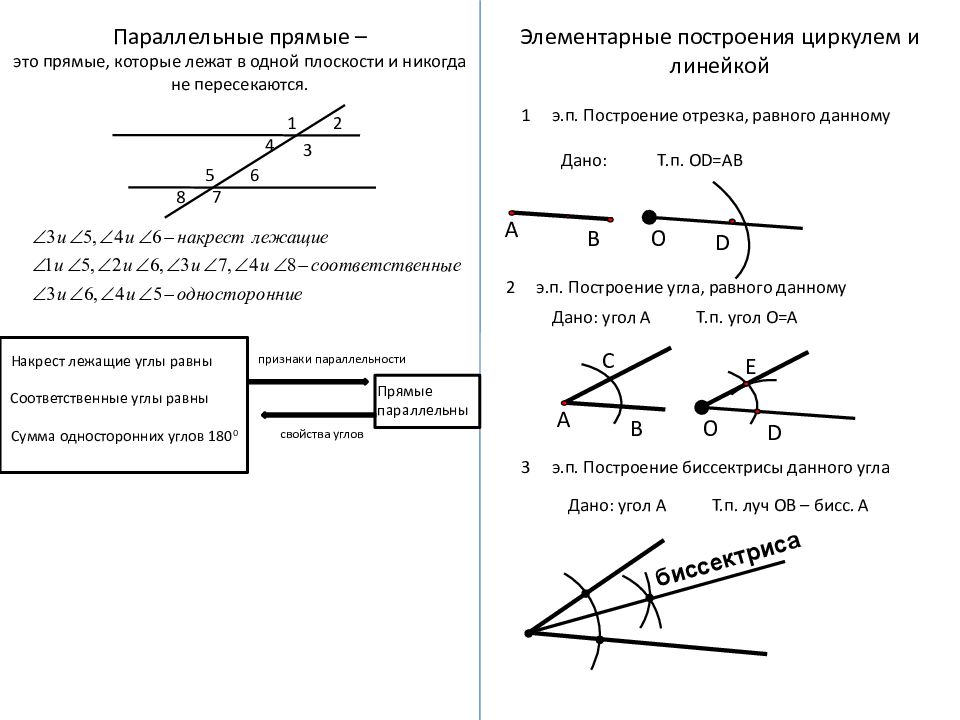
Параллельные прямые – это прямые, которые лежат в одной плоскости и никогда не пересекаются. 1 2 3 4 5 6 7 8 Накрест лежащие углы равны Соответственные углы равны Сумма односторонних углов 180 0 Прямые параллельны признаки параллельности свойства углов Элементарные построения циркулем и линейкой 1 э.п. Построение отрезка, равного данному Дано: Т.п. О D =АВ А В О D А В С О D E 2 э.п. Построение угла, равного данному Дано: угол А Т.п. угол О=А 3 э.п. Построение биссектрисы данного угла Дано: угол А Т.п. луч ОВ – бисс. А биссектриса
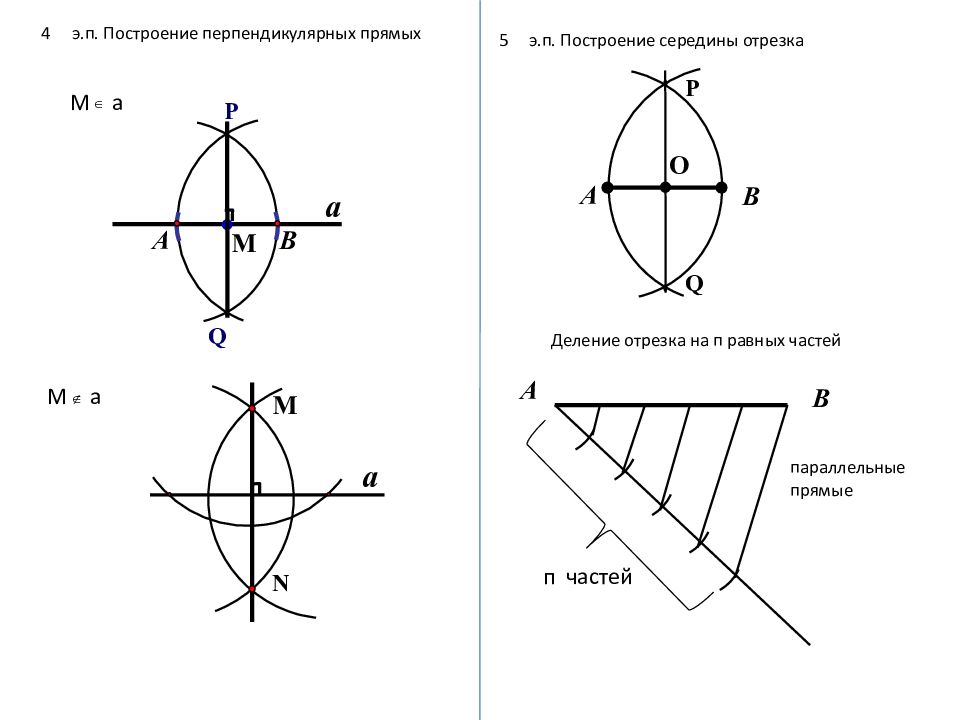
М а 4 э.п. Построение перпендикулярных прямых Q P В А М М а a N М a 5 э.п. Построение середины отрезка Q P В А О Деление отрезка на п равных частей А В п частей параллельные прямые
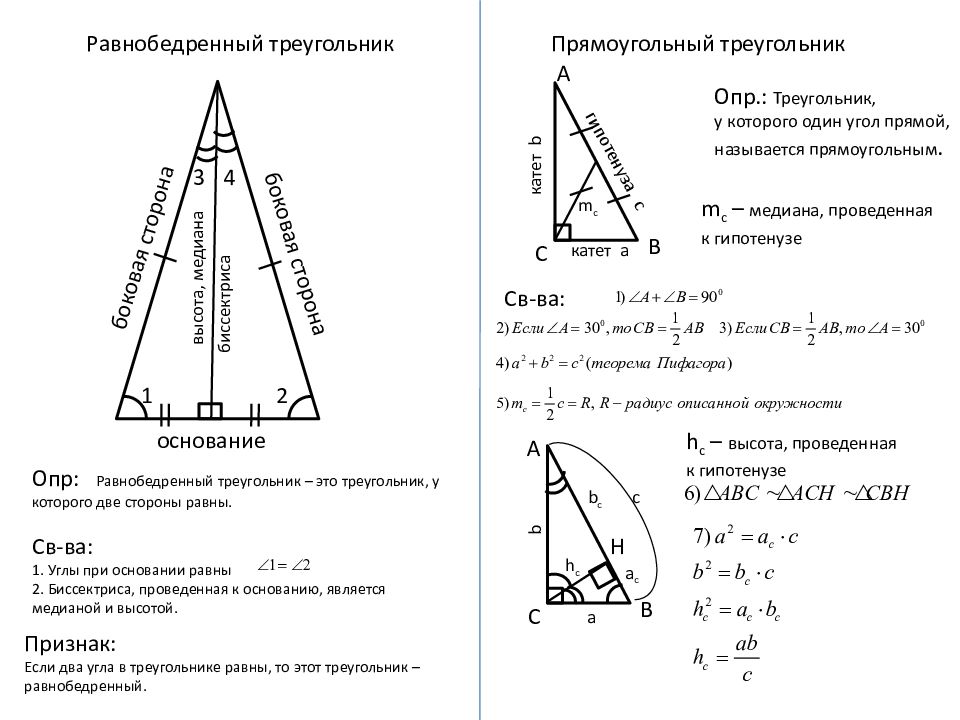
Равнобедренный треугольник Опр : Равнобедренный треугольник – это треугольник, у которого две стороны равны. Св-ва : 1. Углы при основании равны 2. Биссектриса, проведенная к основанию, является медианой и высотой. Признак: Если два угла в треугольнике равны, то этот треугольник – равнобедренный. основание боковая сторона боковая сторона 1 2 3 4 высота, медиана биссектриса Прямоугольный треугольник Опр.: Треугольник, у которого один угол прямой, называется прямоугольным. гипотенуза с a катет а А В С Св-ва : m c В С h c А катет b b a c b c c m c – медиана, проведенная к гипотенузе h c – высота, проведенная к гипотенузе Н
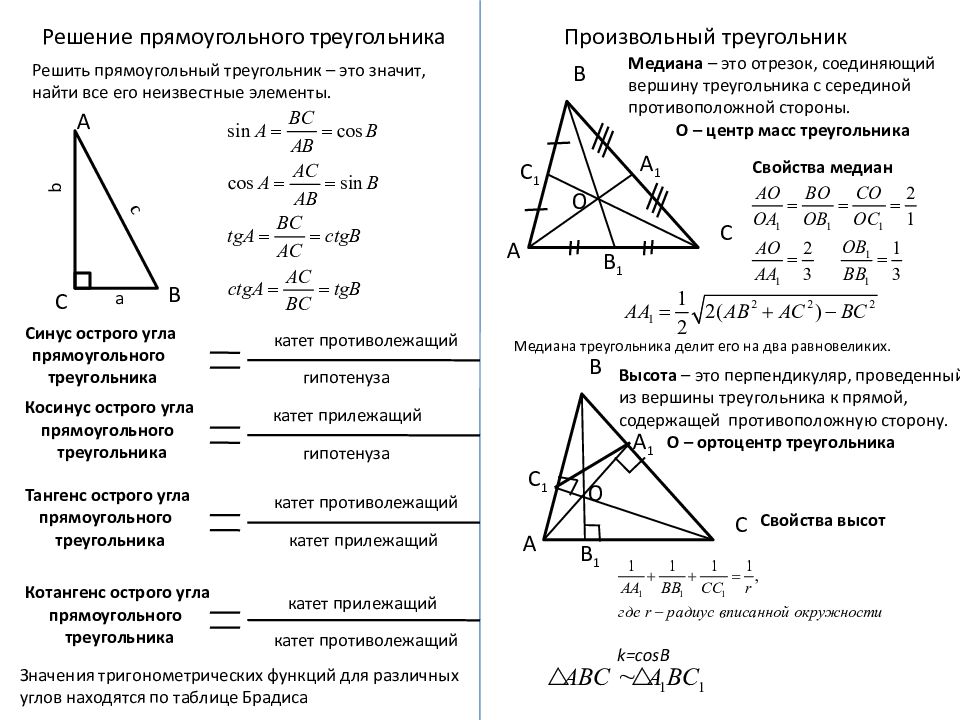
Решение прямоугольного треугольника Решить прямоугольный треугольник – это значит, найти все его неизвестные элементы. с а А В С b Синус острого угла прямоугольного треугольника катет противолежащий гипотенуза Косинус острого угла прямоугольного треугольника катет прилежащий гипотенуза Тангенс острого угла прямоугольного треугольника катет противолежащий катет прилежащий Котангенс острого угла прямоугольного треугольника катет противолежащий катет прилежащий Значения тригонометрических функций для различных углов находятся по таблице Брадиса Произвольный треугольник А С В А С В В 1 А 1 С 1 О Медиана – это отрезок, соединяющий вершину треугольника с серединой противоположной стороны. О – центр масс треугольника О В 1 А 1 С 1 Высота – это перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону. О – ортоцентр треугольника k =со sB Свойства высот Свойства медиан Медиана треугольника делит его на два равновеликих.
А С В В 1 А 1 С 1 О А С В В 1 А 1 С 1 О Биссектриса треугольника – это отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противопо - ложной стороны. О – центр вписанной в треугольник окружности Свойства биссектрисы треугольника Срединный перпендикуляр – это прямая, перпендикулярная стороне треугольника, проходящая через ее середину О – центр описанной около треугольника окружности Соотношения между сторонами и углами произвольного треугольника А С В b a c Теорема косинусов Теорема синусов Теорема о сумме углов треугольника. Неравенство треугольника. Напротив большей стороны треугольника лежит больший угол. Напротив большего угла треугольника лежит большая сторона. Средняя линия треугольника ( MN ) - это отрезок, соединяющий середины двух его сторон. М N
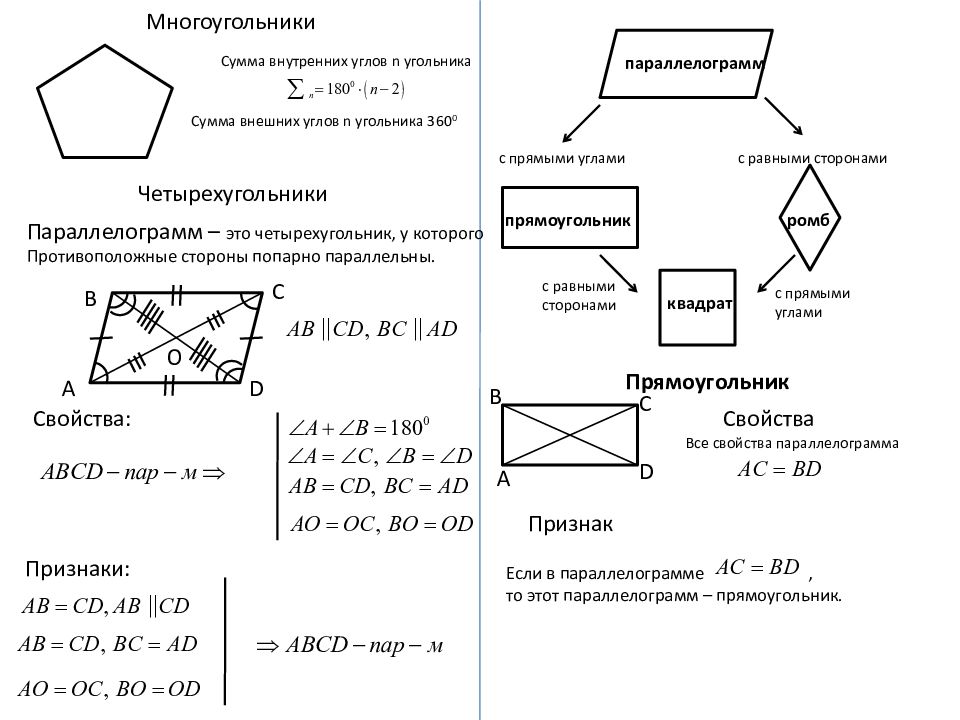
Четырехугольники Параллелограмм – это четырехугольник, у которого Противоположные стороны попарно параллельны. А В С D C войства : Признаки: О с прямыми углами с равными сторонами параллелограмм прямоугольник ромб с равными сторонами с прямыми углами квадрат Многоугольники Сумма внутренних углов n угольника Сумма внешних углов n угольника 360 0 Прямоугольник Свойства Все свойства параллелограмма А В С D Признак Если в параллелограмме, то этот параллелограмм – прямоугольник.
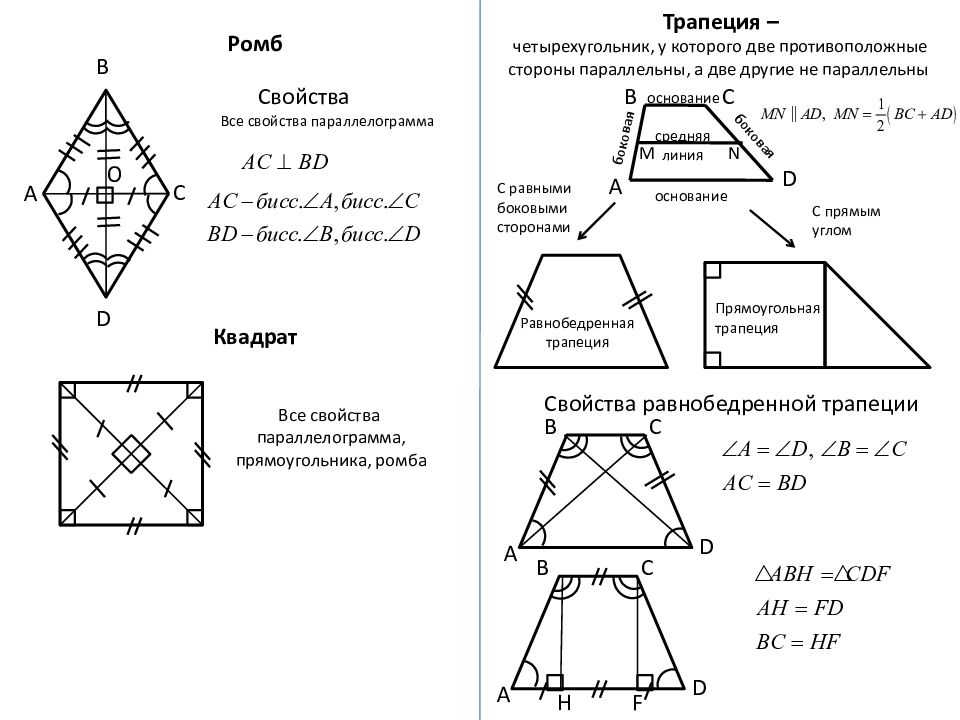
Ромб А В С D O Свойства Все свойства параллелограмма Квадрат Все свойства параллелограмма, прямоугольника, ромба Трапеция – четырехугольник, у которого две противоположные стороны параллельны, а две другие не параллельны основание основание боковая боковая С равными боковыми сторонами С прямым углом Равнобедренная трапеция Прямоугольная трапеция Свойства равнобедренной трапеции А В С D средняя линия В А С D M N А В С D H F
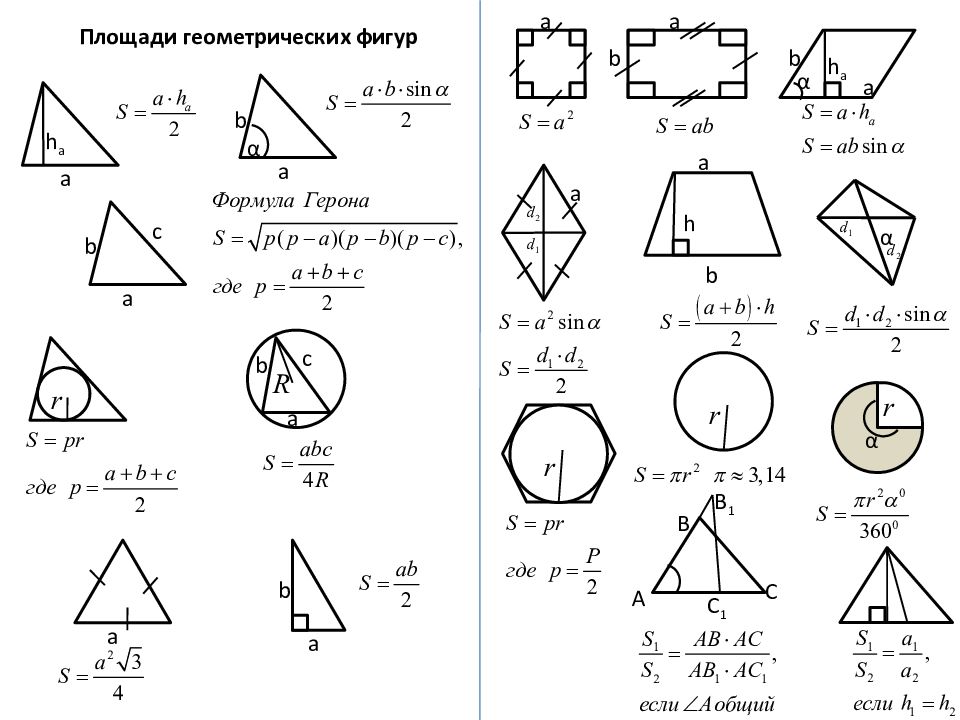
α Площади геометрических фигур а h а a b α b c a a b c a a b a a b a h а b a h a b α α А В С В 1 С 1
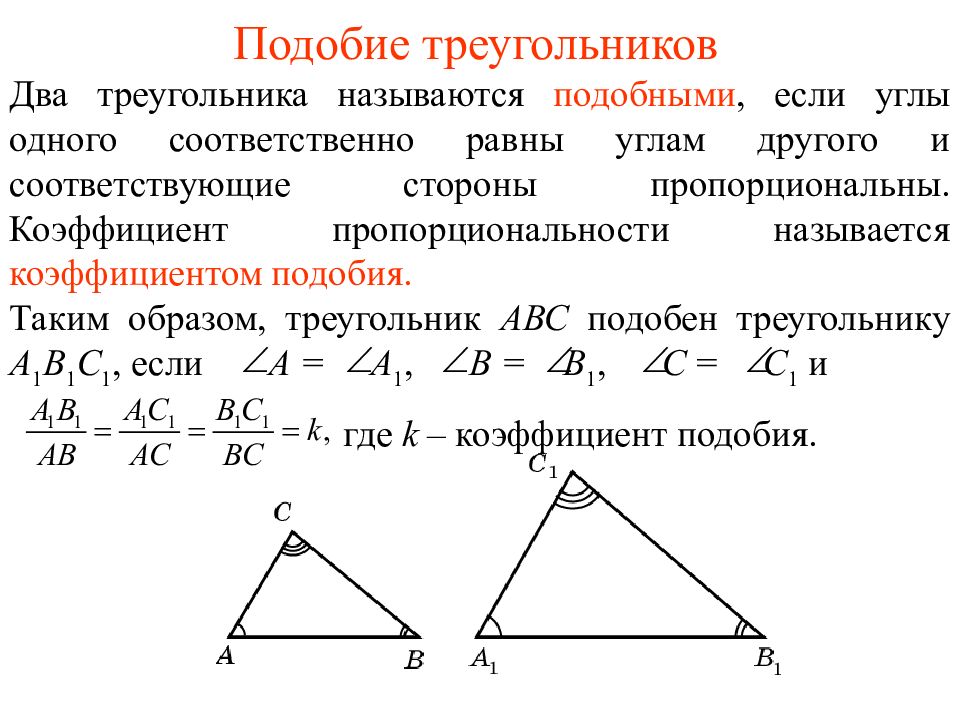
Подобные треугольники Опр.: Подобными называются треугольники у которых соответственные углы равны, и сходственные стороны пропорциональны. А А 1 С В В 1 С 1 Равные углы Подобные фигуры имеют одинаковую форму. k Свойства подобных фигур Признаки подобия треугольников А А 1 С В В 1 С 1 Теорема Фалеса а b А 1 А 2 А 3 А 4 В 1 В 2 В 3 В 4 b А 1 А 2 А 3 В 1 В 2 В 3 а
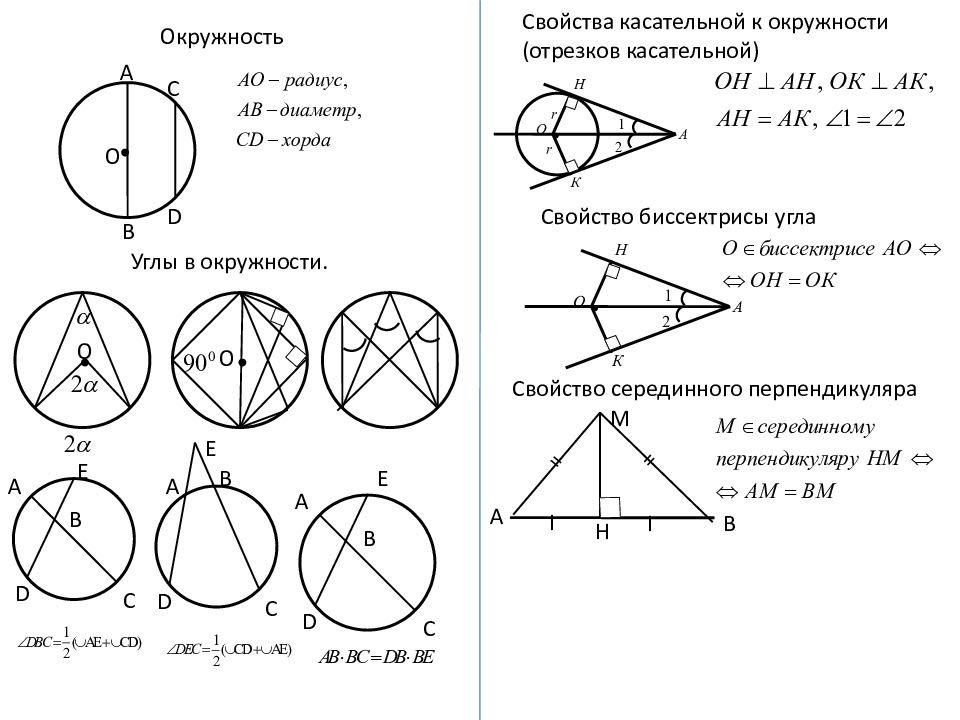
Окружность О А В С D Углы в окружности. О О А В С D Е А В С D А В С D Е Е Свойства касательной к окружности (отрезков касательной) Свойство биссектрисы угла Свойство серединного перпендикуляра В А = = I I Н М
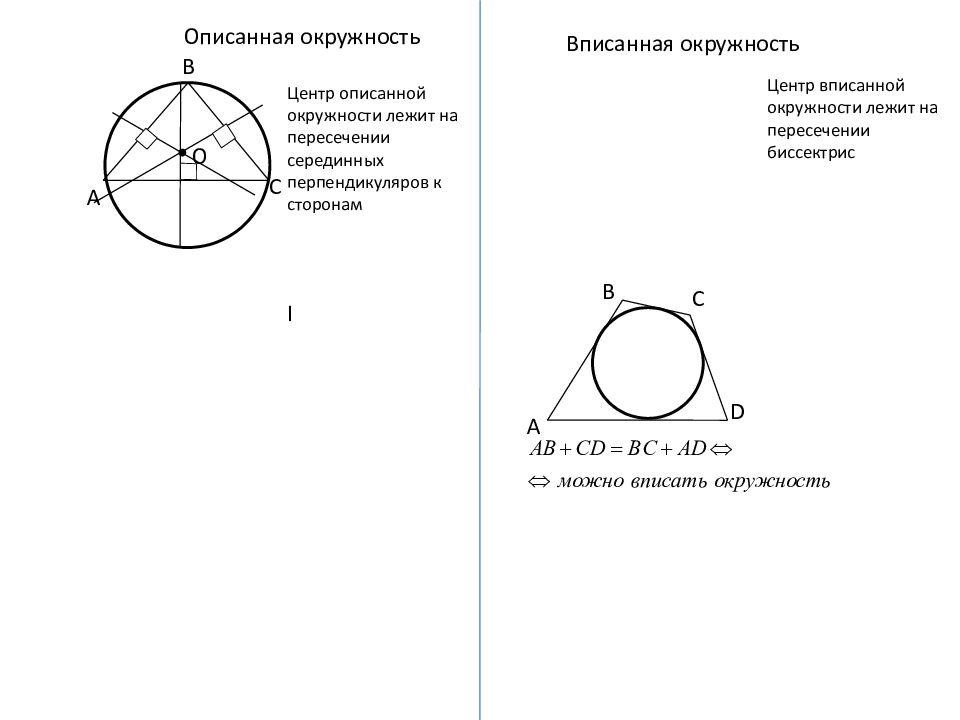
Вписанная окружность А В В С D Центр вписанной окружности лежит на пересечении биссектрис А С О Описанная окружность Центр описанной окружности лежит на пересечении серединных перпендикуляров к сторонам I
