Первый слайд презентации: Проект на тему : «Высоты треугольника»
Курышева Мария Дверник Юлия Гаскевич Александра Голован Сергей Барышникова Анна группа М5
Слайд 2: О пределение
Высотой треугольника называется перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону этого треугольника.
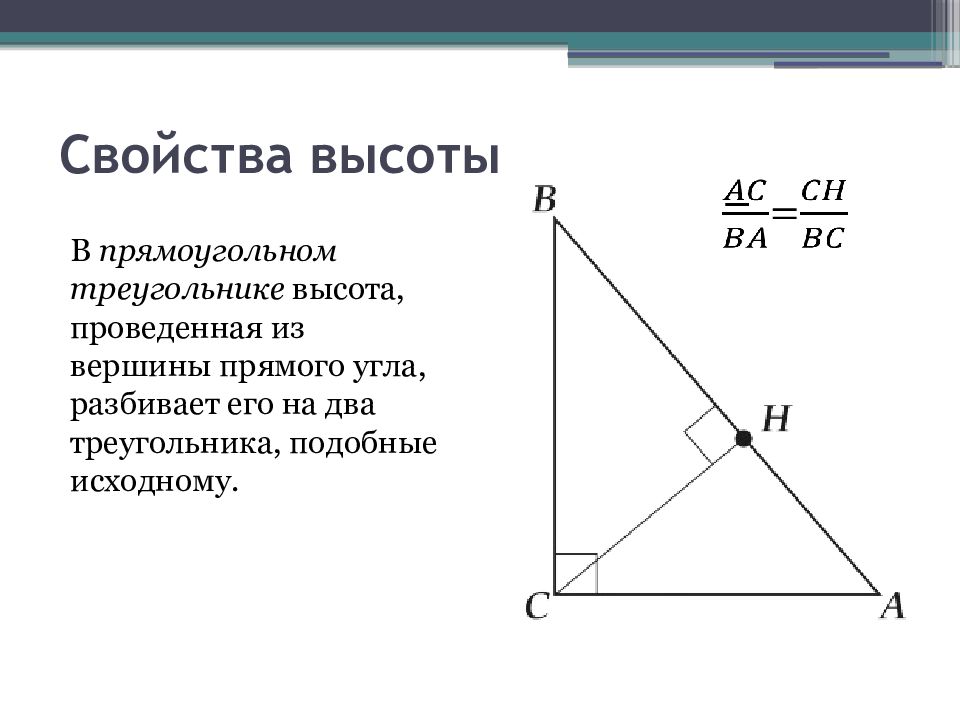
Слайд 3: Свойства высоты
В прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два треугольника, подобныеисходному. =
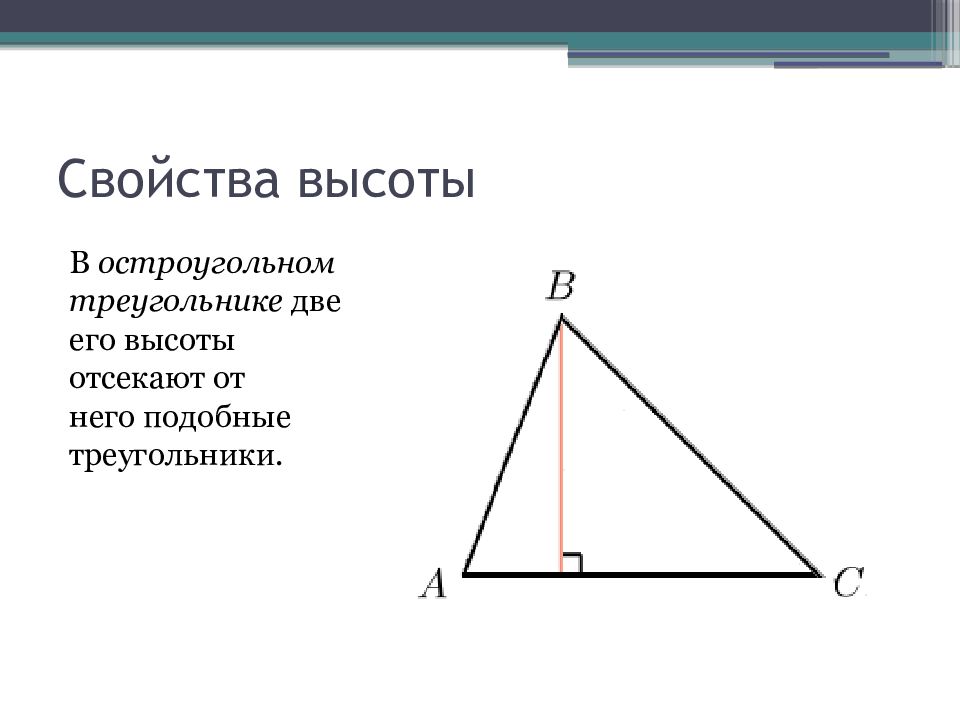
Слайд 4: Свойства высоты
В остроугольном треугольнике две его высоты отсекают от него подобные треугольники.
Слайд 5: Свойства высоты
В равнобедренном треугольнике, третья высота одновременно является медианой и биссектрисой того угла, из которого она выходит.
Если высота в прямоугольном треугольнике ABC длиной h, проведённая из вершины прямого угла, делит гипотенузу длиной C на отрезки m и n, соответствующие катетам b и a, то верны следующие равенства :
Медианы треугольника пересекаются в одной точке, которая делит каждую из них в отношении 2:1, считая от вершины. Эта точка называется центром тяжести треугольника. А в равносторонних треугольниках медианы и высоты - одно и то же.
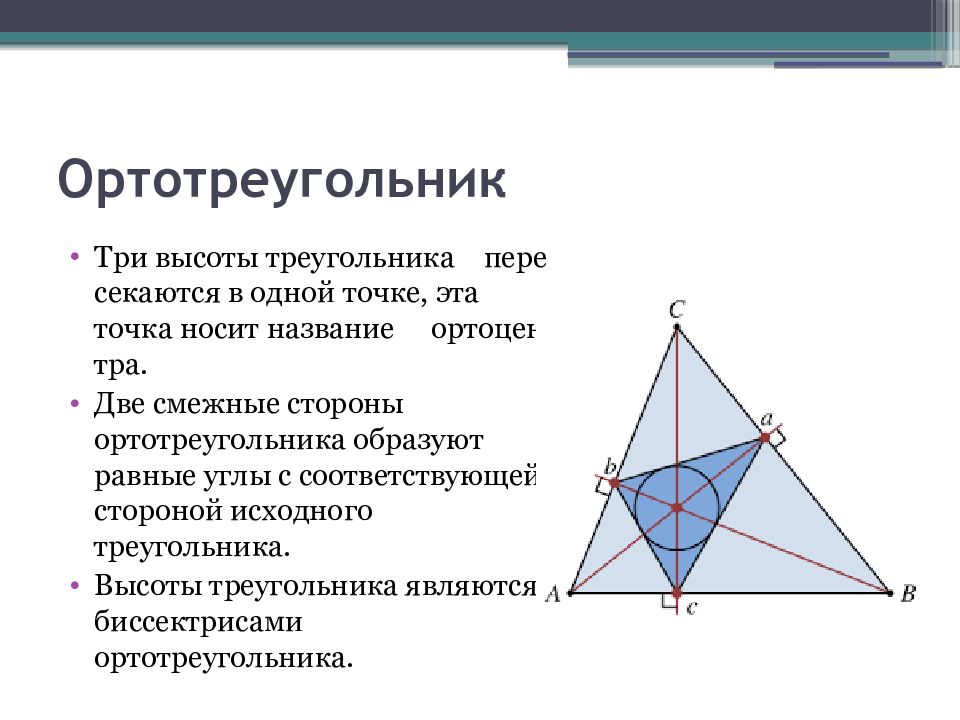
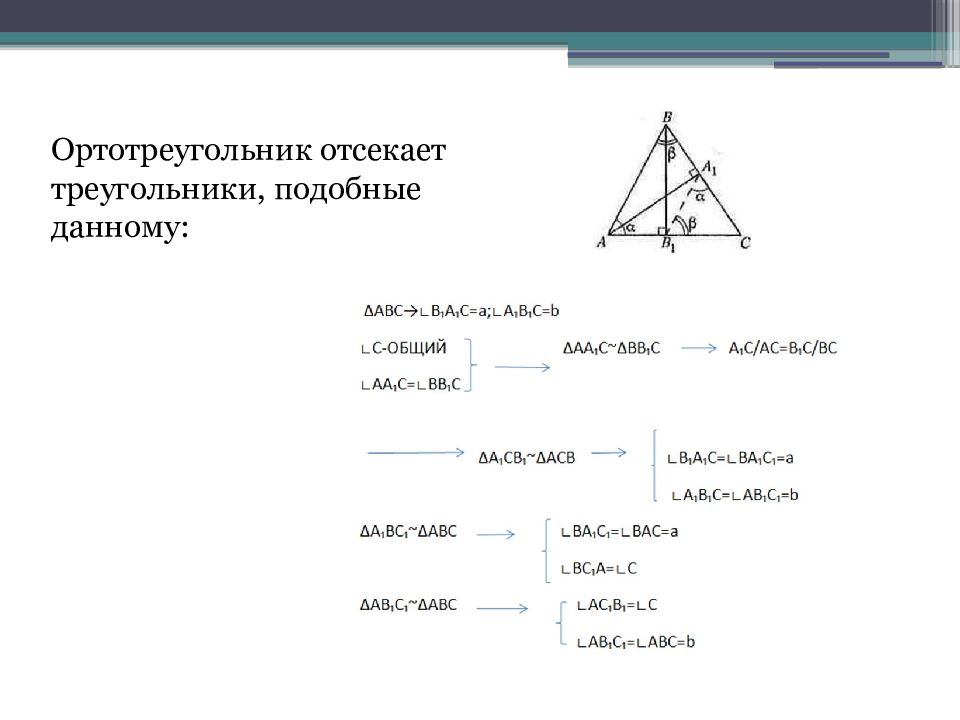
Слайд 8: Ортотреугольник
Три высоты треугольника пересекаются в одной точке, эта точка носит название ортоцентра. Две смежные стороны ортотреугольника образуют равные углы с соответствующей стороной исходного треугольника. Высоты треугольника являются биссектрисами ортотреугольника.
Слайд 11: Окружность девяти точек
О снования высот, середины сторон и середины отрезков, соединяющих ортоцентр —точку пересечения высот —с вершинами треугольника, лежат на одной окружности — окружности девяти точек.
Слайд 12: Прямая Эйлера
Ц ентр описанной окружности, центр тяжести, центр окружности девяти точек и ортоцентр лежат на одной прямой — прямой Эйлера.
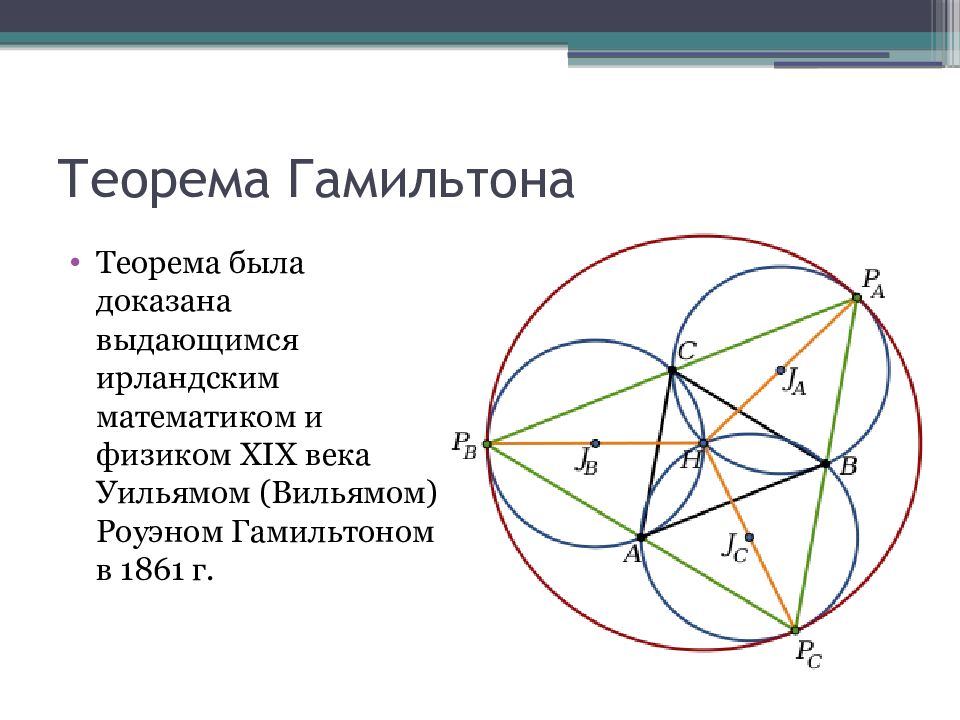
Слайд 13: Теорема Гамильтона
Три отрезка прямых, соединяющих ортоцентр с вершинами остроугольного треугольника, разбивают его на три треугольника Гамильтона, имеющих ту же самую окружность Эйлера (окружность девяти точек), что и исходный остроугольный треугольник.
Слайд 14: Теорема Гамильтона
Теорема была доказана выдающимся ирландским математиком и физиком XIX века Уильямом (Вильямом) Роуэном Гамильтоном в 1861 г.