Первый слайд презентации: Замечательные точки треугольника Теорема о пересечении высот треугольника
Двадцать первое апреля
Слайд 2: Цели:
1) Рассмотреть теорему о точке пересечения высот и следствие из неё; 2) Формировать умения применять известные знания в незнакомой ситуации, сравнивать, анализировать, обобщать.
Слайд 4
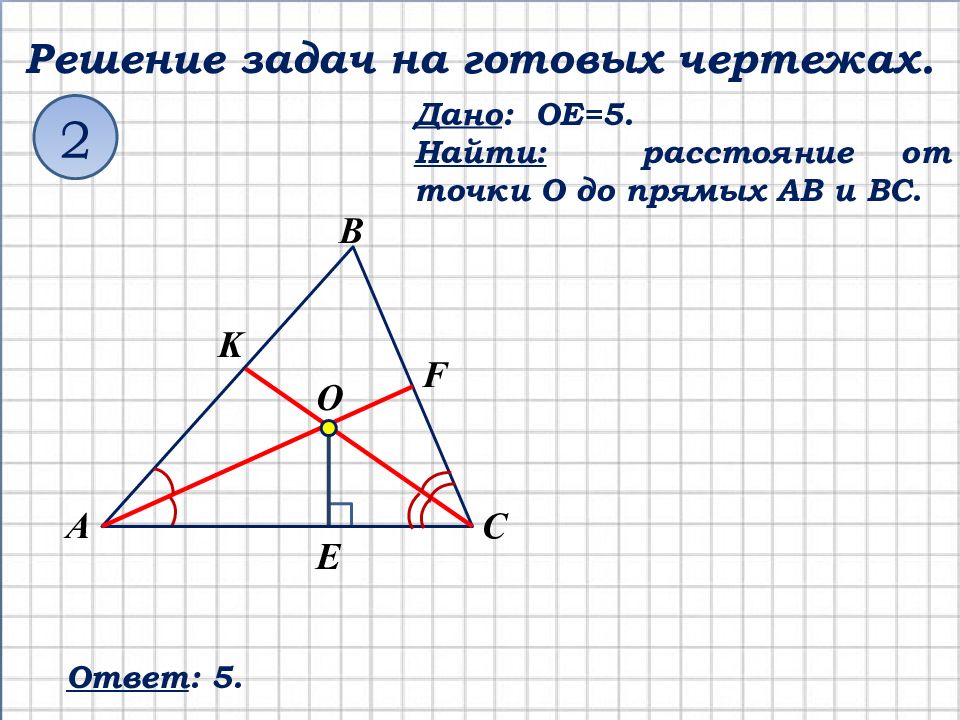
Решение задач на готовых чертежах. Дано : OE =5. Найти: расстояние от точки О до прямых АВ и ВС. 2 Ответ : 5. E С K А В F О
Слайд 5: Устно:
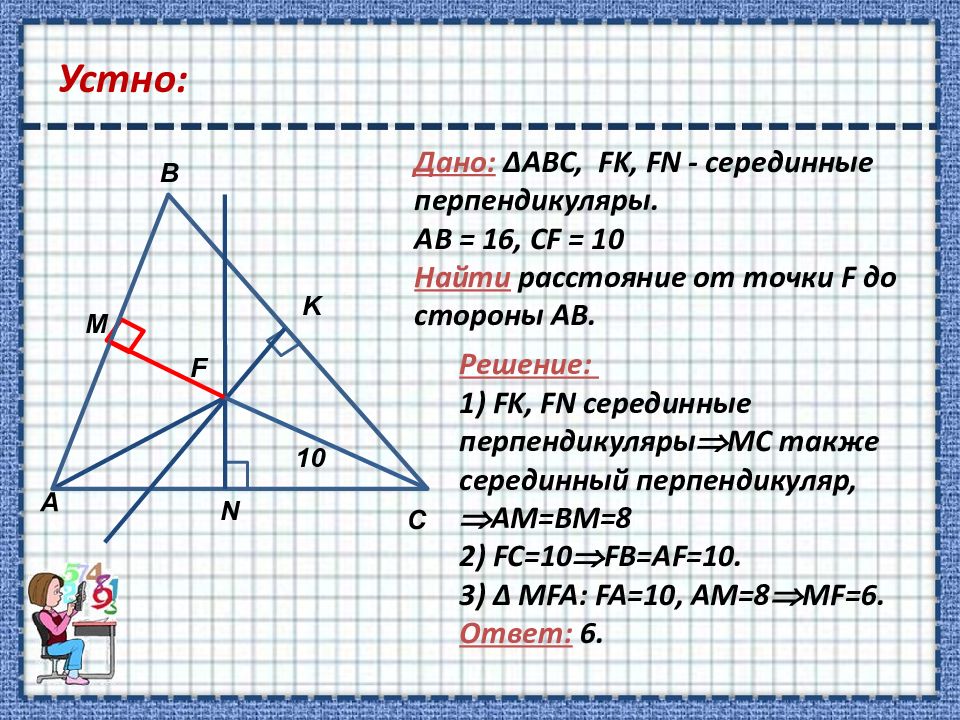
Дано: Δ ABC, FK, FN - серединные перпендикуляры. АВ = 16, СF = 10 Найти расстояние от точки F до стороны АВ. Решение: 1) FK, FN серединные перпендикуляры MC также серединный перпендикуляр, AM = BM =8 2) FC =10 FB = AF =10. 3) Δ MFA : FA =10, А M =8 MF =6. Ответ : 6. F 10 M B K C N А
Теорема. Высоты треугольника или их продолжения пересекаются в одной точке ( ортоцентр). А В С Н М К О Вывод: В остроугольном треугольнике все три высоты пересеклись в одной точке. Эта точка расположена в плоскости треугольника.
Теорема. Высоты треугольника или их продолжения пересекаются в одной точке ( ортоцентр). М А С(К,Н,О) В Вывод: В прямоугольном треугольнике все три высоты пересеклись в одной точке. Эта точка лежит в плоскости треугольника и совпадает с вершиной прямого угла треугольника.
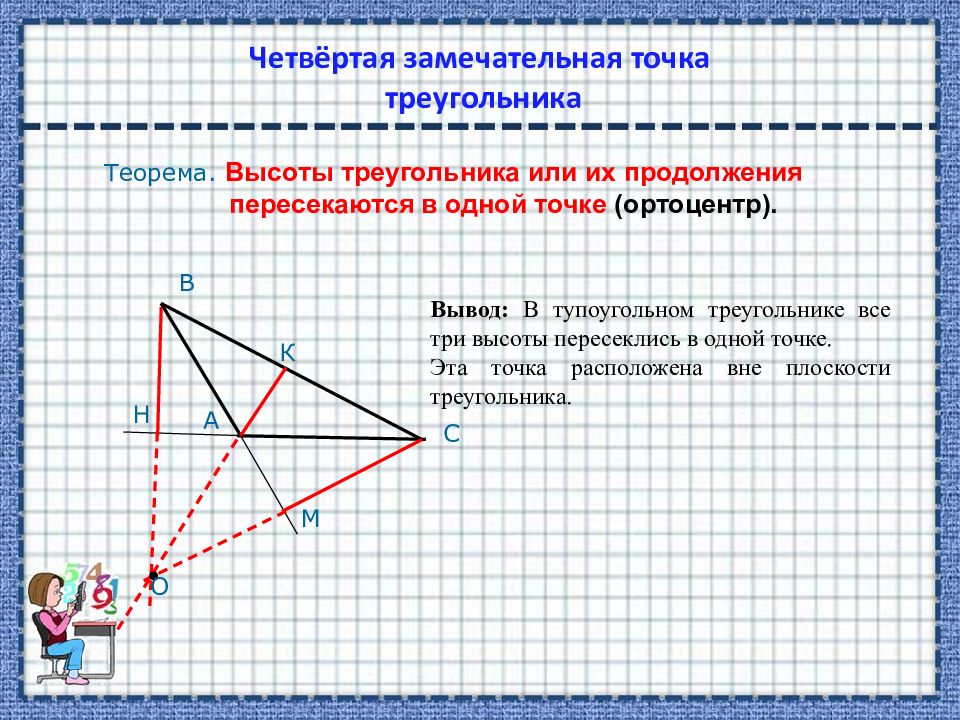
Теорема. Высоты треугольника или их продолжения пересекаются в одной точке ( ортоцентр). В С А Н К М О Вывод: В тупоугольном треугольнике все три высоты пересеклись в одной точке. Эта точка расположена вне плоскости треугольника.
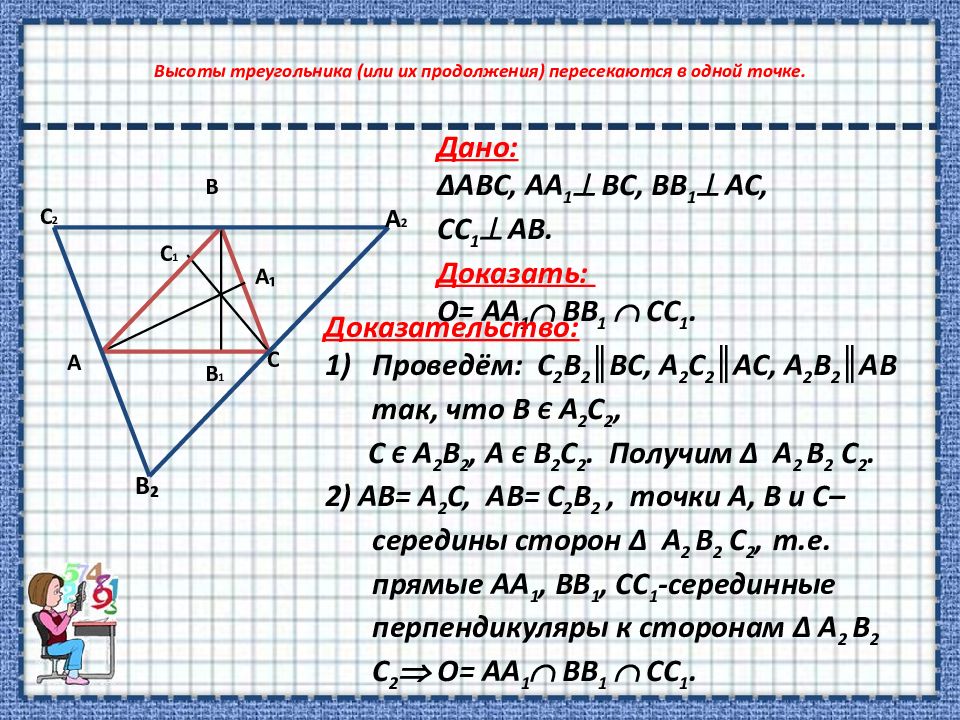
Слайд 9: Высоты треугольника (или их продолжения) пересекаются в одной точке
С 1 А В С В 1 А ₁ А 2 С 2 В₂ Дано: Δ ABC, AA 1 BC, BB 1 AC, CC 1 AB. Доказать: O = AA 1 BB 1 CC 1. Доказательство: Проведём: С 2 B 2 ║ BC, A 2 C 2 ║ AC, A 2 B 2 ║ AB так, что B Є A 2 C 2, C Є A 2 B 2, A Є B 2 C 2. Получим Δ A 2 B 2 C 2. 2) AB = A 2 C, AB = С 2 B 2, точки A, B и C – середины сторон Δ A 2 B 2 C 2, т.е. прямые АА 1, BB 1, CC 1 -серединные перпендикуляры к сторонам Δ A 2 B 2 C 2 O = AA 1 BB 1 CC 1.
Слайд 10
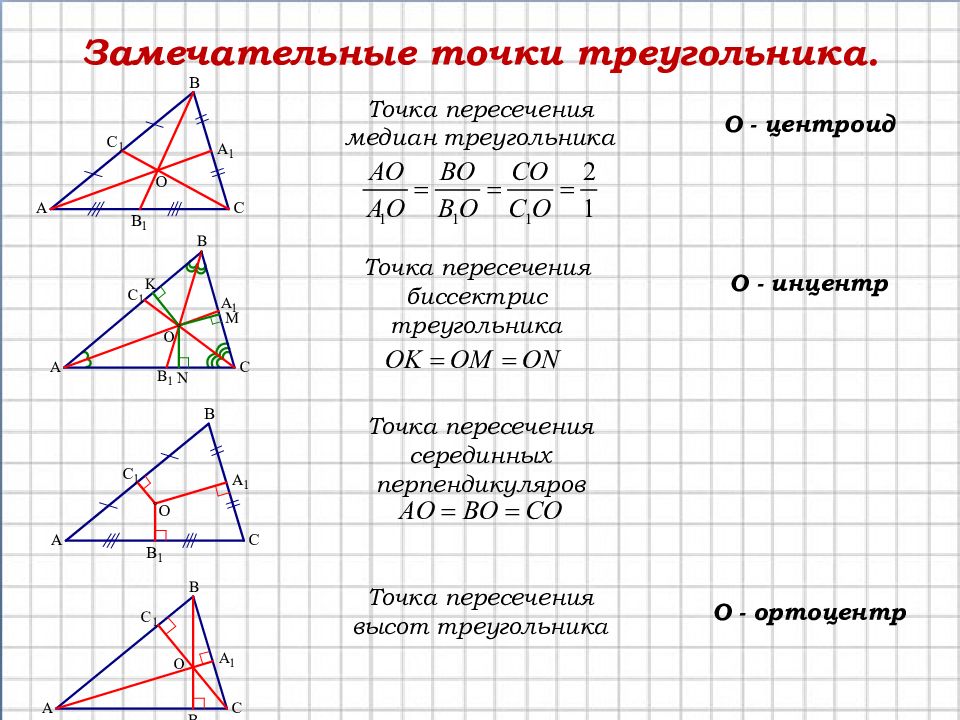
Замечательные точки треугольника. Точка пересечения медиан треугольника О - центроид Точка пересечения высот треугольника О - ортоцентр Точка пересечения серединных перпендикуляров Точка пересечения биссектрис треугольника О - инцентр
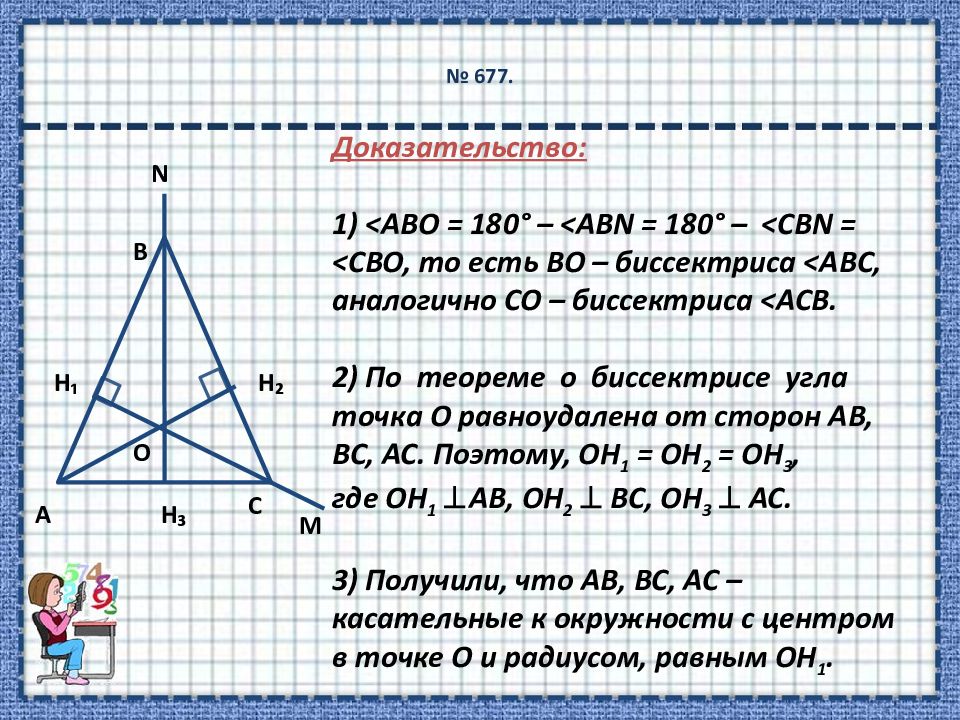
Слайд 11: 677
O N B H₂ M C H ₃ H ₁ А Доказательство: 1) < АВО = 180° – < АВN = 180° – < СВN = < CВО, то есть ВО – биссектриса < АВС, аналогично СО – биссектриса < АСВ. 2) По теореме о биссектрисе угла точка О равноудалена от сторон АВ, ВС, АС. Поэтому, ОН 1 = ОН 2 = ОН 3, где ОН 1 АВ, ОН 2 ВС, ОН 3 АС. 3) Получили, что АВ, ВС, АС – касательные к окружности с центром в точке О и радиусом, равным ОН 1.