Первый слайд презентации: Лекция 11
Взаимное пересечение кривых поверхностей. Частные случаи пересечения поверхностей второго порядка. Метод концентрических сфер. Метод эксцентрических сфер.
При пересечении поверхностей второго порядка линией пересечения в общем случае является пространственная кривая 4-го порядка. Эта кривая пересекается плоскостью в четырех точках (действительных и мнимых) Порядок линии пересечения равен произведению порядков пересекающихся поверхностей. Кривая четвертого порядка может распадаться на две кривые второго порядка
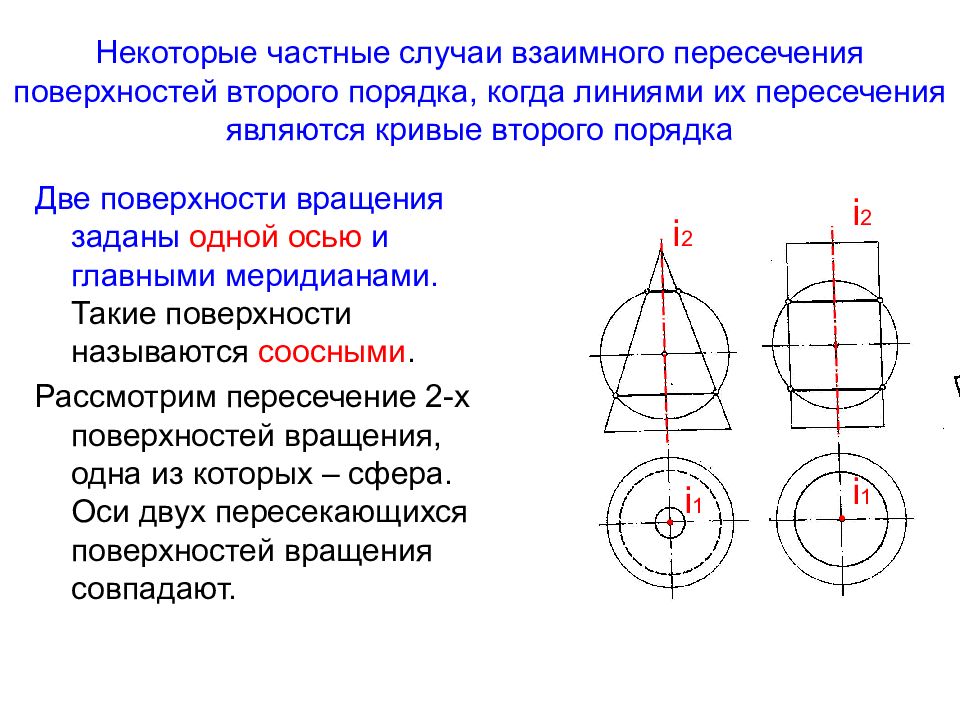
Две поверхности вращения заданы одной осью и главными меридианами. Такие поверхности называются соосными. Рассмотрим пересечение 2-х поверхностей вращения, одна из которых – сфера. Оси двух пересекающихся поверхностей вращения совпадают. ● ● i 2 i 2 i 1 i 1
Слайд 4
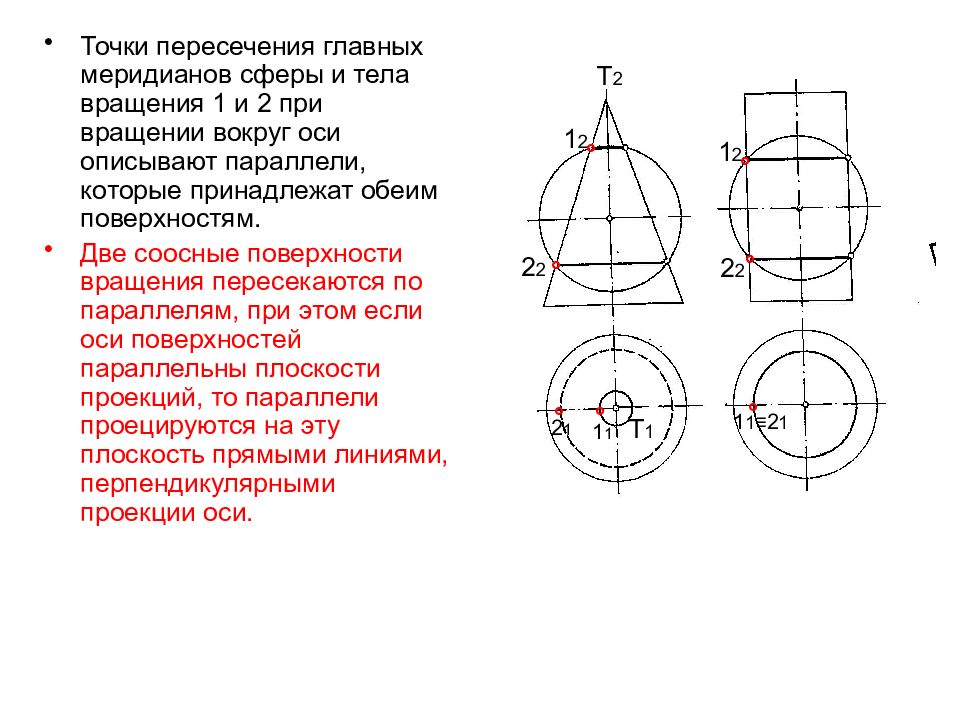
Точки пересечения главных меридианов сферы и тела вращения 1 и 2 при вращении вокруг оси описывают параллели, которые принадлежат обеим поверхностям. Две соосные поверхности вращения пересекаются по параллелям, при этом если оси поверхностей параллельны плоскости проекций, то параллели проецируются на эту плоскость прямыми линиями, перпендикулярными проекции оси. 1 2 2 2 1 2 2 2 Т 2 ° Т 1 1 1 ≡ 2 1 2 1 ° ° 1 1 ° ° ° °
Условия применимости метода концентрических сфер-посредников: Обе пересекающиеся поверхности являются поверхностями вращения. Оси поверхностей пересекаются Поверхности имеют общую плоскость симметрии, параллельную одной из плоскостей проекций.
Слайд 6: Определение рабочей зоны сфер-посредников
Центр сфер выбирается в месте пересечения осей искомых поверхностей вращения Минимальный радиус выбирается так, чтобы сфера касалась обеих поверхностей, или касалась одной и пересекала другую Максимальный радиус равен наибольшему расстоянию от центра сферы до точки наложенных сечений главных меридианов искомых поверхностей
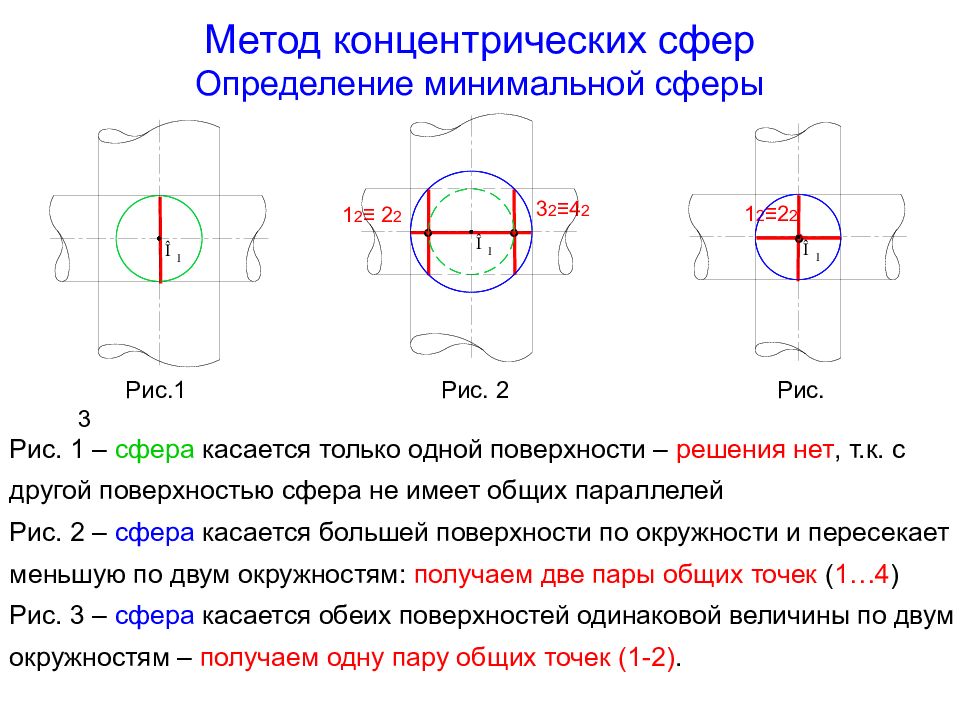
Слайд 7: Метод концентрических сфер Определение минимальной сферы
Рис.1 Рис. 2 Рис. 3 Рис. 1 – сфера касается только одной поверхности – решения нет, т.к. с другой поверхностью сфера не имеет общих параллелей Рис. 2 – сфера касается большей поверхности по окружности и пересекает меньшую по двум окружностям: получаем две пары общих точек ( 1…4 ) Рис. 3 – сфера касается обеих поверхностей одинаковой величины по двум окружностям – получаем одну пару общих точек (1-2). 1 2 ≡ 2 2 3 2 ≡4 2 1 2 ≡2 2 ° ° ° °
Слайд 8
Пересечение поверхностей вращения методом концентрических сфер Задача: Определить линию пересечения конуса и цилиндра Решение: Рассекаем поверхности плоскостью α ┴П1, проходящей по плоскости симметрии поверхностей (по главным меридианам). При пересечении очерков поверхностей получаем фронтальные проекции точек 1 2 и 2 2. Находим горизонтальные проекции этих точек с учетом видимости. 1 2 α 1 х ° ° ● ●
Слайд 9
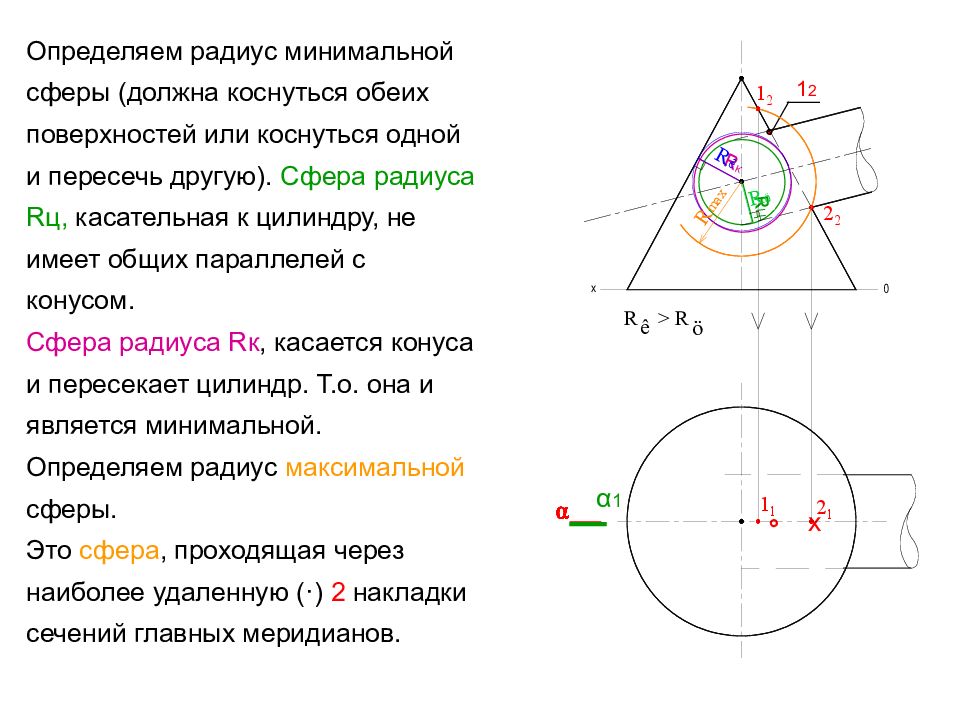
Определяем радиус минимальной сферы (должна коснуться обеих поверхностей или коснуться одной и пересечь другую). Сфера радиуса R ц, касательная к цилиндру, не имеет общих параллелей с конусом. Сфера радиуса R к, касается конуса и пересекает цилиндр. Т.о. она и является минимальной. Определяем радиус максимальной сферы. Это сфера, проходящая через наиболее удаленную ( · ) 2 накладки сечений главных меридианов. 1 2 α 1 х ° R ц R к
Слайд 10
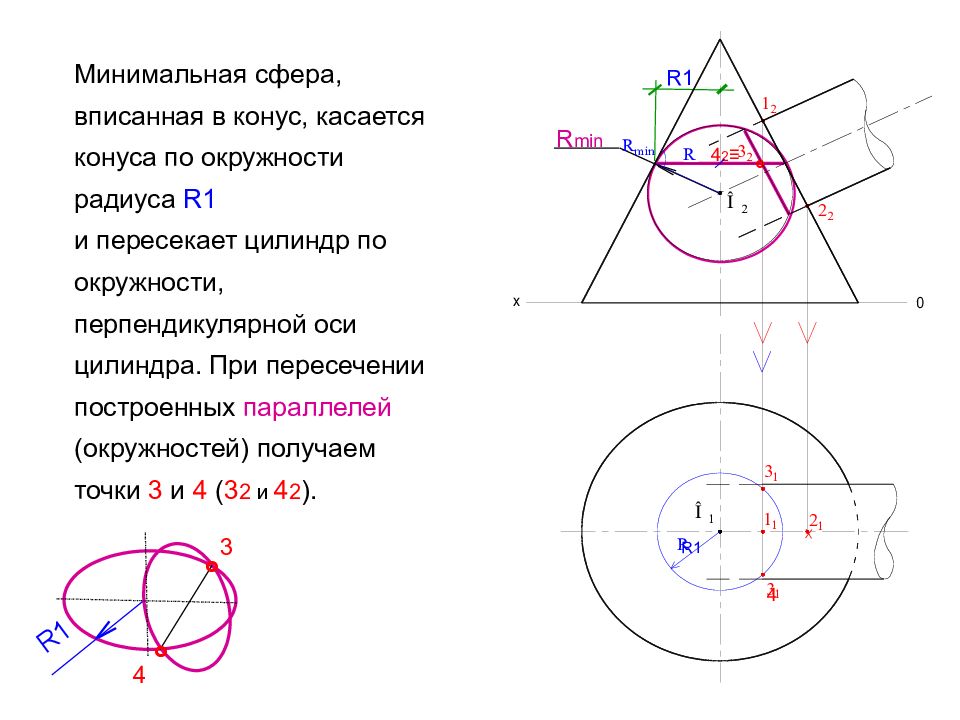
Минимальная сфера, вписанная в конус, касается конуса по окружности радиуса R 1 и пересекает цилиндр по окружности, перпендикулярной оси цилиндра. При пересечении построенных параллелей (окружностей) получаем точки 3 и 4 ( 3 2 и 4 2 ). х ° 4 2 ≡ 4 R min R1 R1 3 4 ° ° R 1
Слайд 11
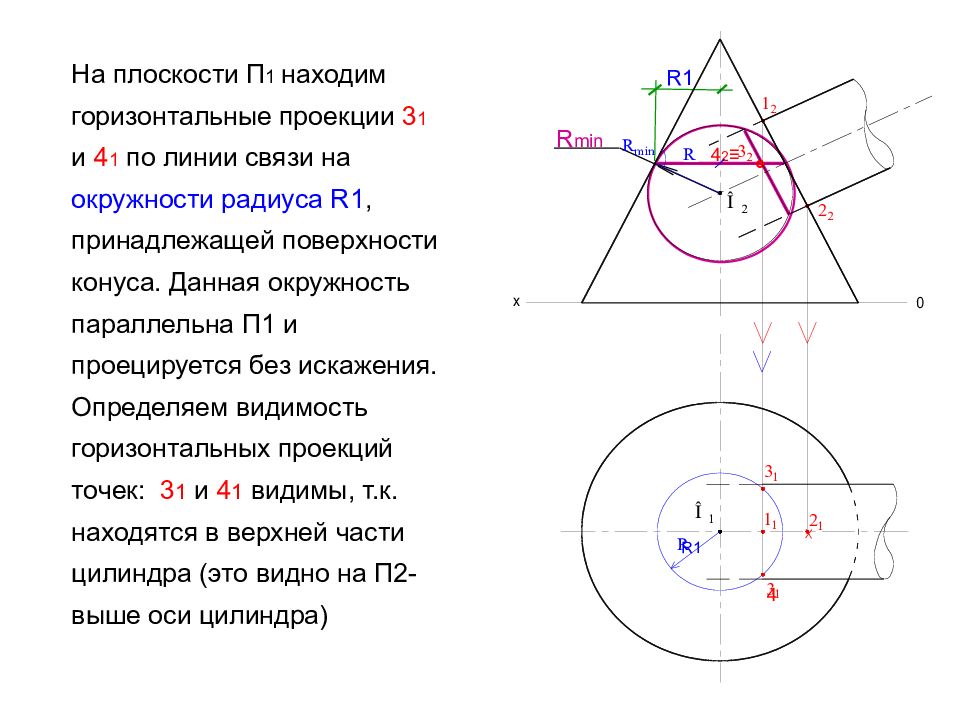
На плоскости П 1 находим горизонтальные проекции 3 1 и 4 1 по линии связи на окружности радиуса R 1, принадлежащей поверхности конуса. Данная окружность параллельна П1 и проецируется без искажения. Определяем видимость горизонтальных проекций точек: 3 1 и 4 1 видимы, т.к. находятся в верхней части цилиндра (это видно на П2- выше оси цилиндра) х ° 4 2 ≡ 4 R min R1 R1
Слайд 12
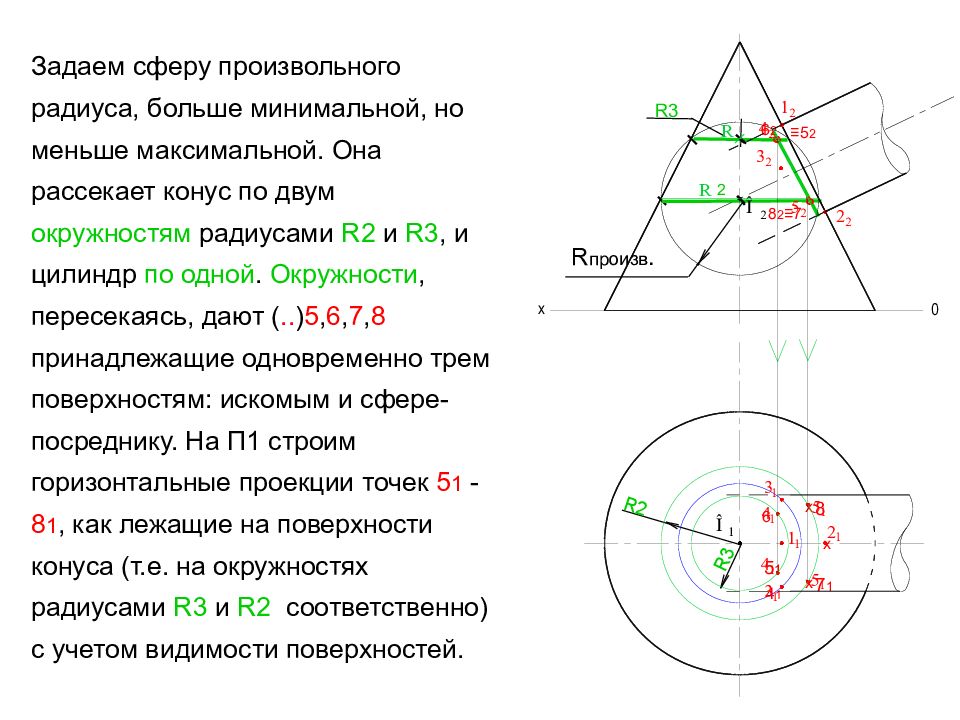
Задаем сферу произвольного радиуса, больше минимальной, но меньше максимальной. Она рассекает конус по двум окружностям радиусами R 2 и R 3, и цилиндр по одной. Окружности, пересекаясь, дают (.. ) 5, 6, 7, 8 принадлежащие одновременно трем поверхностям: искомым и сфере-посреднику. На П1 строим горизонтальные проекции точек 5 1 - 8 1, как лежащие на поверхности конуса (т.е. на окружностях радиусами R 3 и R 2 соответственно) с учетом видимости поверхностей. х х х 2 3 R произв. ° ° R2 R3 5 1 8 7 1 R3 ≡ 5 2 8 2 ≡7 6 2 6 4 1
Слайд 13
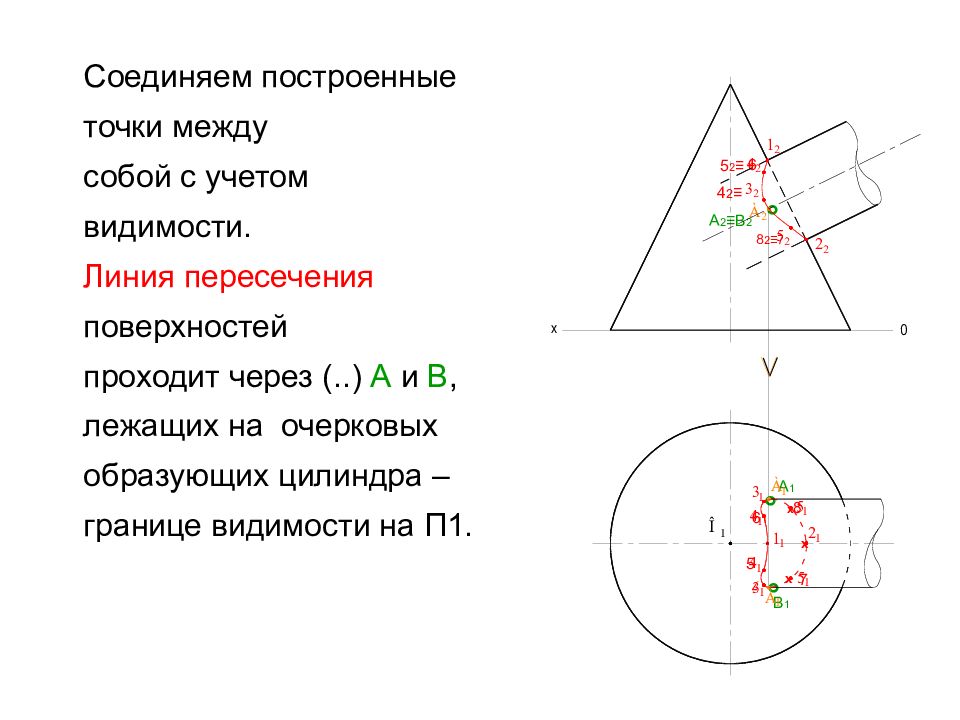
Соединяем построенные точки между собой с учетом видимости. Линия пересечения поверхностей проходит через (.. ) А и В, лежащих на очерковых образующих цилиндра – границе видимости на П1. 5 2 ≡ 8 2 ≡7 5 8 7 1 х х х ° ° ° А 1 В 1 А 2 ≡В 2 6 4 2 ≡ 4 6 1
Слайд 14
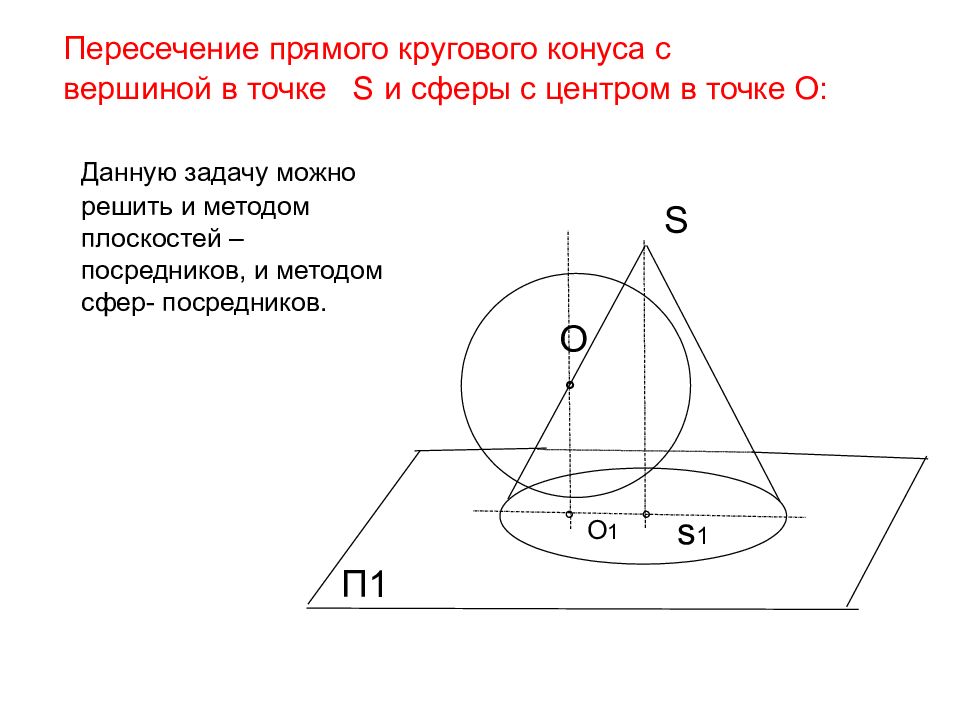
S Пересечение прямого кругового конуса с вершиной в точке S и сферы с центром в точке О: O П1 ° Данную задачу можно решить и методом плоскостей –посредников, и методом сфер- посредников. ° s 1 ° O 1
Слайд 15
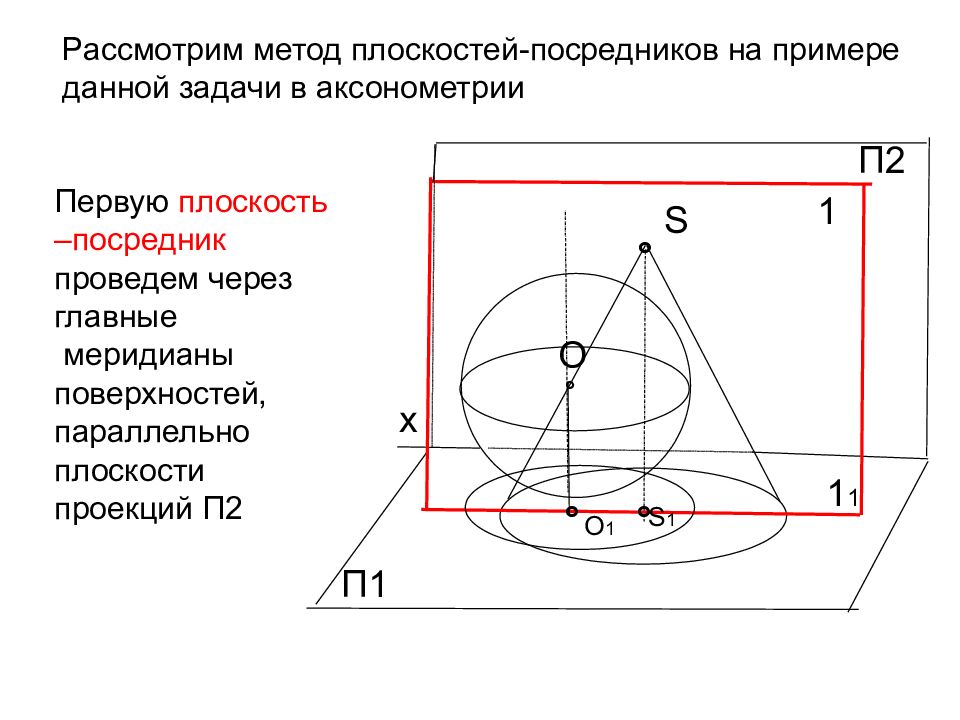
S Рассмотрим метод плоскостей-посредников на примере данной задачи в аксонометрии O П1 ° О 1 S 1 1 Первую плоскость –посредник проведем через главные меридианы поверхностей, параллельно плоскости проекций П2 П2 х 1 1 ° ° °
Слайд 16
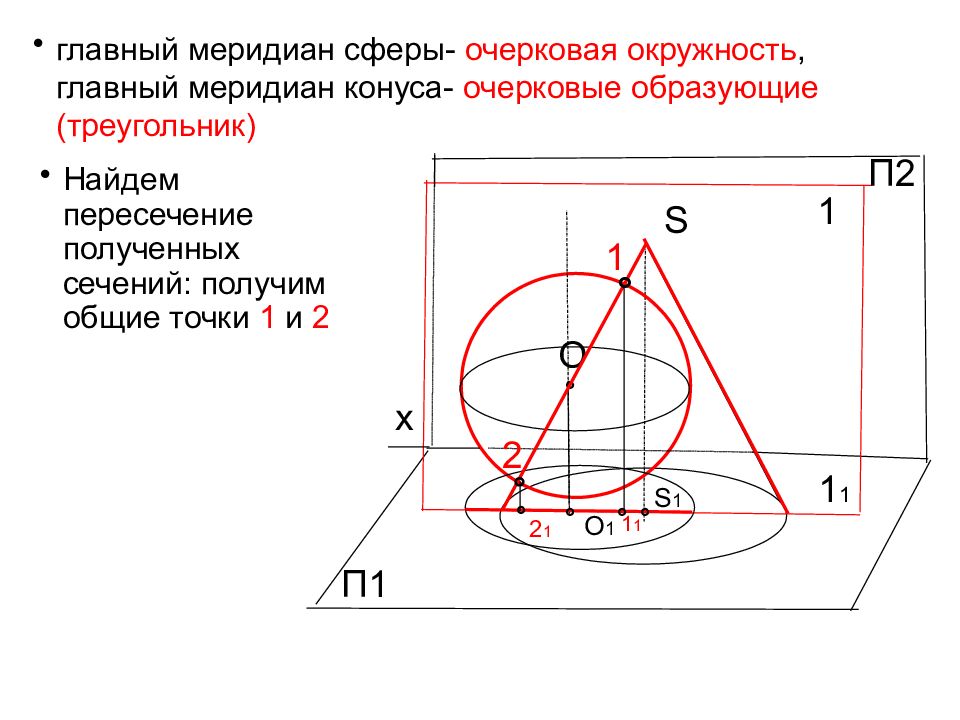
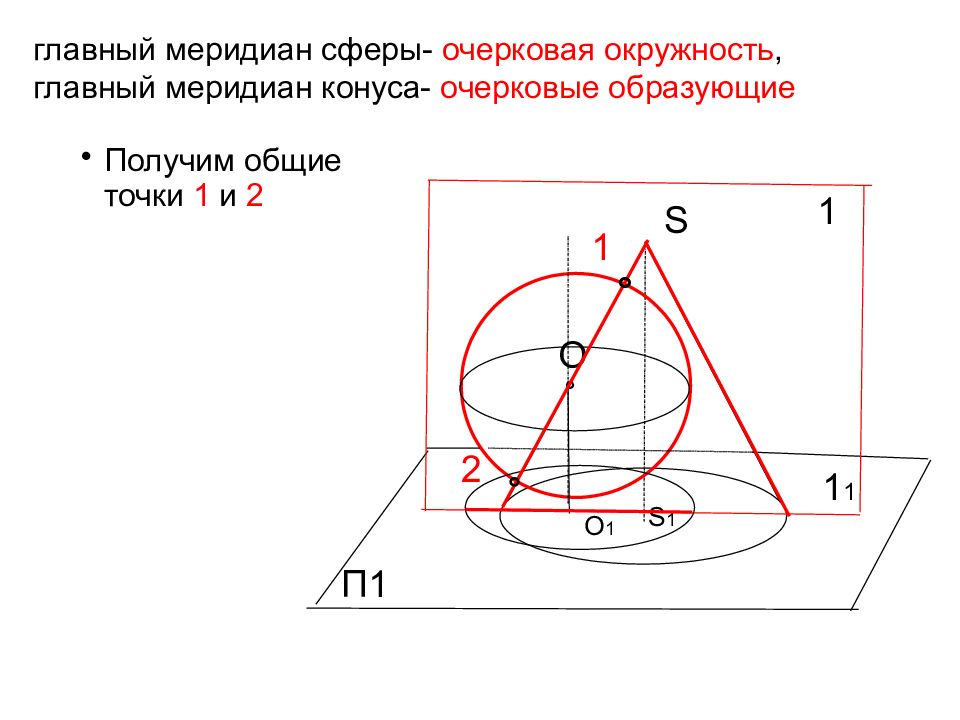
S главный меридиан сферы- очерковая окружность, главный меридиан конуса- очерковые образующие (треугольник) O П1 ° Найдем пересечение полученных сечений: получим общие точки 1 и 2 О 1 S 1 1 ° 1 2 ° х П2 1 1 2 1 1 1 ° ° ° °
Слайд 17
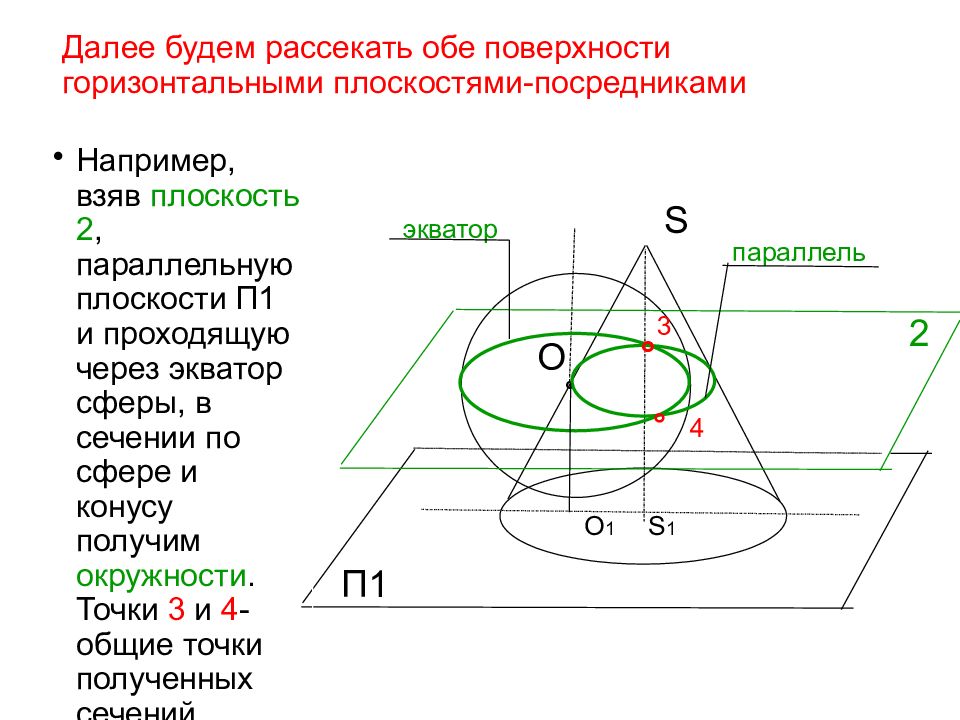
S Далее будем рассекать обе поверхности горизонтальными плоскостями-посредниками O П1 ° Например, взяв плоскость 2, параллельную плоскости П1 и проходящую через экватор сферы, в сечении по сфере и конусу получим окружности. Точки 3 и 4 - общие точки полученных сечений О 1 S 1 2 ° 3 4 ° экватор параллель
Слайд 18
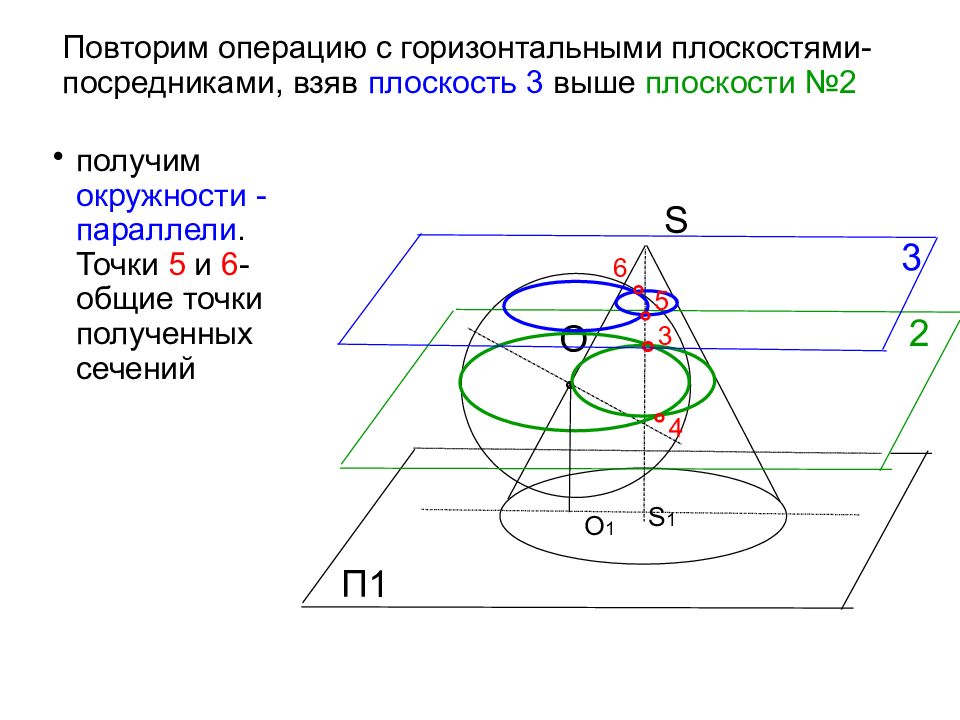
S Повторим операцию с горизонтальными плоскостями-посредниками, взяв плоскость 3 выше плоскости №2 O П1 ° получим окружности - параллели. Точки 5 и 6 - общие точки полученных сечений О 1 S 1 2 ° 3 4 ° 3 ° 5 ° 6
Слайд 19
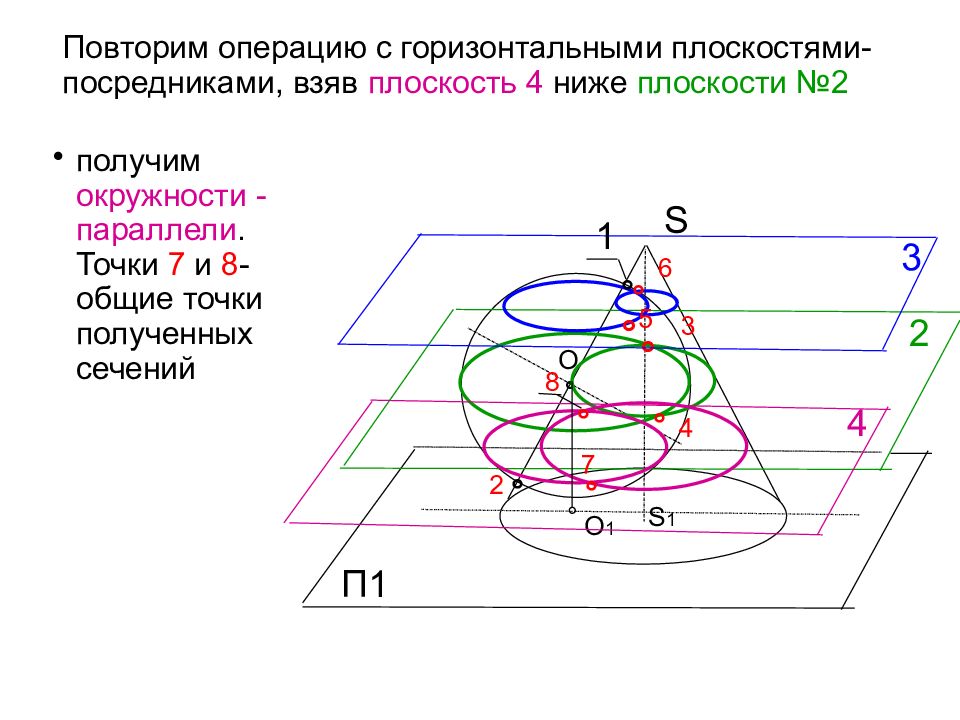
S Повторим операцию с горизонтальными плоскостями-посредниками, взяв плоскость 4 ниже плоскости №2 O П1 ° получим окружности - параллели. Точки 7 и 8 - общие точки полученных сечений О 1 S 1 2 ° 3 4 ° 3 ° 7 ° 8 ° 5 ° ° ° 2 6 1 ° 4
Слайд 20
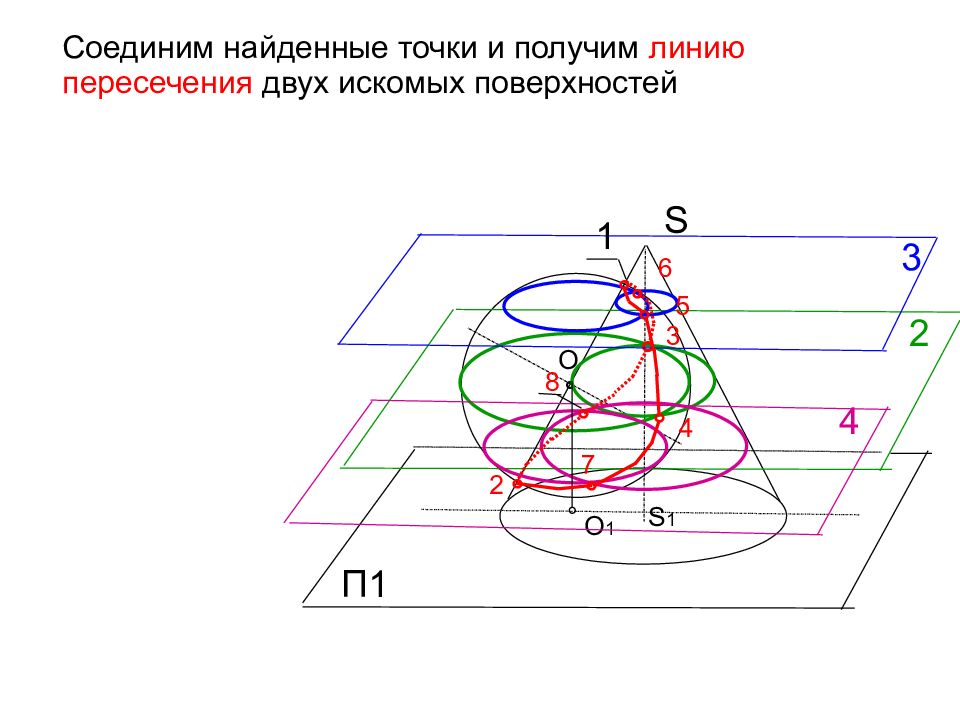
S Соединим найденные точки и получим линию пересечения двух искомых поверхностей O П1 ° О 1 S 1 2 ° 3 4 ° 3 ° 7 ° 8 ° 5 ° ° 2 6 1 ° ° 4
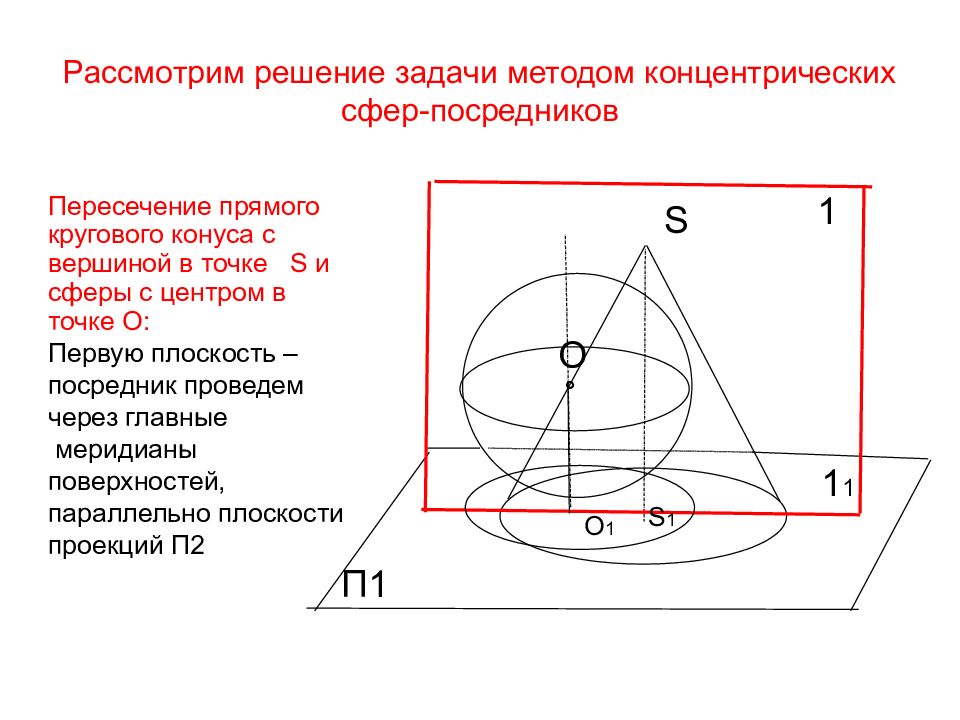
Слайд 21: Рассмотрим решение задачи методом концентрических сфер-посредников
S O П1 ° О 1 S 1 1 Пересечение прямого кругового конуса с вершиной в точке S и сферы с центром в точке О: Первую плоскость –посредник проведем через главные меридианы поверхностей, параллельно плоскости проекций П2 Рассмотрим решение задачи методом концентрических сфер-посредников 1 1
Слайд 22
S главный меридиан сферы- очерковая окружность, главный меридиан конуса- очерковые образующие O П1 ° Получим общие точки 1 и 2 О 1 S 1 1 ° 1 2 ° 1 1
Слайд 23
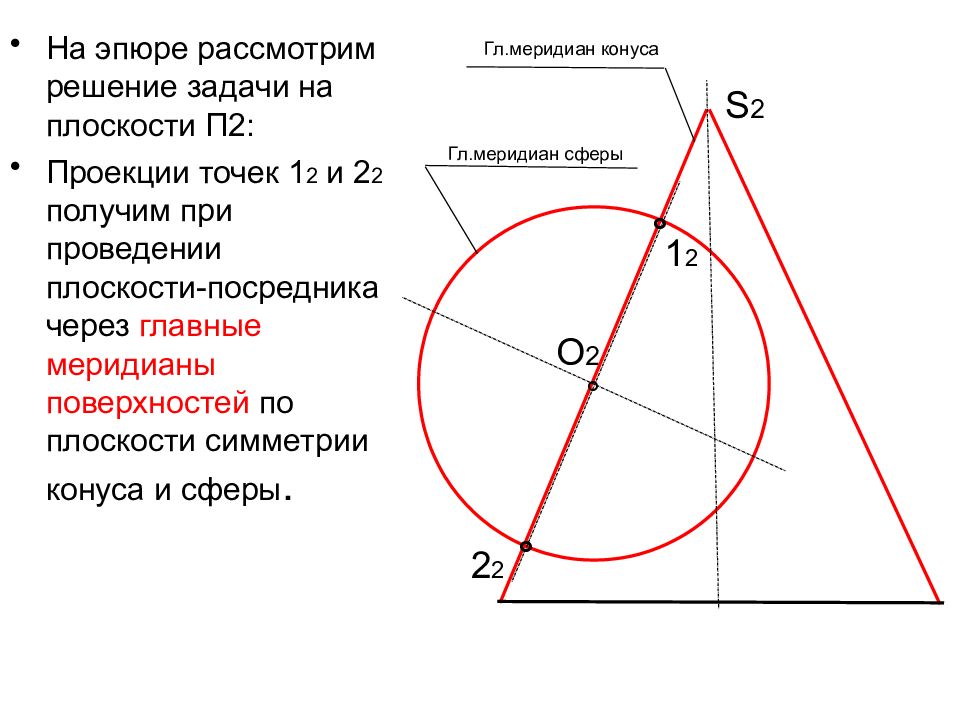
На эпюре рассмотрим решение задачи на плоскости П2: Проекции точек 1 2 и 2 2 получим при проведении плоскости-посредника через главные меридианы поверхностей по плоскости симметрии конуса и сферы. S 2 O 2 ° Гл.меридиан конуса Гл.меридиан сферы ° ° 1 2 2 2
Слайд 24
Т.к. обе поверхности являются поверхностями вращения, они соосны и оси обеих поверхностей параллельны П2-можем применить метод концентрических сфер-посредников. Центр сфер- в точке пересечения осей- (.) S S 2 O 2 ° Гл.меридиан конуса Гл.меридиан сферы ° ° 1 2 2 2
Слайд 25
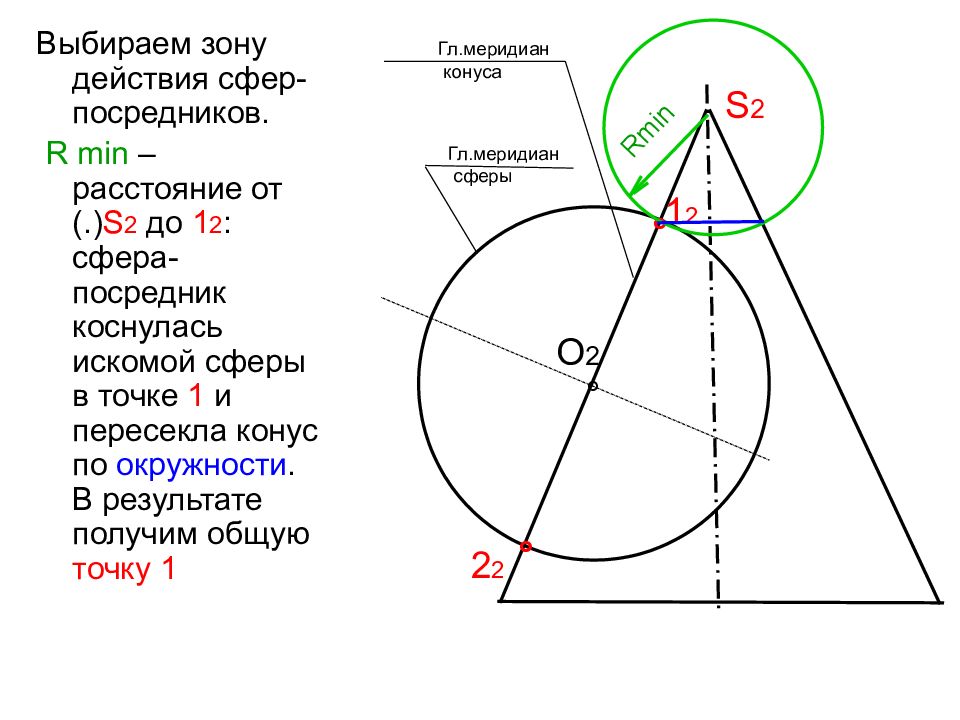
Выбираем зону действия сфер-посредников. R min – расстояние от (.) S 2 до 1 2 : сфера-посредник коснулась искомой сферы в точке 1 и пересекла конус по окружности. В результате получим общую точку 1 S 2 O 2 ° Гл.меридиан конуса Гл.меридиан сферы ° ° 1 2 2 2 Rmin
Слайд 26
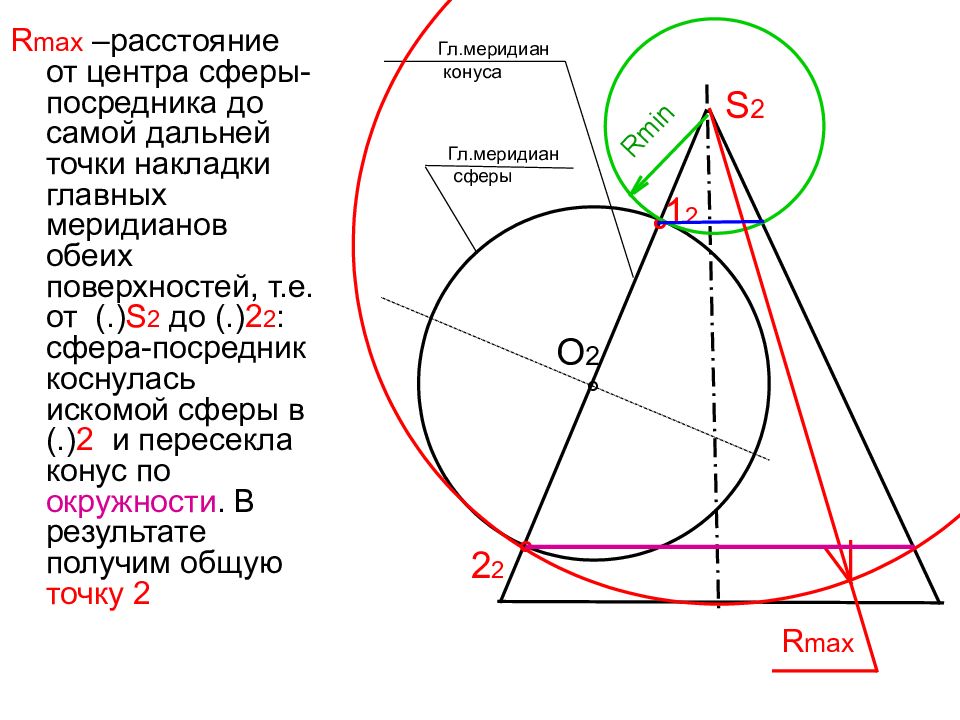
R max –расстояние от центра сферы-посредника до самой дальней точки накладки главных меридианов обеих поверхностей, т.е. от (.) S 2 до (.) 2 2 : сфера-посредник коснулась искомой сферы в (.) 2 и пересекла конус по окружности. В результате получим общую точку 2 S 2 O 2 ° Гл.меридиан конуса Гл.меридиан сферы ° ° 1 2 2 2 Rmin R max
Слайд 27
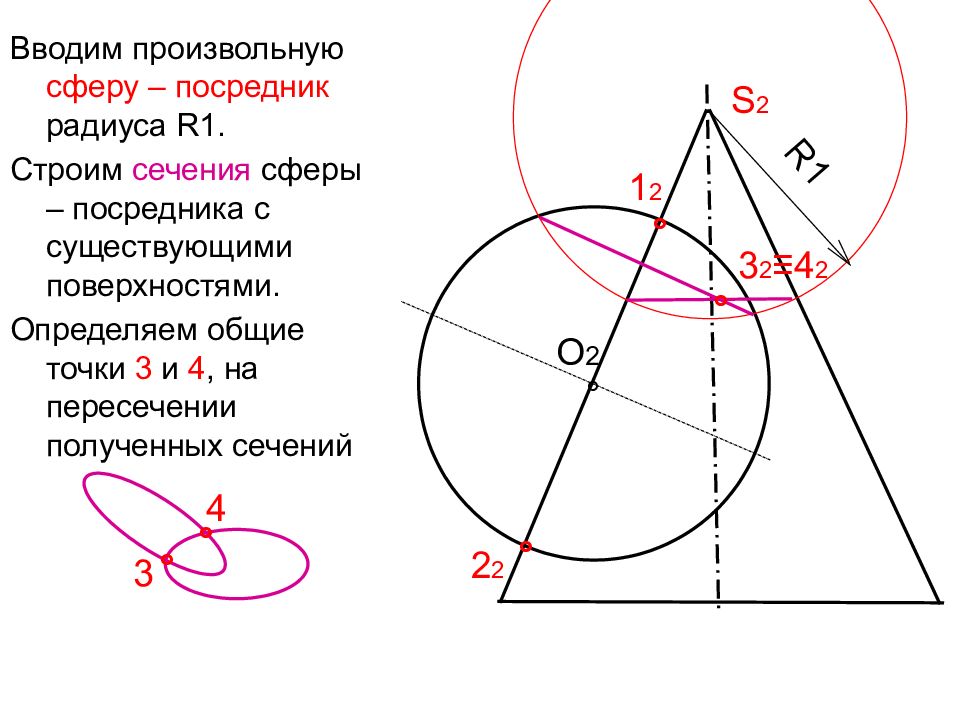
Вводим произвольную сферу – посредник радиуса R1. Строим сечения сферы – посредника с существующими поверхностями. Определяем общие точки 3 и 4, на пересечении полученных сечений O 2 ° ° ° 1 2 2 2 S 2 R1 ° 3 ° 4 ° 3 2 ≡4 2
Слайд 28
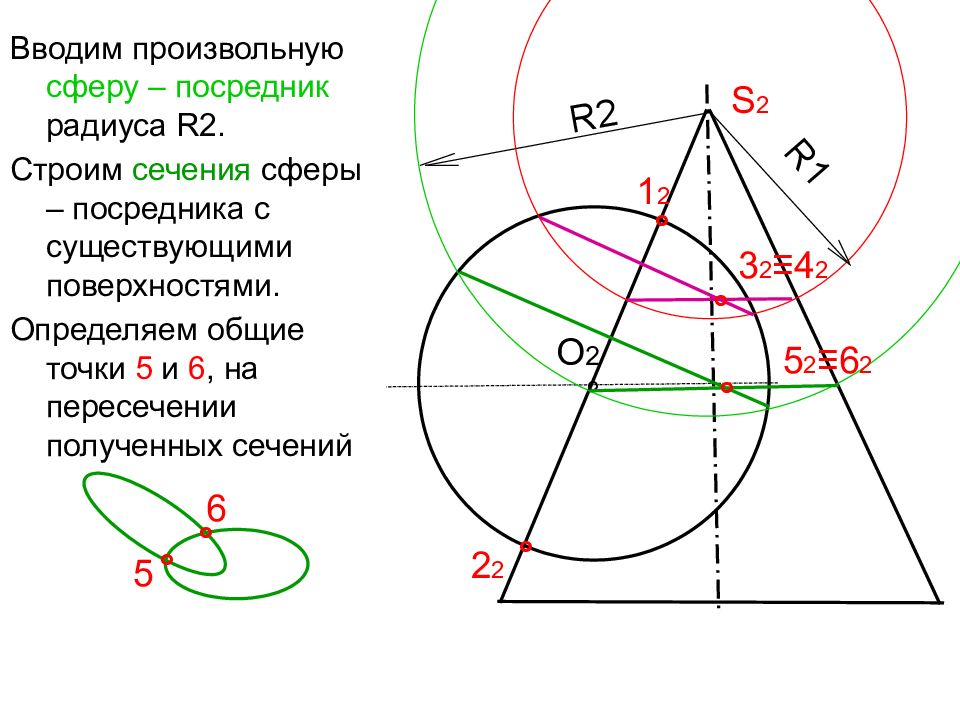
Вводим произвольную сферу – посредник радиуса R 2. Строим сечения сферы – посредника с существующими поверхностями. Определяем общие точки 5 и 6, на пересечении полученных сечений O 2 ° ° ° 1 2 2 2 S 2 R1 ° 5 ° 6 ° 3 2 ≡4 2 R2 ° 5 2 ≡ 6 2
Слайд 29
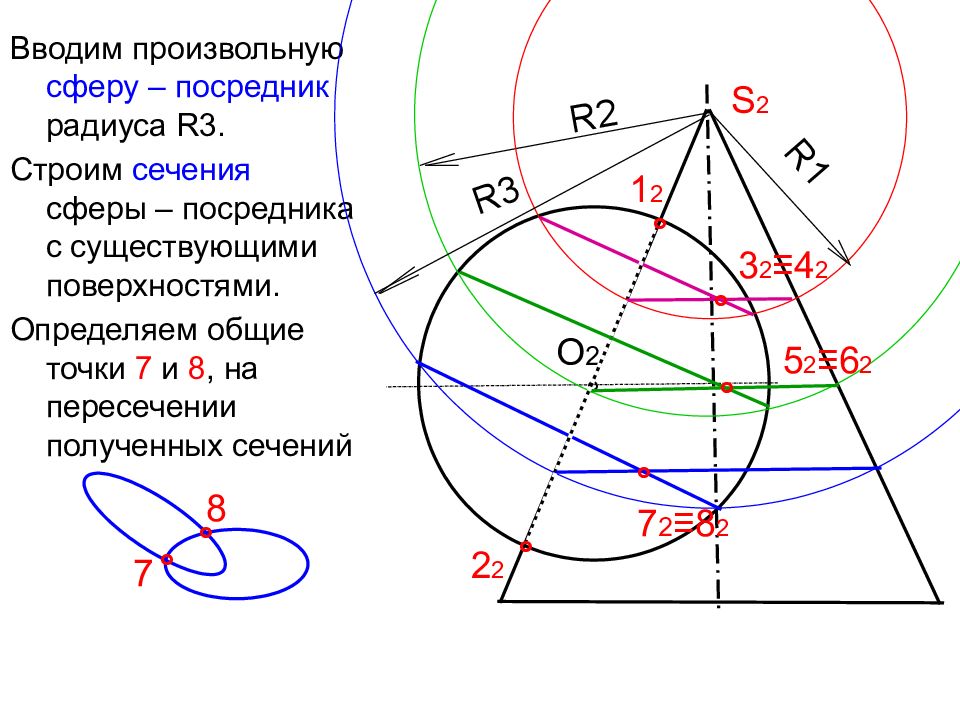
Вводим произвольную сферу – посредник радиуса R3. Строим сечения сферы – посредника с существующими поверхностями. Определяем общие точки 7 и 8, на пересечении полученных сечений O 2 ° ° ° 1 2 2 2 S 2 R1 ° 7 ° 8 ° 3 2 ≡4 2 R2 ° 5 2 ≡ 6 2 R3 ° 7 2 ≡ 8 2
Слайд 30
Соединим найденные точки 1-8, принадлежащие обеим искомым поверхностям. Получим линию пересечения (перехода) сферы и конуса. O 2 ° ° ° 1 2 2 2 S 2 R1 ° 3 2 ≡4 2 R2 ° 5 2 ≡ 6 2 R3 ° 7 2 ≡ 8 2
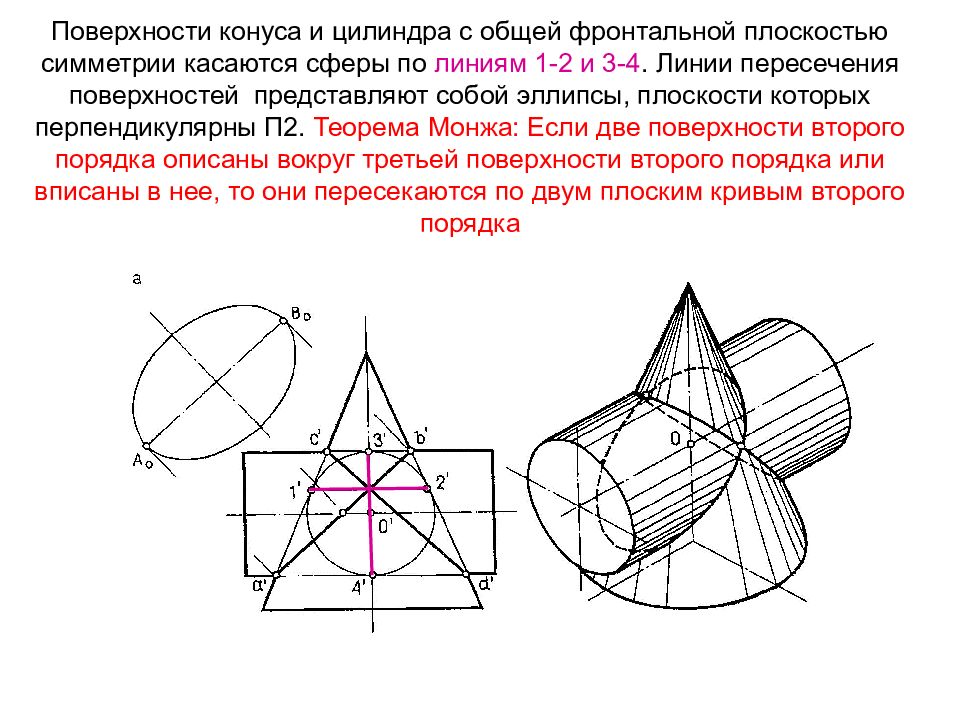
Слайд 31: Поверхности конуса и цилиндра с общей фронтальной плоскостью симметрии касаются сферы по линиям 1-2 и 3-4. Линии пересечения поверхностей представляют собой эллипсы, плоскости которых перпендикулярны П2. Теорема Монжа: Если две поверхности второго порядка описаны вокруг третьей поверхности второго порядка или вписаны в нее, то они пересекаются по двум плоским кривым второго порядка
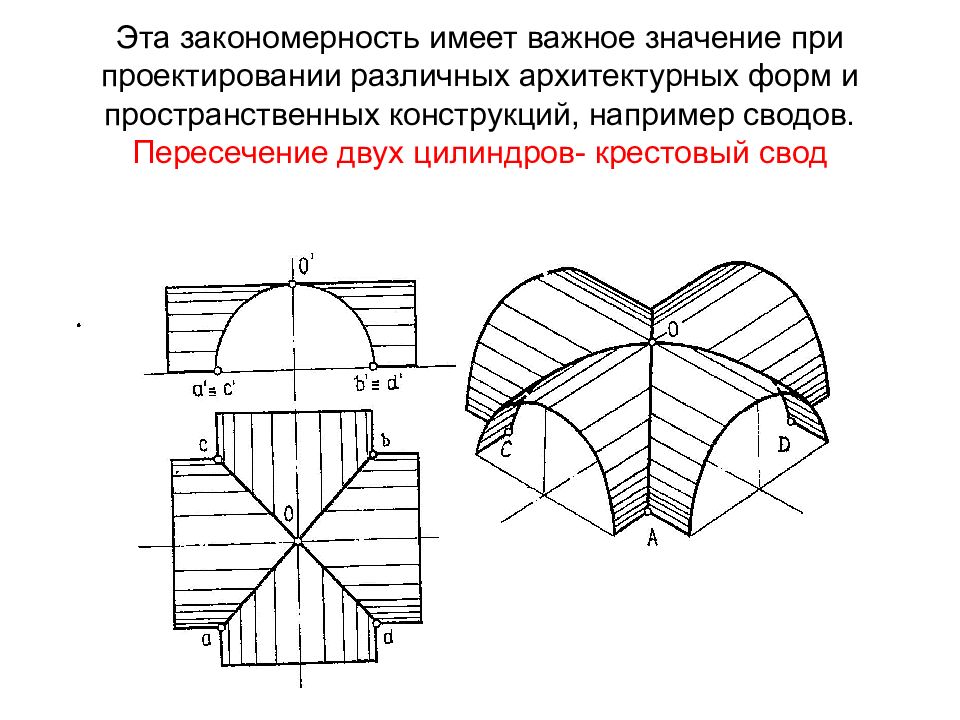
Слайд 32: Эта закономерность имеет важное значение при проектировании различных архитектурных форм и пространственных конструкций, например сводов. Пересечение двух цилиндров- крестовый свод
Слайд 33
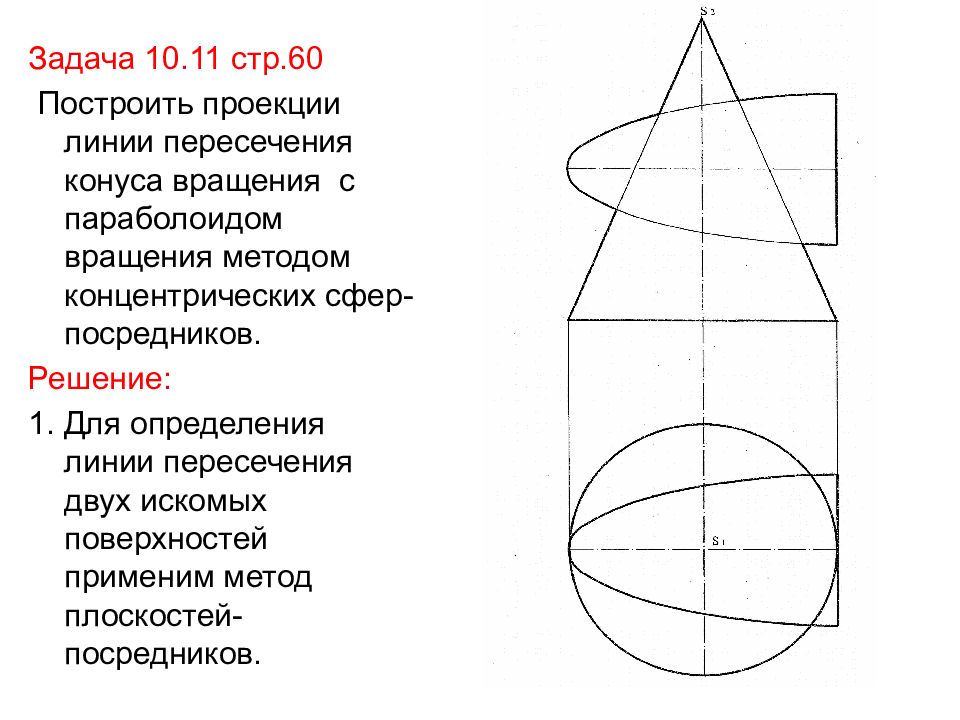
Задача 10.11 стр.60 Построить проекции линии пересечения конуса вращения с параболоидом вращения методом концентрических сфер-посредников. Решение: 1. Для определения линии пересечения двух искомых поверхностей применим метод плоскостей-посредников.
Слайд 34
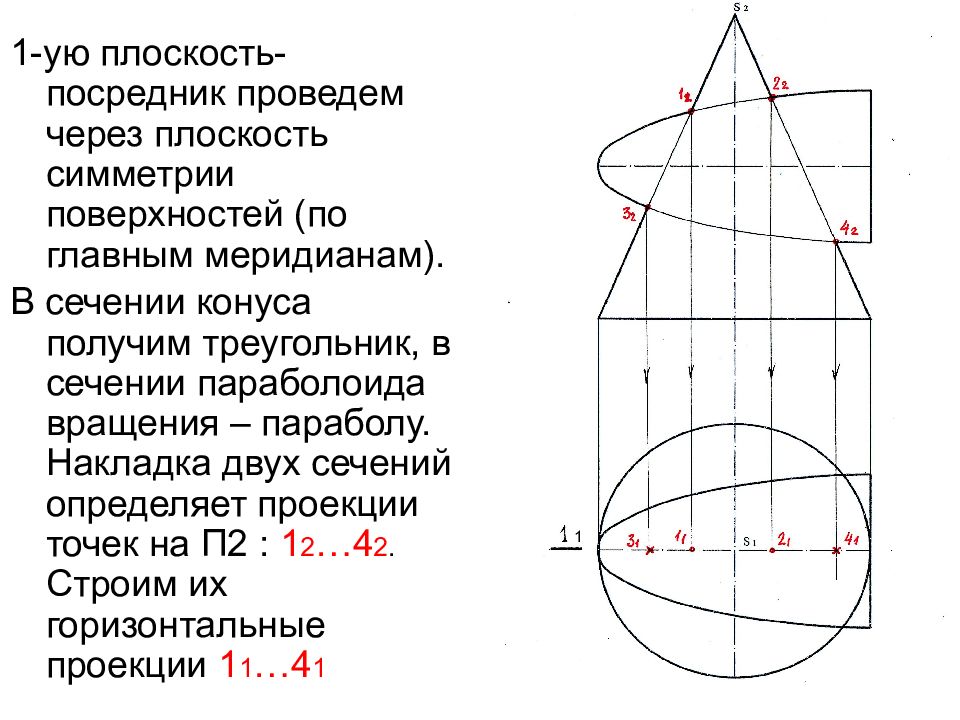
1-ую плоскость- посредник проведем через плоскость симметрии поверхностей (по главным меридианам). В сечении конуса получим треугольник, в сечении параболоида вращения – параболу. Накладка двух сечений определяет проекции точек на П2 : 1 2 …4 2. Строим их горизонтальные проекции 1 1 …4 1 1
Слайд 35
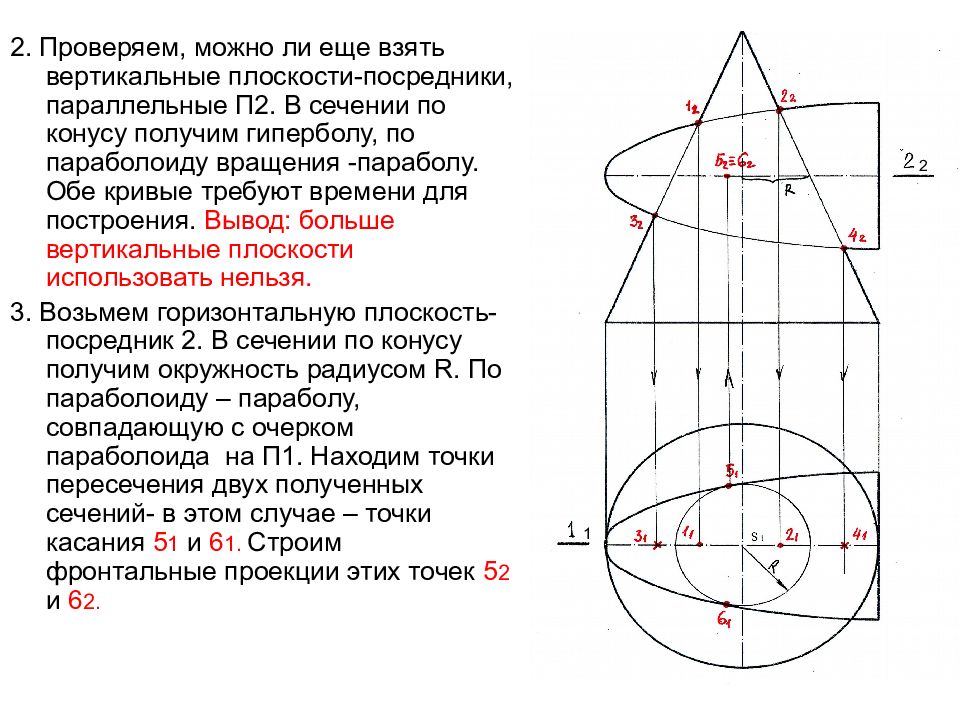
2. Проверяем, можно ли еще взять вертикальные плоскости-посредники, параллельные П2. В сечении по конусу получим гиперболу, по параболоиду вращения -параболу. Обе кривые требуют времени для построения. Вывод: больше вертикальные плоскости использовать нельзя. 3. Возьмем горизонтальную плоскость-посредник 2. В сечении по конусу получим окружность радиусом R. По параболоиду – параболу, совпадающую с очерком параболоида на П1. Находим точки пересечения двух полученных сечений- в этом случае – точки касания 5 1 и 6 1. Строим фронтальные проекции этих точек 5 2 и 6 2. 1 2
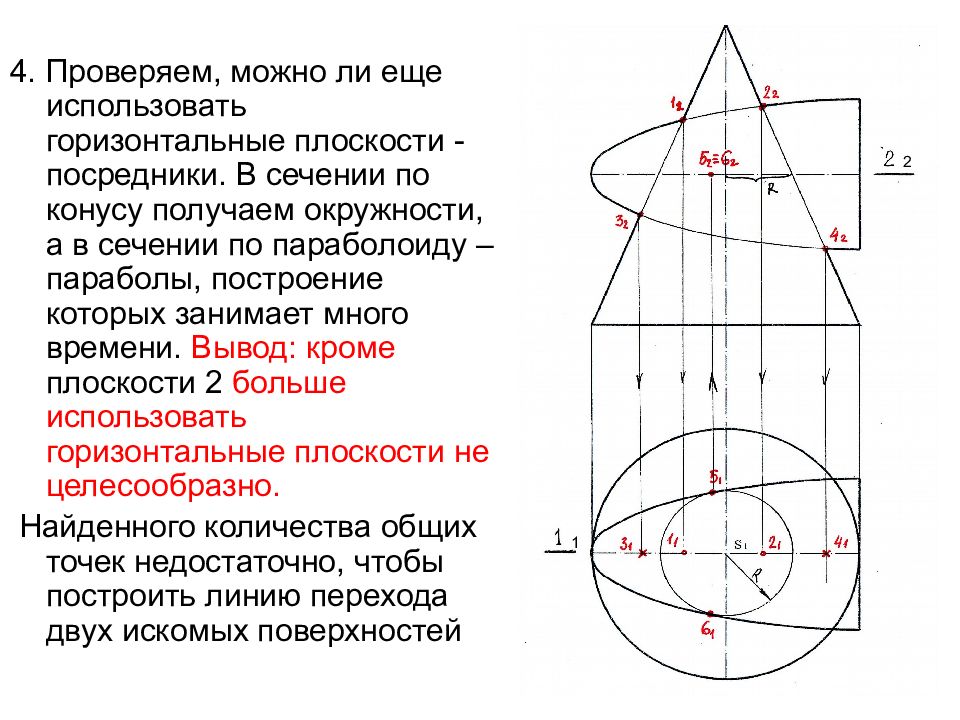
Слайд 36
4. Проверяем, можно ли еще использовать горизонтальные плоскости - посредники. В сечении по конусу получаем окружности, а в сечении по параболоиду – параболы, построение которых занимает много времени. Вывод: кроме плоскости 2 больше использовать горизонтальные плоскости не целесообразно. Найденного количества общих точек недостаточно, чтобы построить линию перехода двух искомых поверхностей 1 2
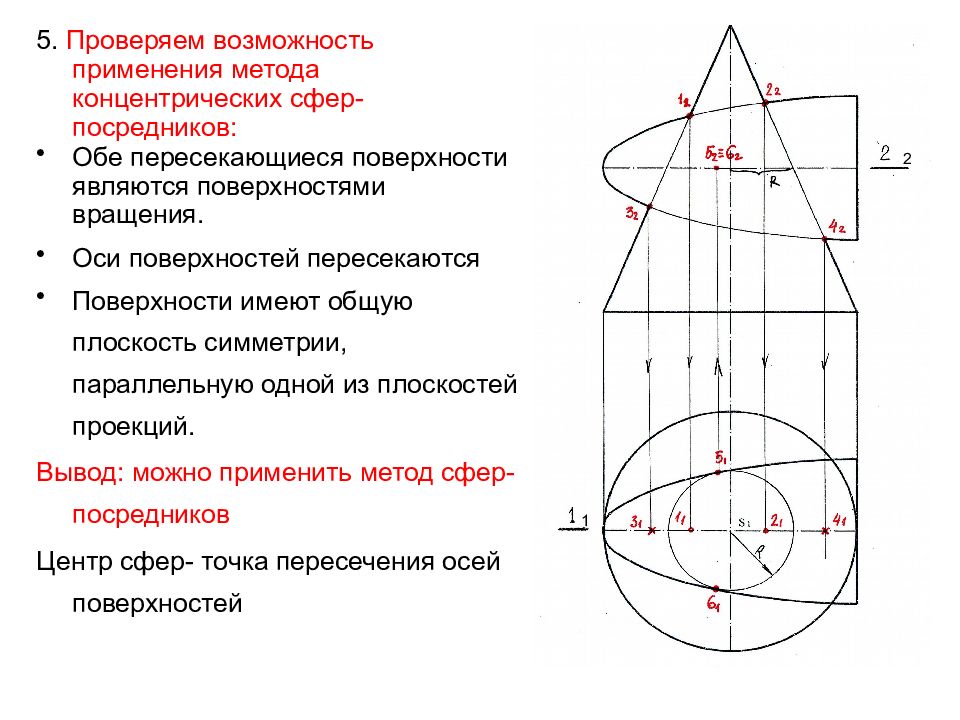
Слайд 37
5. Проверяем возможность применения метода концентрических сфер-посредников: Обе пересекающиеся поверхности являются поверхностями вращения. Оси поверхностей пересекаются Поверхности имеют общую плоскость симметрии, параллельную одной из плоскостей проекций. Вывод: можно применить метод сфер- посредников Центр сфер- точка пересечения осей поверхностей 1 2
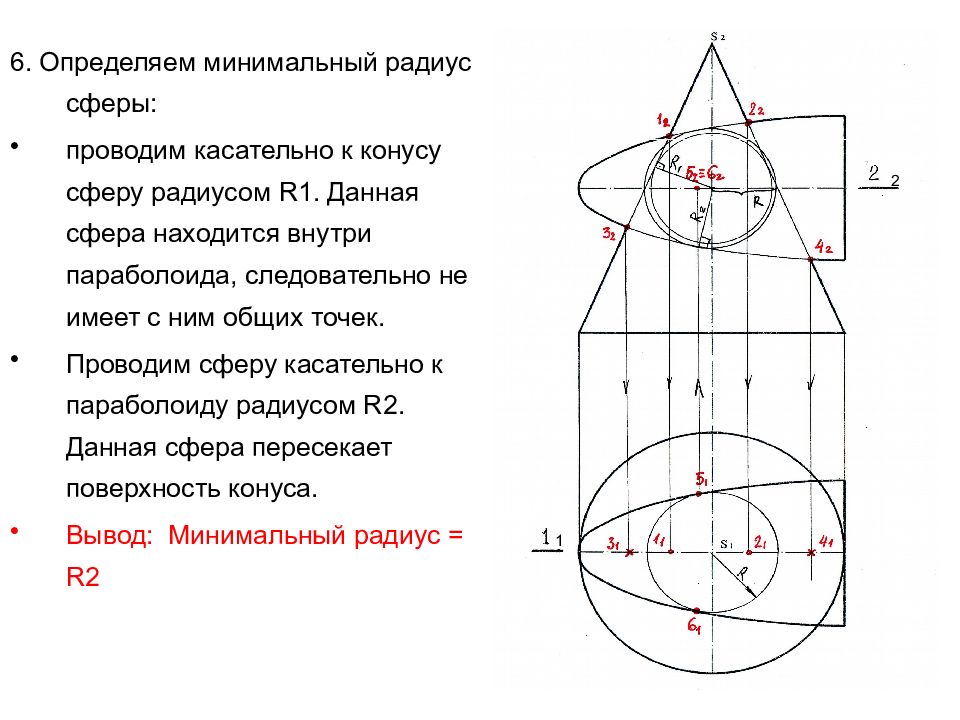
Слайд 38
6. Определяем минимальный радиус сферы: проводим касательно к конусу сферу радиусом R1. Данная сфера находится внутри параболоида, следовательно не имеет с ним общих точек. Проводим сферу касательно к параболоиду радиусом R 2. Данная сфера пересекает поверхность конуса. Вывод: Минимальный радиус = R 2 1 2
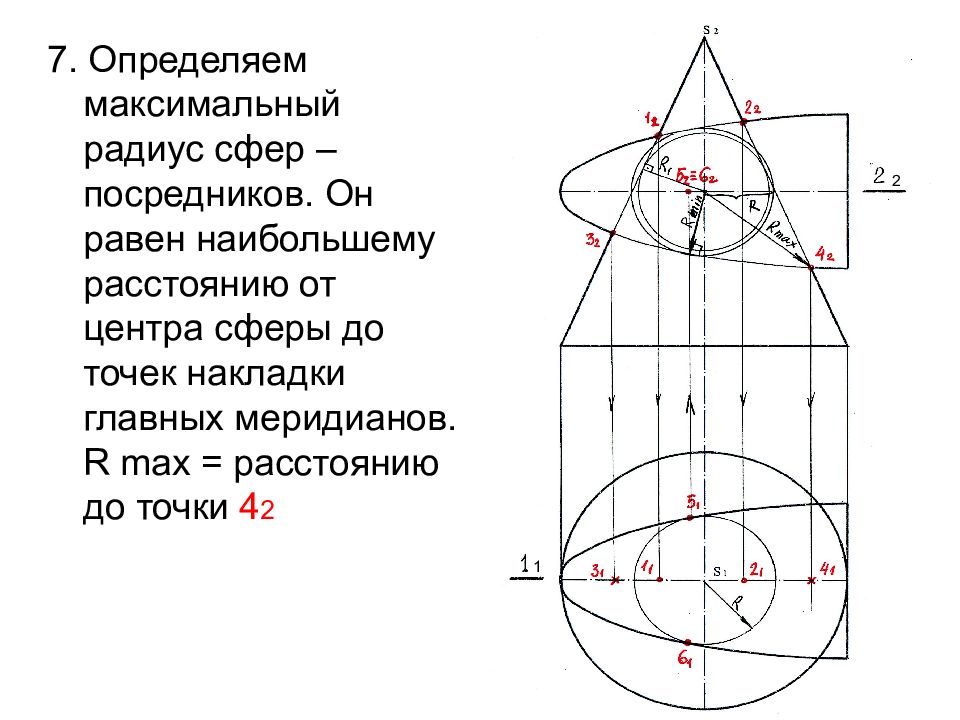
Слайд 39
7. Определяем максимальный радиус сфер – посредников. Он равен наибольшему расстоянию от центра сферы до точек накладки главных меридианов. R max = расстоянию до точки 4 2 1 2
Слайд 40
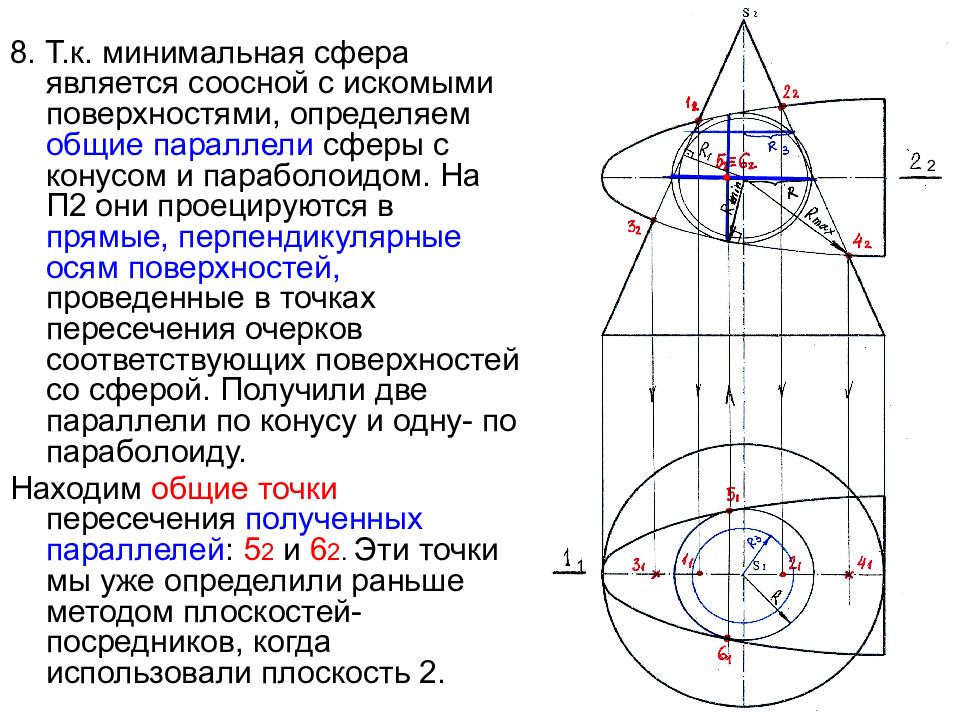
8. Т.к. минимальная сфера является соосной с искомыми поверхностями, определяем общие параллели сферы с конусом и параболоидом. На П2 они проецируются в прямые, перпендикулярные осям поверхностей, проведенные в точках пересечения очерков соответствующих поверхностей со сферой. Получили две параллели по конусу и одну- по параболоиду. Находим общие точки пересечения полученных параллелей : 5 2 и 6 2. Эти точки мы уже определили раньше методом плоскостей-посредников, когда использовали плоскость 2. 1 2 ●
Слайд 41
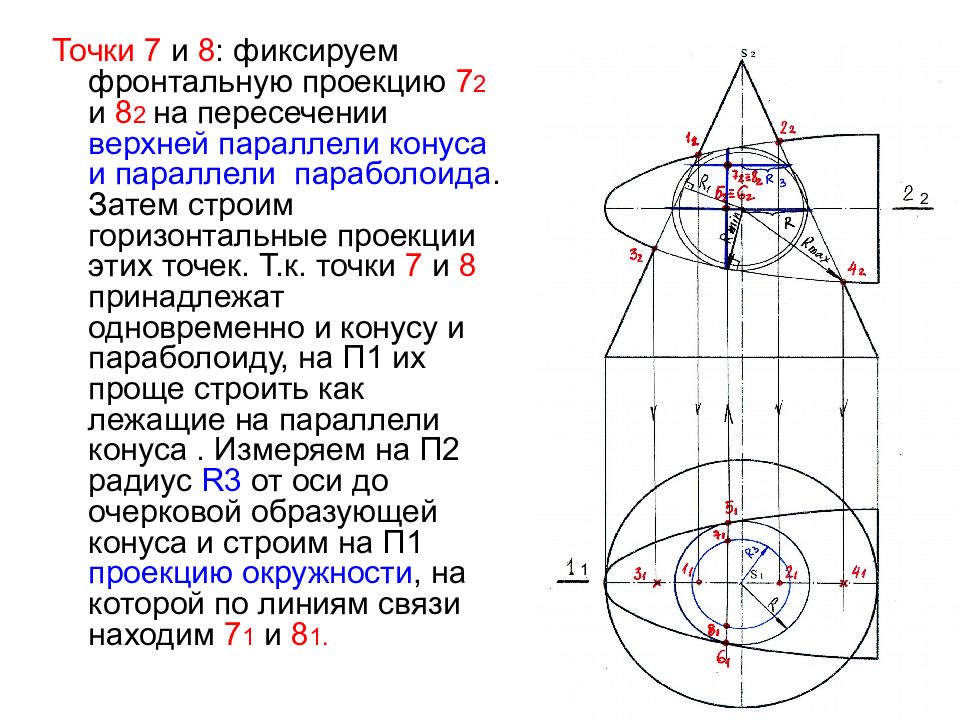
Точки 7 и 8 : фиксируем фронтальную проекцию 7 2 и 8 2 на пересечении верхней параллели конуса и параллели параболоида. Затем строим горизонтальные проекции этих точек. Т.к. точки 7 и 8 принадлежат одновременно и конусу и параболоиду, на П1 их проще строить как лежащие на параллели конуса. Измеряем на П2 радиус R3 от оси до очерковой образующей конуса и строим на П1 проекцию окружности, на которой по линиям связи находим 7 1 и 8 1. 2 1
Слайд 42
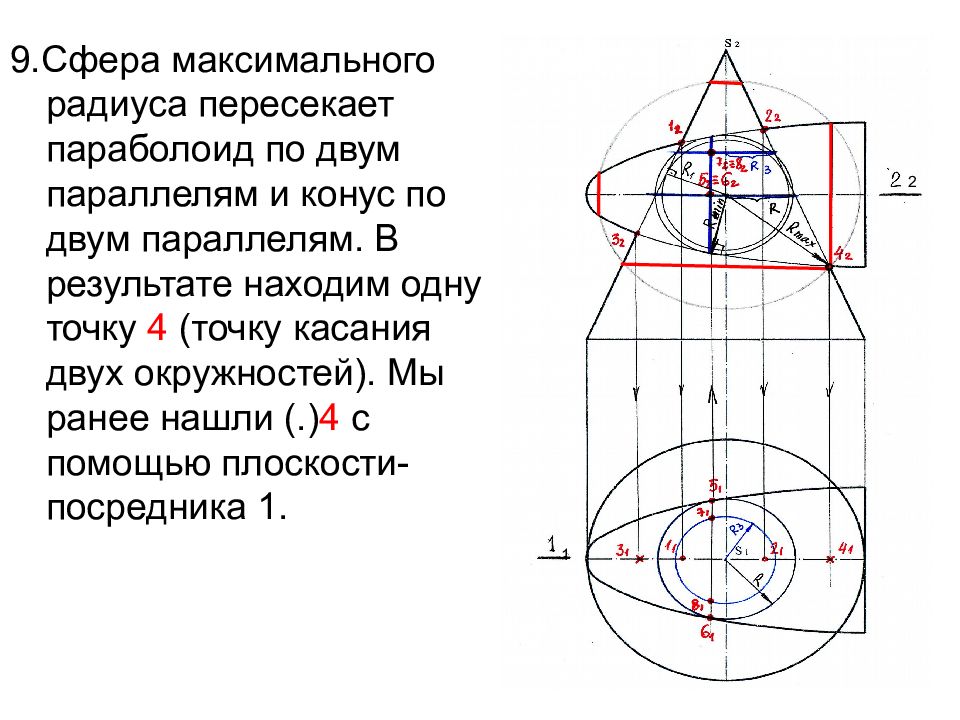
9.Сфера максимального радиуса пересекает параболоид по двум параллелям и конус по двум параллелям. В результате находим одну точку 4 (точку касания двух окружностей). Мы ранее нашли (.) 4 с помощью плоскости- посредника 1. ° 1 2
Слайд 43
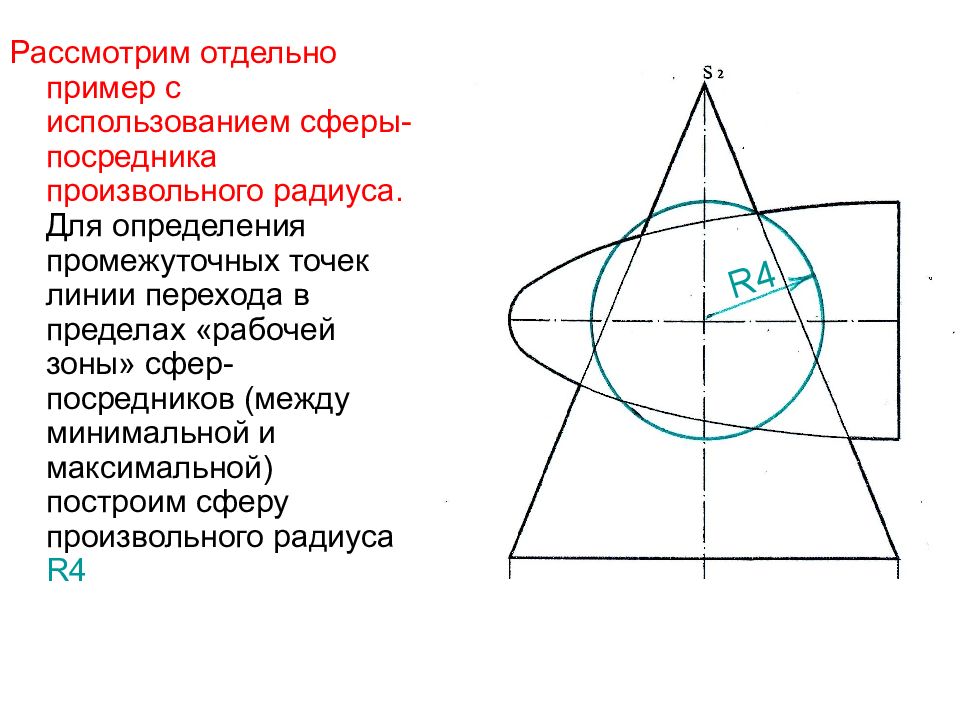
Рассмотрим отдельно пример с использованием сферы-посредника произвольного радиуса. Для определения промежуточных точек линии перехода в пределах «рабочей зоны» сфер - посредников (между минимальной и максимальной) построим сферу произвольного радиуса R4 R4
Слайд 44
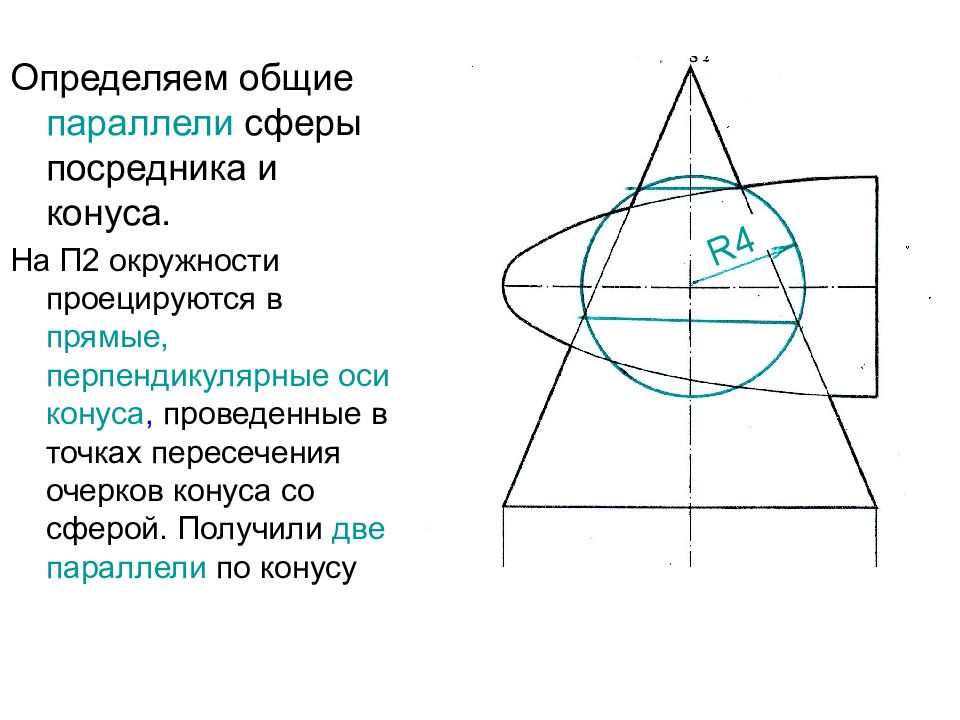
Определяем общие параллели сферы посредника и конуса. На П2 окружности проецируются в прямые, перпендикулярные оси конуса, проведенные в точках пересечения очерков конуса со сферой. Получили две параллели по конусу R4
Слайд 45
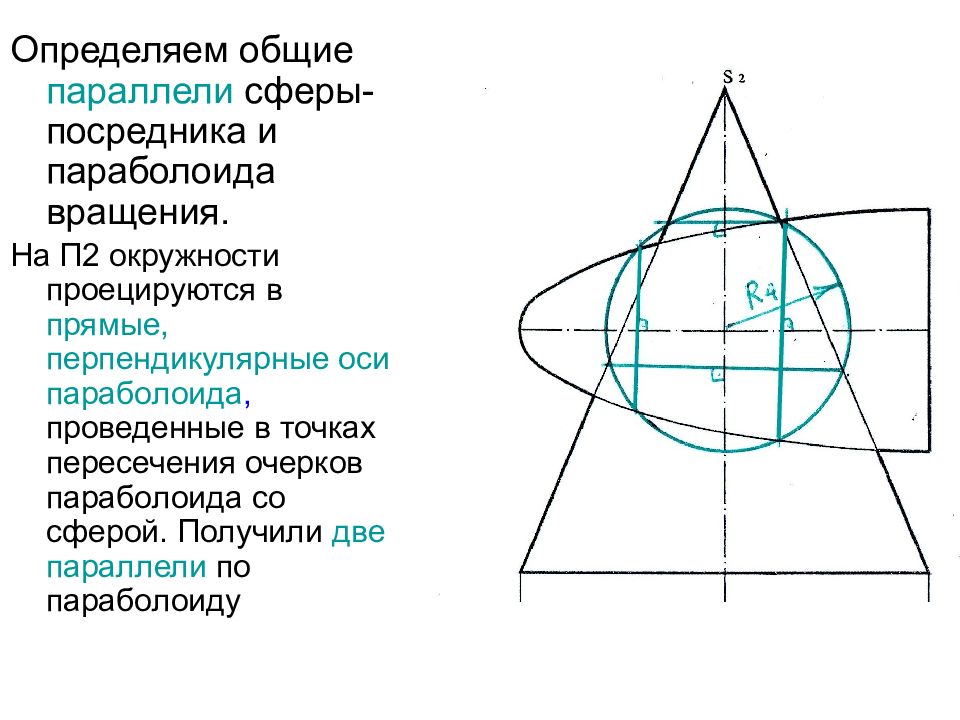
Определяем общие параллели сферы- посредника и параболоида вращения. На П2 окружности проецируются в прямые, перпендикулярные оси параболоида, проведенные в точках пересечения очерков параболоида со сферой. Получили две параллели по параболоиду
Слайд 46
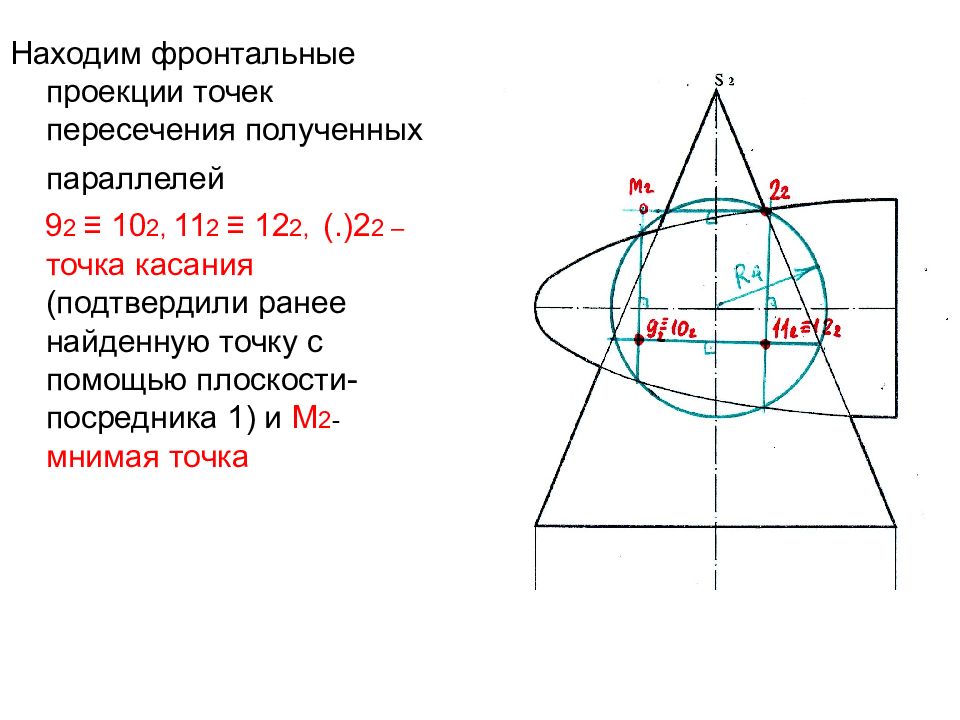
Находим фронтальные проекции точек пересечения полученных параллелей 9 2 ≡ 10 2, 11 2 ≡ 12 2, (.)2 2 – точка касания (подтвердили ранее найденную точку с помощью плоскости-посредника 1) и М 2 - мнимая точка
Слайд 47
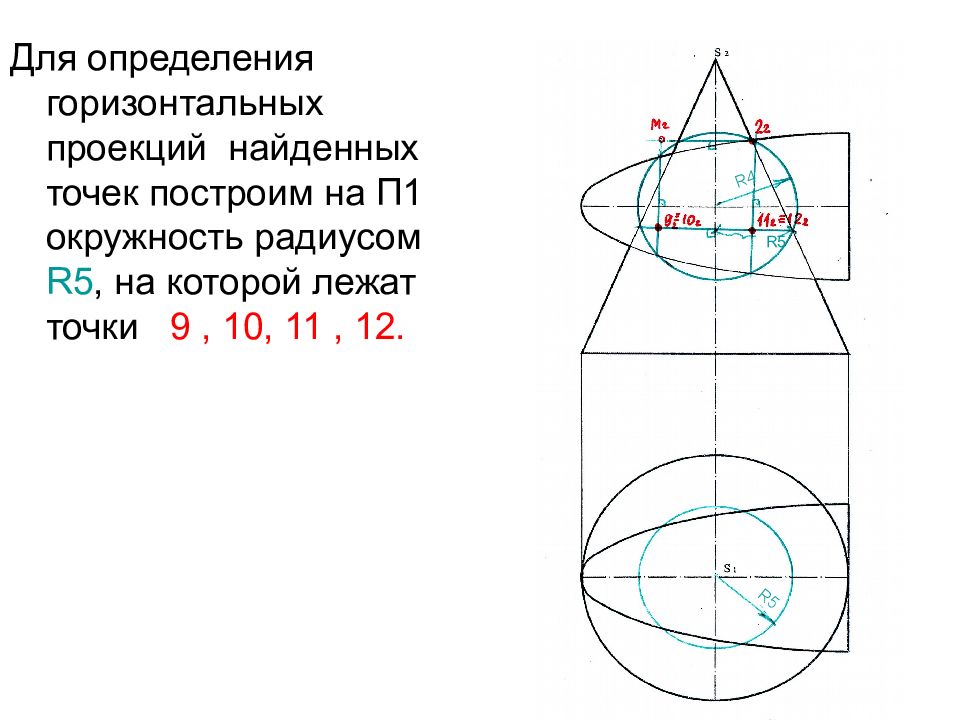
Для определения горизонтальных проекций найденных точек построим на П1 окружность радиусом R5, на которой лежат точки 9, 10, 11, 12. R5 R4 R5
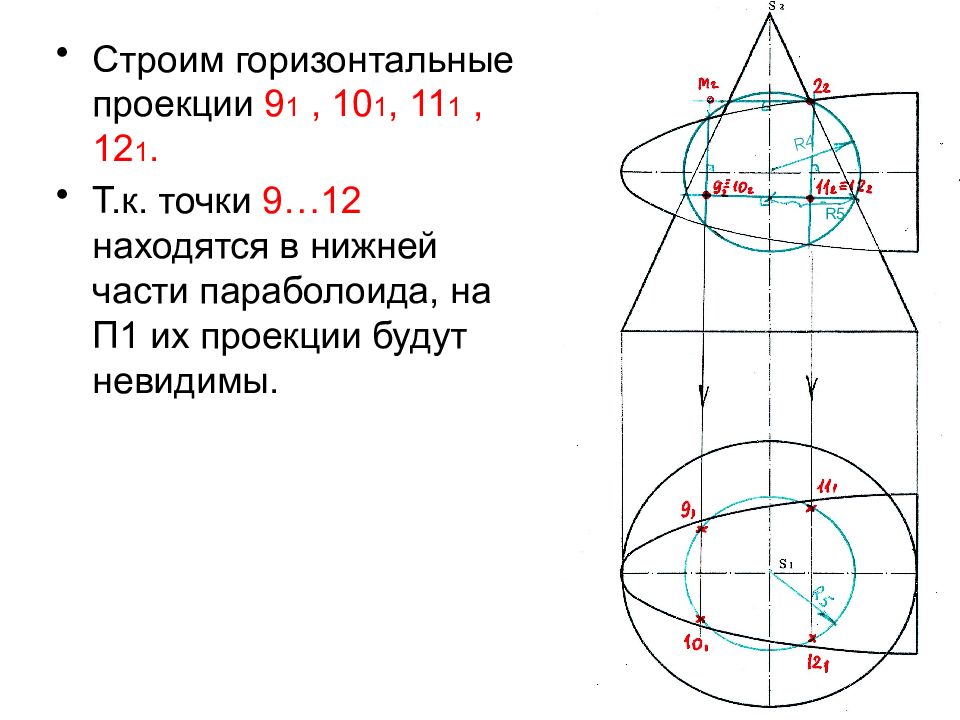
Слайд 48
Строим горизонтальные проекции 9 1, 10 1, 11 1, 12 1. Т.к. точки 9…12 находятся в нижней части параболоида, на П1 их проекции будут невидимы. R4 R5
Слайд 49
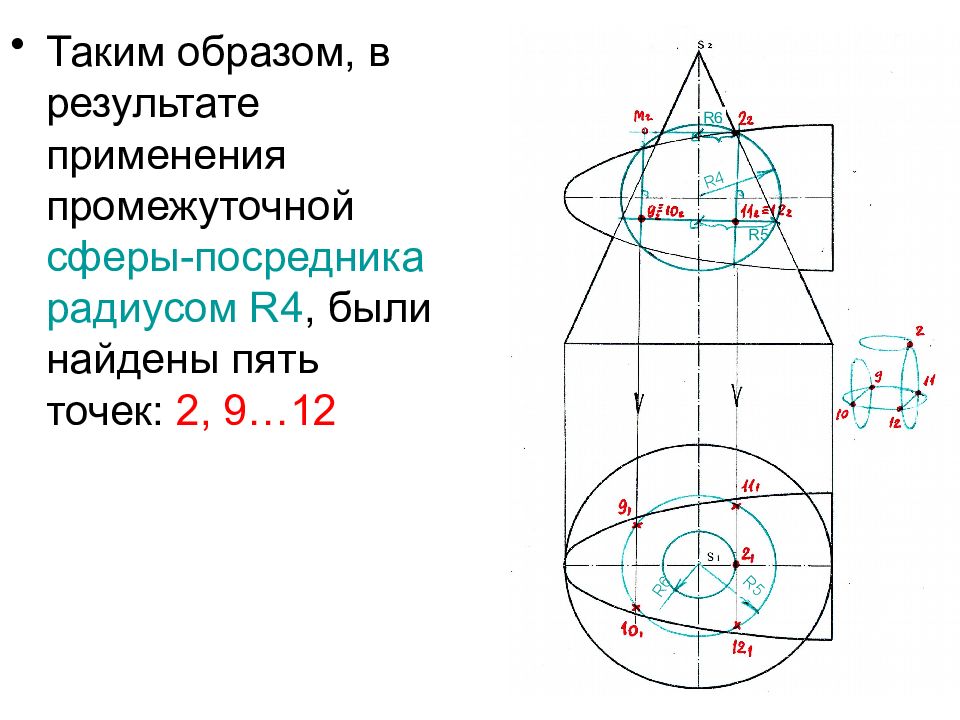
Таким образом, в результате применения промежуточной сферы-посредника радиусом R4, были найдены пять точек: 2, 9…12 R6 R5 R4 R5 R6
Слайд 51
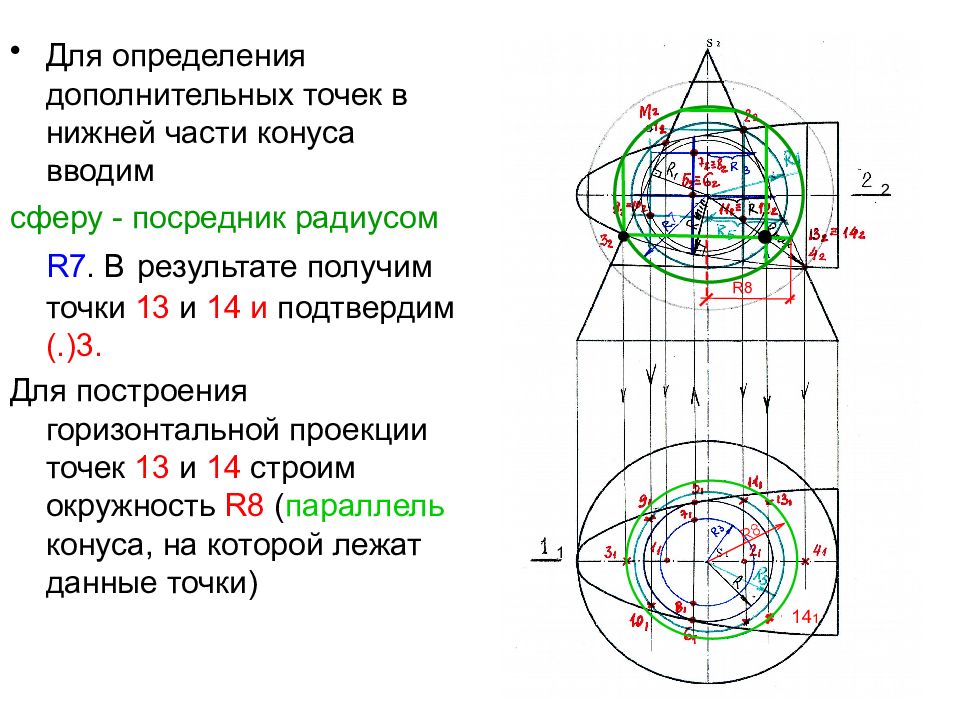
Для определения дополнительных точек в нижней части конуса вводим сферу - посредник радиусом R7. В результате получим точки 13 и 14 и подтвердим (.)3. Для построения горизонтальной проекции точек 13 и 14 строим окружность R8 ( параллель конуса, на которой лежат данные точки) ● ° 14 1 R8 R8 7 ● 1 2
Слайд 52
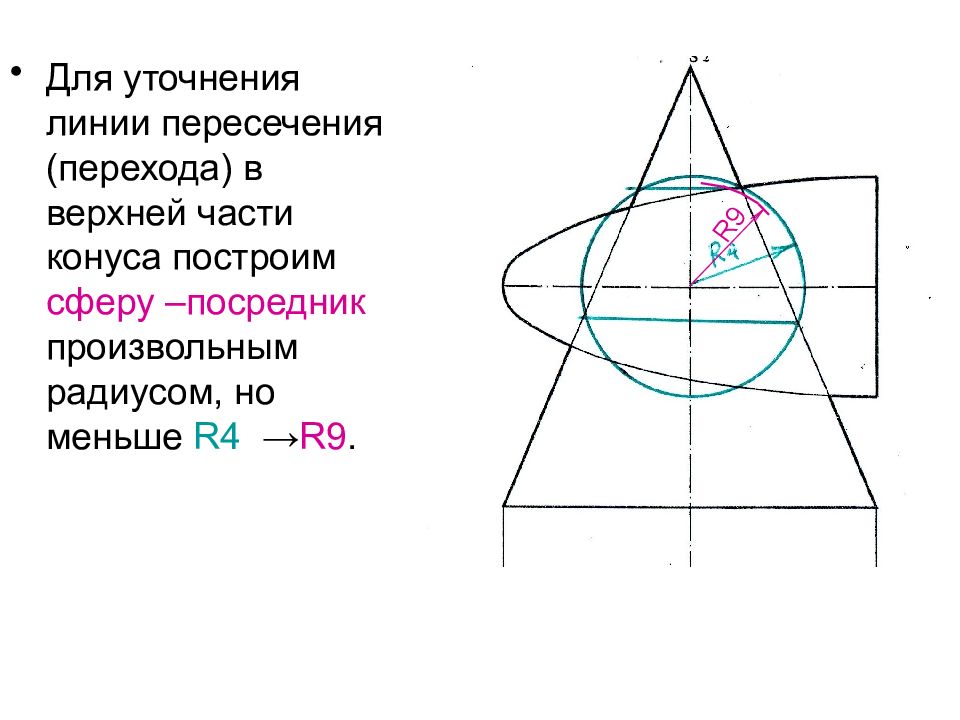
Для уточнения линии пересечения (перехода) в верхней части конуса построим сферу –посредник произвольным радиусом, но меньше R4 → R9. R9
Слайд 53
Построим общие параллели сферы-посредника и искомых поверхностей. Найдем общие точки полученных сечений: 15 и 16 R9 ° R 4 ° Определим фронтальные проекции точек 15 2 и 16 2 16 ° 15 15 2 ≡16 2
Слайд 54
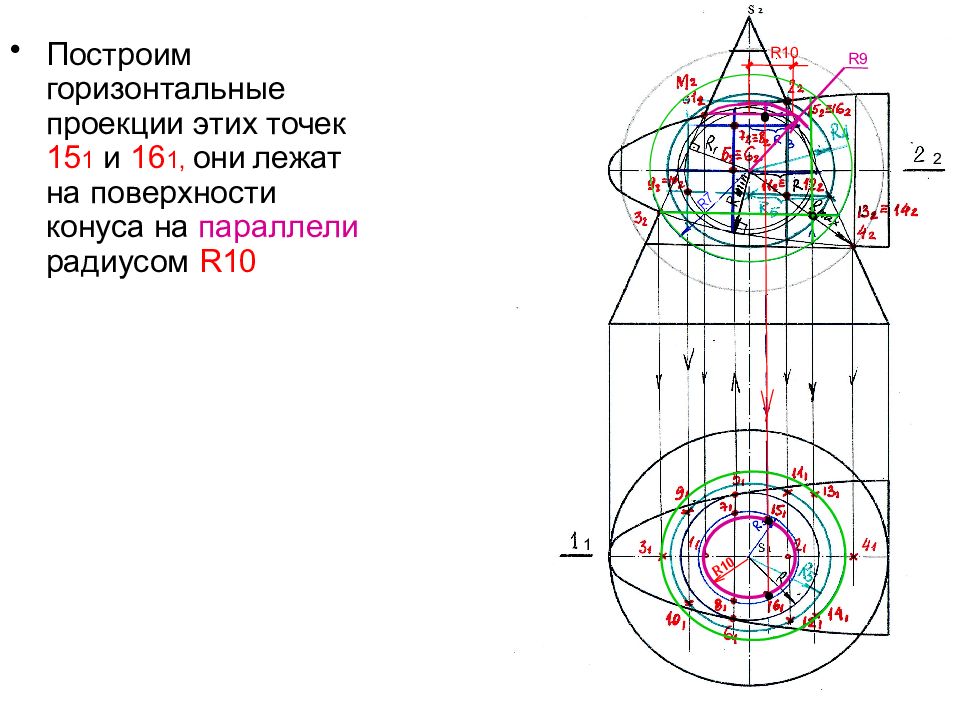
Построим горизонтальные проекции этих точек 15 1 и 16 1, они лежат на поверхности конуса на параллели радиусом R10 ° ° ° ° R9 R10 R10 R7 ● ● ● 1 2
Слайд 55
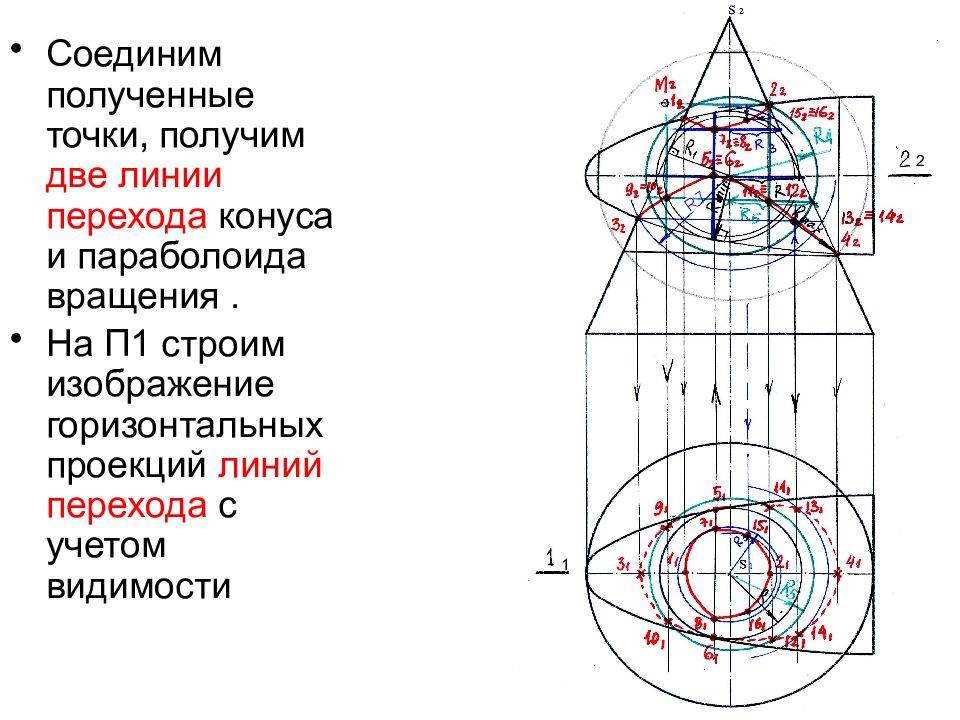
Соединим полученные точки, получим две линии перехода конуса и параболоида вращения. На П1 строим изображение горизонтальных проекций линий перехода с учетом видимости R7 1 2
Слайд 57: Пересечение поверхностей вращения методом эксцентрических сфер
Метод эксцентрических сфер применяется в том случае, когда: Пересекаются две поверхности вращения, или одна из них – циклическая. Оси поверхностей скрещиваются. Поверхности имеют общую плоскость симметрии.
Слайд 58
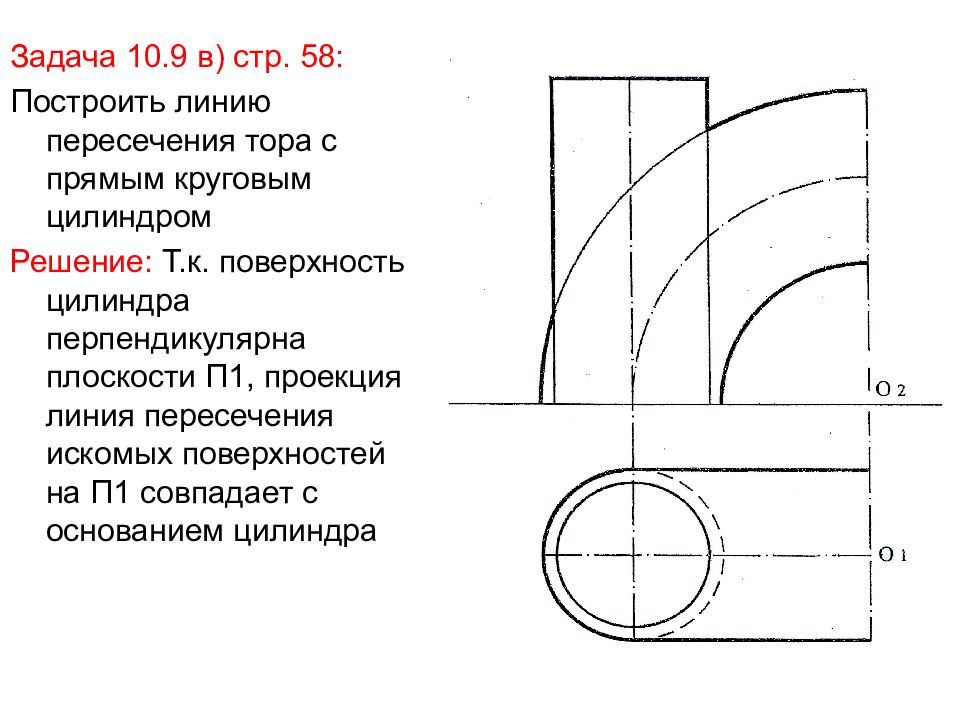
Задача 10.9 в) стр. 58: Построить линию пересечения тора с прямым круговым цилиндром Решение: Т.к. поверхность цилиндра перпендикулярна плоскости П1, проекция линия пересечения искомых поверхностей на П1 совпадает с основанием цилиндра
Слайд 59
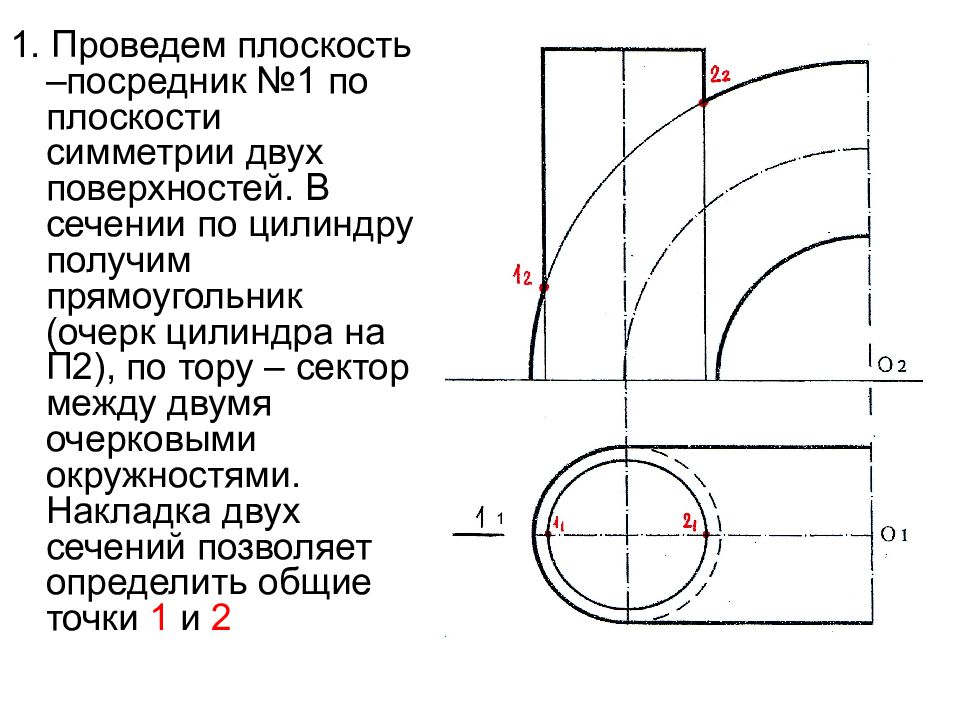
1. Проведем плоскость –посредник №1 по плоскости симметрии двух поверхностей. В сечении по цилиндру получим прямоугольник (очерк цилиндра на П2), по тору – сектор между двумя очерковыми окружностями. Накладка двух сечений позволяет определить общие точки 1 и 2 1
Слайд 60
2. Далее применим метод эксцентрических сфер - посредников. Через ось тора (центр О 2 ) проведем фронтально-проецирующую плоскость 2 (2 2 ), которая разрежет тор по окружности с центром в точке N ( N 2 ) (на П2 окружность совпадает с проекцией плоскости 2 2 ). Восстановим к плоскости окружности перпендикуляр в (.) N ( N 2 ) и найдем его пересечение с осью цилиндра –(.)К (К 2 )- это центр сферы-посредника 1 2 2
Слайд 61
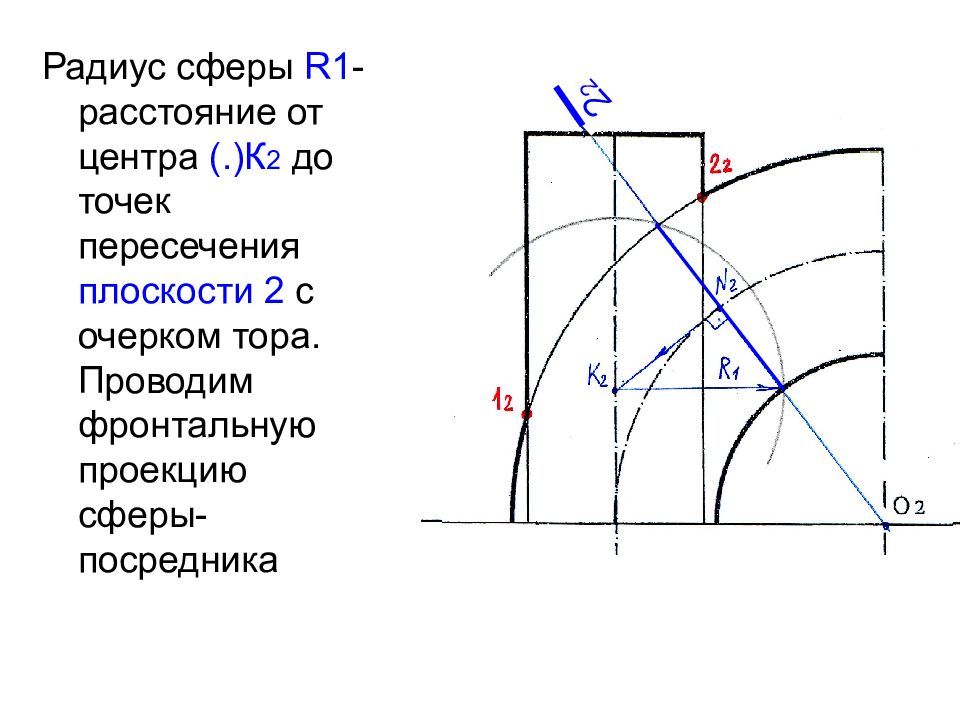
Радиус сферы R1 - расстояние от центра (.)К 2 до точек пересечения плоскости 2 с очерком тора. Проводим фронтальную проекцию сферы-посредника 2 2
Слайд 62
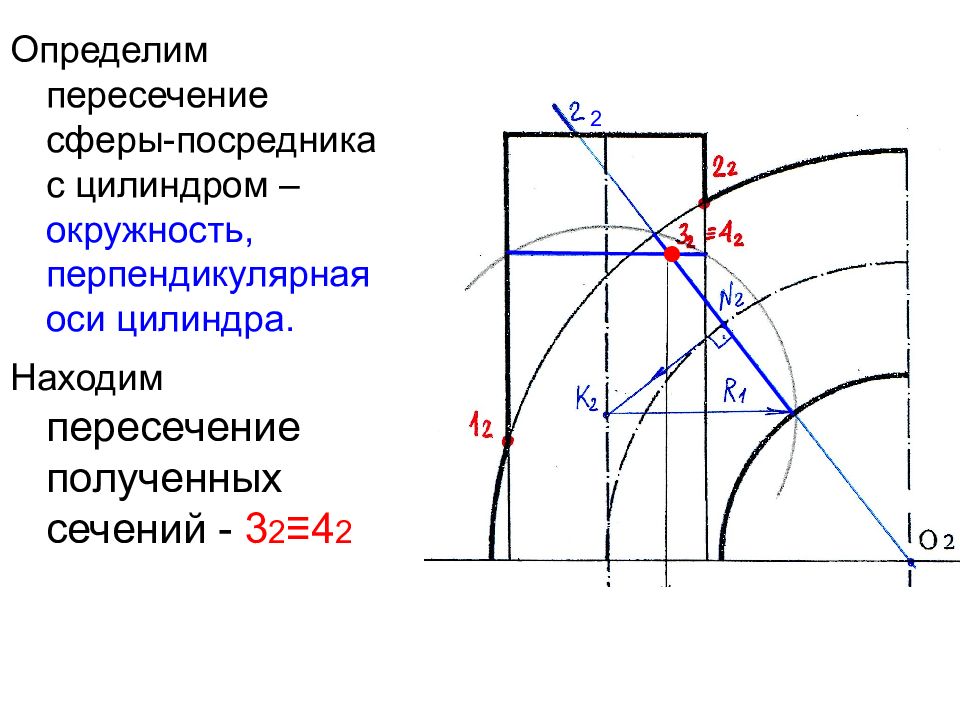
Определим пересечение сферы-посредника с цилиндром – окружность, перпендикулярная оси цилиндра. Находим пересечение полученных сечений - 3 2 ≡4 2 ● 2
Слайд 63
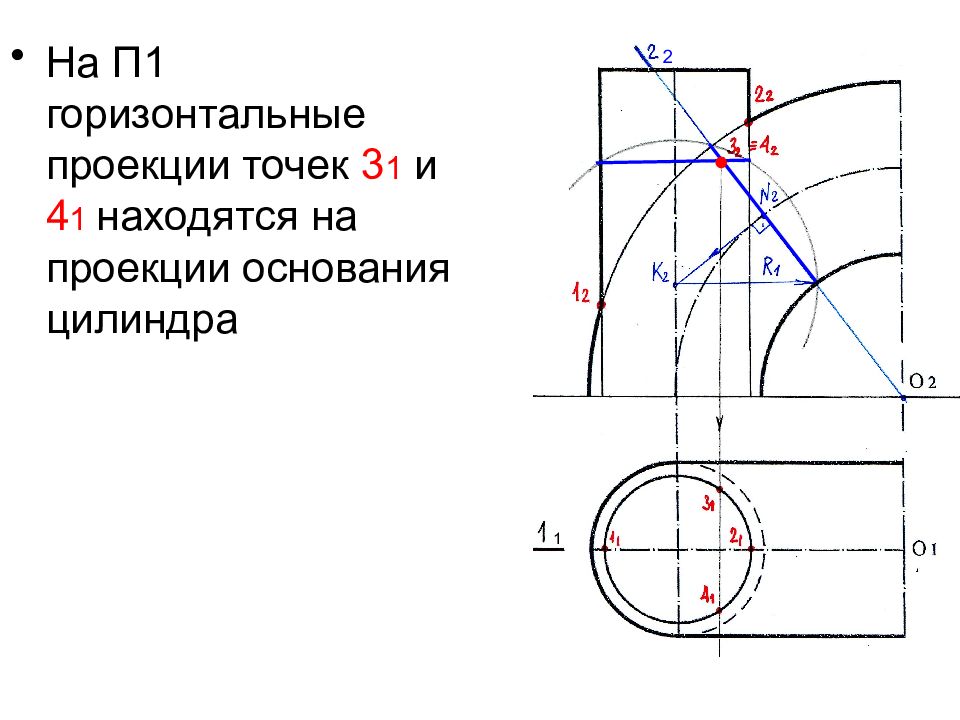
На П1 горизонтальные проекции точек 3 1 и 4 1 находятся на проекции основания цилиндра 1 2 ●
Слайд 64
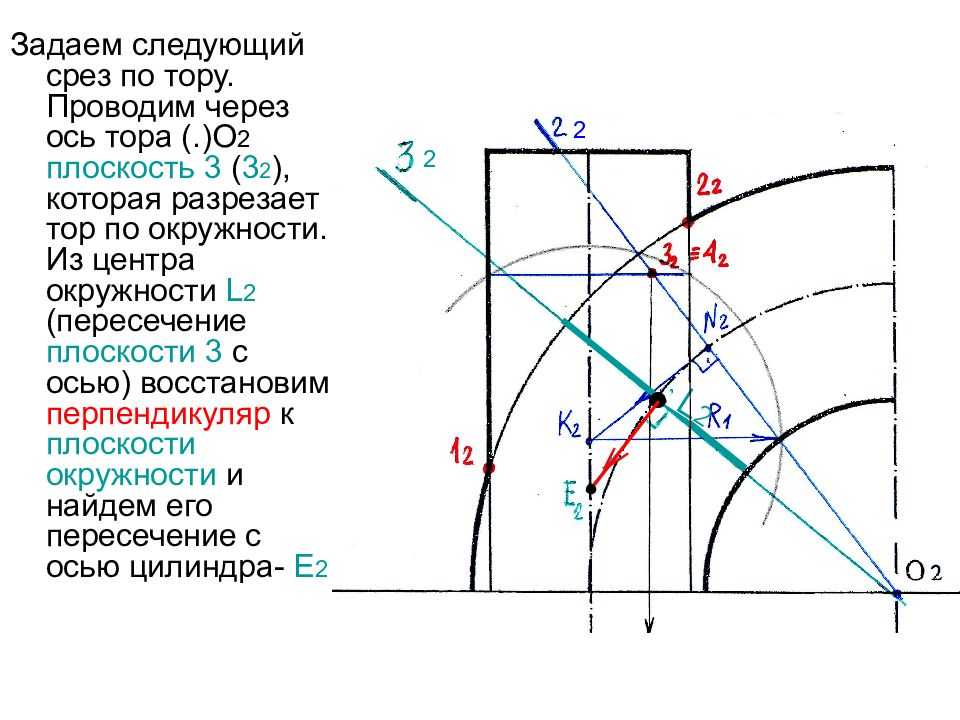
Задаем следующий срез по тору. Проводим через ось тора (.)О 2 плоскость 3 ( 3 2 ), которая разрезает тор по окружности. Из центра окружности L 2 (пересечение плоскости 3 с осью) восстановим перпендикуляр к плоскости окружности и найдем его пересечение с осью цилиндра- Е 2 2 2 ● L 2 ●
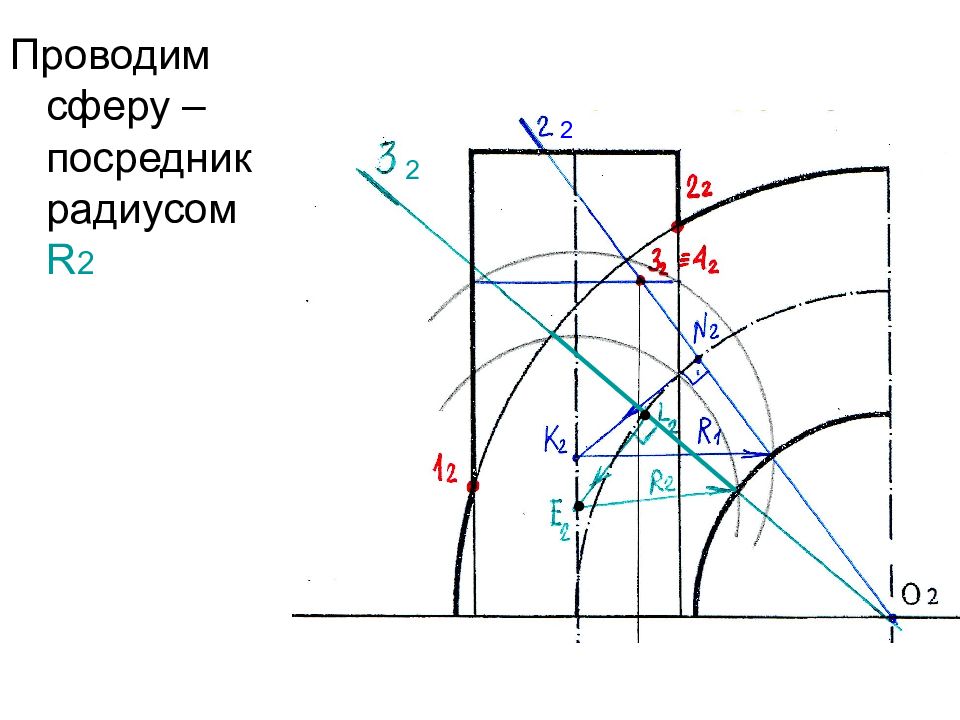
Слайд 66
Находим пересечение построенной сферы с цилиндром и определяем точки 5 2 ≡ 6 2 пересечения двух полученных сечений (окружностей) ° 5 2 ≡ 6 2 1 2 2
Слайд 67
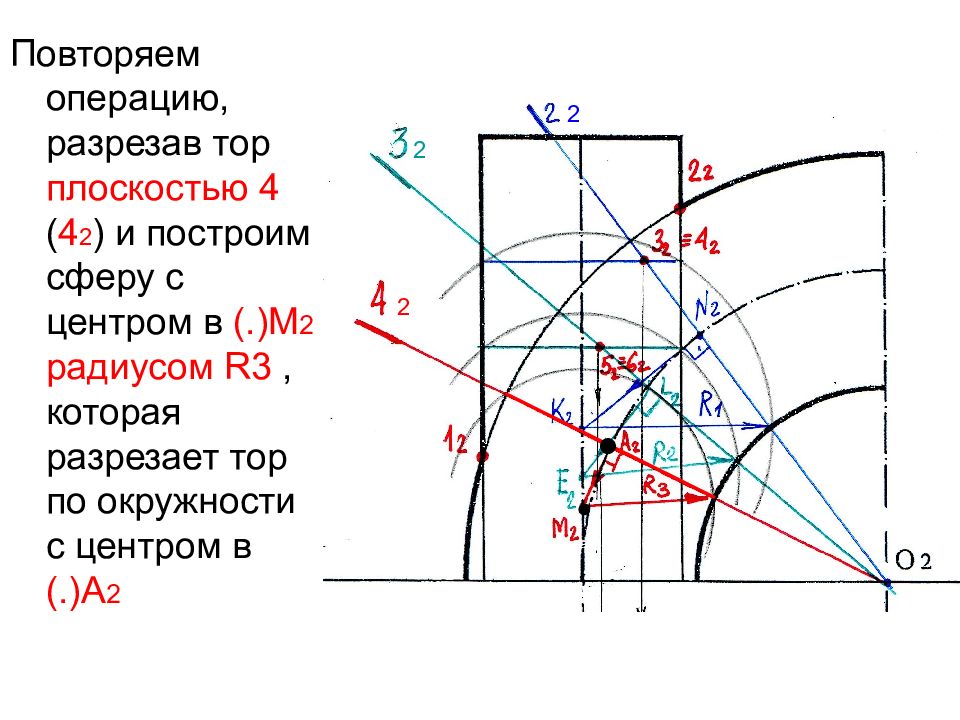
Повторяем операцию, разрезав тор плоскостью 4 ( 4 2 ) и построим сферу с центром в (.)М 2 радиусом R3, которая разрезает тор по окружности с центром в (.)А 2 2 2 2 ● ●
Слайд 68
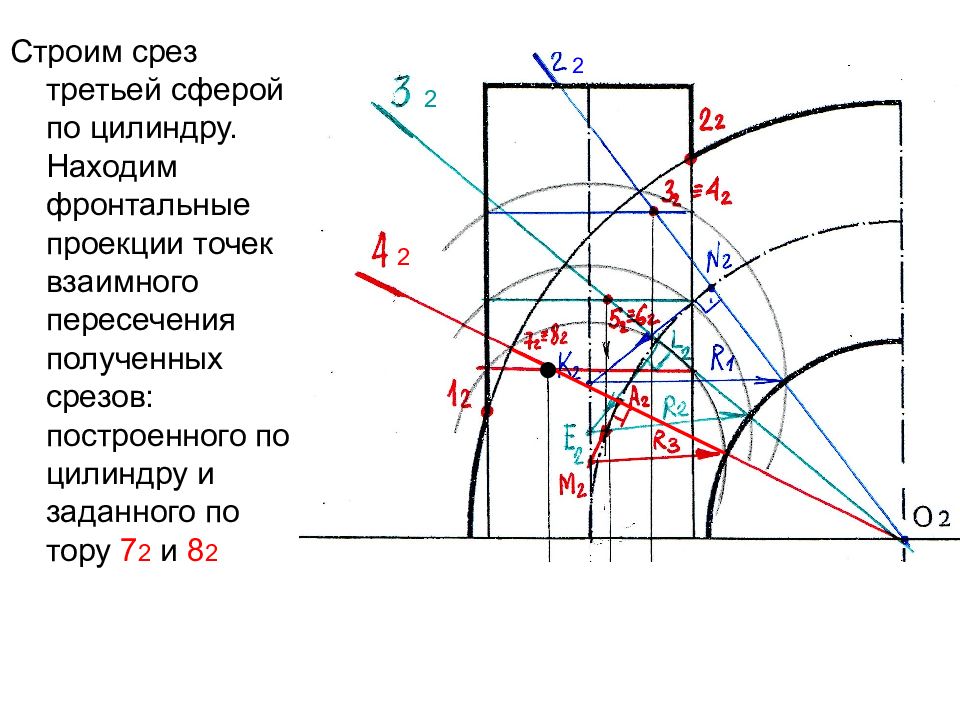
Строим срез третьей сферой по цилиндру. Находим фронтальные проекции точек взаимного пересечения полученных срезов: построенного по цилиндру и заданного по тору 7 2 и 8 2 2 2 2 ●
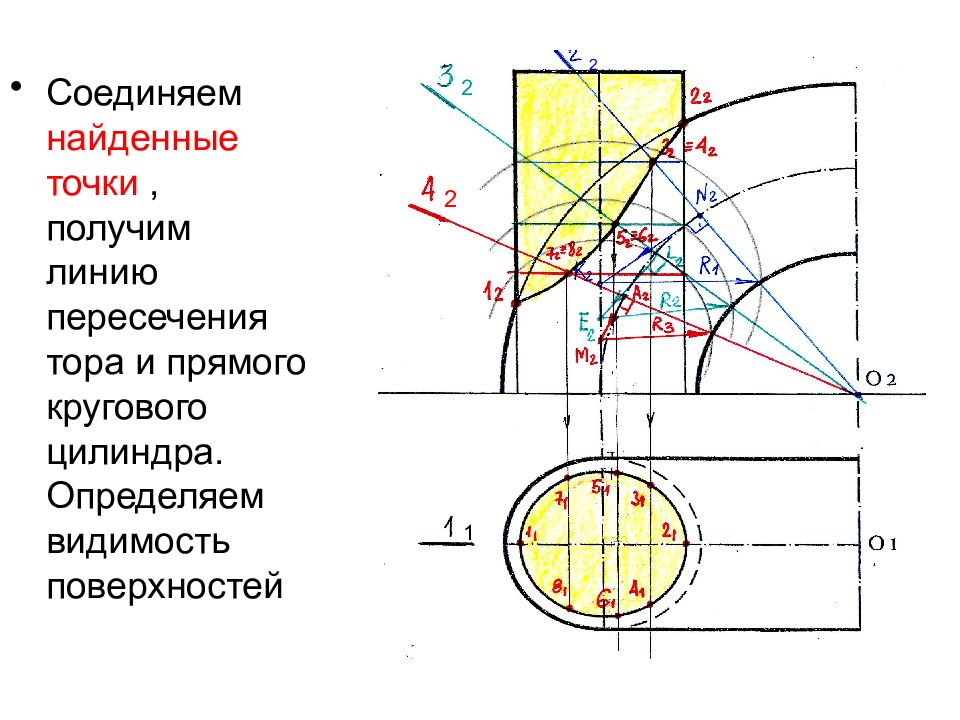
Слайд 69
На П1 горизонтальные проекции точек 7 1 и 8 1 находятся на проекции основания цилиндра 1 2 2 2