Первый слайд презентации: Расстояние между скрещивающимися прямыми
Слайд 2: Определение
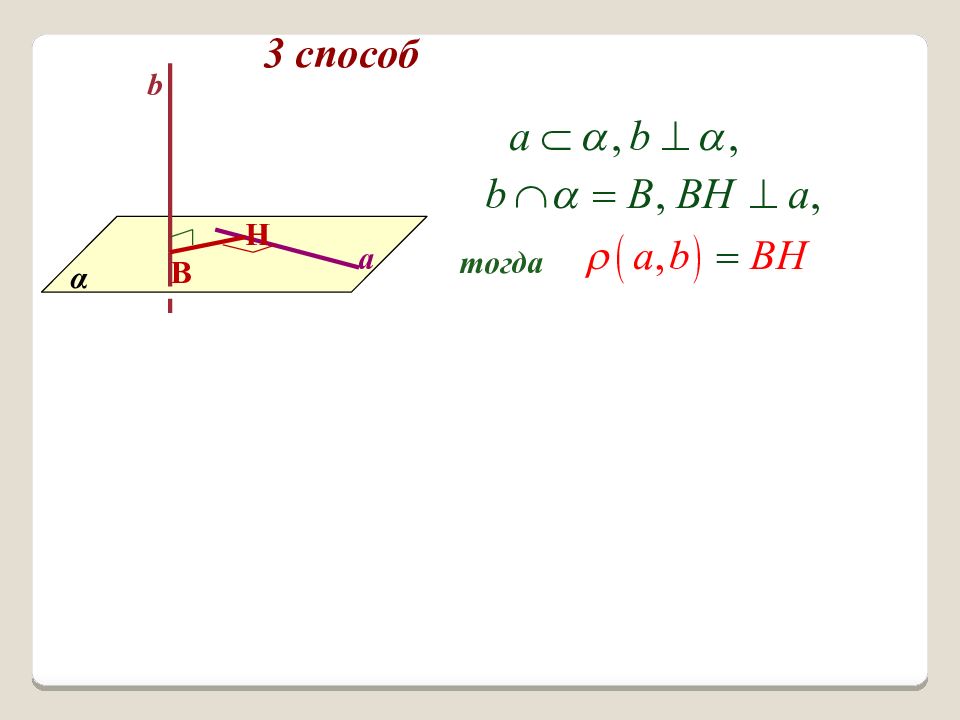
Отрезок, концы которого лежат на скрещивающихся прямых, и перпендикулярный обеим прямым, называется общим перпендикуляром к скрещивающимся прямым.
Слайд 3
Теорема К любым двум скрещивающимся прямым можно провести общий перпендикуляр и притом только один.
Слайд 4
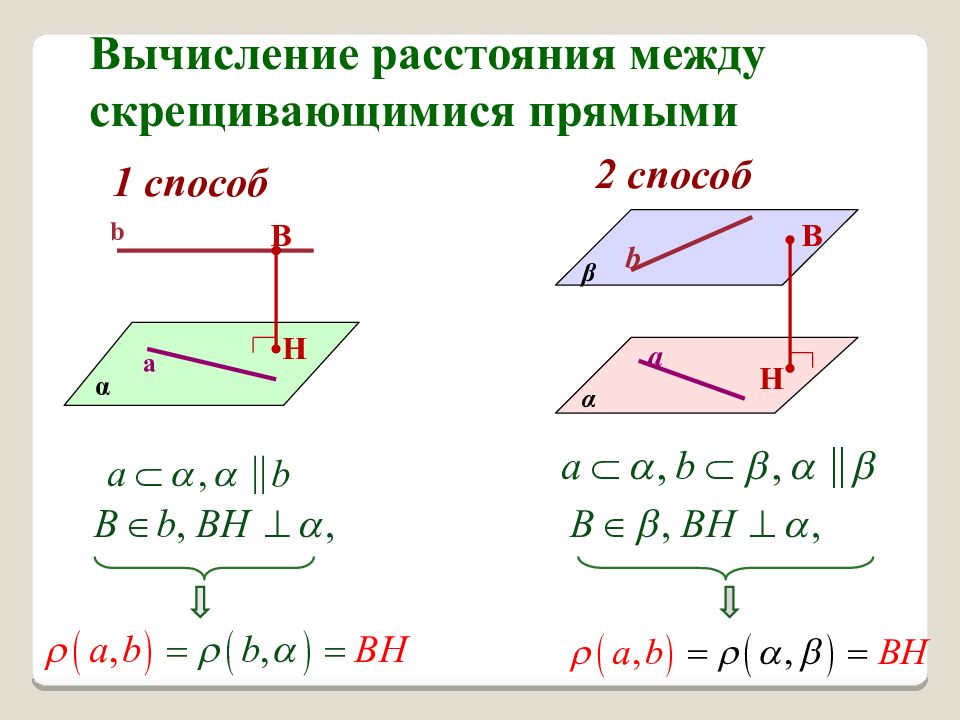
Вычисление расстояния между скрещивающимися прямыми 1 способ α a b B H 2 способ α β b a B H
Слайд 6: Куб 1
В единичном кубе A … D 1 найдите расстояние между прямыми AA 1 и BC. Ответ: 1. Куб 1
Слайд 7: Куб 2
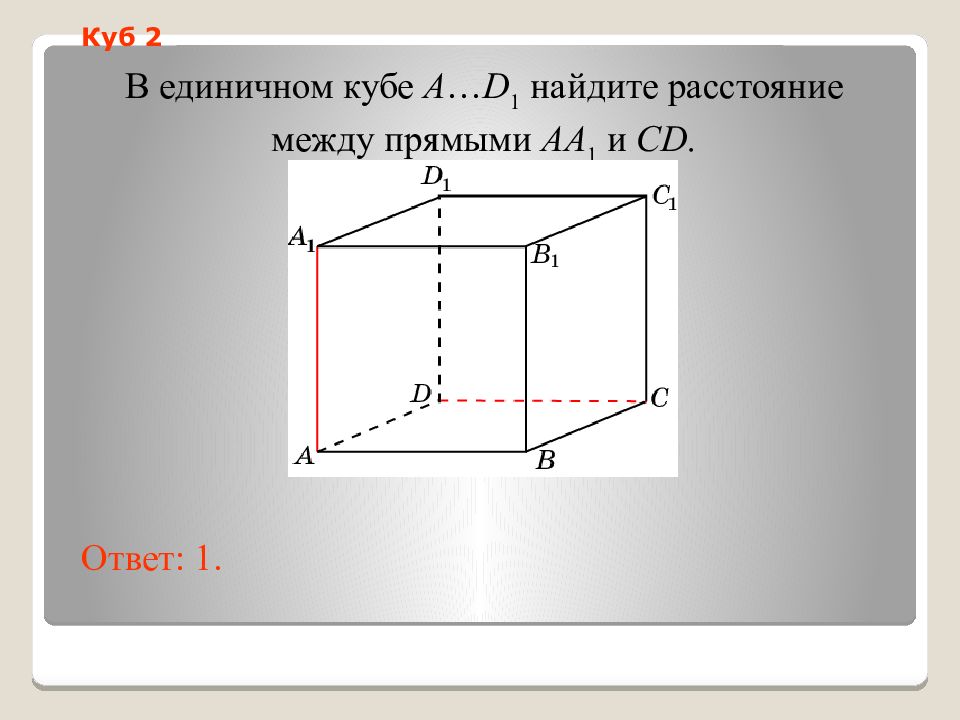
В единичном кубе A … D 1 найдите расстояние между прямыми AA 1 и CD. Ответ: 1. Куб 2
Слайд 8: Куб 3
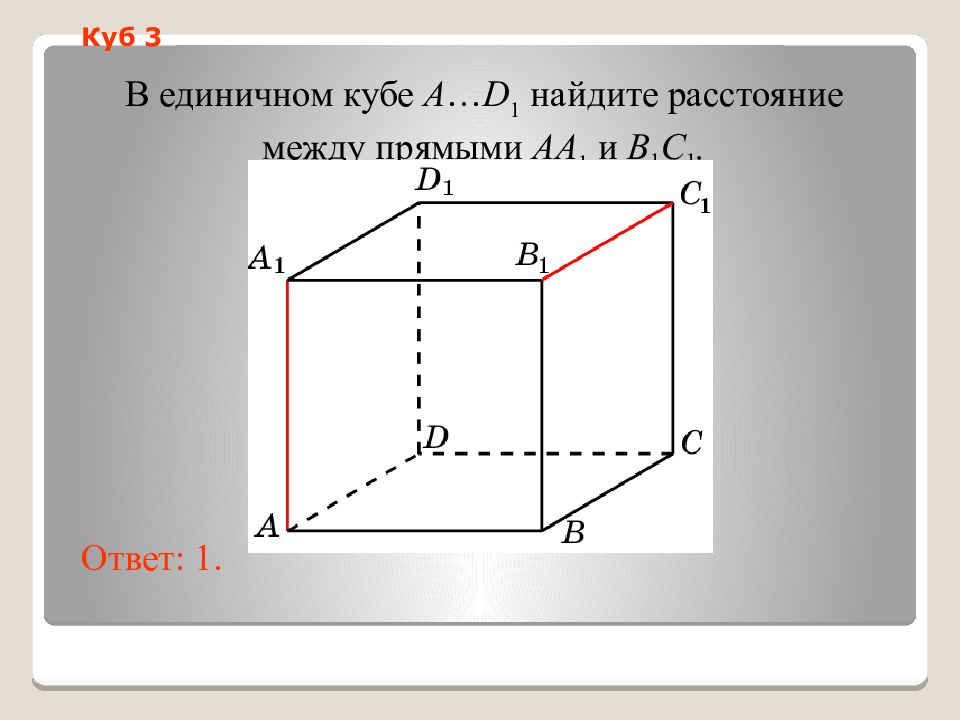
В единичном кубе A … D 1 найдите расстояние между прямыми AA 1 и B 1 C 1. Ответ: 1. Куб 3
Слайд 9: Куб 4
В единичном кубе A … D 1 найдите расстояние между прямыми AA 1 и C 1 D 1. Ответ: 1. Куб 4
Слайд 10: Куб 5
В единичном кубе A … D 1 найдите расстояние между прямыми AA 1 и BC 1. Ответ: 1. Куб 5
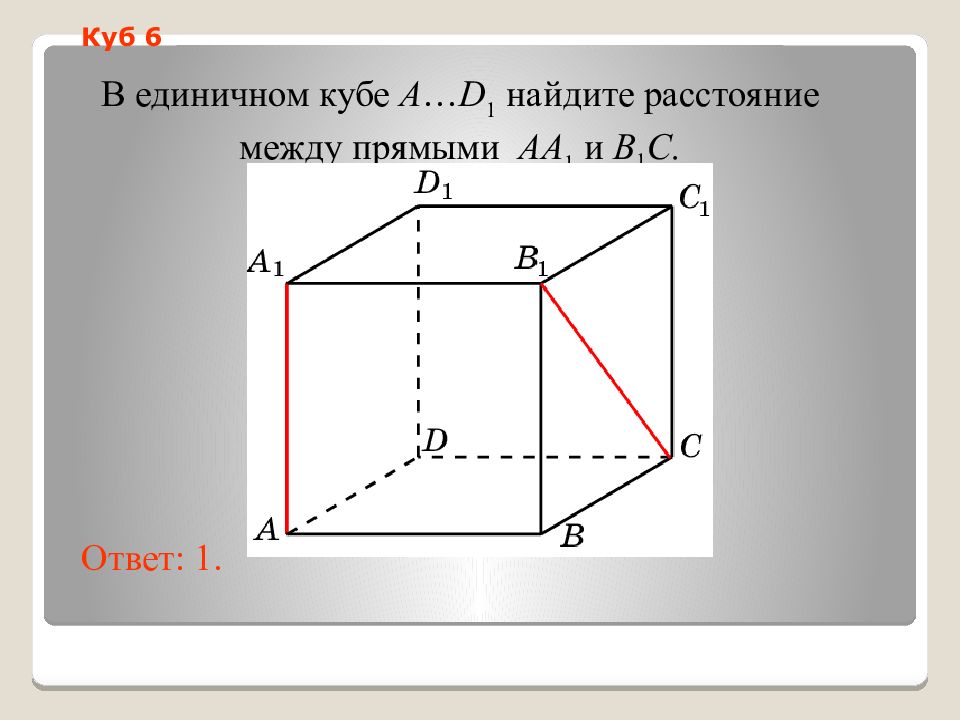
Слайд 11: Куб 6
В единичном кубе A … D 1 найдите расстояние между прямыми AA 1 и B 1 C. Ответ: 1. Куб 6
Слайд 12: Куб 7
В единичном кубе A … D 1 найдите расстояние между прямыми AA 1 и CD 1. Ответ: 1. Куб 7
Слайд 13: Куб 8
В единичном кубе A … D 1 найдите расстояние между прямыми AA 1 и DC 1. Ответ: 1. Куб 8
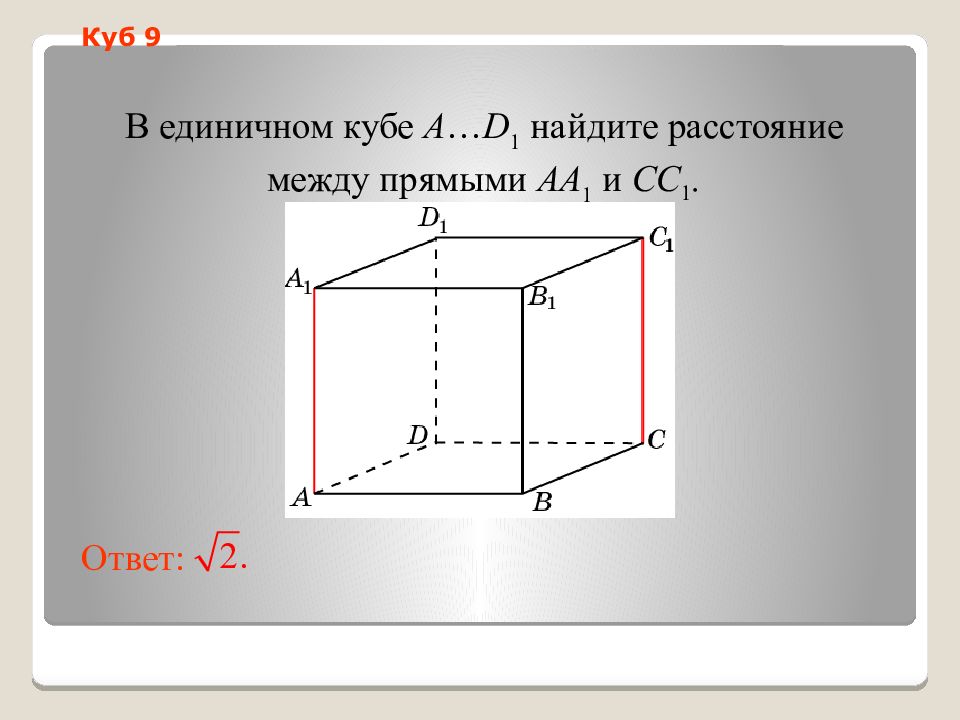
Слайд 14: Куб 9
В единичном кубе A … D 1 найдите расстояние между прямыми AA 1 и CC 1. Ответ: Куб 9
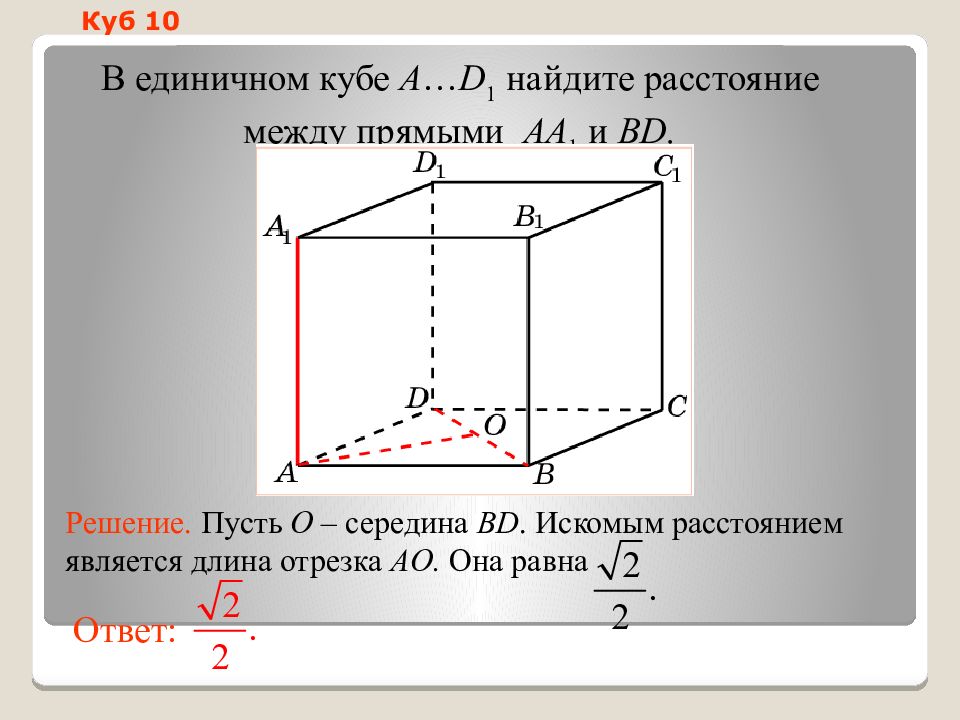
Слайд 15: Куб 1 0
В единичном кубе A … D 1 найдите расстояние между прямыми AA 1 и BD. Ответ: Решение. Пусть O – середина BD. Искомым р асстоянием является длина отрезка AO. Она равна Куб 1 0
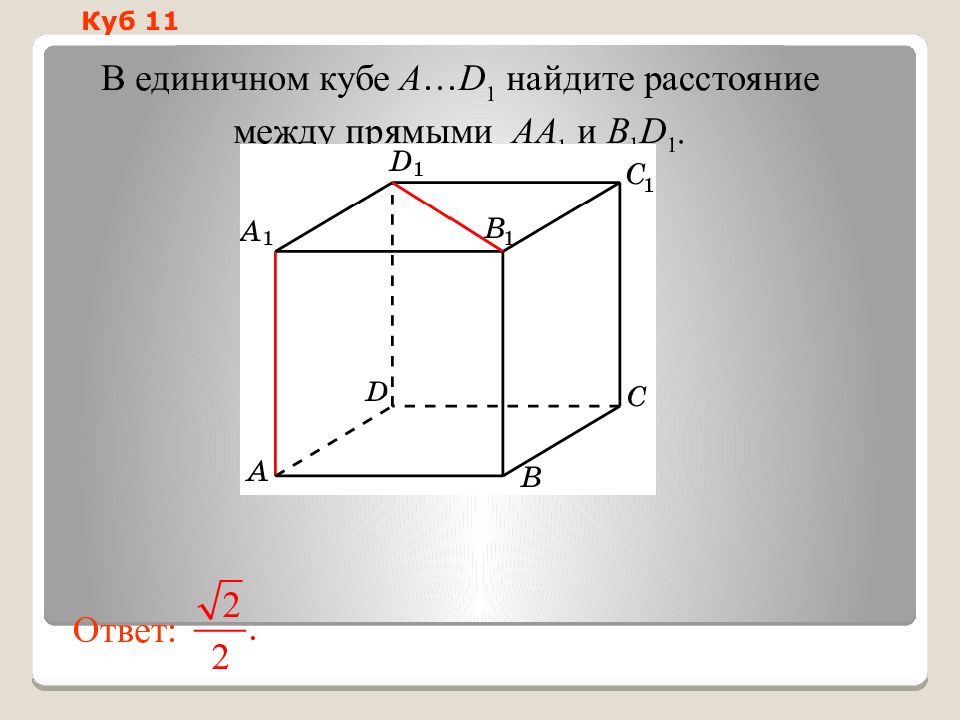
Слайд 16: Куб 1 1
В единичном кубе A … D 1 найдите расстояние между прямыми AA 1 и B 1 D 1. Ответ: Куб 1 1
Слайд 17: Куб 1 2
В единичном кубе A … D 1 найдите расстояние между прямыми AA 1 и BD 1. Ответ: Решение. Пусть P, Q – середины AA 1, BD 1. Искомым расстоянием является длина отрезка PQ. Она равна Куб 1 2
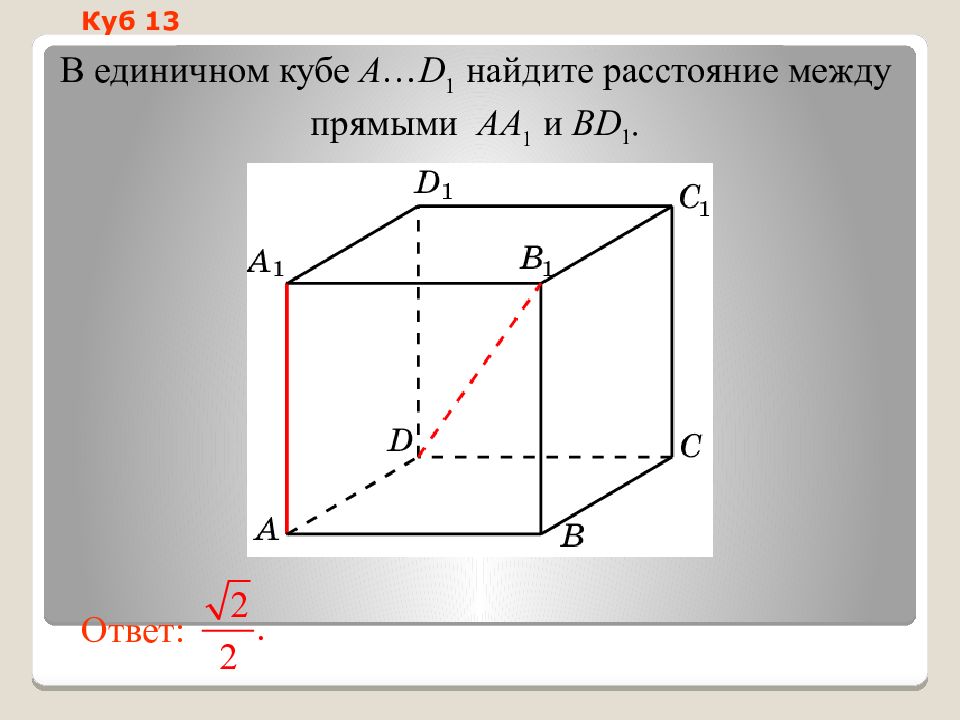
Слайд 18: Куб 1 3
В единичном кубе A … D 1 найдите расстояние между прямыми AA 1 и BD 1. Ответ: Куб 1 3
Слайд 19: Куб 1 4
В единичном кубе A … D 1 найдите расстояние прямыми AB 1 и CD 1. Ответ: 1. Куб 1 4
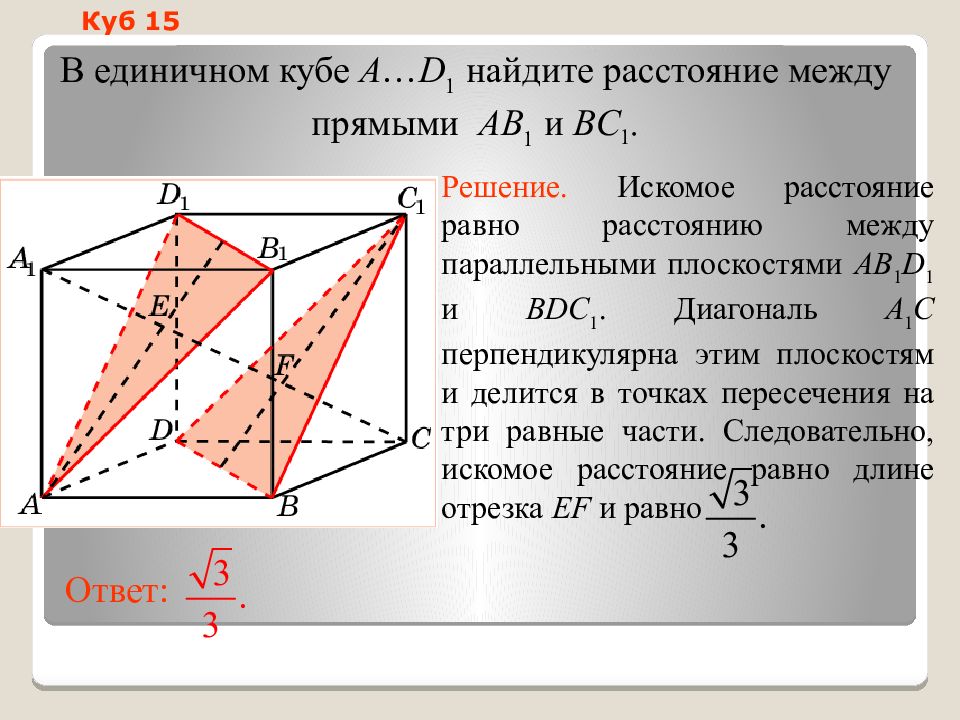
Слайд 20: Куб 1 5
В единичном кубе A … D 1 найдите расстояние между прямыми AB 1 и BC 1. Ответ: Решение. Искомое р асстояние равно расстоянию между параллельными плоскостями AB 1 D 1 и BDC 1. Диагональ A 1 C перпендикулярна этим плоскостям и делится в точках пересечения на три равные части. Следовательно, искомое расстояние равно длине отрезка EF и равно Куб 1 5
Слайд 21: Куб 1 6
В единичном кубе A … D 1 найдите расстояние между прямыми AB 1 и A 1 C 1. Ответ: Решение аналогично предыдущему. Куб 1 6
Слайд 22: Куб 1 7
В единичном кубе A … D 1 найдите расстояние между прямыми AB 1 и BD. Ответ: Решение аналогично предыдущему. Куб 1 7
Слайд 23: Куб 18
В единичном кубе A … D 1 найдите расстояние прямыми AB 1 и BD 1. Ответ: Решение. Диагональ BD 1 перпендикулярна плоскости равностороннего треугольника ACB 1 и пересекает его в центре P вписанной в него окружности. Искомое расстояние равно радиусу OP этой окружности. OP = Куб 18
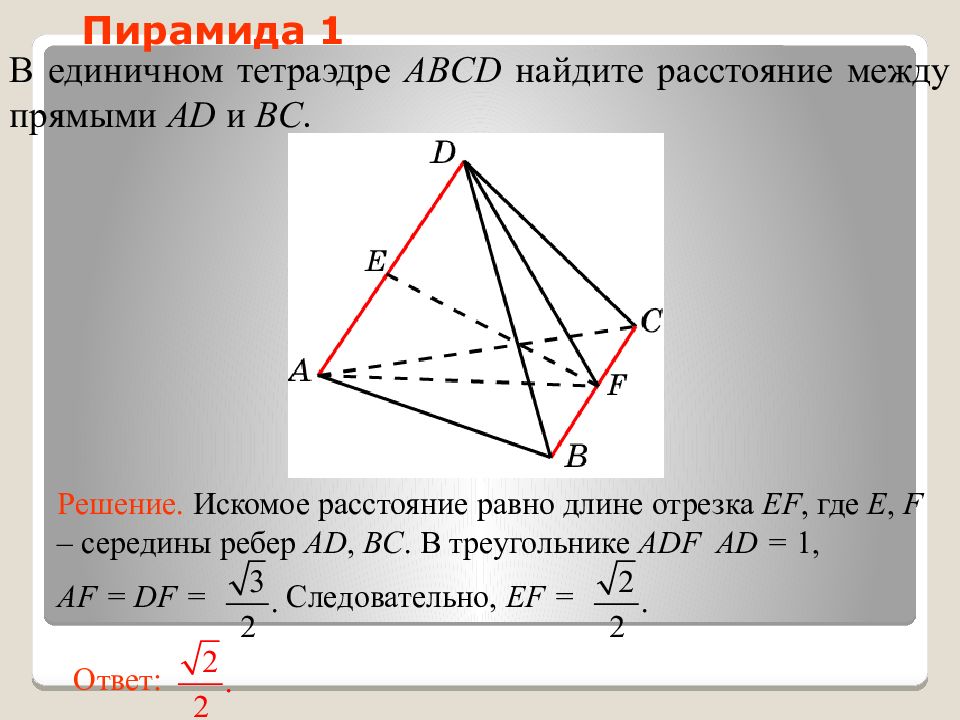
Слайд 24: Пирамида 1
В единичном тетраэдре ABCD н айдите расстояние между прямыми AD и BC. Ответ: Решение. Искомое расстояние равно длине отрезка EF, где E, F – середины ребер AD, BC. В треугольнике ADF AD = 1, AF = DF = Следовательно, EF = Пирамида 1
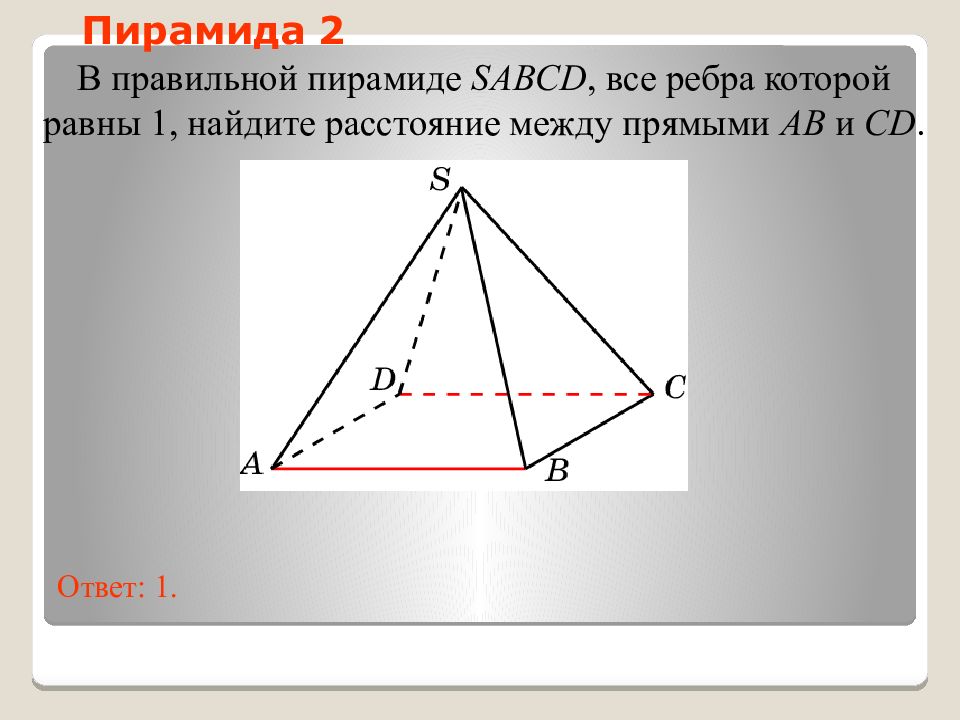
Слайд 25: Пирамида 2
В правильной пирамиде SABCD, все ребра которой равны 1, н айдите расстояние между прямыми AB и CD. Ответ: 1. Пирамида 2
Слайд 26: Пирамида 3
В правильной пирамиде SABCD, все ребра которой равны 1, н айдите расстояние между прямыми SA и BD. Ответ: Решение. Искомое расстояние равно высоте OH треугольника SAO, где O – середина BD. В прямоугольном треугольнике SAO имеем: SA = 1, AO = SO = Следовательно, OH = Пирамида 3
Слайд 27: Пирамида 4
В правильной пирамиде SABCD, все ребра которой равны 1, н айдите расстояние между прямыми SA и BC. Ответ: Решение. Плоскость SAD параллельна прямой BC. Следовательно, искомое расстояние равно расстоянию между прямой BC и плоскостью SAD. Оно равно высоте EH треугольника SEF, где E, F – середины ребер BC, AD. В треугольнике SEF имеем: EF = 1, SE = SF = Высота SO равна Следовательно, EH = Пирамида 4
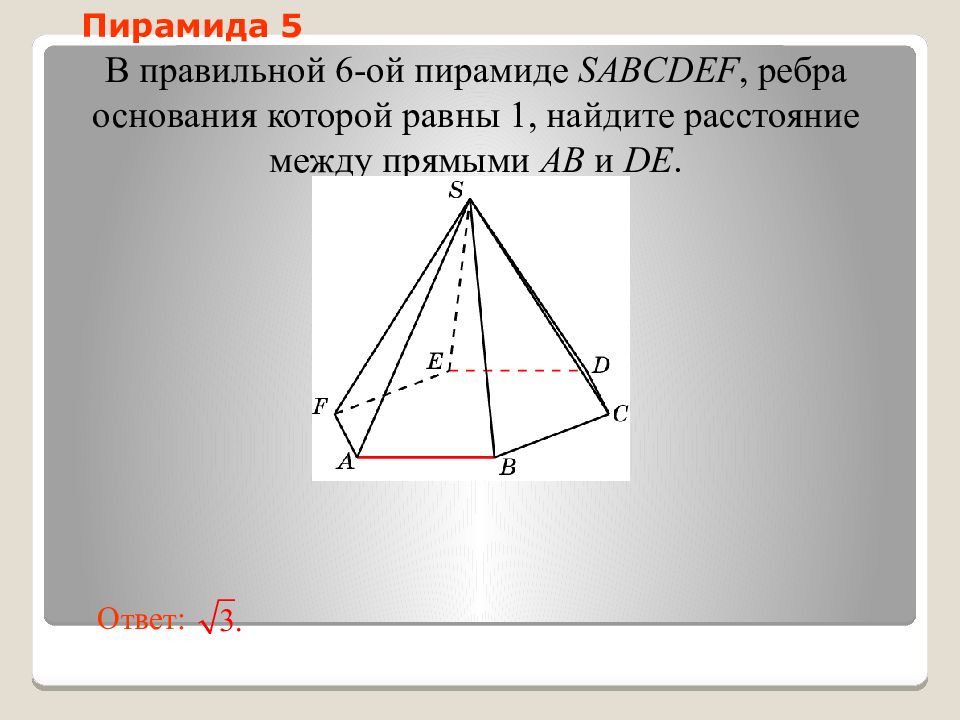
Слайд 28: Пирамида 5
В правильной 6-ой пирамиде SABCDEF, ребра основания которой равны 1, н айдите расстояние между прямыми AB и DE. Ответ: Пирамида 5
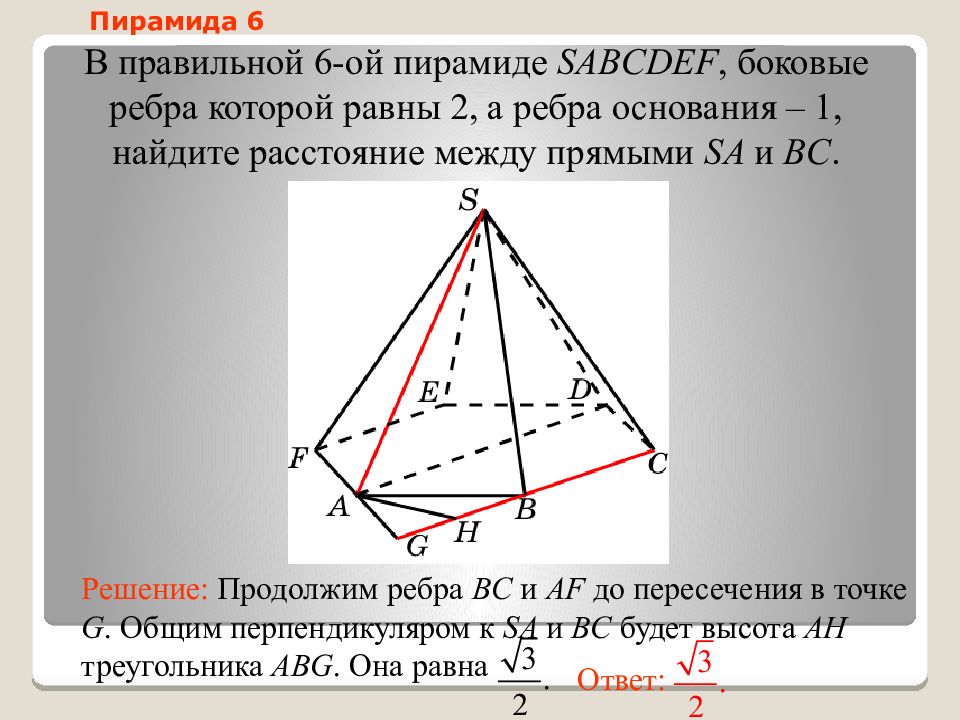
Слайд 29: Пирамида 6
В правильной 6-ой пирамиде SABCDEF, боковые ребра которой равны 2, а ребра основания – 1, н айдите расстояние между прямыми SA и BC. Ответ: Решение: Продолжим ребра BC и AF до пересечения в точке G. Общим перпендикуляром к SA и BC будет высота AH треугольника ABG. Она равна Пирамида 6
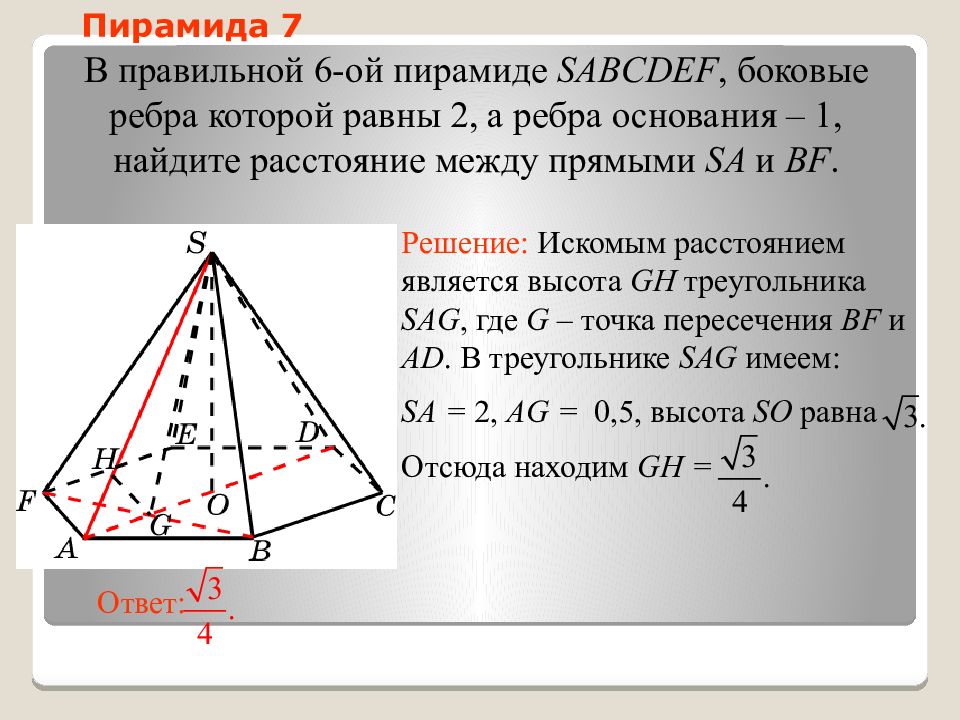
Слайд 30: Пирамида 7
В правильной 6-ой пирамиде SABCDEF, боковые ребра которой равны 2, а ребра основания – 1, н айдите расстояние между прямыми SA и BF. Ответ: Решение: Искомым расстоянием является высота GH треугольника SAG, где G – точка пересечения BF и AD. В треугольнике SAG имеем: SA = 2, AG = 0,5, высота SO равна Отсюда находим GH = Пирамида 7
Слайд 31: Пирамида 8
В правильной 6-ой пирамиде SABCDEF, боковые ребра которой равны 2, а ребра основания – 1, н айдите расстояние между прямыми SA и CE. Ответ: Решение: Искомым расстоянием является высота GH треугольника SAG, где G – точка пересечения CE и AD. В треугольнике SAG имеем: SA = 2, AG =, высота SO равна Отсюда находим GH = Пирамида 8
Слайд 32: Пирамида 9
В правильной 6-ой пирамиде SABCDEF, боковые ребра которой равны 2, а ребра основания – 1, н айдите расстояние между прямыми SA и BD. Ответ: Решение: Прямая BD параллельна плоскости SAE. Искомое расстояние равно расстоянию между прямой BD и этой плоскостью и равно высоте PH треугольника SPQ. В этом треугольнике высота SO равна, PQ = 1, SP = SQ = Отсюда находим PH = Пирамида 9
Слайд 33: Пирамида 10
В правильной 6-ой пирамиде SABCDEF, боковые ребра которой равны 2, а ребра основания – 1, н айдите расстояние между прямыми SA и BG, где G – середина ребра SC. Пирамида 10 Ответ: Решение: Через точку G проведем прямую, параллельную SA. Обозначим Q точку ее пересечения с прямой AC. Искомое расстояние равно высоте QH прямоугольного треугольника ASQ, в котором AS = 2, AQ =, SQ =. Отсюда находим QH =
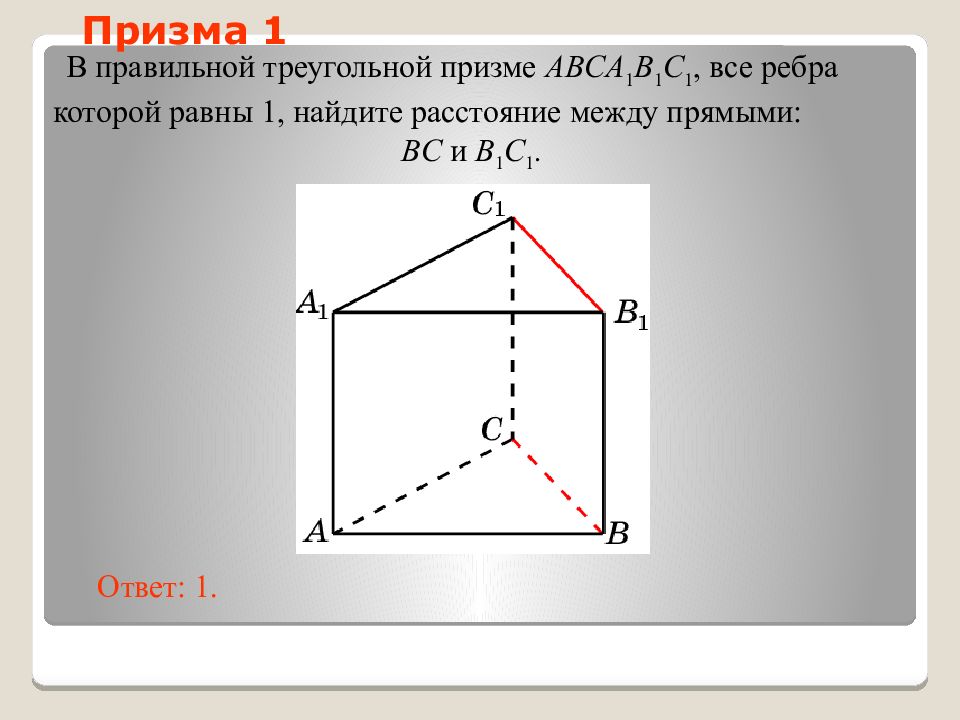
Слайд 34: Призма 1
В правильной треугольной призме ABCA 1 B 1 C 1, все ребра которой равны 1, найдите расстояние между прямыми: BC и B 1 C 1. Ответ: 1. Призма 1
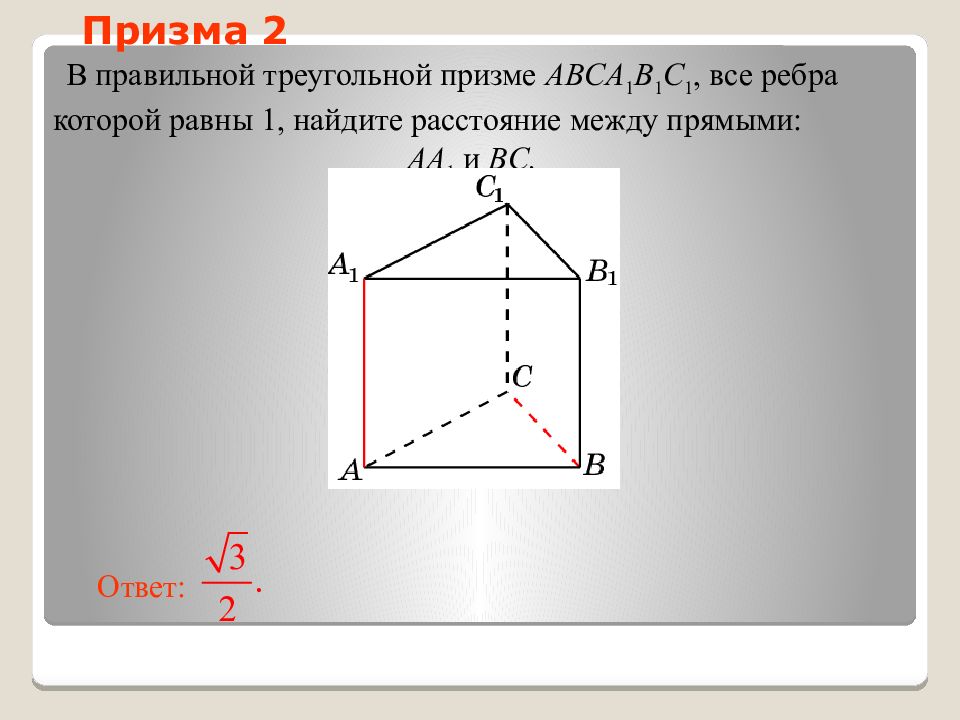
Слайд 35: Призма 2
В правильной треугольной призме ABCA 1 B 1 C 1, все ребра которой равны 1, найдите расстояние между прямыми: AA 1 и BC. Ответ: Призма 2
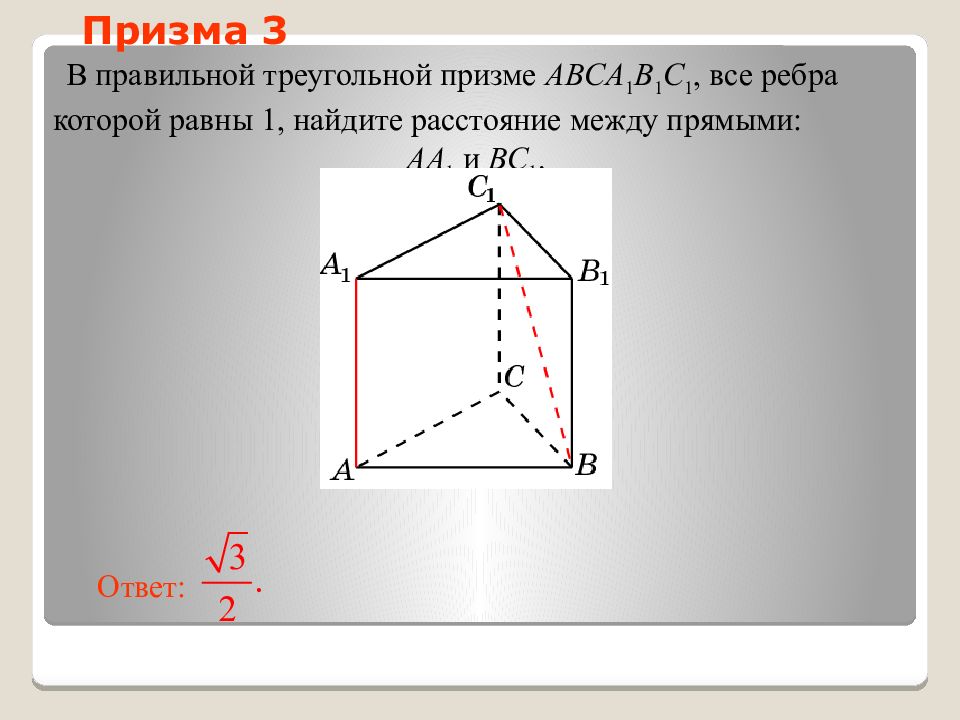
Слайд 36: Призма 3
В правильной треугольной призме ABCA 1 B 1 C 1, все ребра которой равны 1, найдите расстояние между прямыми: AA 1 и BC 1. Ответ: Призма 3
Слайд 37: Призма 4
В правильной треугольной призме ABCA 1 B 1 C 1, все ребра которой равны 1, найдите расстояние между прямыми: AB и A 1 C 1. Ответ: 1. Призма 4
Слайд 38: Призма 5
В правильной треугольной призме ABCA 1 B 1 C 1, все ребра которой равны 1, найдите расстояние между прямыми: AB и A 1 C. Решение: Искомое расстояние равно расстоянию между прямой AB и плоскостью A 1 B 1 C. Обозначим D и D 1 середины ребер AB и A 1 B 1. В прямоугольном треугольнике CDD 1 из вершины D проведем высоту DE. Она и будет искомым расстоянием. Имеем, DD 1 = 1, CD =, CD 1 =. Следовательно, DE = Ответ: Призма 5
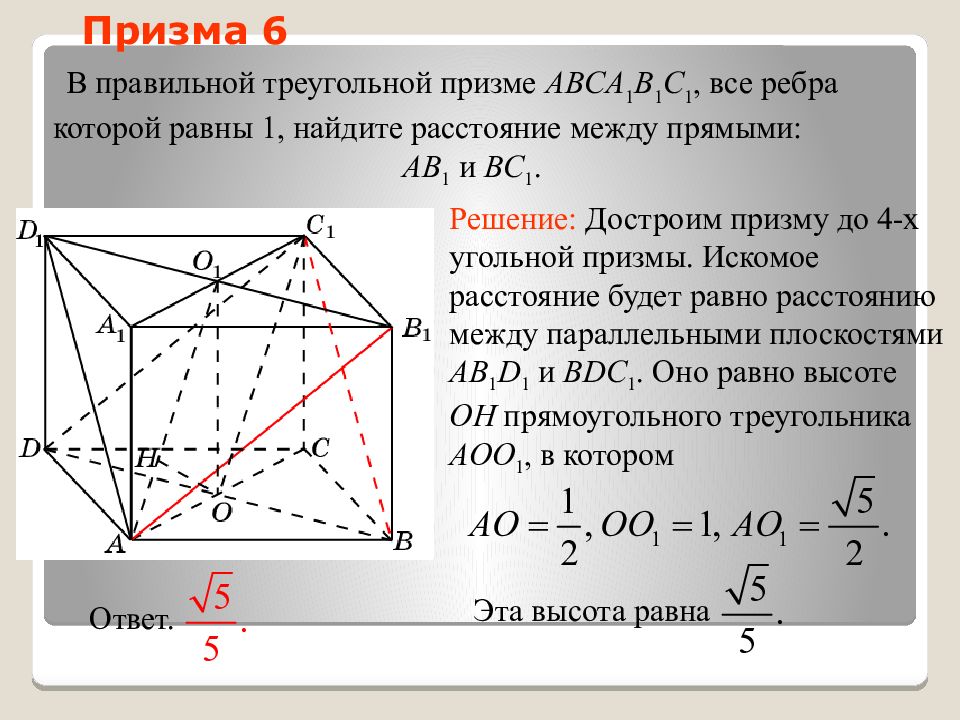
Слайд 39: Призма 6
В правильной треугольной призме ABCA 1 B 1 C 1, все ребра которой равны 1, найдите расстояние между прямыми: AB 1 и BC 1. Призма 6 Решение: Достроим призму до 4-х угольной призмы. Искомое расстояние будет равно расстоянию между параллельными плоскостями AB 1 D 1 и BDC 1. Оно равно высоте OH прямоугольного треугольника AOO 1, в котором Эта высота равна Ответ.
Слайд 40: Призма 7
В правильной 6-й призме A … F 1, ребра которой равны 1, найдите расстояние между прямыми: AB и A 1 B 1. Ответ: 1. Призма 7
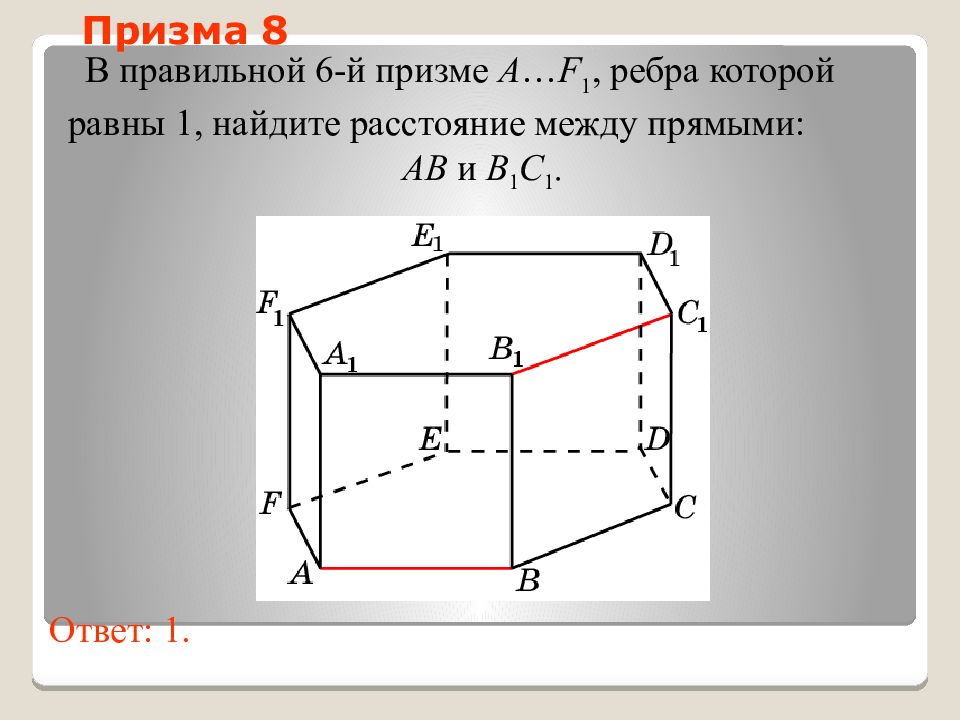
Слайд 41: Призма 8
В правильной 6-й призме A … F 1, ребра которой равны 1, найдите расстояние между прямыми: AB и B 1 C 1. Ответ: 1. Призма 8
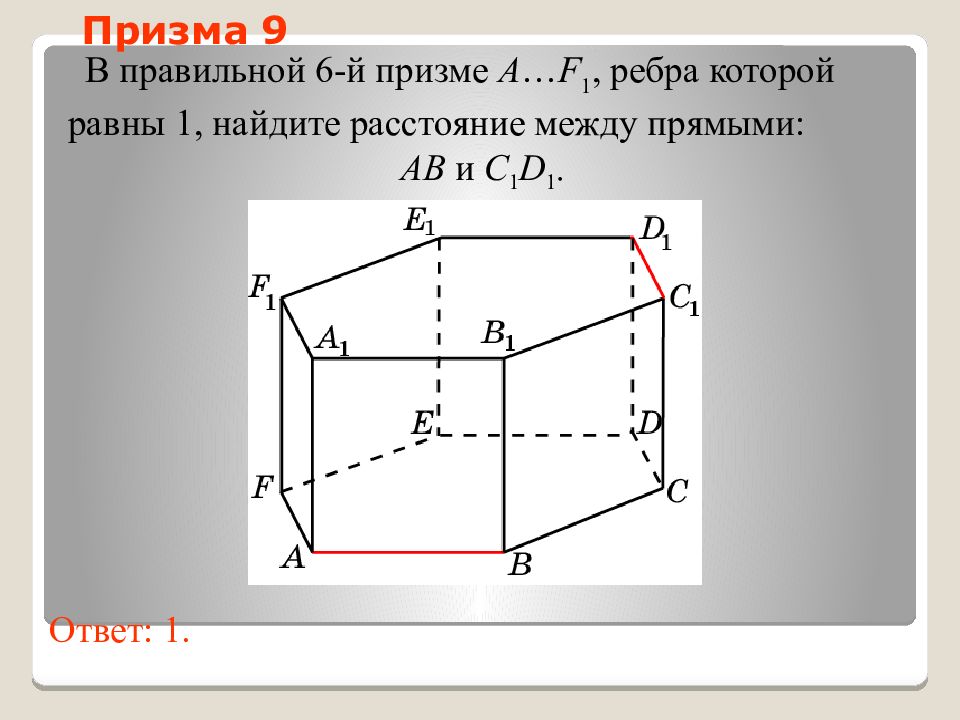
Слайд 42: Призма 9
В правильной 6-й призме A … F 1, ребра которой равны 1, найдите расстояние между прямыми: AB и C 1 D 1. Ответ: 1. Призма 9
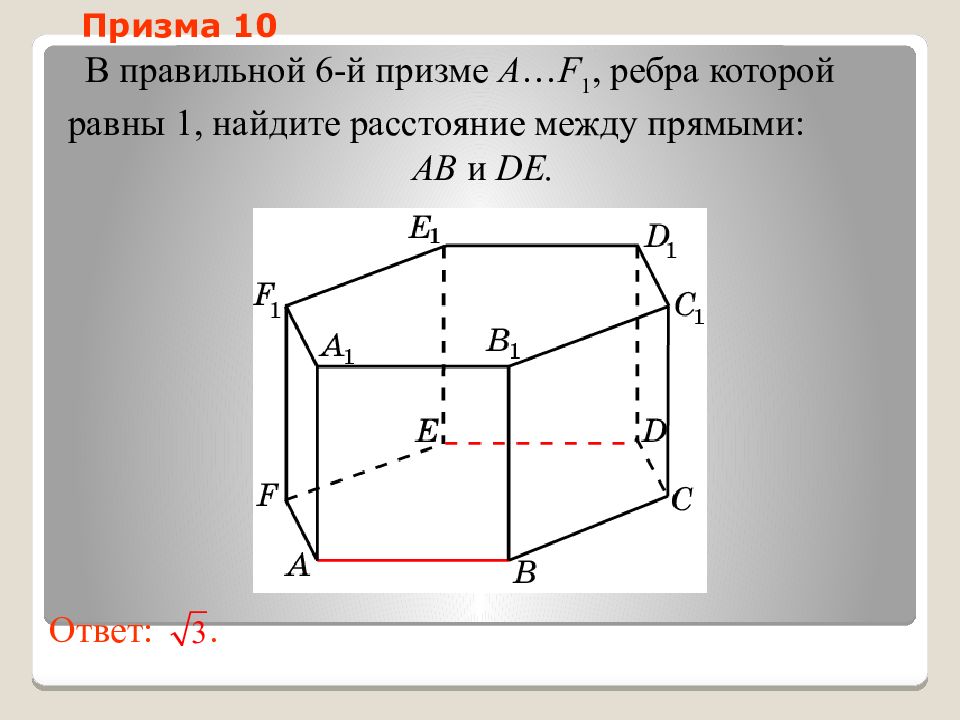
Слайд 43: Призма 10
В правильной 6-й призме A … F 1, ребра которой равны 1, найдите расстояние между прямыми: AB и DE. Ответ:. Призма 10
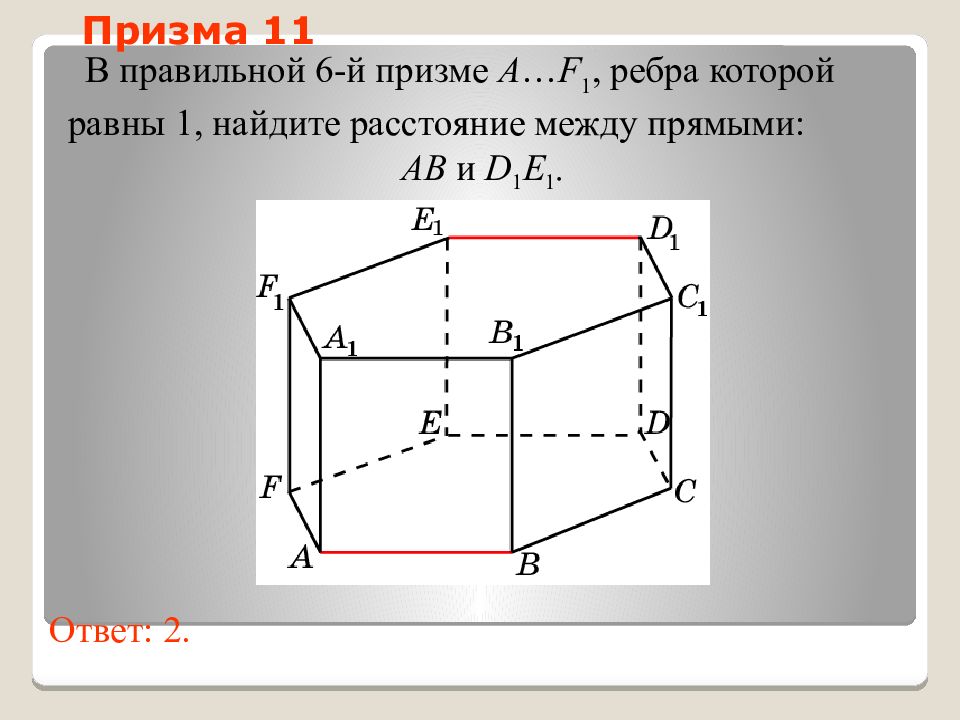
Слайд 44: Призма 11
В правильной 6-й призме A … F 1, ребра которой равны 1, найдите расстояние между прямыми: AB и D 1 E 1. Ответ: 2. Призма 11
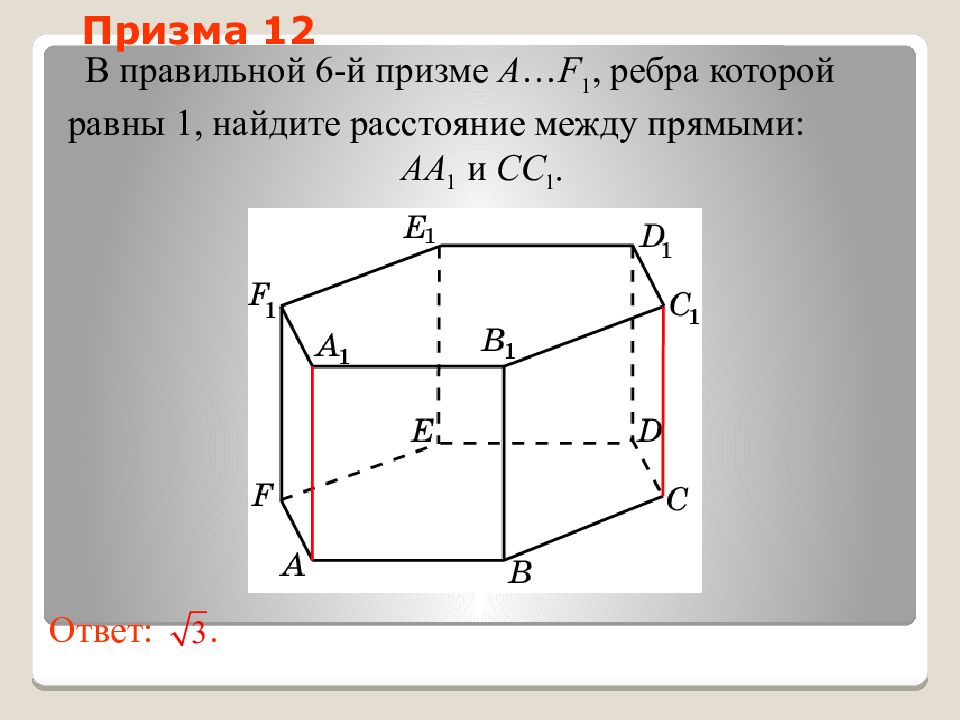
Слайд 45: Призма 12
В правильной 6-й призме A … F 1, ребра которой равны 1, найдите расстояние между прямыми: AA 1 и CC 1. Ответ:. Призма 12
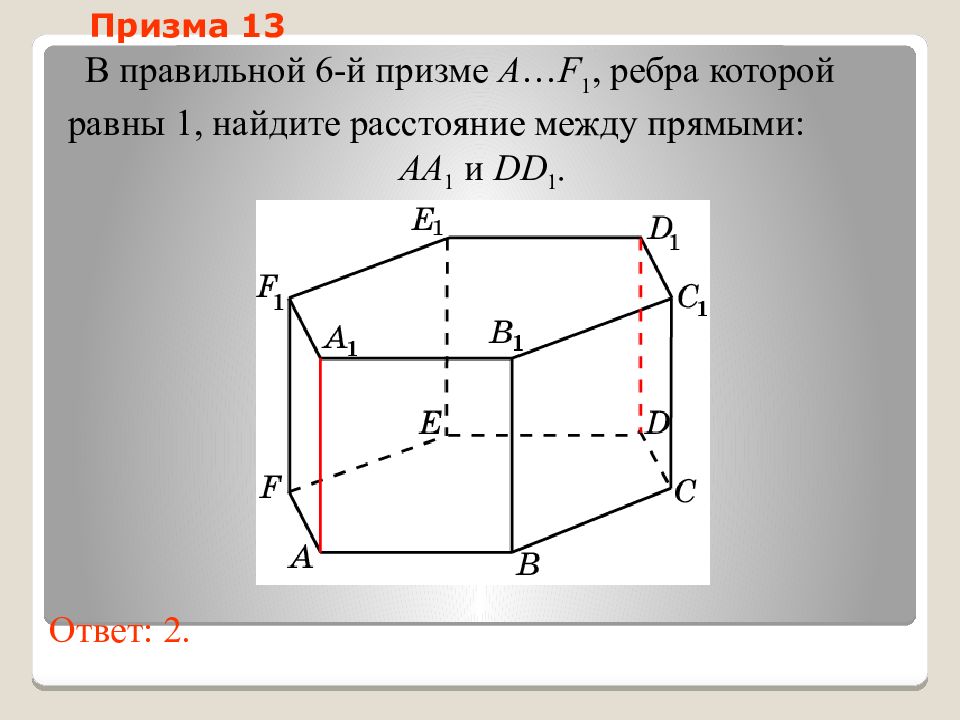
Слайд 46: Призма 13
В правильной 6-й призме A … F 1, ребра которой равны 1, найдите расстояние между прямыми: AA 1 и DD 1. Ответ: 2. Призма 13
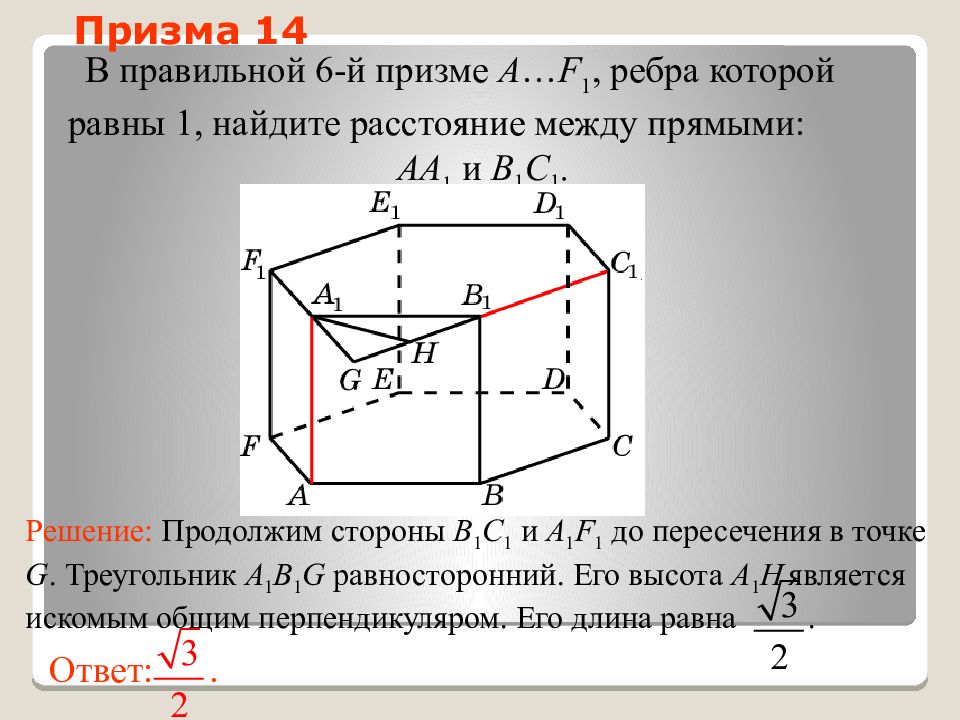
Слайд 47: Призма 14
В правильной 6-й призме A … F 1, ребра которой равны 1, найдите расстояние между прямыми: AA 1 и B 1 C 1. Ответ:. Решение: Продолжим стороны B 1 C 1 и A 1 F 1 до пересечения в точке G. Треугольник A 1 B 1 G равносторонний. Его высота A 1 H является искомым общим перпендикуляром. Его длина равна. Призма 14
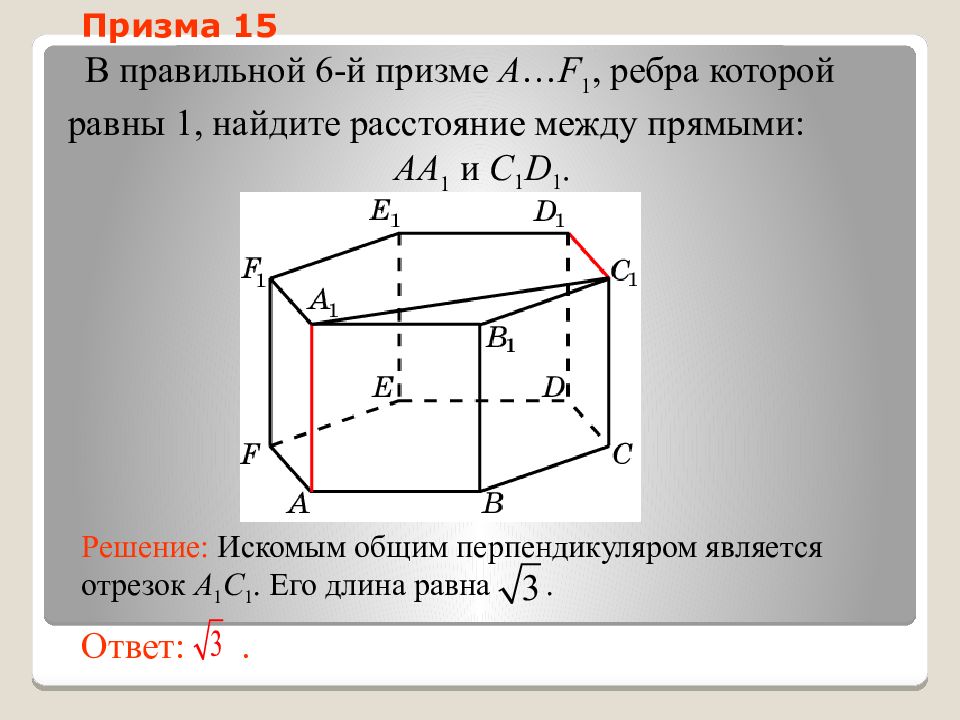
Слайд 48: Призма 15
В правильной 6-й призме A … F 1, ребра которой равны 1, найдите расстояние между прямыми: AA 1 и C 1 D 1. Ответ:. Решение: Искомым общим перпендикуляром является отрезок A 1 C 1. Его длина равна. Призма 15
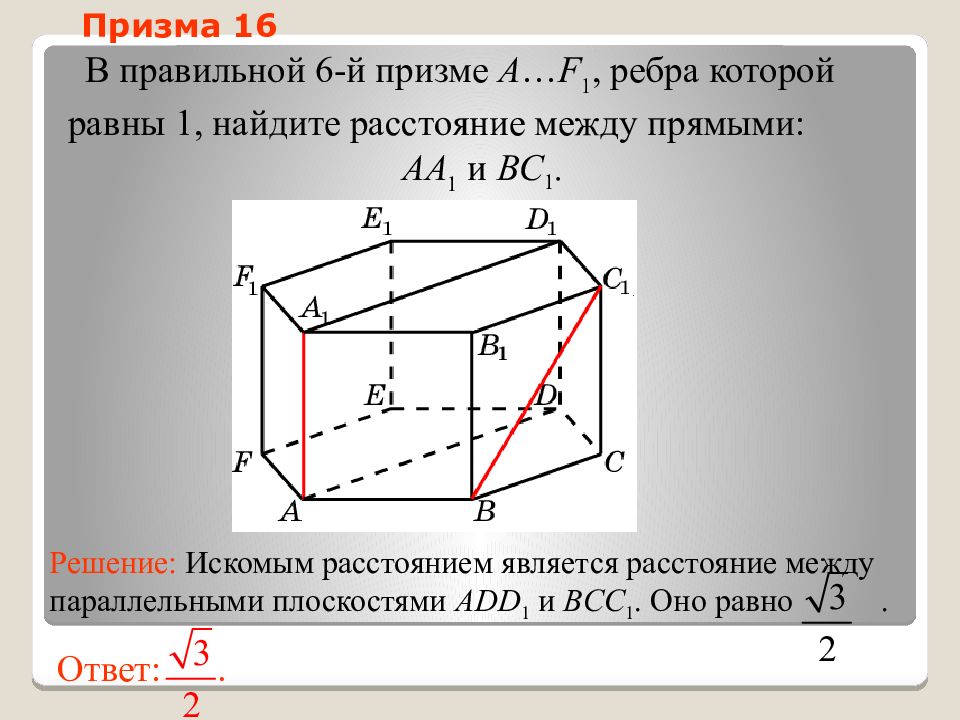
Слайд 49: Призма 16
В правильной 6-й призме A … F 1, ребра которой равны 1, найдите расстояние между прямыми: AA 1 и BC 1. Ответ:. Решение: Искомым расстоянием является расстояние между параллельными плоскостями ADD 1 и BCC 1. Оно равно. Призма 16
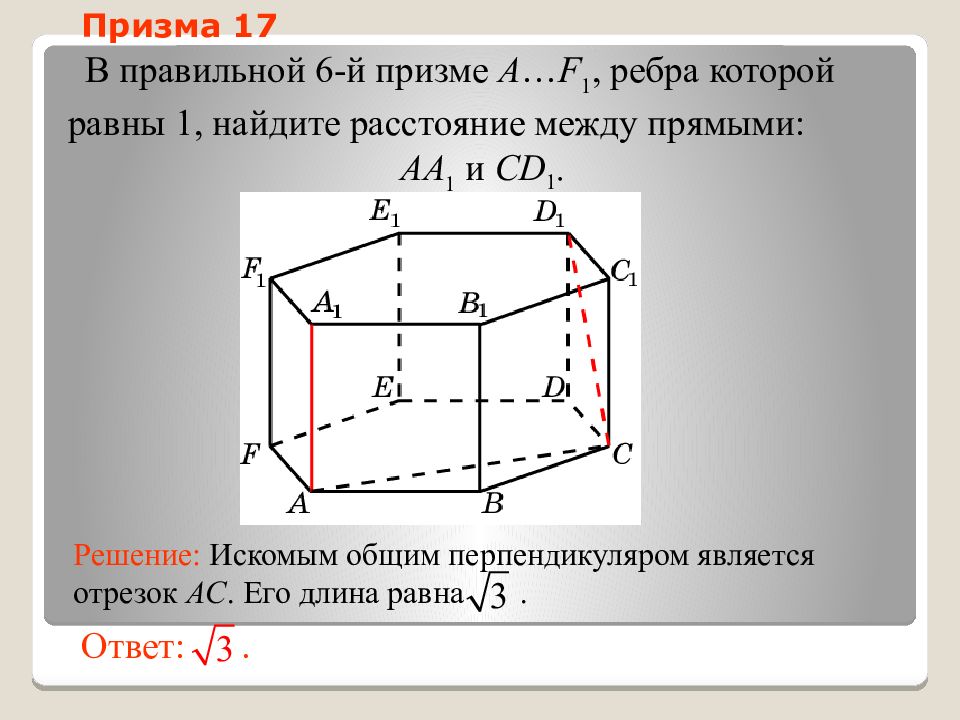
Слайд 50: Призма 17
В правильной 6-й призме A … F 1, ребра которой равны 1, найдите расстояние между прямыми: AA 1 и CD 1. Ответ:. Решение: Искомым общим перпендикуляром является отрезок AC. Его длина равна. Призма 17
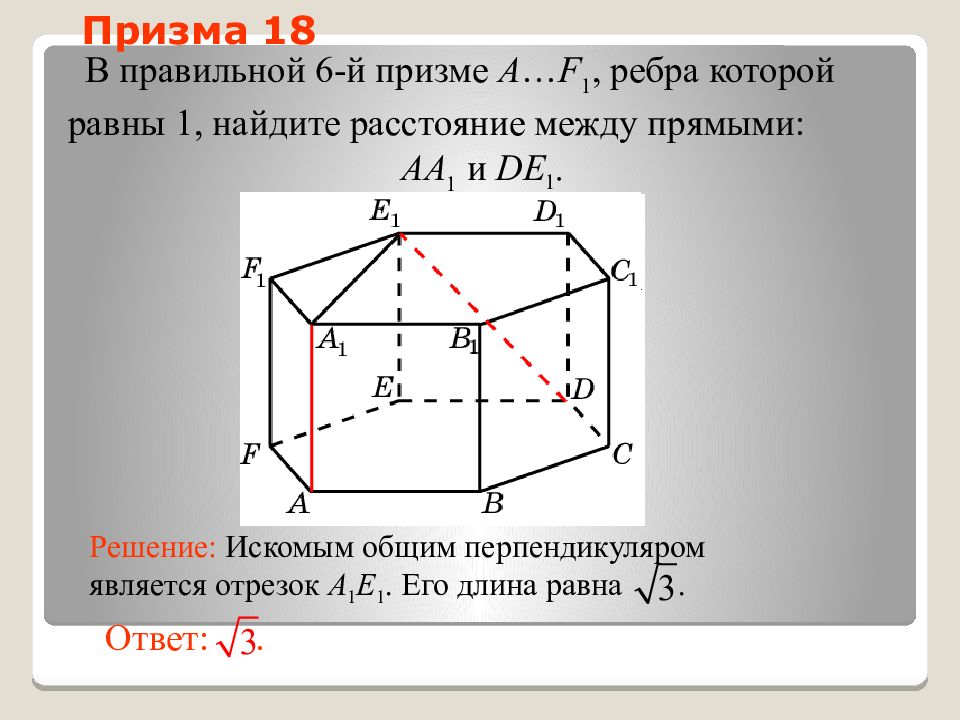
Слайд 51: Призма 18
В правильной 6-й призме A … F 1, ребра которой равны 1, найдите расстояние между прямыми: AA 1 и DE 1. Ответ:. Решение: Искомым общим перпендикуляром является отрезок A 1 E 1. Его длина равна. Призма 18
Слайд 52: Призма 19
В правильной 6-й призме A … F 1, ребра которой равны 1, найдите расстояние между прямыми: AA 1 и BD 1. Решение: Искомым общим перпендикуляром является отрезок AB. Его длина равна 1. Ответ: 1. Призма 19
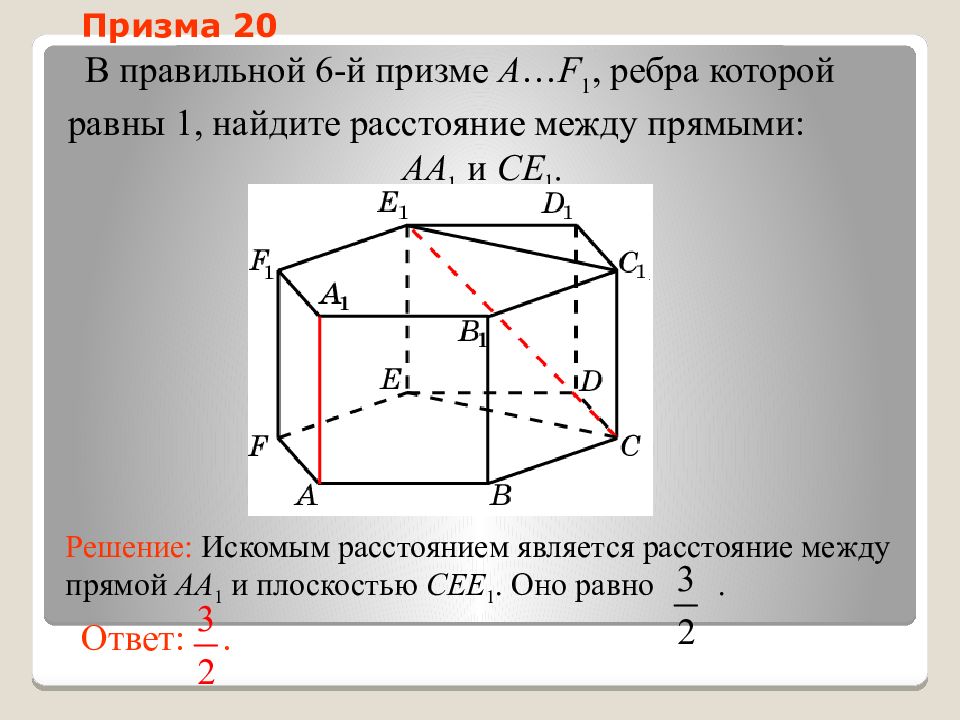
Слайд 53: Призма 20
В правильной 6-й призме A … F 1, ребра которой равны 1, найдите расстояние между прямыми: AA 1 и CE 1. Ответ:. Решение: Искомым расстоянием является расстояние между прямой AA 1 и плоскостью CEE 1. Оно равно. Призма 20
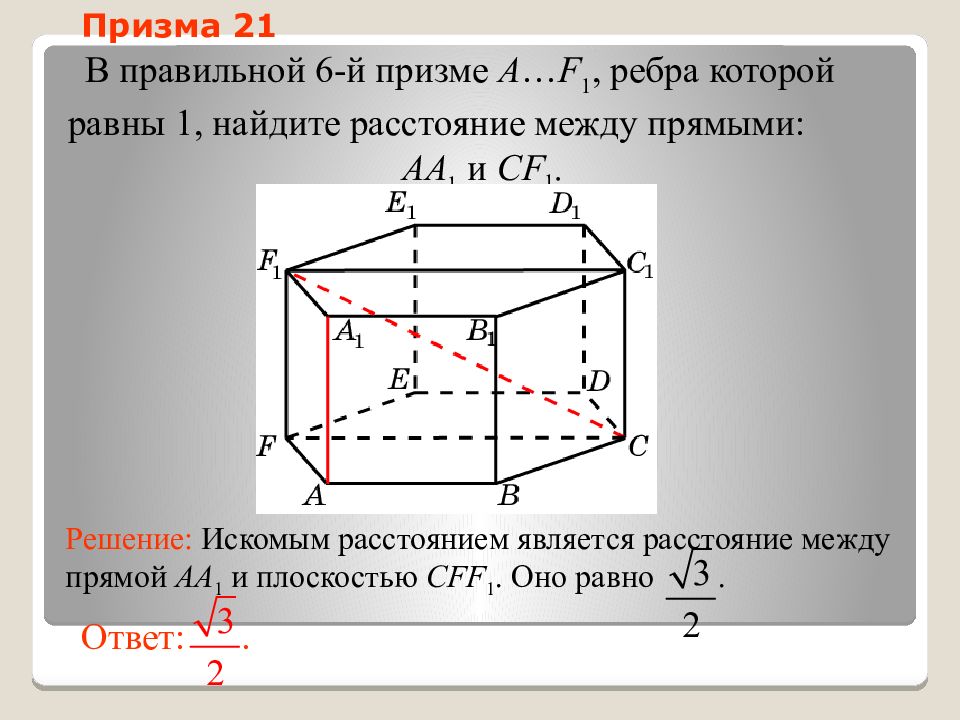
Слайд 54: Призма 21
В правильной 6-й призме A … F 1, ребра которой равны 1, найдите расстояние между прямыми: AA 1 и CF 1. Ответ:. Решение: Искомым расстоянием является расстояние между прямой AA 1 и плоскостью CFF 1. Оно равно. Призма 21
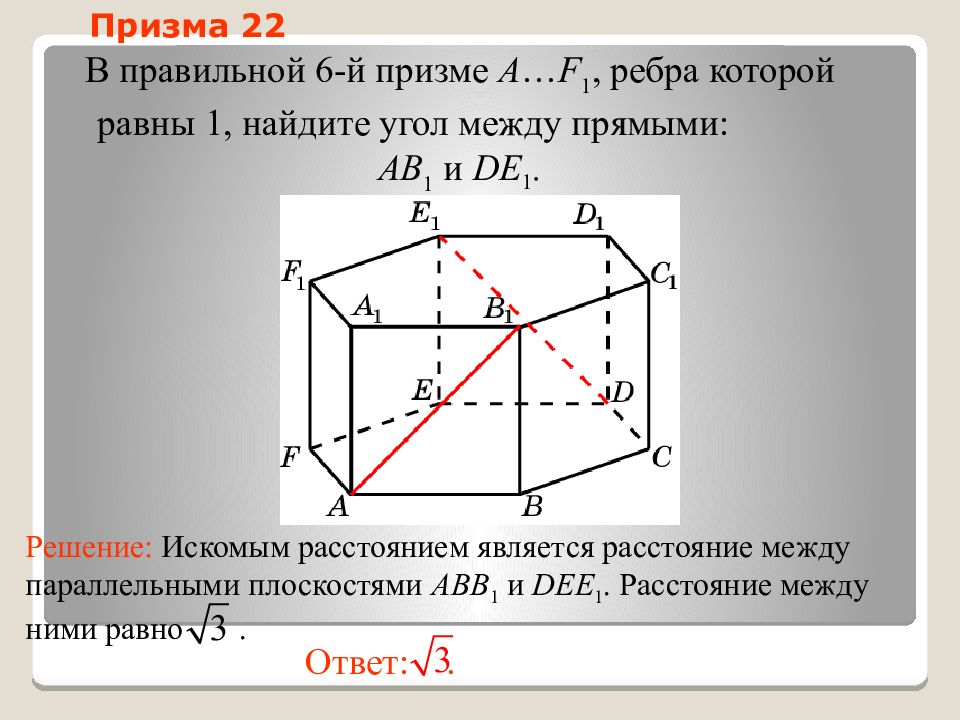
Слайд 55: Призма 22
В правильной 6-й призме A … F 1, ребра которой равны 1, найдите у гол между прямыми: AB 1 и DE 1. Ответ:. Решение: Искомым расстоянием является расстояние между параллельными плоскостями ABB 1 и DEE 1. Расстояние между ними равно. Призма 22
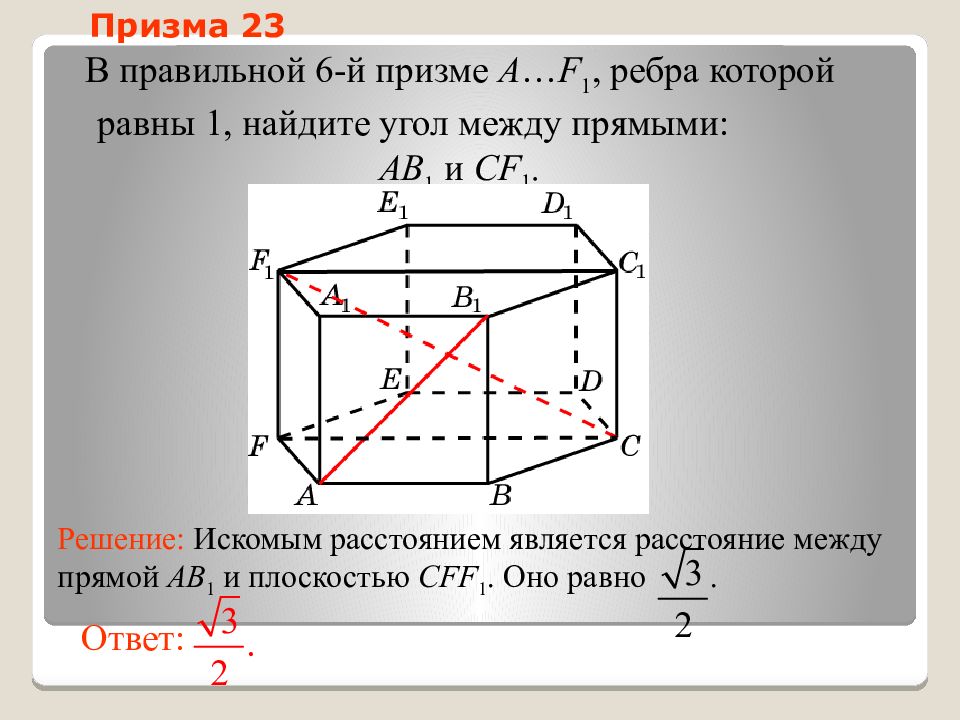
Слайд 56: Призма 23
В правильной 6-й призме A … F 1, ребра которой равны 1, найдите у гол между прямыми: AB 1 и CF 1. Ответ: Решение: Искомым расстоянием является расстояние между прямой AB 1 и плоскостью CFF 1. Оно равно. Призма 23
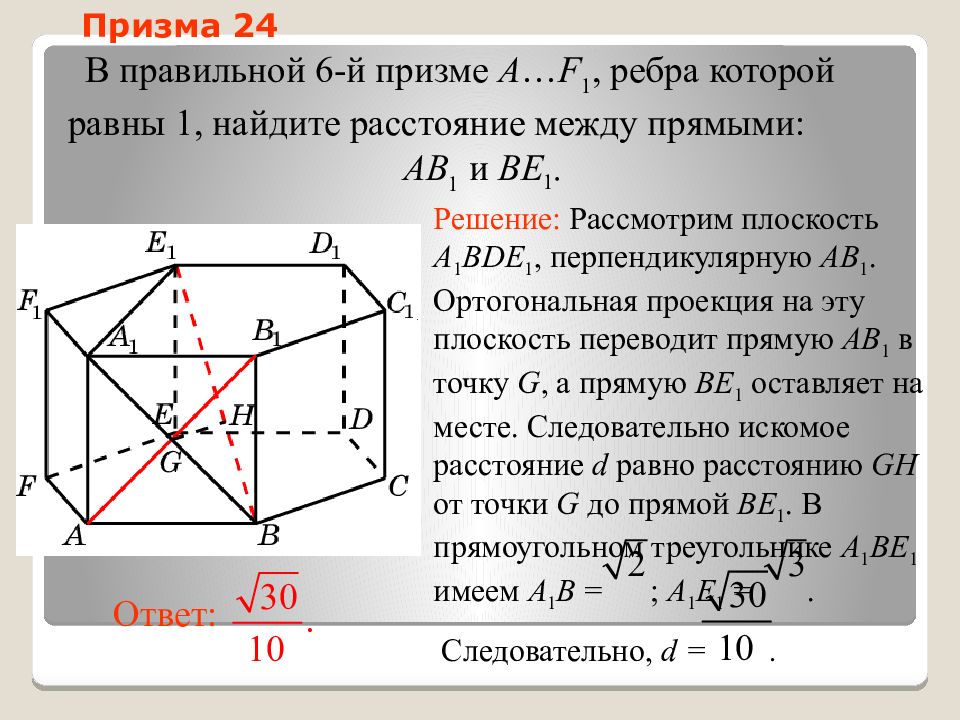
Последний слайд презентации: Расстояние между скрещивающимися прямыми: Призма 24
В правильной 6-й призме A … F 1, ребра которой равны 1, найдите расстояние между прямыми: AB 1 и BE 1. Решение: Рассмотрим плоскость A 1 BDE 1, перпендикулярную AB 1. Ортогональная проекция на эту плоскость переводит прямую AB 1 в точку G, а прямую BE 1 оставляет на месте. Следовательно искомое расстояние d равно расстоянию GH от точки G до прямой BE 1. В прямоугольном треугольнике A 1 BE 1 имеем A 1 B = ; A 1 E 1 =. Следовательно, d =. Ответ: Призма 24