Первый слайд презентации: Системы счисления
Виды систем счисления История непозиционных систем счисления Перевод чисел из десятичной СС в двоичную и обратно Самостоятельная работа
Слайд 2
« Мысль – выражать все числа немногими знаками, придавая им не только значение по форме, но еще и значение по месту, настолько проста, что именно из-за этой простоты трудно оценить, насколько она удивительна …» Пьер Симон Лаплас (1 7 49 – 18 27 гг.)
Слайд 3
Система счисления - это совокупность приемов и правил записи чисел с помощью определенного набора символов (некоторый способ кодирования числовой информации).
Слайд 4
Системы счисления непозиционные позиционные Цифры – знаки которые используются для записи чисел
Слайд 5: История развития систем счисления
Слайд 6: Непозиционные системы счисления
Как только люди начали считать, у них появилась потребность в записи чисел. Находки археологов на стоянках первобытных людей свидетельствуют о том, что первоначально количество предметов отображали равным количеством каких-либо значков (бирок): Зарубок черточек точек
Слайд 7
Позже, для облегчения счета, эти значки стали группировать по три или по пять. Такая система записи чисел называется единичной (унарной), так как любое число в ней образуется путем повторения одного знака, символизирующего единицу. Отголоски единичной системы счисления встречаются и сегодня. Так, чтобы узнать, на каком курсе учится курсант военного училища, нужно сосчитать, какое количество полосок нашито на его рукаве. Сами того не осознавая, единичной системой счисления пользуются малыши, показывая на пальцах свой возраст, а счетные палочки используется для обучения учеников 1-го класса счету
Слайд 8
Единичная система — не самый удобный способ записи чисел. Записывать таким образом большие количества утомительно, и сами записи при этом получаются очень длинными. С течением времени возникли иные, более удобные, системы счисления.
Слайд 9
Древнеегипетская десятичная непозиционная система счисления. Примерно в третьем тысячелетии до нашей эры древние египтяне придумали свою числовую систему, в которой для обозначения ключевых чисел 1, 10, 100 и т.д. использовались специальные значки — иероглифы. Все остальные числа составлялись из этих ключевых при помощи операции сложения. Система счисления Древнего Египта является десятичной, но непозиционной.
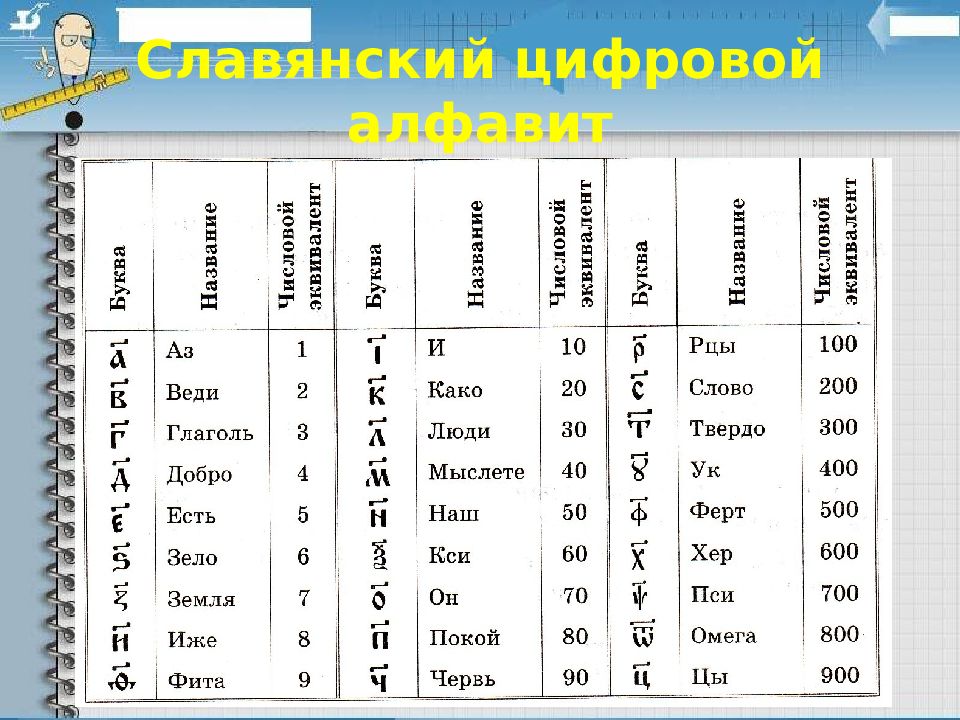
Слайд 11: Алфавитные системы счисления
Слайд 14
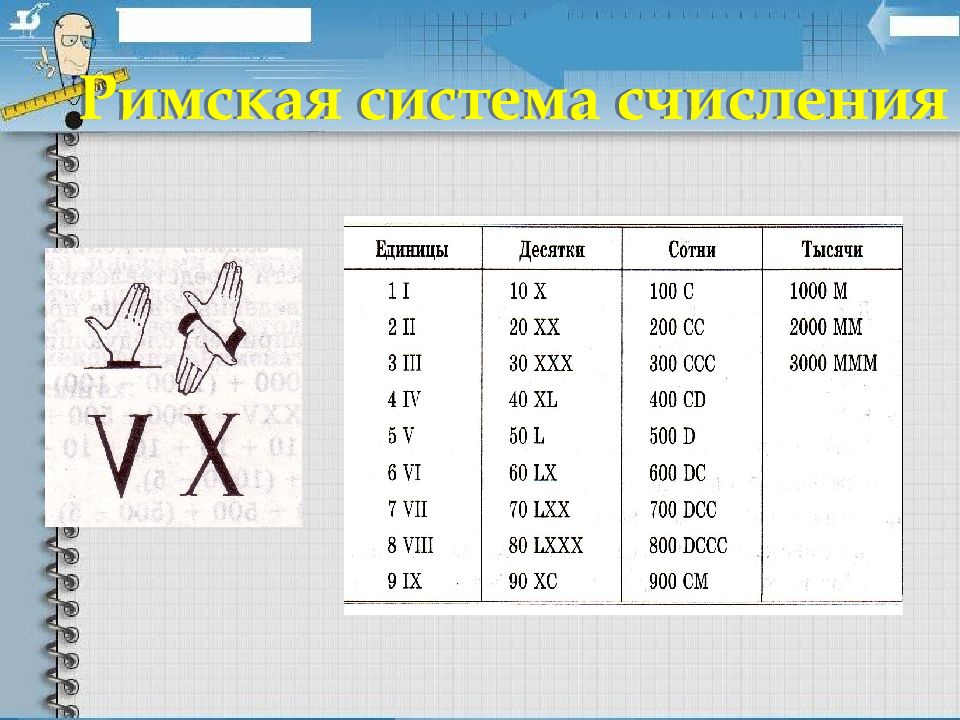
Примером непозиционной системы, которая сохранилась до наших дней, может служить система счисления, которая применялась более двух с половиной тысяч лет назад в Древнем Римскими цифрами пользовались очень долго. Еще 200 лет назад в деловых бумагах числа должны были обозначаться римскими цифрами (считалось, что обычные арабские цифры легко подделать). Римская система счисления сегодня используется, в основном, для наименования знаменательных дат, томов, разделов и глав в книгах.
Слайд 16
В римских числах цифры записываются слева направо в порядке убывания. В таком случае их значения складываются. Если же слева записана меньшая цифра, а справа - большая, то их значения вычитаются. Пример : CCXXXII=100+100+10+10+10+1+1=232 VI=5+1=6 IV=5-1=4 MCMXCVIII= =1000+(-100+1000)+(-10+100)+5+1+1+1=1998
Слайд 17: Позиционные системы счисления
Основные достоинства любой позиционной системы счисления — простота выполнения арифметических операций и ограниченное количество символов (цифр), необходимых для записи любых чисел.
Слайд 18
В позиционных системах счисления количественное значение цифры зависит от ее позиции в числе. Позиция цифры в числе называется разрядом. Каждая позиционная сс имеет определенный алфавит цифр и основание.
Слайд 19
19 Для записи чисел в позиционной системе с основанием п нужно иметь алфавит из п цифр. Обычно для этого при п < 10 используют п первых арабских цифр, а при п >10 к десяти арабским добавляют буквы. Вот примеры алфавитов нескольких систем. Система счисления основание Алфавит Десятичная п=10 0,1,2,3,4,5,6,7,8,9 Двоичная п=2 0,1 Восьмеричная п=8 0,1,2,3,4,5,6,7 Шестнадцатеричная п=16 0,1,2,3,4,5,6,7,8,9, А(10), В(11), C(12), D(13),E(14),F(15)
Слайд 20: Развернутой формулой числа называется запись в виде:
А q =a n *q n +a n-1 *q n-1 +…+a 0 *q 0 +a -1 *q -1 + …+a -m *q -m где А q = само число q -основание системы счисления а – цифры данной системы счисления п – число разрядов Развернутая форма числа в двоичной сс : А 2 =a n *2 n +a n-1 *2 n-1 +…+a 0 *2 0 +a -1 *2 -1 + …+a -m *2 -m
Последний слайд презентации: Системы счисления: Для перевода целого числа из СС с основанием 10 в СС с основанием 2 необходимо:
Это число разделить на 2, полученное частное вновь делят на 2 и так до тех пор пока последнее частное не окажется меньше 2. В результате записать в одну строку последнее частное и все остатки, начиная с последнего. 53 10 = 110101 2 Проверка: 110101 2 =1*2 5 +1*2 4 +0*2 3 +1*2 2 +0*2 1 +1*2 0 + =32+16+4+1=53