Системы счисления. Перевод чисел из одной системы счисления в другую 1.Перевод из десятичной системы а) целое число б) правильная десятичная дробь в) вещественное число. 2. Перевод в десятичную систему 3. Перевод из двоичной в восьмеричную и шестнадцатеричную системы. 4. Перевод из восьмеричной и шестнадцатеричной системы в двоичную 5. Перевод из восьмеричной в шестнадцатеричную систему и обратно. Арифметические операции в позиционных системах счисления 1. сложение 2. вычитание 3. умножение 4. деление Представление чисел в компьютере 1. целые числа 2. вещественные числа Выход
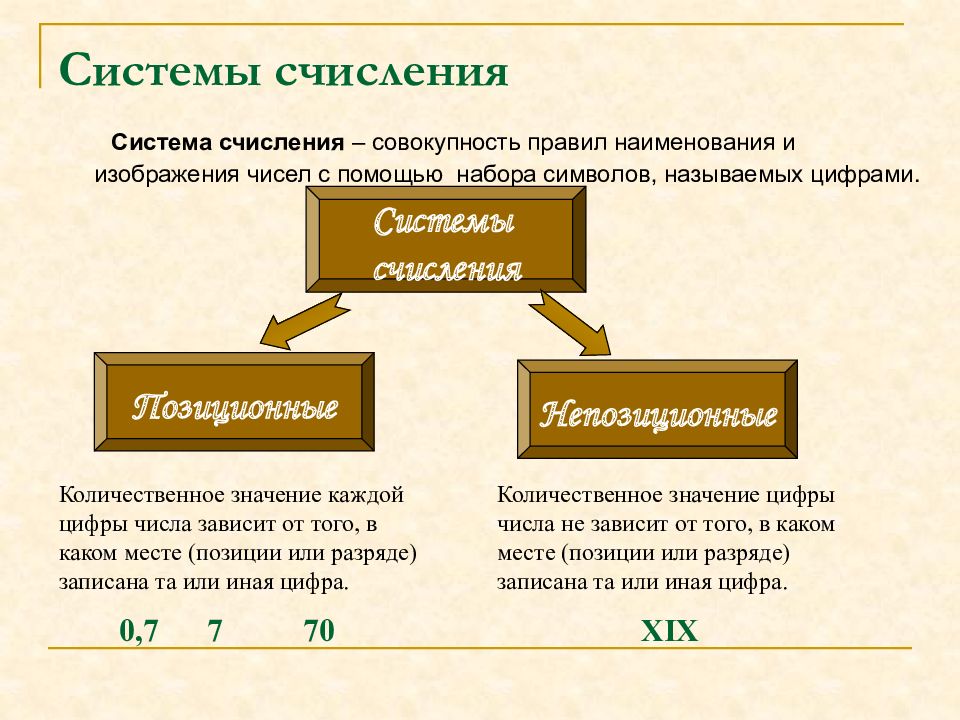
Система счисления – совокупность правил наименования и изображения чисел с помощью набора символов, называемых цифрами. Количественное значение каждой цифры числа зависит от того, в каком месте (позиции или разряде) записана та или иная цифра. 0,7 7 70 Количественное значение цифры числа не зависит от того, в каком месте (позиции или разряде) записана та или иная цифра. XIX Позиционные Непозиционные Системы счисления
Система римских цифр, основанная на употреблении латинских букв для десятичных разрядов I = 1, X = 10, С = 100, М = 1 000 и их половин V = 5, L = 50, D = 500. Число в системе римских чисел записывается по схеме «тысячи — сотни — десятки — единицы ». Пример. Записать число 1974 в системе римских цифр. Решение. Выпишем тысячи, сотни, десятки и единицы: 1 000 — M ; 900 — CM ; 70 — LXX ; 4 — IV. 1974 = MCMLXXIV
сложность представления больших чисел (больше 10 000); сложность выполнения арифметических операций над числами, записанными с помощью этих систем счисления.
Первая позиционная система счисления была придумана еще в Древнем Вавилоне, причем вавилонская нумерация была шестидесятеричная, т.е. в ней использовалось шестьдесят цифр! В XIX веке довольно широкое распространение получила двенадцатеричная система счисления. В настоящее время наиболее распространены десятичная, двоичная, восьмеричная и шестнадцатеричная системы счисления. «Мысль – выражать все числа немногими знаками, придавая им значение по форме, ещё значение по месту, настолько проста, что именно из-за этой простоты трудно оценить, насколько она удивительна» Пьер Симон Лапласс
Количество различных символов, используемых для изображения числа в позиционных системах счисления, называется основанием системы счисления. Позиции цифр называются разрядами. Основание системы счисления показывает во сколько раз изменяется количественное значение цифры при перемещении её на соседнюю позицию За основание системы можно принять любое натуральное число не менее 2.
Компьютеры используют двоичную систему, так как для её реализации нужны технические устройства с двумя устойчивыми состояниями, представление информации с помощью только двух состояний надежно и помехоустойчиво, возможно применение аппарата булевой алгебры для выполнения логических преобразований, двоичная арифметика намного проще десятичной Двоичная система, удобная для компьютера, для человека неудобна из-за её громоздкости и непривычной записи. Для того, чтобы понимать слово компьютера, разработаны восьмеричная и шестнадцатеричная системы счисления. Числа в этих системах требуют в 3/4 раза меньше разрядов, чем в двоичной системе.
Система счисления Основание Алфавит цифр Десятичная 10 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 Двоичная 2 0, 1 Восьмеричная 8 0, 1, 2, 3, 4, 5, 6, 7 Шестнадцатеричная 16 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
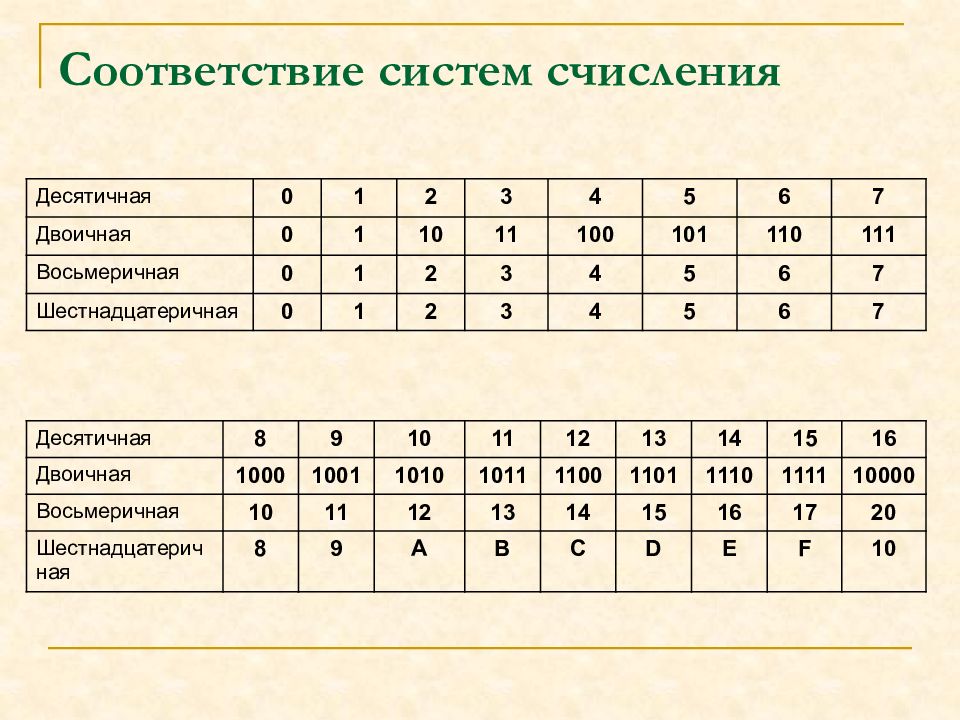
Десятичная 0 1 2 3 4 5 6 7 Двоичная 0 1 10 11 100 101 110 111 Восьмеричная 0 1 2 3 4 5 6 7 Шестнадцатеричная 0 1 2 3 4 5 6 7 Десятичная 8 9 10 11 12 13 14 15 16 Двоичная 1000 1001 1010 1011 1100 1101 1110 1111 10000 Восьмеричная 10 11 12 13 14 15 16 17 20 Шестнадцатеричная 8 9 A B C D E F 10
A q = a n-1 q n-1 +a n-2 q n-2 +…+a 1 q 1 +a 0 q 0 +a -1 q -1 + … +a -m q -m, где a i – цифры системы счисления, n и m –число целых и дробных разрядов соответственно C окращённая форма записи числа A q в системе счисления с основанием q A q = a n-1 a n-2 … a 1 a 0, a -1 … a -m, где a i – цифры системы счисления, n и m –число целых и дробных разрядов соответственно
32478 10 =3*10000+2*1000+4*100+7*10+8= 3*10 4 +2*10 3 +4*10 2 +7*10 1 +8*10 0 26,387 10 =2*10 1 +6*10 0 +3*10 -1 +8*10 -2 +7*10 -3 101101, 011 2 =1*10 101 +0*10 100 +1*10 11 +1*10 10 + +0*10 1 +1*10 0 +0*10 -1 +1*10 -10 +1*10 -11 15 FC 16 =1*10 3 +5*10 2 +F*10 1 +C !!! В любой системе счисление ее основание записывается как 10 В меню назад
Алгоритм перевода: Основание новой системы счисления выразить в десятичной и все последующие действия производить в десятичной системе счисления. Последовательно делить с остатком данное число и получаемые целые частные на основание новой системы счисления до тех пор, пока частное не станет равно нулю. Полученные остатки выразить цифрами алфавита новой системы счисления Записать число в новой системе счисления из полученных остатков, начиная с последнего.
Пример. Перевести число 75 из десятичной системы счисления в двоичную, восьмеричную и шестнадцатеричную. 75 2 74 1 37 2 36 1 18 2 18 0 9 2 8 1 4 2 4 0 2 2 2 0 2 1 0 0 1 75 10 = 1001011 2
Пример 1. Перевести число 75 из десятичной системы счисления в двоичную, восьмеричную и шестнадцатеричную. 75 8 7 2 3 9 8 8 1 1 8 0 1 0 75 10 = 113 8 75 16 64 11 4 16 0 4 0 75 10 = 4B 16 В меню
Алгоритм перевода: Основание новой системы счисления выразить в десятичной и все последующие действия производить в десятичной системе счисления Последовательно умножать десятичную дробь и получаемые дробные части произведений на основание новой системы счисления до тех пор, пока дробная часть не станет равна нулю или не будет достигнута необходимая точность перевода. Полученные целые части произведений выразить цифрами алфавита новой системы счисления. Записать дробную часть числа в новой системе счисления начиная с целой части первого произведения.
Пример. Перевести число 0,1875 из десятичной системы в счисления в двоичную, восьмеричную и шестнадцатеричную. 0,1875 2 0,3750 2 0,7500 2 1,5000 2 1,0000 0,1875 10 = 0,0011 2 0,1875 8 1,5000 8 4,0000 0,1875 10 = 0,14 8 0,1875 16 1,1250 3,0000 0,1875 10 = 0,3 16 1,875
Пример. Перевести число 0,35 из десятичной системы в счисления в двоичную, восьмеричную и шестнадцатеричную. 0,35 2 0,70 2 1,40 2 0,80 2 1,60 2 1,20 0,35 10 0,01011 2 0,35 8 2,80 8 6,40 8 3,20 0,35 10 0,263 8 0,35 16 5,60 16 9,60 0,35 10 0,59 16 В меню
При переводе смешанных дробей отдельно по своим правилам переводятся целая и дробные части, результаты перевода разделяются запятой.
Пример. Перевести число 68, 74 из десятичной системы в счисления в двоичную, восьмеричную и шестнадцатеричную 68 2 68 0 3 4 2 3 4 0 1 7 2 1 6 1 8 2 8 0 4 2 4 0 2 2 2 0 2 1 0 0 1 0,74 2 1,48 2 0,96 2 1,92 2 1,84 2 1,68 68,74 10 = 1000100,10111 2
Пример. Перевести число 68, 74 из десятичной системы в счисления в двоичную, восьмеричную и шестнадцатеричную 68 8 6 4 4 8 8 8 0 1 8 0 1 0 0,74 8 5,92 8 7,36 8 2,88 68,74 10 = 104,572 8
Пример. Перевести число 68, 74 из десятичной системы в счисления в двоичную, восьмеричную и шестнадцатеричную 68 16 6 4 4 4 16 0 4 0 0,74 16 11,84 16 13,44 68,74 10 = 44, BD 8 В меню
При переводе числа из системы счисления с основанием q в десятичную надо представить это число в виде суммы произведений степеней основания его системы счисления на соответствующие цифры числа. a n-1 q n-1 + a n-2 q n-2 + … + a 1 q 1 + a 0 q 0 + a -1 q -1 + … + a -m q -m и выполнить арифметические вычисления. q -основание системы счисления, представленное в десятичной системе
Пример. Перевести число 1011,1 из двоичной системы счисления в десятичную. 1 0 1 1, 1 2 -1 0 1 2 3 = 1∙2 3 + 0∙2 2 + 1∙2 1 + 1∙2 0 + 1∙2 -1 = 11,5 10 разряды число Пример. Перевести число 276,8 из восьмеричной системы счисления в десятичную. 2 7 6, 5 8 -1 0 1 2 = 2∙8 2 + 7∙8 1 + 6∙8 0 + 5∙8 -1 = 190,625 10 разряды число Пример. Перевести число 1 F 3 из шестнадцатеричной системы счисления в десятичную. 1 F 3 16 0 1 2 = 1∙16 2 + 15∙16 1 + 3∙16 0 = 499 10 разряды число В меню
Заменить каждую цифру восьмеричного/шестнадцатеричного числа соответствующим трехразрядным/четырехразрядным двоичным кодом. Пример. Перевести число 527,1 8 в двоичную систему счисления. 527,1 8 = 101 010 111, 001 5 2 7 1 2 Пример. Перевести число 1A3, F 16 в двоичную систему счисления. 1A3, F 16 = 000 1 1 010 00 11, 111 1 1 A 3 F 2 Таблица соответствия В меню
Для перехода от двоичной к восьмеричной/шестнадцатеричной системе счисления поступают следующим образом: двигаясь от запятой влево и вправо, разбивают двоичное число на группы по 3/4 разряда, дополняя при необходимости нулями крайние левую и правую группы. Затем каждую группу из 3/4 разрядов заменяют соответствующей восьмеричной/шестнадцатеричной цифрой. Пример 1 0 1 0 1 0 0 1,1 0 1 1 1 2 1 5 0 6 0 2 5 = 251,65 8 1 0 1 0 1 0 0 1,1 0 1 1 1 2 9 B A 0 00 8 = A9, B8 16 Таблица соответствия В меню
При переходе из восьмеричной системы счисления в шестнадцатеричную и обратно вначале производится перевод чисел из исходной системы счисления в двоичную, а затем – в конечную систему. Пример. Перевести число 527,1 8 в шестнадцатеричную систему счисления. 527,1 8 = Пример. Перевести число 1A3, F 16 в восьмеричную систему счисления. 1A3, F 16 = 101010111,011 2 7 6 0 5 =157,6 16 000 1 110100011,1111 2 3 7 4 00 6 4 =643,74 8 Таблица соответствия В меню
Правила выполнения основных арифметических операций в любой позиционной системе счисления подчиняются тем же законам, что и в десятичной системе. При сложении цифры суммируются по разрядам, и если при этом возникает переполнение разряда, то производится перенос в старший разряд. Переполнение разряда наступает тогда, когда величина числа в нем становится равной или большей основания системы счисления. При вычитании из меньшей цифры большей в старшем разряде занимается единица, которая при переходе в младший разряд будет равна основанию системы счисления
Если при умножении однозначных чисел возникает переполнение разряда, то в старший разряд переносится число кратное основанию системы счисления. При умножении многозначных чисел в различных позиционных системах применяется алгоритм перемножения чисел в столбик, но при этом результаты умножения и сложения записываются с учетом основания системы счисления. Деление в любой позиционной системе производится по тем же правилам, как и деление углом в десятичной системе, то есть сводится к операциям умножения и вычитания.
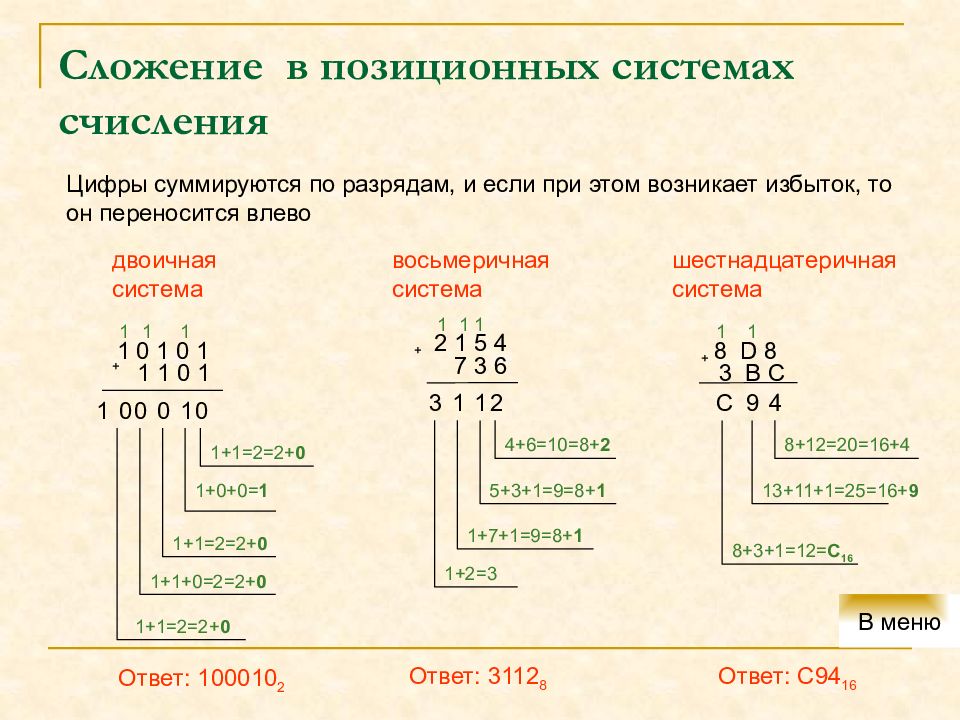
Цифры суммируются по разрядам, и если при этом возникает избыток, то он переносится влево 1 0 1 0 1 + 1 1 0 1 двоичная система 0 1+1=2=2+ 0 1 1 1+0+0= 1 0 1+1=2=2+ 0 1 0 1+1+0=2=2+ 0 1 0 1+1=2=2+ 0 1 Ответ: 100010 2 2 1 5 4 + 7 3 6 2 4+6=10=8+ 2 1 1 5+3+1=9=8+ 1 1 1+7+1=9=8+ 1 1 3 1+2=3 восьмеричная система 1 Ответ: 3112 8 шестнадцатеричная система 8 D 8 + 3 B C 4 8 + 12 = 2 0= 16 + 4 1 9 13 + 11 +1= 25 = 16 + 9 8 + 3 +1= 12 = C 16 C 1 Ответ: C94 16 В меню
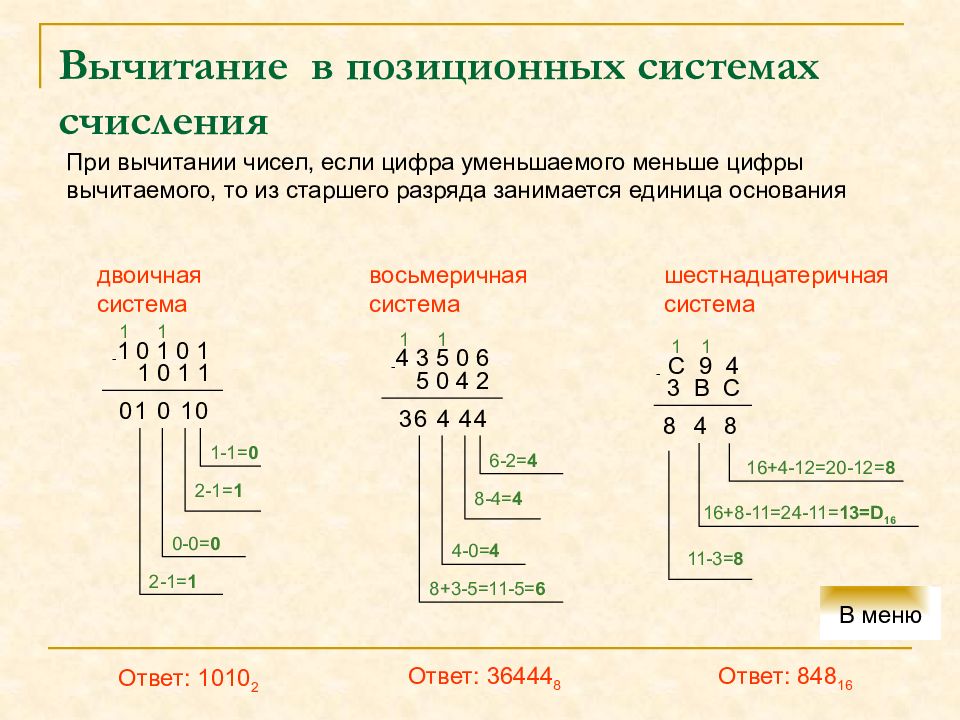
При вычитании чисел, если цифра уменьшаемого меньше цифры вычитаемого, то из старшего разряда занимается единица основания двоичная система Ответ: 1010 2 восьмеричная система Ответ: 36444 8 шестнадцатеричная система Ответ: 848 16 1 0 1 0 1 - 1 0 1 1 0 1-1= 0 1 1 2-1= 1 0 0-0= 0 1 2-1= 1 1 0 4 3 5 0 6 - 5 0 4 2 4 6-2= 4 1 4 8-4= 4 4 4-0= 4 6 8+3-5=11-5= 6 1 3 С 9 4 - 3 В С 8 16+4-12=20-12= 8 1 4 16+8-11=24-11= 13= D 16 8 11 - 3 = 8 1 В меню
3 ∙3=9=8+ 1 Умножение в позиционных системах счисления При умножении многозначных чисел в различных позиционных системах применяется алгоритм перемножения чисел в столбик, но при этом результаты умножения и сложения записываются с учетом основания системы счисления двоичная система Ответ: 101011111 2 восьмеричная система Ответ: 13351 8 1 1 0 1 1 х 1 1 0 1 1 1 0 1 1 1 1 0 1 1 1 1 0 1 1 1 0 1 0 1 1 1 1 1 1+1+1=3=2+ 1 1 1+1+1=3=2+ 1 1 1+1=2=2+ 0 1 1 1 6 3 х 6 3 5 3 1 1 6 ∙3+1=19=16+ 3 =2∙8+ 3 2 1 ∙3+2= 5 1 2 6 2 6 ∙3=18=16+ 2 =8∙2+ 2 6 ∙6+2=38=32+ 6 =4∙8+ 6 2 4 6 ∙1+4=10=8+ 2 1 3 3 5 1 6+5=11=8+ 3 1 В меню
Деление в любой позиционной системе производится по тем же правилам, как и деление углом в десятичной системе. При этом необходимо учитывать основание системы счисления. двоичная система Ответ: 10,1 2 восьмеричная система Ответ: 63 8 1 0 0 0 1 1 1 1 1 0 1 1 1 1 0 1 1 1 0 1 1 1 , 0 0 1 0 1 3 3 5 1 1 6 3 6 1 2 6 2 5 3 1 3 5 3 1 0 В меню
Числа в компьютере могут храниться в формате с фиксированной запятой – целые числа и в формате с плавающей запятой – вещественные числа. Целые числа без знака занимают в памяти один или два байта. Целые числа со знаком занимают в памяти компьютера один, два или четыре байта, при этом самый левый (старший) разряд содержит информацию о знаке числа Применяются три формы записи (кодирования) целых чисел со знаком: прямой код, обратный код и дополнительный код. Вещественные числа хранятся и обрабатываются в компьютере в формате с плавающей запятой. Этот формат базируется на экспоненциальной форме записи, в которой может быть представлено любое число
Целые числа в компьютере могут представляться со знаком или без знака. Целые числа без знака занимают в памяти один или два байта. в однобайтовом формате принимают 2 8 =256 различных значений от 00000000 2 до 11111111 2, в двухбайтовом формате 2 16 =65536 значений от 00000000 00000000 2 до 1111111111111111 2 Формат числа в байтах Запись с порядком Обычная запись 1 2 0 … 2 8 – 1 0 … 2 16 – 1 0 …255 0 …65535
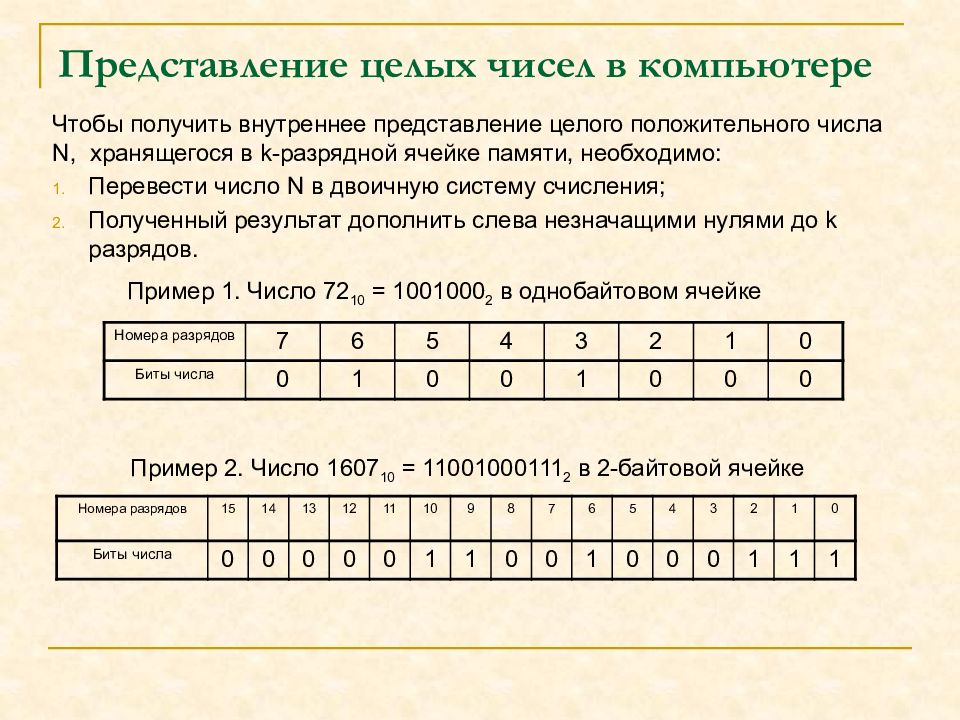
Чтобы получить внутреннее представление целого положительного числа N, хранящегося в k- разрядной ячейке памяти, необходимо: Перевести число N в двоичную систему счисления; Полученный результат дополнить слева незначащими нулями до k разрядов. Пример 1. Число 72 10 = 1001000 2 в однобайтовом ячейке Номера разрядов 7 6 5 4 3 2 1 0 Биты числа 0 1 0 0 1 0 0 0 Пример 2. Число 1607 10 = 11001000111 2 в 2-байтовой ячейке Номера разрядов 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0 Биты числа 0 0 0 0 0 1 1 0 0 1 0 0 0 1 1 1
Формат числа в байтах Запись с порядком Обычная запись 1 2 4 - 2 7 … 2 7 – 1 - 2 15 … 2 15 – 1 - 2 31 … 2 31 – 1 -128 …127 -32 768 …32 767 - 2 147 483 648 …2 147 483 647 Целые числа со знаком занимают в памяти компьютера один, два или четыре байта, при этом самый левый (старший) разряд содержит информацию о знаке числа. Знак «плюс» кодируется нулем, а «минус» - единицей
Пример. Число 62 10 = 111110 2 в однобайтовом формате 0 0 1 1 1 1 1 0 В компьютерной технике применяются три формы записи (кодирования) целых чисел со знаком: прямой код, обратный код и дополнительный код. Положительные числа в прямом, обратном и дополнительных кодах изображаются одинаково – двоичными кодами с цифрой 0 в знаковом разряде. Знак числа
Пример. Число -57 10 = -111001 2 в однобайтовом формате 1 0 1 1 1 0 0 1 Отрицательные числа в прямом, обратном и дополнительных кодах имеют разное изображение.. Знак числа Прямой код. В знаковый разряд помещается цифра 1, а в разряды цифровой части числа – двоичный код его абсолютной величины. прямой код
Пример. Число -57 10 = -111001 2 в однобайтовом формате 1 1 0 0 0 1 1 0 Знак числа Обратный код. Для образования обратного кода отрицательного двоичного числа необходимо в знаковом разряде поставить 1, а в цифровых разрядах единицы заменить нулями, а нули - единицами. обратный код
Пример. Число -57 10 = -111001 2 в однобайтовом формате 1 1 0 0 0 1 1 1 Знак числа Дополнительный код отрицательного числа получается образованием обратного кода с последующим прибавлением единицы к его младшему разряду дополнительный код
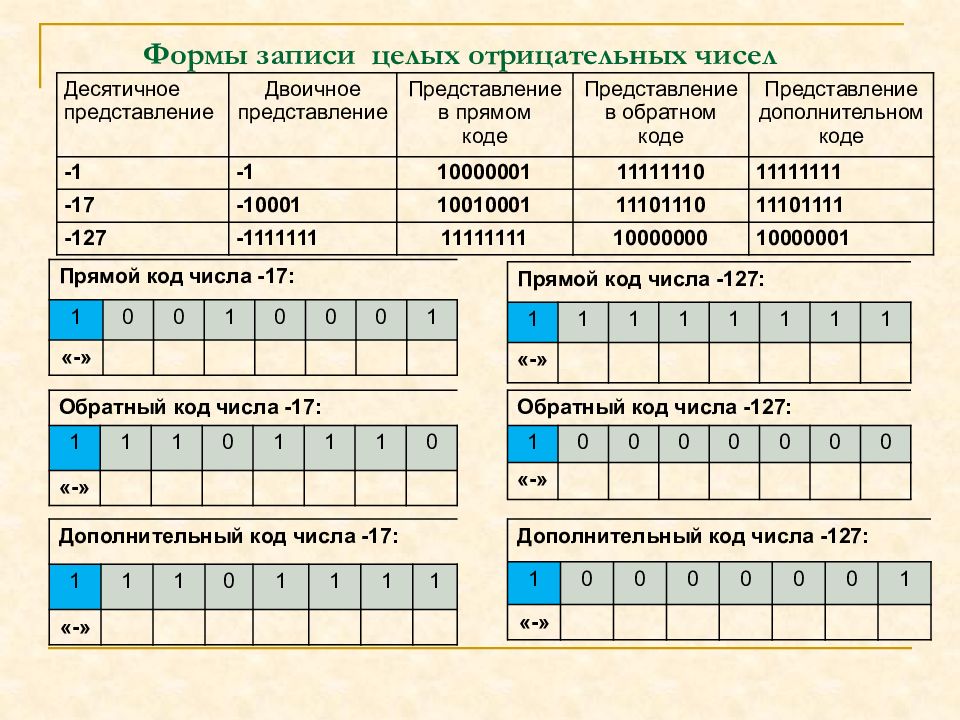
Десятичное представление Двоичное представление Представление в прямом коде Представление в обратном коде Представление дополнительном коде -1 -1 10000001 11111110 11111111 -17 -10001 10010001 11101110 11101111 -127 - 1111111 11111111 10000000 10000001 Прямой код числа -17: 1 0 0 1 0 0 0 1 «-» Прямой код числа -127: 1 1 1 1 1 1 1 1 «-» Обратный код числа -17: 1 1 1 0 1 1 1 0 «-» Обратный код числа -127: 1 0 0 0 0 0 0 0 «-» Дополнительный код числа -17: 1 1 1 0 1 1 1 1 «-» Дополнительный код числа -127: 1 0 0 0 0 0 0 1 «-»
Отрицательные десятичные числа при вводе в компьютер автоматически преобразуются в обратный или дополнительный код и в таком виде хранятся, перемещаются и участвуют в операциях. При выводе таких чисел из компьютера происходит обратное преобразование в отрицательные десятичные числа В меню
Любое число N в системе счисления с основанием q можно записать в виде N = ±M ∙ q p, где М - мантисса числа (значащая часть числа); р – порядок числа. Такой способ записи чисел называется представлением числа с плавающей точкой Мантиссу и порядок q - ичного числа записывают в системе счисления с основанием q, а само основание – в десятичной системе
где q — основание системы счисления. Это условие означает, что первая цифра после запятой не равна нулю, а абсолютное значение мантиссы не превышает единицы. Число с нормализованной мантиссой называется нормализованным.
Представить числа - 245,62 и 0,00123 в форме числа с плавающей точкой. Р е ш е ни е. Число - 245,62 можно представить в форме числа с порядком –245,62 × 10 0. Мантисса этого числа не нормализована, поэтому поделим его на 10 3, увеличив при этом порядок: – 0,24562 × 10 3. В результате число - 0,24562 × 10 3 нормализовано. Число 0,00123 в форме числа с порядком 0,00123 × 10 0 не нормализовано, так как не нормализована мантисса. Умножим мантиссу на 10 2, уменьшив при этом порядок: 0,123 × 10 –2. В результате число 0,123 × 10 –2 нормализовано. Для нормализации мантиссы запятая сдвигалась вправо или влево. Поэтому такие числа называются числами с плавающей точкой. В отличие от чисел с фиксированной точкой они значительно ускоряют арифметические операции, при этом каждый раз необходимо нормализовывать мантиссу чисел с плавающей точкой.
Для основанного на стандарте IEEE -754 представления вещественного числа в ЭВМ используются m + p + 1 бит, распределяемые следующим образом 1 разряд знака мантиссы, p разрядов порядка, m разрядов мантиссы. Это представление называется ( m, p )-форматом. Диапазон представления чисел X ( m, p )-форматом определяется из неравенства: При этом порядок числа P должен удовлетворять условию - 2 p - 1 + 1 ≤ P ≤ 2 p - 1 - 1
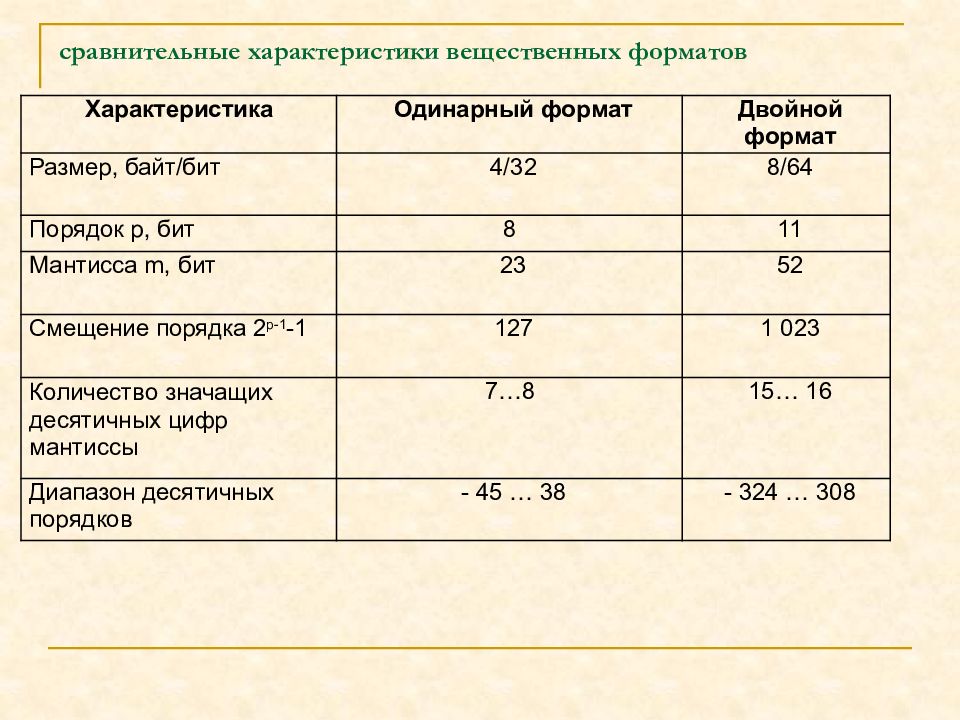
сравнительные характеристики вещественных форматов Характеристика Одинарный формат Двойной формат Размер, байт/бит 4/32 8/64 Порядок p, бит 8 11 Мантисса m, бит 23 52 Смещение порядка 2 p-1 -1 127 1 023 Количество значащих десятичных цифр мантиссы 7…8 15… 16 Диапазон десятичных порядков - 45 … 38 - 324 … 308
Форматы вещественных чисел Формат числа Диапазон абсолютных значений Размер в байтах одинарный вещественный двойной расширенный 10 -45 … 10 38 10 -39 … 2 38 10 -324 … 10 308 10 -4932 … 10 4932 4 6 8 10
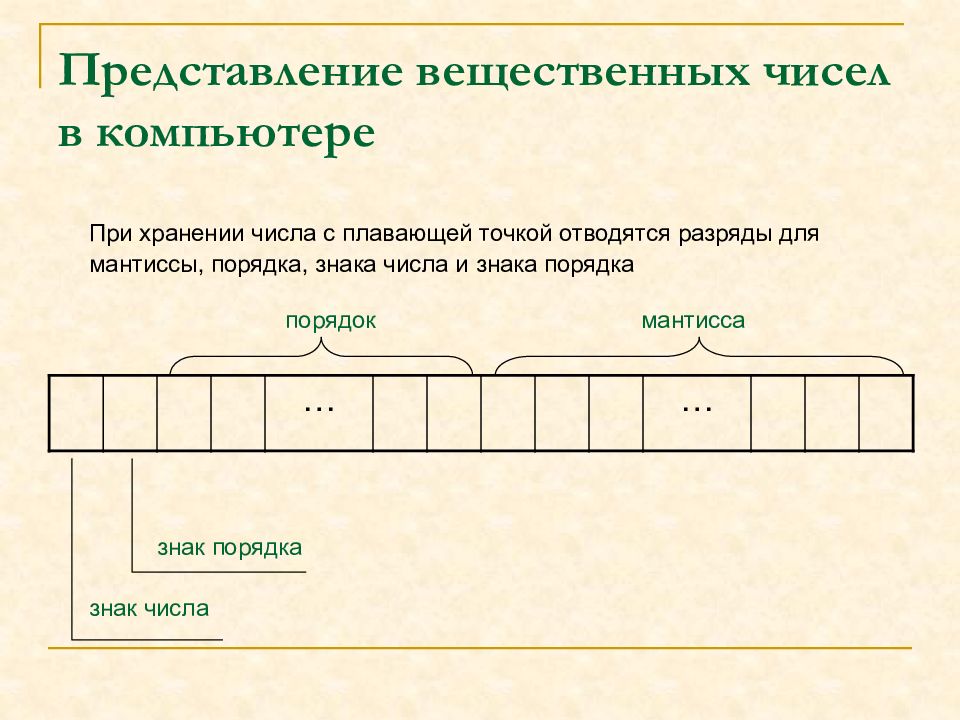
При хранении числа с плавающей точкой отводятся разряды для мантиссы, порядка, знака числа и знака порядка … … знак числа знак порядка порядок мантисса
если Х = 0, то принять знаковый разряд, порядок и мантиссу за ноль и закончить алгоритм ; если X > 0, то принять знаковый разряд 0, иначе принять 1. Знаковый разряд сформирован ; перевести целую и дробную часть абсолютного значения числа X в двоичную систему счисления. Если число дробное, то получить m + 1 разрядов. Принять порядок равный нулю ; если X ≥ 1, то перенести запятую влево до самого старшего разряда и увеличить порядок, иначе перенести запятую вправо до первого ненулевого ( единичного ) разряда и уменьшить порядок ; если число разрядов дробной части меньше m, то дополнить дробную часть нулями справа до m разрядов. Отбросить единицу из целой части. Мантисса сформирована ; прибавить к порядку смещение 2 p - 1 - 1 и перевести порядок в двоичную систему счисления. Порядок сформирован. Код, в котором представлен порядок, называется смещенным. Смещенный порядок упрощает сравнение, сложение и вычитание порядков при арифметических операциях ; записать знаковый разряд, порядок и мантиссу в соответствующие разряды формата.
Пример. Число 6,25 10 записать в нормализованном виде в четырехбайтовом формате с семью разрядами для записи порядка 6,25 10 = 110,01 2 = 0,11001 ∙ 2 11 … … знак числа знак порядка порядок мантисса 31 30 22 0 0 1 1 0 0 0 1 1 1 0 0 0 0
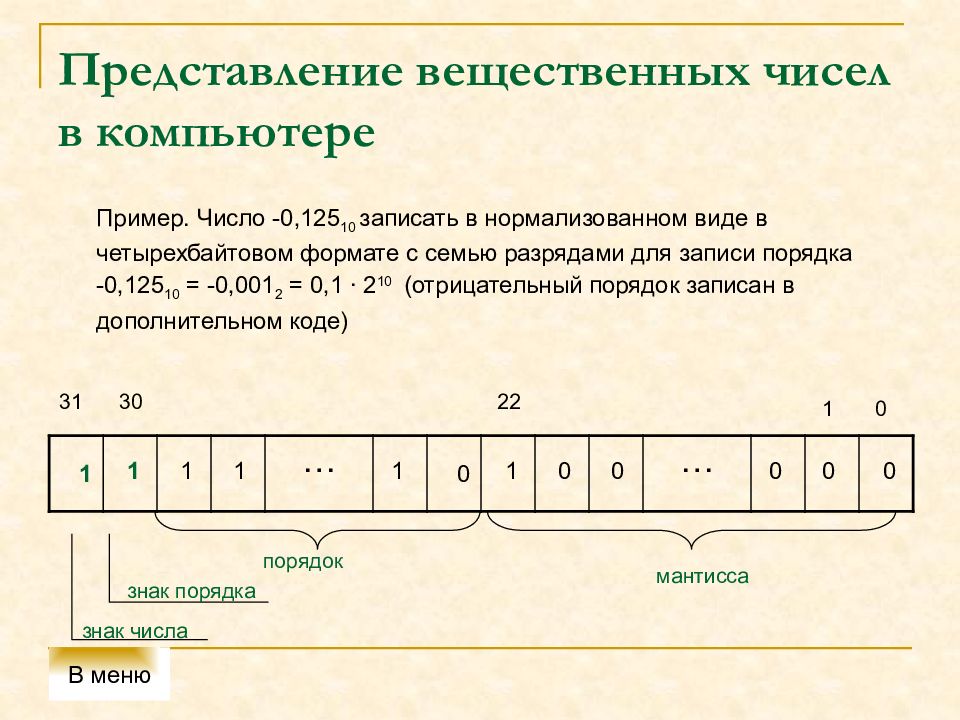
Пример. Число -0,125 10 записать в нормализованном виде в четырехбайтовом формате с семью разрядами для записи порядка -0,125 10 = -0,001 2 = 0,1 ∙ 2 10 (отрицательный порядок записан в дополнительном коде) … … знак числа знак порядка порядок мантисса 31 30 22 1 1 0 1 1 1 0 1 1 0 0 0 0 0 В меню
