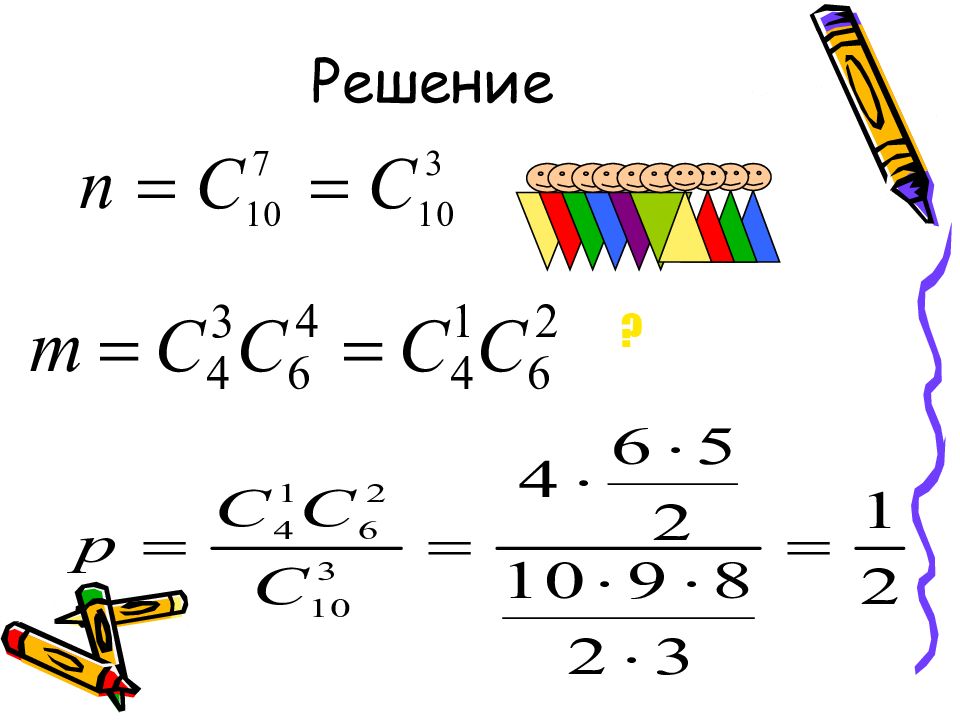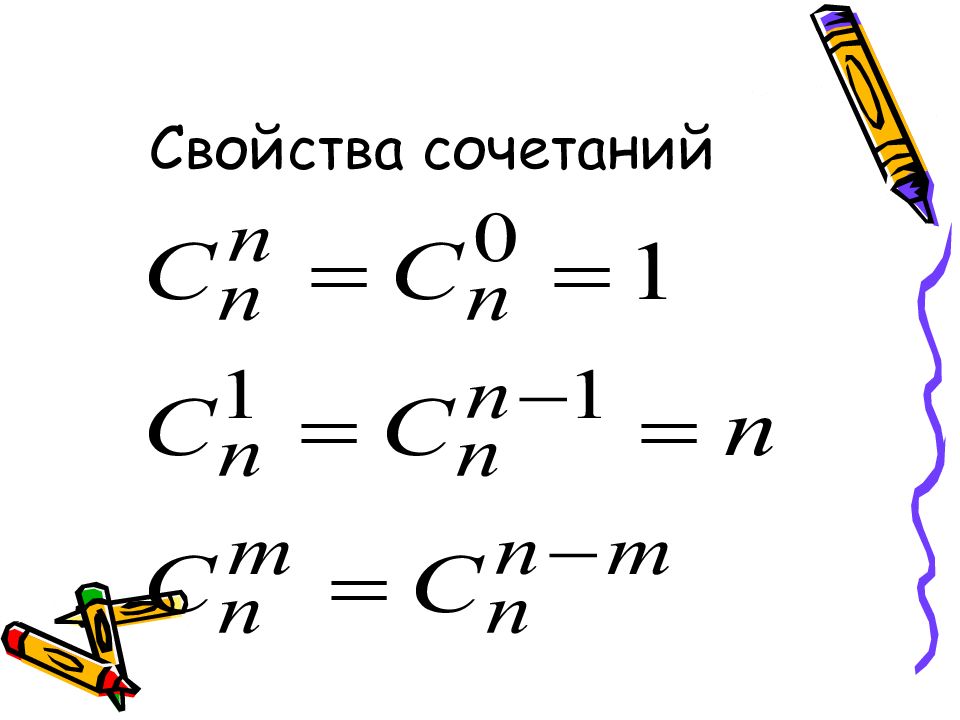Слайд 2: Случайное событие
Опыт, эксперимент, наблюдение явления называется испытанием. Результат, исход испытания называется событием. Случайное событие
Слайд 3: Классическое определение вероятности
Вероятностью Р ( А ) события А называется отношение числа m элементарных событий, благоприятствующих событию А, к числу n всех элементарных событий, т.е.
Слайд 4: Событие А называется благоприятствующим событию В,
если наступление события А влечет за собой наступление события В.
Слайд 5: элементарные события
События U 1, U 2,…, U n, образующие полную группу попарно несовместимых и равновозможных событий, называются элементарными событиями.
Слайд 6: совокупность событий образует полную группу событий для данного испытания,
если его результатом обязательно становится хотя бы одно из них.
Слайд 7: Совместимые события
События называются совместимыми, если появление одного из них не исключает появление другого в одном и том же испытании. В противном случае они называются несовместимыми. Совместимые события
Слайд 8: Равновозможные события
События U i ( i = 1, 2, 3,..., n ) считаются равновозможными, если условия испытания не создают преимущества в появлении какого-либо события перед другими возможными.
Слайд 9: Задача 1
10 9 8 7 6 5 4 3 2 Задача 1 В урне 10 пронумерованных шаров с номерами от 1 до 10. Вынули один шар. Какова вероятность того, что номер вынутого шара не превосходит 10? 1
Слайд 10: Событие называется достоверным,
если в данном испытании оно является единственно возможным его исходом.
Слайд 11: Задача 2
В урне 15 шаров: 5 белых и 10 черных. Какова вероятность вынуть из урны синий шар? ?
Слайд 12: Событие называется невозможным,
если в данном испытании оно заведомо не может произойти.
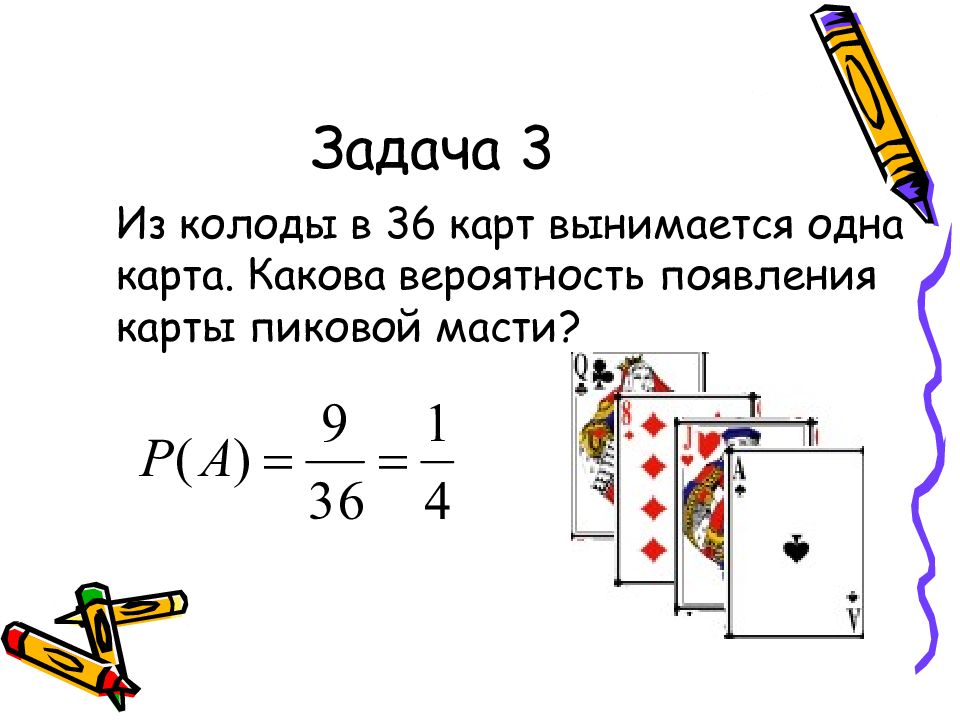
Слайд 13: Задача 3
Из колоды в 36 карт вынимается одна карта. Какова вероятность появления карты пиковой масти?
Слайд 14: Задача 4
Бросаются одновременно две монеты. Какова вероятность выпадения цифры на обеих монетах?
Слайд 15: Решение
Составим схему возможных случаев. Всего случаев 4. Благоприятствующих случаев 1. Р = 1/4. Первая монета Вторая монета 1 случай 2 случай 3 случай 4 случай герб герб цифра цифра герб цифра герб цифра
Слайд 16: Задача 5
В урне 10 шаров: 6 белых и 4 черных. Вынули два шара. Какова вероятность, что оба шара белые?
Слайд 18: Задача 6
В цехе работают 6 мужчин и 4 женщины. По табельным номерам наудачу отобраны 7 человек. Найти вероятность того, что среди отобранных лиц три женщины. ?
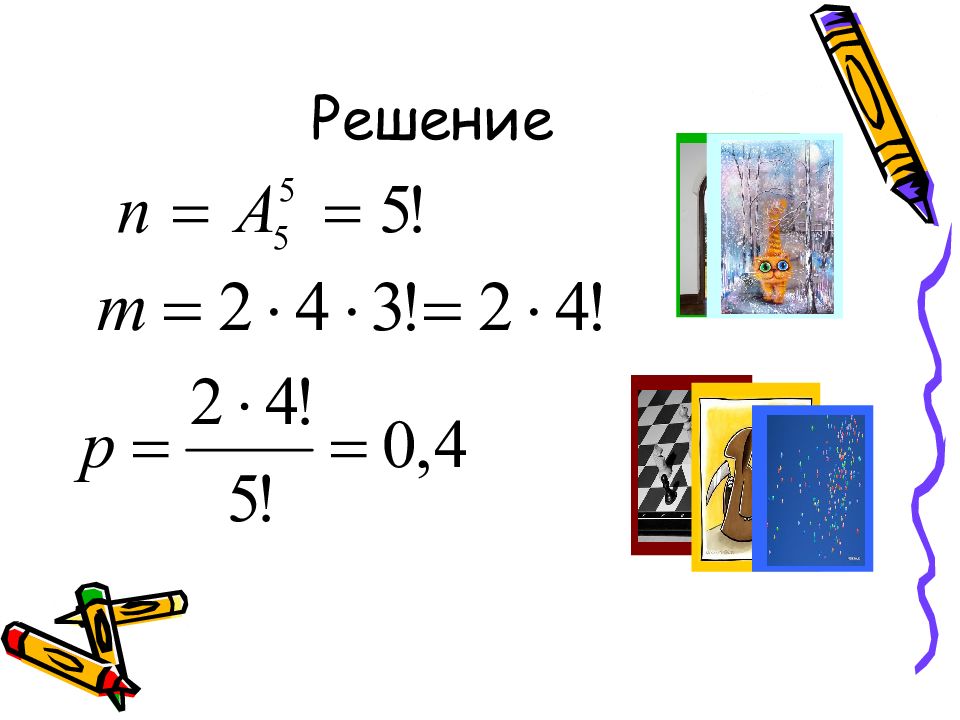
Слайд 21: Задача 7
Пять книг расставляются на полку. Найти вероятность того, что две определенные книги окажутся рядом.
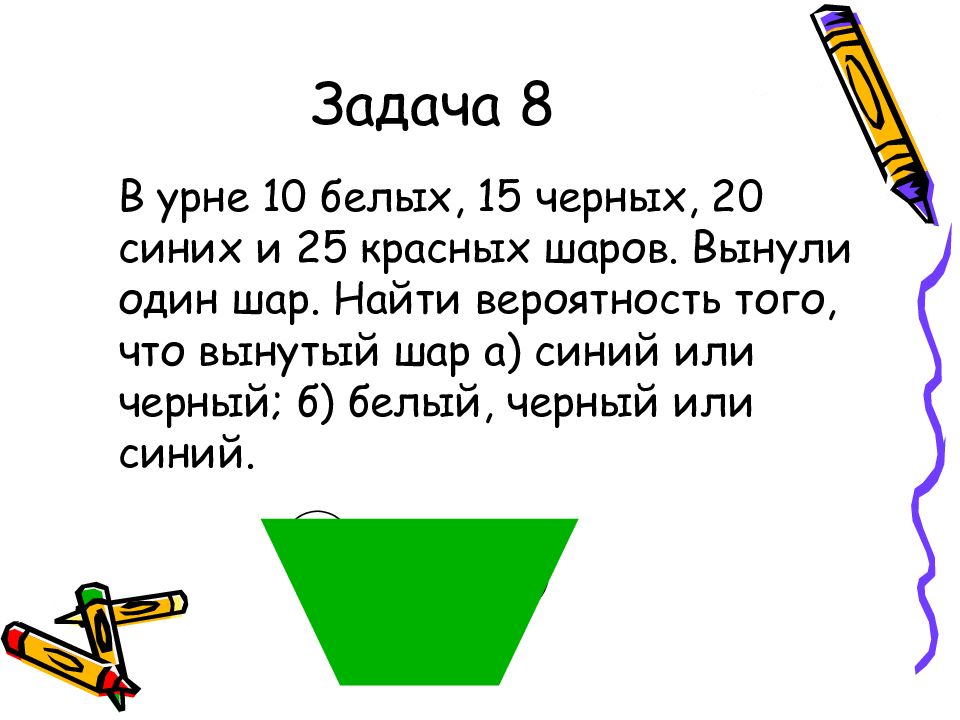
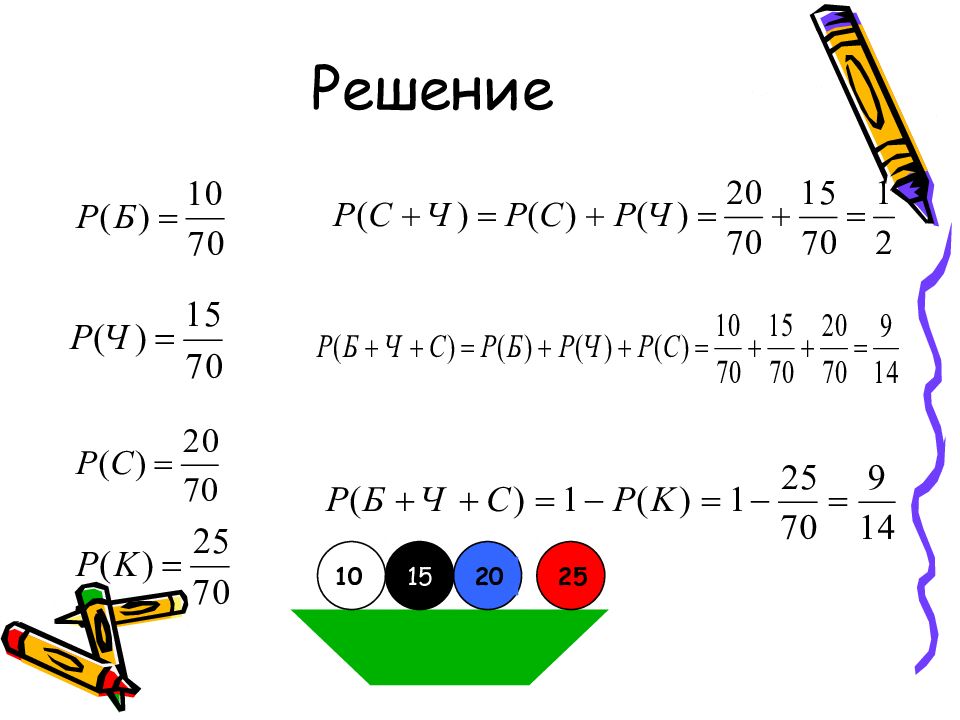
Слайд 23: Задача 8
В урне 10 белых, 15 черных, 20 синих и 25 красных шаров. Вынули один шар. Найти вероятность того, что вынутый шар а) синий или черный; б) белый, черный или синий. 10 15 20 25
Слайд 25: Задача 9
На стеллаже в библиотеке стоит 15 учебников, причем 5 из них в переплете. Библиотекарь берет три учебника. Найти вероятность того, что хотя бы один из взятых учебников окажется в переплете. 1? 2? 3?
Слайд 26: Решение
I способ. А – хотя бы один учебник в переплете: В – один в переплете, два – без переплета; С – два в переплете, один без переплета; D – все три в переплете. А = В + С + D. ?
Слайд 28: Решение
II способ. А – хотя бы один учебник в переплете; - ни один из взятых учебников не имеет переплета. NB!
Слайд 30: Теорема умножения вероятностей
Вероятность произведения двух зависимых событий А и В равна произведению вероятности одного из них на условную вероятность другого, найденную в предположении, что первое событие уже наступило: Р ( АВ ) =Р ( А ) Р ( В А ).
Слайд 31: Вероятность произведения двух независимых событий
равна произведению вероятностей этих событий: Р ( АВ ) =Р ( А ) Р ( В ).
Слайд 32: Теорема сложения вероятностей совместных событий
Вероятность суммы двух совместных событий А и В равна сумме вероятностей этих событий минус вероятность их произведения: Р ( А+В ) = Р ( А ) +Р ( В ) - Р ( АВ ).
Слайд 33: Задача 10
В первом ящике 2 белых и 7 черных шаров, во втором 8 белых и 4 черных шара. Из каждого ящика вынули по шару. Найти вероятность того, что один из вынутых шаров белый, а другой – черный. 2 8 7 4
Слайд 34: Решение
А –белый шар из I ящика, - черный шар из I ящика, В – белый шар из II ящика, - черный шар из II ящика, 2 7 8 4
Слайд 35: Задача 11
Вероятность попадания в цель у первого стрелка 0,8, у второго – 0,9. Стрелки делают по выстрелу. Найти вероятность: а) двойного попадания; б) хотя бы одного попадания; г) одного попадания.
Слайд 36: Задача 12
Студент разыскивает нужную ему формулу в трех справочниках. Вероятности того, что формула содержится в первом, втором и третьем справочниках равны 0,6; 0,7 и 0,8. Найти вероятности того, что формула содержится 1) только в одном справочнике; 2) только в двух справочниках; 3) во всех трех справочниках.
Слайд 37: Задача 13
Из 10 деталей 7 – стандартные. Наудачу берут 6 деталей. Найти вероятность того, что среди них: а) не более одной нестандартной; б) не более двух нестандартных.
Слайд 38: Задача 14
На полке 10 пар разных перчаток. Наудачу выбираются 4 перчатки. Найдите вероятность того, что среди них окажется хотя бы одна пара.