Для матриц A, B, C одинаковых размеров : 1) A + B = B + A ( коммутативность ), 2) ( A + B ) +C = A +( B + C ) ( ассоциативность ). Для матриц A, B одинаковых размеров и чисел s, t : 1) ( s t ) A= s ( t A ); 2) s ( A+B )= s A+ s B ; 3) ( s + t ) A= s A+ t A. Свойства о пераци и умножения матриц : 1) ( A B ) C= A ( B C ) ( ассоциативность ), 2) A ( B+C )= A B+ A C, ( A+B ) C= A C+ B C ( дистрибутивность ), 3) t ( A B )= ( t A ) B=A ( t B ).
Докажем ассоциативность умножения 1). Пусть A ( m x n ), B ( n x p ), C ( p x q ).
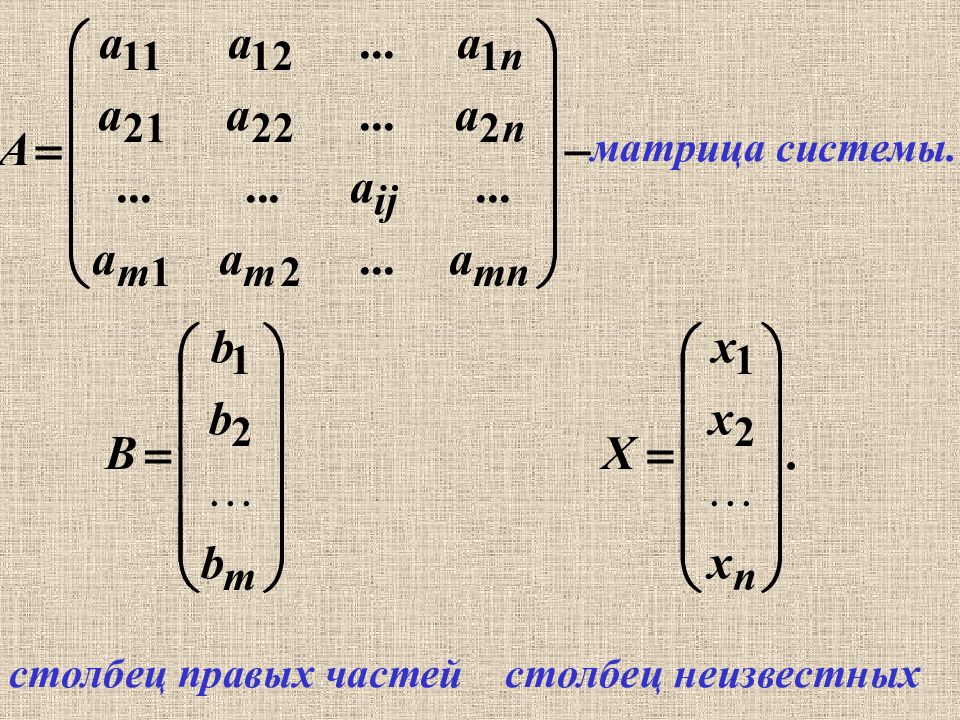
Матричная запись системы линейных алгебраических уравнений (СЛАУ). m уравнений, n неизвестных.
матрица системы. столбец правых частей столбец неизвестных
Определение Квадратная матрица B называется обратной по отношению к к вадратн ой матрице A того же порядка, если AB = BA = I. Обозначение: Пример :
1) A ( n x n ), B ( n x m ), X ( n x m ): AX = B. Если 2) A ( n x n ), B ( m x n ), X ( m x n ): XA = B. Если Пример
