Слайд 2: Литература
В.Л. Клюшин «Высшая математика для экономистов» (учебное пособие) В.Л. Клюшин «Высшая математика для экономистов: задачи, тесты, упражнения» 2
Слайд 3: Понятие матрицы
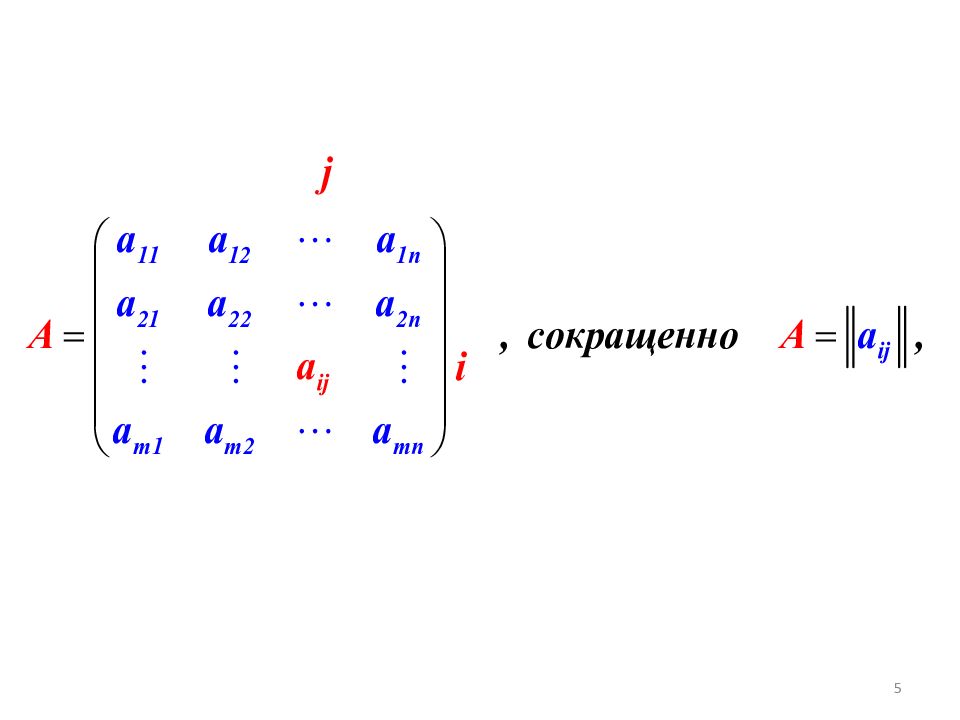
Определение. Числовая таблица с m строками и n столбцами называется mxn матрицей. 3x4 - матрица - элемент матрицы, стоящий на пересечении i- ой строки и j- го столбца 3
Слайд 6: Экономический пример
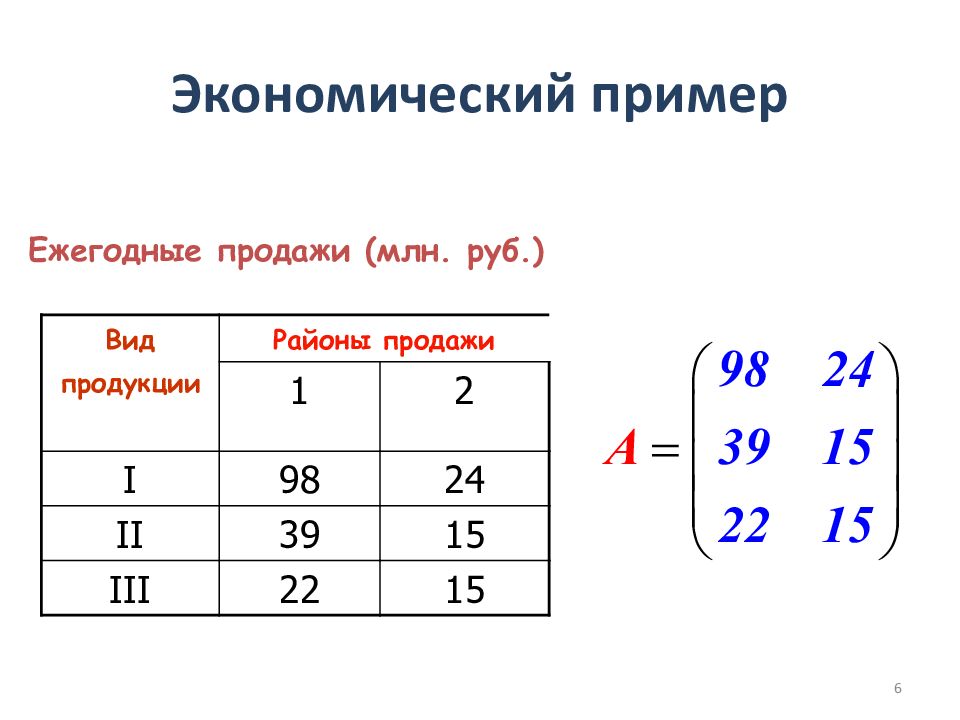
Вид продукции Районы продажи 1 2 I 98 24 II 39 15 III 22 15 Ежегодные продажи (млн. руб.) 6
Слайд 11: Экономический пример
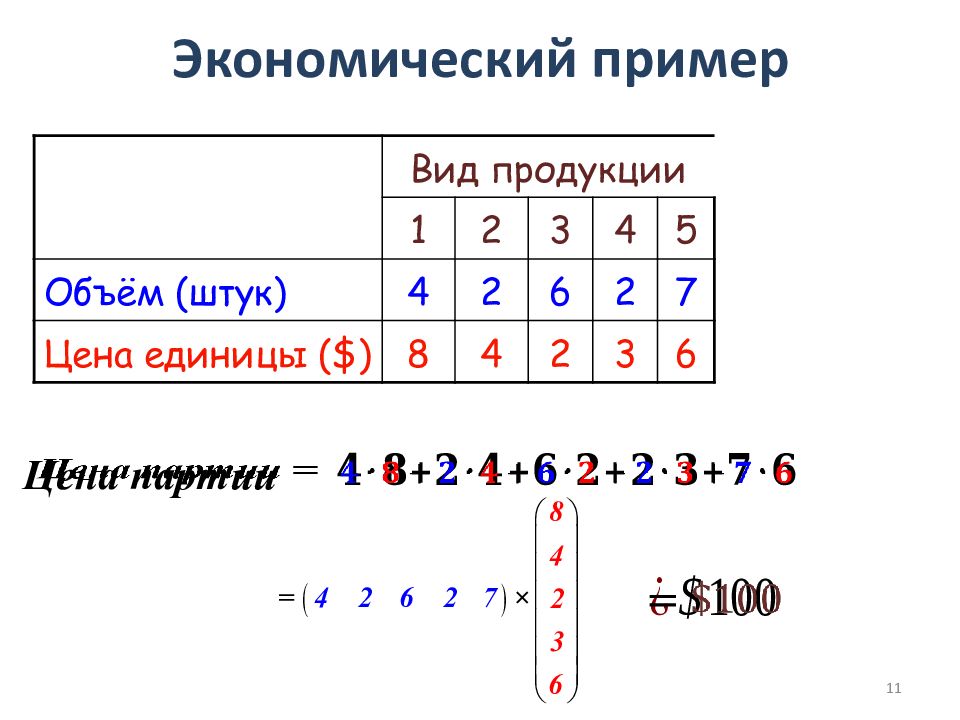
Вид продукции 1 2 3 4 5 Объём (штук) 4 2 6 2 7 Цена единицы ( $ ) 8 4 2 3 6 Цена партии 11
Слайд 12: Умножение строки на столбец
Пример. Умножить каждую строку матрицы A на каждый столбец матрицы B, где 12
Слайд 13: Умножение матрицы на матрицу
При умножении матрицы на матрицу, каждая строка матрицы умножается на каждый столбец матрицы. При этом результат умножения - ой строки матрицы на - ый столбец матрицы, записывается на пересечение - ой строки и - го столбца матрицы. 13
Слайд 14: Пример
. Р езультат умножения матриц содержит столько же строк как первый сомножитель и столько же столбцов как второй сомножитель 14
Слайд 16: Транспонирование матриц
При транспонировании меняются местами строки и столбцы исходной матрицы. ( Первая строка становится первым столбцом, вторая строка становится вторым столбцом и т.д.) Матрица, транспонированная к A обозначается A ’ или A t. Пример. 16
Слайд 18: Специальные виды матриц
Строка Столбец Квадратная Диагональная Нулевая Верхнетреугольная Нижнетреугольная 18
Слайд 19: П ример
Определить типы следующих матриц ( выбрать из строка, столбец, квадратная, диагональная, нулевая, верхнетреугольная, нижнетреугольная ). 19
Слайд 20: Определители квадратных матриц
Определитель матрицы – это число, обозначаемое и вычисляемое по конкретным правилам. Матрица 1-го порядка – таблица, состоящая из од - ного числа и её определитель равен этому числу. 20
Слайд 22: Геометрический смысл определителя 2-го порядка
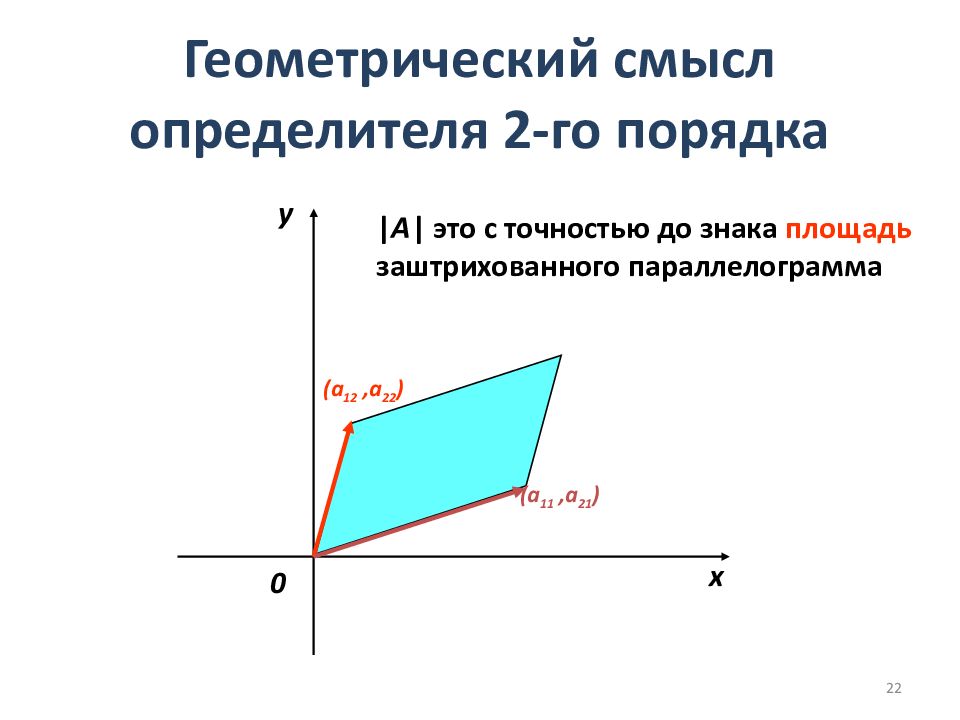
| А | это с точностью до знака площадь заштрихованного параллелограмма (a 12,a 22 ) ( a 11,a 21 ) x y 0 22
Слайд 23: Решить систему уравнений:
Для решения системы двух линейных уравнений с двумя неизвестными и можно умножить первое уравнение на коэффициент при во втором уравнении и умножить второе уравнение на коэффициент при в первом уравнении. Затем вычесть из первого уравнения второе: 23
Слайд 27: Теорема Крамера
Пусть дана система уравнений Если, где обозначает матрицу ко э ффициентов при неизвестных, то и, где матрицы и получаются из матрицы заменой первого и второго столбца на столбец свободных членов соответственно Теорема Крамера . 27
Слайд 29: Разложение определителя по элементам строки или столбца
Минором определителя матрицы называется такой новый определитель, который получается из данного вычеркиванием -ой строки и -го столбца. 29
Слайд 34: Разложение определителя по элементам строки или столбца
Алгебраическим дополнением элемента определителя матрицы называется минор этого элемента, взятый со знаком Пример: 34
Слайд 36: Разложение определителя по элементам строки или столбца
Теорема Лапласа. Определитель матрицы равен сумме произведений элементов любой строки (столбца) на их алгебраическ ие дополнени я. 36
Слайд 37: Разложение определителя по элементам строки или столбца
Пример. Найти определитель матрицы при помощи разложения по элементам третьего столбца. 37
Слайд 38: Свойства определителей
Определитель не меняется при транспонировании : Пример : 38
Слайд 39: Свойства определителей
Определитель меняет знак при перестановки любых двух строк или любых двух столбцов. Пример : 39
Слайд 40: Свойства определителей
3. Общий множитель элементов какой-либо строки или столбца можно вынести за знак определителя. Пример : 40
Слайд 41: Свойства определителей
4. Определитель матрицы, содержащий строку или столбец, целиком состоящий из нулей, равен нулю. Пример : 41
Слайд 42: Свойства определителей
5. Определитель матрицы, содержащий равные или пропорциональные строку и столбец, равен нулю. Пример : 42
Слайд 43: Свойства определителей
6. Если каждый элемент некоторой строки матрицы представим в виде суммы двух слагаемых, то определитель есть сумма определителей, где все строки матриц и, кроме указанной строки, совпадают с соответствующими строками матрицы, а все элементы указанной строки матриц и являются, соответственно, первыми и вторыми слагаемыми указанной строки матрицы. 43
Слайд 45: Свойства определителей
Определитель не изменится, если к элементам некоторой строки ( столбца ) прибавить соответствующие элементы другой строки ( столбца ), предварительно умножив их на один и тот же множитель. 45
Слайд 47: Свойства определителей
Определитель верхнетреугольной матрицы равен произведению диагональных элементов. Пример : 47
Слайд 48: Свойства определителей
( Теорема Лапласа.) Определитель равен сумме произведений элементов любой строки (столбца) на их алгебраическ и е дополнени я. Пример : 48
Слайд 49: Свойства определителей
Если является единственным ненуле-вым элементом в своей строке или столбце, то Пример : 49
Слайд 50: Свойства определителей
Определитель произведения матриц равен произведению определителей : 50
Слайд 51: Обратная матрица
Число 1 обладает свойством : Д ля любого числа. Например, Для любого ненулевого числа определено Ч исло, обратное к ( обозначается или ) такое, что 51
Слайд 52: Обратная матрица
Вопрос : существует ли аналог числа 1 и аналог обратного числа среди матриц ? 52
Слайд 53: Обратная матрица
Квадратная матрица называется диагональной, если все её элементы вне главной диагонали равны нулю. Пример : Диагональная матрица называется единичной, если все её диагональные элементы – единицы. Пример : 53
Слайд 54: Обратная матрица
Единичная матрица обозначается или. Единичная матрица размера обозначается так же или : 54
Слайд 55: Обратная матрица
Если для матрицы определено произведение, то Аналогично, Пример : 55
Слайд 56: Обратная матрица
Матрица называется обратной к матрице и обозначается, если Если существует, то матрица A называется обратимой. 56
Слайд 58: Обратная матрица
Теорема. Обратная матрица существует только для невырожденной квадратной матрицы. Пример : существует, так как 58
Слайд 60: Нахождение обратной матрицы методом присоединённой матрицы
Пусть – квадратная матрица. Найти. Если, то не существует. Для каждого элемента матрицы вычислить его алгебраическое дополнение. Записать все алгебраические дополнения в виде матрицы и транспонировать её. Получится присоединённая матрица, обозначаемая или или. 60
Слайд 62: Нахождение обратной матрицы методом присоединённой матрицы
Обратная матрица вычисляется по формуле 62
Слайд 63: Нахождение обратной матрицы методом присоединённой матрицы
Пример. Найти методом присоединённой матрицы, где Решение. 1. , следовательно существует. 63
Слайд 65: Нахождение обратной матрицы методом присоединённой матрицы
2. ( продолжение ) 65
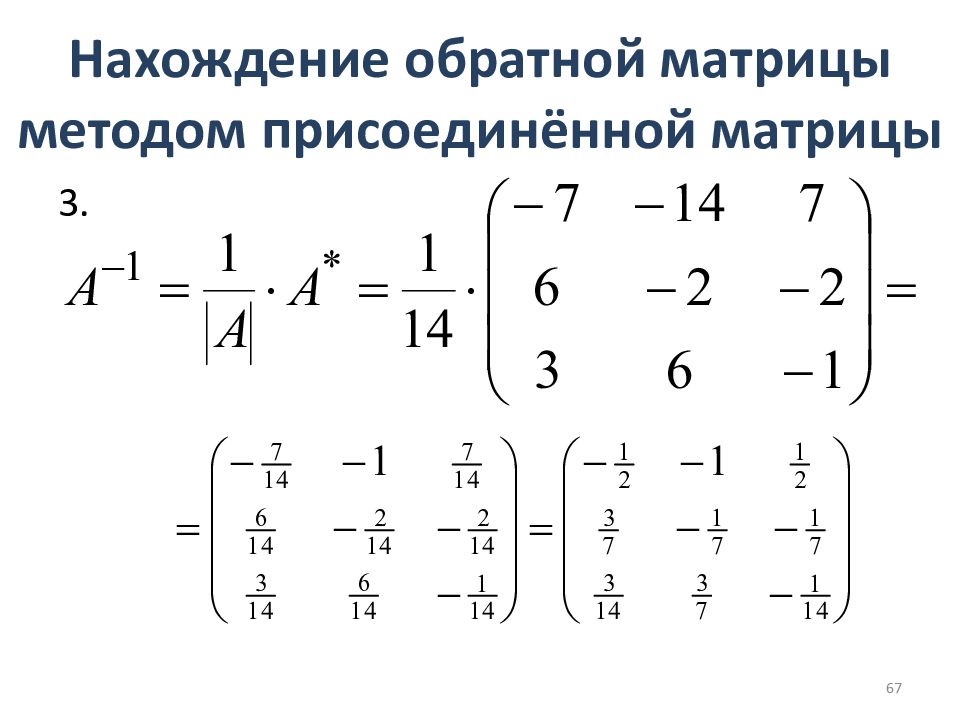
Слайд 66: Нахождение обратной матрицы методом присоединённой матрицы
(продолжение) 66
Слайд 68: Нахождение обратной матрицы методом присоединённой матрицы
Проверка: Ответ: 68
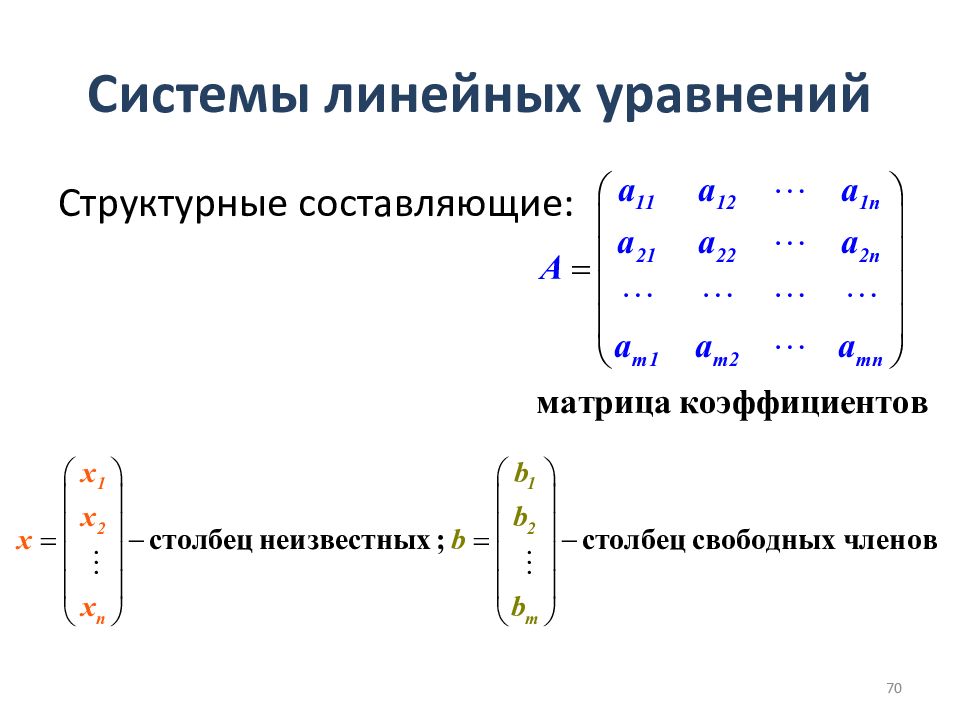
Слайд 69: Системы линейных уравнений
В общем случае система с уравнениями и неизвестными имеет вид (1) 69
Слайд 72: Системы линейных уравнений
Решением системы называется такой набор чисел ( с 1, с 2,…, с n ), что при его подстановке в систему вместо соответствующих неизвестных ( с 1 вместо х 1, …, с n вместо х n ) каждое из уравнений системы обращается в тождество. Если система ( 1 ) имеет хотя бы одно решение, то она называется совместной ; система, не имеющая ни одного решения, называется несовместной. 72
Слайд 73: Системы линейных уравнений
Система называется определенной, если она имеет единственное решение; и неопределенной, если она имеет более одного решения. 73
Слайд 74: Метод обратной матрицы
Система уравнений Р авносильна матричному уравнению 74
Слайд 75: Метод обратной матрицы
Мы сможем решить систему, если сможем решить данное матричное уравнение. 75