Первый слайд презентации: Тема 1.6 ЦЕНТР ТЯЖЕСТИ
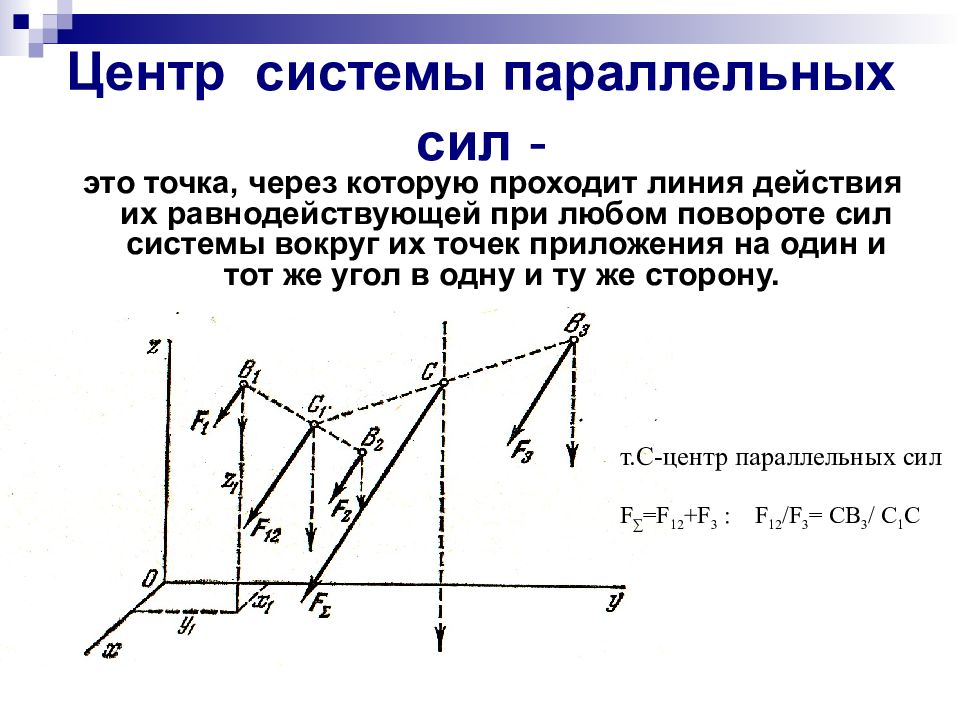
Слайд 2: Центр системы параллельных сил -
это точка, через которую проходит линия действия их равнодействующей при любом повороте сил системы вокруг их точек приложения на один и тот же угол в одну и ту же сторону. т.С-центр параллельных сил F ∑ = F 12 + F 3 : F 12 / F 3 = C В 3 / С 1 C
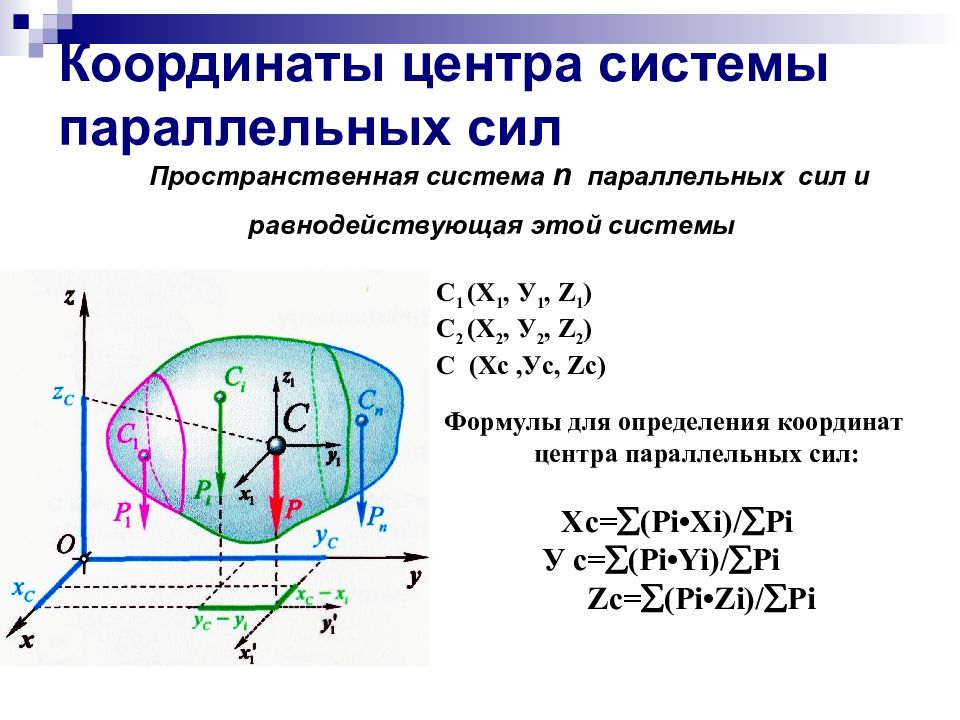
Слайд 3: Координаты центра системы параллельных сил
Пространственная система n параллельных сил и равнодействующая этой системы F 2 Формулы для определения координат центра параллельных сил: Xc= ( Р i•Xi)/ Р i У c= ( Р i•Yi)/ Р i Zc = (Р i • Zi )/ Р i С 1 ( Х 1, У 1, Z 1 ) С 2 ( Х 2, У 2, Z 2 ) C ( Х c, У c, Zc)
Слайд 4: Определение положения центра тяжести
Сила тяжести или вес тела- сила, с которой тело притягивается к земле. Любое тело можно представить в виде элементарных частиц, которые имеют определенный вес. Сила тяжести каждой элементарной частицы направлена к центру земли и образует систему параллельных сил. Таким образом центр тяжести тела- есть цент параллельных сил тяжести всех элементарных частиц тела. Центр тяжести- геометрическая точка, которая может быть расположена в самом теле или вне тела( цилиндр с отверстием). В этой точке условно считают сосредоточенным вес всего тела.
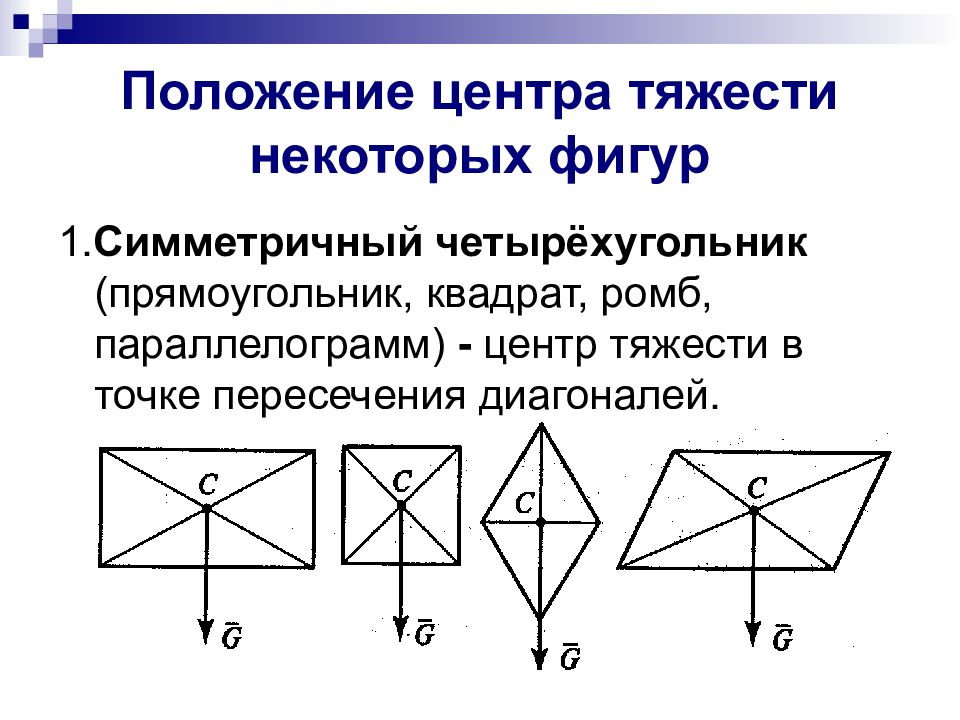
1. Симметричный четырёхугольник (прямоугольник, квадрат, ромб, параллелограмм) - центр тяжести в точке пересечения диагоналей.
Слайд 6: Положение центра тяжести некоторых фигур
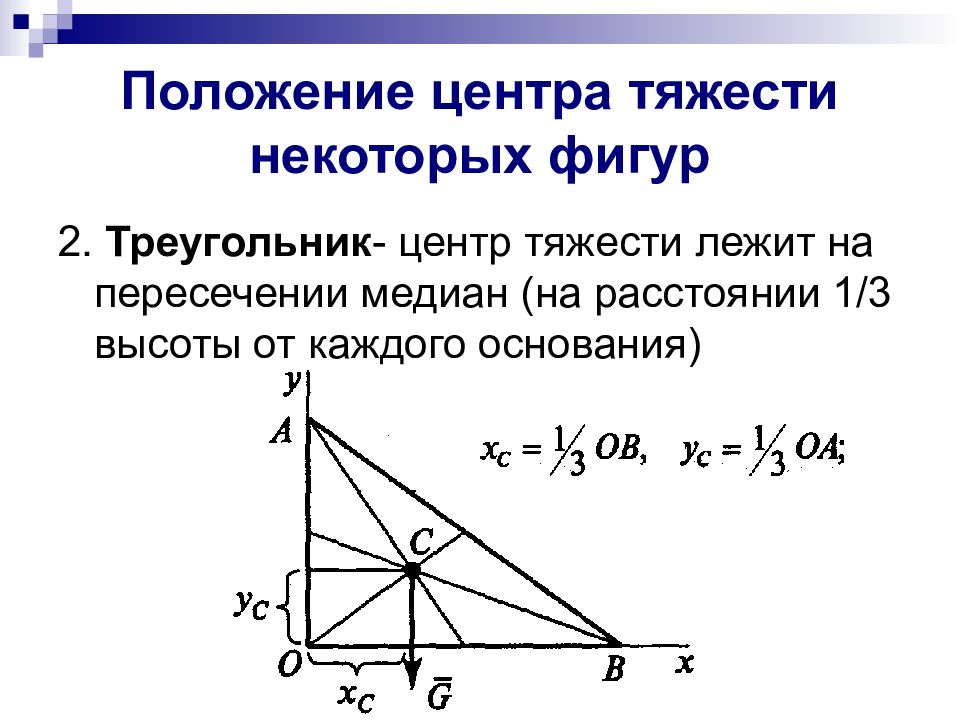
2. Треугольник - центр тяжести лежит на пересечении медиан (на расстоянии 1/3 высоты от каждого основания)
Слайд 7: Положение центра тяжести некоторых фигур
3. Полукруг — центр тяжести в точке с координатами: а) Xc = R, У c =4 R /3π (рис. а) б) Xc =4 R /3π, У c = R (рис. б)
Слайд 8: Положение центра тяжести некоторых фигур
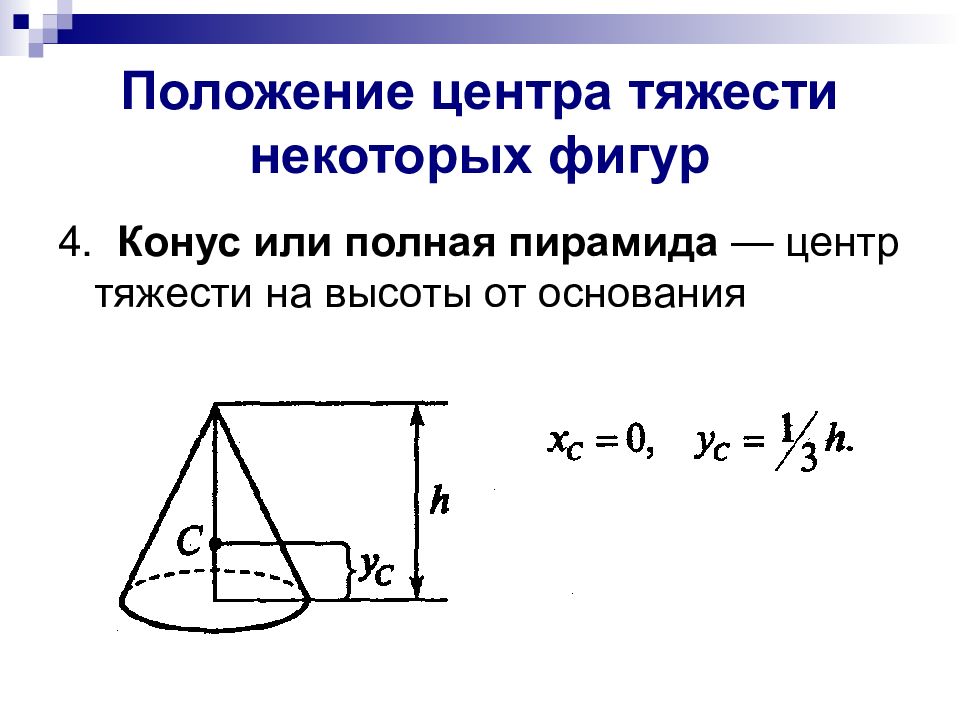
4. Конус или полная пирамида — центр тяжести на высоты от основания
Слайд 9: Положение центра тяжести некоторых фигур
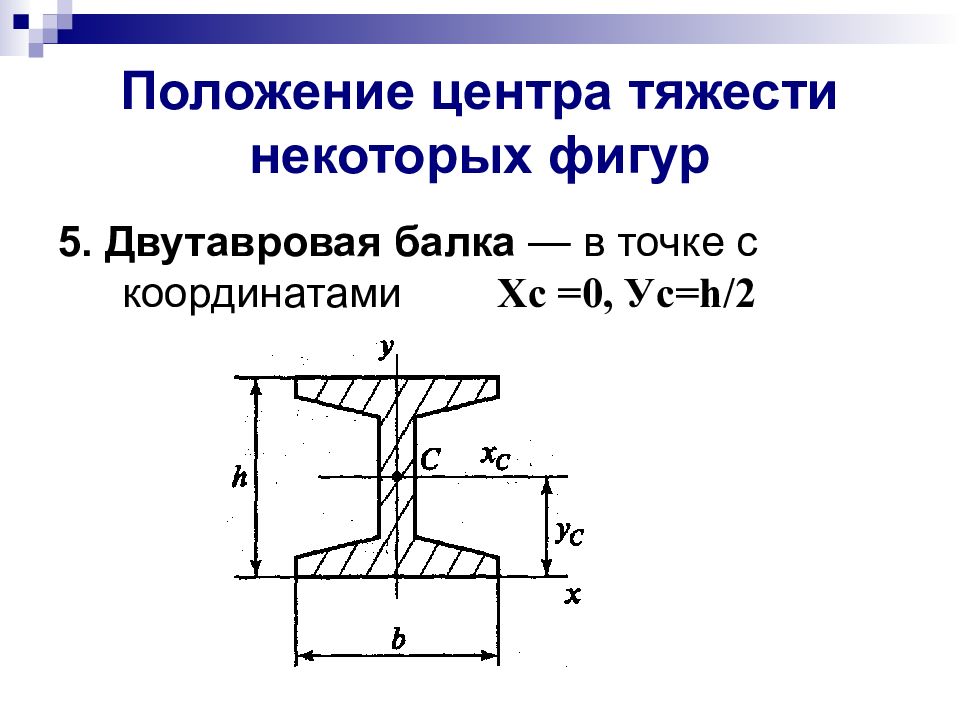
5. Двутавровая балка — в точке с координатами Xc =0, У c = h /2
Слайд 10: Положение центра тяжести некоторых фигур
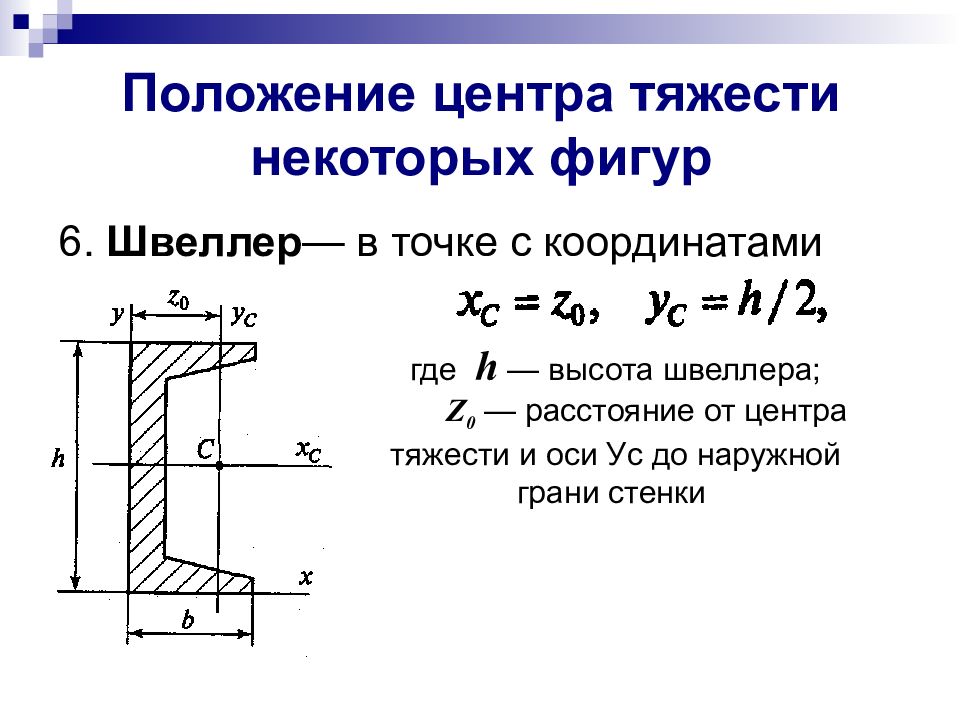
6. Швеллер — в точке с координатами где h — высота швеллера; Z 0 — расстояние от центра тяжести и оси У c до наружной грани стенки
Слайд 11: Положение центра тяжести некоторых фигур
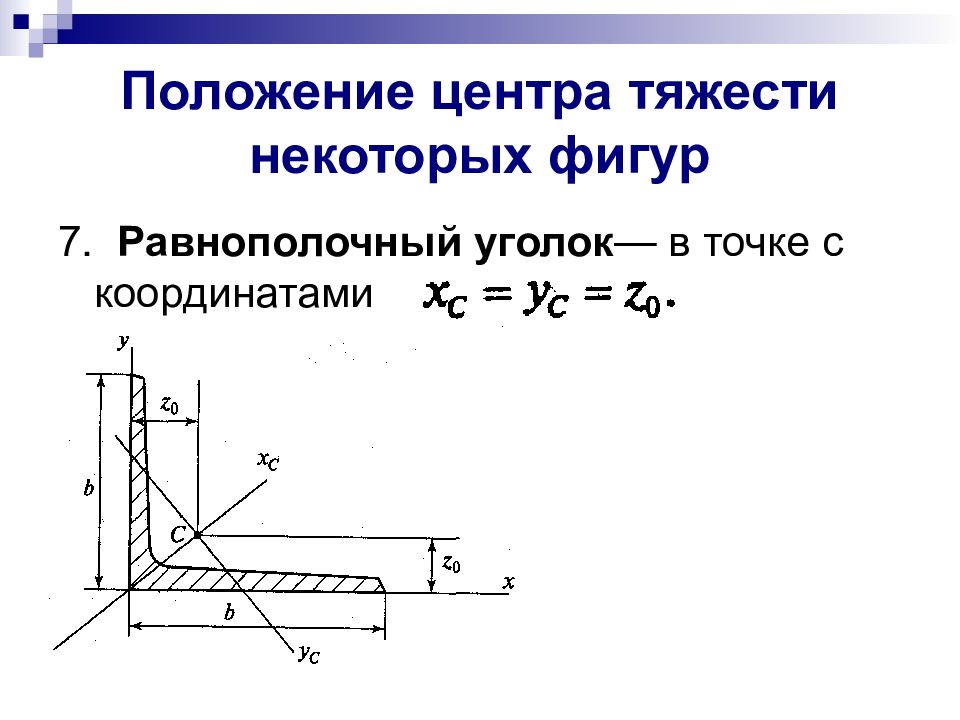
7. Равнополочный уголок — в точке с координатами
Слайд 12: Методы нахождения центра тяжести
Метод симметрии - этот метод используется для определения центра тяжести однородных симметричных тел и симметричных плоских фигур. Если однородное тело имеет ось симметрии, то центр тяжести лежит на этой оси Если две оси симметрии, то центр тяжести находится в точке их пересечения. Центр тяжести тела вращения лежит на оси вращения.
Слайд 13: Методы нахождения центра тяжести
Если плоская фигура имеет неправильную геометрическую форму, то центр тяжести такой фигуры можно определить двумя способами: 1 ) практическим методом - подвешивания фигуры на острие; 2) теоретическим методом
Слайд 14: 2 Теоретические методы
А) Метод разбиения - заключается в том, что тело разбивают на фигуры простейшей геометрической формы. Затем определяется положение центра тяжести и площади каждой элементарной фигуры. Для того чтобы найти координаты центра тяжести заданной сложной фигуры, используются следующие формулы: Где Ai — площади элементарных фигур, на которые разбита сложная фигура; Xi, Yi — координаты центра тяжести каждой элементарной фигуры относительно случайных осей x и у.
Слайд 15: 2 Теоретические методы
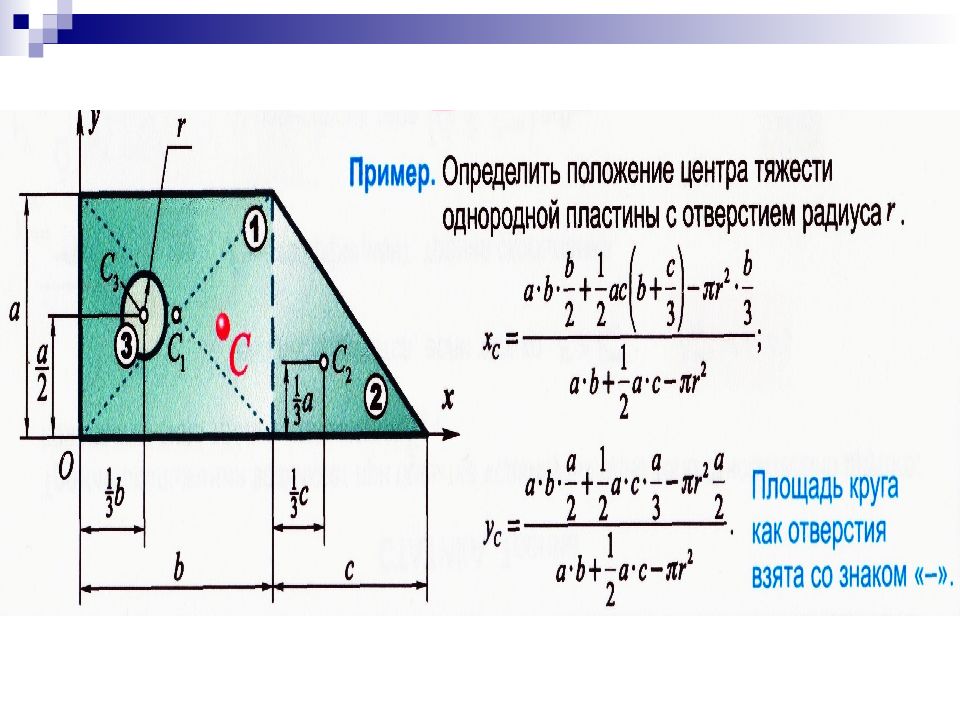
Б) Метод отрицательных масс - если тело имеет полости или плоская фигура вырезы, то тело вначале рассматривают как единое целое, а затем при подстановке в формулы полости и вырезы будем подставлять со знаком минус.