Геометрия, 9 класс. Теоремы синусов и косинусов.
Самостоятельная работа: 1 вариант: 2 вариант: 8 ? 8 5 ? 6
Утверждения, обобщающие теорему Пифагора и эквивалентные теореме косинусов, были сформулированы отдельно для случаев острого и тупого угла в 12 и 13 предложениях II книги «Начал» Евклида.
Утверждения, эквивалентные теореме косинусов для сферического треугольника, применялись в сочинениях математиков стран Средней Азии. Теорему косинусов для сферического треугольника в привычном нам виде сформулировал Региомонтан, назвав её «теоремой Альбатегния » (по имени ал-Баттани ).
В Европе теорему косинусов популяризовал Франсуа Виет в XVI столетии. В начале XIX столетия её стали записывать в принятых по сей день алгебраических обозначениях.
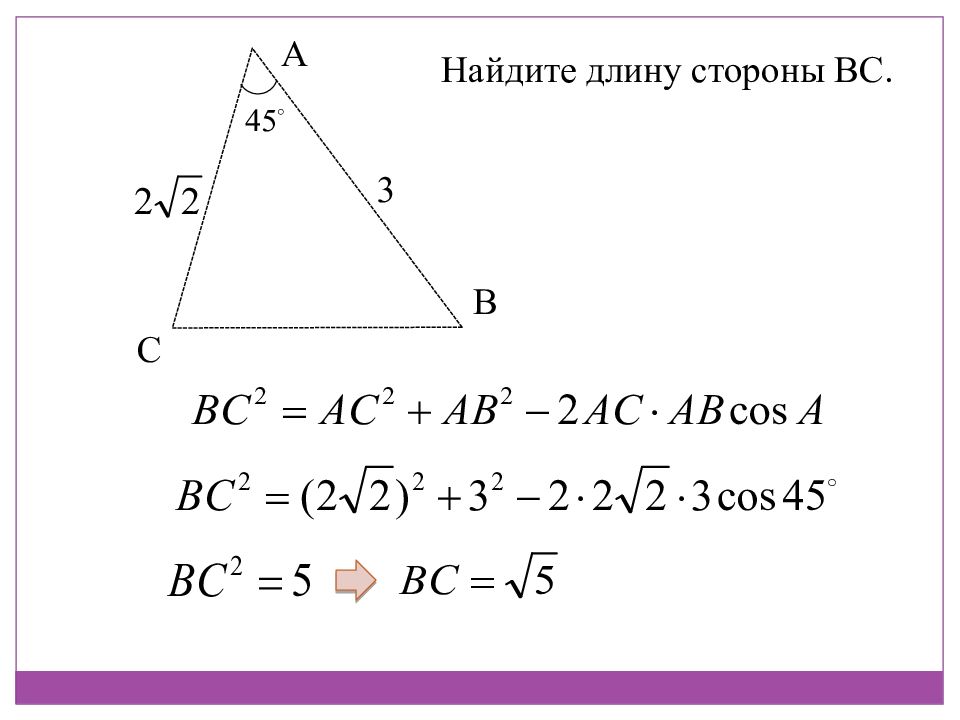
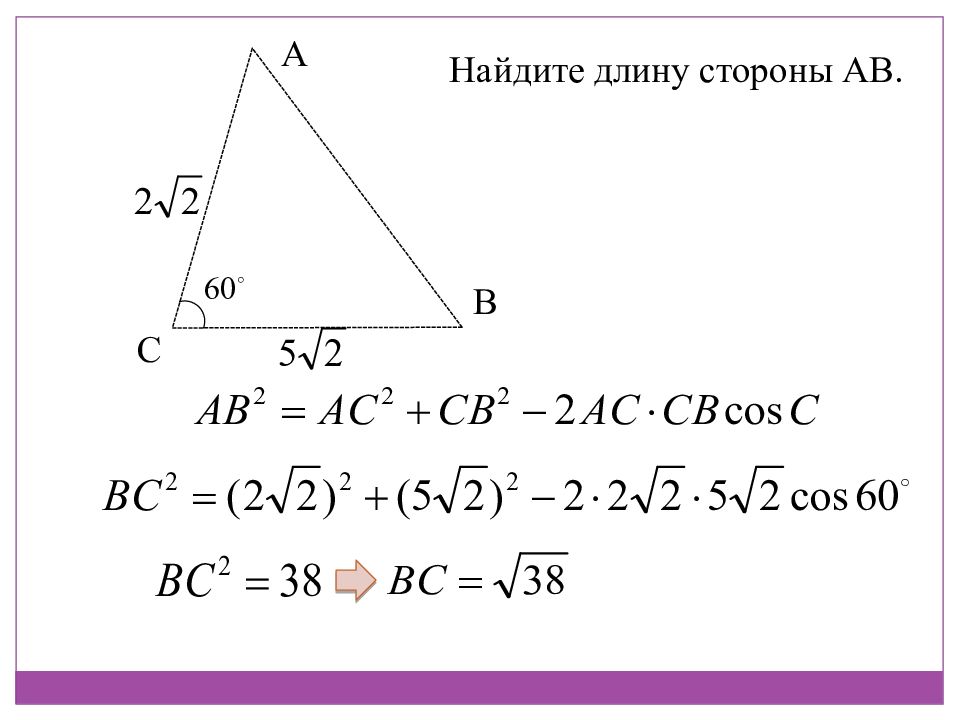
A B C Теорема косинусов: Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними а с b
Самое древнее доказательство для теоремы синусов на плоскости описано в книге Насир ад-Дин Ат-Туси «Трактат о полном четырёхстороннике » написанной в XIII веке. Теорема синусов для сферического треугольника была доказана математиками средневекового Востока ещё в X веке. В труде Ал-Джайяни XI века «Книга о неизвестных дугах сферы» приводилось общее доказательство теоремы синусов на сфере Насир ад-Дин Ат-Туси
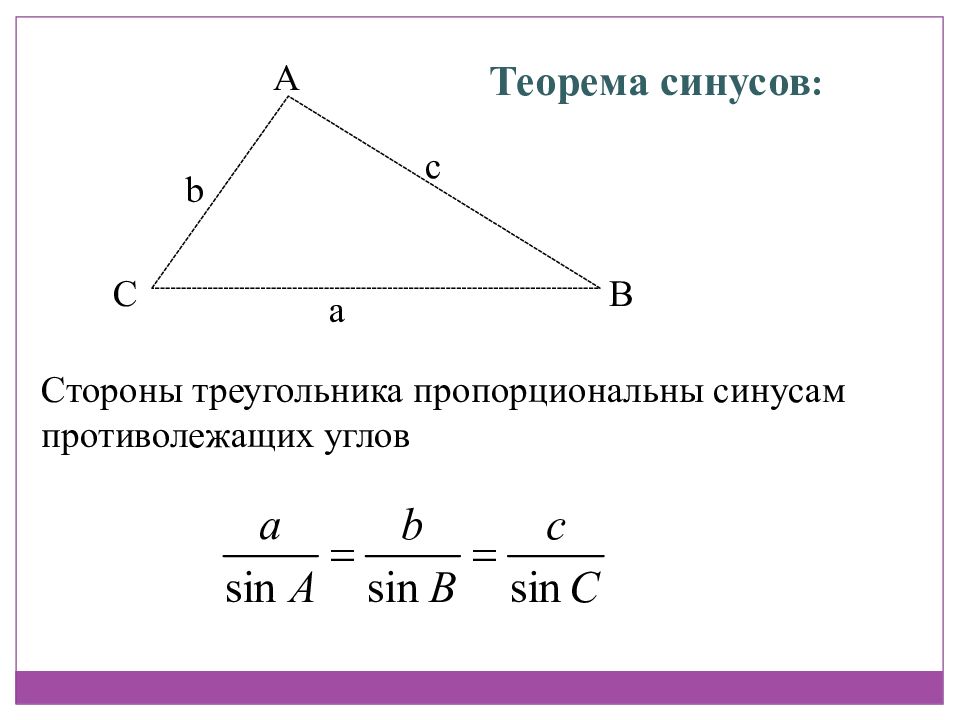
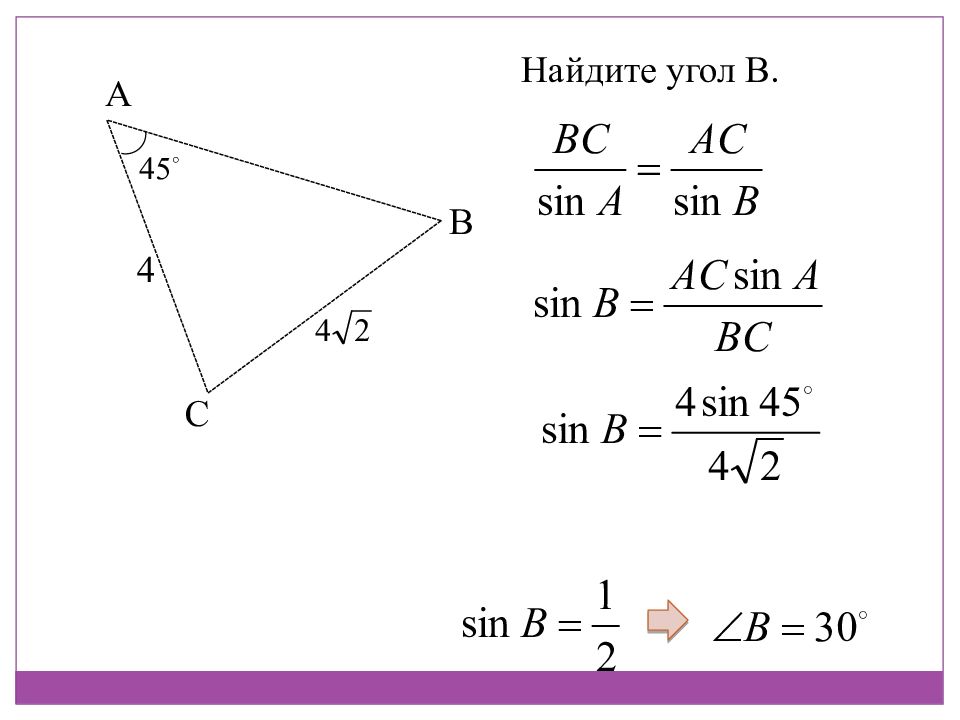
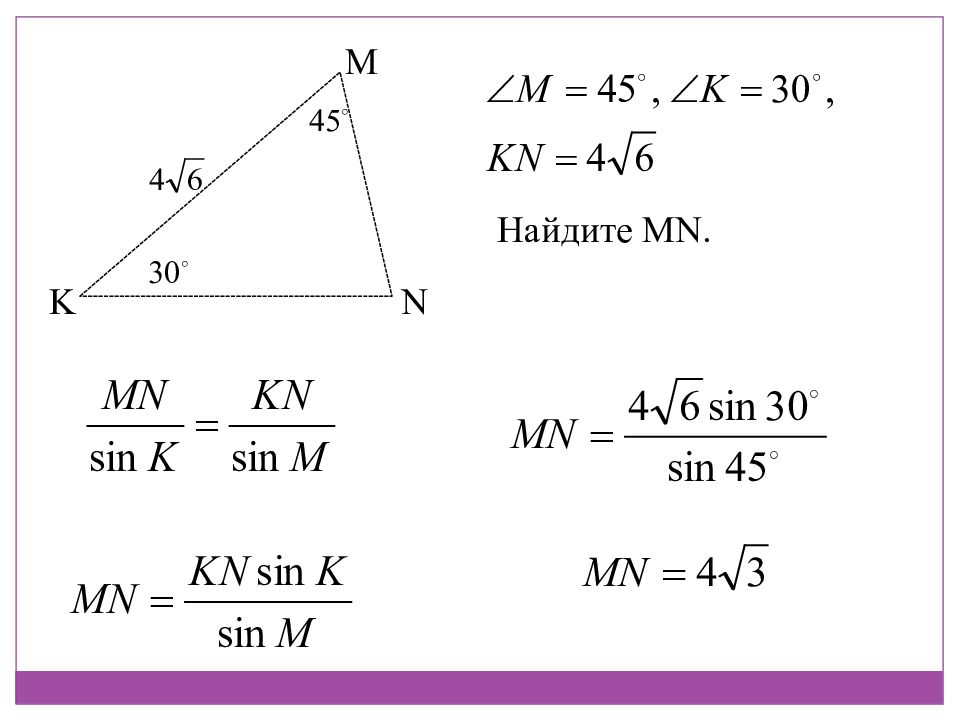
A B C Теорема синусов : Стороны треугольника пропорциональны синусам противолежащих углов а с b
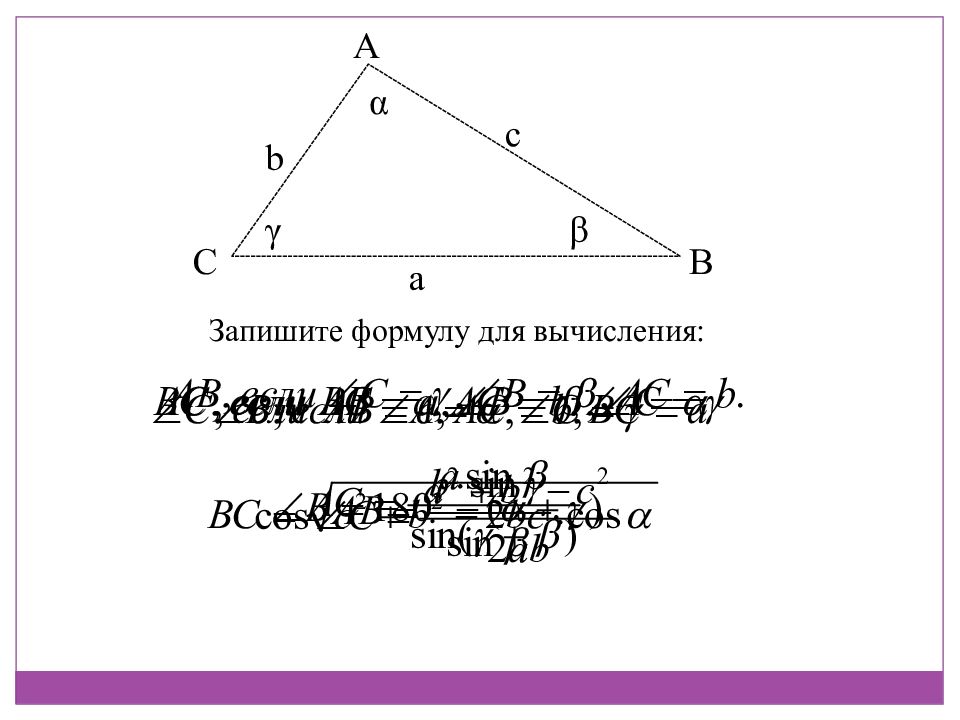
Замечание: Можно доказать, что отношение стороны треугольника к синусу противолежащего угла равно диаметру описанной окружности. Следовательно, для любого треугольника ABC со сторонами AB=c, BC=a, CA=b имеют место равенства Где R – радиус описанной окружности.
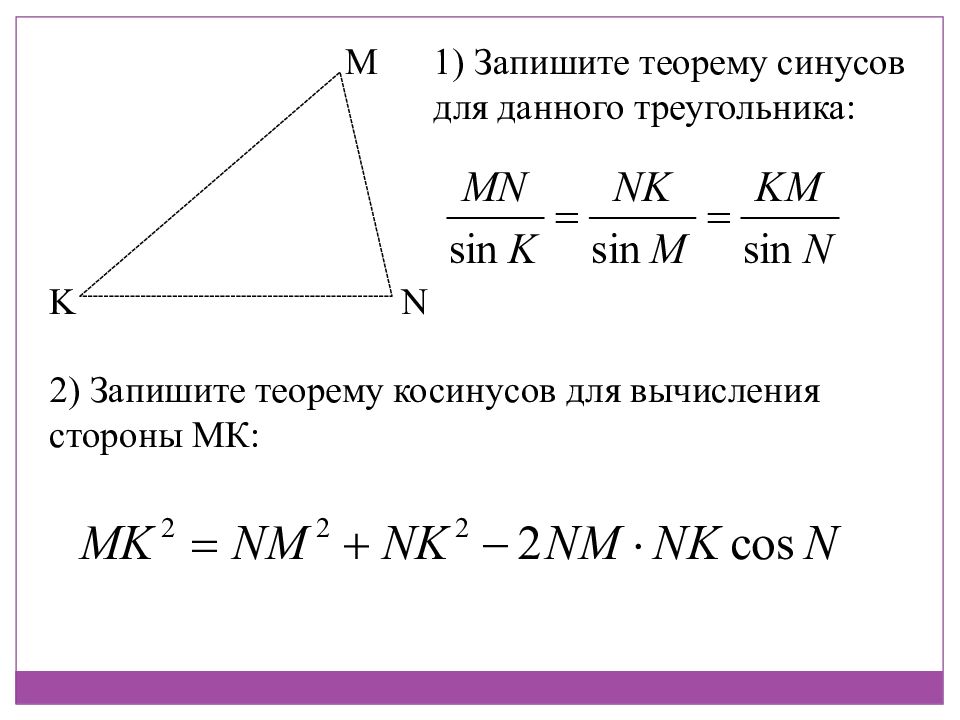
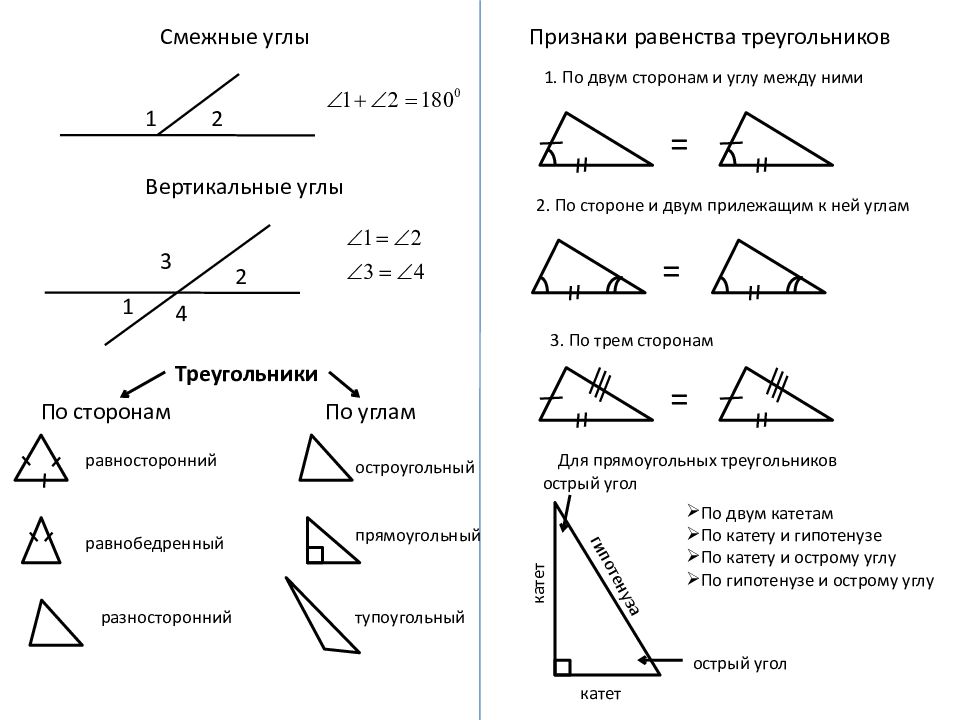
M N K 1) Запишите теорему синусов для данного треугольника: 2) Запишите теорему косинусов для вычисления стороны МК:
Найдите угол В. А С В 4
Найдите длину стороны ВС. А С В 3
Найдите длину стороны АВ. А С В
M N K Найдите MN.
A B C а с b α β γ Запишите формулу для вычисления:
http://ppt4web.ru/geometrija/teoremy-sinusov-i-kosinusov0.html http://nsportal.ru/shkola/geometriya/library/2014/10/15/teorema-sinusov-i-kosinusov https://upload.wikimedia.org/wikipedia/commons/thumb/1/14/Johannes_Regiomontanus2.jpg/500px-Johannes_Regiomontanus2.jpg http://img1.liveinternet.ru/images/attach/c/10/110/217/110217775_Nesreddi_tusi.jpg http://www.biografguru.ru/about/evklid/?q=3117
