Первый слайд презентации: Теорема Пифагора
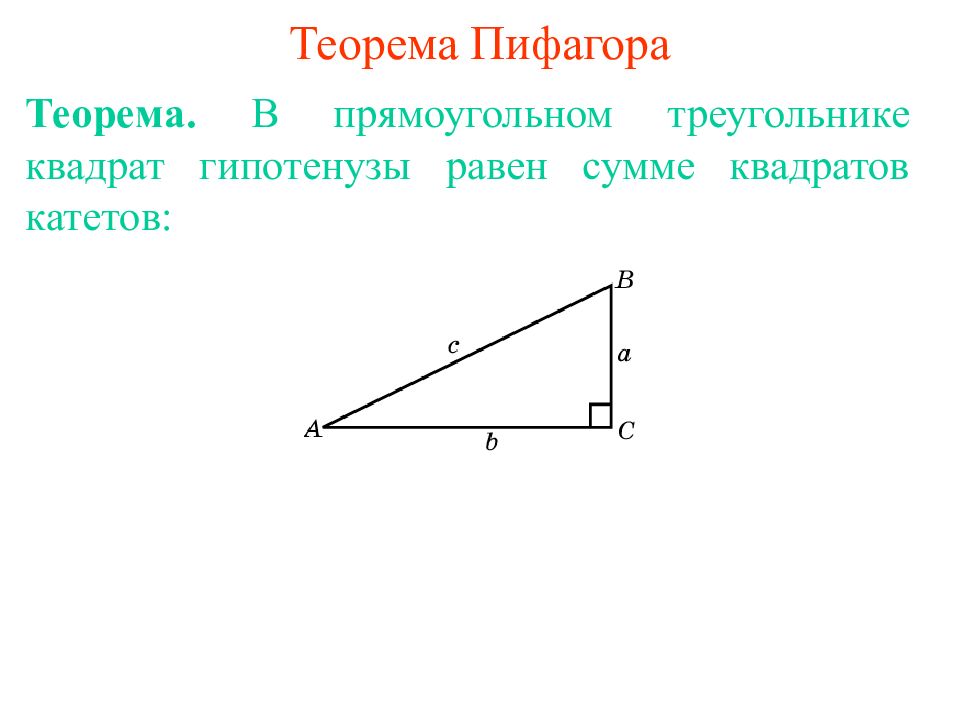
Теорема. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов:
Слайд 2: Синус и косинус
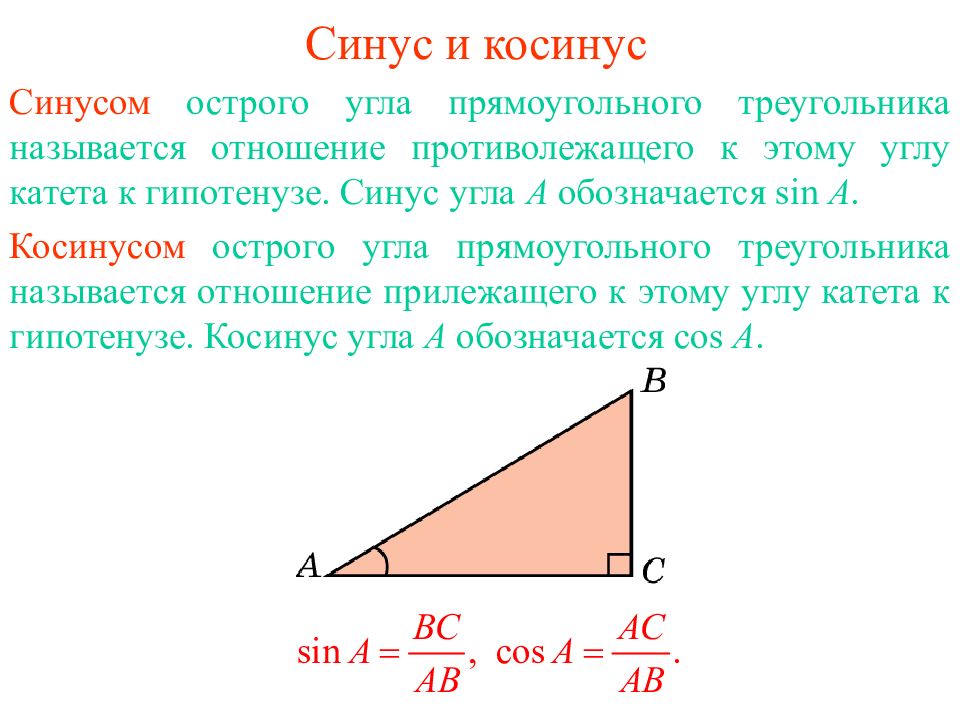
Синусом острого угла прямоугольного треугольника называется отношение противолежащего к этому углу катета к гипотенузе. Синус угла А обозначается sin A. Кос инусом острого угла прямоугольного треугольника называется отношение п ри лежащего к этому углу катета к гипотенузе. Кос инус угла А обозначается cos A.
Слайд 3: Тангенс и котангенс
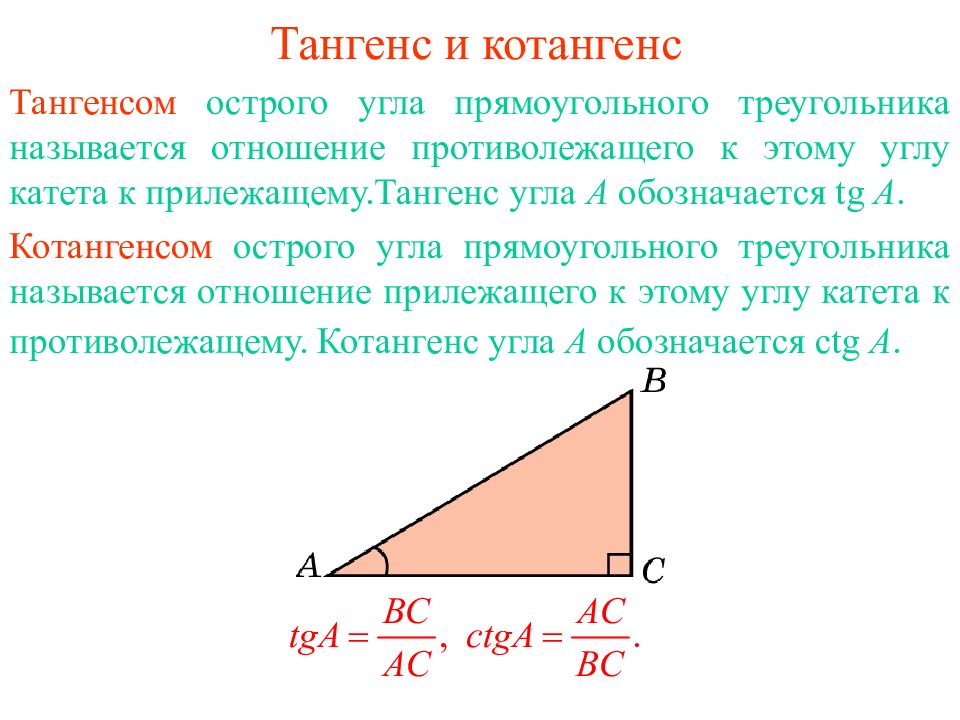
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего к этому углу катета к прилежащему.Тангенс угла А обозначается tg A. Котангенсом острого угла прямоугольного треугольника называется отношение прилежащего к этому углу катета к противолежащему. Котангенс угла А обозначается с tg A.
Слайд 4: Теорема косинусов
Теорема. Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними: c 2 = a 2 + b 2 – 2 ab cos C.
Слайд 5: Теорема синусов
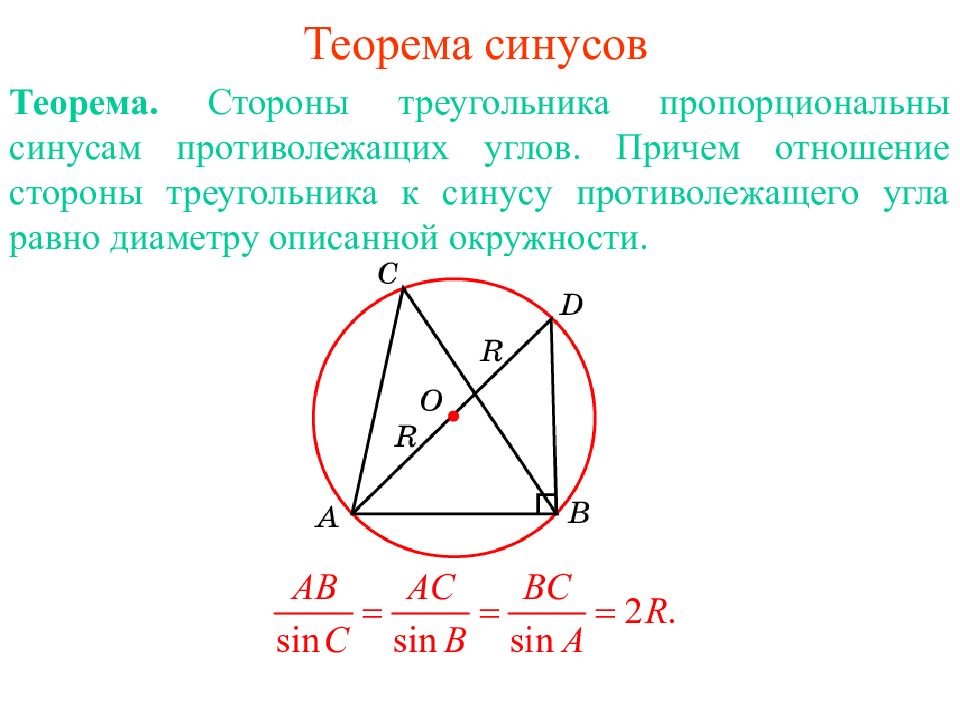
Теорема. Стороны треугольника пропорциональны синусам противолежащих углов. Причем отношение стороны треугольника к синусу противолежащего угла равно диаметру описанной окружности.
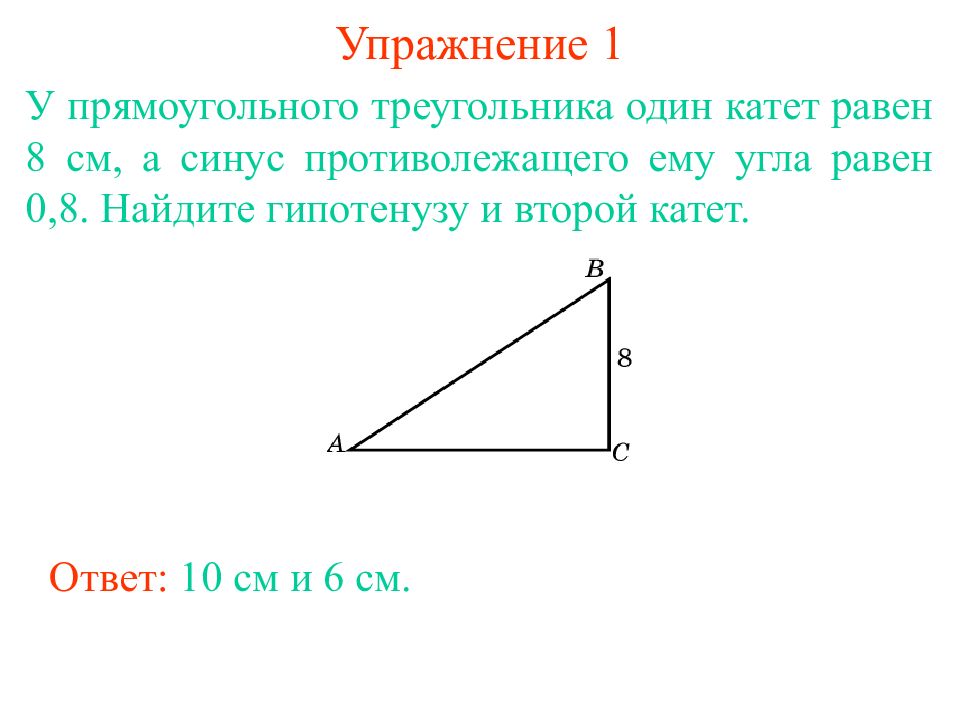
Слайд 6: Упражнение 1
У прямоугольного треугольника один катет равен 8 см, а синус противолежащего ему угла равен 0,8. Найдите гипотенузу и второй катет. Ответ: 10 см и 6 см.
Слайд 7: Упражнение 2
В прямоугольном треугольнике ABC sin A = 1/3, AB = 6. Найдите BC. Ответ: 2.
Слайд 8: Упражнение 3
В прямоугольном треугольнике ABC sin A = 3/4, BC = 6. Найдите AB. Ответ: 8.
Слайд 9: Упражнение 4
В прямоугольном треугольнике ABC cos A = 2/3, AB = 6. Найдите AC. Ответ: 4.
Слайд 10: Упражнение 5
В прямоугольном треугольнике ABC cos A = 2/3, AC = 6. Найдите AB. Ответ: 9.
Слайд 11: Упражнение 6
В прямоугольном треугольнике ABC tg A = 2/3, AC = 6. Найдите BC. Ответ: 4.
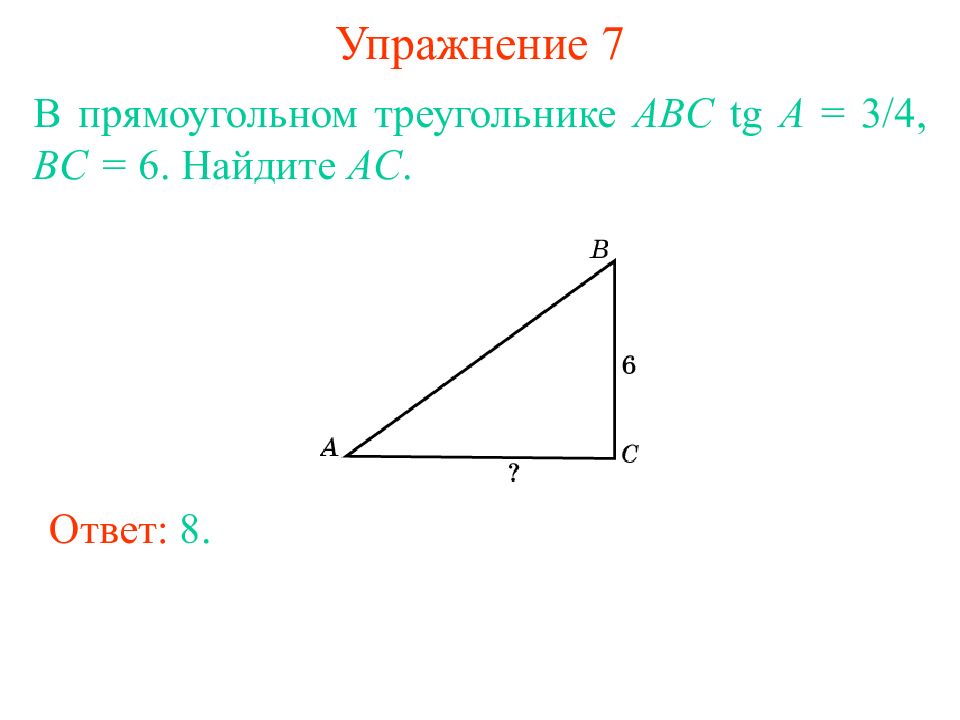
Слайд 12: Упражнение 7
В прямоугольном треугольнике ABC tg A = 3/4, BC = 6. Найдите AC. Ответ: 8.
Слайд 13: Упражнение 8
В прямоугольном треугольнике ABC, AC = 6. Найдите BC. Ответ: 4.
Слайд 14: Упражнение 9
Катеты прямоугольного треугольника равны 3 и 4. Найдите гипотенузу. Ответ: 5.
Слайд 15: Упражнение 10
Гипотенуза прямоугольного треугольника равна 13. Один из его катетов равен 5. Найдите другой катет. Ответ: 12.
Слайд 16: Упражнение 11
В треугольнике ABC AC = BC = 2, угол C равен 120 о. Найдите высоту, опущенную на сторону AB. Ответ: 1.
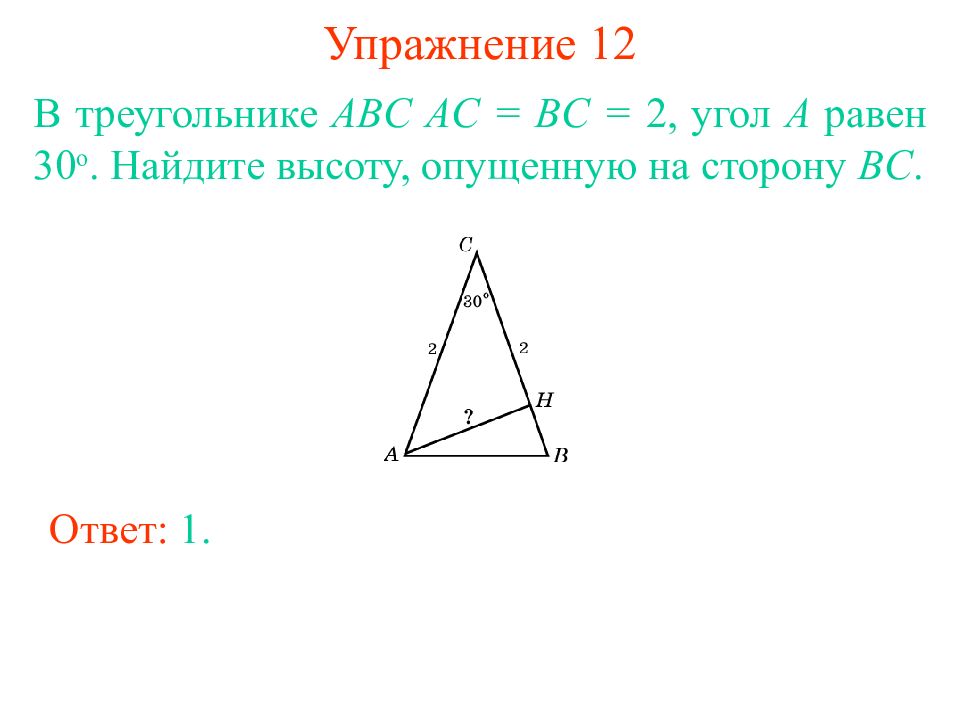
Слайд 17: Упражнение 12
В треугольнике ABC AC = BC = 2, угол A равен 30 о. Найдите высоту, опущенную на сторону BC. Ответ: 1.
Слайд 18: Упражнение 13
В треугольнике ABC AC = BC, угол C равен 90 о, AB = 6. Найдите высоту, опущенную на сторону AB. Ответ: 3.
Слайд 19: Упражнение 14
В треугольнике ABC AB = BC, угол B равен 120 о, AC = 4. Найдите высоту, опущенную из вершины C. Ответ: 2.
Слайд 20: Упражнение 15
Боковые стороны равнобедренного треугольника равны 10. Высота, опущенная на основание, равна 8. Найдите основание. Ответ: 12.
Слайд 21: Упражнение 16
В треугольнике ABC AB = 6, BC = 4, угол B равен 90 о. Найдите медиану, проведенную из вершины C. Ответ: 5.
Слайд 22: Упражнение 17
Сторона равностороннего треугольника равна. Найдите биссектрису этого треугольника. Ответ: 3.
Слайд 23: Упражнение 18
В прямоугольном треугольнике ABC угол C равен 90 о, угол B равен 30 о, катет AC равен. Найдите биссектрису, проведенную из вершины A. Ответ: 2.
Слайд 24: Упражнение 19
В треугольнике ABC угол A равен 60 о, угол B равен 45 о, сторона AC равна. Найдите сторону BC. Ответ: 3.
Слайд 25: Упражнение 20
Найдите сторону треугольника, лежащую против угла в 120 о, если прилежащие к нему стороны равны 6 и 10. Ответ: 14.
Слайд 26: Упражнение 21
В прямоугольном треугольнике ABC AB = 6, Найдите BC. Ответ: 2.
Слайд 27: Упражнение 22
В прямоугольном треугольнике ABC AB = 6, Найдите AC. Ответ: 4.
Слайд 28: Упражнение 23
В прямоугольном треугольнике ABC AB = 5, Найдите AC. Ответ: 4.
Слайд 29: Упражнение 2 4
В прямоугольном треугольнике ABC Найдите 5 sin A. Ответ: 3.
Слайд 30: Упражнение 25
Гипотенуза прямоугольного треугольника равна 10, а разность катетов равна 2. Найдите меньший катет. Ответ: 6.
Слайд 31: Упражнение 26
Найдите высоту, опущенную на гипотенузу, прямоугольного треугольника с катетами 15 и 20. Ответ: 12.
Слайд 32: Упражнение 27
Гипотенуза прямоугольного треугольника равна 25, а высота, опущенная на нее, равна 12. Найдите больший катет этого треугольника. Ответ: 20.
Слайд 33: Упражнение 28
В прямоугольном треугольнике проекции катетов на гипотенузу равны 1 и 3. Найдите его меньший острый угол. Ответ: 30 o.
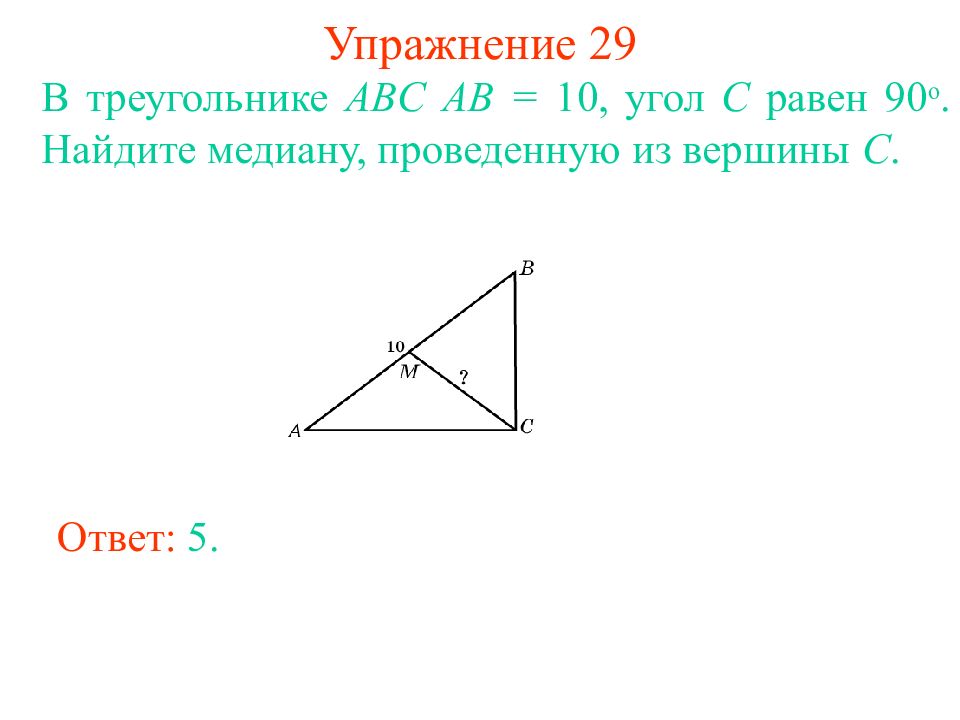
Слайд 34: Упражнение 29
В треугольнике ABC AB = 10, угол C равен 90 о. Найдите медиану, проведенную из вершины C. Ответ: 5.
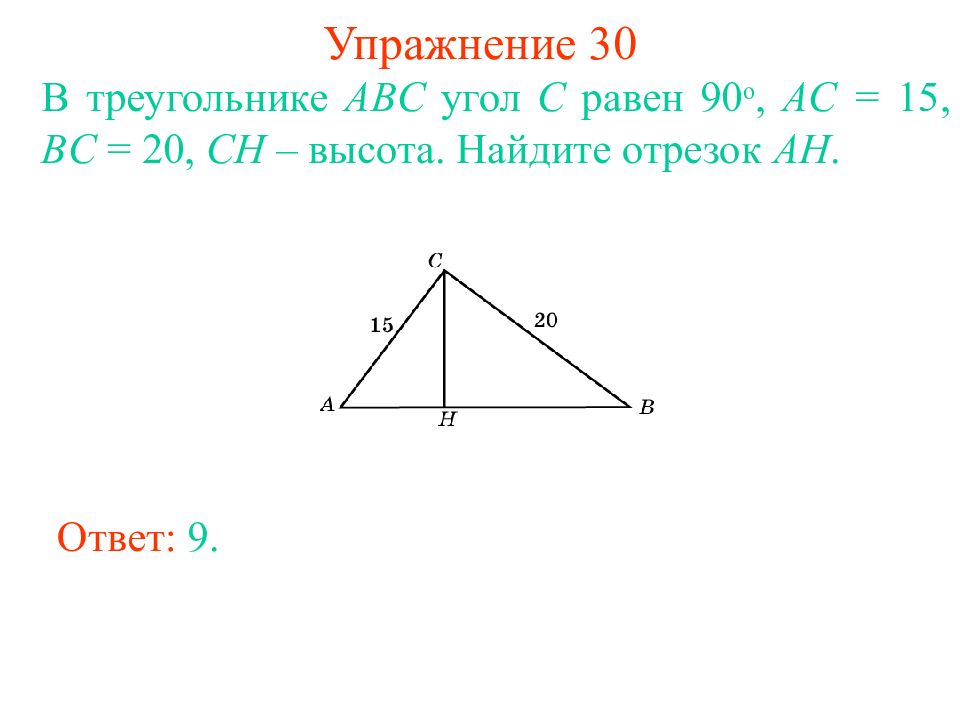
Слайд 35: Упражнение 30
В треугольнике ABC угол C равен 90 о, AC = 15, BC = 20, CH – высота. Найдите отрезок AH. Ответ: 9.
Слайд 36: Упражнение 31
В треугольнике ABC угол A равен 60 о, угол B равен 45 о, высота CH равна. Найдите сторону AB. Ответ: 2.
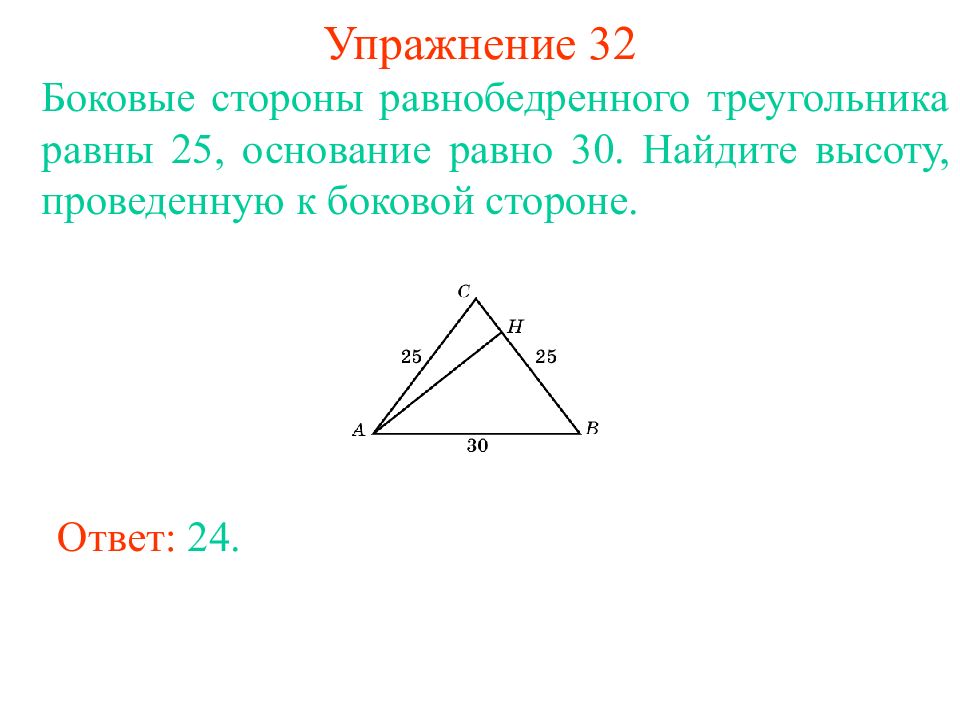
Слайд 37: Упражнение 32
Боковые стороны равнобедренного треугольника равны 25, основание равно 30. Найдите высоту, проведенную к боковой стороне. Ответ: 24.
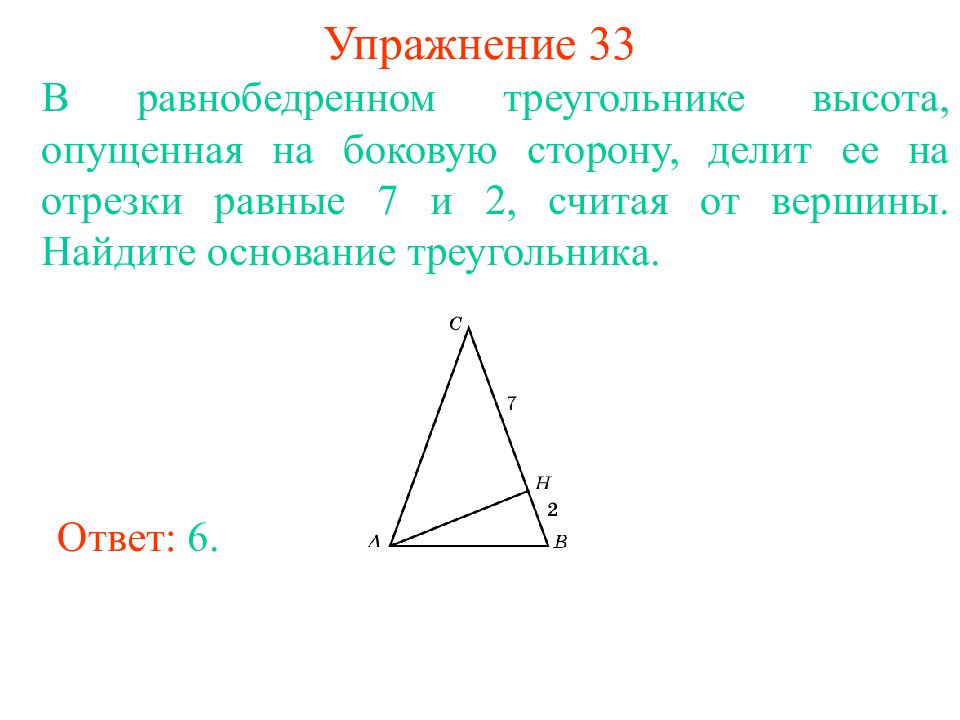
Слайд 38: Упражнение 33
В равнобедренном треугольнике высота, опущенная на боковую сторону, делит ее на отрезки равные 7 и 2, считая от вершины. Найдите основание треугольника. Ответ: 6.
Слайд 39: Упражнение 34
В треугольнике ABC AC = BC, AB = 1, угол C равен 36 о. Найдите биссектрису, проведенную из вершины A. Ответ: 1.
Слайд 40: Упражнение 35
Боковые стороны равнобедренного треугольника равны, основание равно. Найдите медиану, проведенную к боковой стороне. Ответ: 3.
Слайд 41: Упражнение 36
Боковые стороны равнобедренного треугольника равны, основание равно. Найдите биссектрису, проведенную к боковой стороне. Ответ: 10.
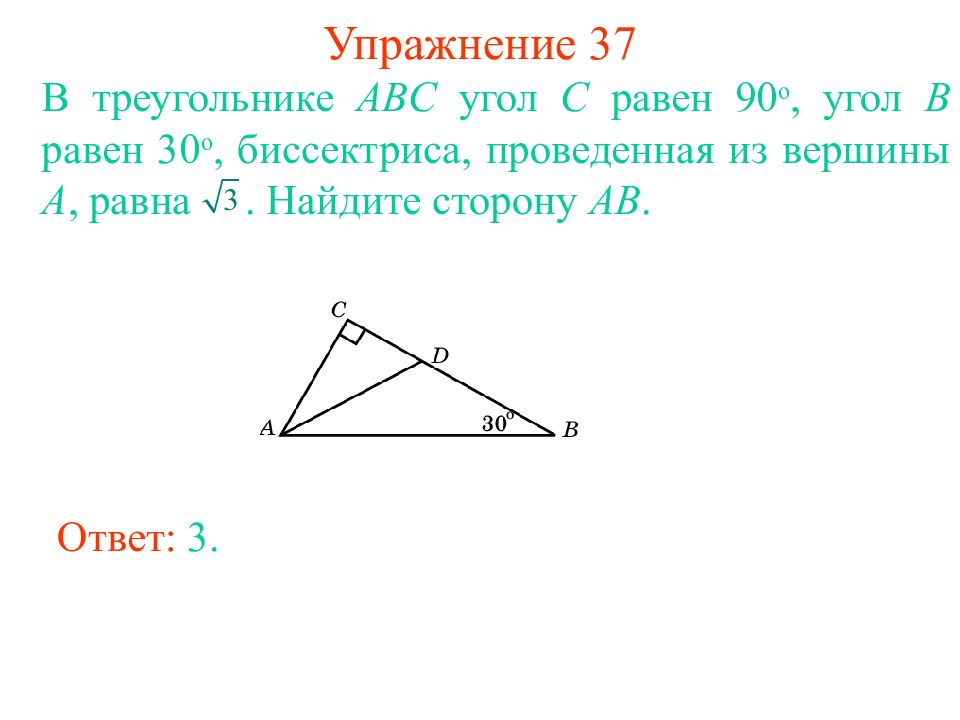
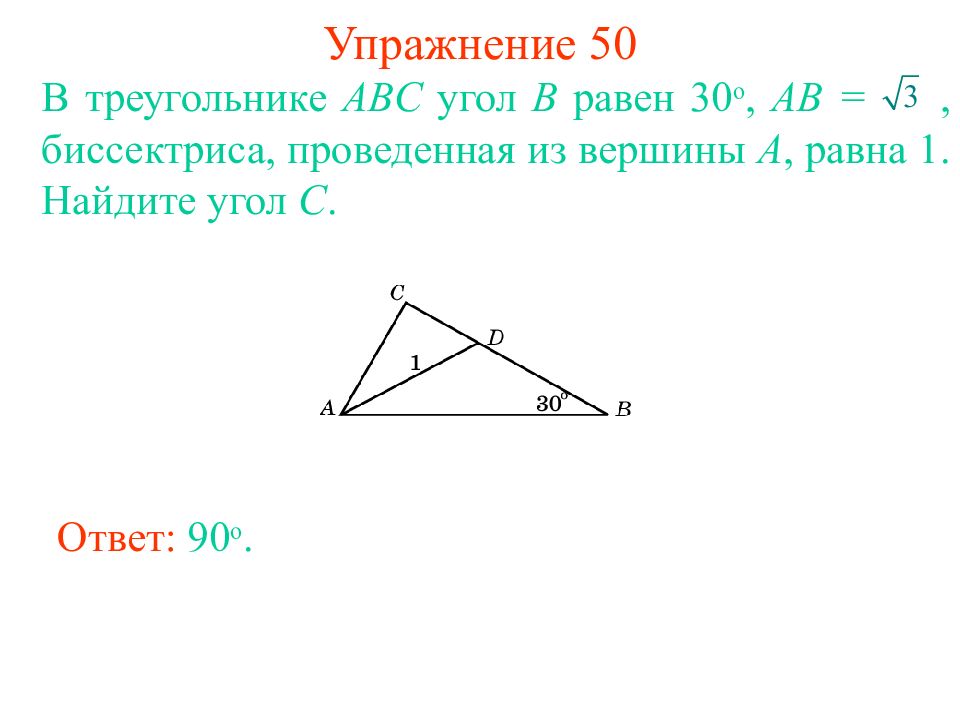
Слайд 42: Упражнение 37
В треугольнике ABC угол C равен 90 о, угол B равен 30 о, биссектриса, проведенная из вершины A, равна. Найдите сторону AB. Ответ: 3.
Слайд 43: Упражнение 38
В треугольнике ABC сторона AC равна, сторона BC равна 3, угол A равен 60 о. Найдите угол B. Ответ: 45 o.
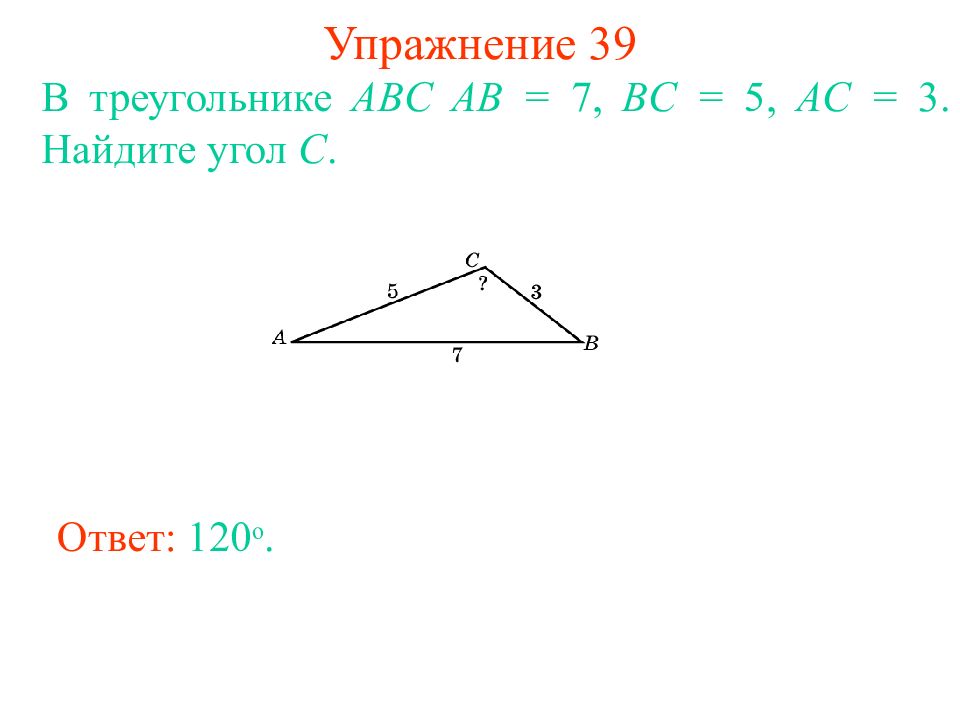
Слайд 44: Упражнение 39
В треугольнике ABC AB = 7, BC = 5, AC = 3. Найдите угол C. Ответ: 120 o.
Слайд 45: Упражнение 40
Одна из сторон треугольника равна 13, а угол, лежащий против этой стороны, равен 120 о, сумма двух других сторон треугольника равна 15. Найдите наименьшую сторону треугольника. Ответ: 7.
Слайд 46: Упражнение 41
В прямоугольном треугольнике ABC cos A = 3/5, AB = 10. Найдите AC. Ответ: 6.
Слайд 47: Упражнение 42
У прямоугольного треугольника один катет равен 6 см, а синус противолежащего ему угла равен 2/3. Найдите гипотенузу. Ответ: 9.
Слайд 48: Упражнение 43
Гипотенуза прямоугольного треугольника равна 10. Один из его катетов на 2 больше другого. Найдите больший катет. Ответ: 8.
Слайд 49: Упражнение 44
В треугольнике ABC AC = 4, угол A равен 30 о. Найдите высоту, опущенную на сторону BC. Ответ: 2.
Слайд 50: Упражнение 45
Боковые стороны равнобедренного треугольника равны 13. Высота, опущенная на основание, равна 12. Найдите основание. Ответ: 10.
Слайд 51: Упражнение 46
В прямоугольном треугольнике ABC AB = 10, tg A = 3/4. Найдите AC. Ответ: 8.
Слайд 52: Упражнение 47
В треугольнике ABC AC = 8, BC = 6, угол C равен 90 о. Найдите медиану, проведенную из вершины C. Ответ: 5.
Слайд 53: Упражнение 48
В треугольнике ABC BC = 3, AB =, угол С равен 45 о. Найдите угол A. Ответ: 60 o.
Слайд 54: Упражнение 49
В треугольнике ABC AB = 3, AC = 2, BC =. Найдите угол A. Ответ: 60 o.