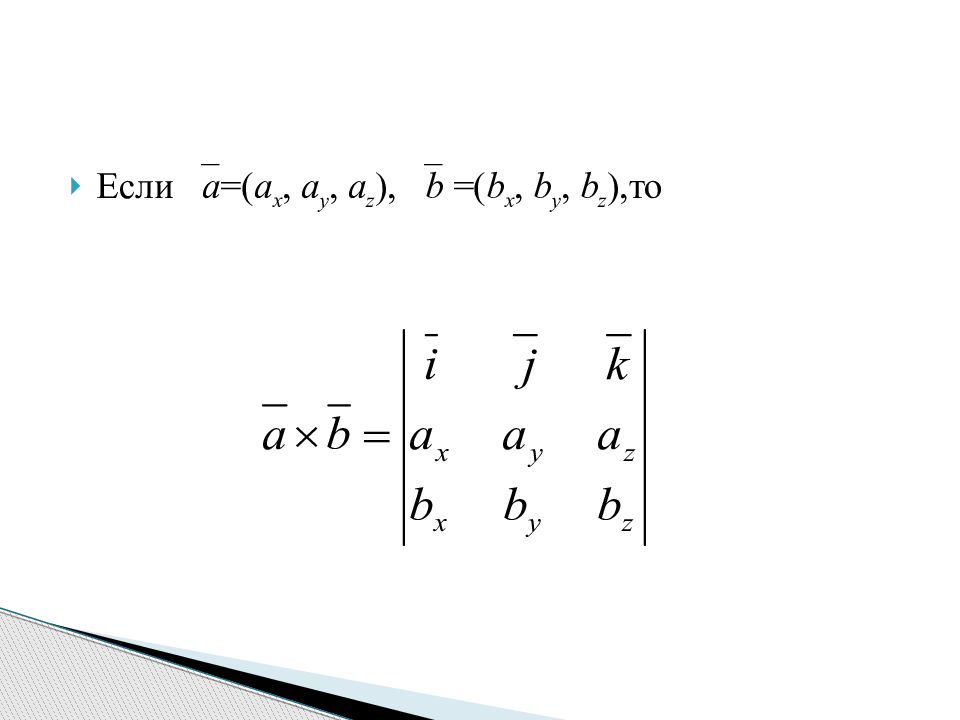Первый слайд презентации: ВЕКТОРЫ И ДЕЙСТВИЯ НАД НИМИ
Основные понятия. Линейные операции над векторами. Векторное пространство. Разложение вектора по базису. Нелинейные операции над векторами.
Слайд 2: Основные понятия
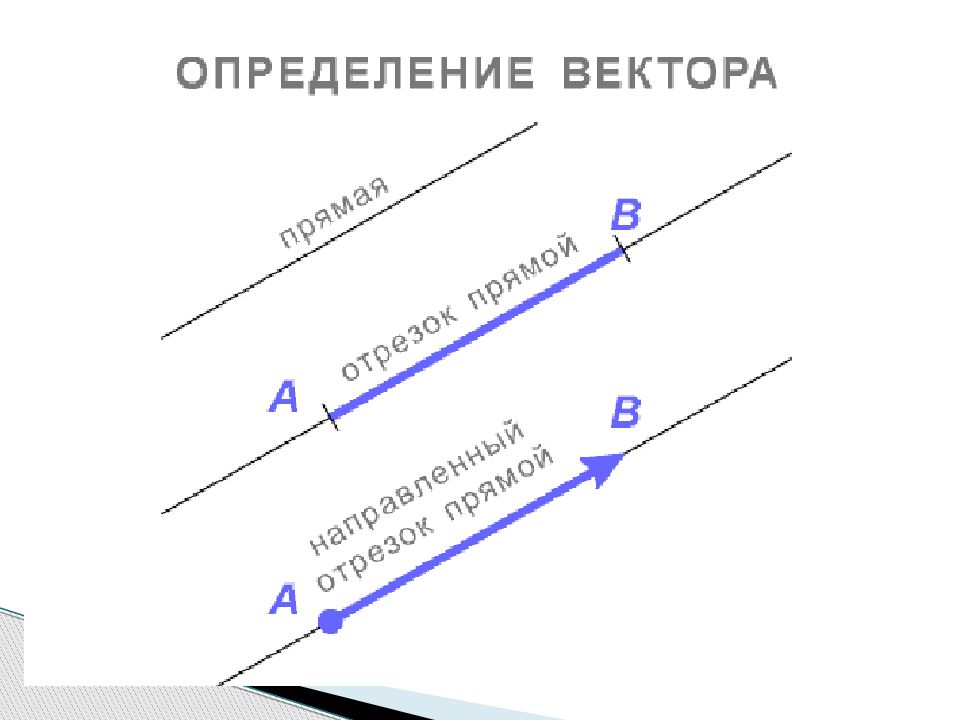
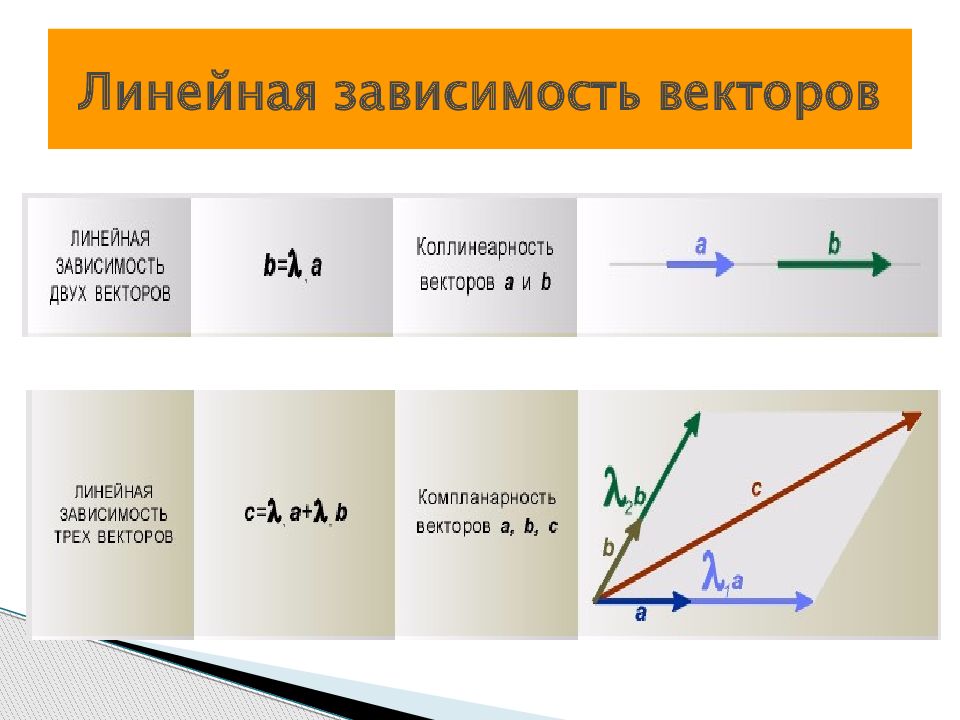
вектор; длина вектора; свободные векторы; равные векторы; нулевой вектор; коллинеарные векторы; компланарные векторы; n – мерный вектор и его координаты; векторное пространство; линейная комбинация векторов; линейно-зависимая и линейно-независимая система векторов; базис векторного пространства; проекция вектора на ось; проекция точки на ось; координаты вектора в ДСК; направляющие косинусы вектора Основные понятия
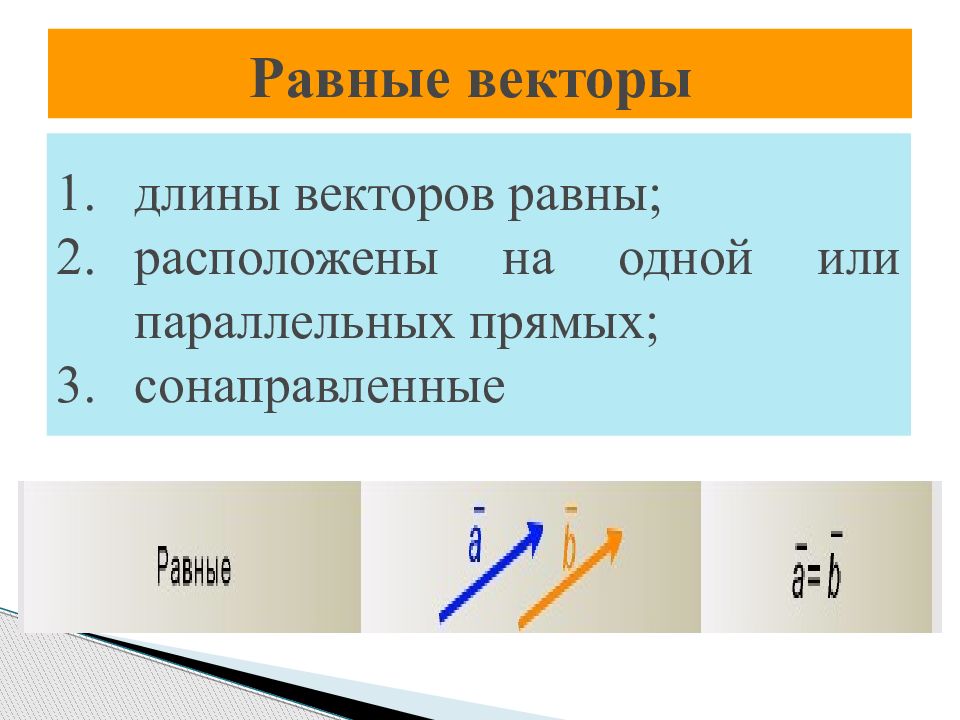
Слайд 5: Равные векторы
длины векторов равны; расположены на одной или параллельных прямых; сонаправленные
Слайд 6: Нулевой вектор
Слайд 7: Взаимное расположение векторов
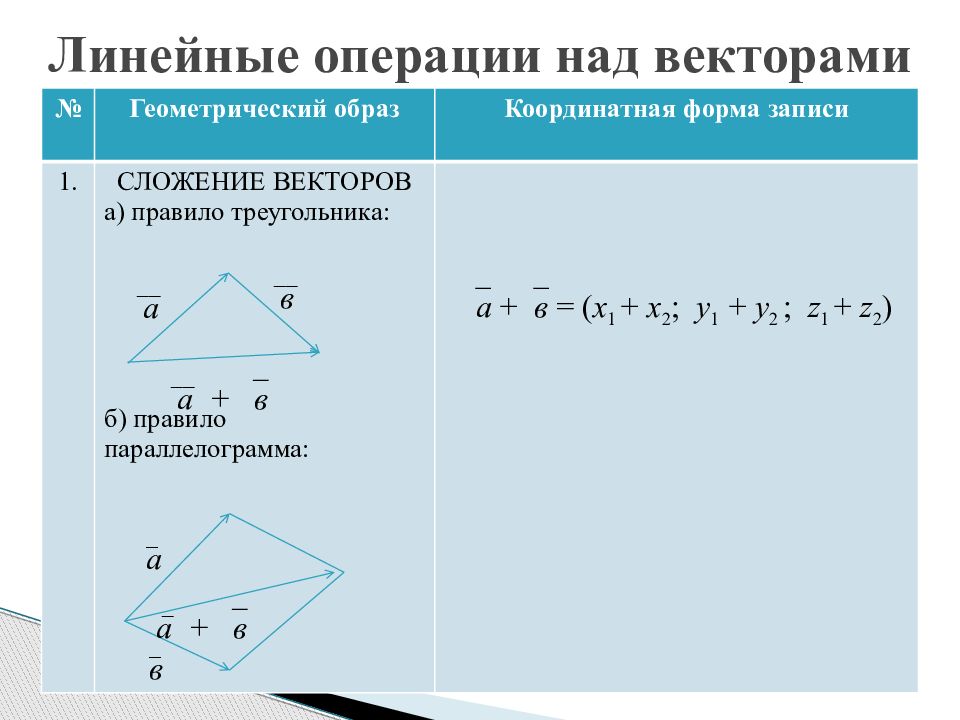
Слайд 10: Линейные операции над векторами
№ Геометрический образ Координатная форма записи 1. СЛОЖЕНИЕ ВЕКТОРОВ а) правило треугольника: б) правило параллелограмма: а + в = ( х 1 + х 2 ; y 1 + y 2 ; z 1 + z 2 ) в а а + в а в а + в
Слайд 11
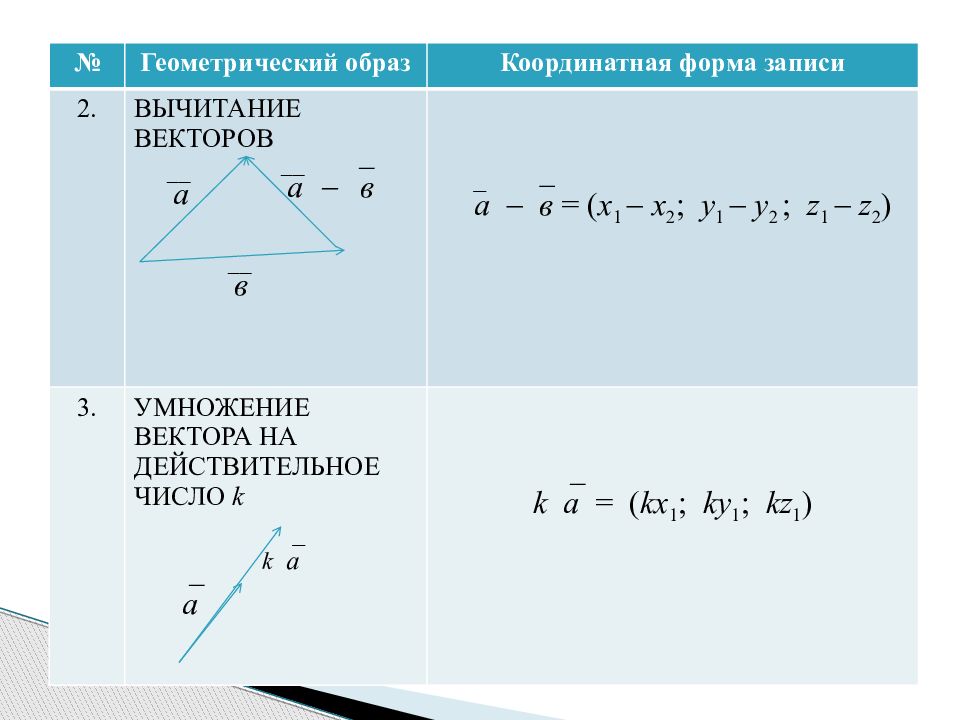
№ Геометрический образ Координатная форма записи 2. ВЫЧИТАНИЕ ВЕКТОРОВ а в = ( х 1 х 2 ; y 1 y 2 ; z 1 z 2 ) 3. УМНОЖЕНИЕ ВЕКТОРА НА ДЕЙСТВИТЕЛЬНОЕ ЧИСЛО k ka = ( k х 1 ; ky 1 ; kz 1 ) a k a в а а в
Слайд 17: Основные формулы
Если вектор, то: ; ; , где - угол между вектором a и положительным направлением оси l
Слайд 18: Примеры:
№1. Найти длины диагоналей параллелограмма, построенного на векторах: = (3; -5; 8) и = (-1; 1; -4). №2. Вектор, заданный в трехмерном пространстве составляет с координатными осями Ох и Оу углы =60˚, β = 120˚. Вычислить его координаты если a = 2. №3. Даны четыре точки,,.,. Выяснить, коллинеарны ли векторы и ? Примеры:
Слайд 20: НЕЛИНЕЙНЫЕ ОПЕРАЦИИ НАД ВЕКТОРАМИ
скалярное произведение двух векторов; векторное произведение двух векторов; смешанное произведение трех векторов НЕЛИНЕЙНЫЕ ОПЕРАЦИИ НАД ВЕКТОРАМИ
Слайд 22: Свойства скалярного произведения
(переместительное); (сочетательное); (распределительное); ; ; Свойства скалярного произведения
Слайд 23: Координатная форма скалярного произведения
Если a =( a x, a y, a z ), b =( b x, b y, b z ),то Координатная форма скалярного произведения
Слайд 26: Свойства векторного произведения
; ; ; (условие коллинеарности ) Свойства векторного произведения
Слайд 30: Свойства смешанного произведения
; если три данных вектора компланарны, то (и наоборот); ; ; если три вектора заданы координатами a =( x 1 ; y 1 ; z 1 ), b =( x 2 ; y 2 ; z 2 ), c =( x 3 ; y 3 ; z 3 ), то смешанное произведение вычисляется по формуле: Свойства смешанного произведения
Слайд 32
Приложения нелинейных операций над векторами Скалярное произведение Геометрические приложения Физические приложения
Слайд 33
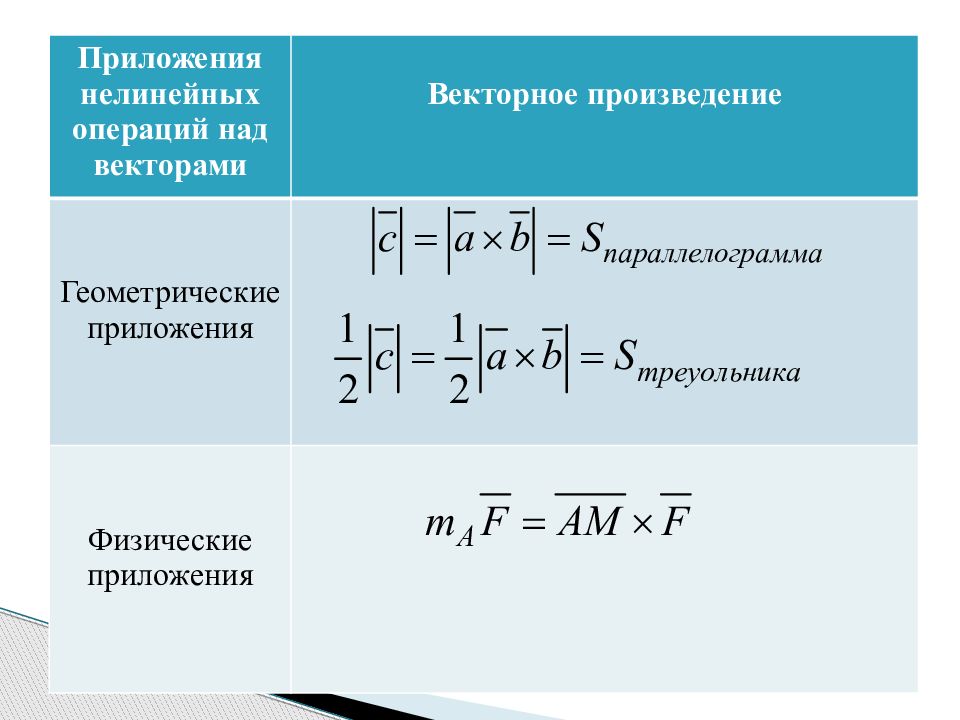
Приложения нелинейных операций над векторами Векторное произведение Геометрические приложения Физические приложения
Слайд 34
Приложения нелинейных операций над векторами Смешанное произведение Геометрические приложения Физические приложения