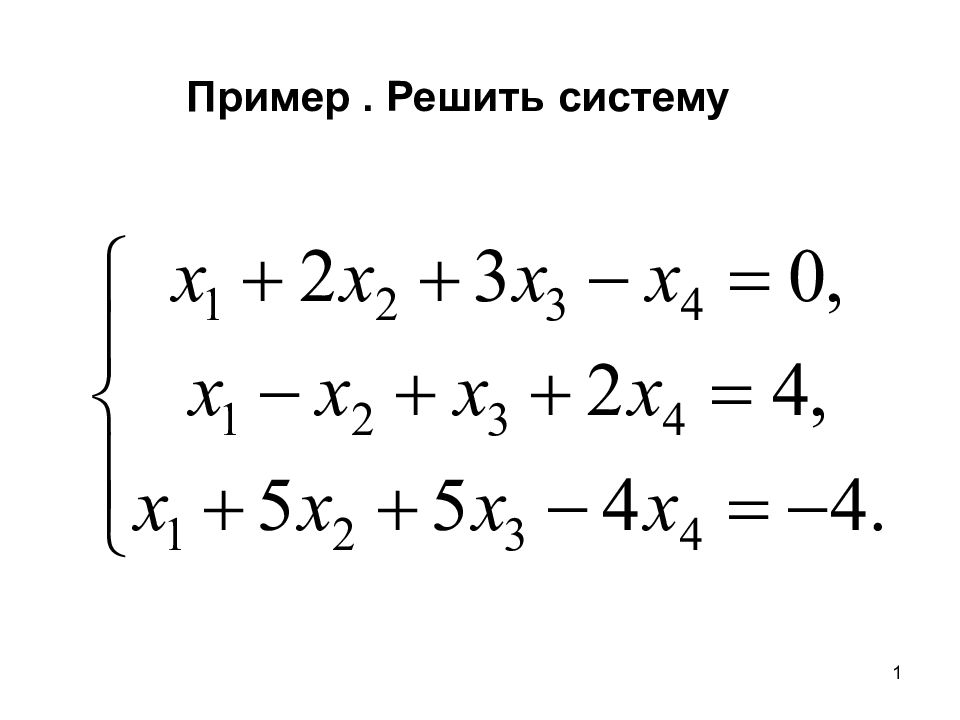Слайд 2: Основные понятия
Математическая величина Скалярная величина (характеризуется численным значением) Векторная величина (Характеризуется численным значением и направлением) 2
Слайд 3: Основные понятия
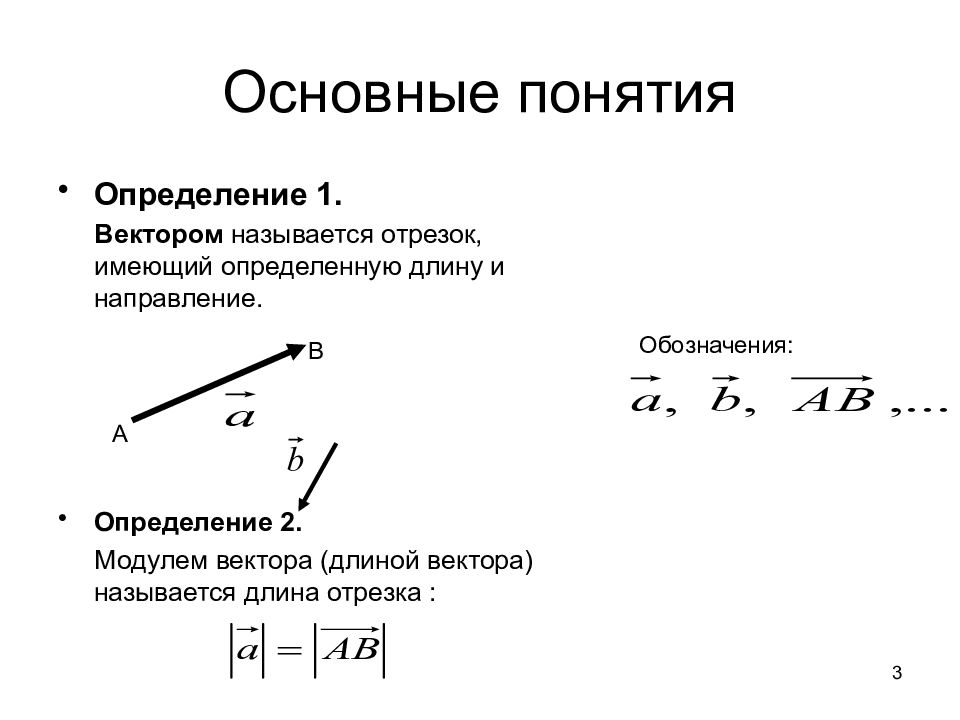
Определение 1. Вектором называется отрезок, имеющий определенную длину и направление. Определение 2. Модулем вектора (длиной вектора) называется длина отрезка : А В Обозначения: 3
Слайд 4: Основные понятия
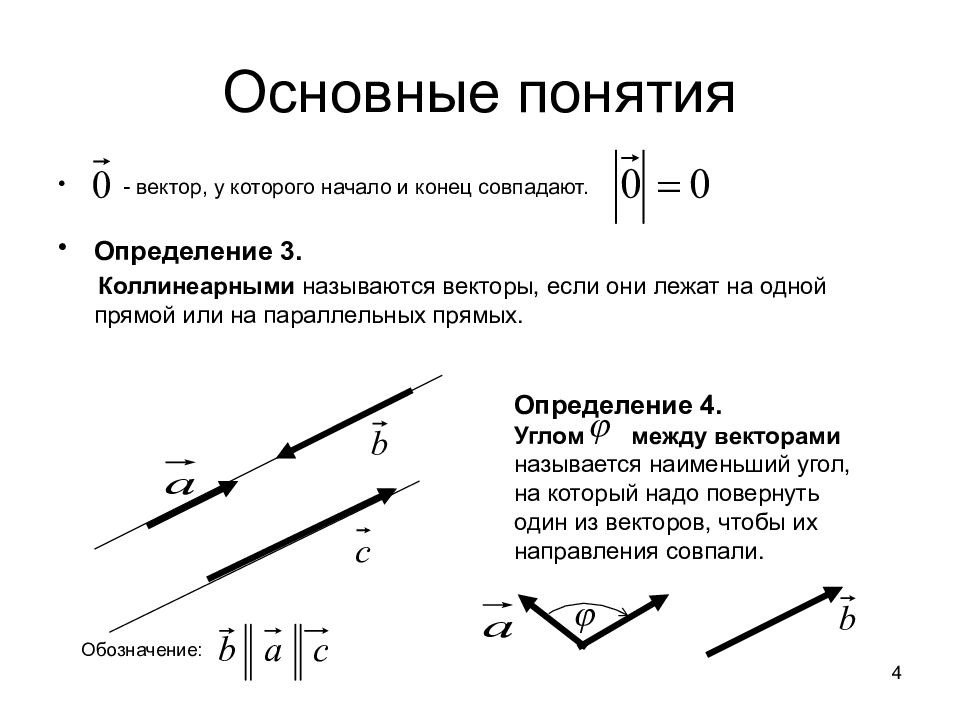
- вектор, у которого начало и конец совпадают. Определение 3. Коллинеарными называются векторы, если они лежат на одной прямой или на параллельных прямых. Определение 4. Углом между векторами называется наименьший угол, на который надо повернуть один из векторов, чтобы их направления совпали. Обозначение: 4
Слайд 5: Основные понятия
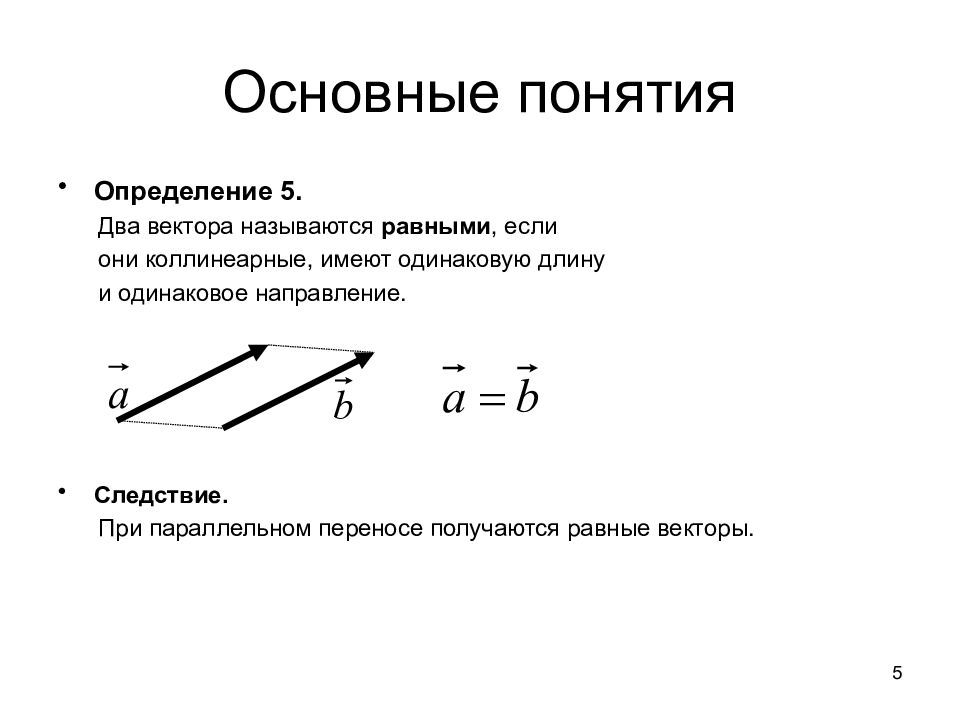
Определение 5. Два вектора называются равными, если они коллинеарные, имеют одинаковую длину и одинаковое направление. Следствие. При параллельном переносе получаются равные векторы. 5
Слайд 6: Основные понятия
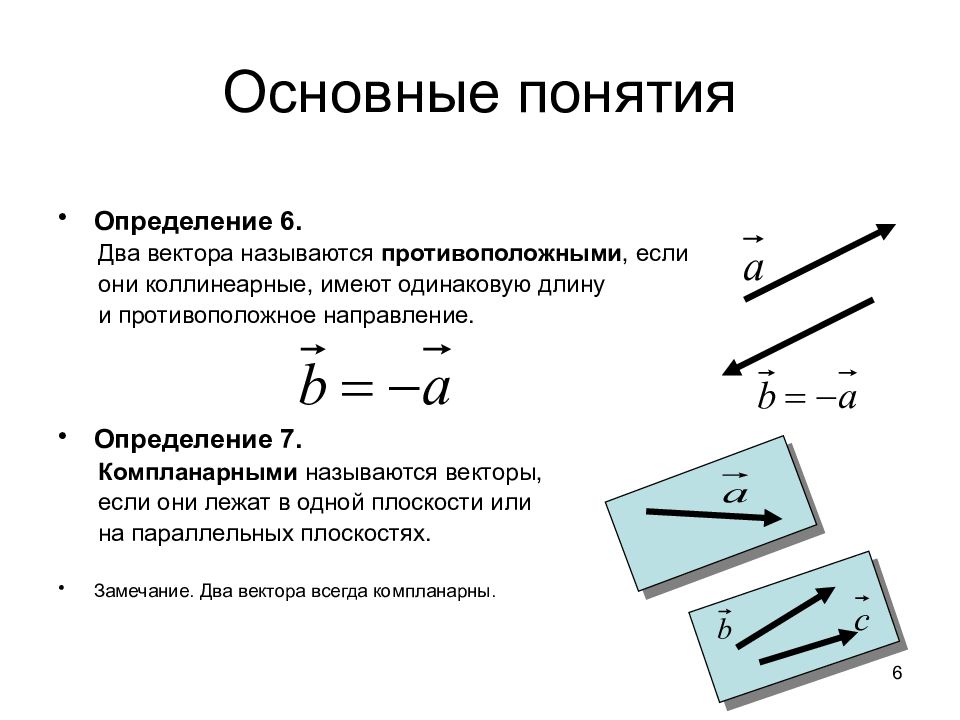
Определение 6. Два вектора называются противоположными, если они коллинеарные, имеют одинаковую длину и противоположное направление. Определение 7. Компланарными называются векторы, если они лежат в одной плоскости или на параллельных плоскостях. Замечание. Два вектора всегда компланарны. 6
Слайд 7: Операции с векторами
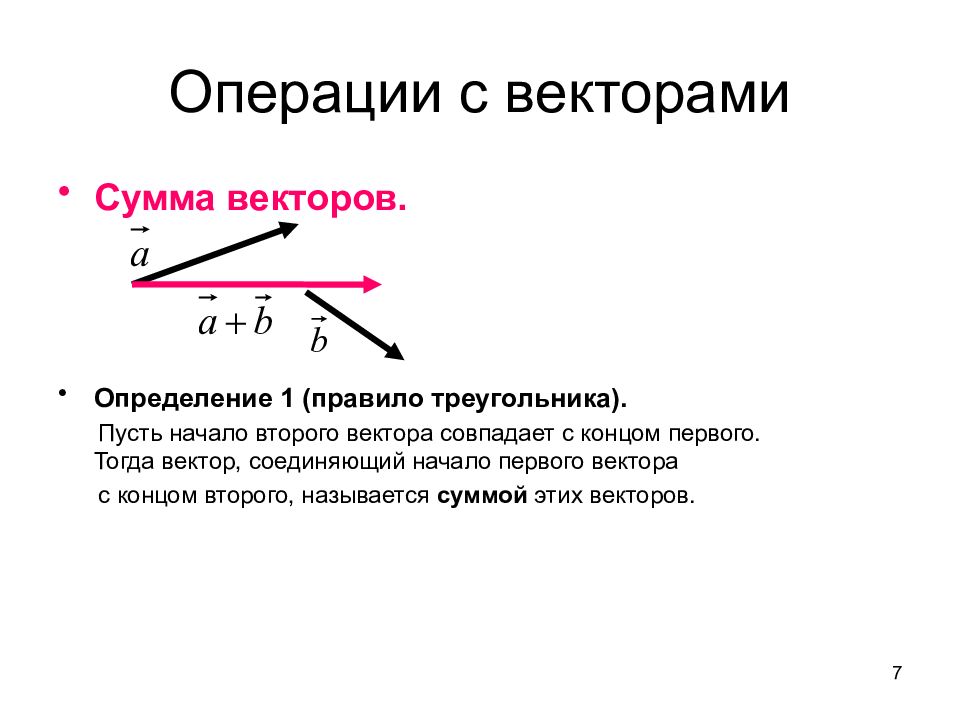
Сумма векторов. Определение 1 (правило треугольника). Пусть начало второго вектора совпадает с концом первого. Тогда вектор, соединяющий начало первого вектора с концом второго, называется суммой этих векторов. 7
Слайд 8: Операции с векторами
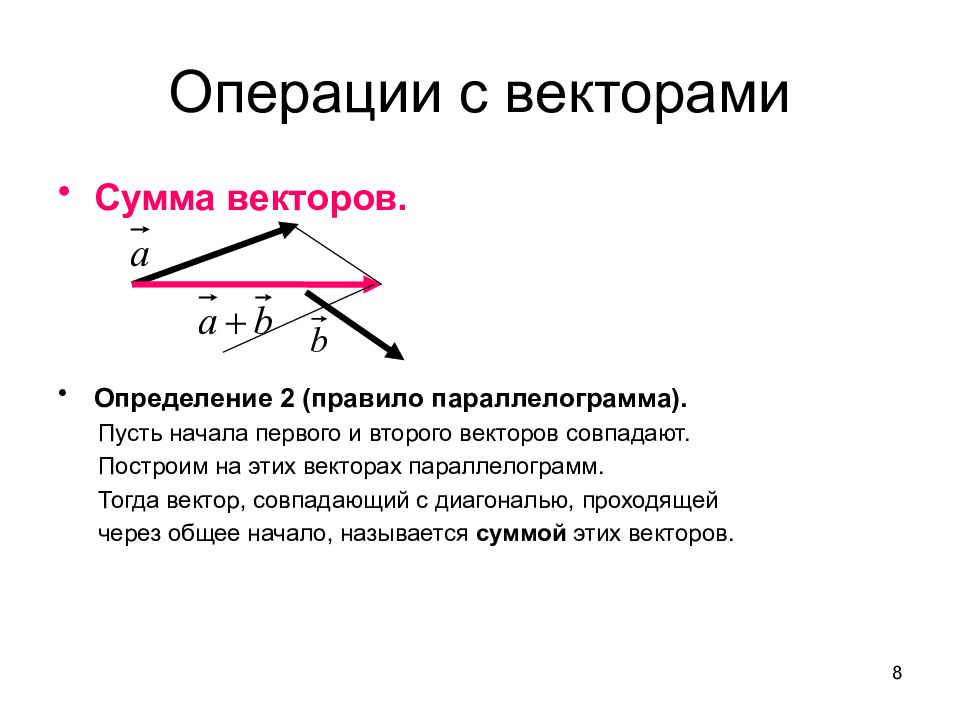
Сумма векторов. Определение 2 (правило параллелограмма). Пусть начала первого и второго векторов совпадают. Построим на этих векторах параллелограмм. Тогда вектор, совпадающий с диагональю, проходящей через общее начало, называется суммой этих векторов. 8
Слайд 9: Операции с векторами
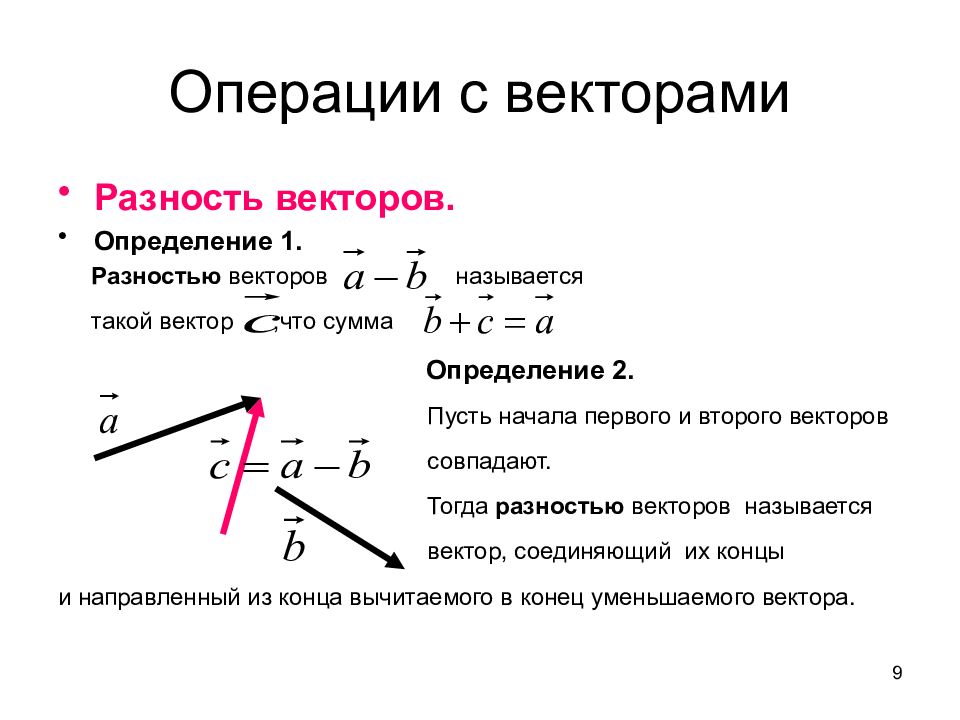
Разность векторов. Определение 1. Разностью векторов называется такой вектор,что сумма Определение 2. Пусть начала первого и второго векторов совпадают. Тогда разностью векторов называется вектор, соединяющий их концы и направленный из конца вычитаемого в конец уменьшаемого вектора. 9
Слайд 10: Операции с векторами
Произведение вектора на число. Определение. Произведением вектора на число называется вектор, коллинеарный вектору, равный по модулю, направленный при в ту же сторону, что и, и в противоположную сторону, если. 10
Слайд 11: Операции с векторами
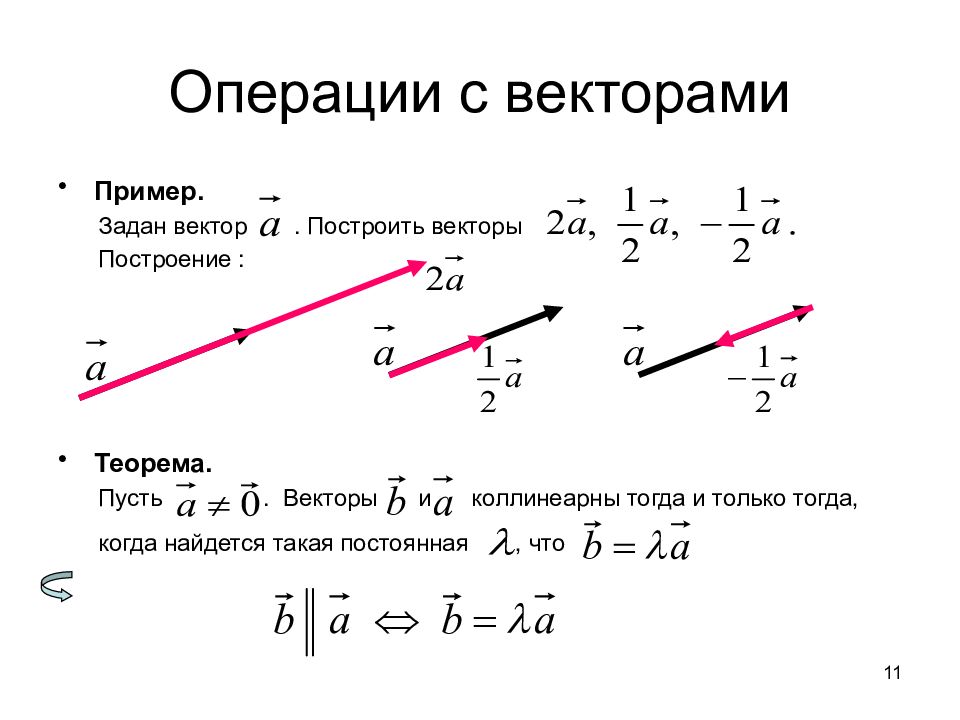
Пример. Задан вектор. Построить векторы Построение : Теорема. Пусть. Векторы и коллинеарны тогда и только тогда, когда найдется такая постоянная, что 11
Слайд 12: Разложение векторов
Разложение векторов по ортам. Определение 1. Ортом вектора называется вектор, имеющий единичную длину и то же направление, что и вектор. 12
Слайд 13: Разложение векторов
Рассмотрим прямоугольную систему координат. Теорема 3. В пространстве любой вектор можно разложить по ортонормированному базису : Такое разложение единственное. x y z 0 Векторы -единичные (орты), направленные по осям x, y, z ( соответственно ) Определение 2. Тройка векторов называется ортонормированным базисом в пространстве. 13
Слайд 14: Разложение векторов
Определение 3. Коэффициенты x, y, z разложения называются прямоугольными координатами вектора : Частный случай. Если вектор расположен на координатной плоскости хо y, то разложение будет иметь вид Коэффициенты х, у называются прямоугольными координатами вектора на плоскости : 14
Слайд 15: Проекции вектора
Рассмотрим вектор и ось Определение. Проекцией вектора на ось называется разность проекций конца и начала вектора на эту ось; 0 15
Слайд 16: Проекции вектора
В пространстве: Следствие. Если вектор задан двумя точками, - начало, - конец, то 16
Слайд 17: Действия с векторами в координатной форме
Сумма и разность векторов, произведение вектора на число. Пусть Тогда 1. 2. Модуль вектора Орт вектора 17
Слайд 18: Действия с векторами в координатной форме
Необходимое и достаточное условие коллинеарности векторов, заданных в координатной форме. Два ненулевых вектора коллинеарны тогда и только тогда, когда соответствующие координаты пропорциональны. Пусть Тогда Доказательство. 18
Слайд 19: Скалярное произведение
Определение. Скалярным произведением двух векторов называется число, равное произведению модулей векторов на косинус угла между ними. Физический смысл. Пусть материальная точка под действием силы перемещается из положения в положение Работа силы по перемещению материальной точки равна скалярному произведению вектора силы на вектор перемещения. Обозначения : 19
Слайд 20: Скалярное произведение
Свойства скалярного произведения. 1. 2. 3. 4. Следствия из формулы 4 : 20
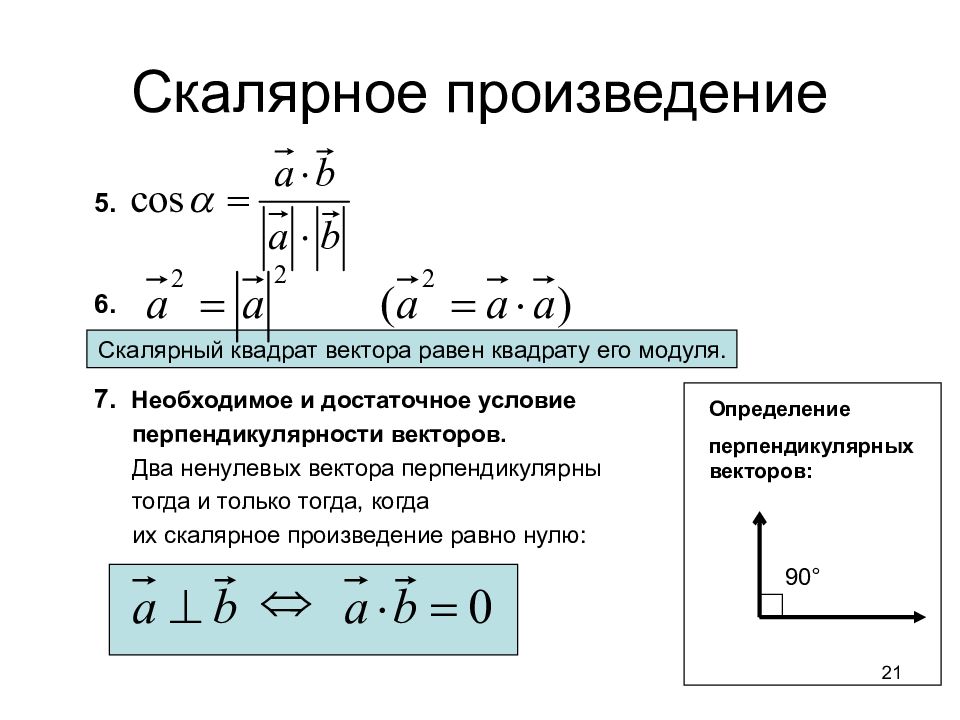
Слайд 21: Скалярное произведение
5. 6. Скалярный квадрат вектора равен квадрату его модуля. 7. Необходимое и достаточное условие перпендикулярности векторов. Два ненулевых вектора перпендикулярны тогда и только тогда, когда их скалярное произведение равно нулю: Определение перпендикулярных векторов: 90 ° 21
Слайд 22: Скалярное произведение
Скалярное произведение векторов, заданных в координатной форме. Пусть Тогда Скалярное произведение векторов равно сумме произведений соответствующих координат. Условие перпендикулярности векторов в координатной форме : 22
Слайд 23: Векторное произведение
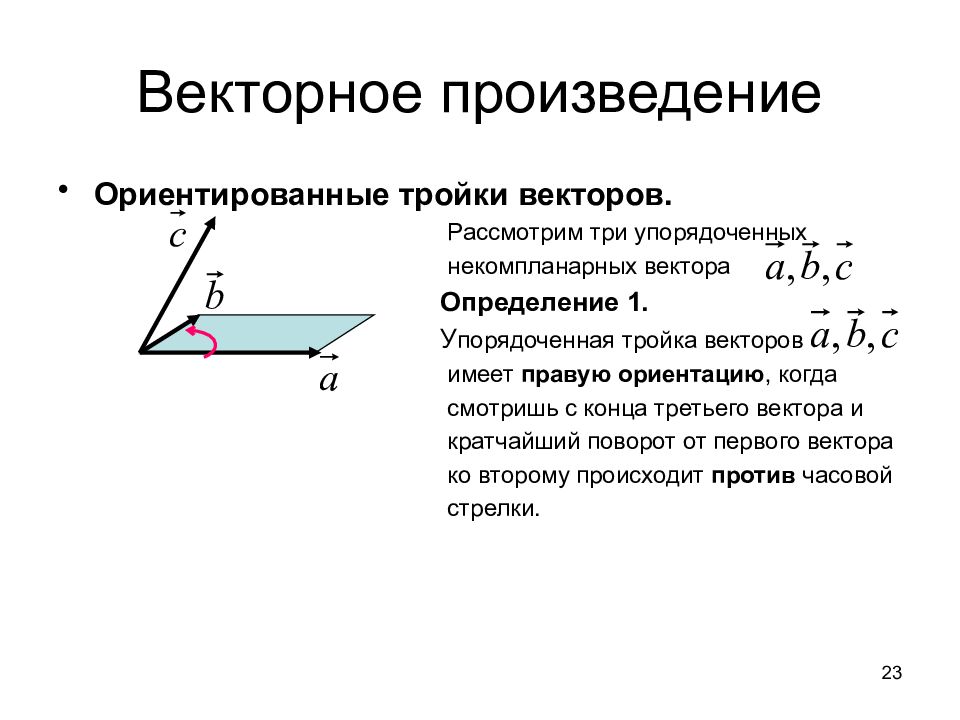
Ориентированные тройки векторов. Рассмотрим три упорядоченных некомпланарных вектора Определение 1. У порядоченная тройка векторов имеет правую ориентацию, когда смотришь с конца третьего вектора и кратчайший поворот от первого вектора ко второму происходит против часовой стрелки. 23
Слайд 24: Векторное произведение
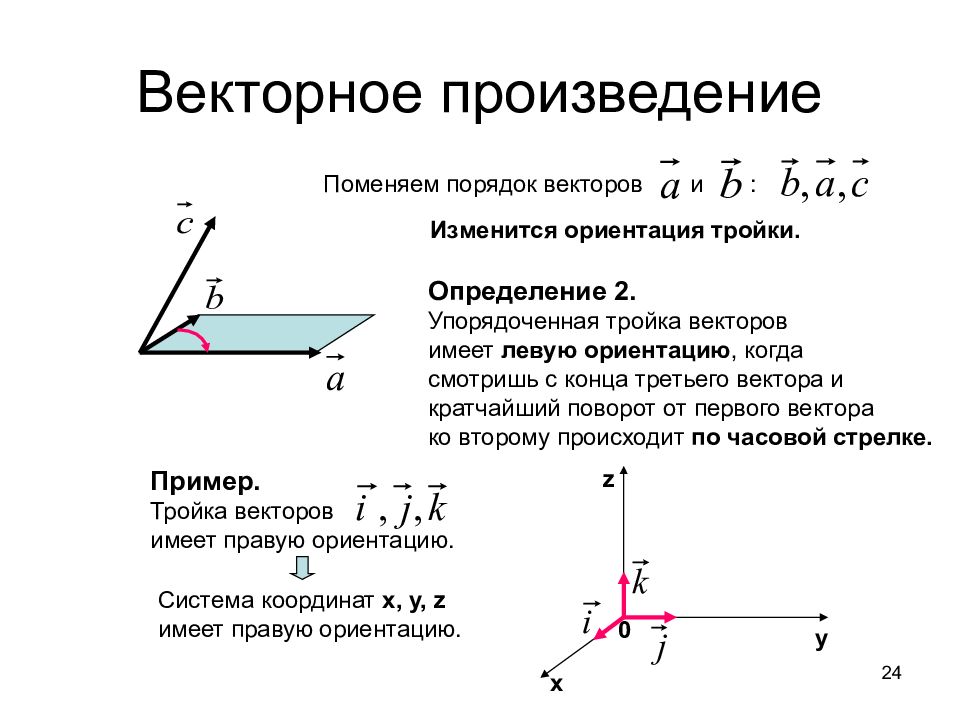
Поменяем порядок векторов и : Изменится ориентация тройки. Определение 2. Упорядоченная тройка векторов имеет левую ориентацию, когда смотришь с конца третьего вектора и кратчайший поворот от первого вектора ко второму происходит по часовой стрелке. Пример. Тройка векторов имеет правую ориентацию. x y z 0 Система координат х, у, z имеет правую ориентацию. 24
Слайд 25: Векторное произведение
Определение 3. Векторным произведением двух векторов называется третий вектор, удовлетворяющий трем условиям : 1. 2. 3. Тройка векторов имеет правую ориентацию. Обозначения : 25
Слайд 26: Векторное произведение
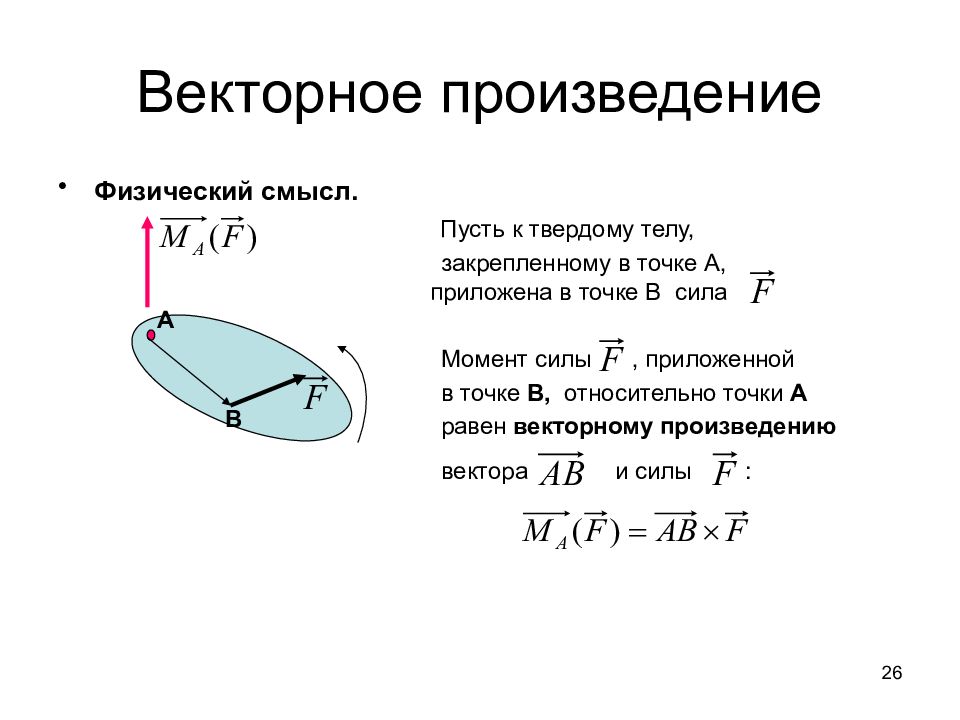
Физический смысл. Пусть к твердому телу, закрепленному в точке А, приложена в точке В сила Момент силы, приложенной в точке В, относительно точки А равен векторному произведению вектора и силы : А В 26
Слайд 27: Векторное произведение
Свойства векторного произведения. 1. 2. 3. 4. Геометрический смысл. Модуль векторного произведения двух векторов численно равен площади параллелограмма, построенного на этих векторах: 27
Слайд 28: Векторное произведение
5. Необходимое и достаточное условие коллинеарности двух векторов. Два ненулевых вектора коллинеарны тогда и только тогда, когда их векторное произведение равно нулевому вектору: 6. 28
Слайд 29: Векторное произведение
Векторное произведение векторов, заданных в координатной форме. Пусть Тогда 29
Слайд 30: Смешанное произведение
Определение. Смешанным произведением трех векторов называется векторное произведение первых двух векторов, умноженное скалярно на третий вектор: Обозначения: Замечание. Результат смешанного произведения трех векторов является скалярной величиной. 30
Слайд 31: Смешанное произведение
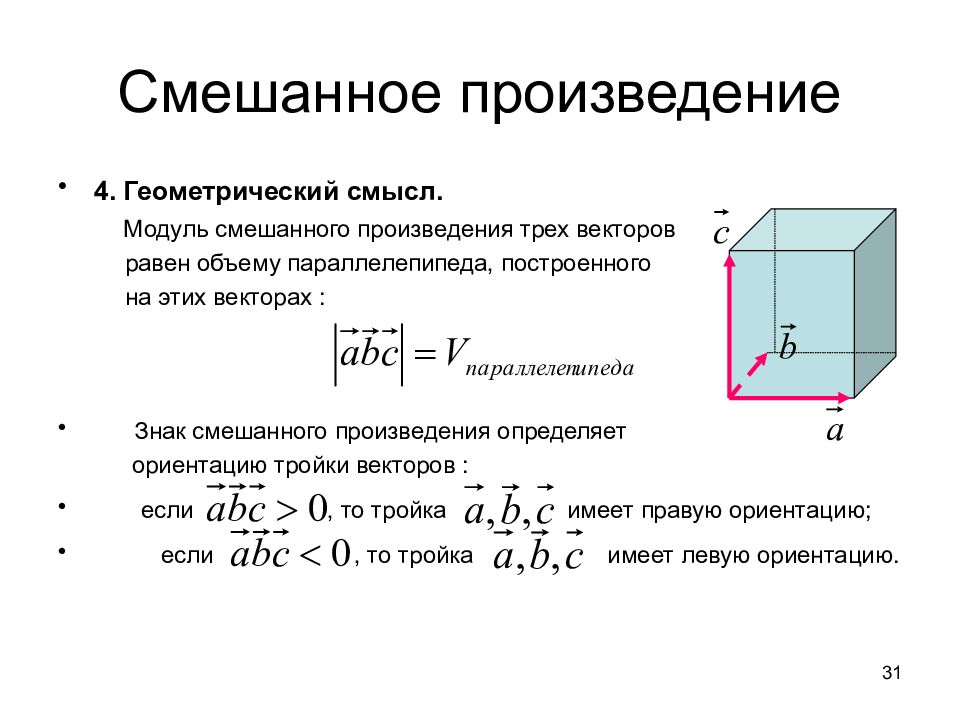
4. Геометрический смысл. Модуль смешанного произведения трех векторов равен объему параллелепипеда, построенного на этих векторах : Знак смешанного произведения определяет ориентацию тройки векторов : если, то тройка имеет правую ориентацию; если, то тройка имеет левую ориентацию. 31
Последний слайд презентации: Векторная алгебра: Смешанное произведение
5. Необходимое и достаточное условие компланарности трех векторов. Три ненулевых вектора компланарны тогда и только тогда, когда смешанное произведение этих векторов равно нулю. Смешанное произведение векторов, заданных в координатной форме. Пусть Тогда 32