Первый слайд презентации: А.А. Башев ЭЛЕКТРОТЕХНИКА И ЭЛЕКТРОНИКА
Кафедра “Теоретическая и общая электротехника” Для студентов электротехнических специальностей всех форм обучения Федеральное агентство по образованию Нижегородский государственный технический университет им. Р.Е. АЛЕКСЕЕВА
Слайд 2: Тема 8
ЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПРИ НЕСИНУСОИДАЛЬНЫХ ПЕРИОДИЧЕСКИХ ТОКАХ Тема 8
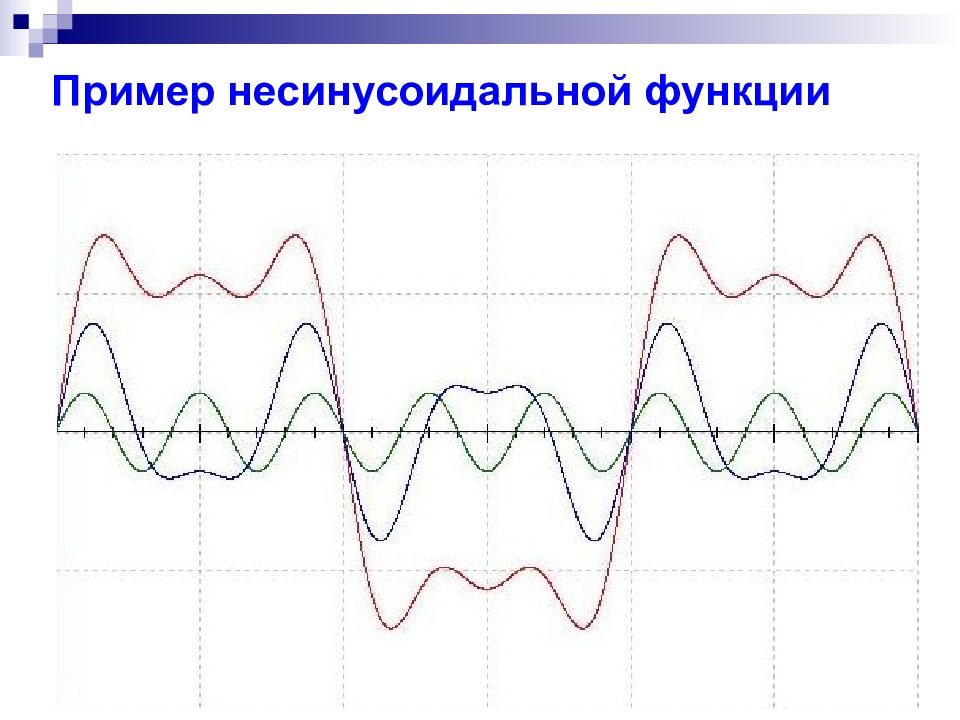
Слайд 3: Несинусоидальные токи
Периодическими несинусоидальными токами и напряжениями называются токи и напряжения, изменяющиеся во времени по периодическому несинусоидальному закону
Слайд 4: Разложение периодических функций. Характеристики несинусоидальных величин
Для анализа процессов в линейных электрических цепях при воздействии на них несинусоидальных токов или напряжений последние обычно разлагаются в ряд Фурье.
Слайд 5
Электротехника и электроника Ряд Фурье в тригонометрической форме 5 Ряд Фурье в тригонометрической форме – угловая частота первой гармоники
Слайд 6
Электротехника и электроника Ряд Фурье в тригонометрической форме 6 Коэффициенты a n и b n вычисляются по формулам – постоянная составляющая, равная среднему значению функции f ( t ) за период:
Слайд 7
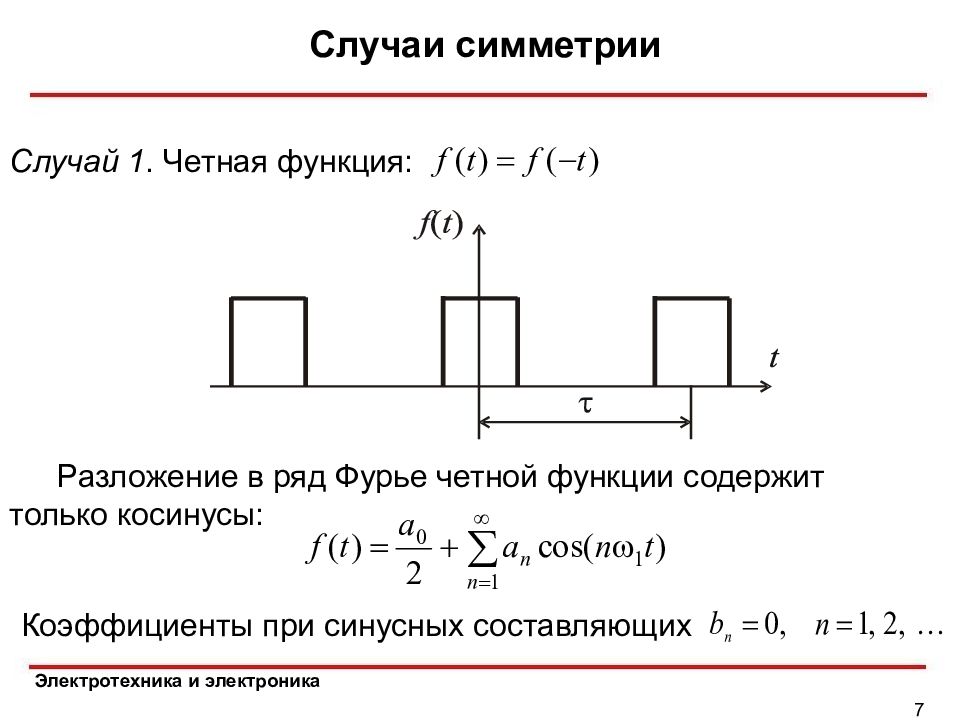
Электротехника и электроника Случаи симметрии 7 Случай 1. Четная функция: Разложение в ряд Фурье четной функции содержит только косинусы: Коэффициенты при синусных составляющих
Слайд 8
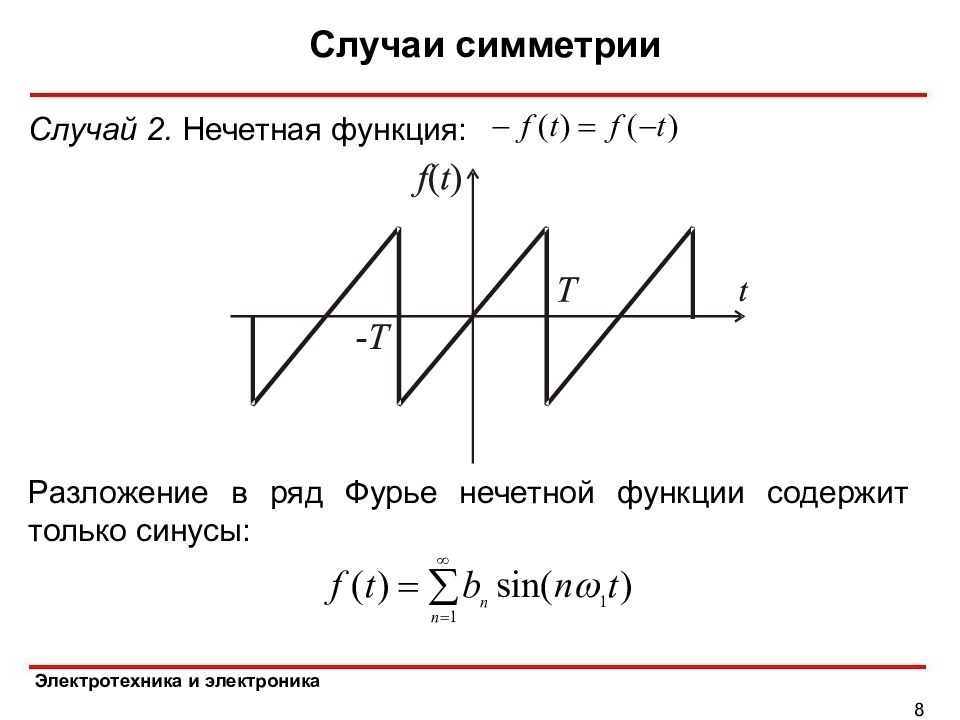
Электротехника и электроника Случаи симметрии 8 Случай 2. Нечетная функция: Разложение в ряд Фурье нечетной функции содержит только синусы:
Слайд 9
Электротехника и электроника Случаи симметрии 9 Случай 3. Функция f ( t ) симметрична относительно оси абсцисс при совмещении двух полупериодов во времени, т. е. Четные гармоники, а также составляющая равны нулю, т. е.
Слайд 10
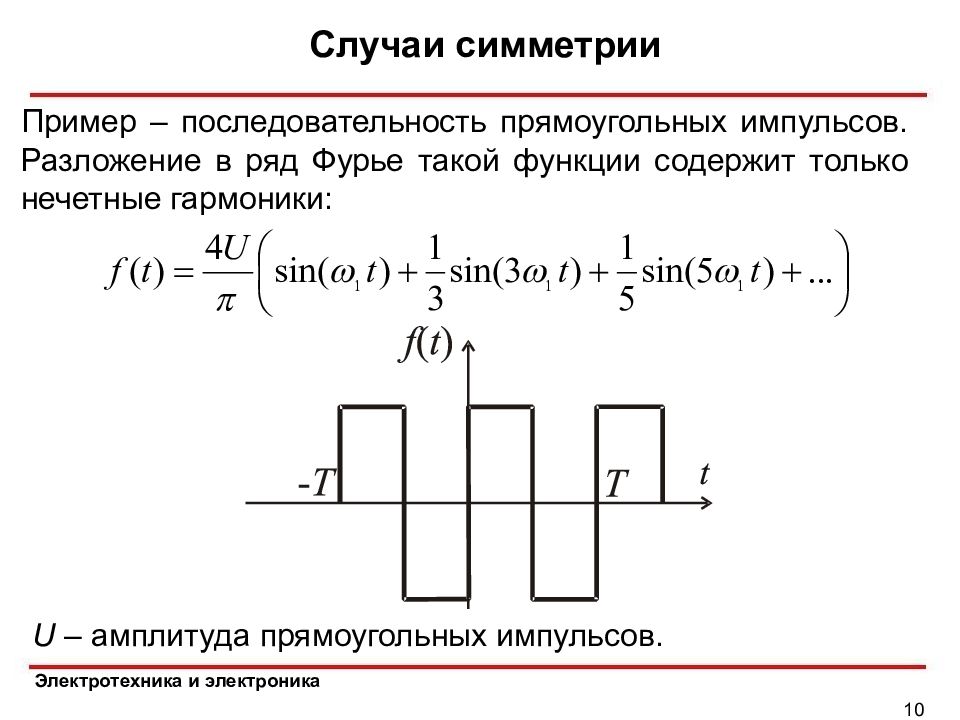
Электротехника и электроника Случаи симметрии 10 Пример – последовательность прямоугольных импульсов. Разложение в ряд Фурье такой функции содержит только нечетные гармоники: U – амплитуда прямоугольных импульсов.
Слайд 11
Электротехника и электроника Комплексная форма ряда Фурье 11 Ряд Фурье в тригонометрической форме Воспользуемся равенствами:
Слайд 12
Электротехника и электроника Комплексная форма ряда Фурье 12 Ряд Фурье примет вид: Коэффициент a n – четная, а b n – нечетная функция индекса n : Поэтому элемент - jb n можно рассматривать как слагаемое с отрицательным индексом. ,
Слайд 13
Электротехника и электроника Комплексная форма ряда Фурье 13 Изменив нижний предел суммирования на, получим – комплексный коэффициент ряда Фурье. В показательной форме: ,
Слайд 14
Электротехника и электроника Комплексный частотный спектр 14 Амплитуды гармоник образуют амплитудный спектр. Совокупность комплексных коэффициентов гармоник называют комплексным частотным спектром функции Начальные фазы образуют фазовый спектр.
Слайд 15
Электротехника и электроника Комплексный частотный спектр 15 Используя равенства Комплексная амплитуда n -й гармоники получим, что комплексный коэффициент ряда Фурье
Слайд 18: Величины, характеризующие несинусоидальные токи
Максимальное значение – I max Действующее значение Среднее по модулю значение Среднее за период значение (постоянная составляющая)
Слайд 19: Величины, характеризующие несинусоидальные токи
Коэффициент амплитуды Коэффициент формы Коэффициент искажений Коэффициент гармоник
Слайд 20: Величины, характеризующие несинусоидальные токи
Действующим значением периодической несинусоидальной переменной называется среднеквадратичное за период значение величины:
Слайд 21: Величины, характеризующие несинусоидальные токи
На практике действующее значение переменной определяется на основе информации о действующих значениях конечного ряда гармонических.
Слайд 22: Мощность в цепях периодического несинусоидального тока
Допустим, ток и напряжение являются периодическими несинусоидальными функциями:
Слайд 23: Мощность в цепях периодического несинусоидального тока
Среднее за период значение произведения синусоидальных функций различной частоты равно нулю, тогда Где Реактивная мощность
Слайд 24
Полная мощность где Т – мощность искажений, определяемая произведениями действующих значений разнопорядковых гармонических тока и напряжения. Мощность в цепях периодического несинусоидального тока
Слайд 25: Рекомендуемая литература
Электротехника и электроника Рекомендуемая литература 1. Алтунин Б.Ю., Панкова Н.Г. Теоретические основы электротехники : Комплекс учебно - методических материалов: Часть 1 / Б.Ю. Алтунин, Н.Г. Панкова; НГТУ им. Р.Е. Алексеева. Н.Новгород, 2007.-130 с. 2. Алтунин Б.Ю., Кралин А.А. Электротехника и электроника: комплекс учебно-методических материалов: Ч.1/ Б.Ю. Алтунин, А.А. Кралин; НГТУ им. Р.Е. Алексеева. Н.Новгород, 2007.-98 с. 3. Алтунин Б.Ю., Кралин А.А. Электротехника и электроника: комплекс учебно-методических материалов: Ч.2/ Б.Ю. Алтунин, А.А. Кралин; НГТУ им. Р.Е. Алексеева. Н.Новгород, 2008.-98 с 4. Касаткин, А.С. Электротехника /А.С. Касаткин, М.В. Немцов.-М.: Энергоатомиздат, 2000. 5. Справочное пособие по основам электротехники и электроники /под. ред. А.В. Нетушила.-М.: Энергоатомиздат, 1995. 6. Манаев Е.И. Основы радиоэлектроники.-3-е изд., перераб. И доп.-М.: Радио и связь, 1990.-512 с.: ил. 7. Новожилов, О. П. Электротехника и электроника: учебник / О. П. Новожилов. – М.: Гардарики, 2008. – 653 с. 25