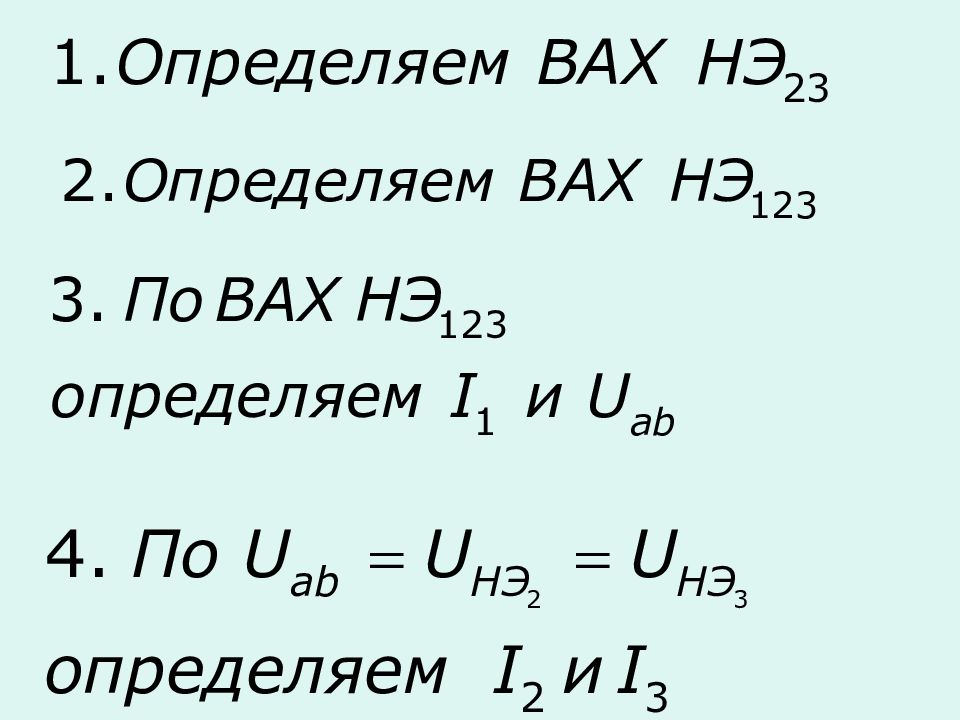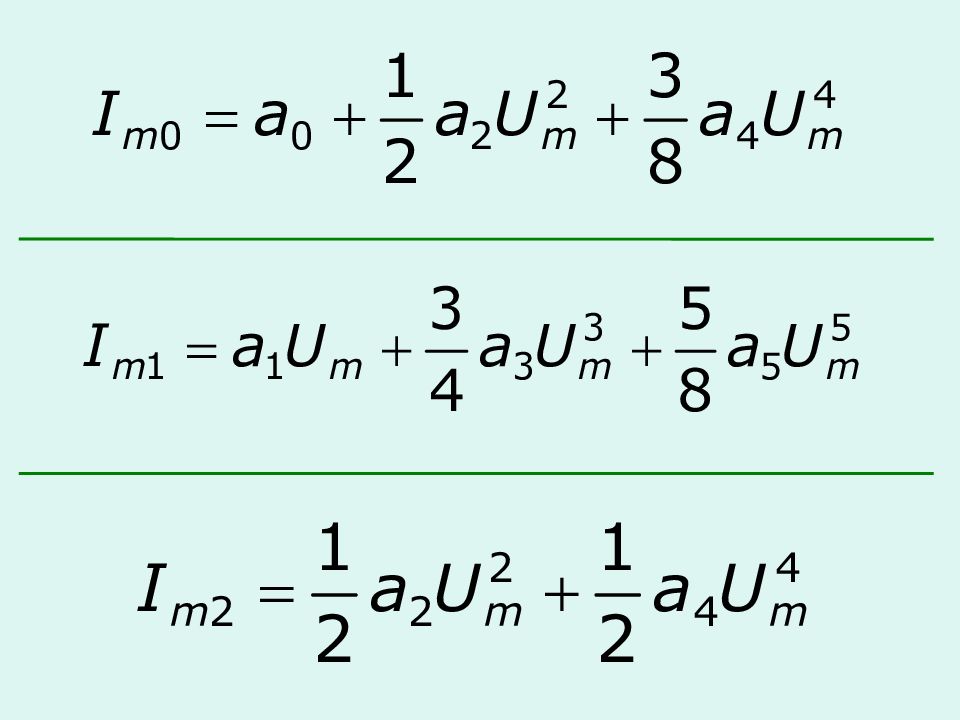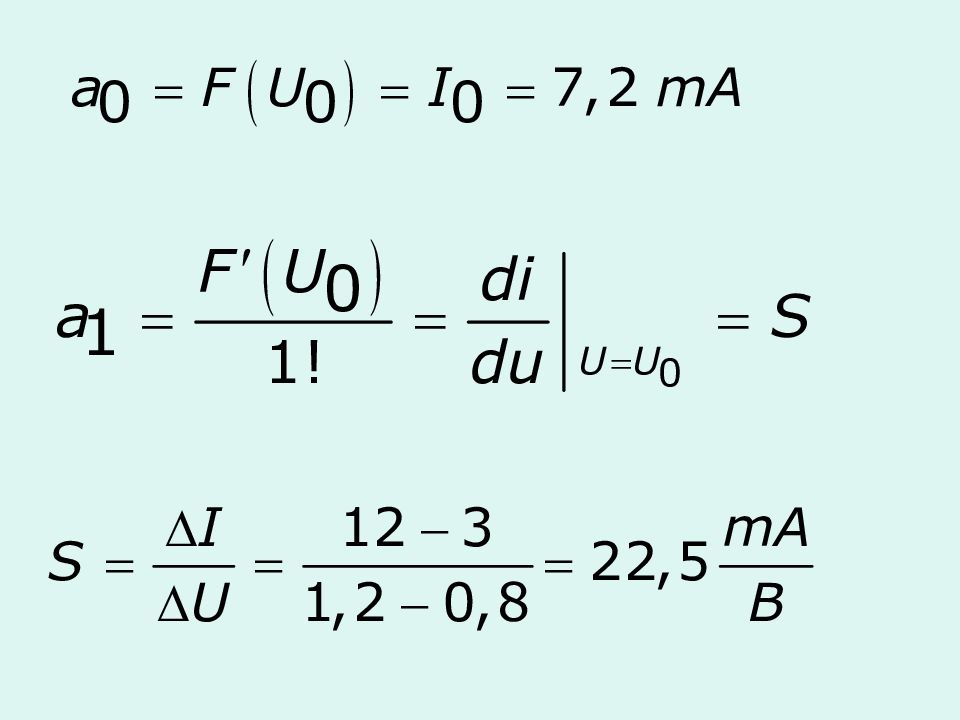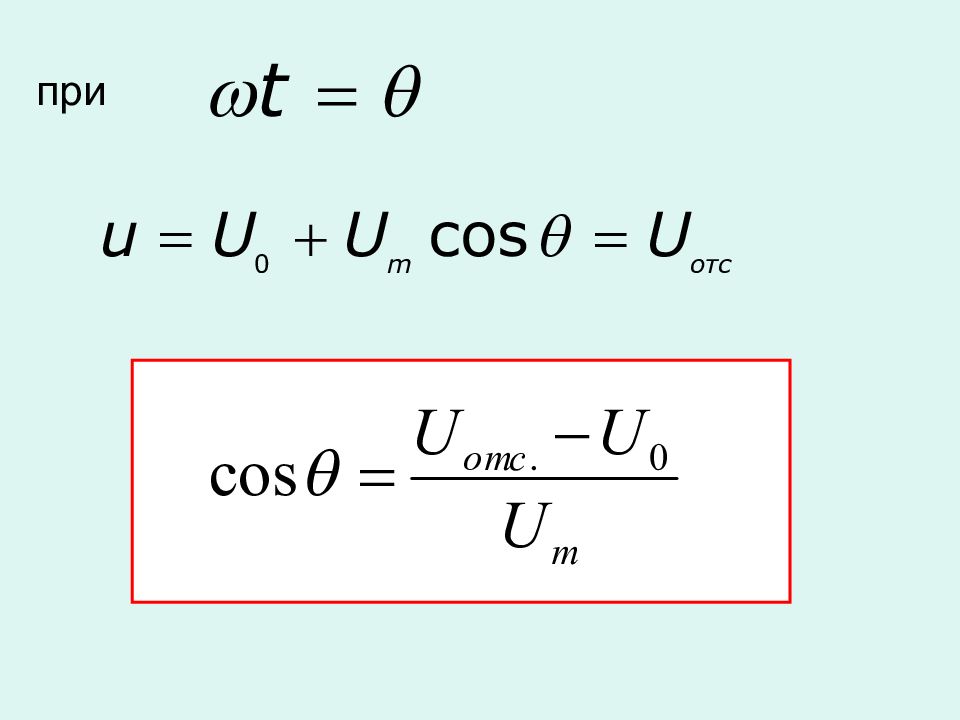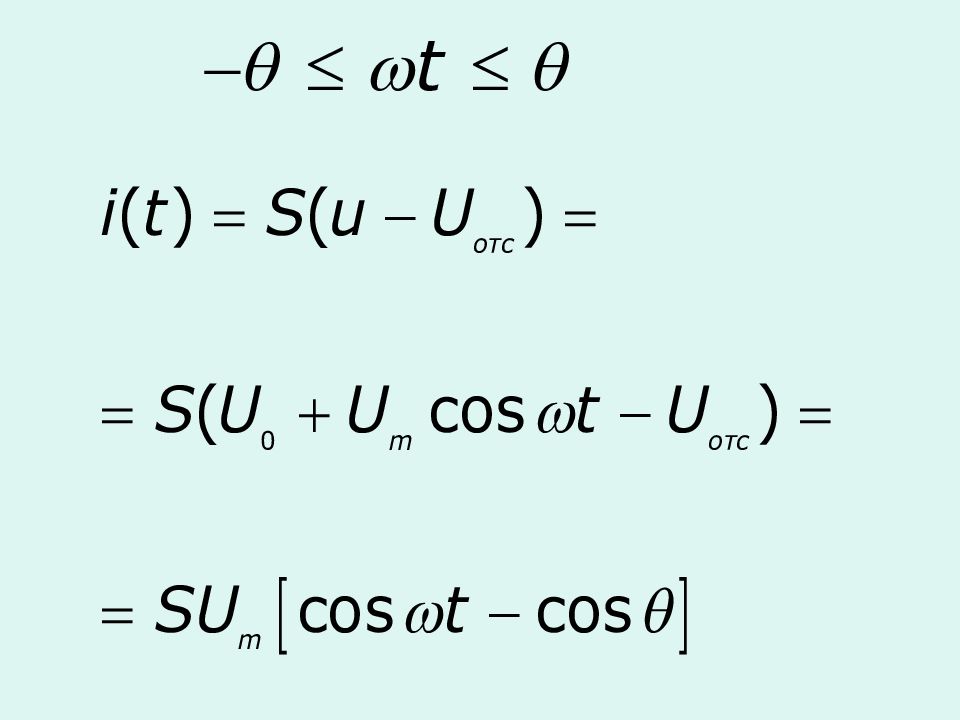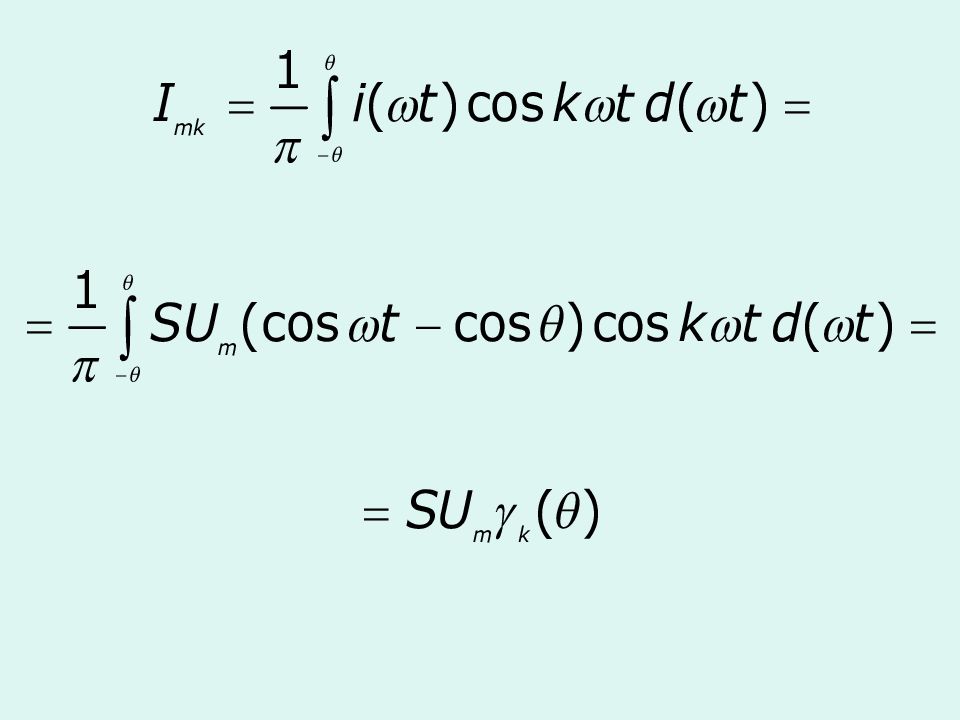Первый слайд презентации: X Нелинейные цепи
Слайд 3
Элемент электрической цепи, параметры которого зависят от значения и направления тока, протекающего через элемент, или напряжения, приложенного к элементу, называется нелинейным
Слайд 4
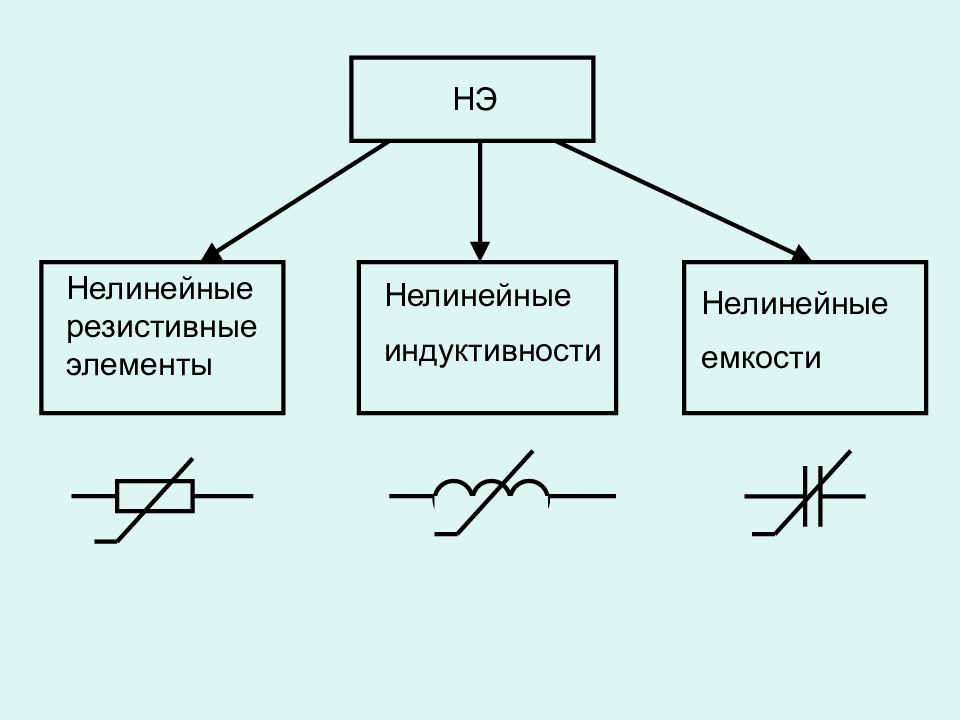
НЭ Нелинейные резистивные элементы Нелинейные индуктивности Нелинейные емкости
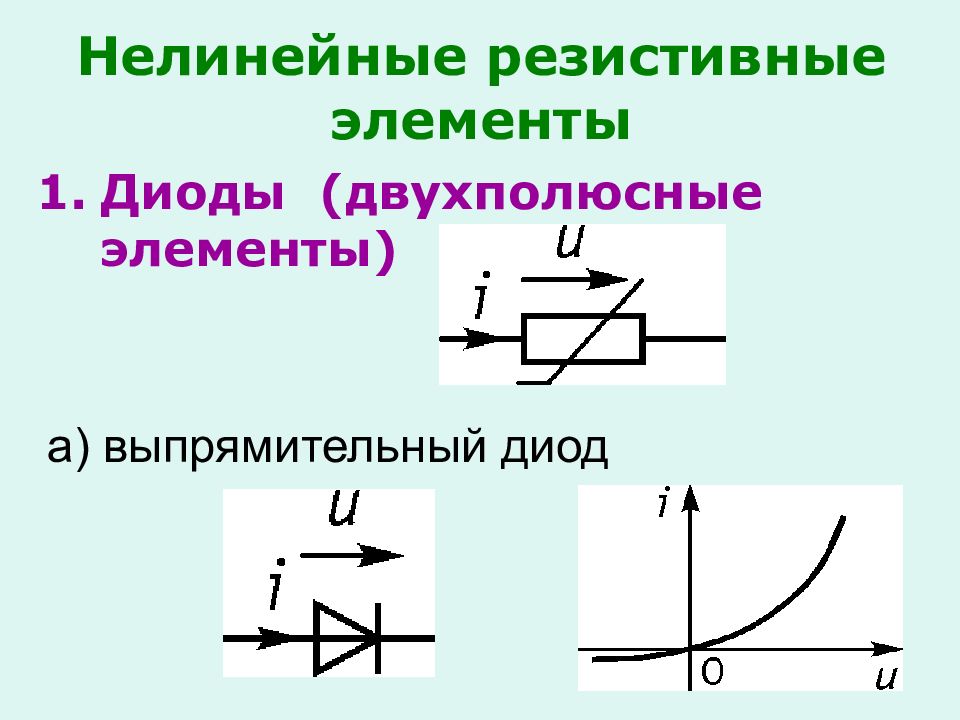
Слайд 5: Нелинейные резистивные элементы
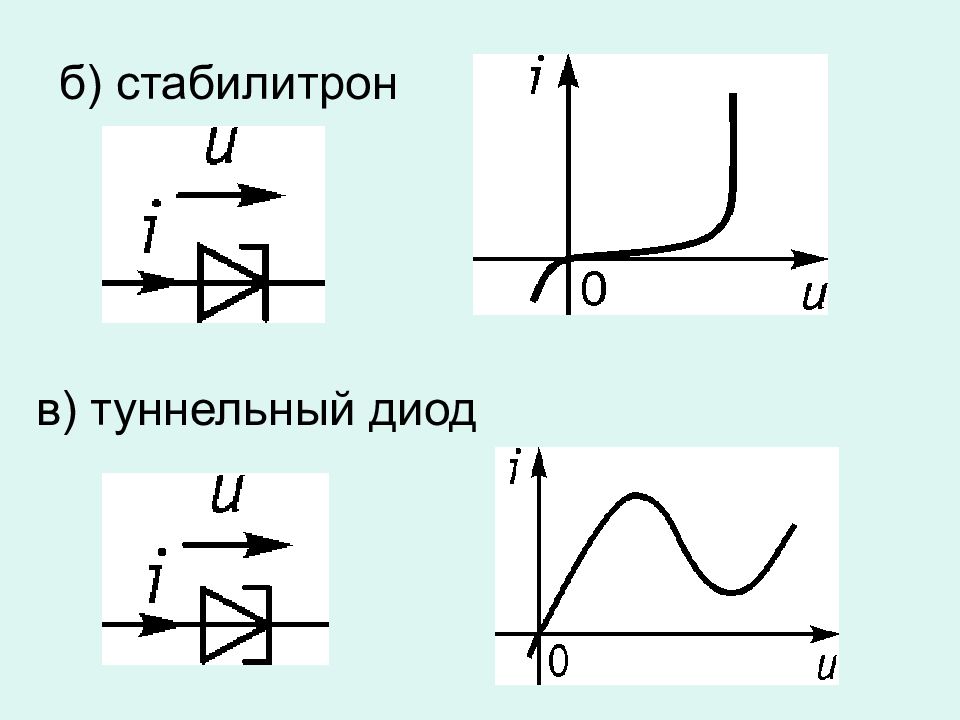
Диоды (двухполюсные элементы) а) выпрямительный диод
Слайд 8
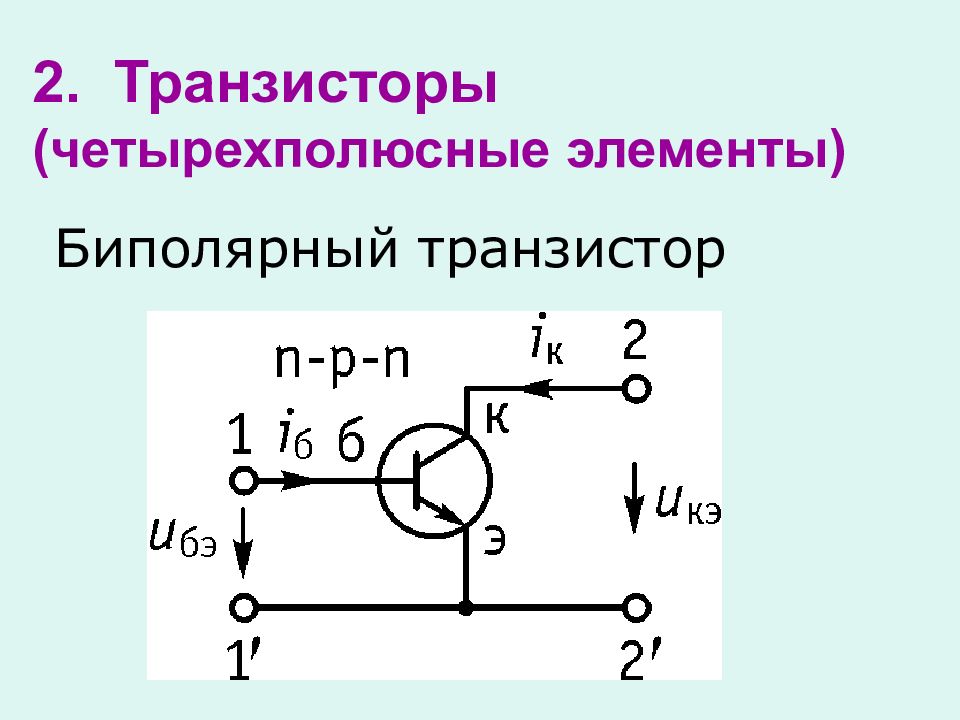
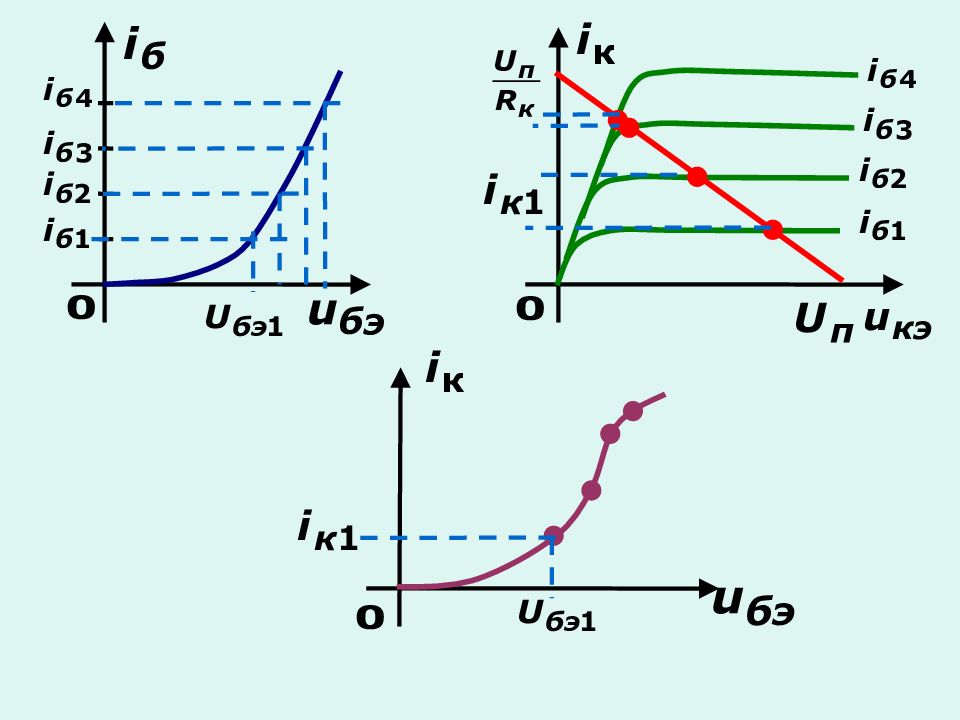
Для анализа работы транзистора построим проходную характеристику по заданным входной характеристике и выходным характеристикам Транзистор характеризуется семейством входных и выходных характеристик
Слайд 10: Параметры нелинейных элементов
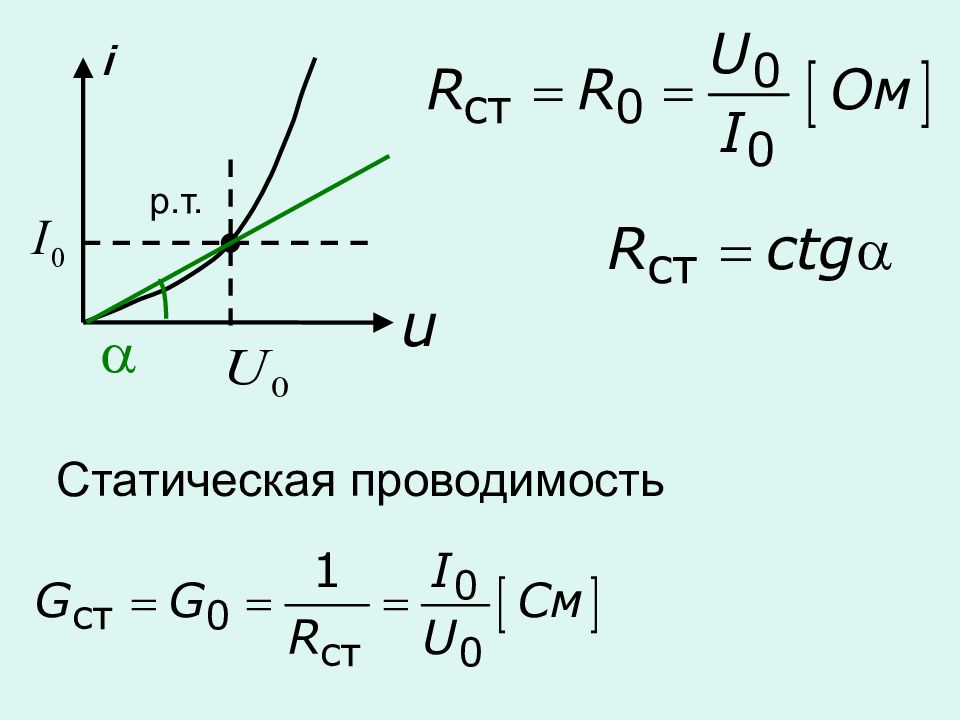
Статическое сопротивление – сопротивление НЭ постоянному току в рабочей точке
Слайд 12
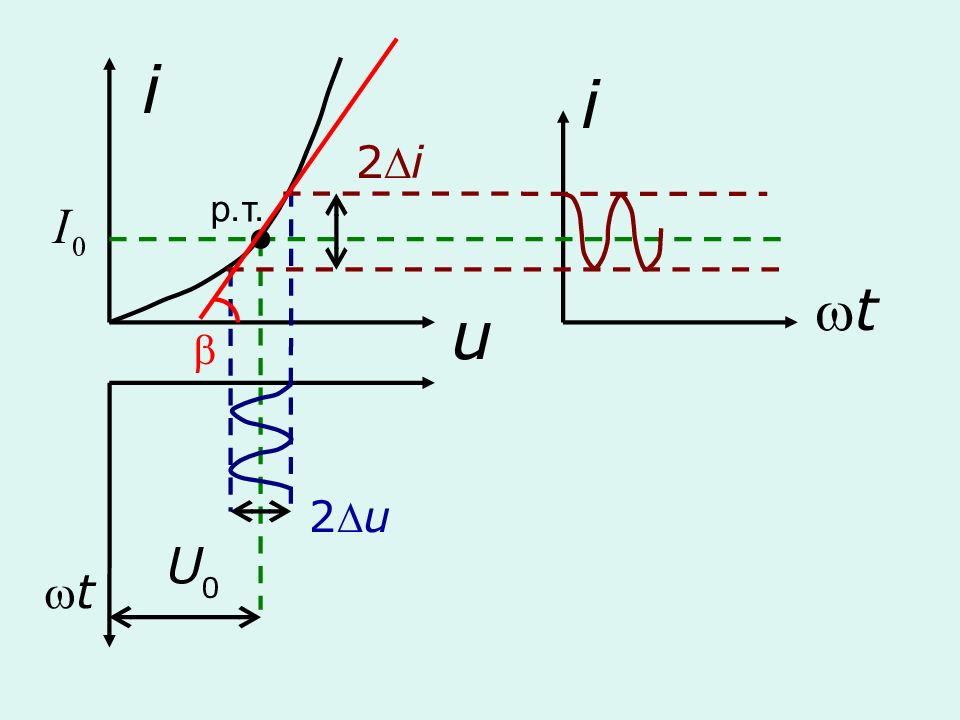
2. Динамическое (дифференциальное) сопротивление – сопротивление нелинейного элемента переменному току малой амплитуды
Слайд 16: Особенности нелинейных цепей
Не соблюдается принцип взаимности (обратимости) Для нелинейного элемента не выполняется закон Ома Особенности нелинейных цепей
Слайд 20
5. На выходе цепи появляются дополнительные спектральные составляющие, которых не было во входном сигнале
Слайд 23
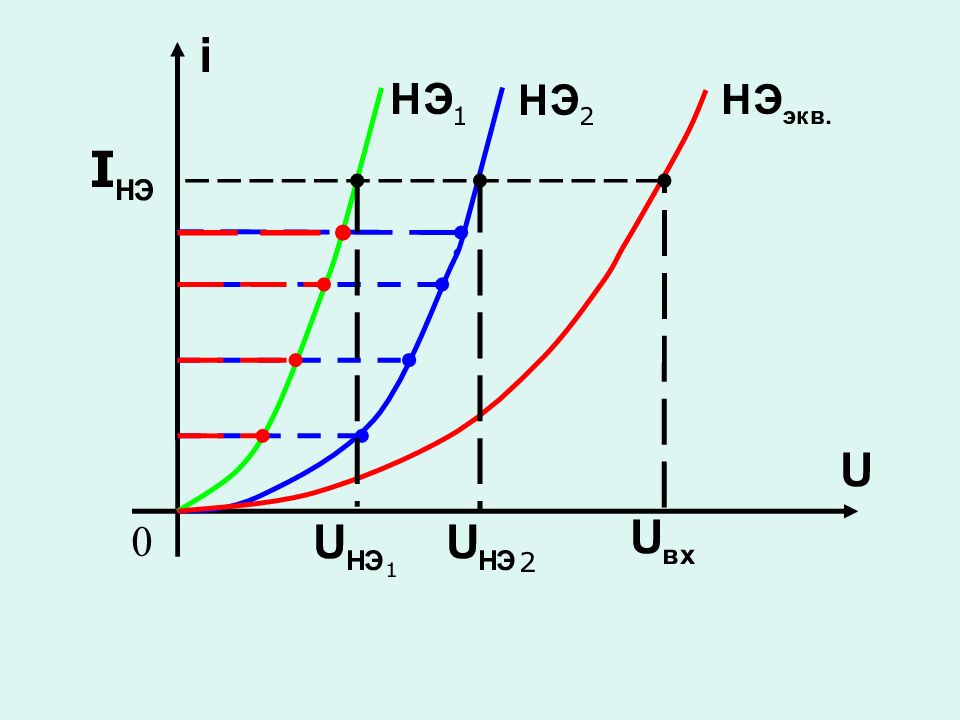
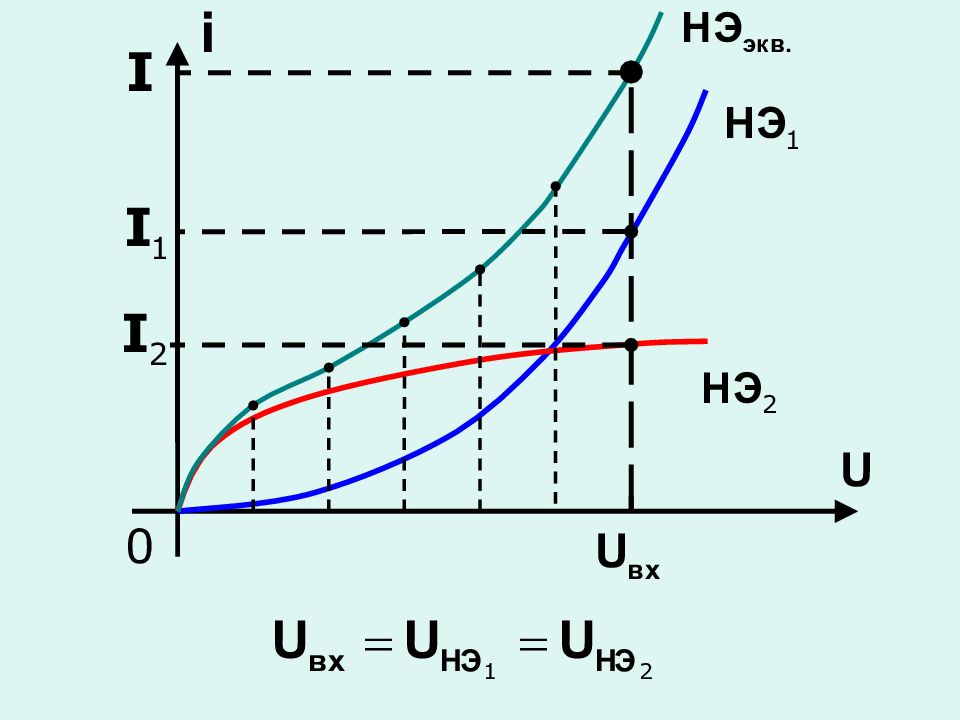
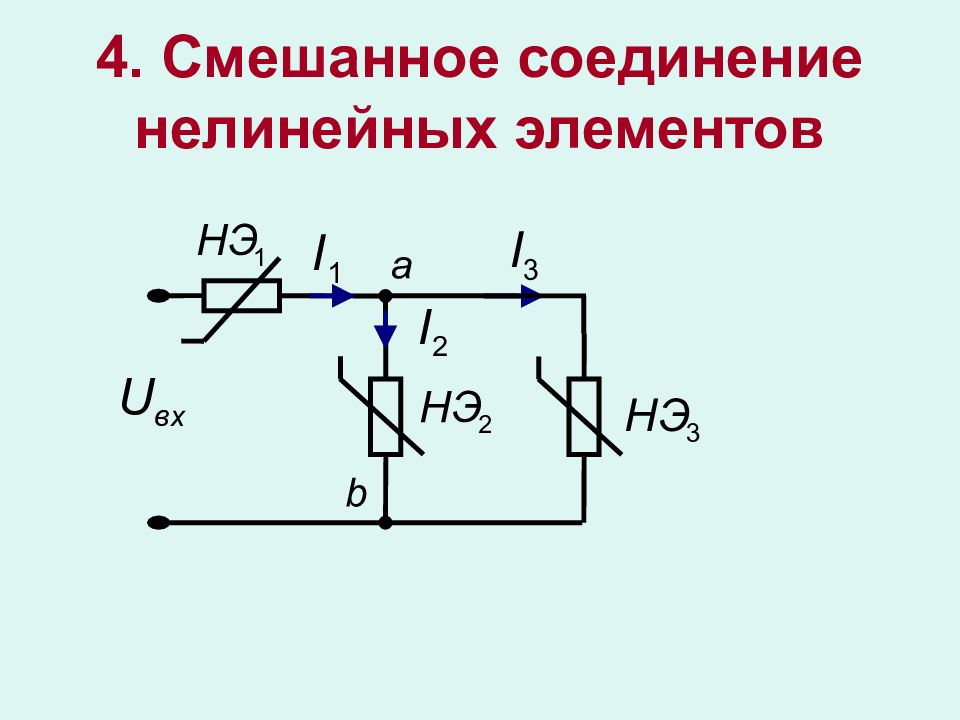
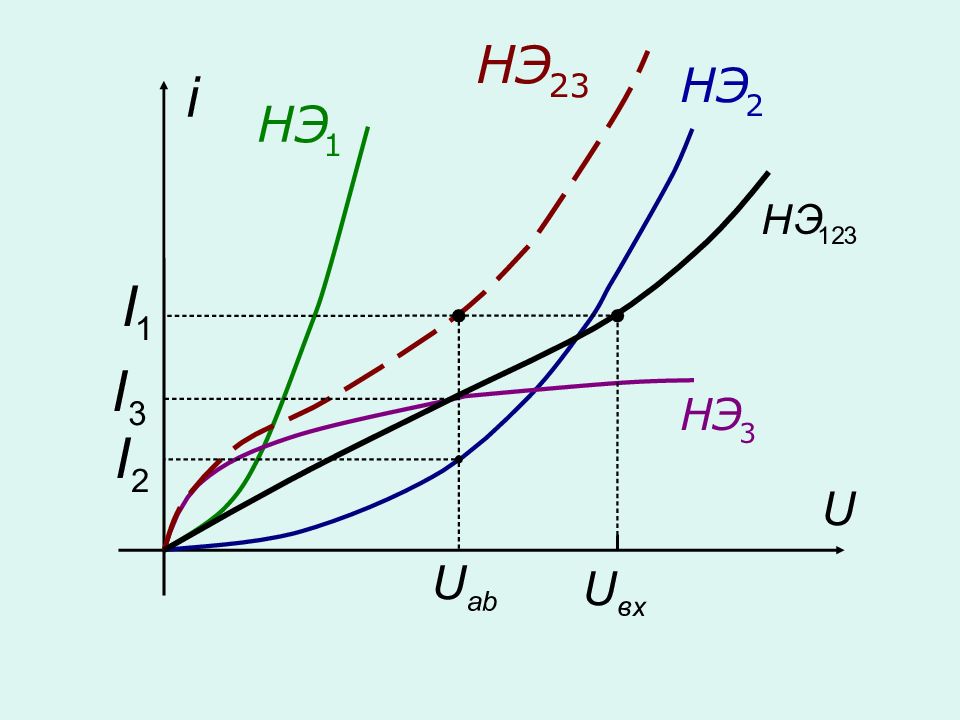
Графоаналитические методы – ВАХ нелинейного элемента задана таблицей или графиком
Слайд 34
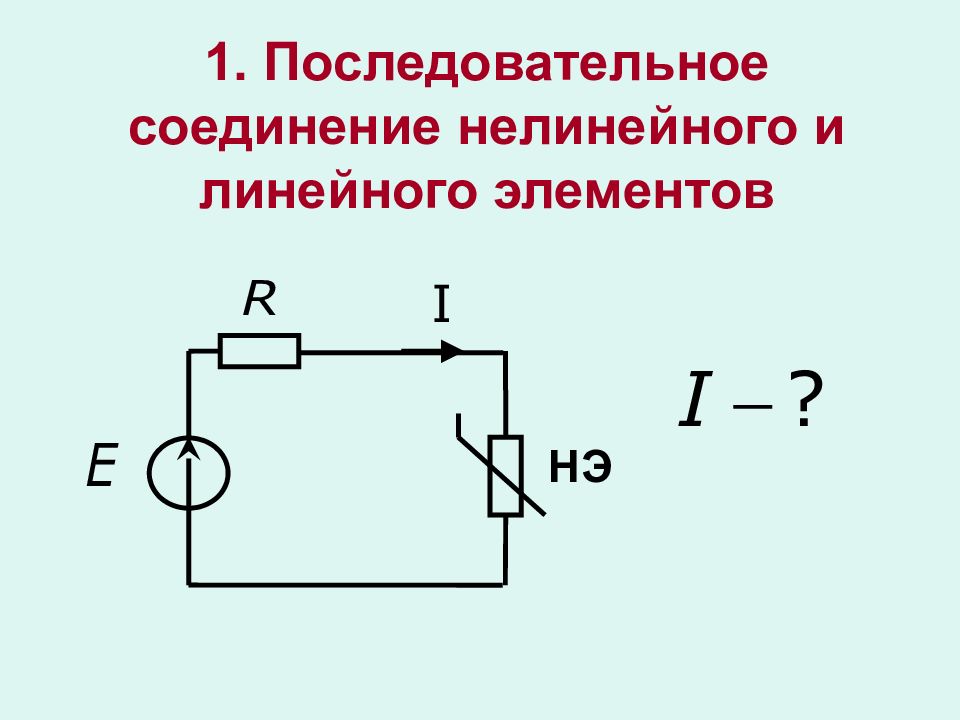
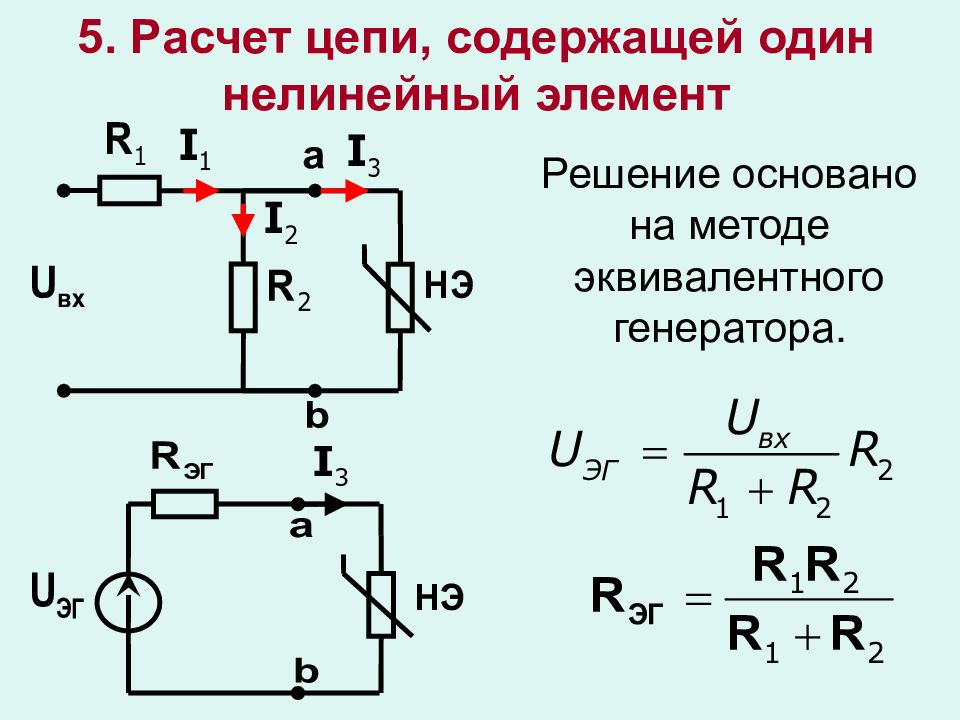
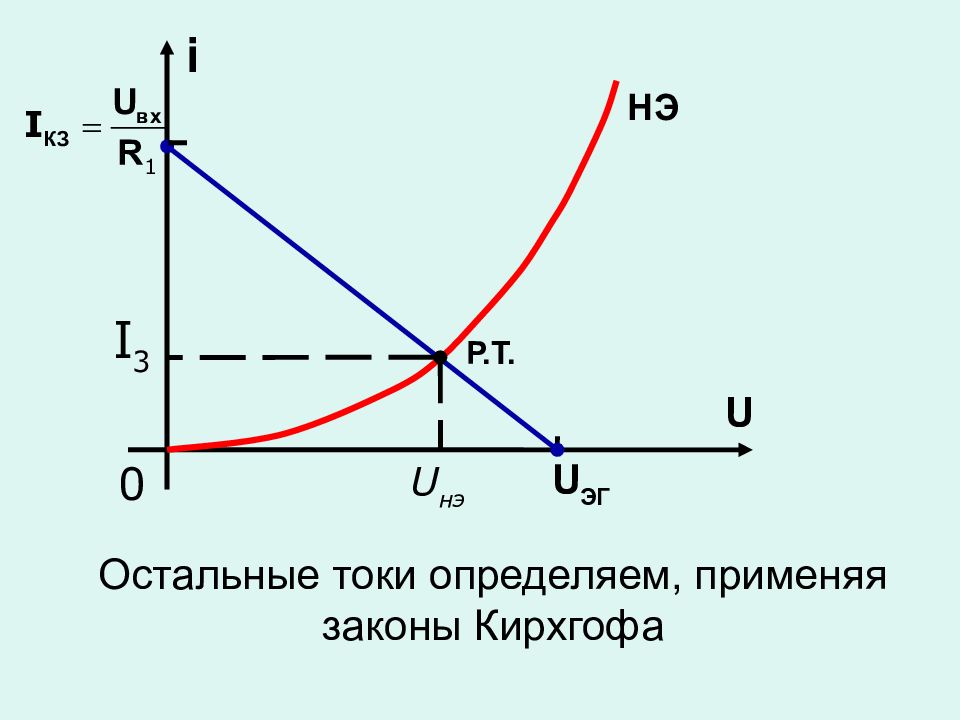
5. Расчет цепи, содержащей один нелинейный элемент Решение основано на методе эквивалентного генератора.
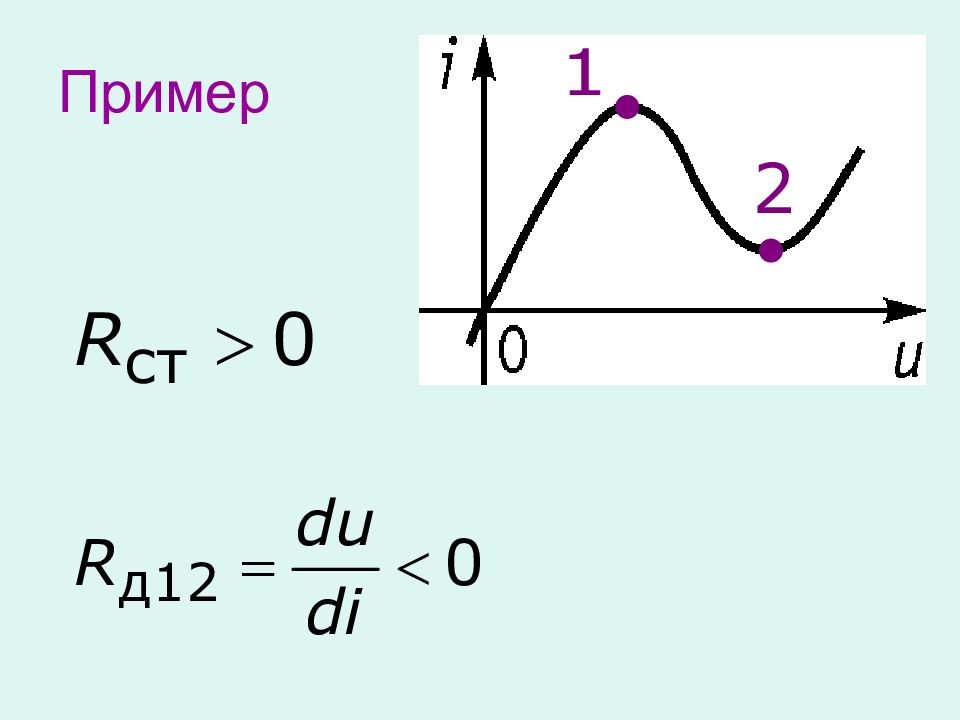
Слайд 36: Пример
Аналитические методы – ВАХ нелинейного элемента задана аналитически по законам Кирхгофа
Слайд 38
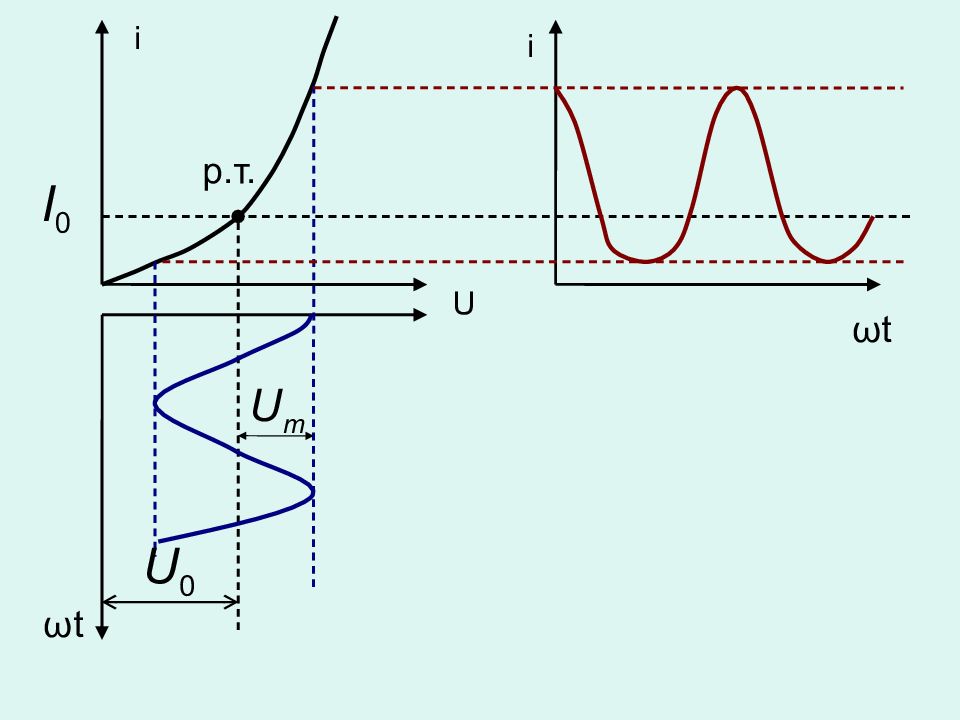
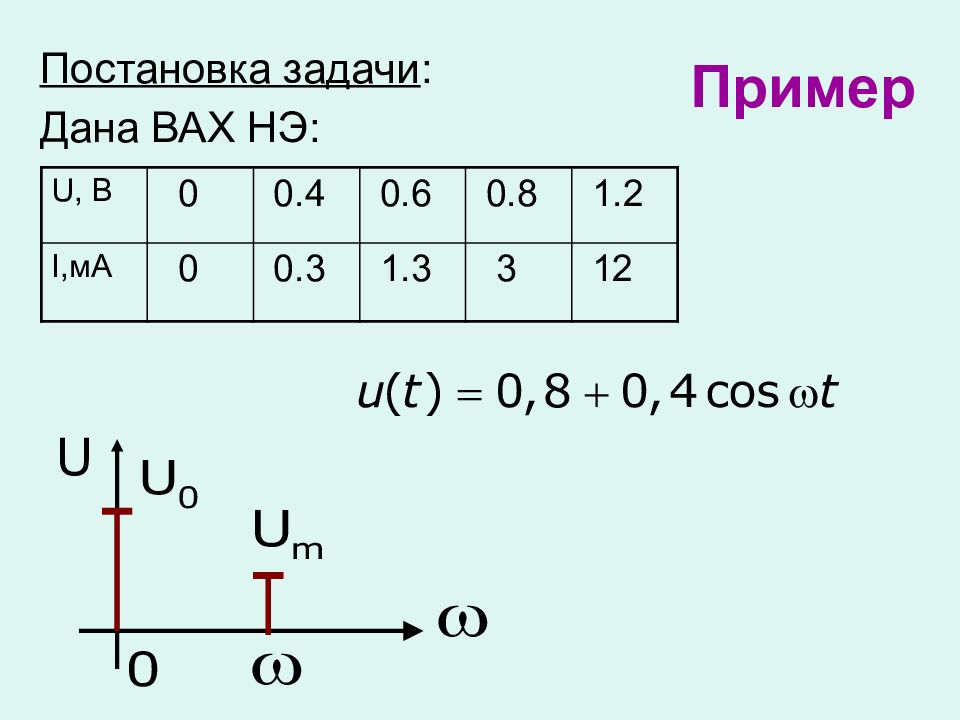
Постановка задачи : на вход нелинейного элемента (НЭ) подается сумма напряжений: постоянного и гармонического, т.е. Найти: закон изменения тока на НЭ спектр тока
Слайд 40
ток i ( t ) - периодическая функция времени, которая может быть представлена рядом Фурье: - постоянная составляющая - гармоники
Слайд 42
Аналитические методы вычисления спектра тока через нелинейный элемент основаны на аппроксимации ВАХ Аппроксимация – представление функции, заданной таблично или графически, в аналитическом виде, т.е. в виде формулы
Слайд 43: Этапы аппроксимации
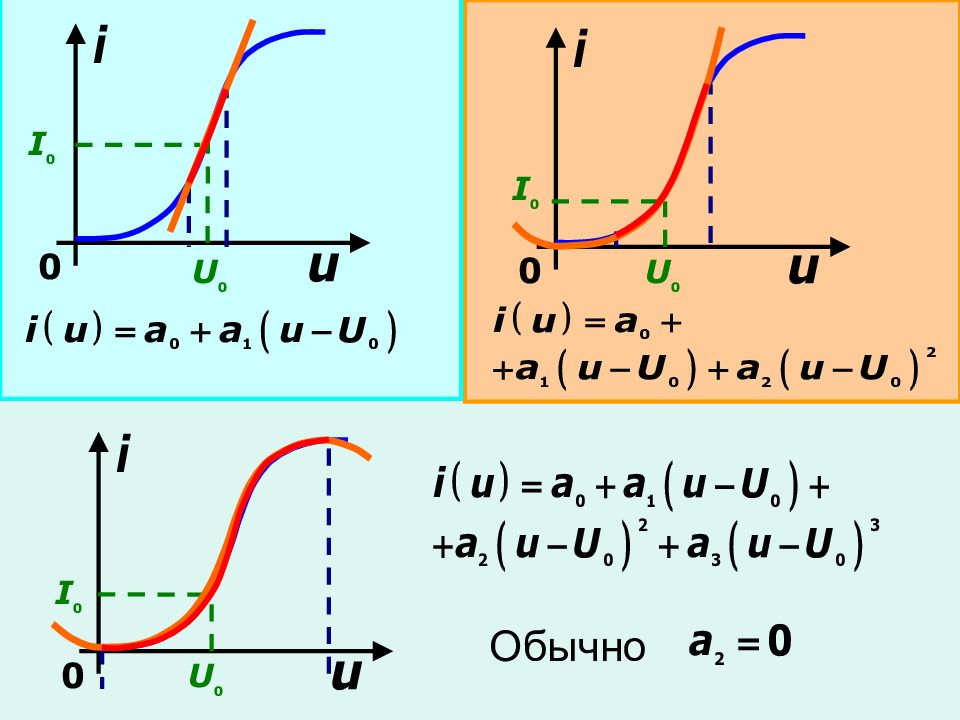
Выбор класса функций, которыми аппроксимируется характеристика а) степенной полином б) кусочно-линейная (отрезки прямых) в) экспонента г) гиперболический тангенс
Слайд 44
2. Определение коэффициентов аппроксимации а) метод интерполяции (метод выбранных точек) б) метод Тейлора в) метод Чебышева г) метод среднеквадратического приближения
Слайд 46
Применяется для точного воспроизведения ВАХ при работе с сигналами малой амплитуды Пусть функция задана графически или таблично Найдем аппроксимирующую функцию
Слайд 47
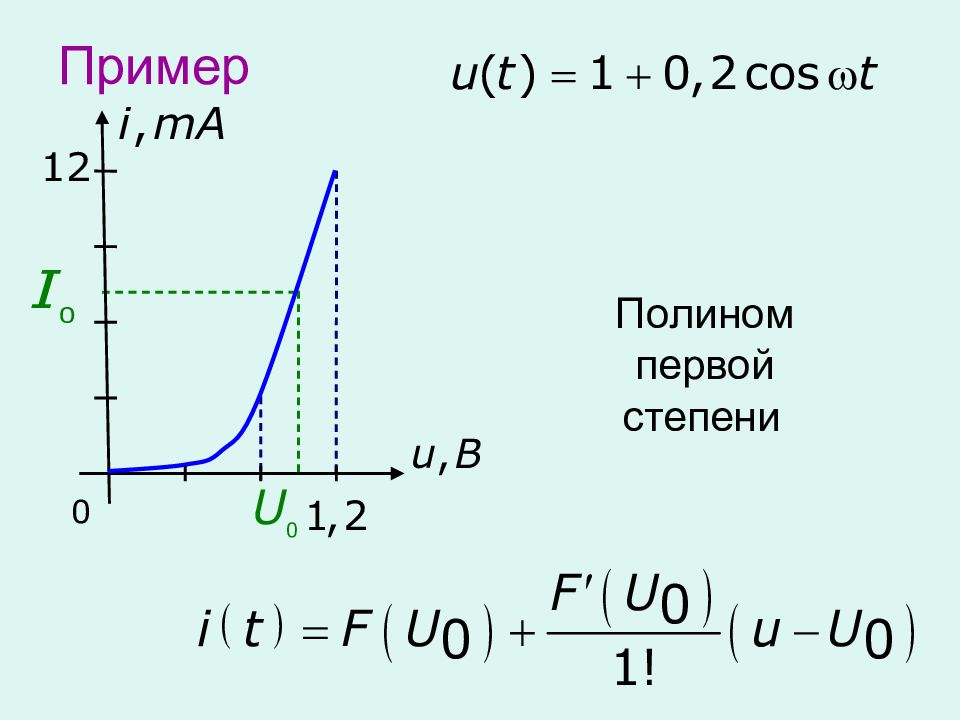
При работе с напряжениями малой амплитуды нет необходимости аппроксимировать всю ВАХ Достаточно выполнить аппроксимацию в окрестностях рабочей точки Степень полинома выбирают по виду рабочего участка
Слайд 49: Спектр тока при полиномиальной аппроксимации
Пусть ВАХ НЭ выражается полиномом 5 степени
Слайд 55
Выводы: Нелинейность ВАХ НЭ приводит к искажению формы сигнала и изменению его спектра. Число гармоник тока определяется степенью аппроксимирующего полинома.
Слайд 56
3) Постоянная составляющая и четные гармоники определяются четными членами полинома 4) Амплитуды нечетных гармоник зависят от коэффициентов при нечетных степенях
Слайд 57
Выбирая при аппроксимации степень полинома, мы тем самым задаем ширину спектра выходного сигнала
Слайд 58: Определение коэффициентов методом интерполяции
Выбираем узлы интерполяции Число узлов интерполяции n+1 - на 1 больше степени полинома Функции F(u) и f(u) в узлах интерполяции совпадают
Слайд 59: Пример
Постановка задачи : Дана ВАХ НЭ: U, B 0 0.4 0.6 0.8 1.2 I, мА 0 0.3 1.3 3 12
Слайд 69
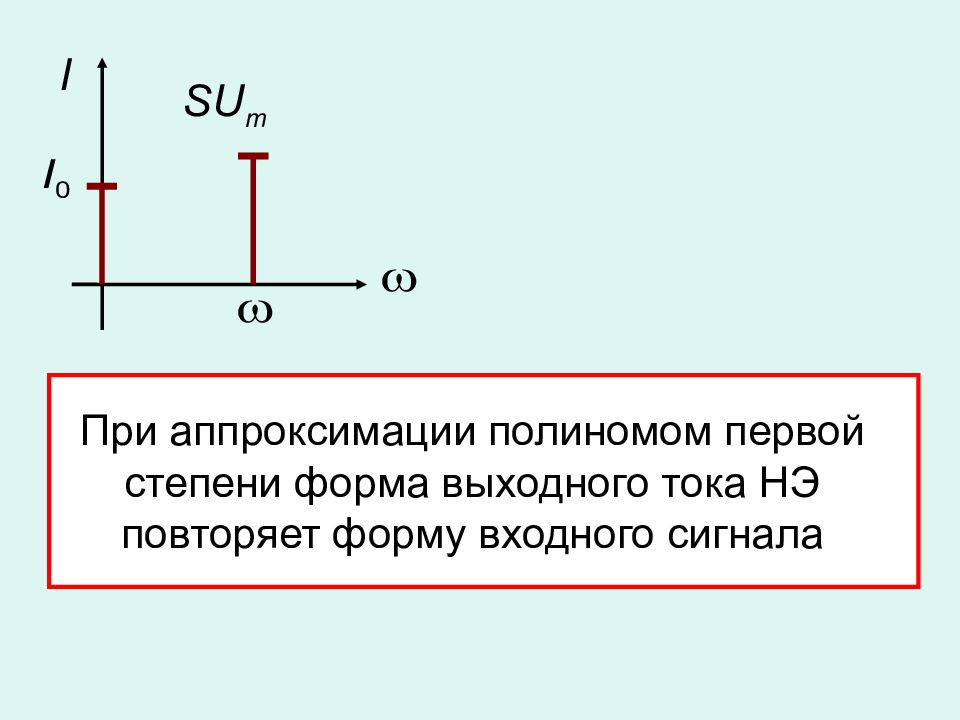
При аппроксимации полиномом первой степени форма выходного тока НЭ повторяет форму входного сигнала
Слайд 71
Режим большого сигнала Замена ВАХ отрезками прямых линий, образующих в интервале аппроксимации непрерывную функцию f(x). напряжение отсечки S – крутизна полученной ВАХ в области изменения тока НЭ
Слайд 72
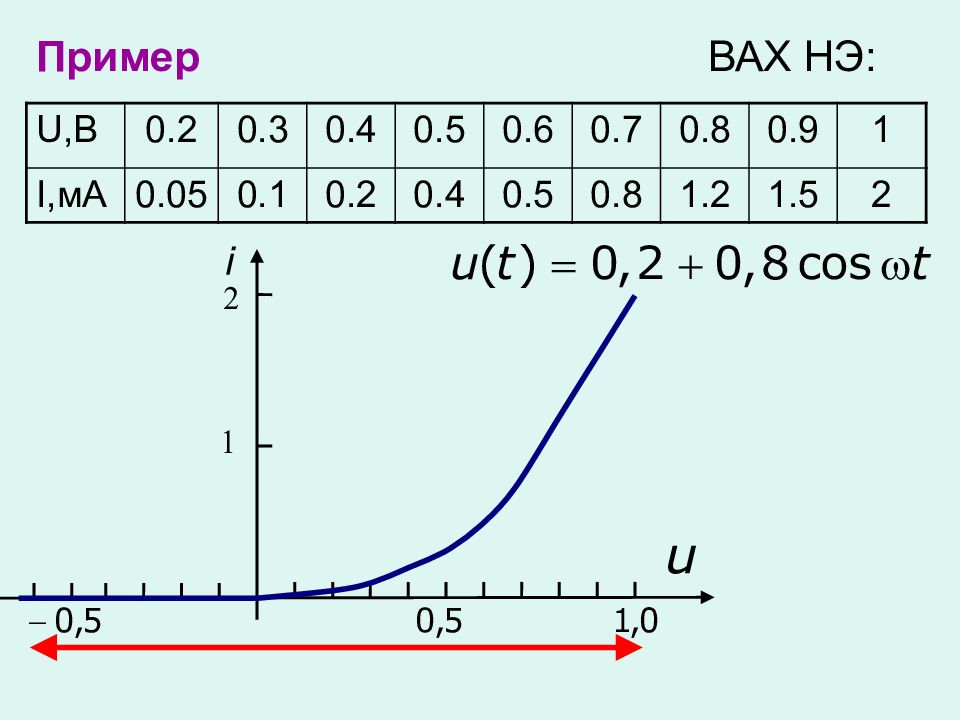
Пример ВАХ НЭ: U, В 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 I, мА 0.05 0.1 0.2 0.4 0.5 0.8 1.2 1.5 2
Слайд 73
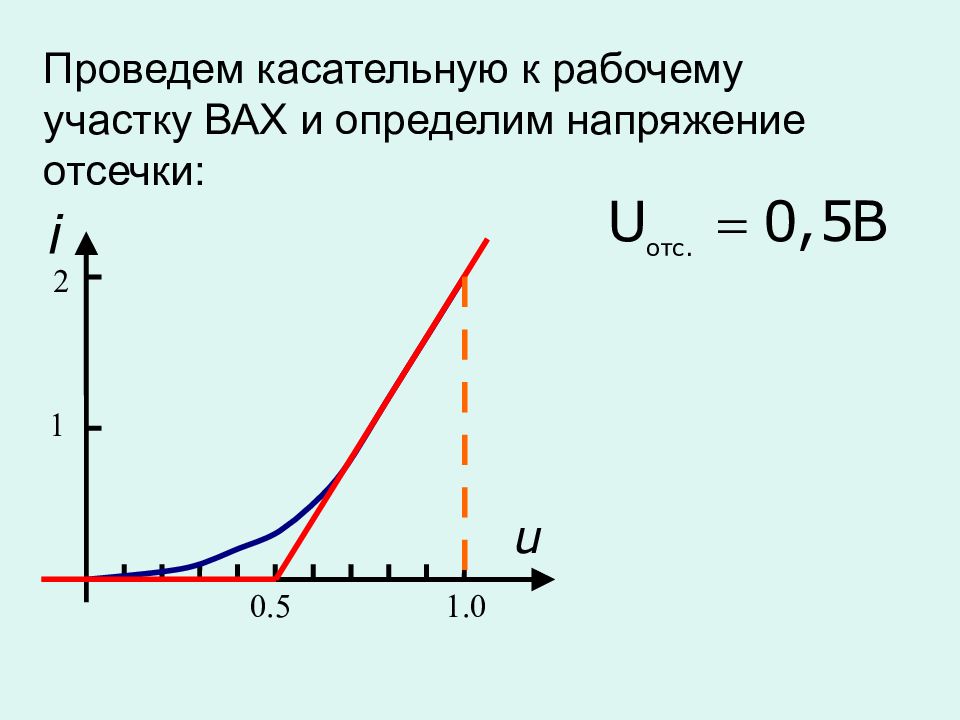
Проведем касательную к рабочему участку ВАХ и определим напряжение отсечки:
Слайд 75
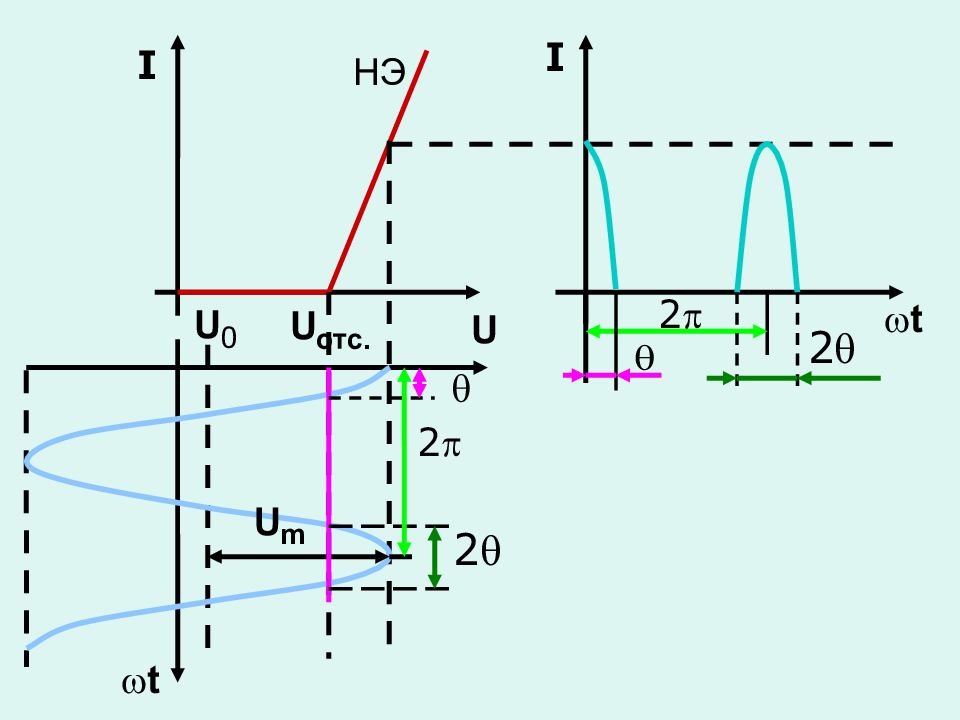
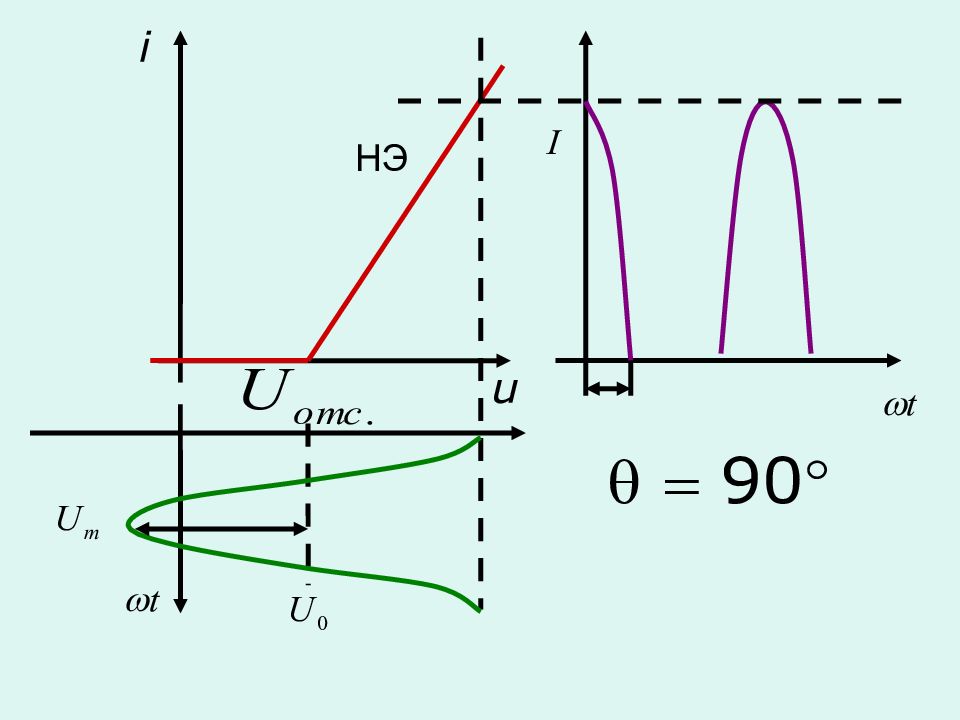
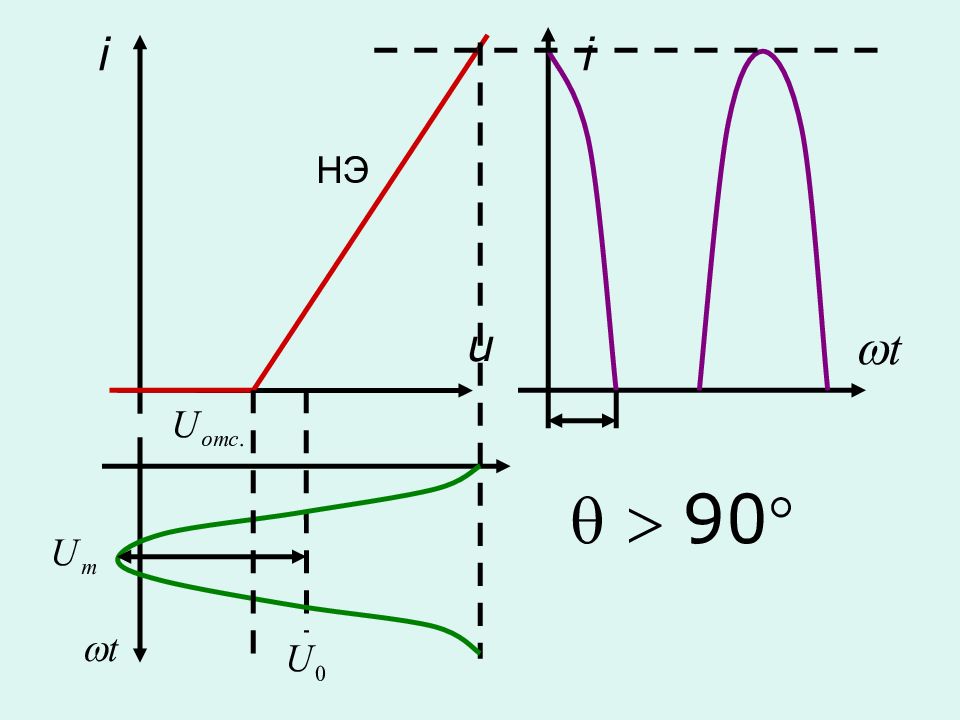
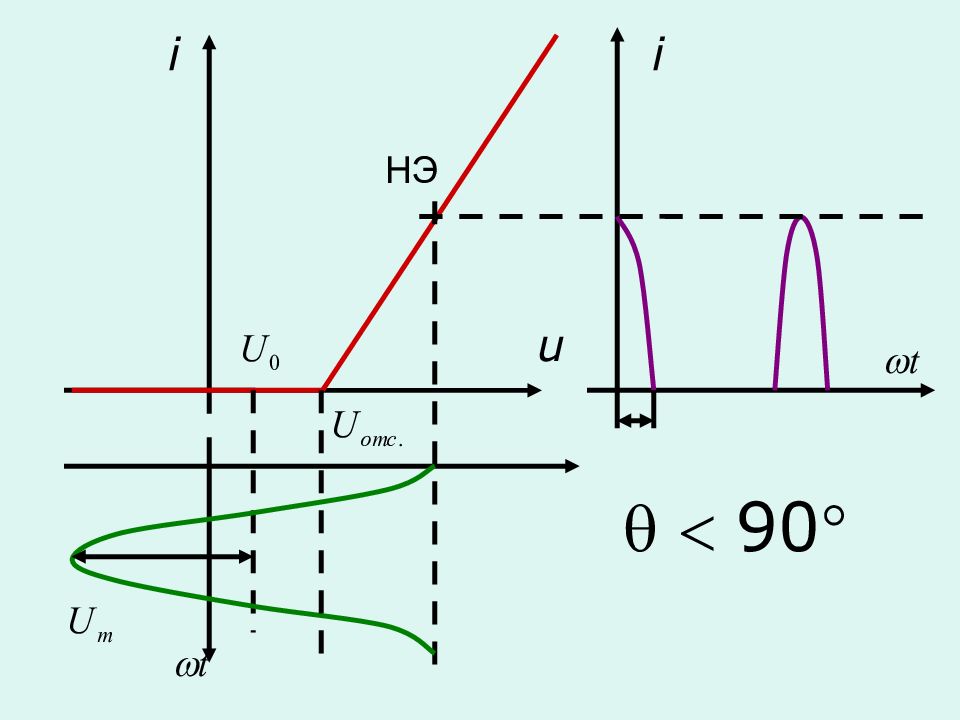
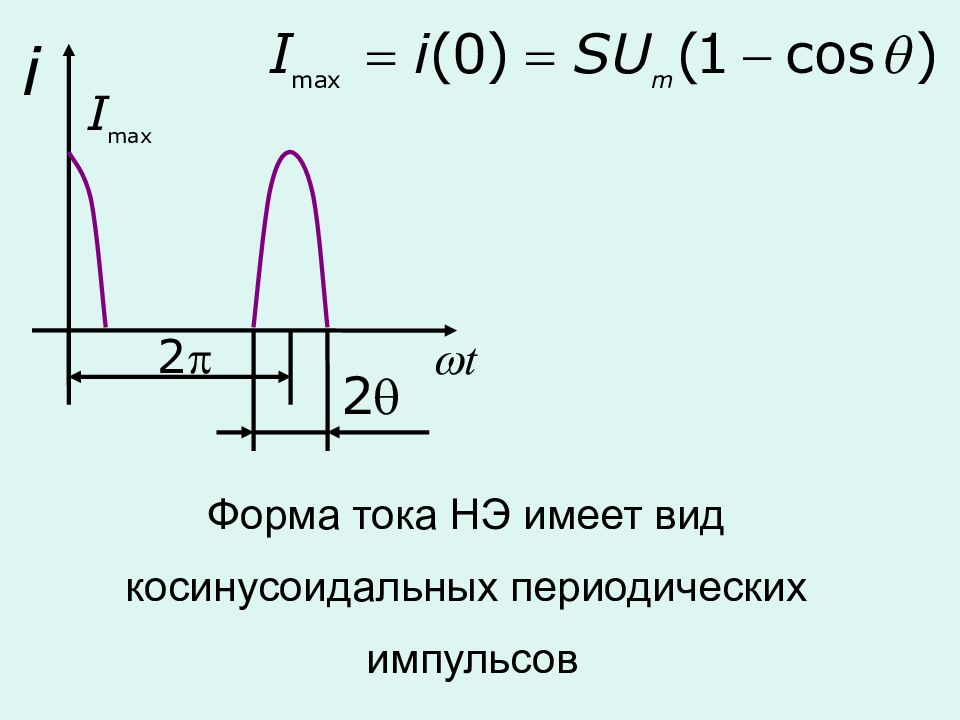
Спектр выходного тока при кусочно-линейной аппроксимации (метод угла отсечки)
Слайд 77
Часть полупериода ( в координатах ), в течение которого существует ток в цепи нелинейного элемента, называется углом отсечки Диапазон изменения угла отсечки
Слайд 78
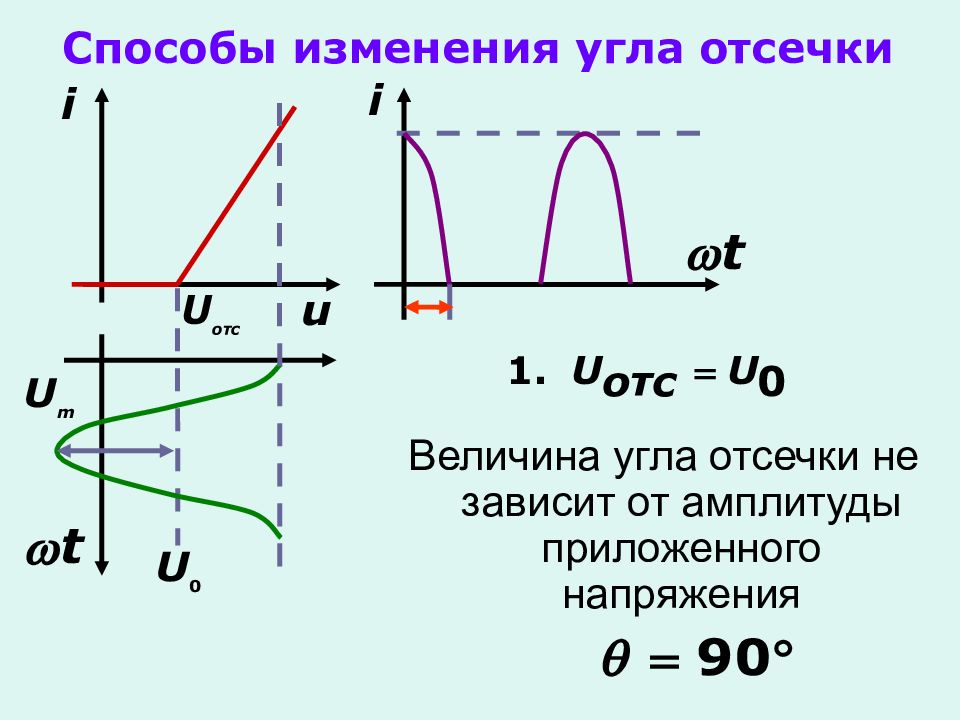
Величина угла отсечки не зависит от амплитуды приложенного напряжения Способы изменения угла отсечки
Слайд 93
Чаще всего коэффициенты (функции) Берга представлены либо в графическом виде, либо в виде таблицы:
Слайд 94
Оптимальный угол отсечки - позволяет определить угол отсечки для получения максимального значения амплитуды требуемой гармоники k - номер требуемой гармоники
Слайд 97
Выводы: При кусочно-линейной аппроксимации число гармонических составляющих реакции бесконечно велико. Чем меньше угол отсечки, тем медленнее убывают амплитуды гармоник.
Слайд 98
3. В общем случае амплитуды гармоник нелинейно зависят от амплитуды гармонического воздействия в силу нелинейного характера зависимости угла отсечки от Um