Алгебра 8 класс «Решение систем двух линейных уравнений с двумя неизвестными»
Определите, какая из пар чисел (1; 2) (-1; 2) (-8/7;-7) (1; -2) является решением системы уравнений: 7х – 3у = 13, 2х + 5у = -8.
Определи ть, какая из пар чисел ( 1 ; 2 ) (-1; 2) (-8/7;-7) (1; -2) является решением системы уравнений. Решение: 7 1 – 3 2 = 13, 2 1 + 5 2 = -8 . . . . 7 (-1) – 3 2 = 13, 2 (-1) + 5 2 = -8 . . . . (ложь) (ложь) Образец оформления решения:
Решите систему графически: у – 3х = 0, 3х + у = -6.
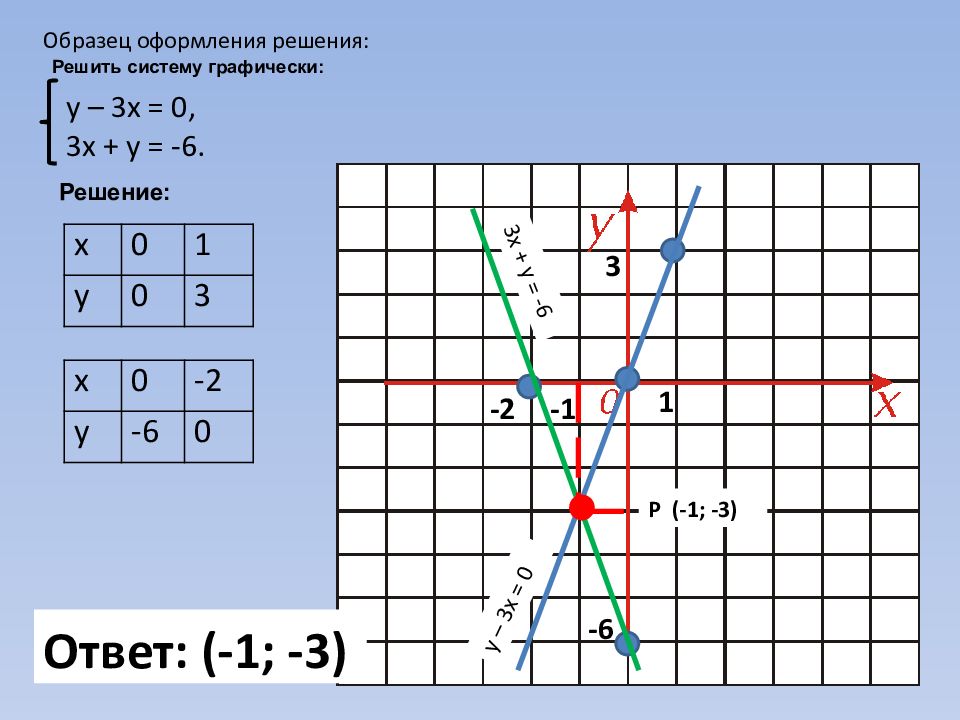
Реши ть систему графически: у – 3х = 0, 3х + у = -6. Образец оформления решения: Решение: Даны линейные уравнения. Их графиками являются прямые. Для построения прямых необходимо знать координаты двух точек, принадлежащих каждой прямой. Построим таблицу значений для каждой прямой: х 0 1 у 0 3 х 0 -2 у -6 0
Решить систему графически: у – 3х = 0, 3х + у = -6. Образец оформления решения: Решение: х 0 1 у 0 3 х 0 -2 у -6 0 1 3 -6 -1 -2 у – 3х = 0 3х + у = -6 Р (-1; -3) Ответ: (-1; -3)
Решите систему методом подстановки: у – 3х = 8, 3х + 2у = 7.
Реши ть систему методом подстановки: у – 3х = 8, 3х + 2у = 7. Образец оформления решения: Решение: у – 3х = 8, 3х + 2у = 7; = > у = 8 + 3х, 3х + 2у = 7; = > у = 8+3x, 3х + 2 (8+3x) = 7; = > у = 8+3x, 3х + 16+6x = 7;
Решить систему методом подстановки: у – 3х = 8, 3х + 2у = 7. Образец оформления решения: Решение: у – 3х = 8, 3х + 2у = 7; = > у = 8 + 3х, 3х + 2у = 7; = > у = 8+3x, 3х + 2 (8+3x) = 7; = > у = 8+3x, 3х + 16+6x = 7; = > у = 8+3x, 9 х = 7 -16 ; = > у = 8+3x, 9 х = -9 ; = > у = 8+3 (-1), х = -1 ; .
Решить систему методом подстановки: у – 3х = 8, 3х + 2у = 7. Образец оформления решения: Решение: у – 3х = 8, 3х + 2у = 7; = > = > у = 5, х = -1. ... Ответ: (-1; 5 ) у = 8+3 (-1), х = -1 ; . = >
Решите систему методом алгебраического сложения: 3х + 2у = 6, 5х + 3у = 11.
Реши ть систему методом алгебраического сложения: 3х + 2у = 6, 5х + 3у = 11; Образец оформления решения: Решение: = > 9 х + 6 у = 18, -10 х +( -6 у) = -22 ; х 3 х (-2) = > 9х + 6у = 18, - х = - 4 ; = > 9х+ 6у = 18, х = 4 ; = > 9 4 + 6у = 18, х = 4 ; . = > 6у = 18 - 36, х = 4; = > у = -3, х = 4. Ответ: (4; -3)
Прямая у= kx+m проходит через точки А(2;-1) и В ( 3;4). Найдите уравнение прямой.
Най ти уравнение прямой, проходящей через точки А(2;-1) и В ( 3;4). -1=2k+m, 4=3k+m. Образец оформления решения: Решение: Запишем уравнение всех прямых, проходящих через точку А (2;-1): -1 = 2 k + m Запишем уравнение всех прямых, проходящих через точку В (3;4): 4 = 3 k + m Уравнение искомой прямой удовлетворяет обоим равенствам. Составим и решим систему уравнений:
Най ти уравнение прямой, проходящей через точки А(2;-1) и В ( 3;4). -1=2k+m, 4=3k+m ; Образец оформления решения: Решение: = > х (-1) -1=2k+m, - 4= - 3k - m ; = > -1=2k+m, -5 = - k ; = > -1= 10 +m, k = 5 ; = > m= -11, k = 5. Ответ: y= 5 x -11
