Первый слайд презентации: Аналитическая геометрия в пространстве
Слайд 2
«Аналитическая геометрия в пространстве» курса «Высшая математика» включает четыре основные темы: 1. Плоскость 2. Прямая в пространстве 3. Взаимное расположение прямой и плоскости в пространстве 4. Поверхности 2-го порядка
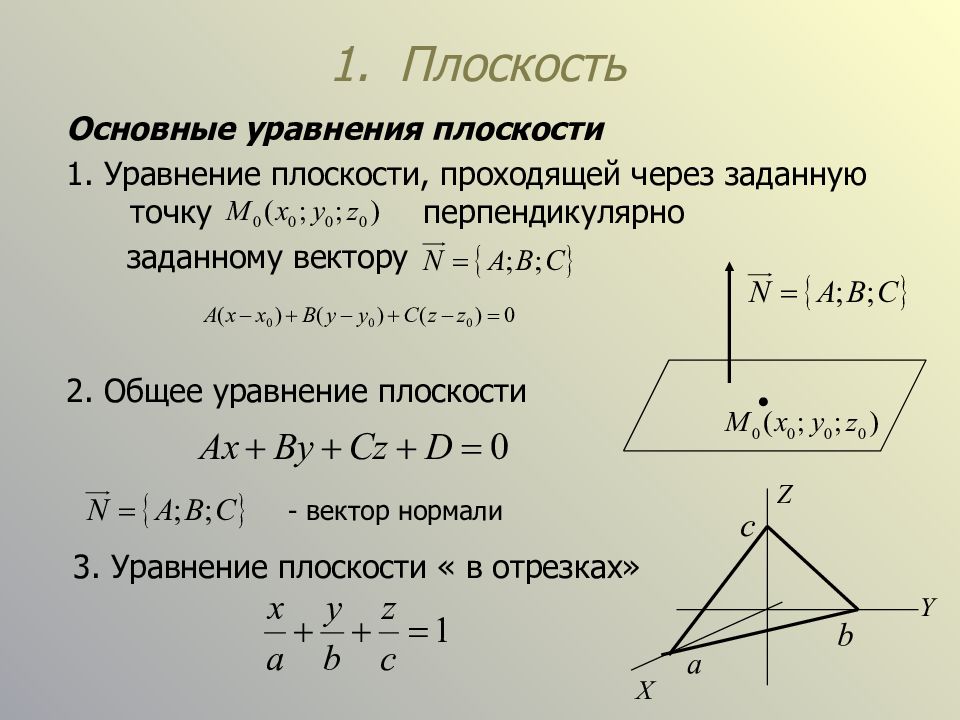
Слайд 3: 1. Плоскость
Основные уравнения плоскости 1. Уравнение плоскости, проходящей через заданную точку перпендикулярно заданному вектору 2. Общее уравнение плоскости - вектор нормали 3. Уравнение плоскости « в отрезках»
Слайд 4: Уравнения плоскости
4. Уравнение плоскости, проходящей через три точки Условие компланарности векторов
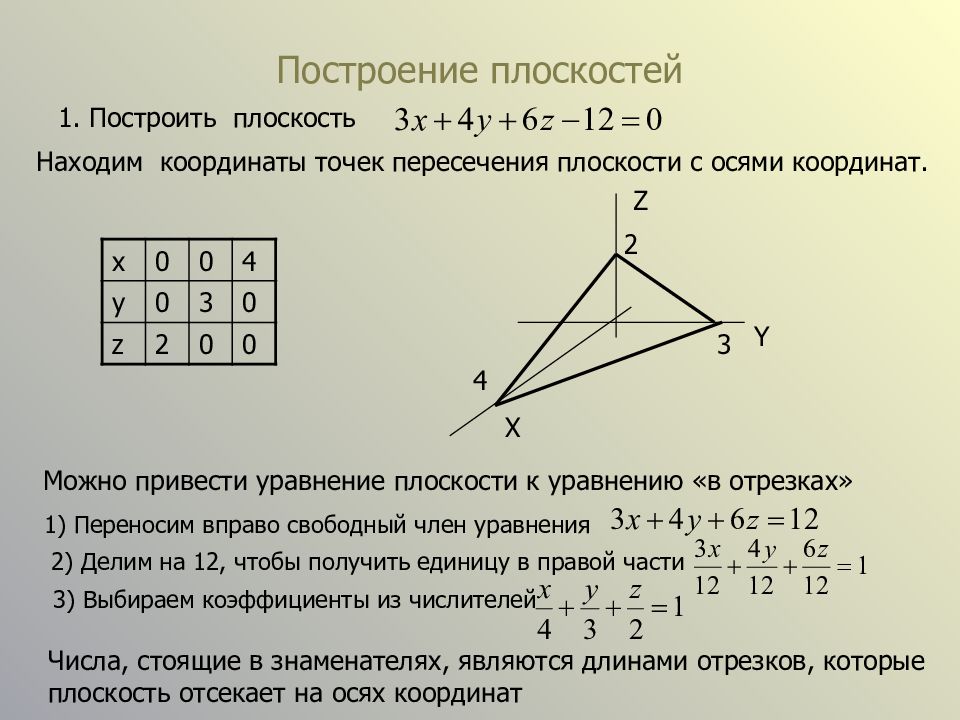
Слайд 5: Построение плоскостей
1. Построить плоскость Находим координаты точек пересечения плоскости с осями координат. x 0 0 4 y 0 3 0 z 2 0 0 Z Y X 2 3 4 Можно привести уравнение плоскости к уравнению «в отрезках» 1) Переносим вправо свободный член уравнения 2) Делим на 12, чтобы получить единицу в правой части 3) Выбираем коэффициенты из числителей Числа, стоящие в знаменателях, являются длинами отрезков, которые плоскость отсекает на осях координат
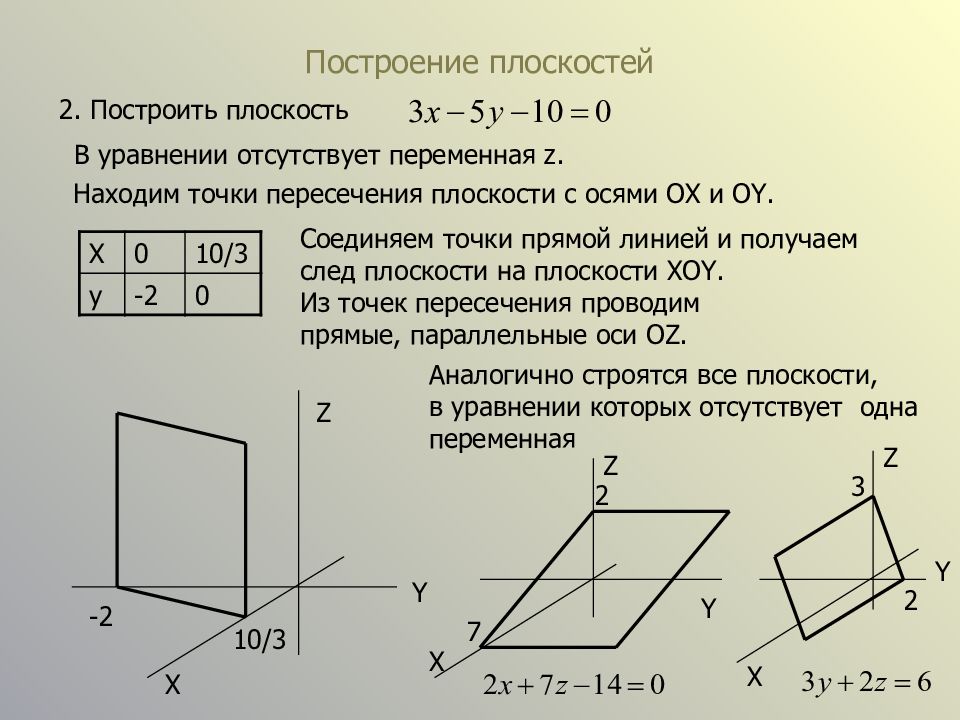
Слайд 6: Построение плоскостей
2. Построить плоскость В уравнении отсутствует переменная z. Находим точки пересечения плоскости с осями OX и OY. X 0 10/3 y -2 0 Соединяем точки прямой линией и получаем след плоскости на плоскости XOY. Из точек пересечения проводим прямые, параллельные оси OZ. Z Y X 10/3 -2 Аналогично строятся все плоскости, в уравнении которых отсутствует одна переменная X Y Z 7 2 X Y Z 2 3
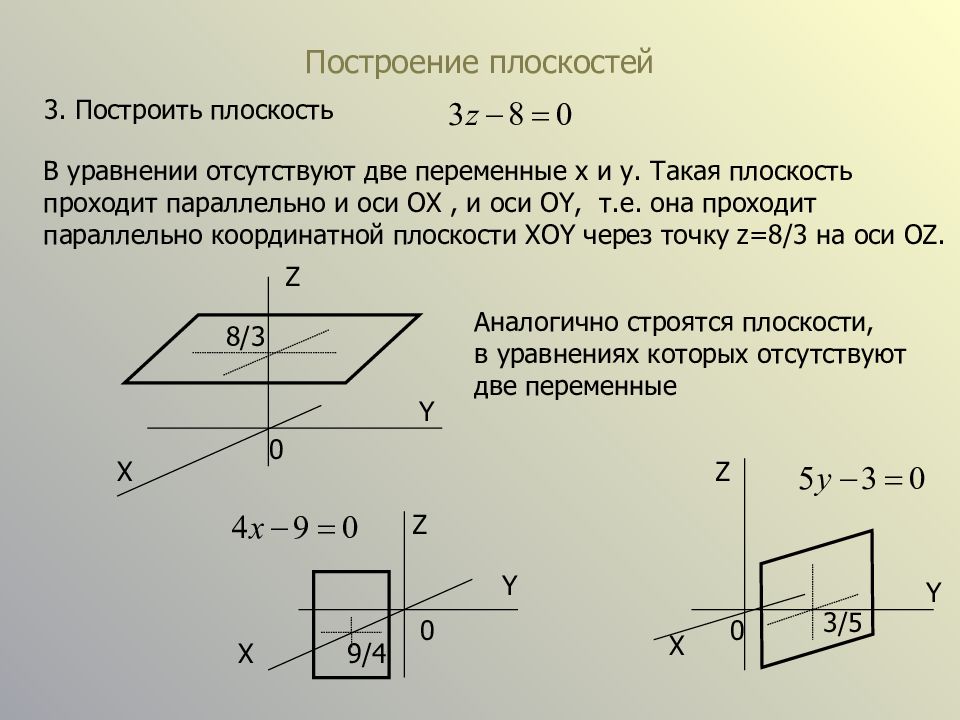
Слайд 7: Построение плоскостей
3. Построить плоскость В уравнении отсутствуют две переменные x и y. Такая плоскость проходит параллельно и оси OX, и оси OY, т.е. она проходит параллельно координатной плоскости XOY через точку z= 8/3 на оси OZ. Z Y X 8/3 0 Аналогично строятся плоскости, в уравнениях которых отсутствуют две переменные Z X Y 0 Z X Y 9/4 3/5 0
Слайд 8
Таким образом, 1. если в уравнении плоскости отсутствует одна переменная, то плоскость проходит параллельно той оси координат, переменной которой нет в уравнении. 2. если в уравнении плоскости отсутствует свободный член, то плоскость проходит через начало координат. 3. Если в уравнении плоскости отсутствуют две переменные, то плоскость проходит параллельно координатной плоскости, переменных которой нет в уравнении. Уравнения координатных плоскостей - уравнение плоскости YOZ - уравнение плоскости XOZ - уравнение плоскости XOY
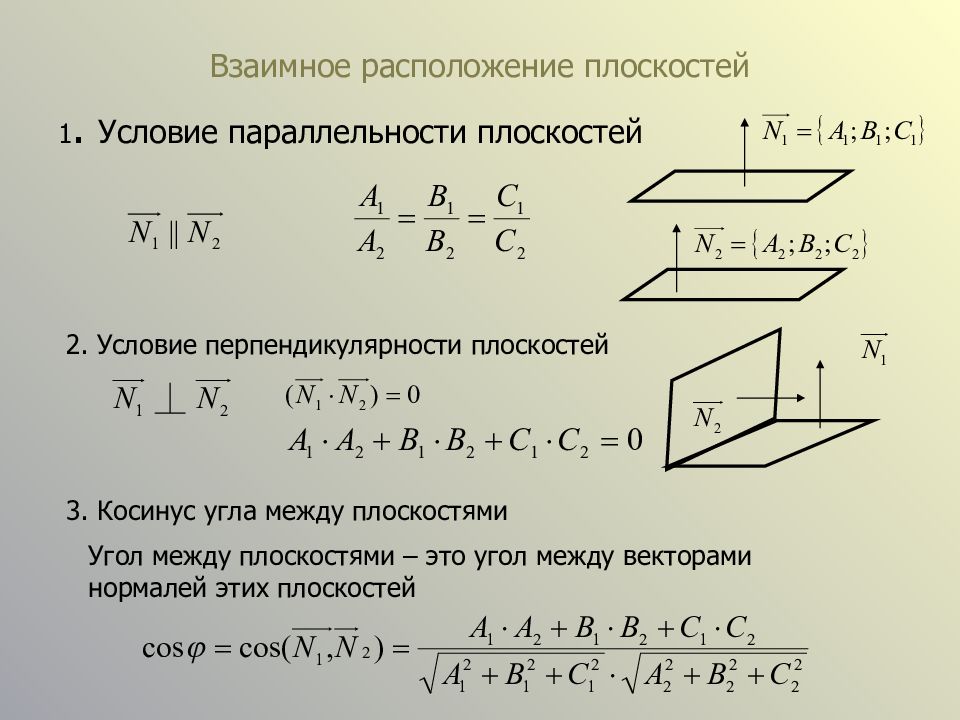
Слайд 9: Взаимное расположение плоскостей
1. Условие параллельности плоскостей 2. Условие перпендикулярности плоскостей 3. Косинус угла между плоскостями Угол между плоскостями – это угол между векторами нормалей этих плоскостей
Слайд 10: Расстояние от точки до плоскости
Расстояние от точки до плоскости находится по формуле Правило : для нахождения расстояния от точки до плоскости нужно координаты точки подставить в левую часть уравнения плоскости, разделить на длину вектора нормали плоскости и полученное значение взять по абсолютной величине. Расстояние – величина всегда положительная ! Расстояние – это длина перпендикуляра, опущенного из точки на плоскость
Слайд 11: 2. Прямая в пространстве. Основные уравнения
1. Уравнение прямой, проходящей через заданную точку параллельно заданному вектору - канонические уравнения - направляющий вектор 2. Параметрические уравнения 3. Уравнение прямой, проходящей через две заданные точки и
Слайд 12: Прямая в пространстве. Основные уравнения
4. Общее уравнение прямой в пространстве а) Направляющий вектор б) Нахождение точки на прямой - канонические уравнения прямой
Слайд 13: Взаимное расположение прямых в пространстве
1. Нахождение угла между прямыми. Прямые в пространстве заданы каноническими уравнениями, поэтому угол между прямыми – это угол между направляющими векторами 2. Условия параллельности и перпендикулярности прямых Условие параллельности прямых Условие перпендикулярности прямых
Слайд 14: 3. Взаимное расположение прямой и плоскости в пространстве
1. Условие параллельности прямой и плоскости 2. Условие перпендикулярности прямой и плоскости
Слайд 15: Взаимное расположение прямой и плоскости в пространстве
3. Нахождение угла между прямой и плоскостью Углом между прямой и плоскостью считается угол между этой прямой и ее ортогональной проекцией на эту плоскость. На рисунке это угол. Из уравнений прямой и плоскости известны направляющий вектор прямой и вектор нормали плоскости. Косинус угла между этими векторами легко можно найти. Легко заметить, что углы и в сумме дают 90 градусов, а значит Поэтому при нахождении угла между прямой и плоскостью находят не косинус, а синус угла. Кроме того, в формуле стоит модуль, так как синус угла в данной ситуации может быть только положительным
Слайд 16
Нахождение точки пересечения прямой и плоскости Для нахождения точки пересечения прямой и плоскости нужно составить систему из уравнений прямой и плоскости Для того, чтобы решить систему, переводим уравнение прямой в параметрический вид Подставляем эти уравнения в уравнение плоскости Из этого уравнения находим параметр и подставляем его значение в параметрические уравнения, получим координаты точки пересечения
Слайд 17: 4. Поверхности 2-го порядка
Общее уравнение плоскости или прямой в пространстве – есть уравнения линейные относительно переменных и Уравнение поверхности 2-го порядка квадратичная часть линейная часть . К поверхностям 2-го порядка относятся : сфера, эллипсоид, гиперболоиды, конусы, параболоиды и цилиндры. Основная задача состоит в умении по уравнению определить тип поверхности, привести само уравнение к каноническому виду и построить поверхность в системе координат. ,
Слайд 18: Классификация поверхностей второго порядка
Название поверхности Каноническое уравнение Сфера Эллипсоид Однополостной гиперболоид Двуполостной гиперболоид Эллиптический параболоид Гиперболический параболоид Конус Эллиптический цилиндр Гиперболический цилиндр Параболический цилиндр или
Слайд 19
Поверхности второго порядка СФЕРА ПАРАБОЛОИДЫ ЭЛЛИПСОИДЫ КОНУСЫ ГИПЕРБОЛОИДЫ ЦИЛИНДРЫ ГИПЕРБОЛОИДЫ
Слайд 20: 1. Сфера
Определение. Сферой называется множество точек пространства, равноудаленных от одной точки, называемой центром Уравнение сферы со смещенным центром Уравнение сферы с центром в начале координат В уравнение сферы входят квадраты трех переменных, причем коэффициенты при квадратах и знаки при них одинаковые. !
Слайд 21: Эллипсоид
Каноническое уравнение трехосного эллипсоида имеет вид a b c полуоси эллипсоида. Центр этого эллипсоида находится в начале координат. Уравнение эллипсоида с центром в точке имеет вид Признаки уравнения эллипсоида: Наличие квадратов всех трех переменных Одинаковые знаки при квадратах переменных Разные коэффициенты при квадратах переменных
Слайд 22: Гиперболоиды
Канонические уравнения гиперболоидов Каноническое уравнение однополостного гиперболоида Признаки уравнения однополостного гиперболоида: Наличие квадратов всех трех переменных Разные знаки при квадратах переменных Один знак минус при квадрате переменной в левой части уравнения, в правой части плюс 1. полуоси В зависимости от знака перед единицей в правой части гиперболоиды делятся на одно и двуполостные.
Слайд 23: Разные ориентации однополостных гиперболоидов
Ориентация гиперболоида зависит от того, перед какой переменной в каноническом уравнении стоит знак минус. Однополостный гиперболоид с осью симметрии OY Однополостный гиперболоид с осью симметрии OX
Слайд 24: Гиперболоиды
Каноническое уравнение двуполостного гиперболоида Признаки уравнения двуполостного гиперболоида: Наличие квадратов всех трех переменных Разные знаки при квадратах переменных Два знака минус в уравнении: один при квадрате переменной в левой части уравнения, другой в правой части при 1. полуоси Если из уравнения выразить z, то получим Т.к. , то получается, что Двуполостный гиперболоид на проходит через начало координат.
Слайд 25: Разные ориентации двуполостного гиперболоида
Каноническое уравнение двуполостного гиперболоида содержит два знака минус в уравнении. Один знак минус оставляем в левой части уравнения, а второй поставим перед единицей в правой части. В таком случае легко определить ось симметрии гиперболоида: перед квадратом какой переменной в левой части уравнения знак минус, та ось системы координат и будет являться осью симметрии.
Слайд 26: Конусы 2-го порядка
Каноническое уравнение конуса Признаки уравнения конуса: Наличие квадратов всех трех переменных Разные знаки при квадратах переменных Свободный член в правой части уравнения равен нулю. Каноническое уравнение конуса от уравнений гиперболоидов отличает то, что в правой части уравнения стоит не единица, а ноль. Если один знак минус оставляем в левой части уравнения, то ось симметрии конуса определится также, как и для гиперболоидов: перед квадратом какой переменной в левой части уравнения знак минус, та ось системы координат и будет являться осью симметрии. Для данного уравнения – это ось OZ.
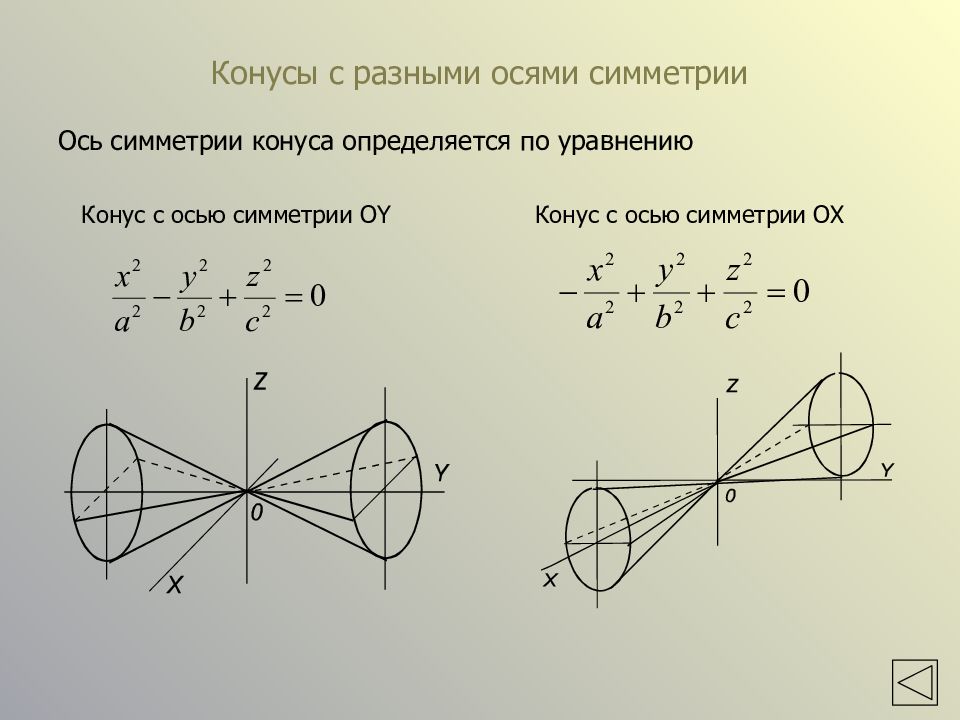
Слайд 27: Конусы с разными осями симметрии
Ось симметрии конуса определяется по уравнению Конус с осью симметрии OY Конус с осью симметрии OX
Слайд 28: Параболоиды
Канонические уравнения параболоидов можно записать в общем виде Таким образом, в уравнении отсутствует квадрат одной переменной. В зависимости от знака между квадратами двух других переменных различают эллиптические и гиперболические параболоиды Признаки уравнения эллиптического или кругового параболоида : Отсутствие квадрата одной из переменных Одинаковые знаки при квадратах переменных в левой части уравнения Эллиптический параболоид Круговой параболоид Если то
Слайд 29: Различные ориентации эллиптических параболоидов
Характерным признаком уравнения эллиптического параболоида является присутствие всех трех переменных, но одно из них входит в уравнение только в первой степени, т.е. в уравнении параболоида отсутствует квадрат одной переменной. Ось симметрии параболоида параллельна той оси, координата которой в уравнении только в первой степени. параболоид с осью симметрии OY параболоид с осью симметрии OX Можно записать один из видов параболоидов со смещенной вершиной - вершина параболоида Возможна также смена направления чаши параболоида. Если в каноническом уравнении в правой части стоит знак минус, то параболоид направлен в отрицательном направлении оси симметрии. где
Слайд 30: Гиперболический параболоид
Каноническое уравнение гиперболического параболоида имеет вид Признаки уравнения гиперболического параболоида: Отсутствие квадрата одной из переменных Разные знаки при квадратах переменных в левой части уравнения Отличительным признаком уравнения гиперболического параболоида является то что в левой части уравнения между квадратами переменных знак минус. Эта поверхность имеет форму седла. Возможны различные варианты ориентации гиперболического параболоида в зависимости от оси симметрии, знаков при квадратах.
Слайд 31: Цилиндрические поверхности
Цилиндрическая поверхность-это поверхность, которую описывает прямая линия (образующая), которая оставаясь параллельно самой себе движется вдоль некоторой кривой, называемой направляющей. По названию направляющей получают свое название и цилиндры. Если образующая параллельна какой-либо оси координат, то каноническое уравнение цилиндра не содержит в уравнении соответствующую переменную. В этом случае уравнение цилиндра повторяет уравнение своей направляющей. Вариантов различных уравнений цилиндров достаточно много. Для построения цилиндра нужно построить направляющую в той плоскости, в которой она задана, а затем «тянуть» эту линию вдоль той оси, координата которой отсутствует в уравнении. Признаки уравнения цилиндрической поверхности: В уравнении цилиндрической поверхности отсутствует одна переменная.
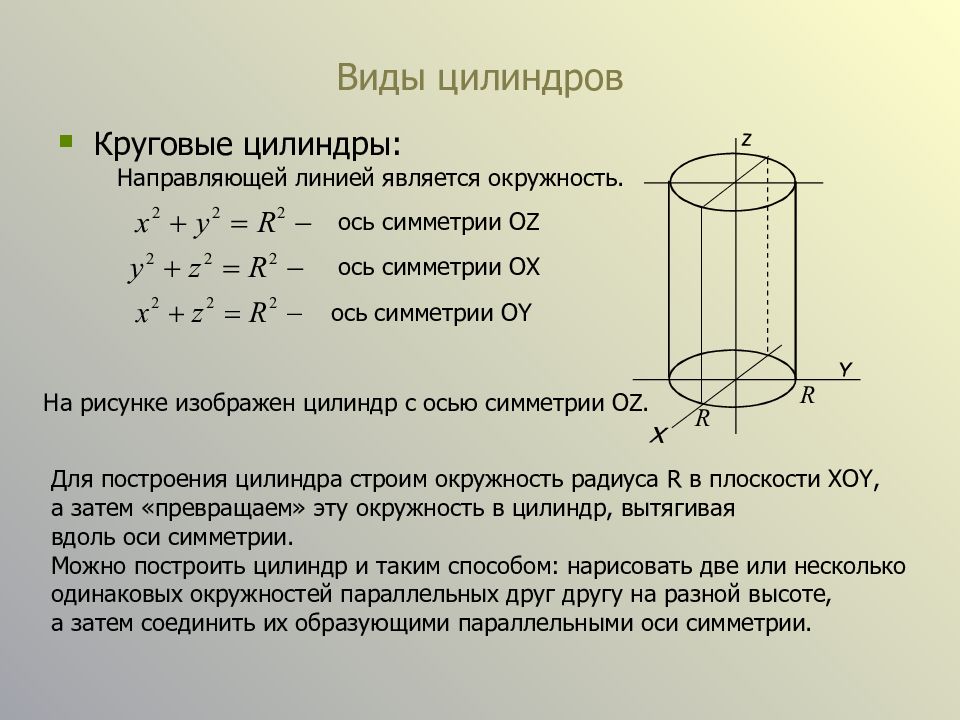
Слайд 32: Виды цилиндров
Круговые цилиндры: ось симметрии OZ ось симметрии OX ось симметрии OY На рисунке изображен цилиндр с осью симметрии OZ. Для построения цилиндра строим окружность радиуса R в плоскости XOY, а затем «превращаем» эту окружность в цилиндр, вытягивая вдоль оси симметрии. Можно построить цилиндр и таким способом: нарисовать две или несколько одинаковых окружностей параллельных друг другу на разной высоте, а затем соединить их образующими параллельными оси симметрии. Направляющей линией является окружность.
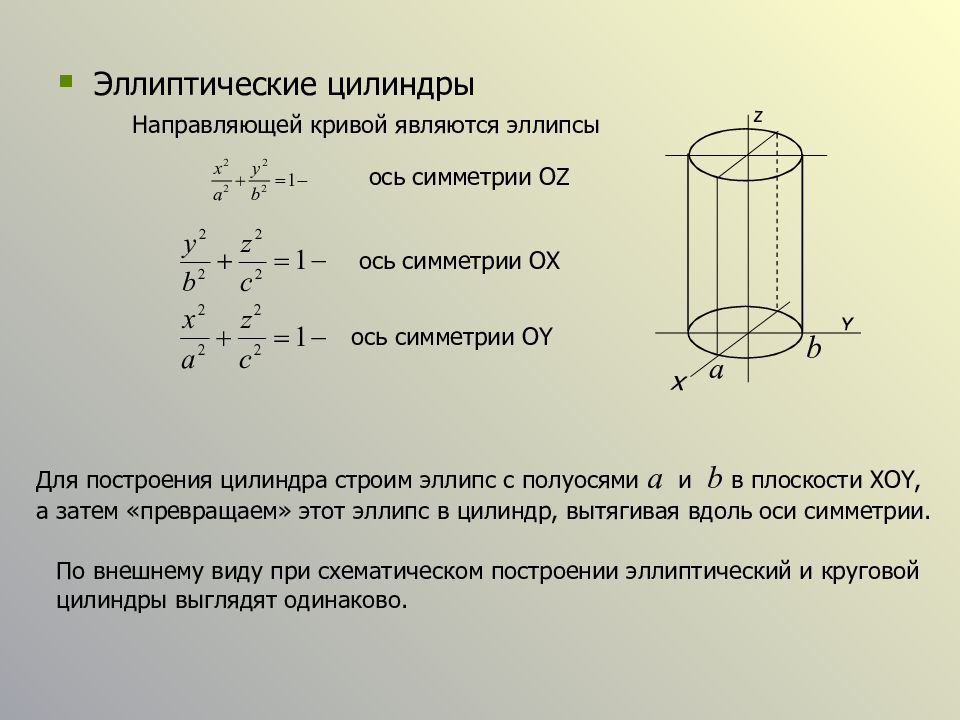
Слайд 33
Эллиптические цилиндры ось симметрии OZ ось симметрии OX ось симметрии OY Для построения цилиндра строим эллипс с полуосями a и b в плоскости XOY, а затем «превращаем» этот эллипс в цилиндр, вытягивая вдоль оси симметрии. По внешнему виду при схематическом построении эллиптический и круговой цилиндры выглядят одинаково. Направляющей кривой являются эллипсы
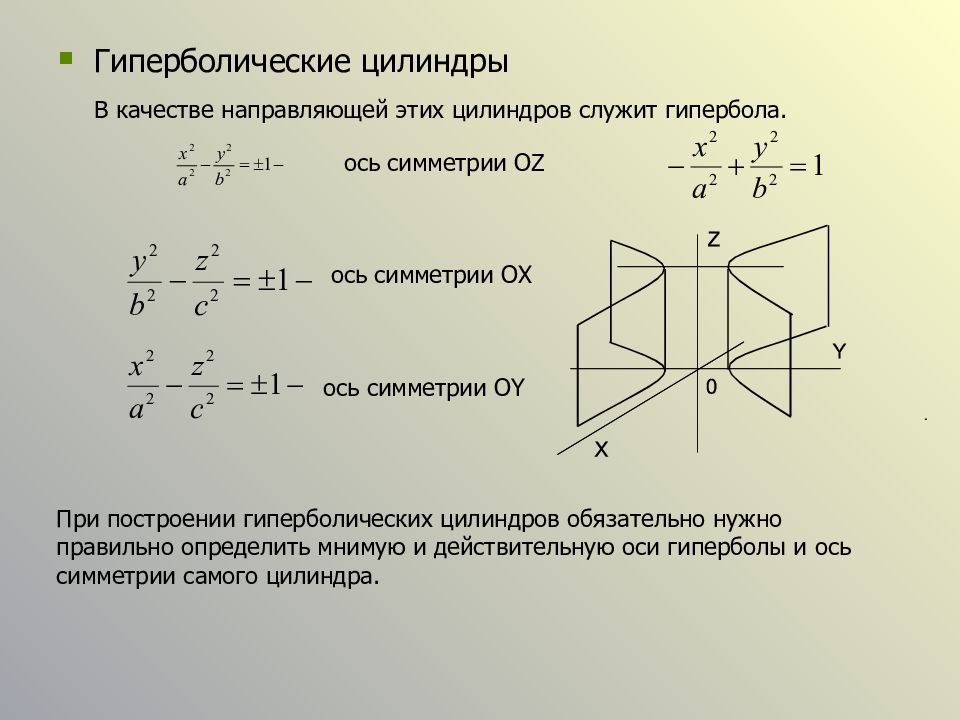
Слайд 34
Гиперболические цилиндры ось симметрии OZ ось симметрии OX ось симметрии OY При построении гиперболических цилиндров обязательно нужно правильно определить мнимую и действительную оси гиперболы и ось симметрии самого цилиндра. В качестве направляющей этих цилиндров служит гипербола.
Слайд 35
Параболические цилиндры ось симметрии OZ ось симметрии OZ ось симметрии OX ось симметрии OX ось симметрии OY ось симметрии OY При построении цилиндра нужно определить основные параметры параболы: координаты вершины, ось симметрии и направление ветвей, построить параболу, а затем уже строить цилиндр с соответствующей осью симметрии. Направляющей этих цилиндров является парабола.