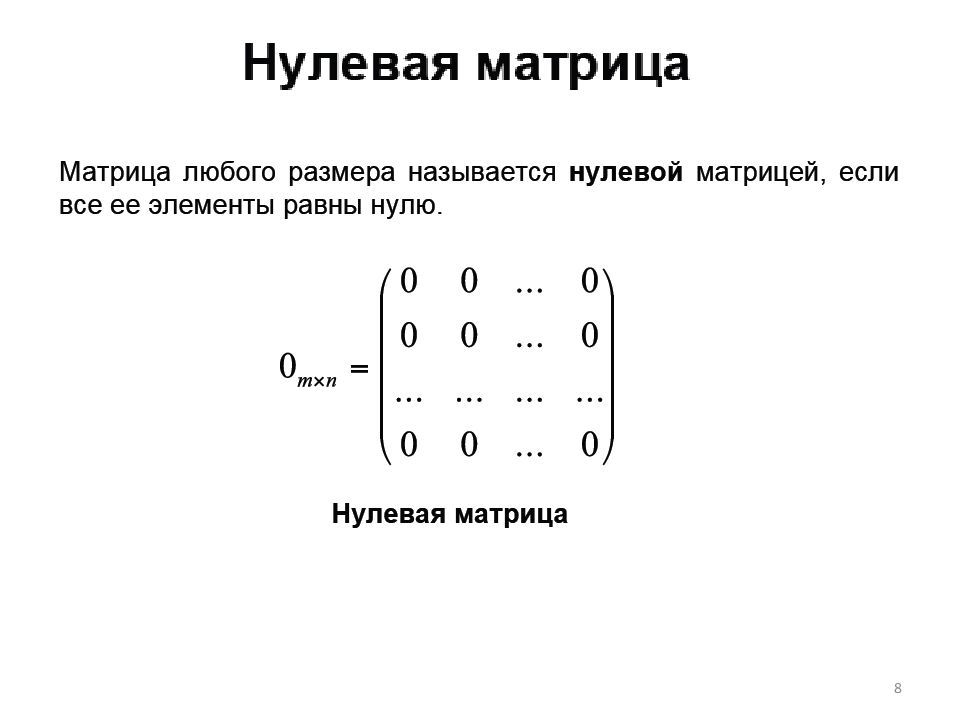
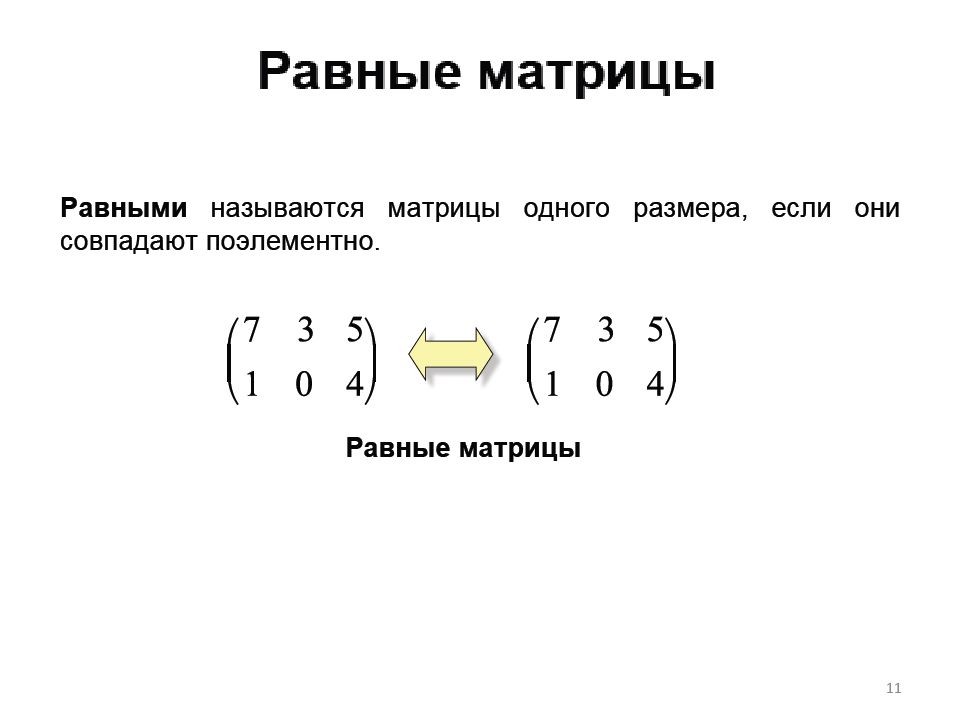
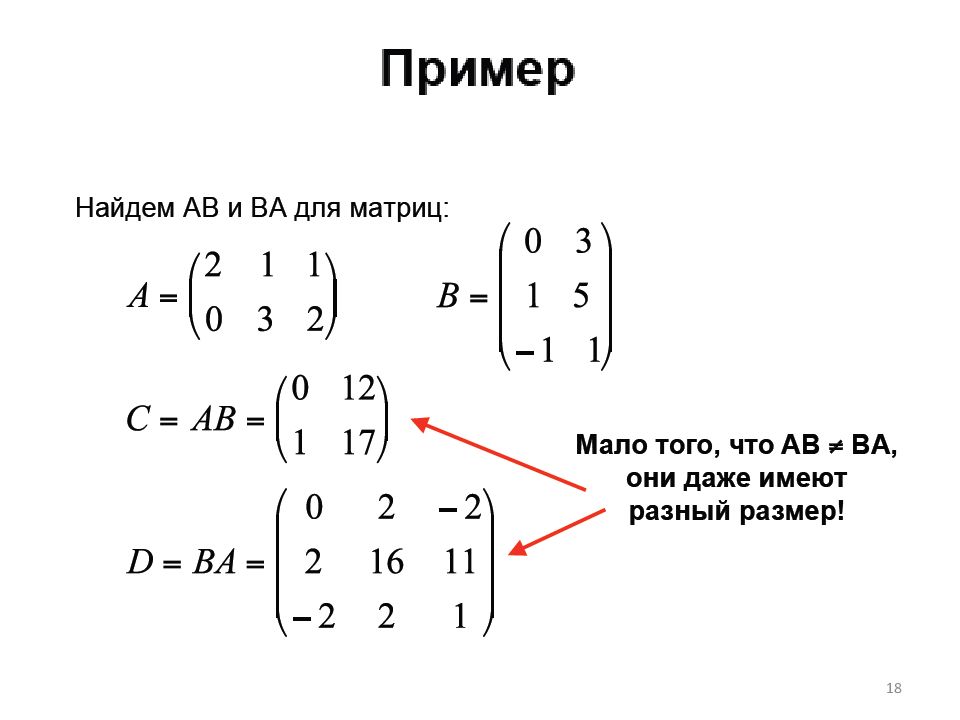
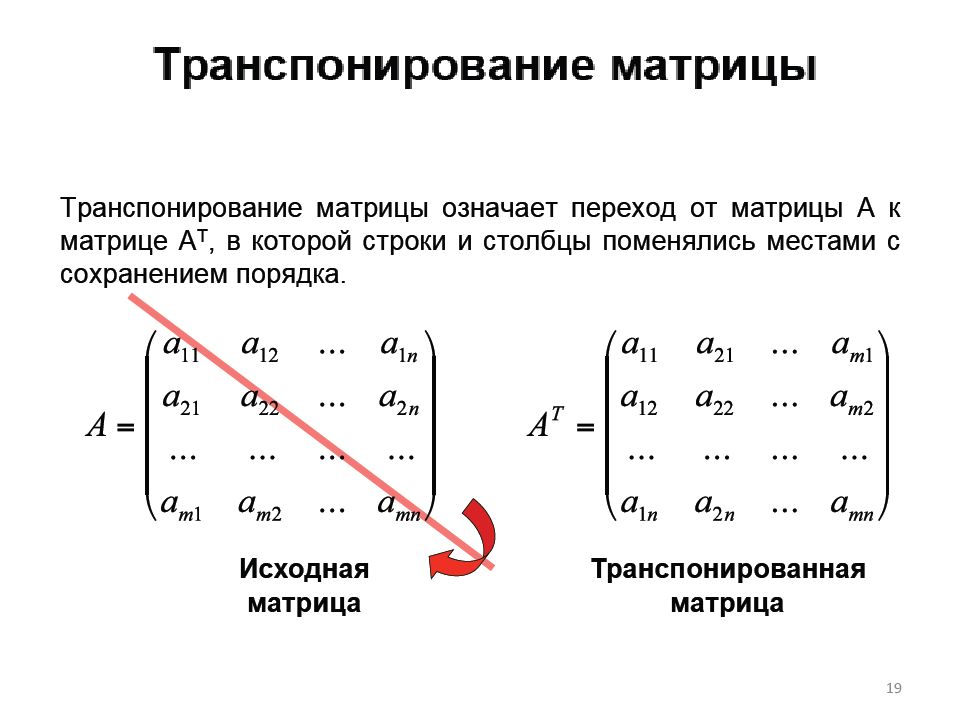
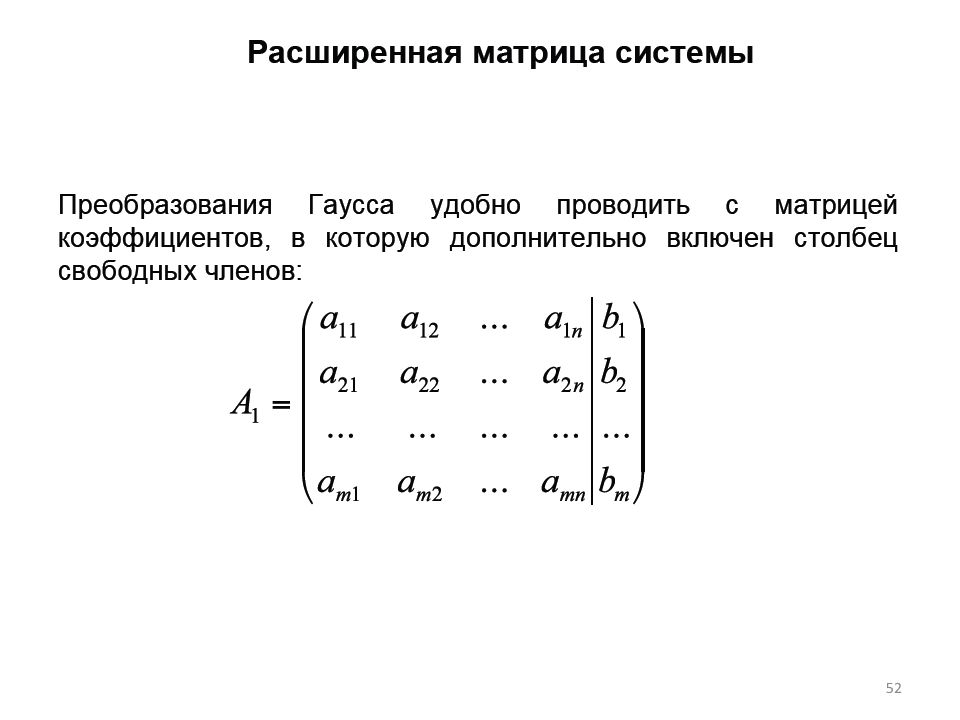
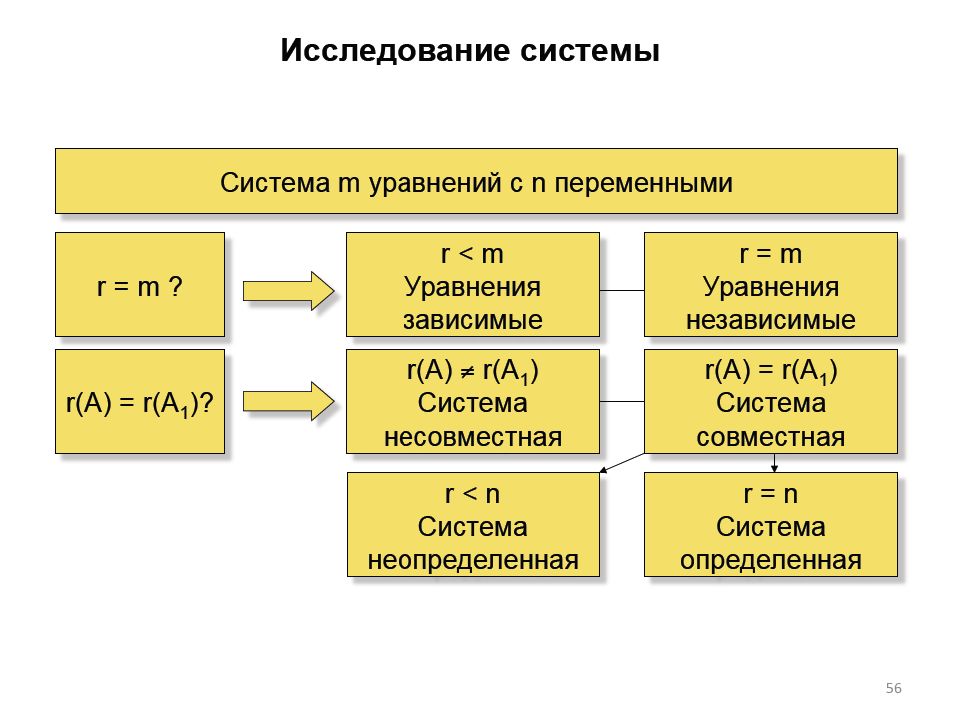
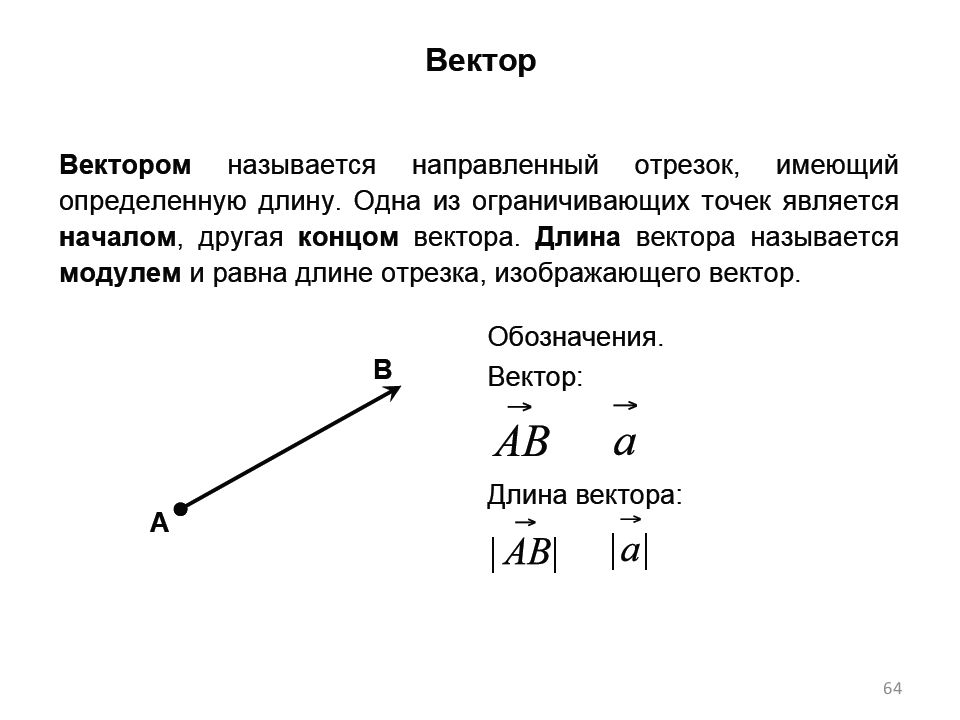
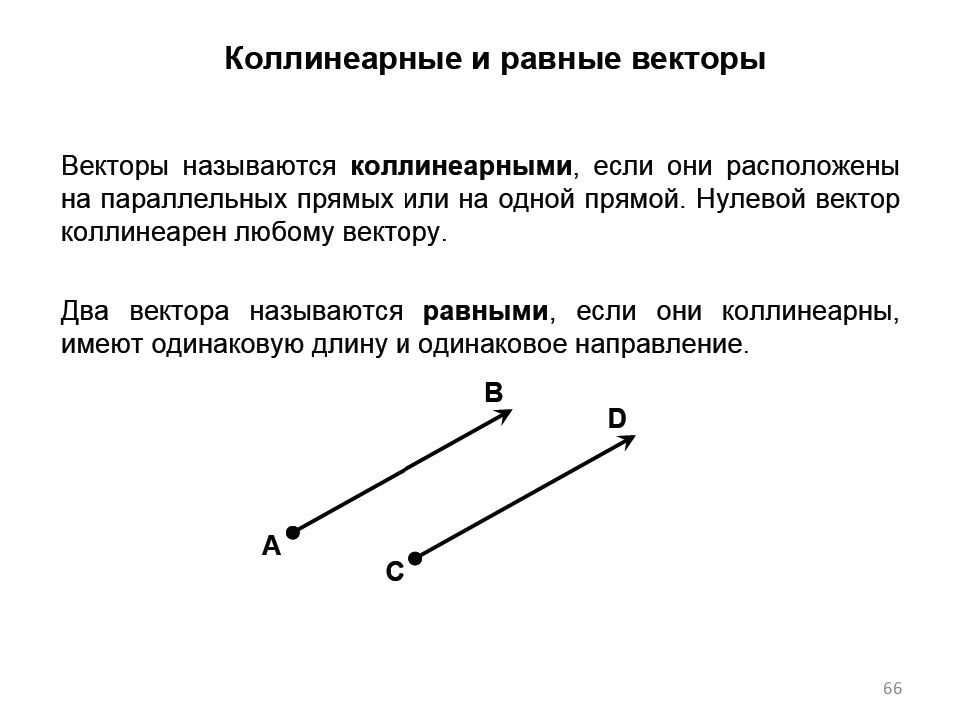
Первый слайд презентации: Линейная алгебра
Лекции – 12 часов Практические занятия – 8 часов Контрольная работа № 1 – зачет Компьютерное тестирование – зачет Экзамен Попов Валерий Андреевич Консультации по пятницам с 15-00 Кафедра математики и информатики (701) 1
Слайд 2: Рекомендуемая литература
Высшая математика для экономистов. Учебник. /Под ред. Н. Ш. Кремера. – М.: ЮНИТИ, 2010. Высшая математика для экономистов. Практикум. /Под ред. Н. Ш. Кремера. – М.: ЮНИТИ, 2010. Высшая математика для экономических специальностей. Учебник и практикум. /Под ред. Н. Ш. Кремера. – М.: Высшее образование, 2009. 2
3
Слайд 85: Векторное пространство
85 Множество векторов с действительными компонентами, в котором определены операции сложения векторов и умножения вектора на число, удовлетворяющее выше приведенным свойствам (аксиомам), называется векторным пространством. Размерность пространства – это максимальное число содержащихся в нем линейно независимых векторов. Совокупность n линейно независимых векторов n -мерного пространства называется базисом.
Слайд 97: 5. Квадратичные формы
97 Квадратичной формой от n переменных называется сумма, каждый член которой является либо квадратом одной из переменных, либо произведением двух разных переменных, взятых с некоторым коэффициентом: Матрица A, составленная из коэффициентов, называется матрицей квадратичной формы. Матрица A, у которой все элементы, называется симметрической матрицей.
Слайд 98: Матричная запись квадратичной формы
98 В матричной записи квадратичная форма с указанием элементов имеет вид: Квадратичная форма называется канонической, если при всех i ≠ j :
Слайд 99: Невырожденное линейное преобразование
99 Линейное преобразование называется невырожденным, если матрица C линейного преобразования X = CY является невырожденной:. Если X и Y – матрицы-столбцы, то квадратичная форма п ри невырожденном линейном преобразовании имеет вид:. Теорема : Любая квадратичная форма с помощью невырожденного преобразования может быть приведена к каноническому виду.
Слайд 100: Закон инерции квадратичных форм
100 Теорема. Число слагаемых с положительными, или отрицательными коэффициентами канонической формы не зависит от способа приведения формы к этому виду. Теорема. Ранг квадратичной формы (ранг квадратичной формы ) равен числу отличных от нуля коэффициентов квадратичной формы и не меняется при линейных преобразованиях. Каноническая форма называется положительно ( отрицательно ) определенной, если при всех значениях переменных, из которых хотя бы одно отлично от нуля, имеет место неравенство:
Слайд 101: Знакоопределенная квадратичная форма
101 Теорема. Для того, чтобы квадратичная форма была положительно (отрицательно) определенной, необходимо и достаточно, чтобы все собственные значения матрицы этой квадратичной формы были положительны ( отрицательны). Теорема (критерий Сильвестра). Для того, чтобы квадратичная форма была положительно определенной, необходимо и достаточно, чтобы все главные миноры матрицы квадратичной формы были положительны. Для отрицательно определенной квадратичной формы знаки главных миноров чередуются, начиная со знака (-) для минора первого порядка.
Слайд 102: 6. Элементы аналитической геометрии
102 Уравнением линии на плоскости Oxy называется уравнение, которому удовлетворяют координаты x и y каждой точки данной линии и не удовлетворяют координаты любой точки, не лежащей на этой линии. Уравнение y = kx + b называется уравнением прямой с угловым коэффициентом k = tg α. У равнение прямой, проходящей через данную точку (, ) в данном направлении :. Если в уравнении угловой коэффициент является произвольным, то это уравнение определяет пучок прямых, проходящих через точку (, ).
Слайд 103: Уравнение прямой
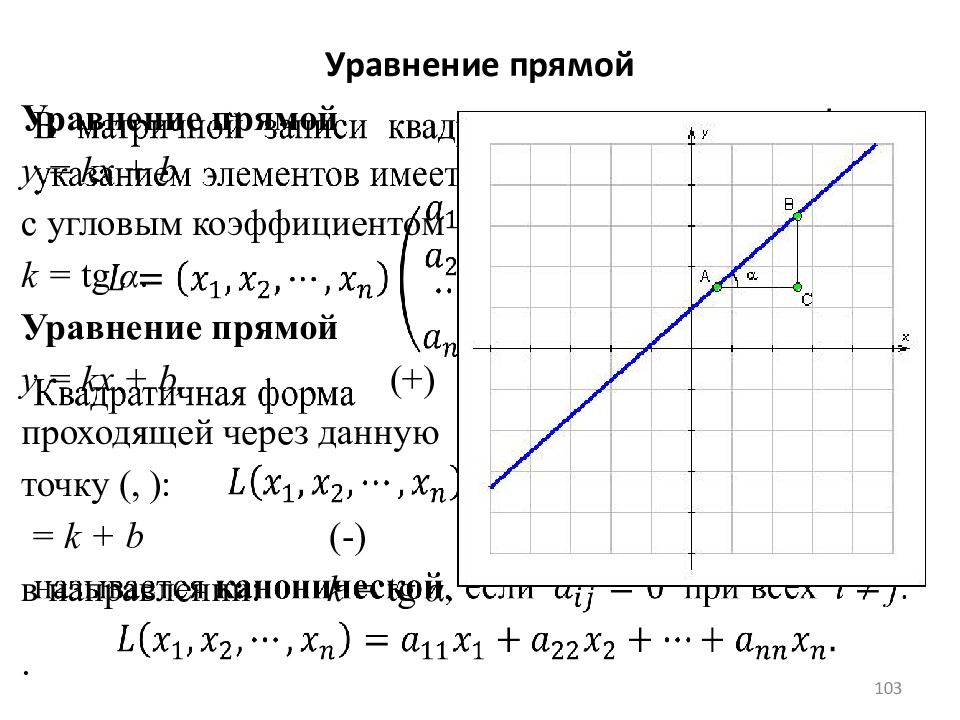
103 Уравнение прямой y = kx + b с угловым коэффициентом k = tg α. Уравнение прямой y = kx + b, (+) проходящей через данную точку (, ): = k + b (-) в направлении : k = tg α. .
Слайд 104: Уравнение прямой, проходящей через две данные точки
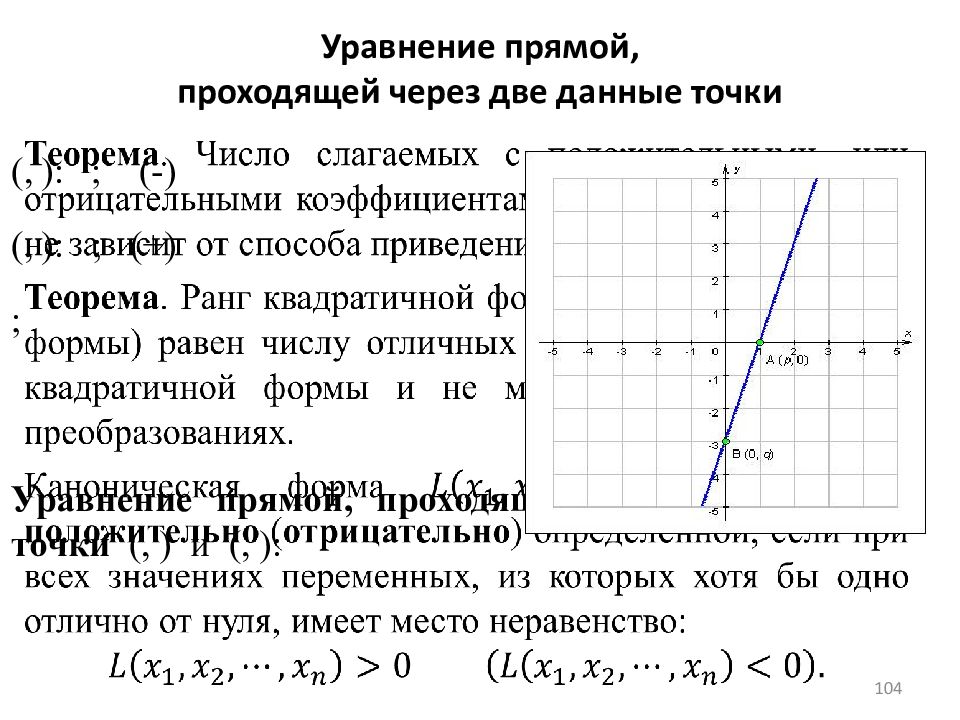
104 (, ) : ; (-) (, ) : ; (+) ; Уравнение прямой, проходящей через две данные точки (, ) и (, ) :
Слайд 105: Общее уравнение прямой и его исследование
105 – уравнение первой степени. При имеем уравнение прямой: , где При, имеем уравнение прямой, параллельной оси Oy :, где При имеем уравнение оси Oy :. – общее уравнение прямой при любых значениях коэффициентов A, B, C, причем и одновременно.
Слайд 106: Координаты точки пересечения двух прямых
106 Координаты точки пересечения двух прямых могут быть найдены в результате решения этой системы. Если прямые не параллельны, то есть, то решение системы дает единственную точку пересечения этих прямых с координатами.
Слайд 107: Условие параллельности двух прямых
107 Равенство угловых коэффициентов является необходимым и достаточным условием параллельности прямых
Слайд 108: Условие перпендикулярности двух прямых
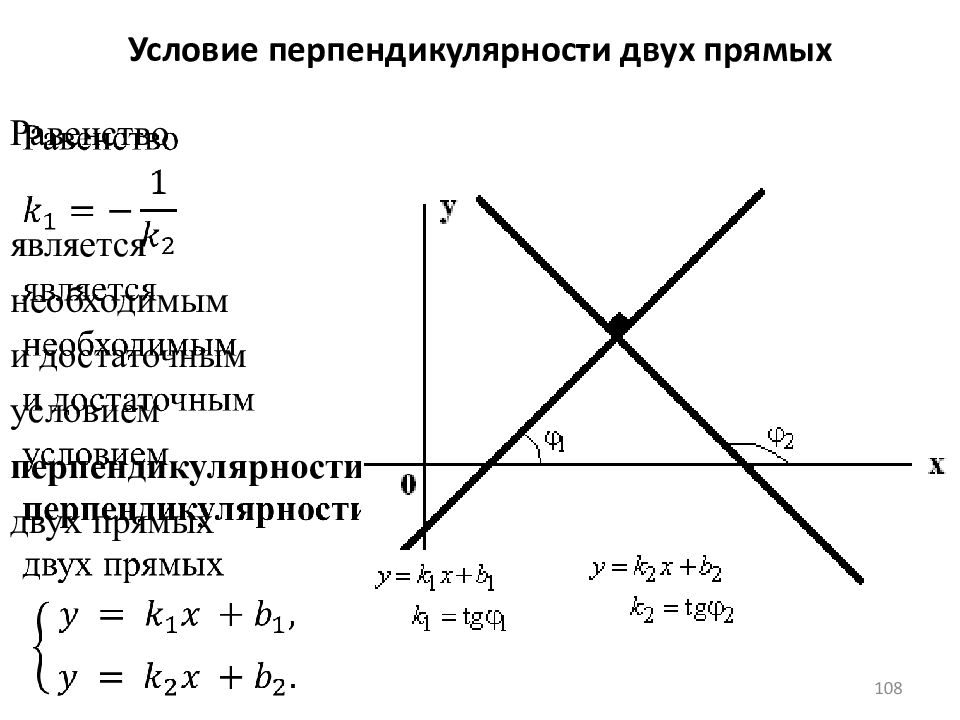
108 Равенство я вляется н еобходимым и достаточным условием перпендикулярности двух прямых
Слайд 109: Кривые второго порядка
109 Кривой 2-го порядка называется линия на плоскости, которая в декартовой системе координат определяется уравнением ax 2 + 2 bxy + cy 2 + 2 dx + 2 ey + f = 0. a, b, c, d, e, f – вещественные коэффициенты, причем a 2 + b 2 + c 2 ≠ 0. Для каждой кривой 2-го порядка (для каждого уравнения) существует такая система координат, в которой уравнение кривой имеет вид окружности, эллипса, гиперболы или параболы.
Слайд 110: Окружность
110 Окружностью называется замкнутая плоская кривая, все точки которой одинаково удалены от данной точки ( центра О ), лежащей в той же плоскости, что и кривая. Уравнение н азывается нормальным уравнением окружности. – координаты центра О, – радиус окружности.
Слайд 111: Эллипс
111 Эллипс – геометрическое место точек X евклидовой плоскости, для которых сумма расстояний до двух данных точек и ( называемых фокусами ) постоянна и больше расстояния между фокусами. a – большая полуось ; b – малая полуось ; c – фокальный радиус ; p – фокальный параметр ; – каноническое уравнение эллипса.
Слайд 112: Гипербола
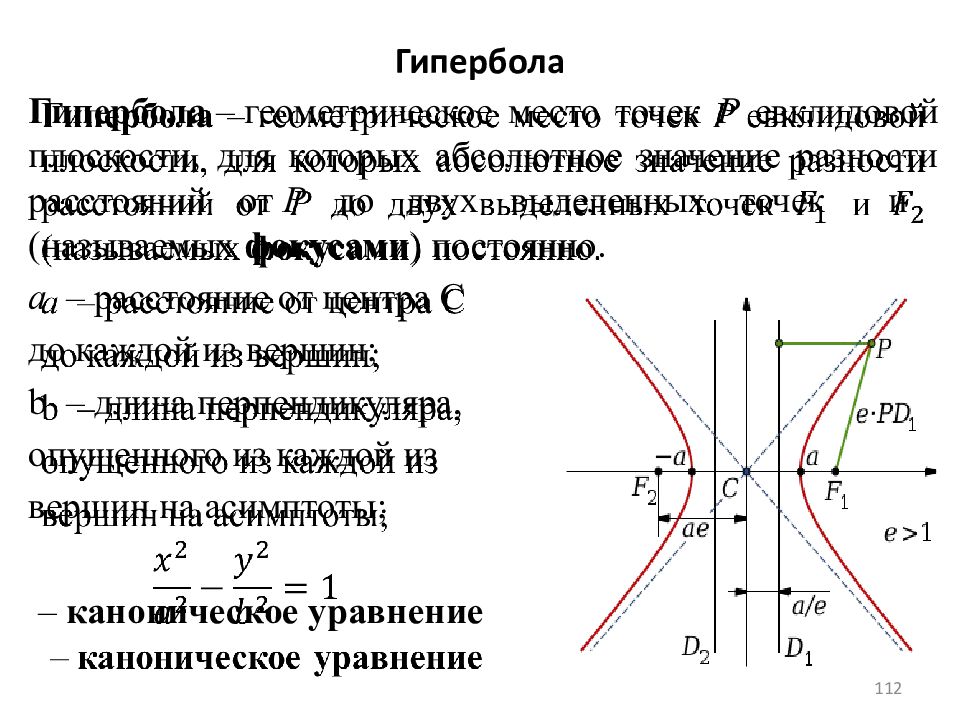
112 Гипербола – геометрическое место точек P евклидовой плоскости, для которых абсолютное значение разности расстояний от P до двух выделенных точек и ( называемых фокусами ) постоянно. a – расстояние от центра C до каждой из вершин ; b – длина перпендикуляра, опущенного из каждой из вершин на асимптоты ; – каноническое уравнение
Слайд 113: Парабола
113 Парабола – множество всех точек М, равноудалённых от данной прямой l (называемой директрисой параболы) и данной точки F (называемой фокусом параболы ). – каноническое уравнение параболы ; – параметр параболы ; – фокусное расстояние ; Ox – ось параболы ;
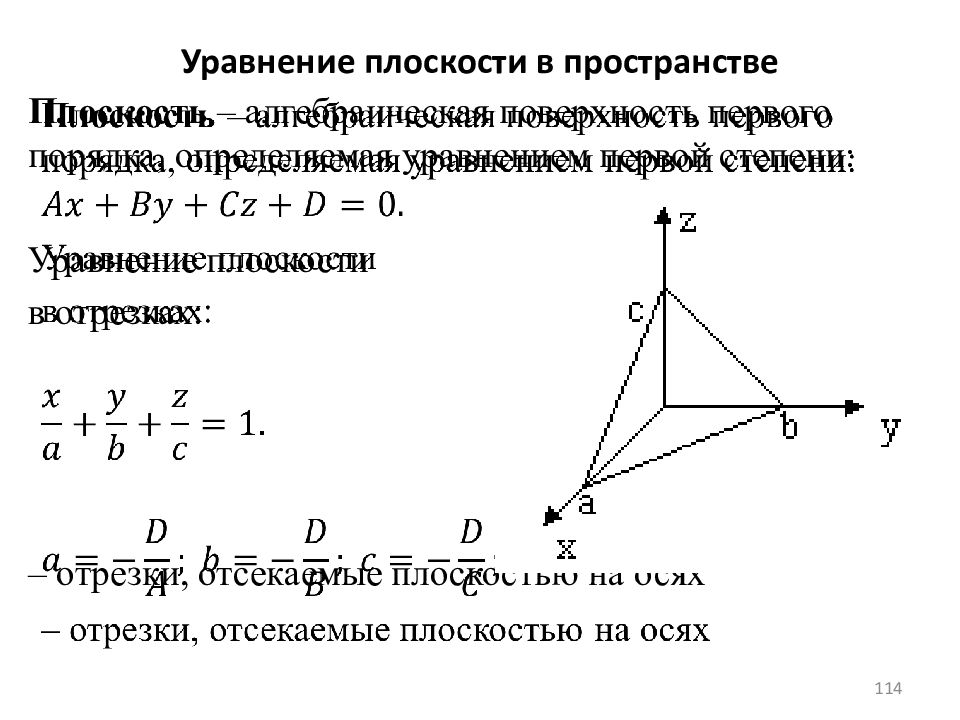
Слайд 114: Уравнение плоскости в пространстве
114 Плоскость – алгебраическая поверхность первого порядка, определяемая уравнением первой степени: Уравнение плоскости в отрезках: – отрезки, отсекаемые плоскостью на осях
Слайд 115: Условие перпендикулярности и параллельности плоскостей
115 Плоскости параллельны, если перпендикулярны, если и ли образуют угол, определяемый соотношением
Слайд 116: Уравнение прямой в пространстве
116 Прямая, образованная пересечением двух не параллельных плоскостей, определяется равенствами Уравнение прямой, проходящей через точку, н азывают каноническим уравнением, где