Первый слайд презентации: Кривые второго порядка
К кривым второго порядка относятся: эллипс, частным случаем которого является окружность, гипербола и парабола. Общее уравнение кривой второго порядка В некоторых частных случаях это уравнение может определять также две прямые, точку или мнимое геометрическое место.
Слайд 3: Окружность
Окружностью называется геометрическое место точек на плоскости, равноудаленных от точки А( a; b ) на расстояние R. y 0 х А R М (x; y) Для любой точки М справедливо: Каноническое уравнение окружности
Слайд 4: Эллипс
Эллипсом называется геометрическое место точек, сумма расстояний от каждой из которых до двух точек той же плоскости F 1 и F 2, называемых фокусами, есть величина постоянная, равная 2а. y 0 х F 1 F 2 -c c M(x; y) r 1 r 2 Зададим систему координат и начало координат выберем в середине отрезка [ F 1 F 2 ]
Слайд 6
ИССЛЕДОВАНИЕ КАНОНИЧЕСКОГО УРАВНЕНИЯ ЭЛЛИПСА Из уравнения эллипса получаем: Эллипс лежит внутри прямоугольника, ограниченного x = a, y = b. Эллипс имеет центр симметрии (начало координат) и две оси симметрии (оси Ox и Oy ). Центр симметрии эллипса называют центром эллипса.
Слайд 7
функция возрастает при x (– a ; 0) ( y > 0) , убывает при x (0; a ) ( y < 0) , экстремум (максимум) в точке x = 0 , y (0) = b ; кривая всюду выпуклая.
Слайд 8: Эллипс
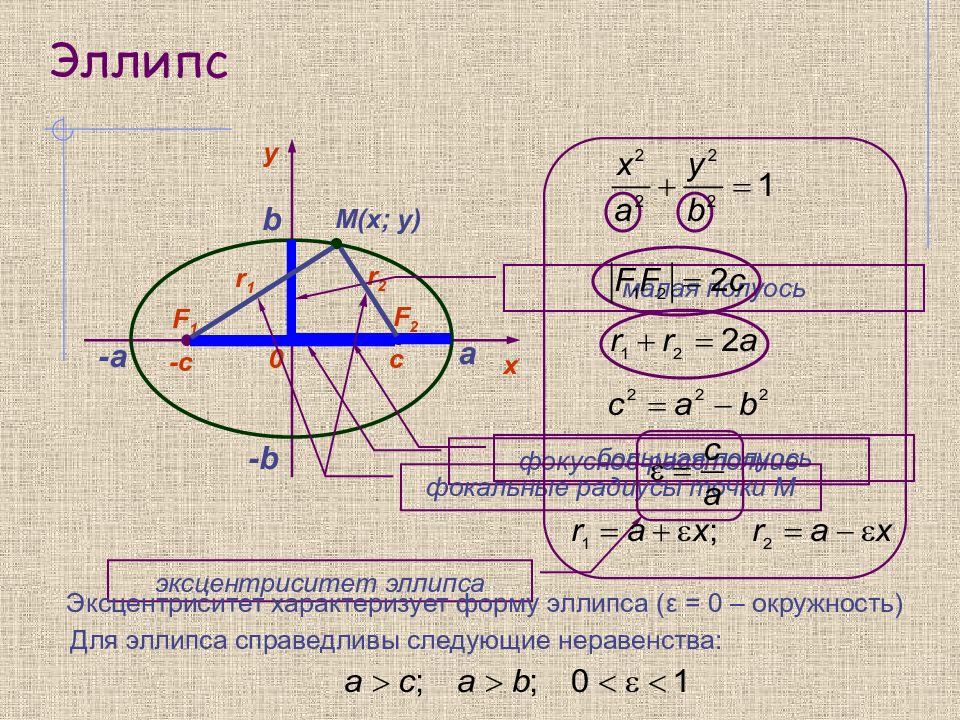
y 0 х F 1 F 2 -c c M(x; y) r 1 r 2 а -а большая полуось малая полуось b -b фокусное расстояние фокальные радиусы точки М эксцентриситет эллипса Для эллипса справедливы следующие неравенства: Эксцентриситет характеризует форму эллипса ( ε = 0 – окружность)
Слайд 9: Директрисы эллипса
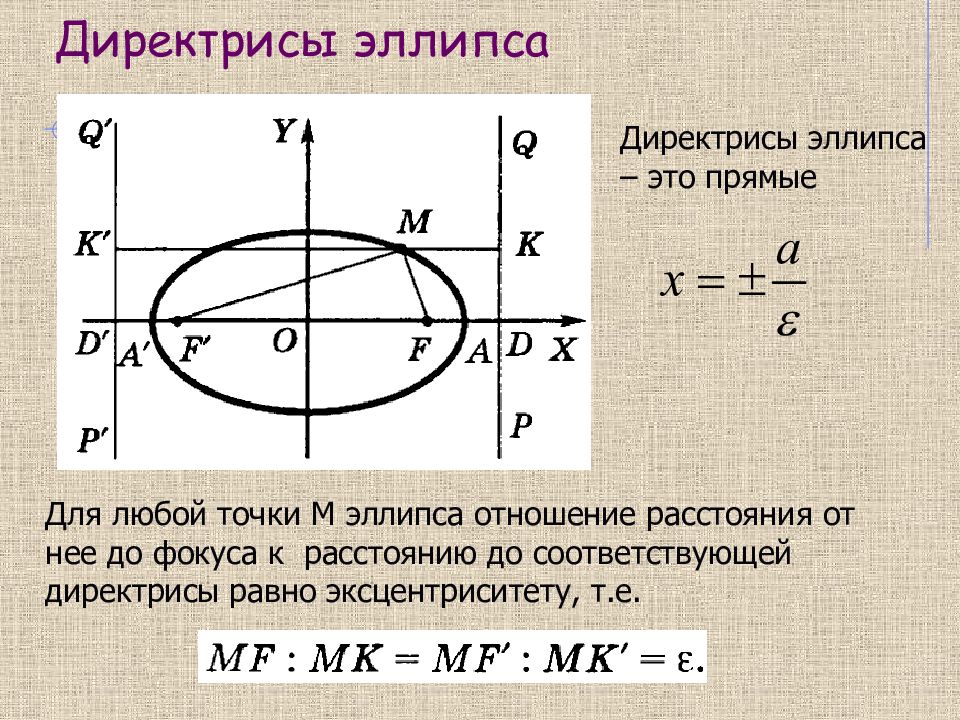
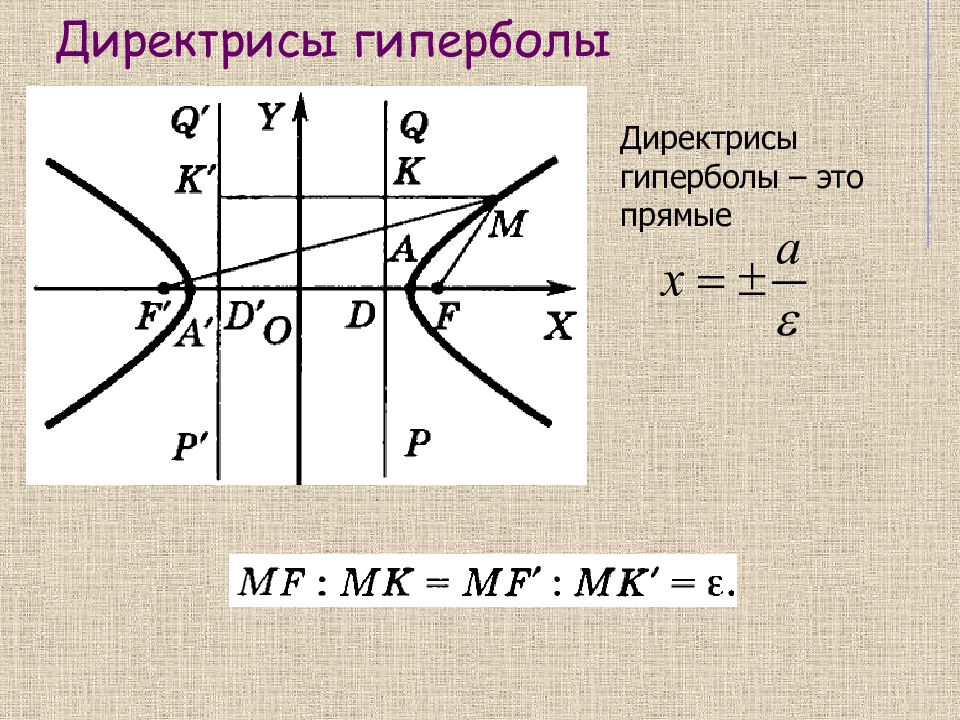
Для любой точки М эллипса отношение расстояния от нее до фокуса к расстоянию до соответствующей директрисы равно эксцентриситету, т.е. Директрисы эллипса – это прямые
Слайд 10: Пример
Составить уравнение эллипса, фокусы которого лежат в точках F 1 (-4; 0) F 2 (4; 0), а эксцентриситет равен 0,8. Каноническое уравнение эллипса: y 0 х - 5 5 - 3 3
Слайд 11
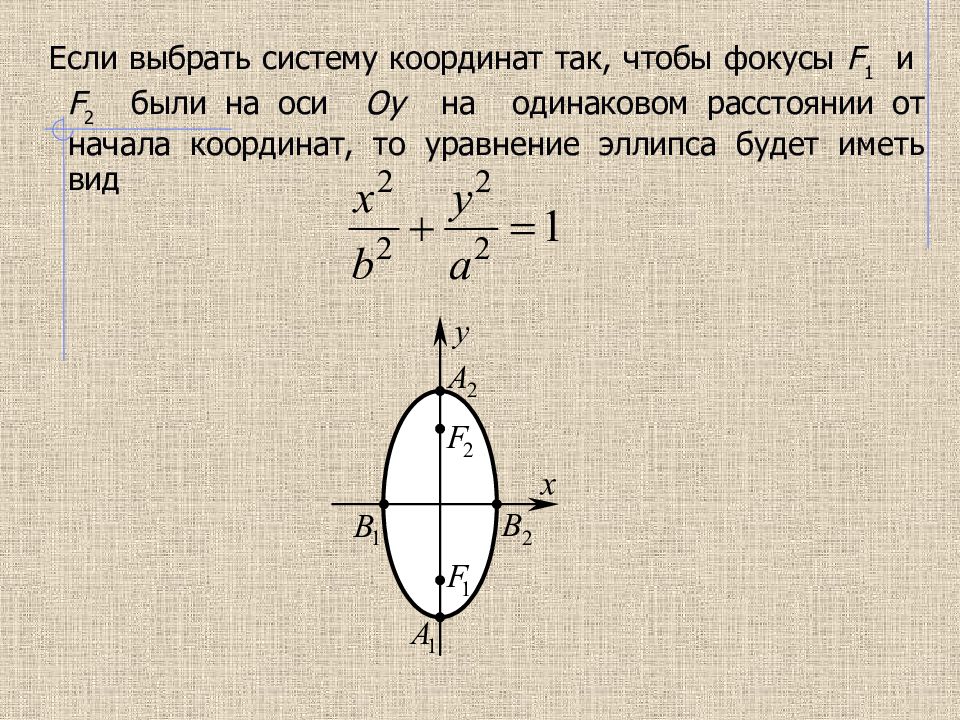
Если выбрать систему координат так, чтобы фокусы F 1 и F 2 были на оси Oy на одинаковом расстоянии от начала координат, то уравнение эллипса будет иметь вид
Слайд 12: Гипербола
Гиперболой называется геометрическое место точек, разность расстояний от каждой из которых до двух точек той же плоскости F 1 и F 2, называемых фокусами, есть величина постоянная, равная 2а. y 0 х F 1 F 2 -c c M(x; y) r 1 r 2
Слайд 13: Гипербола
b 2 b 2 b 2 Каноническое уравнение гиперболы После тождественных преобразований уравнение примет вид:
Слайд 14
ИССЛЕДОВАНИЕ КАНОНИЧЕСКОГО УРАВНЕНИЯ ГИПЕРБОЛЫ 1) Т очек гиперболы нет в полосе, ограниченной прямыми x = a. 2) Гипербола имеет центр симметрии (начало координат) и две оси симметрии (оси Ox и Oy ). Центр симметрии гиперболы называют центром гиперболы. Ось симметрии гиперболы, проходящую через фокусы (ось Ox ) называют действительной (или фокальной ) осью симметрии, а вторую ось (ось Oy ) – мнимой осью. 3) Из уравнения гиперболы получаем: Исследуем кривую методами, разработанными в математическом анализе:
Слайд 15
а) D ( y ) = (– ;– a ] ∪ [ a ; + ) , y ( a ) = 0 ; б) линия имеет асимптоты Напомним: П рямая ℓ называется асимптотой кривой, если расстояние от точки M кривой до прямой ℓ стремится к нулю при удалении точки M от начала координат. Существуют два вида асимптот – вертикальные и наклонные. Вертикальные асимптоты кривая y = f ( x ) имеет в тех точках разрыва II рода функции y = f ( x ), в которых хотя бы один из односторонних пределов функции равен бесконечности. Наклонные асимптоты кривой y = f ( x ) имеют уравнение y = k 1,2 x + b 1,2, где
Слайд 16
в) функция возрастает при x ( a ; + ) ( y > 0) , убывает при x ( – ; – a ) ( y < 0) , экстремум ов нет ( критические точки x = 0 D ( y ) и x = a – граничные) ; г) кривая всюду выпуклая.
Слайд 17: Гипербола
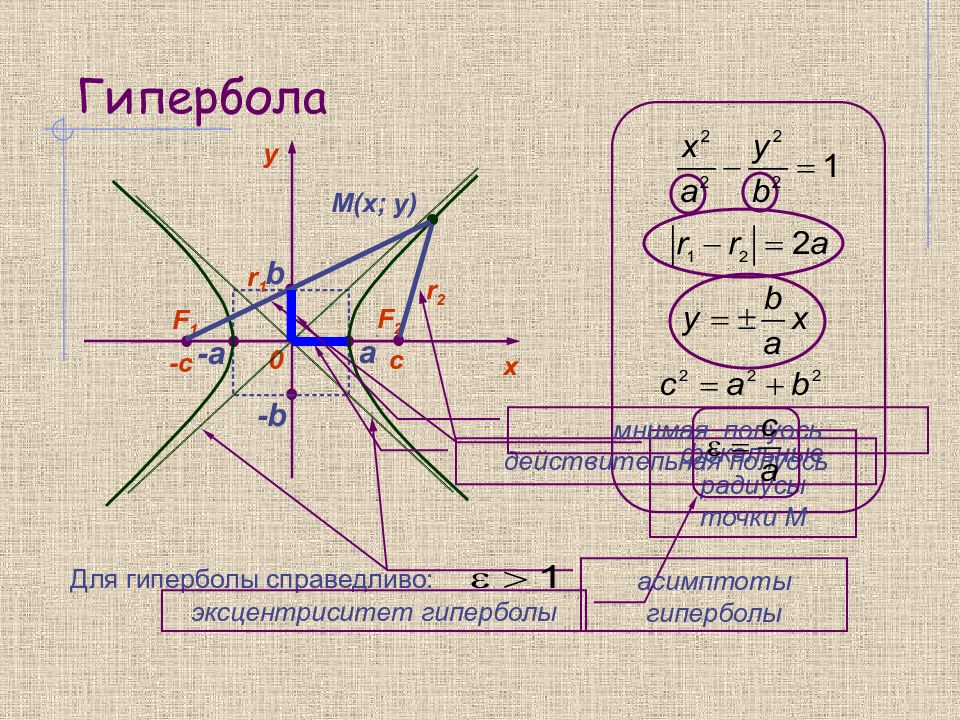
y 0 х F 1 F 2 -c c M(x; y) а - а -b b Для гиперболы справедливо: r 1 r 2 фокальные радиусы точки М действительная полуось мнимая полуось эксцентриситет гиперболы асимптоты гиперболы
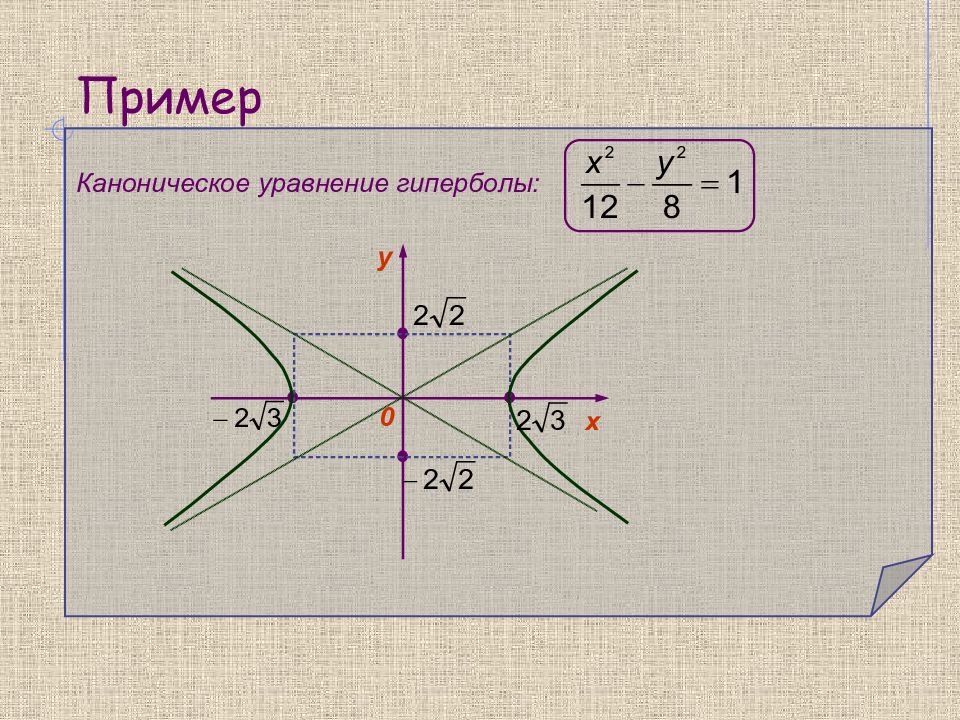
Слайд 19: Пример
Составить уравнение гиперболы, проходящей через точку А(6; -4), если ее асимптоты заданы уравнениями: Решим систему: Точка А лежит на гиперболе
Слайд 21: Парабола
y 0 х F M(x; y) d r Параболой называется геометрическое место точек на плоскости, для каждой из которых расстояние до некоторой фиксированной точки той же плоскости , называемой фокусом, равно расстоянию до прямой:
Слайд 22: Парабола
y 0 х F M(x; y) d r каноническое уравнение параболы директриса параболы фокус параболы фокальный радиус Эксцентриситет параболы:
Слайд 23
ИССЛЕДОВАНИЕ КАНОНИЧЕСКОГО УРАВНЕНИЯ ПАРАБОЛЫ 1) П арабола лежит в полуплоскости x ≥ 0. 2) Парабола имеет ось симметрии (ось Ox ). Ось симметрии параболы называют осью параболы. 3) Из уравнения параболы получаем: Исследуем кривую методами, разработанными в математическом анализе: а) D ( y ) = [0; + ) , y (0) = 0 ; б) асимптот нет (проверить самим); в) функция всюду возрастает; г) кривая всюду выпуклая.
Общее уравнение кривой называется пятичленным, если 2Bxy =0: Приведение пятичленного уравнения к каноническому виду рассмотрим на примере:
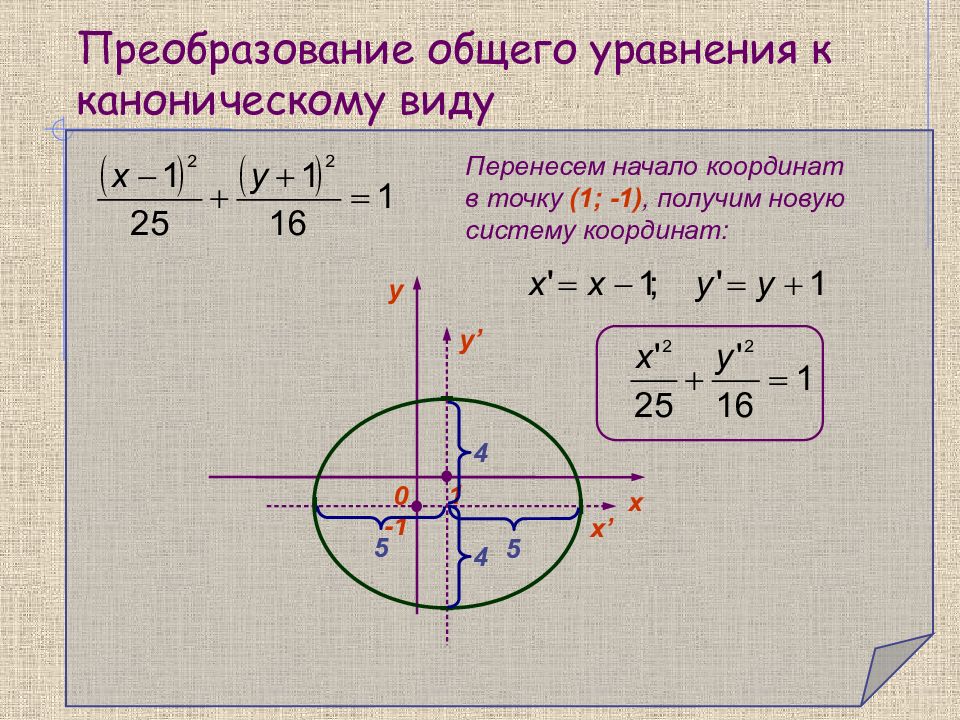
Слайд 26: Преобразование общего уравнения к каноническому виду
y 0 х - 1 1 5 5 4 4 y’ x’ Перенесем начало координат в точку (1; -1), получим новую систему координат:
Последний слайд презентации: Кривые второго порядка: Преобразование общего уравнения к каноническому виду
Если слагаемое 2Bxy в общем уравнении не равно нулю, то для приведения уравнения к каноническому виду необходимо повернуть оси координат на угол α. При этом зависимость между старыми координатами и новыми определяются формулами: Угол α удовлетворяет условию: В случае, если A = C, то