2003г. Переменный ток Четырехполюсники Основные уравнения четырехполюсника Уравнения четырехполюсника при питании со стороны выходных зажимов. Холостой ход и короткое замыкание четырехполюсников. Опытное определение коэффициентов четырехполюсника. Эквивалентные схемы замещения четырехполюсников. Волновое сопротивление четырехполюсника. Коэффициент распространения Уравнения четырехполюсника в гиперболических функциях
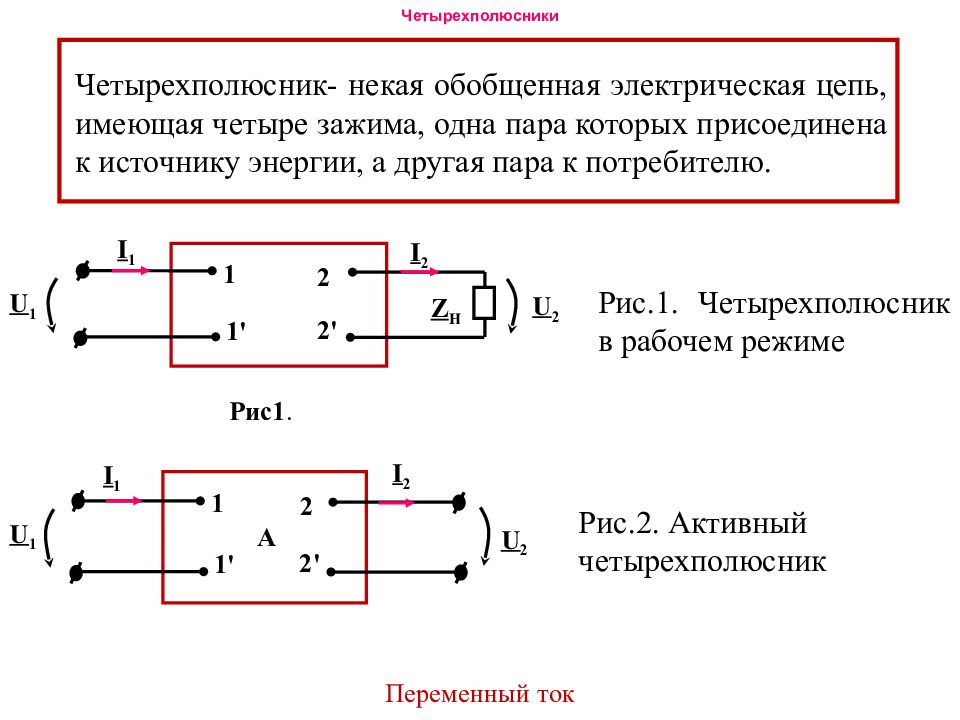
Переменный ток Четырехполюсник- некая обобщенная электрическая цепь, имеющая четыре зажима, одна пара которых присоединена к источнику энергии, а другая пара к потребителю. 1 1 ' U 1 2 2 ' I 1 I 2 U 2 А 1 1 ' U 1 2 2 ' I 1 I 2 Z H U 2 Рис1. Рис.1. Четырехполюсник в рабочем режиме Рис.2. Активный четырехполюсник
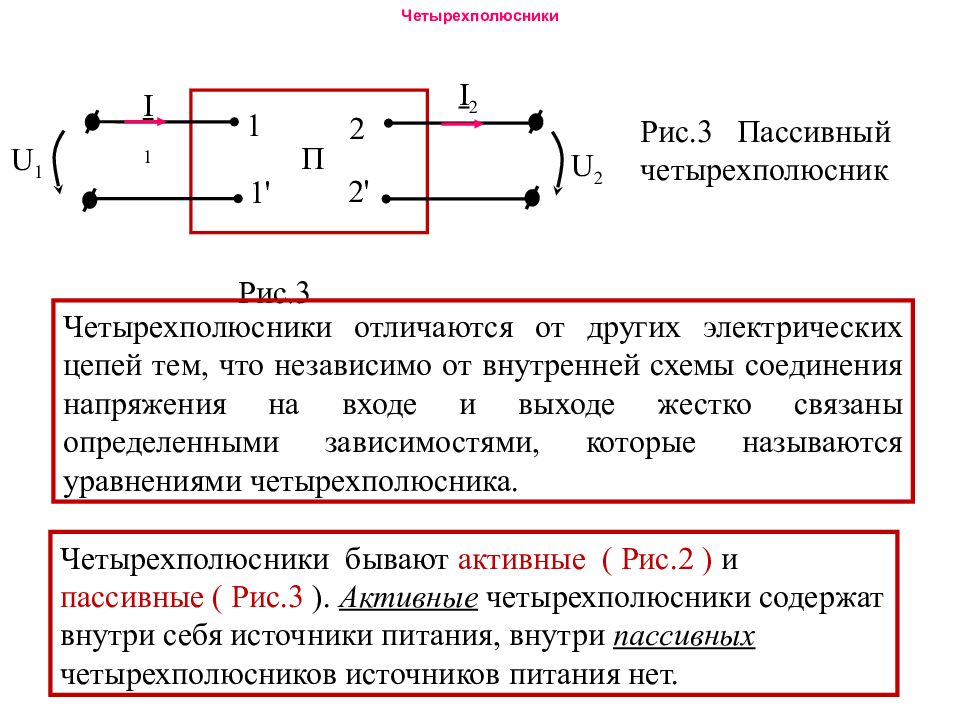
1 1 ' U 1 2 2 ' I 1 I 2 U 2 П Рис. 3 Рис.3 Пассивный четырехполюсник Четырехполюсники отличаются от других электрических цепей тем, что независимо от внутренней схемы соединения напряжения на входе и выходе жестко связаны определенными зависимостями, которые называются уравнениями четырехполюсника. Четырехполюсники бывают активные ( Рис.2 ) и пассивные ( Рис.3 ). Активные четырехполюсники содержат внутри себя источники питания, внутри пассивных четырехполюсников источников питания нет.
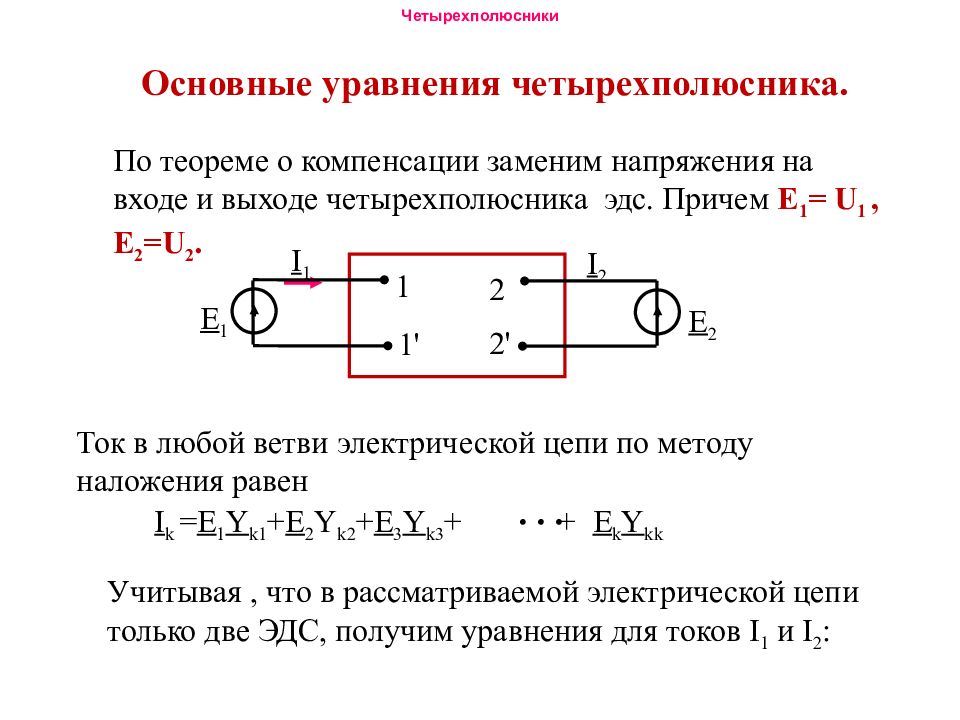
Основные уравнения четырехполюсника. По теореме о компенсации заменим напряжения на входе и выходе четырехполюсника эдс. Причем Е 1 = U 1, Е 2 = U 2. 1 1 ' 2 2 ' I 1 I 2 E 2 E 1 Ток в любой ветви электрической цепи по методу наложения равен I k = E 1 Y k1 + E 2 Y k2 + E 3 Y k3 + + Е k Y kk Учитывая, что в рассматриваемой электрической цепи только две ЭДС, получим уравнения для токов I 1 и I 2 :
I 1 = E 1 Y 11 – E 2 Y 12 I 2 = - E 2 Y 22 + E 1 Y 21 1. I 1 = U 1 Y 11 – U 2 Y 12 I 2 = - U 2 Y 22 + U 1 Y 21 2. Из второго уравнения системы (2) выразим напряжение U 1 А В 3. 4. Подставим в первое уравнение системы (2) уравнение (3) C D
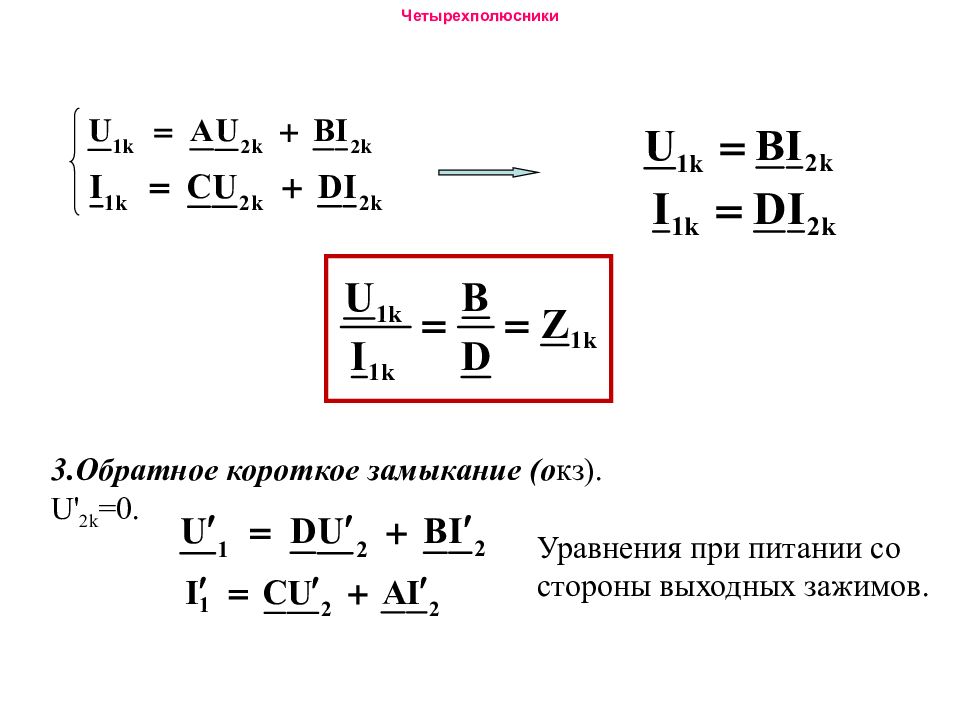
I 1 = С U 2 + D I 2 5. В результате получим систему уравнений (6),связывающих входные значения тока и напряжения с выходными. I 1 = С U 2 + D I 2 (6) Система (6) - основные уравнения четырехполюсника относительно входных зажимов. Коэффициенты четырехполюсника А, В, С, D могут быть действительными либо комплексными числами, а также некоторыми функциями связанными с параметрами четырехполюсника.
Коэффициенты четырехполюсника связаны между собой уравнением А D – B C = 1 Доказательство Полученное уравнение справедливо для любых линейных четырехполюсников
1 1 ' 2 2 ' I ' 1 U 1 ' U 2 ' Уравнения четырехполюсника при питании со стороны выходных зажимов. U 1 U ' 2 U 2 U ' 1 (6) I ' 2 I 1 - I ' 2 I 2 - I ' 1 D B C A X X X X 7. 8. Вычтем из (7) уравнение (8)
9. 10. 11. Вычтем из (10) уравнение (11) 12. 13. Система 13- основные уравнения четырехполюсника при питании со стороны выходных зажимов.
Таким образом, при питании со стороны выходных зажимов, структура уравнений остается той же, что и при питании со стороны входных зажимов, только меняются местами коэффициенты А и D. Если А = D, то входные и выходные зажимы связаны одними и теми же зависимостями, независимо с какой стороны питается четырехполюсник. Такие четырехполюсники называются симметричными и условием симметрии является A = D
Холостой ход и короткое замыкание четырехполюсника. Покажем, что любой рабочий режим четырехполюсника может быть получен наложением двух режимов: холостого хода и короткого замыкания. I. Холостой ход. ( Z H = ∞, I 2xx = 0) Опыт холостого хода проводим таким образом,чтобы U 2xx = U 2H 1 1 ' U 1 2 2 ' I 1 I 2H Z H U 2H 1. 2. а)
II. Короткое замыкание ( Z H =0, U 2xx =0) 3. 4. Опыт короткого замыкания проводим таким образом, чтобы I 2k =I 2H I 1 = С U 2H + D I 2 H (9) С учетом замечаний ( a,b ) уравнения 1,2,3,4 будут иметь вид (5,6,7,8) 5. 6. 7. 8. Сравнив уравнения 5-8 с уравнениями системы (9), получим b)
(10) Система уравнений 10 показывает, что любой режим работы четырехполюсника может быть определен наложением двух независимых режимов ( хх и кз ) при соблюдении условий (а, b). Вывод:
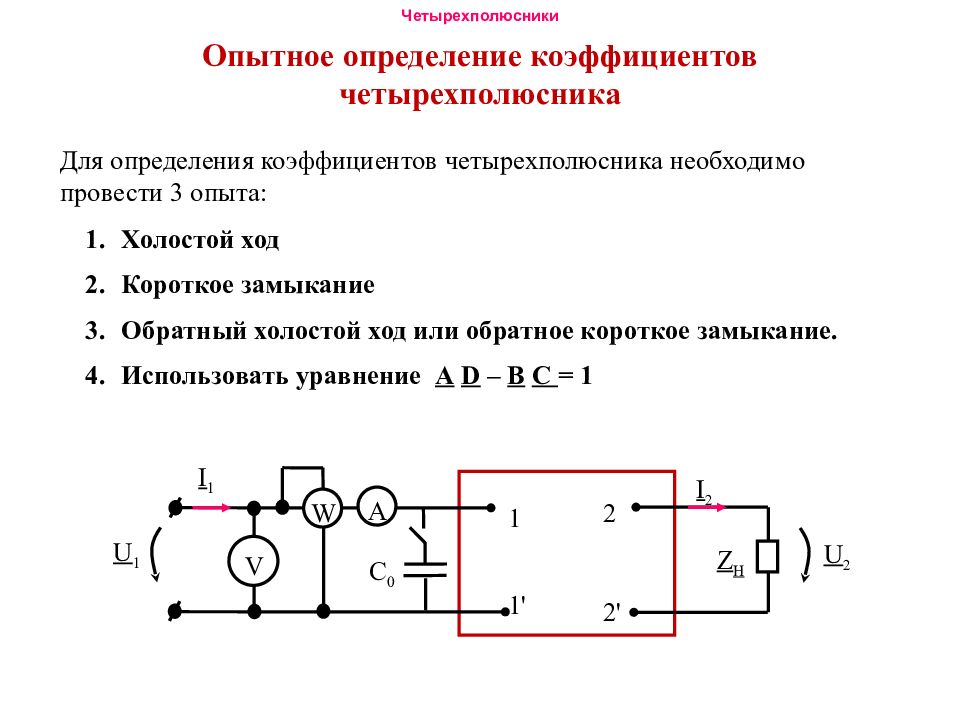
Для определения коэффициентов четырехполюсника необходимо провести 3 опыта: Холостой ход Короткое замыкание Обратный холостой ход или обратное короткое замыкание. Использовать уравнение А D – B C = 1 1 1 ' U 1 I 1 2 2 ' I 2 Z H V А W U 2 С 0
При проведении опытов измеряем I, U, P 1. Опыт холостого хода (ХХ). I 2x =0, Z H =∞ 2. Опыт короткого замыкания (кз). U 2k =0, Z H =0.
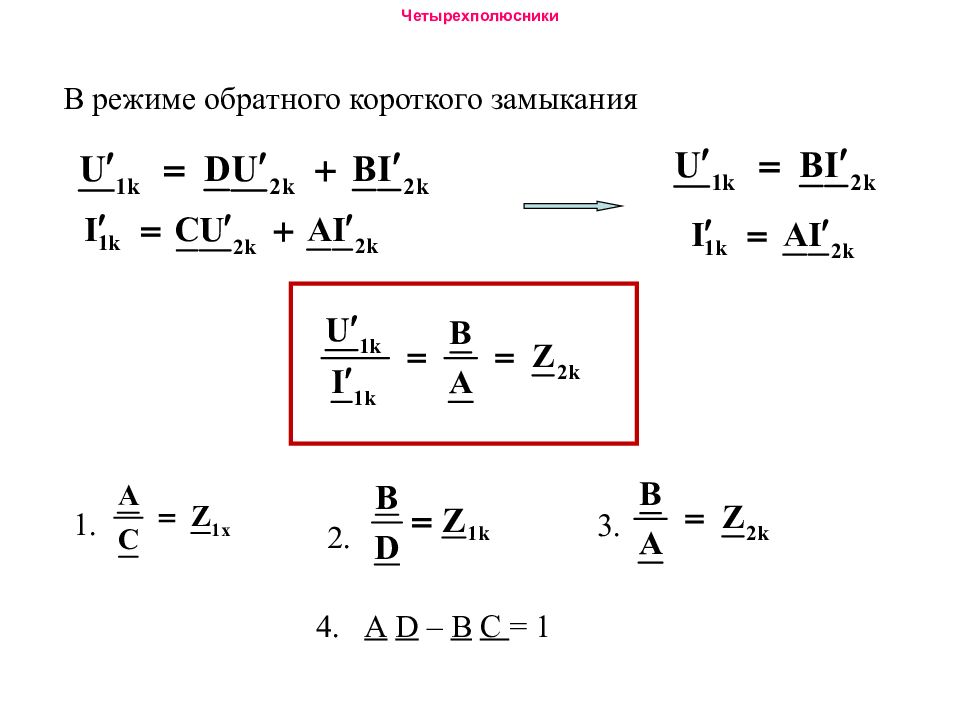
3. Обратное короткое замыкание (о кз). U' 2k =0. Уравнения при питании со стороны выходных зажимов.
В режиме обратного короткого замыкания 1. 2. 3. 4. А D – B C = 1
Решим совместно 1, 2, 3, 4. Подставим полученные выражения в (4) (5) (6)
Если четырехполюсник симметричный, то Z 1k = Z 2k и коэффициент А определяется по уравнению (6) Для определения характера нагрузки ( знака аргумента у входного сопротивления) служит емкость, подключаемая параллельно исследуемому четырехполюснику. Если при подключении емкости показание амперметра уменьшаются, то характер цепи индуктивный, если наоборот –емкостной. Эквивалентные схемы замещения четырехполюсника U 1 1 1 ' 2 2 ' I 1 I 2 U 2 Рис.1 Рис.2 Z 1T U 2 Z 2T Y 2T U 1 I 1 I 2 U 0 Z 2T
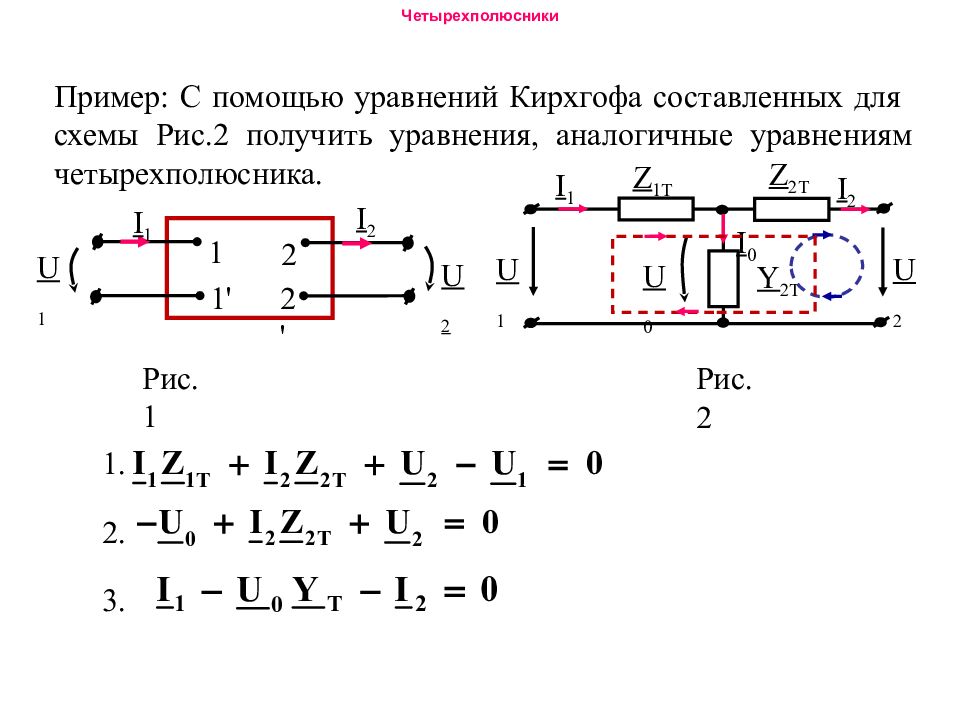
Пример: С помощью уравнений Кирхгофа составленных для схемы Рис.2 получить уравнения, аналогичные уравнениям четырехполюсника. U 1 1 1 ' 2 2 ' I 1 I 2 U 2 Z 1T Z 2T Y 2T I 1 I 2 U 1 U 2 I 0 U 0 Рис.1 Рис.2 1. 2. 3.
Выразим из (3) ток I 1 5. 6. 7. 8. Таким образом получили систему:
9. 10. I 1 = С U 2 + D I 2 (11) Сравнив уравнения 9 и 10 с системой (6) получим 12. 13. 14. 15.
Сопротивления Т-образной схемы замещения: Т-образная схема замещения может использоваться как для симметричных, так и для не симметричных четырехполюсников. Для схемы замещения симметричных четырехполюсников Z 1T =Z 2T. П-образная схема замещения может быть получена путем из Т-образной схемы замещения, если преобразовать звезду сопротивлений в треугольник.
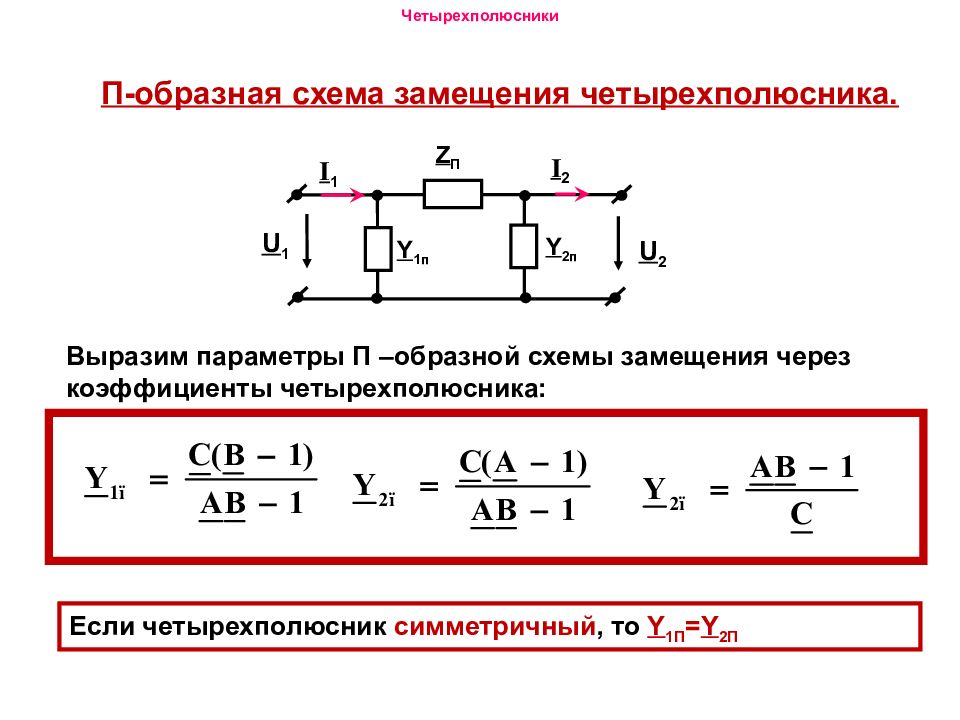
U 1 Z П Y 2 п I 1 I 2 U 2 Y 1 п П-образная схема замещения четырехполюсника. Выразим параметры П –образной схемы замещения через коэффициенты четырехполюсника: Если четырехполюсник симметричный, то Y 1 П = Y 2П
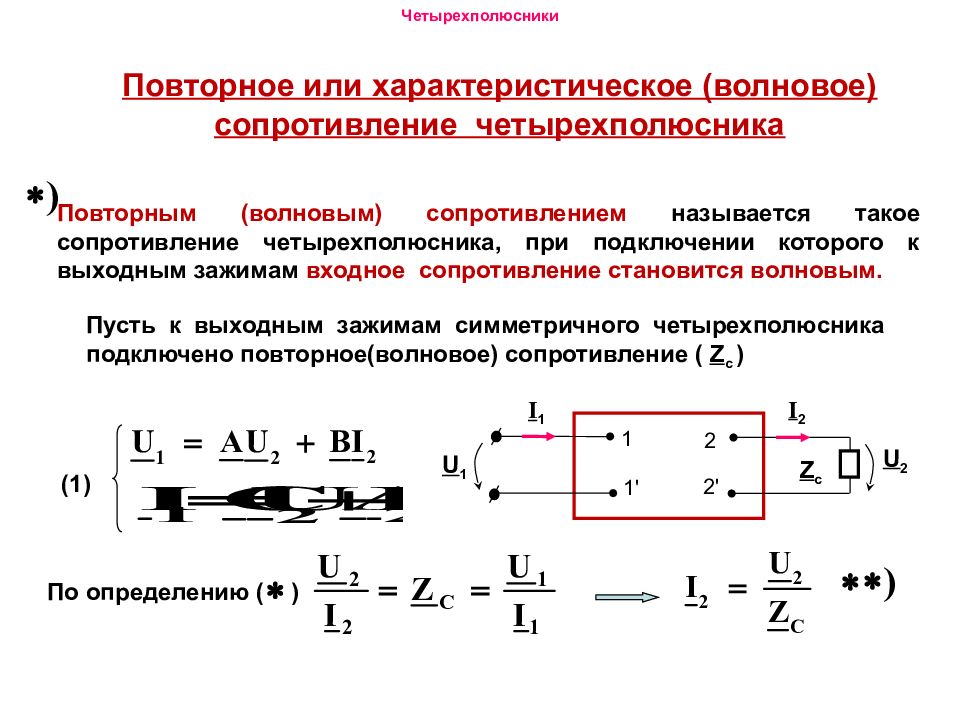
Повторное или характеристическое (волновое) сопротивление четырехполюсника Повторным (волновым) сопротивлением называется такое сопротивление четырехполюсника, при подключении которого к выходным зажимам входное сопротивление становится волновым. Пусть к выходным зажимам симметричного четырехполюсника подключено повторное(волновое) сопротивление ( Z c ) 1 1 ' U 1 2 2 ' I 1 I 2 Z c U 2 По определению ( ) (1)
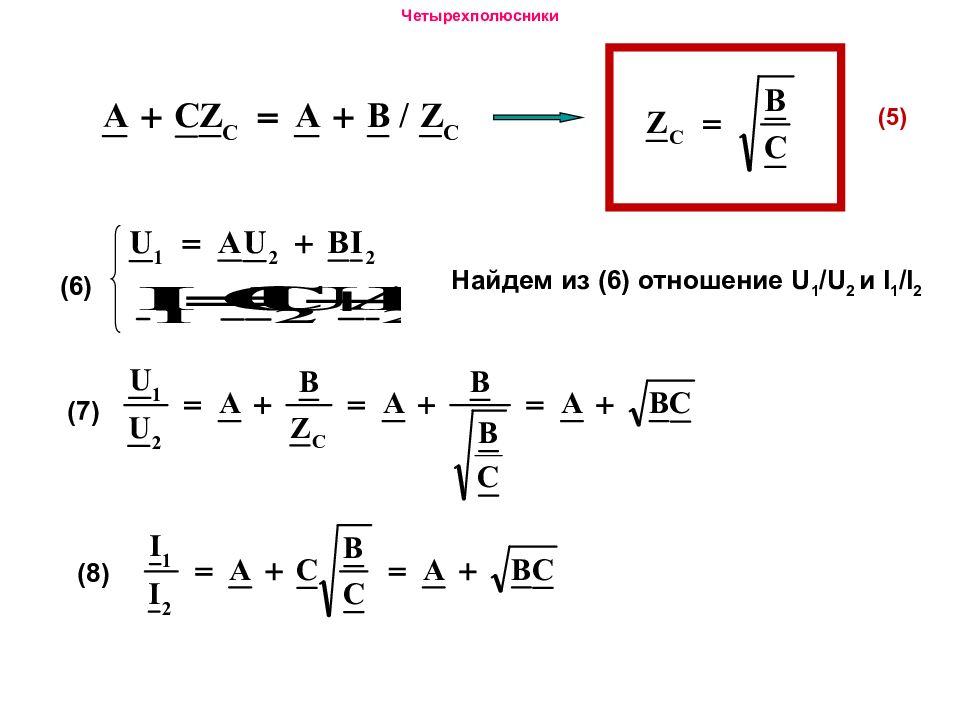
Определим величину волнового сопротивления. С учетом (1) и (2) (3) (4) Поделим (3) на (4)
(5) (6) Найдем из (6) отношение U 1 /U 2 и I 1 /I 2 (7) (8)
(9) (10) Отношение токов и напряжений на входе и выходе четырехполюсника одинаково и обозначается - коэффициент распространения, комплексное число - коэффициент затухания - коэффициент фазы Коэффициент затухания показывает во сколько раз изменились ток и напряжение на выходе по отношению к напряжению и току на входе четырехполюсника.
2003г. Переменный ток Коэффициент фазы показывает на сколько изменились фазы токов и напряжений при переходе от входных зажимов четырехполюсника к выходным, Уравнения четырехполюсника в гиперболических функциях Некоторые предварительные формулы гиперболический синус гиперболический косинус
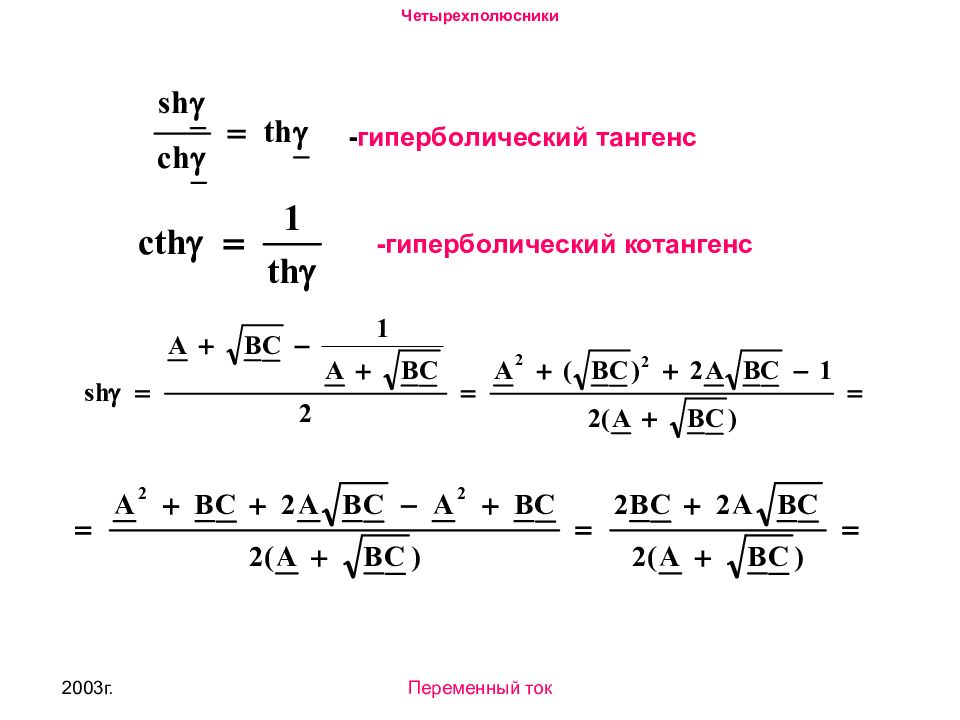
2003г. Переменный ток - гиперболический тангенс -гиперболический котангенс
2003г. Переменный ток Можно сделать вывод иначе
2003г. Переменный ток 11.
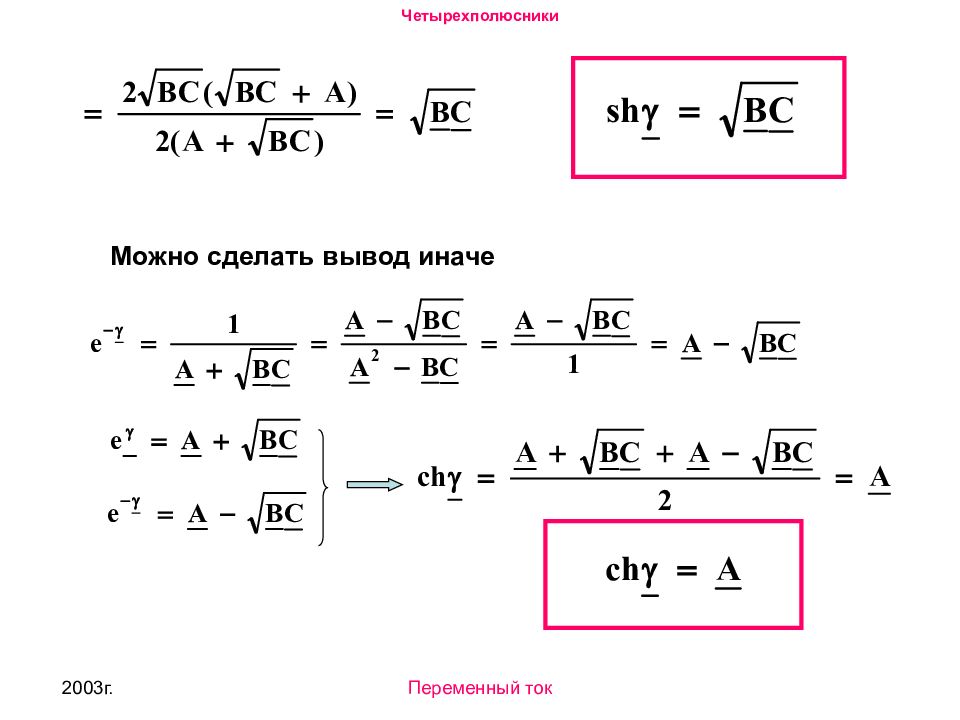
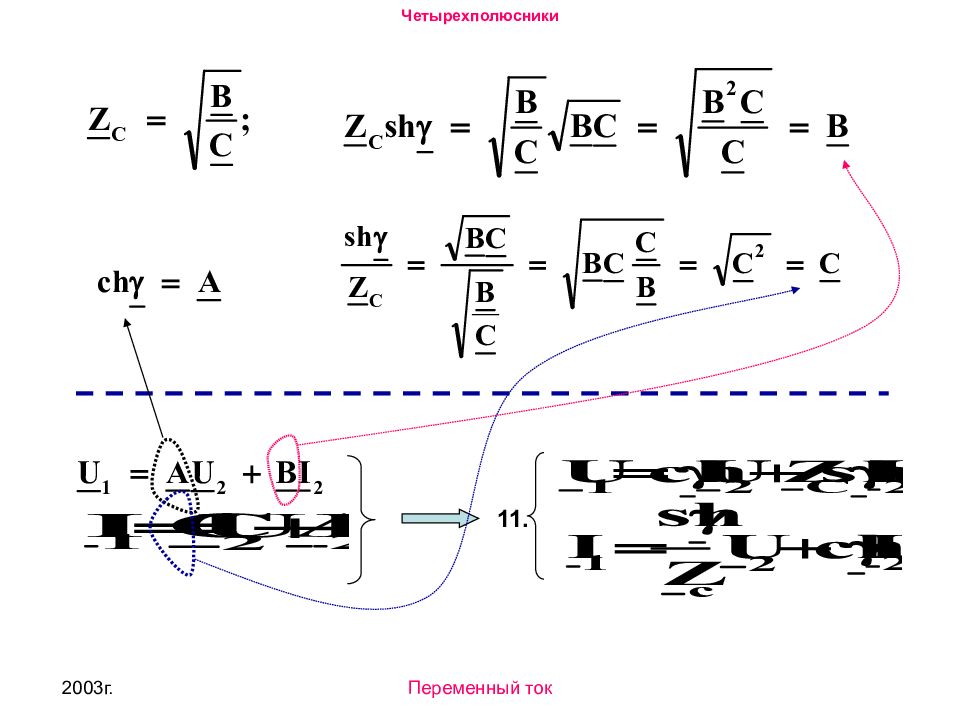
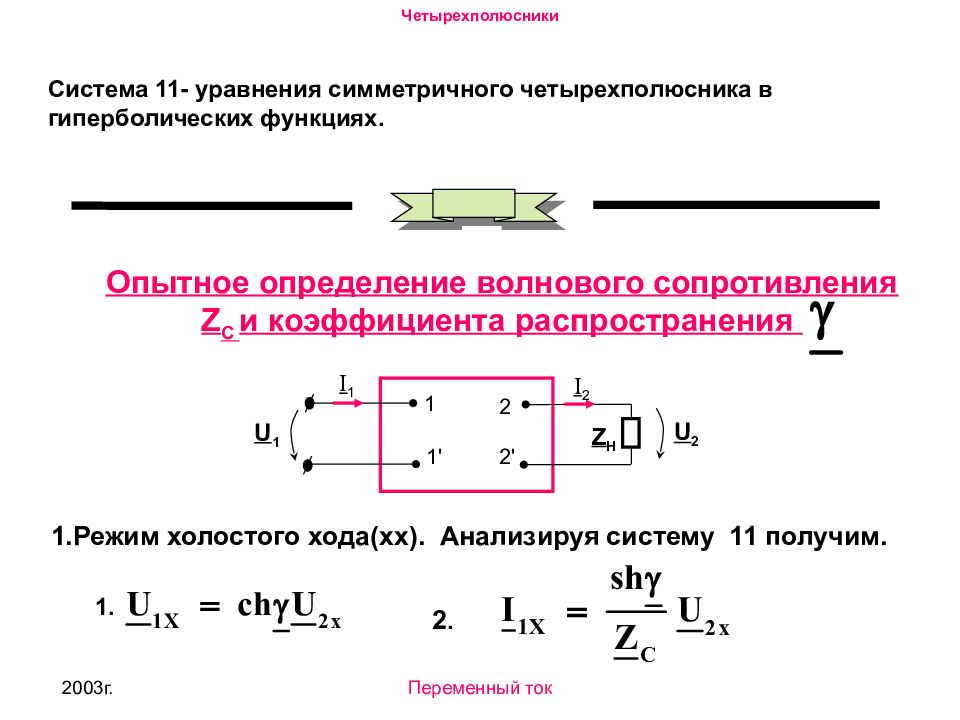
2003г. Переменный ток Система 11- уравнения симметричного четырехполюсника в гиперболических функциях. Опытное определение волнового сопротивления Z C и коэффициента распространения 1 1 ' U 1 2 2 ' I 1 I 2 Z H U 2 1. Режим холостого хода (xx). Анализируя систему 11 получим. 1. 2.
2003г. Переменный ток 3. 2.Режим короткого замыкания U 2 =0
