Численное дифференцирование Рассмотрим функцию y = f ( x ). По определению производной
Численное дифференцирование Рассмотрим функцию y = f ( x ). По определению производной Из определения предела получаем приближенное равенство
Численное дифференцирование Рассмотрим функцию y = f ( x ). По определению производной Из определения предела получаем приближенное равенство Рассмотрим функцию y=f(x), заданную на интервале [ a ; b ]. Разделим интервал [ a ; b ] на n равных частей. Занумеруем полученные точки x i начиная с нулевого номера a = x o < x 1 < … < x n = b. Длину каждого интервала будем называть шагом h =( b - a )/ n, а полученные точки {x i } и шаг h разбиением интервала [ a ; b ].
Численное дифференцирование Рассмотрим функцию y = f ( x ). По определению производной Из определения предела получаем приближенное равенство Рассмотрим функцию y=f(x), заданную на интервале [ a ; b ]. Разделим интервал [ a ; b ] на n равных частей. Занумеруем полученные точки x i начиная с нулевого номера a = x o < x 1 < … < x n = b. Длину каждого интервала будем называть шагом h =( b - a )/ n, а полученные точки {x i } и шаг h разбиением интервала [ a ; b ]. В каждой точке x i вычислим значение функции y i = f ( x i ). Полученную пару ( x i ; y i ) будем называть узлами функции.
По формуле приближенного значения производной (если возьмем x ; x = h ) имеем: или (1)
Однако если возьмем x = – h, тогда получим Или. (2)
Аналогично взяв x = 2 h, получим или (3)
Аналогично взяв x = 2 h, получим или (3) Полученные формулы (1) – (3) называются соответственно правой, левой и центральной разностными формулами численного дифференцирования для первой производной.
Рассмотрим функцию y=f( x ), заданную на интервале [0;1] и протабулированную с шагом 0,1. Найдем первую производную этой функции. Мы вывели для этого три различные формулы (1), (2) и (3). i x y 0 0 0 1 0,1 0,01 2 0,2 0,04 3 0,3 0,09 4 0,4 0,16 5 0,5 0,25 6 0,6 0,36 7 0,7 0,49 8 0,8 0,64 9 0,9 0,81 10 1 1
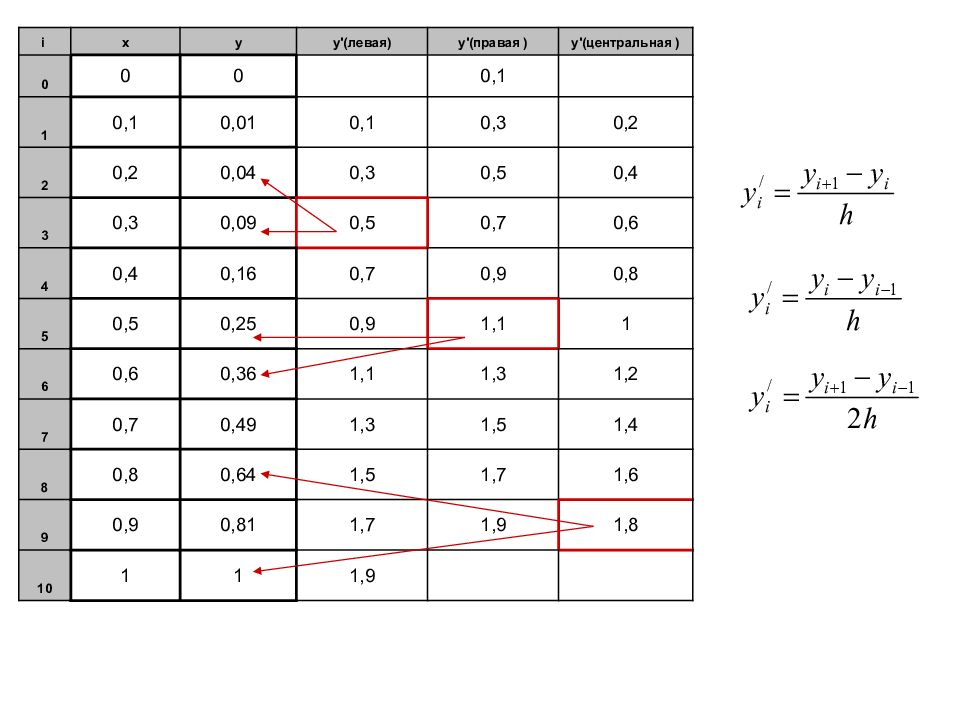
i x y y'( левая ) y'( правая ) y'( центральная ) 0 0 0 0,1 1 0,1 0,01 0,1 0,3 0,2 2 0,2 0,04 0,3 0,5 0,4 3 0,3 0,09 0,5 0,7 0,6 4 0,4 0,16 0,7 0,9 0,8 5 0,5 0,25 0,9 1,1 1 6 0,6 0,36 1,1 1,3 1,2 7 0,7 0,49 1,3 1,5 1,4 8 0,8 0,64 1,5 1,7 1,6 9 0,9 0,81 1,7 1,9 1,8 10 1 1 1,9
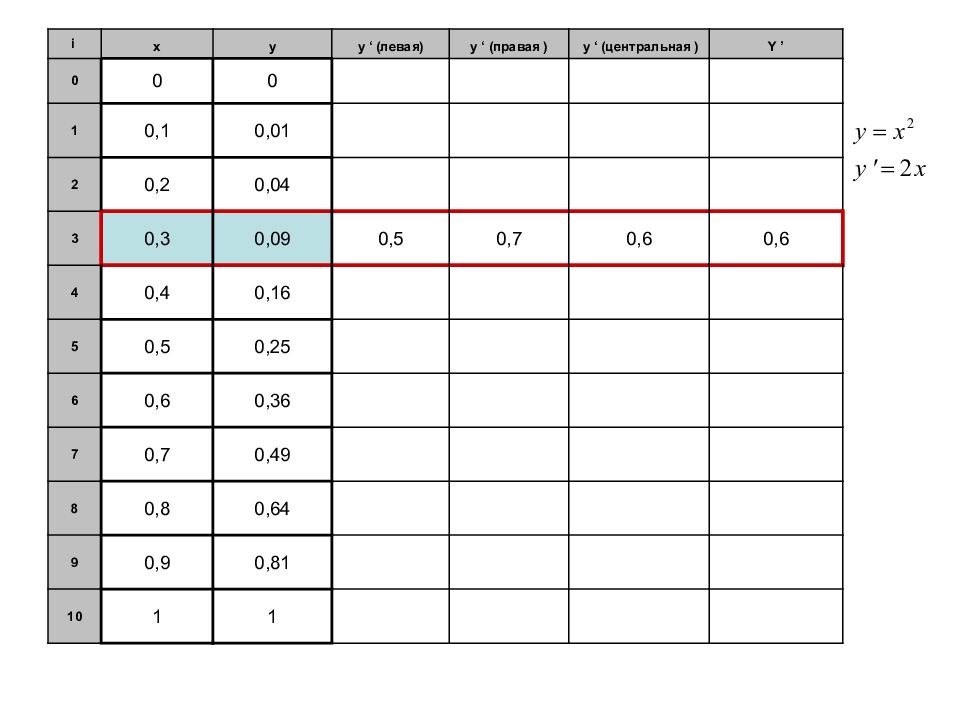
i x y y ‘ ( левая ) y ‘ ( правая ) y ‘ ( центральная ) Y ’ 0 0 0 1 0,1 0,01 2 0,2 0,04 3 0,3 0,09 0,5 0,7 0,6 0,6 4 0,4 0,16 5 0,5 0,25 6 0,6 0,36 7 0,7 0,49 8 0,8 0,64 9 0,9 0,81 10 1 1
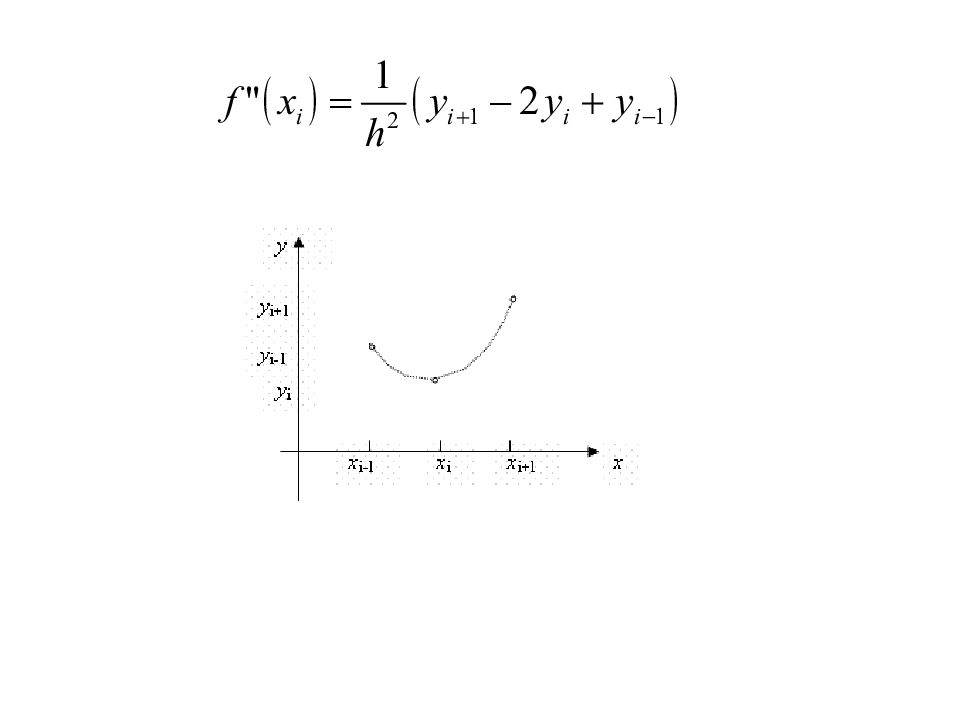
Аналогично определяются разностные формулы и для старших производных. Или
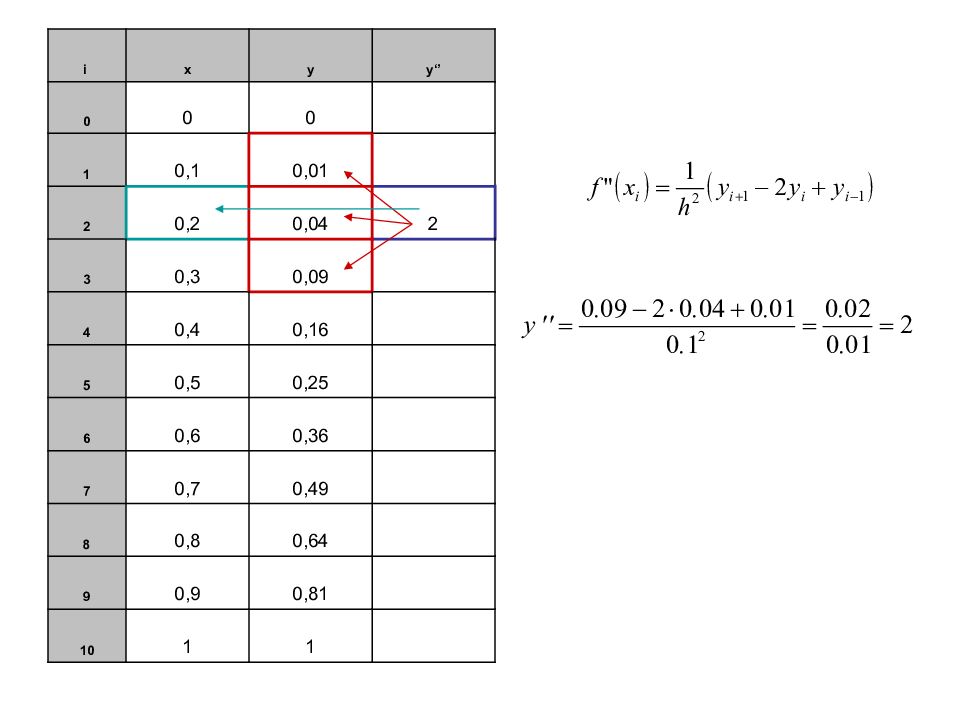
i x y y‘’ 0 0 0 1 0,1 0,01 2 0,2 0,04 2 3 0,3 0,09 4 0,4 0,16 5 0,5 0,25 6 0,6 0,36 7 0,7 0,49 8 0,8 0,64 9 0,9 0,81 10 1 1
Неравномерная сетка Рассмотрим функцию y = f ( x ), заданную узлами M i =( x i ; y i ) Будем говорить, что функция задана неравномерной сеткой, если h i = x i +1 – x i =/= h j = x j +1 – x j h i -1 h i Y i-1 Y i+1 Y i
Неравномерная сетка Рассмотрим функцию y = f ( x ), заданную узлами M i =( x i ; y i ) Будем говорить, что функция задана неравномерной сеткой, если h i = x i +1 – x i =/= h j = x j +1 – x j Тогда - правая производная, где h i = x i +1 – x i левая производная, где h i -1 = x i – x i -1 центральная производная, где h i + h i -1 = x i +1 – x i -1 h i -1 h i Y i-1 Y i+1 Y i
Неравномерная сетка Рассмотрим функцию y = f ( x ), заданную узлами M i =( x i ; y i ) Будем говорить, что функция задана неравномерной сеткой, если h i = x i +1 – x i =/= h j = x j +1 – x j Тогда - правая производная, где h i-1 = x i +1 – x i h i -1 h i-1 X i-1 X i+1 X i
Неравномерная сетка Рассмотрим функцию y = f ( x ), заданную узлами M i =( x i ; y i ) Будем говорить, что функция задана неравномерной сеткой, если h i = x i +1 – x i =/= h j = x j +1 – x j Тогда - правая производная, где h i-1 = x i +1 – x i левая производная, где h i -1 = x i – x i -1 h i -1 h i-1 X i-1 X i+1 X i
Неравномерная сетка Рассмотрим функцию y = f ( x ), заданную узлами M i =( x i ; y i ) Будем говорить, что функция задана неравномерной сеткой, если h i = x i +1 – x i =/= h j = x j +1 – x j Тогда - правая производная, где h i-1 = x i +1 – x i левая производная, где h i -1 = x i – x i -1 центральная производная, где h i + h i -1 = x i +1 – x i -1 h i -1 h i+1 X i-1 X i+1 X i
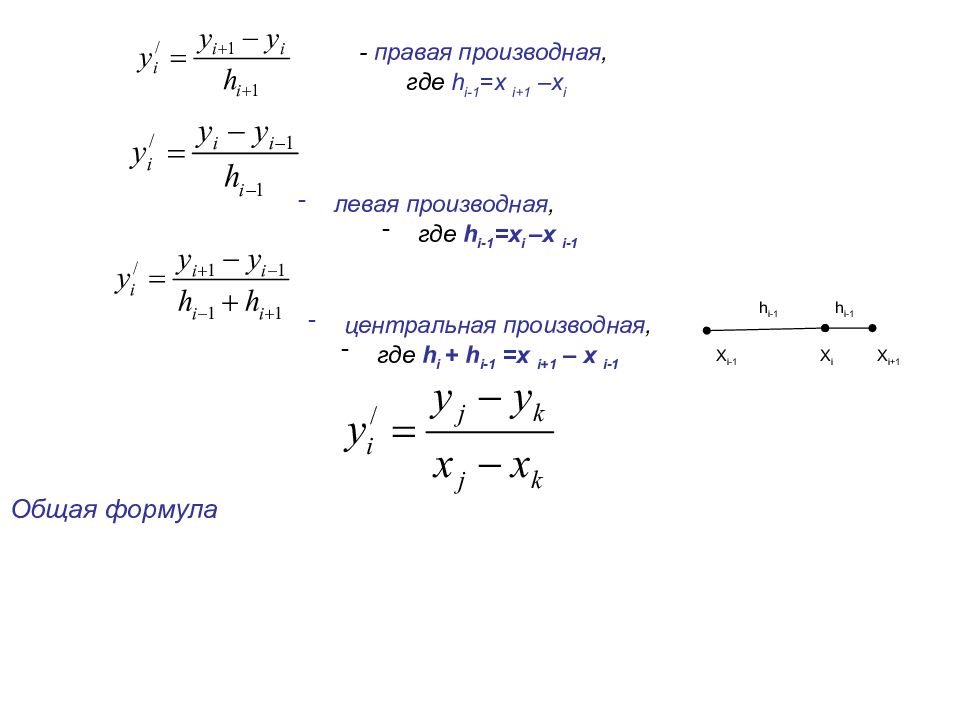
- правая производная, где h i-1 = x i +1 – x i левая производная, где h i -1 = x i – x i -1 центральная производная, где h i + h i -1 = x i +1 – x i -1 Общая формула h i -1 h i-1 X i-1 X i+1 X i
Вторая производная задается формулой
Пример. Рассмотрим функцию, заданную таблицей Найти Y / ( 0.2 ) и Y // ( 0.2 ) - Правая x 0 0.2 0.5 y 0 0.04 0.25
Пример. Рассмотрим функцию, заданную таблицей Найти Y / ( 0.2 ) и Y // ( 0.2 ) - Правая Y // ( 0.2 )=( 0.2 *0.25 - ( 0.2+0.3 )* 0.04 + 0.3 *0) /( 0.3 * 0. 2 *0.2 ) = 1.67 Погрешность вычисленного значения производной зависит от шага h. h 0.2 0.3 x 0 0.2 0.5 y 0 0.04 0.25 x 0 0.2 0.5 y 0 0.04 0.25
