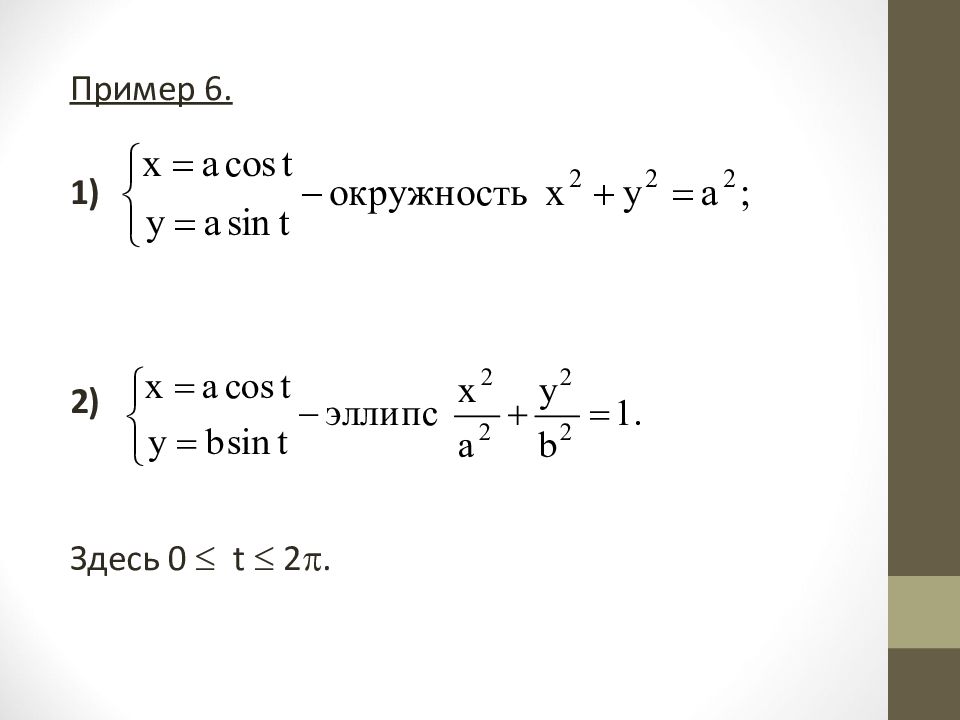Логарифмическое дифференцирование. Дифференцирование функций, заданных неявно. Дифференцирование функций, заданных параметрически. Производные высших порядков.
Пусть у = lnu, где u = φ ( х ) - дифференцируемая функция. Применяя правило дифференцирования сложной функции, получим
Таким образом, имеем или ( 1) Производная называется логарифмической производной функции u = φ ( х ).
О.1.1. Операция, состоящая в последовательном применении к функции сначала логарифмирования (по основанию е), а затем дифференцирования, называется логарифмическим дифференцированием, а ее результат - логарифмической производной данной функции. О.1.2. Степенно-показательной функцией ( показательно-степенной или сложной показательной ) называется функция вида у = u v, где u = u(х) и v = v(х) - заданные дифференцируемые функции от х.
Найдем производную данной функции логарифмическим дифференцированием: lny = vlnu. Отсюда по формуле (1) получим откуда
Подставив у = u v, получим или Замечание Производная степенно-показательной функции состоит из двух слагаемых. Первое слагаемое получается, если функцию дифференцировать как степенную функцию, считая v = const, а u - переменной; а второе слагаемое – если функцию дифференцировать как показательную функцию, считая u = const, а v - переменной от x.
Логарифмическое дифференцирование может быть применено для отыскания производных не только степенно-показательных функций, но и таких, непосредственное дифференцирование которых громоздко (произведение большого числа сомножителей, радикалы, дроби и т.д.).
Пример 1. Найти у′, если Решение Прологарифмируем данную функцию: Отсюда Если воспользоваться выражением (1), то получится такой же результат.
Пример 2. Найти у′, если Решение Прологарифмируем данную функцию: Умножая на у и подставляя его значение, получим:
2.1. Неявное задание функции О.2.1. Если функция задана уравнением у = f(х), разрешенным относительно у, то говорят, что функция задана в явном виде (явная функция). О.2.2.Под неявным заданием функции понимают задание функции у в виде уравнения F( x,y ) = 0, (2) не разрешенного относительно у.
Всякую явно заданную функцию у = f(х) можно записать как неявно заданную уравнением у ‒ f(х) = 0, но не наоборот. Чтобы выразить функцию у из уравнения (2), необходимо разрешить данное уравнение относительно у. В общем случае, при заданном х, уравнение (2) может иметь несколько корней у, т.е. неявная функция может быть многозначной.
Пример 3. х 2 + у 2 = 1 - неявная функция Не всегда легко, а иногда и невозможно, разрешить уравнение (2) относительно у. Пример 4. у + 2 у х = 0 - нельзя явно выразить у через х.
Пусть неявная функция у задана уравнением (2) F( x,y ) = 0, не разрешенным относительно у. Правило дифференцирования неявной функции Для того чтобы найти производную неявной функции, заданной уравнением (2), нужно продифференцировать уравнение (2), помня, что у является функцией от х и его производная равна у′. Затем разрешить полученное уравнение относительно у′. Производная неявной функции выражается через аргумент х и функцию у, т.е. сама является функцией неявной.
Пример 5. Найти производную функции у, заданной уравнением х 3 + у 3 ‒ 3ху = 0. Решение Дифференцируем данное уравнение по х, помня, что у есть функция от х, т.е. у = f(х). В результате получим: Откуда
3.1. Параметрическое задание функции О.3.1. Параметрическим заданием функции у = f(х) называется определение данной функции в виде системы двух уравнений относительно новой промежуточной переменной t, называемой параметром: (3) Выражение непосредственной зависимости у от х ( у = f(х)) может быть получено путем исключения параметра t из уравнений (3).
Пример 6. 1 ) 2 ) Здесь 0 t 2 .
Пусть зависимость между аргументом х и функцией у задана параметрически в виде системы двух уравнений (3), где t - параметр. Т.3.1. (дифференцирование функции, заданной параметрически) Если функция у от аргумента х задана параметрически системой (3), где функции х(t) и у(t) дифференцируемы, причем х′(t) 0, то производная этой функции выражается формулой или
Пример 7. Пусть. Найти у′ х. Решение
Производная у′ = f′(х) функции у = f(х) есть так же функция от х и называется производной первого порядка или первой производной. Возможно, что эта функция сама имеет производную. О.4.1. Производная от первой производной функции у = f(х) называется производной второго порядка или второй производной данной функции и обозначается одним из символов
Таким образом О.4.2. Производная от второй производной функции у = f(х) называется производной третьего порядка или третьей производной данной функции и обозначается одним из символов Таким образом
Производные, начиная со второй, называются производными высших порядков. О.4.3. Производная от (n‒1)-й производной функции у = f(х) называется производной n- го порядка или n-й производной данной функции и обозначается одним из символов Таким образом
Начиная с производной 4-го порядка, производные обозначают римскими цифрами или числами в скобках. Пример 8. у V или у (5) - производная 5-го порядка. Для некоторых элементарных функций можно вывести формулы нахождения производных любого порядка.
Пример 9. Найти производную n- го порядка функции у = а х. Решение
Механический ( физический) смысл второй производной Пусть материальная точка движется прямолинейно по закону S = S(t). Известно, что ʋ = S′(t) - скорость точки в данный момент времени t. Можно показать, что вторая производная от пути по времени есть величина ускорения прямолинейного движения точки, т.е.
Пусть неявная функция у задана уравнением (2), т.е. F( x,y ) = 0. Продифференцировав уравнение (2) по х и разрешив полученное уравнение относительно у′, найдем первую производную. Продифференцировав по х первую производную, получим вторую производную у″ от неявной функции. В нее войдут х, у и у′. Подставляя уже найденное значение у′ в выражение второй производной, выразим у″ через х и у. Аналогично поступаем для нахождения третьей производной и т.д.
Пример 10. Найти у‴, если х 2 + у 2 = 1. Решение F( x,y ) = 0 х 2 + у 2 ‒ 1= 0.
Пусть функция у = f(х) задана параметрически в виде системы уравнений (3): Первая производная у′ х находится по формуле (4)
Найдем вторую производную от функции, заданной параметрически. Из определения второй производной и равенства (4) следует, что Таким образом, Аналогично получаются формулы:
Пример 11. Найти вторую производную функции Решение
