Числовая последовательность 25.11.2013 1 Р. Мунипов
Определение 1. Если каждому значению из натурального ряда чисел ставится в соответствие по определенному закону некоторое вещественное число, то множество занумерованных вещественных чисел называется числовой последовательностью или просто последовательностью. Последовательность обозначается символом, при этом называют членом или элементом этой последовательности, — номером члена. Числовая последовательность — это функция, область определения которой есть множество всех натуральных чисел; множество значений этой функции, т. е. совокупность чисел, называют множеством значений последовательности. 25.11.2013 2 Р. Мунипов
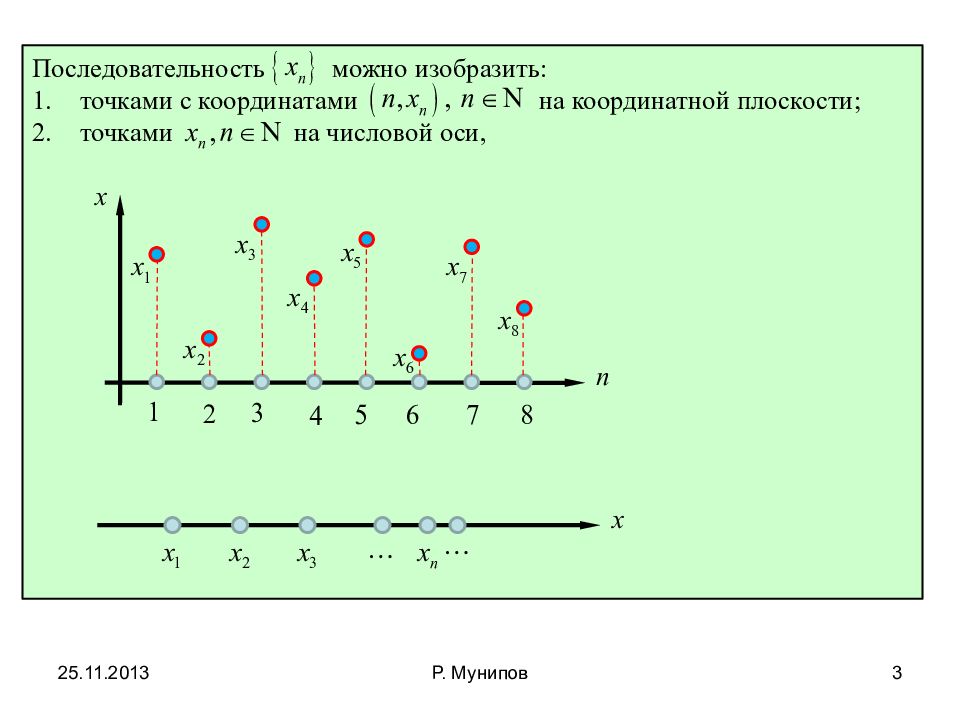
Последовательность можно изобразить: точками с координатами на координатной плоскости; точками на числовой оси, 25.11.2013 3 Р. Мунипов
Множество значений последовательности может быть как конечным, так и бесконечным, в то время как множество ее элементов всегда является бесконечным: любые два разных элемента последовательности отличаются своими номерами. множество значений состоит лишь из двух чисел 1 и (-1) множество значений бесконечно большое 25.11.2013 4 Р. Мунипов
Последовательность может быть задана с помощью формулы, позволяющей вычислить каждый член последовательности по его номеру. Например, то каждый нечётный член последовательности равен 0, а каждый чётный член равен 1. Иногда последовательность задается рекуррентной формулой, позволяющей находить члены последовательности по известным предыдущим. При таком способе задания последовательности обычно указывают: первый член последовательности (или несколько членов); формулу, связывающую - й член с соседними (например, с -м и -м членами). 25.11.2013 5 Р. Мунипов
Арифметическая прогрессия с разностью задаются рекуррентными формулами или Например, Геометрическая прогрессия со знаменателем задаются рекуррентными формулами или Например, Последовательность Фибоначчи задаётся рекуррентной формулой 25.11.2013 6 Р. Мунипов
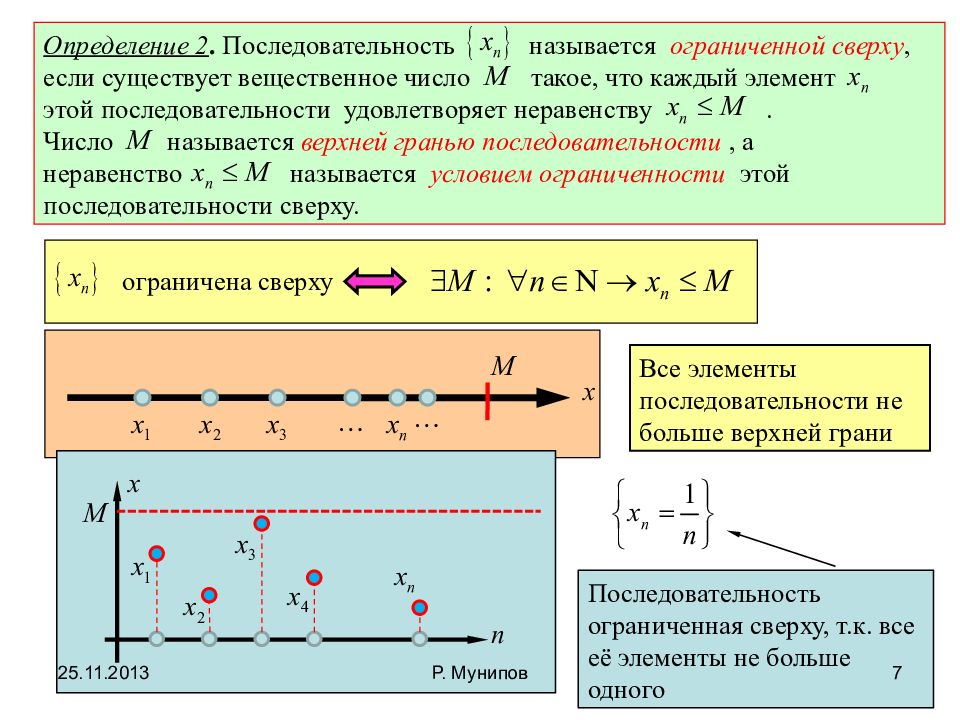
Определение 2. Последовательность называется ограниченной сверху, если существует вещественное число такое, что каждый элемент этой последовательности удовлетворяет неравенству. Число называется верхней гранью последовательности, а неравенство называется условием ограниченности этой последовательности сверху. ограничена сверху Все элементы последовательности не больше верхней грани Последовательность ограниченная сверху, т.к. все её элементы не больше одного 25.11.2013 7 Р. Мунипов
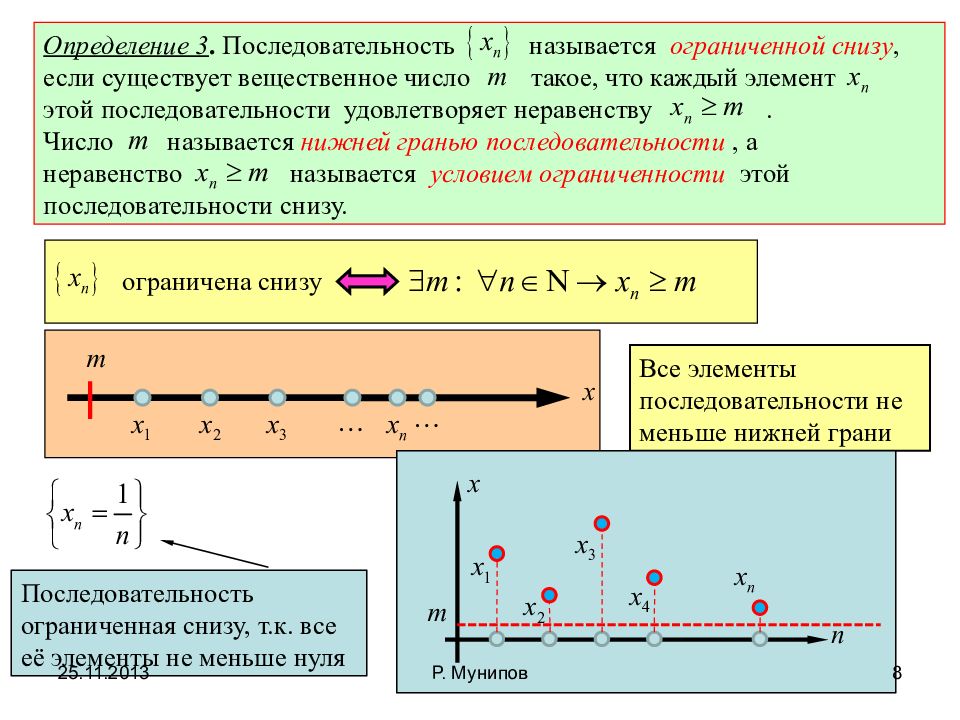
Определение 3. Последовательность называется ограниченной снизу, если существует вещественное число такое, что каждый элемент этой последовательности удовлетворяет неравенству. Число называется нижней гранью последовательности, а неравенство называется условием ограниченности этой последовательности снизу. ограничена снизу Все элементы последовательности не меньше нижней грани Последовательность ограниченная снизу, т.к. все её элементы не меньше нуля 25.11.2013 8 Р. Мунипов
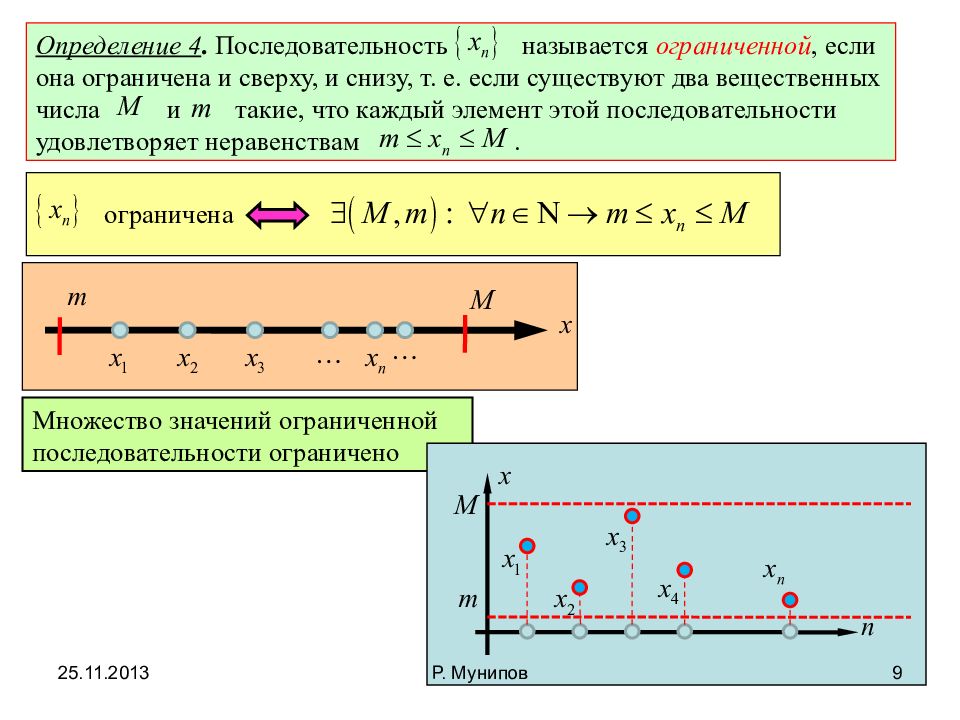
Определение 4. Последовательность называется ограниченной, если она ограничена и сверху, и снизу, т. е. если существуют два вещественных числа и такие, что каждый элемент этой последовательности удовлетворяет неравенствам. ограничена Множество значений ограниченной последовательности ограничено 25.11.2013 9 Р. Мунипов
Необходимое и достаточное условие ограниченности последовательности. Последовательность является ограниченной тогда и только тогда, когда существует положительное вещественное число такое, что каждый элемент последовательности удовлетворяет неравенству ограничена Необходимость : последовательность ограниченная то, найдётся положительное число, что все элементы последовательности по модулю не больше этого числа, Достаточность : все элементы последовательности удовлетворяют неравенству, тогда она ограничена, Геометрически ограниченность последовательности означает, что все члены последовательности содержатся в -окрестности точки ноль. 25.11.2013 10 Р. Мунипов
Определение 5. Последовательность называется неограниченной если для любого положительного вещественное числа найдется хотя бы один элемент последовательности, удовлетворяющий неравенству неограниченная последовательность ограниченная лишь снизу последовательность ограниченная, 25.11.2013 11 Р. Мунипов
Определение 6. Последовательность называется бесконечно большой, если для любого положительного вещественного числа найдется номер, начиная с которого, элементы этой последовательности удовлетворяют неравенству. бесконечно большая бесконечно большая последовательность, Всякая бесконечно большая последовательность будет неограниченной, поскольку, по определению бесконечно большой последовательности, всякому все элементы последовательности удовлетворяют неравенству, а определение неограниченной последовательности требует, чтобы любому удовлетворял хотя бы один элемент последовательности. Вместе с тем не всякая неограниченная последовательность, будет бесконечно большой. неограниченная последовательность, но не является бесконечно большой 25.11.2013 12 Р. Мунипов
Определение 7. Последовательность называется бесконечно малой, если для любого положительного вещественного числа найдется номер, начиная с которого, элементы этой последовательности удовлетворяют неравенству. бесконечно малая Последовательность бесконечно малая, значит для любого сколь угодно малого положительного числа, найдется номер, начиная с которого, все элементы последовательности по модулю будут меньше этого числа Из определяющего неравенства бесконечно малой последовательности следует все элементы последовательности начиная с некоторого номера, будут находится в некоторой –окрестности числа ноль для любого сколь угодно малого положительного числа, найдется номер, начиная с которого, все элементы последовательности по модулю будут меньше этого числа 25.11.2013 13 Р. Мунипов
14 Р. Мунипов 25.11.2013 Замечание. Последовательность будет бесконечно малой если, и бесконечно большой если. есть бесконечно малая есть бесконечно большая Рассмотрим случай. Положим, или. Используя неравенство Бернулли получим, или. Пусть, выберем номер так чтобы, или. Номер определим равенством для которого также справедливо. В силу для всех справедливо. Получили, что для любого найдётся номер такой, что при всех выполняется неравенство. Это доказывает, что при последовательность будет бесконечно малой.
Рассмотрим случай. Положим, или. Используя неравенство Бернулли получим. Пусть, выберем номер так чтобы, или. Номер определим равенством, для которого также справедливо. В силу для всех справедливо. Получили, что для любого найдётся номер такой, что при всех выполняется неравенство. Это доказывает, что при последовательность будет бесконечно большой. Выражение называется функция антье, или целая часть числа Неравенство Бернулли, 25.11.2013 15 Р. Мунипов
Пример бесконечно малая последовательность бесконечно малая последовательность бесконечно большая последовательность 25.11.2013 16 Р. Мунипов
Теорема. Сумма двух бесконечно малых последовательностей и будет бесконечно малой последовательностью. Доказательство бесконечно малая: бесконечно малая: Пусть Рассмотрим Значит есть бесконечно малая последовательность 25.11.2013 17 Р. Мунипов
Теорема. Разность двух бесконечно малых последовательностей и будет бесконечно малой последовательностью. Доказательство бесконечно малая: бесконечно малая: Пусть Рассмотрим Значит есть бесконечно малая последовательность 25.11.2013 18 Р. Мунипов Замечание. Алгебраическая сумма конечного числа бесконечно малых последовательностей будет бесконечно малой последовательностью
Теорема. Произведение ограниченной последовательности на бесконечно малую последовательность будет бесконечно малой последовательностью. Доказательство ограниченная: бесконечно малая: Замечание. Если бесконечно малую последовательность умножить на число, то получим бесконечно малую последовательность Пусть Рассмотрим произведение Значит произведение ограниченной и бесконечно малой последовательностей есть бесконечно малая последовательность 25.11.2013 19 Р. Мунипов
Теорема. Всякая бесконечно малая последовательность есть ограниченная последовательность. Замечание. Произведение конечного числа бесконечно малых последовательностей будет бесконечно малой последовательностью Доказательство Пусть последовательность бесконечно малая, по определению Пусть число такое, что, тогда очевидно для всех членов последовательности справедливо. Значит бесконечно малая последовательность ограничена. ограниченная: 25.11.2013 20 Р. Мунипов
Теорема. Если есть бесконечно большая последовательность, то начиная с некоторого номера определена последовательность которая будет бесконечно малой. Доказательство Поскольку последовательность бесконечно большая, по крайней мере начиная с некоторого номера её элементы будут отличны от нуля и значит определена последовательность. Покажем, что она будет бесконечно малой последовательностью. Пусть, тогда, по определению бесконечно большой последовательности найдётся номер, начиная с которого для всех элементов справедливо неравенство, или, что то же самое,. Это значит последовательность будет бесконечно малой последовательностью. 25.11.2013 21 Р. Мунипов
Теорема. Если все элементы бесконечно малой последовательности отличны от нуля, то последовательность будет бесконечно большой. Доказательство Поскольку последовательность бесконечно малая, элементы которой отличны от нуля и значит определена последовательность. Покажем, что она будет бесконечно большой последовательностью. Пусть, тогда, по определению бесконечно малой последовательности найдётся номер, начиная с которого для всех элементов справедливо неравенство, или, что то же самое,. Это значит последовательность будет бесконечно большой последовательностью. Последовательность бесконечно большая, тогда последовательность будет бесконечно малой 25.11.2013 22 Р. Мунипов Последовательность бесконечно малая, тогда последовательность будет бесконечно большой
Определение 9. Последовательность называется сходящейся, если существует число, что для любого положительного вещественного числа найдется номер, начиная с которого, элементы этой последовательности удовлетворяют неравенству. сходящаяся Замечание. Из определения предела последовательности следует, что последовательность сходится к числу, тогда и только тогда, когда разность есть бесконечно малая последовательность, значит: а) разность сходящейся последовательности с её предельным значением есть бесконечно малая последовательность, б) сходящуюся последовательность можно представить как сумму её предельного значения и бесконечно малой последовательности 25.11.2013 23 Р. Мунипов
Замечание. Предел бесконечно малой последовательности равен нулю: бесконечно малая Замечание. Из определения предела последовательности следует, что последовательность сходится к числу, тогда и только тогда, когда последовательность имеет предел равный нулю: Замечание. Из определения предела последовательности следует, что удаление конечного числа ее членов не изменяет ее сходимости, 25.11.2013 24 Р. Мунипов
Замечание. Из определения предела последовательности следует, т.е. последовательность сходится к числу тогда и только тогда, когда для любого наперед заданного положительного числа найдется номер, начиная с которого все элементы последовательности будут находится в окрестности точки Число — предел последовательности, если для всякой окрестности точки найдется номер, начиная с которого все члены последовательности принадлежат этой окрестности, так что вне этой окрестности либо нет ни одного члена последовательности, либо содержится лишь конечное число членов. -окрестность точки 25.11.2013 25 Р. Мунипов
Пусть имеется утверждение { число есть предел последовательности } тогда отрицание этого, т.е. число не является пределом последовательности будет иметь вид Пусть имеется утверждение { последовательность сходящаяся } тогда отрицание этого, т.е. последовательность не является сходящейся, будет иметь вид 25.11.2013 26 Р. Мунипов Замечание. Последовательность, не являющуюся сходящейся, называют расходящейся ; т.е. последовательность называют расходящейся, если никакое число не является ее пределом.
Пример Покажем, что последовательность, где, имеет Действительно, справедливо, тогда. Пусть. Неравенство будет выполнятся, если или. Пусть номер такой, что, например,, где целая часть числа, т.е. наибольшее целое число, не превосходящее числа. Тогда для всех будет выполнятся неравенство. По определению предела это значит, т.е. 25.11.2013 27 Р. Мунипов
Пример Покажем, что последовательность, где, имеет Действительно, справедливо тогда. Пусть. Неравенство будет выполнятся, если справедливо, или. Пусть, тогда для всех выполняются неравенства. По определению предела это значит, т.е. 25.11.2013 28 Р. Мунипов
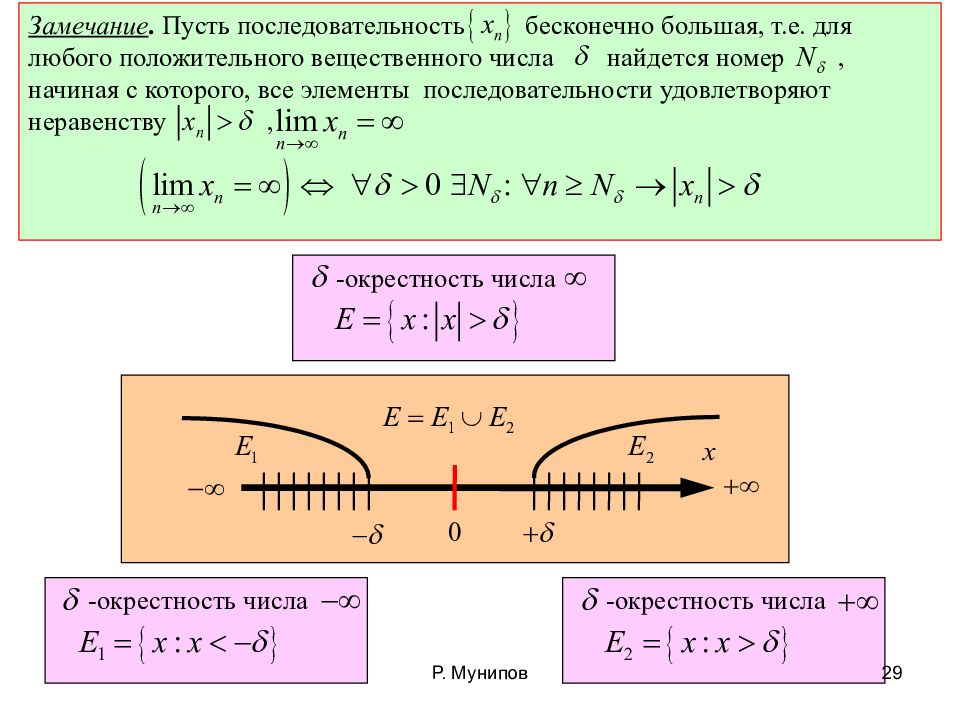
25.11.2013 Замечание. Пусть последовательность бесконечно большая, т.е. для любого положительного вещественного числа найдется номер, начиная с которого, все элементы последовательности удовлетворяют неравенству, -окрестность числа -окрестность числа -окрестность числа 29 Р. Мунипов
Замечание. Последовательность имеет предел минус бесконечность, т.е. в –окрестности числа содержатся все члены последовательности, быть может, за исключением конечного числа членов. Замечание. Последовательность имеет предел плюс бесконечность, т.е. в –окрестности числа содержатся все члены последовательности, быть может, за исключением конечного числа членов. 25.11.2013 30 Р. Мунипов
Теорема. Сходящаяся последовательность имеет один и только один предел. Доказательство. Справедливость теоремы докажем от противного. Предположим, что последовательность имеет два различных между собой предела Причём, не ограничивая общности можно предположить. Пусть и окрестности и не пересекались (не имели общих точек). Так как число — предел последовательности, то по заданному можно найти номер такой, что для всех. Поэтому вне интервала может оказаться лишь конечное число членов последовательности. Тогда, интервал может содержать лишь конечное число членов последовательности. Это противоречит тому, что — предел последовательности (любая окрестность точки должна содержать бесконечное число членов последовательности). Полученное противоречие показывает, что последовательность не может иметь два различных предела. 25.11.2013 31 Р. Мунипов
25.11.2013 Теорема. Если последовательность имеет предел, то она ограниченная. Замечание. Не всякая ограниченная последовательность сходится. Последовательность ограничена, но предела не имеет Доказательство. Докажем справедливость теоремы. Пусть последовательность имеет предел, равный. По определению предела для найдем номер такой, что при всех имеет место неравенство. Так как модуль суммы не превосходит суммы модулей, то Поэтому при всех выполняется неравенство. Положим тогда при всех, значит последовательность ограничена. 32 Р. Мунипов
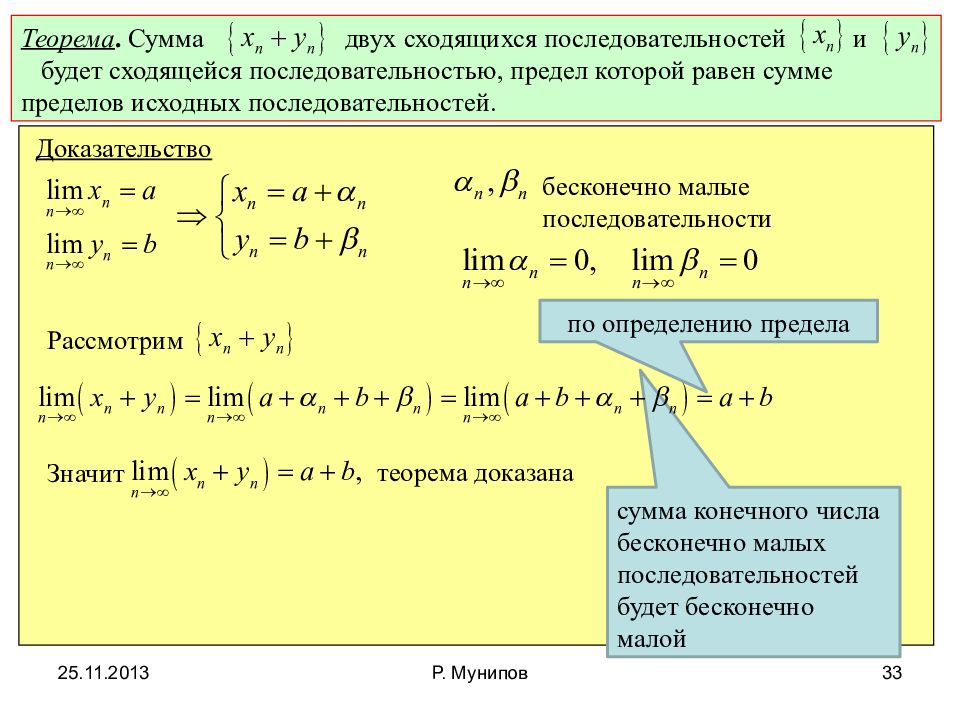
Теорема. Сумма двух сходящихся последовательностей и будет сходящейся последовательностью, предел которой равен сумме пределов исходных последовательностей. Доказательство бесконечно малые последовательности Рассмотрим Значит теорема доказана по определению предела сумма конечного числа бесконечно малых последовательностей будет бесконечно малой 25.11.2013 33 Р. Мунипов
Теорема. Разность двух сходящихся последовательностей и будет сходящейся последовательностью, предел которой равен разности пределов исходных последовательностей. Доказательство бесконечно малые последовательности Рассмотрим Значит теорема доказана сумма конечного числа бесконечно малых последовательностей будет бесконечно малой по определению предела 25.11.2013 34 Р. Мунипов
Р. Мунипов 25.11.2013 Теорема. Произведение двух сходящихся последовательностей и будет сходящейся последовательностью, предел которой равен произведению пределов исходных последовательностей. Доказательство бесконечно малые последовательности Произведение бесконечно малой последовательности на число есть бесконечно малая последовательность Произведение конечного числа бесконечно малых последовательностей есть бесконечно малая последовательность Рассмотрим Значит теорема доказана 35
Р. Мунипов Замечание. Из существования предела произведения последовательностей не следует существования конечного предела каждого сомножителя. Например: Замечание. Постоянный сомножитель можно выносить за знак предела, если постоянная величина, а последовательность имеет конечный предел, то Замечание. Если последовательность имеет конечный предел отличный от нуля, и есть целое отрицательное число, то 25.11.2013 36
Теорема. Пусть. Частное двух сходящихся последовательностей и, будет сходящейся последовательностью, предел которой равен отношению пределов исходных последовательностей. 25.11.2013 37 Р. Мунипов
Р. Мунипов Доказательство Докажем, что есть бесконечно малая последовательность. Имеем Так как и — бесконечно малые последовательности, то и будет бесконечно малой. По условию, поэтому последовательность является ограниченной. Отсюда следует, что последовательность — бесконечно малая как произведение бесконечно малой последовательности на ограниченную последовательность. Таким образом, — бесконечно малая последовательность, и поэтому 25.11.2013 38
25.11.2013 Р. Мунипов Теорема. Если для всех элементов последовательностей и или по крайней мере начиная с некоторого номера, справедливы неравенства а последовательности имеют конечный равные пределы, то последовательность сходится и её предел равен пределу этих последовательностей Доказательство. По определению предела для любого найдутся номера и такие, что при всех и при всех Отсюда, поскольку справедливы неравенства следует, что при всех выполняется условие. Это означает, что существует Теорема о трёх последовательностях, или теорема о «зажатой» последовательности 39
Пример Пусть. Покажем, что Для всех элементов последовательности справедливо действительно, если, то если, то Значит справедливы неравенства (*). Поскольку и, то по теореме о трёх последовательностях получаем, что 25.11.2013 40 Р. Мунипов
Пример Докажем, что если, то Действительно, поскольку, то. Обозначая, получаем, где, тогда, в силу неравенства Бернулли, справедливо. Т.к., то, или. Поскольку, то по теореме о трёх последовательностях получаем, что, или 25.11.2013 41 Р. Мунипов
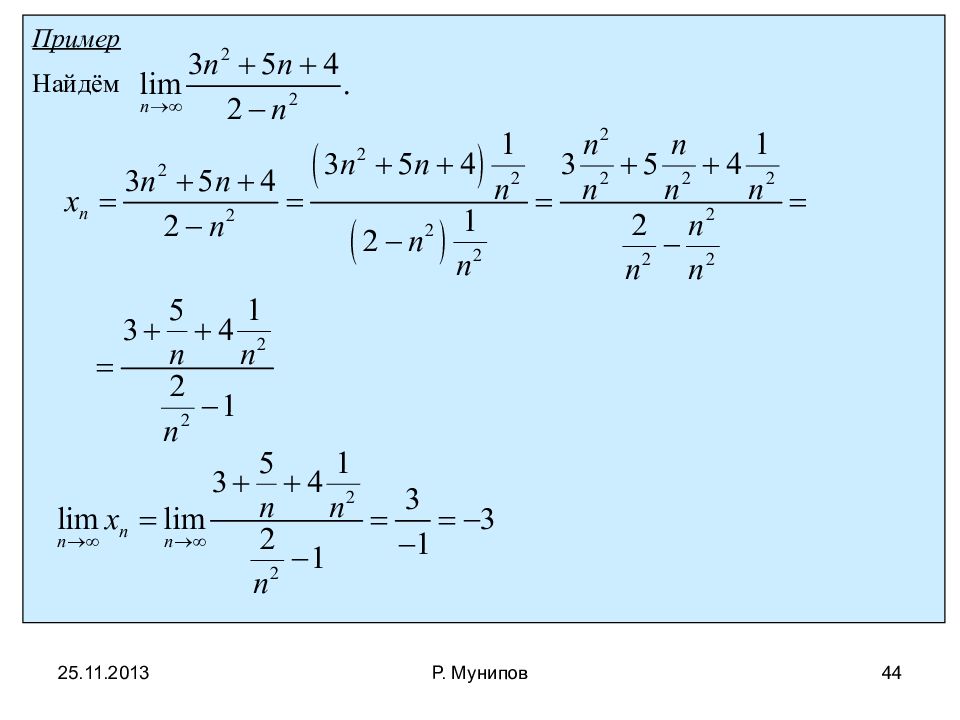
Пример Докажем, что Справедливо Тогда,, или. Т.к. для значений выполняется неравенство, то получаем, или. Поскольку, то. Для последовательности её предел тогда, по теореме о трёх последовательностях получаем, значит Функция корня и подкоренное выражение ведут себя в бесконечности одинаково 25.11.2013 42 Р. Мунипов
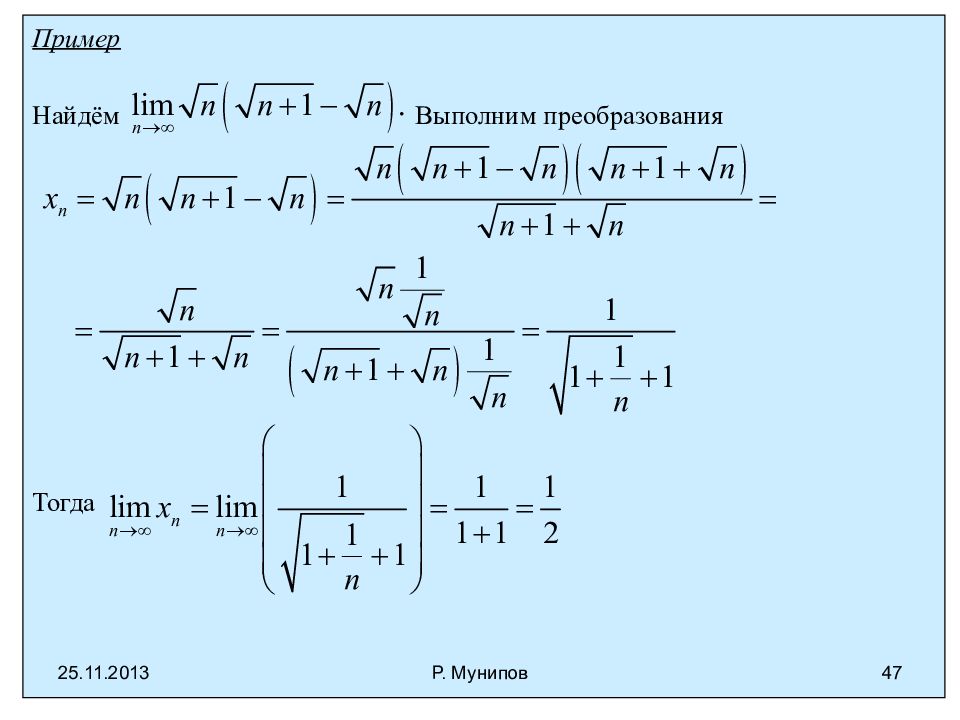
Пример Докажем, что, если и, то Если, то справедливо Тогда для, т.к. при выполняется неравенство. Если представить, то получаем, для исходной последовательности тогда справедливо двойное неравенство. Поскольку тогда, по теореме о трёх последовательностях получаем Показательная функция с основанием большим единицы быстрее стремится к бесконечности, чем любая степенная функция с показателем большим одного 25.11.2013 43 Р. Мунипов
Пример Найдём 25.11.2013 44 Р. Мунипов
Пример Найдём 25.11.2013 45 Р. Мунипов
Пример Докажем, что, если, то Действительно, Вместе с тем, значит 25.11.2013 46 Р. Мунипов
Пример Найдём Выполним преобразования Тогда 25.11.2013 47 Р. Мунипов
Р. Мунипов Теорема. Если последовательности и имеют конечные пределы, для которых выполняется неравенство, то, начиная с некоторого номера, для всех элементов последовательностей будет справедливо это неравенство, Доказательство. Согласно определению предела, выберем таким, чтобы – окрестности точек и не пересекались,, тогда существуют номера и, такие что для и для. Пусть, тогда для выполняется неравенство, что и требовалось доказать. 25.11.2013 48
Замечание. Очевидно теорема справедлива для неравенства больше. Замечание. Если и, то, или если и, то Замечание. Если и, то 25.11.2013 49 Р. Мунипов
Замечание. Если для сходящейся последовательности выполняется для всех (или для всех ) неравенство, то для предела справедливо. Отсюда следует, что если все члены сходящейся последовательности принадлежат отрезку, т. е. для всех (или для всех ), то и предел этой последовательности принадлежит отрезку, т. е.. Замечание. Если соответствующие члены двух сходящихся последовательностей связаны знаком нестрогого неравенства, то такое же неравенство справедливо и для пределов этих последовательностей. Т.е. предельный переход сохраняет знак нестрогого неравенства. Однако знак строгого неравенства, вообще говоря, не сохраняется, т. е. если при и последовательности сходятся, то Например, 25.11.2013 50 Р. Мунипов
Замечание. Теорема Штольца. Если для последовательностей и справедливо а последовательность, по крайней мере начиная с некоторого номера, удовлетворяет неравенству, то Пример. Применяя теорему Штольца, весьма просто находится предел, 25.11.2013 51 Р. Мунипов
Пример. Из теоремы Штольца следует, или Ранее было показано, что. Тогда рассматривая предел получаем, 25.11.2013 52 Р. Мунипов
Пример. Рассмотрим последовательность её предел, применяя теорему Штольца, получаем Вместе с тем,, тогда для разности Значит, 25.11.2013 53 Р. Мунипов
Р. Мунипов 25.11.2013 Определение 9. Последовательность называется возрастающей ( неубывающей), если каждый элемент этой последовательности, начиная со второго, не меньше предыдущего её элемента, т. е. если для всех номеров справедливо неравенство. неубывающая Определение 10. Последовательность называется убывающей ( невозрастающей ), если каждый элемент этой последовательности, начиная со второго, не больше предыдущего ее элемента, т. е. если для всех номеров справедливо неравенство. невозрастающая Определение 11. Последовательность называется монотонной, если она является либо невозрастающей, либо неубывающей. невозрастающая неубывающая монотонная 54
Определение 12. Последовательность называется строго возрастающей, если каждый элемент этой последовательности, начиная со второго, больше предыдущего ее элемента, т. е. если для всех номеров справедливо неравенство. возрастающая Определение 13. Последовательность называется строго убывающей, если каждый элемент этой последовательности, начиная со второго, меньше предыдущего ее элемента, т. е. если для всех номеров справедливо неравенство. убывающая 25.11.2013 55 Р. Мунипов
Определение 14. Точной верхней гранью последовательности называется число, для которого все элементы последовательности не превосходят этого числа, и для любого положительного числа найдётся номер, что соответствующий этому номеру элемент последовательности будет больше разности, Определение 15. Точной нижней гранью последовательности называется число, для которого все элементы последовательности не меньше этого числа, и для любого положительного числа найдётся номер, что соответствующий этому номеру элемент последовательности будет меньше суммы, 25.11.2013 56 Р. Мунипов
Р. Мунипов 25.11.2013 Теорема. Если последовательность возрастающая и ограничена сверху, то существует её предел равный точной верхней грани этой последовательности,. Если последовательность убывающая и ограничена снизу, то существует её предел равный точной нижней грани этой последовательности,. Доказательство Рассмотрим случай возрастающей и ограниченной последовательности. По определению точной верхней грани для любого элемента последовательности справедливо Пусть, по определению точной верхней грани найдётся номер, что соответствующий ему элемент удовлетворяет неравенству. По условию последовательность возрастающая, т.е. для всех элементов выполняется неравенство. Поэтому для справедливо или, сравнивая это неравенство с, получаем Значит что и требовалось доказать. Аналогично доказывается, если последовательность убывающая и ограниченная снизу. 57
Замечание. Чтобы монотонная последовательность сходилась необходимо и достаточно, чтобы она была ограниченной. Необходимость следует из теоремы, что всякая сходящаяся последовательность ограничена. Замечание. Не всякая сходящаяся последовательность монотонная. Например, однако эта последовательность не является монотонной Замечание. Все элементы неубывающей, ограниченной сверху последовательности не больше её предела. Все элементы невозрастающей, ограниченной снизу последовательности не меньше её предела. 25.11.2013 58 Р. Мунипов
Пример Докажем, что для предел Для всех элементов последовательности справедливо то при всех, где. Значит заданная последовательность убывающая при. Кроме этого, при всех, т.е. ограничена снизу. Тогда, по теореме о сходимости монотонной последовательности, сходится, пусть. Рассматривая предел получаем, в итоге Функция факториала быстрее стремится в бесконечность, чем любая показательная функция 25.11.2013 59 Р. Мунипов
Пример Найдём предел последовательности ( корней) Для всех элементов последовательности справедливо Очевидно, последовательность возрастающая, и ограничена сверху, действительно, для первого и второго члена получаем Предположим, тогда Значит последовательность ограничена. По теореме сходимости монотонной ограниченной последовательности получаем существование конечного предела искомой последовательности, обозначим, очевидно 25.11.2013 60 Р. Мунипов
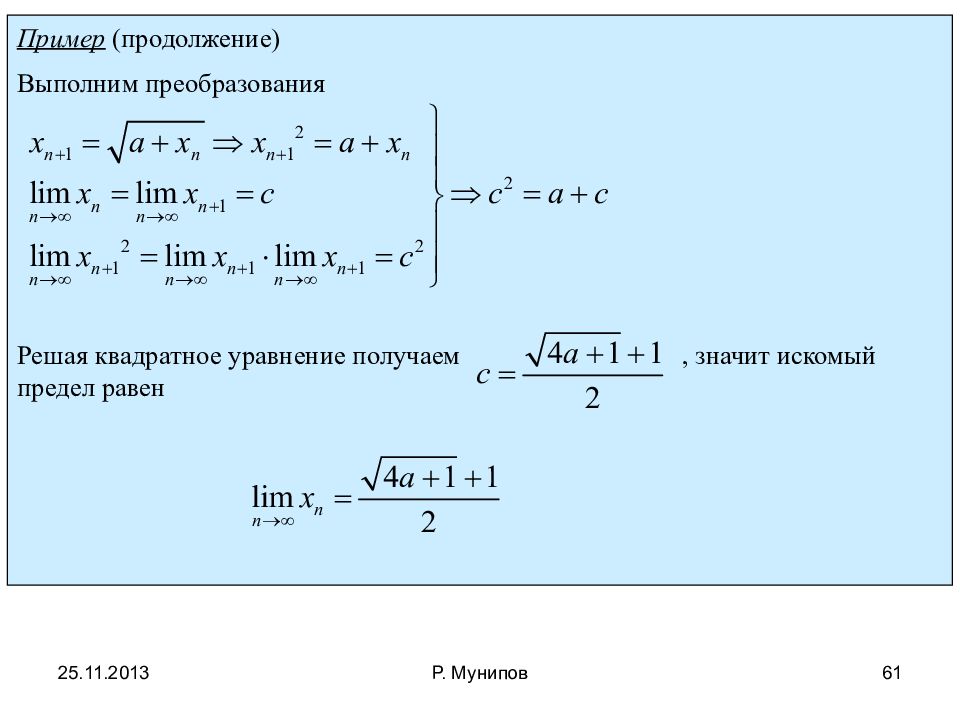
Пример (продолжение) Выполним преобразования Решая квадратное уравнение получаем, значит искомый предел равен 25.11.2013 61 Р. Мунипов
25.11.2013 Пример Докажем, что для предел Очевидно, в силу, для всех элементов последовательности справедливо. Применим для неравенство для среднеарифметического и среднегеометрического, тогда для т.е., значит заданная последовательность ограниченная снизу. Покажем её монотонность, т.к. и, то значит убывающая, у которой существует. Рассматривая или 62 Р. Мунипов
Пример Рекуррентное выражение можно использовать для приближённого вычисления квадратного корня числа 25.11.2013 63 Р. Мунипов
Замечание. Итак, если, то предел Обобщением, этого примера есть последовательность для которой, что позволяет с достаточной точностью вычислять целые корни из положительного числа 25.11.2013 64 Р. Мунипов
Замечание. Среднее арифметическое двух чисел и равно Среднее геометрическое двух чисел и равно Очевидно, Значит среднее арифметическое двух чисел не меньше их среднего геометрического, Если, то их среднее арифметическое, среднее геометрическое для которых также справедливо 25.11.2013 65 Р. Мунипов
Число е. Рассмотрим последовательность где Покажем существование предела этой последовательности. Рассмотрим дополнительную последовательность, Эта последовательность ограничена снизу, действительно, в силу неравенства Бернулли 25.11.2013 66 Р. Мунипов
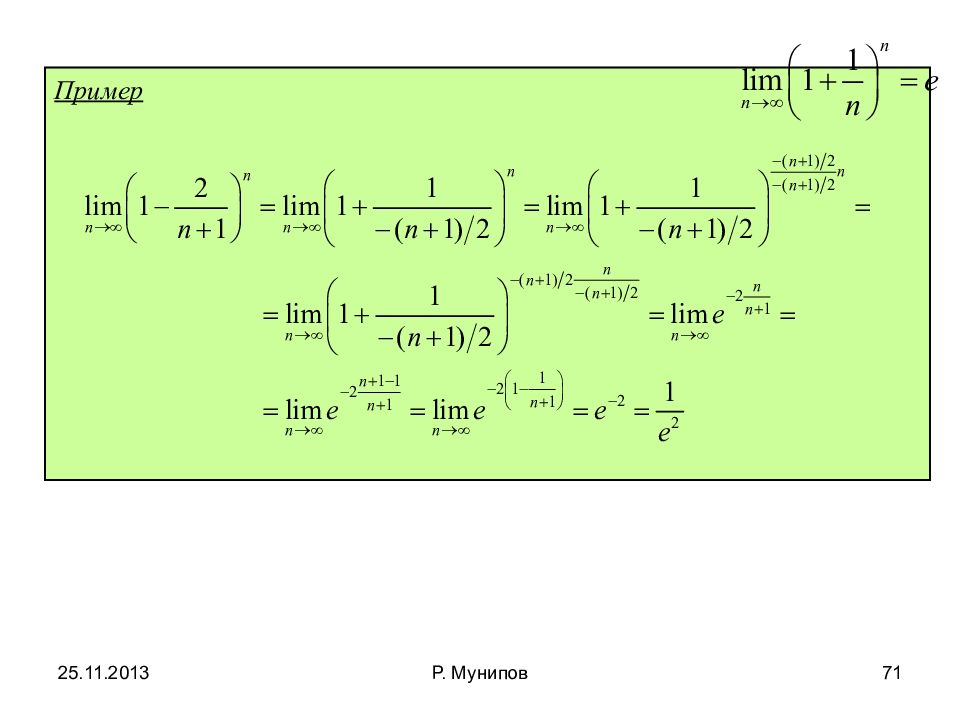
25.11.2013 Число е. (продолжение 1) Покажем монотонность или, применяя неравенство Бернулли, или. Итак последовательность монотонно убывает и ограничена снизу, значит у неё существует предел, обозначим этот предел символом, т.е.. Тогда выполняя преобразования получаем, 67 Р. Мунипов
Число е. (продолжение 2) Тогда выполняя преобразования получаем, Значит 25.11.2013 68 Р. Мунипов
Р. Мунипов Теорема. Если в последовательности все элементы отличны от 0 и -1, причём, то Доказательство Условие означает, что возможно и Пусть, тогда в последовательности лишь конечное членов меньше единицы, значит не ограничивая общности можно считать, исключив из последовательности конечное число членов. Обозначим — функция антье, наибольшее целое число не превосходящее, причём,. Для положительном основании и степени справедливы неравенства Если равно 0 или -1 то выражение не определено 25.11.2013 69
Р. Мунипов Доказательство (продолжение1) Поскольку целые положительные (натуральные) числа и, то Значит Аналогично, 25.11.2013 70
Пример 25.11.2013 71 Р. Мунипов
Р. Мунипов 25.11.2013 Определение 16. Последовательность отрезков, где называется стягивающейся, если каждый последующий принадлежит предыдущему, длина –ого отрезка стремится к нулю при, Замечание. Из определения стягивающихся отрезков следует, что значит 72
Теорема (Кантор). Если последовательность отрезков является стягивающейся, то существует и при том единственная точка, принадлежащая всем отрезкам этой последовательности. 25.11.2013 73 Р. Мунипов Доказательство Обозначим эту точку через. Покажем её существование, т.е. точка принадлежит всем отрезкам. Действительно, т.к. система отрезков стягивающая, то последовательность левых концов не убывает, а последовательность правых концов не возрастает. Вместе с тем, обе эти последовательности ограничены, Значит по теореме о сходимости монотонной ограниченной последовательности следует существование пределов, По определению стягивающей отрезков, поэтому причём для всех. Значит точка является общей для всех отрезков. Единственность этой точки доказывается аналогично, предполагая противное, что существуют две точки и, и справедливо. Тогда выполняется, значит. Это невозможно поскольку при, получили противоречие.
Георг Кантор (1845-1918) Немецкий учёный математик основоположник современной теории множеств 25.11.2013 74 Р. Мунипов
Пример Определение 17. Пусть возрастающая последовательность натуральных чисел,. Тогда последовательность, образованная из последовательности, называется подпоследовательностью этой последовательности, Замечание. Очевидно, всякая последовательность является подпоследовательностью для самой себя. 25.11.2013 75 Р. Мунипов Замечание. По определению, подпоследовательность образована из членов исходной последовательности, причем порядок следования членов в подпоследовательности такой же, как и исходной. Для элемента число означает порядковый номер члена последовательности, а — номер этого члена в исходной последовательности. Поэтому, откуда следует, что при.
Замечание. Очевидно, всякая подпоследовательность образуется из исходной последовательности прореживанием её членов. Замечание. Для последовательности и её подпоследовательностей справедливы свойства: Если последовательность сходится к некоторому числу, то и всякая её подпоследовательность также сходится к этому числу. Если все подпоследовательности некоторой последовательности сходятся, то все они сходятся к одному и тому же числу, к этому же числу сходится и исходная последовательность. Замечание. Очевидно, всякая подпоследовательность бесконечной последовательности будет бесконечно большой последовательностью. 25.11.2013 76 Р. Мунипов
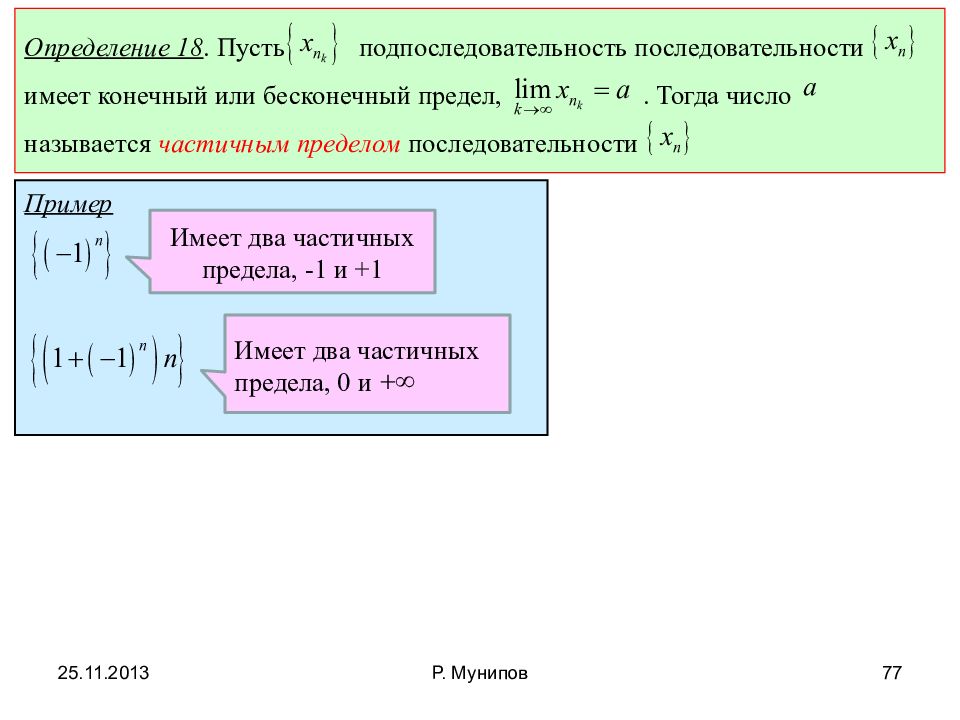
Определение 18. Пусть подпоследовательность последовательности имеет конечный или бесконечный предел,. Тогда число называется частичным пределом последовательности Пример Имеет два частичных предела, -1 и +1 Имеет два частичных предела, 0 и 25.11.2013 77 Р. Мунипов
25.11.2013 Р. Мунипов Пример Определение 19. Пусть ограниченная последовательность, а есть множество её частичных пределов. Верхним пределом последовательности называют точную верхнюю грань множества, Определение 20. Пусть ограниченная последовательность, а есть множество её частичных пределов. Нижним пределом последовательности называют точную нижнюю грань множества, 78
Теорема ( Больцано-Вейерштрасса ). Из любой ограниченной последовательности можно выделить сходящуюся подпоследовательность. Доказательство Пусть — ограниченная последовательность, тогда все члены последовательности принадлежат некоторому отрезку, т. е. Разобьем отрезок пополам точкой. Тогда по крайней мере один из отрезков содержит бесконечное число членов. Если оба отрезка обладают этим свойством, возьмем, например, правый отрезок (и будем так поступать в дальнейшем). Выбранный отрезок, содержащий бесконечное число членов данной последовательности, обозначим, его длина равна. Разделив отрезок пополам, выберем указанным выше способом из двух получившихся отрезков отрезок, содержащий бесконечное число членов последовательности. Продолжая эти рассуждения, получим последовательность отрезков таких, что: 25.11.2013 79 Р. Мунипов
Доказательство (продолжение) Значит, — стягивающаяся последовательность отрезков. По теореме Кантора существует единственная точка, принадлежащая всем отрезкам, Покажем, что найдется подпоследовательность последовательности такая, что. Действительно, отрезок содержит бесконечное число членов последовательности,. Отрезок также содержит бесконечное число членов данной последовательности,. Вообще, следовательно, существует подпоследовательность последовательности такая, что справедливы неравенства. Полученное означает что точки и принадлежат отрезку, и поэтому расстояние между ними не превосходит длины отрезка, т. е. Отсюда следует,. Теорема доказана. 25.11.2013 80 Р. Мунипов
Больцано Бернард (1781-1848) Чешский учёный математик и логик Вейерштрасс Карл Теодор Вильгельм (1815-1897) Немецкий учёный математик, разработал систему логического обоснования математического анализа 25.11.2013 81 Р. Мунипов
Замечание. Из теоремы Больцано-Вейерштрасса следует, что всякая ограниченная последовательность имеет хотя бы один конечный частичный предел. Т.е. из всякой ограниченной последовательности можно выделить сходящуюся к конечному числу подпоследовательность. Всякая неограниченная последовательность содержит бесконечно большую подпоследовательность. Т.е. из любой неограниченной последовательности можно выделить бесконечно большую подпоследовательность. Чтобы число, где есть конечное число, или число, или число, было частичным пределом последовательности, необходимо и достаточно, чтобы в любой окрестности этого числа содержалось бесконечное число членов этой последовательности. Из всякой последовательности можно выделить либо сходящуюся к конечному числу подпоследовательность, либо бесконечно большую подпоследовательность, все элементы которой, начиная с некоторого номера имеют один знак. Метод последовательного деления рассматриваемых промежутков пополам называют методом Больцано. 25.11.2013 82 Р. Мунипов
Определение 20. Последовательность называют фундаментальной, если она удовлетворяет условию Коши : для каждого существует такое натуральное число, что для любого и любого справедливо неравенство, или Замечание. Для фундаментальной последовательности справедливы свойства: Для любого найдётся номер, начиная с которого все элементы последовательности будут находиться в – окрестности элемента этой последовательности. Фундаментальная последовательность ограничена. 25.11.2013 83 Р. Мунипов Замечание. Очевидно, фундаментальность последовательности означает, что с возрастанием номера последовательности, разность между её достаточно близкими элементами будет меньше любого наперёд заданного положительного числа.
Покажем справедливость ограниченности фундаментальной последовательности. Пусть. Тогда т.к. последовательность фундаментальная, найдётся номер, начиная с которого все элементы последовательности будут находится в –окрестности значения (в силу первого свойства для фундаментальных последовательностей), Обозначим, тогда для всех номеров справедливо неравенство, что означает ограниченность последовательности. 25.11.2013 84 Р. Мунипов
Теорема (Критерий Коши). Чтобы последовательность имела конечный предел необходимо и достаточно, чтобы она была фундаментальной. Доказательство Необходимость, что если последовательность имеет конечный предел, то она фундаментальная. Действительно, пусть по определению предела, Тогда для и получаем, что означает фундаментальность последовательности, необходимость доказана. Достаточность, что фундаментальная последовательность имеет конечный предел. Действительно, из определения фундаментальной последовательности получаем (*) 25.11.2013 85 Р. Мунипов
Доказательство (продолжение) Так как фундаментальная последовательность является ограниченной, то по теореме Больцано-Вейерштрасса она содержит сходящуюся подпоследовательность, пусть. Покажем, что число является также пределом. По определению предела, (**) Пусть, тогда для и из (*) получаем Из неравенства (**) при следует, Значит, теорема доказана. 25.11.2013 86 Р. Мунипов
Замечание. Критерий Коши устанавливает факт сходимости последовательности, не указывая значение предела. Замечание. Очевидно, если последовательность не удовлетворяет критерию Коши, то она не имеет конечного предела, т.е. является расходящейся. 25.11.2013 87 Р. Мунипов Пример Докажем, что последовательность, где расходится. Последовательность расходится, если не выполняется условие Коши. Положим тогда, Условие Коши не выполняется при, значит расходится
