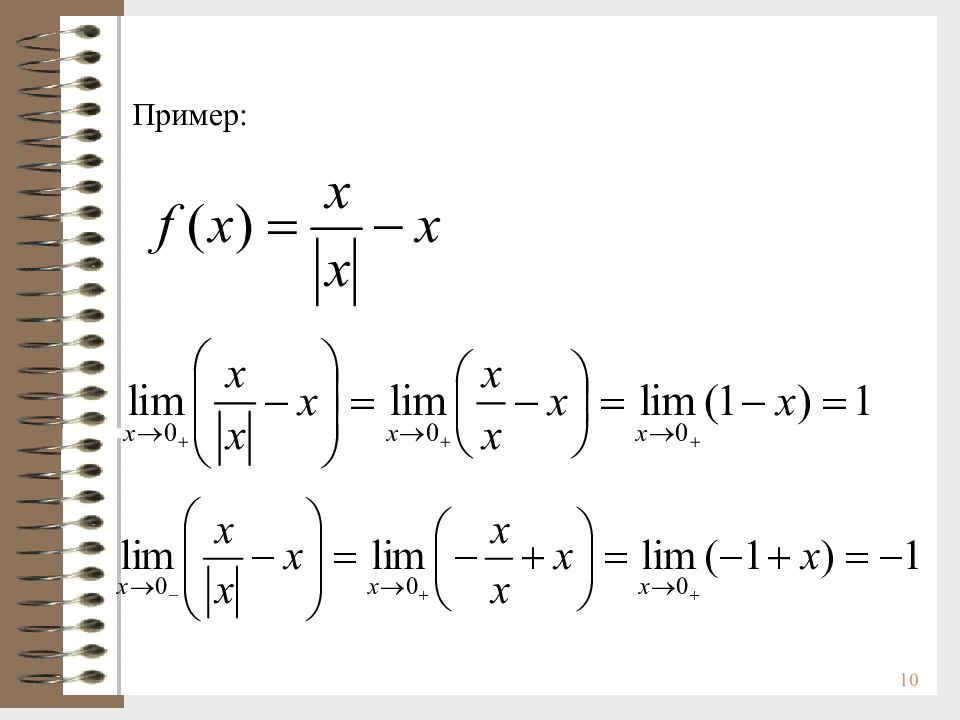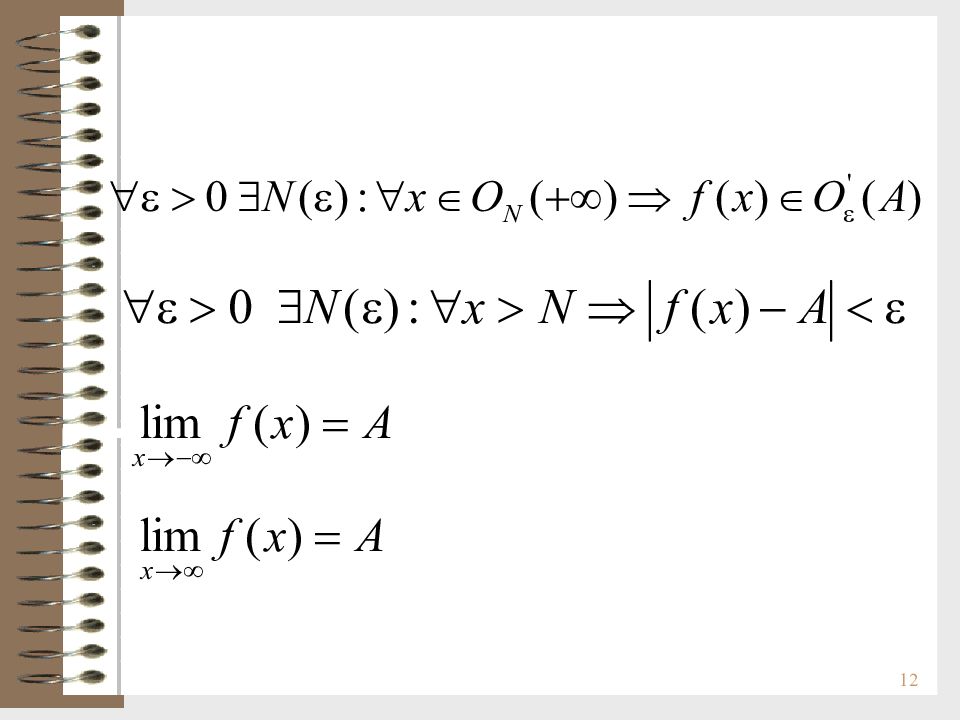Лекция № 5
2 Предел функции Предел по Гейне: Число А называется пределом функции f ( x ) в точке а, если для любой, сходящейся к точке а последовательности значений аргумента х (отличных от а ), соответствующая последовательность значений функции сходится к числу А.
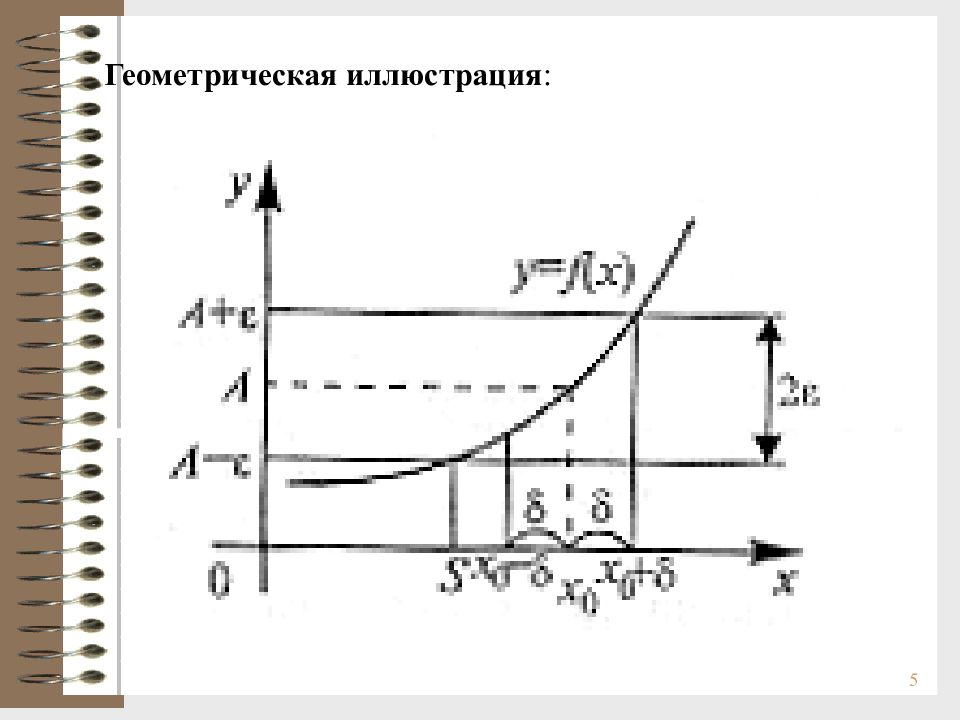
3 Предел по Коши: Число А называется пределом функции f ( x ) в точке а, если для любого e - окрестности точки А, можно найти проколотую d - окрестность точки а, такую, что для всех х из этой окрестности соответствующие значения функции принадлежат e - окрестности точки А. Определение без использования окрестностей (на языке e - d ) :
4 Замечания : 1. Использование в определении предела проколотой окрестности является существенным, т.к. сама функция может и не существовать в точке а. 2. Можно обобщить понятие предела, если под а и А понимать не только числа, но и и использовать соответствующие окрестности. 3. В отличие от последовательностей говорить о пределе функции без указания точки, в которой вычисляется предел бессмысленно! Функции имеют в разных точках различные пределы!
5 Геометрическая иллюстрация :
6 Примеры:
7 Данная функция не имеет предела в точке а = 0 Это означает, что не существует e такое, что для любого числа А не существует нужного нам числа d
8 Односторонние пределы Определение 1. Число А называется правым ( левым ) пределом функции f ( x ) в точке а, если для любой сходящейся к а последовательности x 1, x 2, …, x n, … такой, что x n > a ( x n < a ), соответствующая последовательность f ( x 1 ), f ( x 2 ), …, f ( x n ), … сходится к А.
9 Определение 2. ( на языке - ) Число А называется правым (левым) пределом функции в точке а, если для любого >0 существует такое >0, что для всех х из правой ( левой) -окрестности точки а, т.е. a <x<a+ ( a- <x<a ), выполняется неравенство | f ( x ) – A |< . Теорема. Функция f ( x ) имеет в точке а предел тогда и только тогда, если в этой точке существуют правый и левый пределы, причем они равны. В этом случае предел функции равен односторонним пределам.
10 Пример:
11 Различные виды пределов Пределы на бесконечности: Определение 1. Число А называется пределом функции f ( x ) при х +, если для любой бесконечно большой последовательности значений аргумента x 1, x 2, …, x n, … ( x n >0 ) соответствующая последовательность значений функции f ( x 1 ), f ( x 2 ), …, f ( x n ), … сходится к А. Число А называется пределом функции f ( x ) в + бесконечности, если для любой e - окрестности точки А, можно найти N - окрестность + бесконечности, такую, что для всех х из этой окрестности соответствующие значения функции принадлежат e - окрестности точки А.
12
13 Бесконечные пределы: ( бесконечно большие функции ) Функция f ( x ) имеет в точке а предел равный плюс бесконечности ( является положительной бесконечно большой в окрестности точки а ), если для любой N - ок-рестности плюс бесконечности, можно найти проколотую d - окрестность точки а, такую, что для всех х из этой окрестности соответствующие значения функции принадлежат N - окрестности плюс бесконечности.
14 Геометрическая иллюстрация, пример Аналогично можно ввести понятие бесконечно большой функции бесконечности: и т.д.
15 Функция f ( x ) называется бесконечно малой в окрестности точки а (в точке а ), если ее предел в этой точке равен 0. Теорема. Для того, чтобы функция f ( x ) имела конечный предел в точке а н еобходимо и достаточно, чтобы функция ( х ) = f ( x ) – A была бесконечно малой при х а. Свойства бесконечно малых : Алгебраическая сумма конечного числа бесконечно малых величин есть величина бесконечно малая. Произведение бесконечно малой величины на ограниченную функцию есть величина бесконечно малая Величина обратная бесконечно малой есть величина бесконечно большая Величина обратная бесконечно большой есть величина бесконечно малая
16 Пусть при х а функции ( х ) и ( х ) являются бесконечно малыми. Тогда : 1) если, то ( х ) – бесконечно малая более высокого порядка, чем ( х ). 2) если ( А – число), то ( х ) и ( х ) – бесконечно малые одного порядка. Сравнение бесконечно малых и бесконечно больших функций 3) если, то ( х ) и ( х ) – эквивалентные бесконечно малые. Обозначается : ( х ) ~ ( х ) 4) если, то ( х ) – бесконечно малая n - го порядка относительно ( х ).
17 Теорема. Если ( х ) ~ 1 ( х ) и ( х ) ~ 1 ( х ) при х а и существует, то существует причем Сравнение бесконечно больших функций: Для бесконечно больших функций также имеют место аналогичные правила, учитывая, что вместо термина “ порядок малости ” употребляется термин “ порядок роста ”. Примеры эквивалентных бесконечно малых (при x 0 ):
18 Основные теоремы о пределах Т1. (О единственности предела) Если функция f ( x ) имеет предел в точке а, то этот предел единственный. Т2. (О предельном переходе в неравенстве ) Пусть функции f ( x ) и g ( x ) определены на одном и том же промежутке Х и существуют пределы этих функций в т. а Кроме того, существует такое число d > 0, что для всех х из d- окрестности числа а f ( x ) g ( x ). Тогда A B. Т3. (Об ограниченности функции имеющей предел) Если функция f ( x ) имеет конечный предел в точке а, то существуют числа М > 0 и > 0 такие, что для всех х из - окрестности точки а
19 Т4. Пусть функции f ( x ), g ( x ) и h ( x ) определены в некоторой окрестности точки а, за исключением, быть может, самой точки а, функции f ( x ) и h ( x ) имеют в точке а предел, равный А, т.е. Т5. (Связь предела с алгебраическими операциями) Пусть функции f ( x ) и g ( x ) имеют в точке а пределы В и С. Тогда функции f ( x ) g ( x ), f ( x ) g( x ) и f ( x ) / g ( x ) (при С 0) имеют в точке а пределы, равные В С, В С и B/C соответственно. Тогда если f ( x ) g ( x ) h ( x ), то
20 Некоторые важные пределы 1. 2. Первый замечательный предел:
21 3. Второй замечательный предел Делая замену переменной, имеем 4. или
