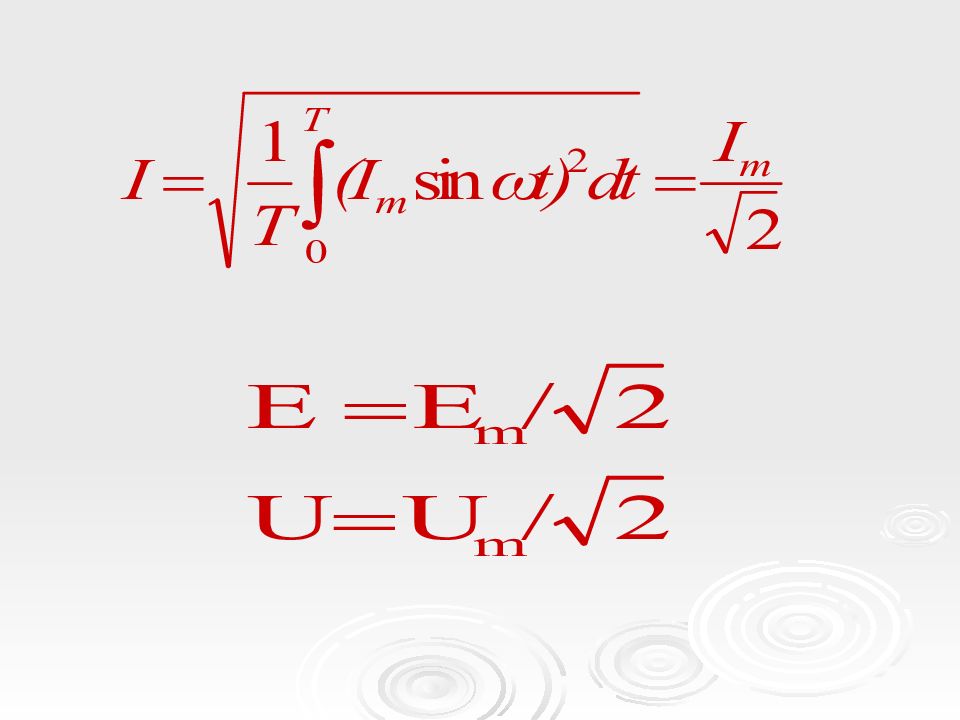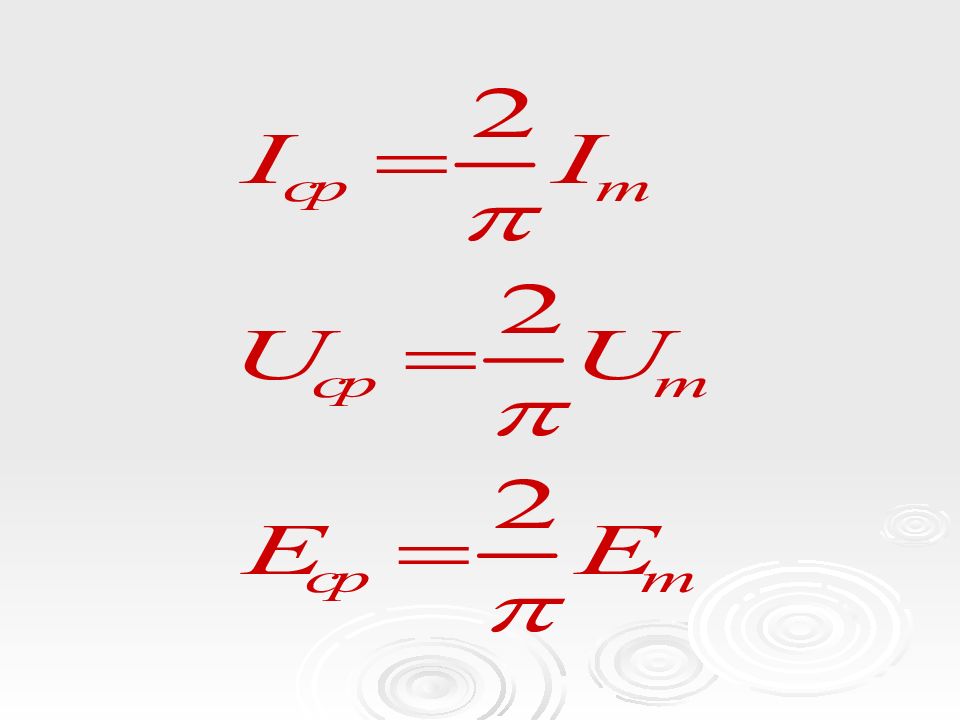Первый слайд презентации: ЭЛЕКТРИЧЕСКИЕ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА
1. Основные параметры, характеризующие синусоидальные токи, напряжения и ЭДС 2. Идеальные резистивный, индуктивный и емкостный элементы в цепях синусоидального тока
Токи, напряжения и ЭДС, значения которых периодически изменяются во времени по синусоидальному закону, называют синусоидальными (гармоническими). По сравнению с постоянным током синусоидальный имеет ряд преимуществ: производство, передача и использование электрической энергии наиболее экономичны при синусоидальном токе; в цепях синусоидального тока относительно просто преобразовывать форму напряжения, а также создавать трехфазные системы напряжения. В зависимости от типа решаемой задачи синусоидальные величины представляют: - в виде аналитических выражений; - графически, посредством временной или векторной диаграмм;
Переменный электрический ток – это ток, изменяющийся с течением времени. Значение этой величины в рассматриваемый момент времени называется мгновенным значением тока i.
Слайд 4
Переменный синусоидальный сигнал характеризуется: периодом Т, который выражается в секундах (с), частотой f - величиной, обратной периоду, выражается в герцах (Гц). В России f =50 Гц круговой частотой ω = 2 π f (рад/с).
Слайд 5
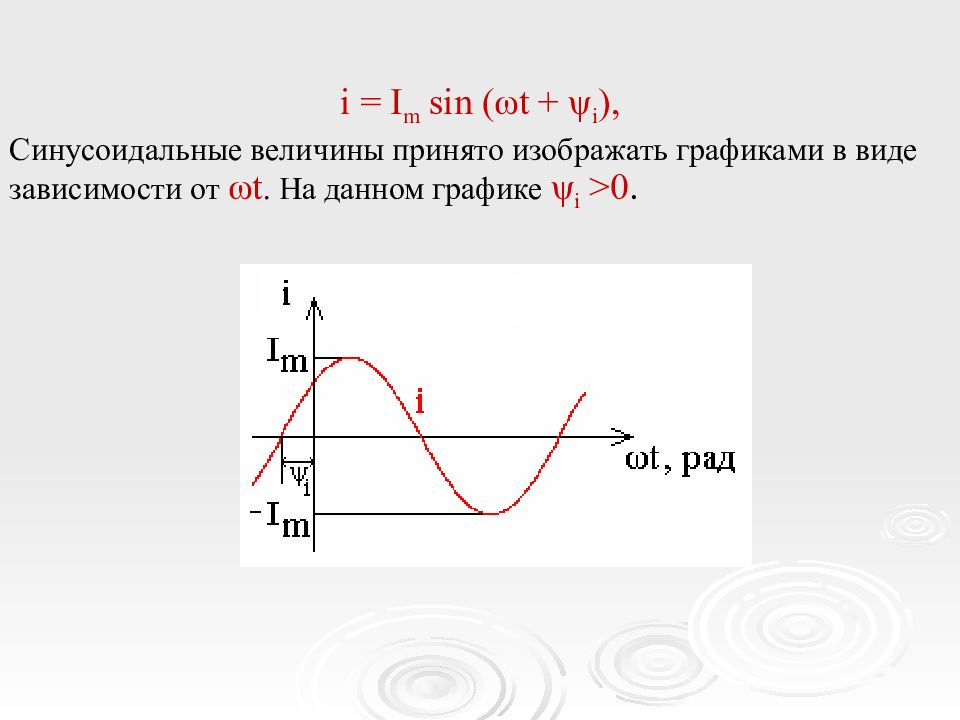
Мгновенное значения тока: i = I m sin ( ω t + ψ i ), где i – мгновенное значение тока, А; I m – амплитудное значение тока, А; ω – круговая (угловая) частота, рад/с; t – время, с; ψ i – начальная фаза тока.
Слайд 6
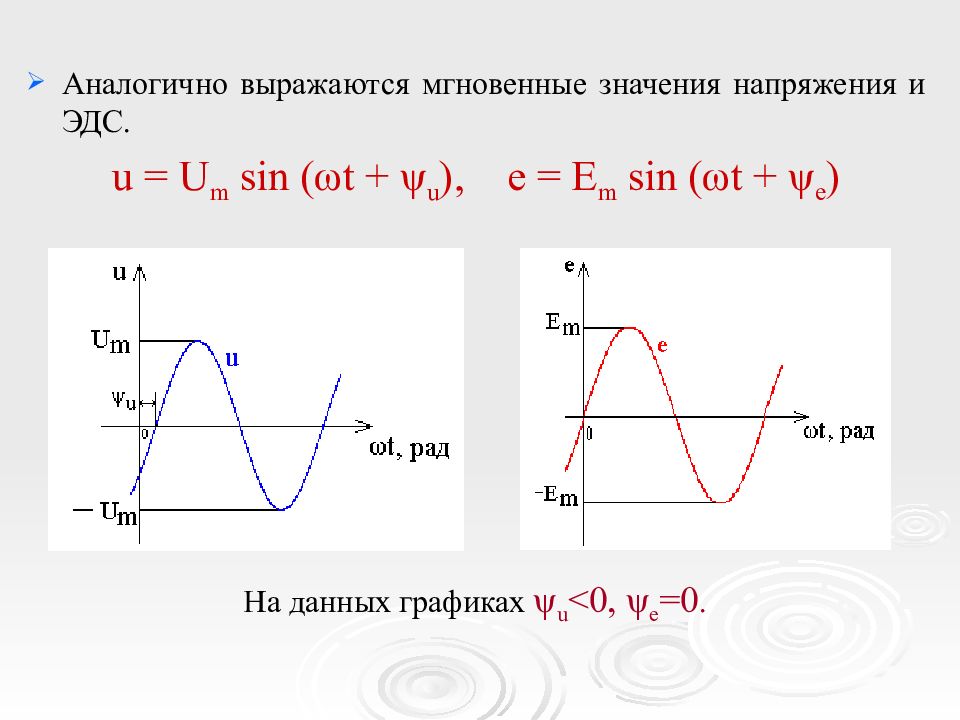
Аналогично выражаются мгновенные значения напряжения и ЭДС. u = U m sin ( ω t + ψ u ), e = E m sin ( ω t + ψ e ) Для расчета электрических цепей аналитические выражения синусоидальных величин неудобны, т. к. алгебраические действия с тригонометрическими функциями приводят к громоздким вычислениям.
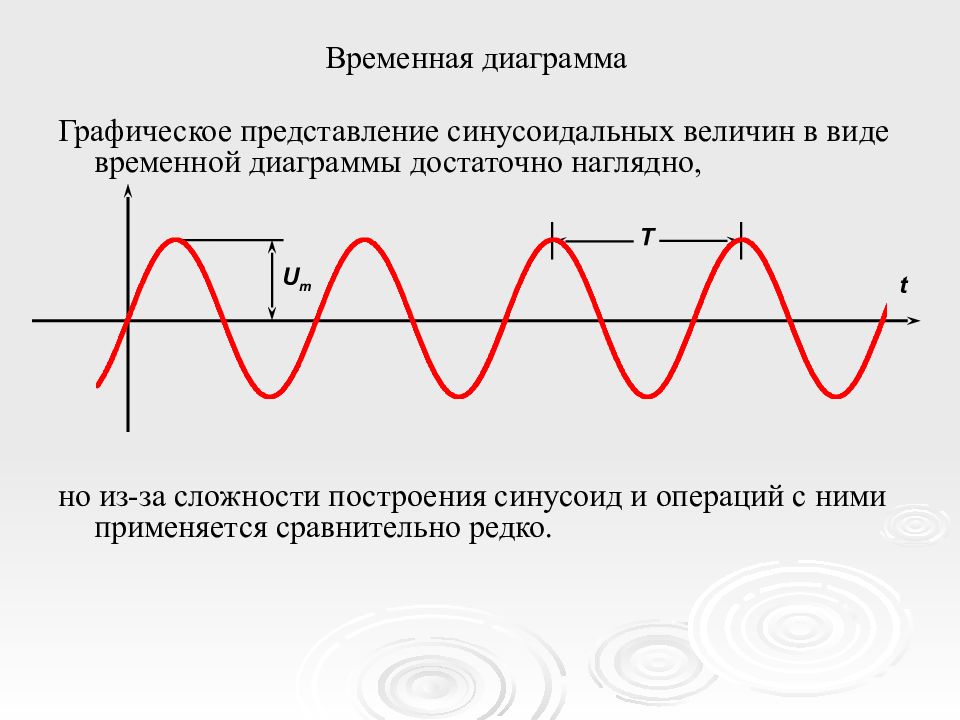
Слайд 7: Временная диаграмма
Графическое представление синусоидальных величин в виде временной диаграммы достаточно наглядно, но из-за сложности построения синусоид и операций с ними применяется сравнительно редко. t U m Т
Слайд 8
i = I m sin ( ω t + ψ i ), Синусоидальные величины принято изображать графиками в виде зависимости от ω t. На данном графике ψ i > 0.
Слайд 9
Аналогично выражаются мгновенные значения напряжения и ЭДС. u = U m sin ( ω t + ψ u ), e = E m sin ( ω t + ψ e ) На данных графиках ψ u <0, ψ e =0.
Слайд 10
Начальная фаза тока ( ЭДС, напряжения) ψ i, ψ e, ψ u – это значение фазы в момент времени t = 0. Разность начальных фаз двух синусоидальных величин одной и той же частоты называют сдвигом фаз. Сдвиг фаз между напряжением и током определяется вычитанием начальной фазы тока из начальной фазы напряжения: φ = ψ u – ψ i
Слайд 11
Действующее значение переменного тока (ЭДС, напряжения) – это среднеквадратичное значение переменного тока (ЭДС, напряжения) за период Т.
Слайд 13
Среднее значение синусоидальной функции за период Т равно нулю. Среднее значение переменного тока (ЭДС, напряжения) определяют за положительный полупериод
Слайд 15
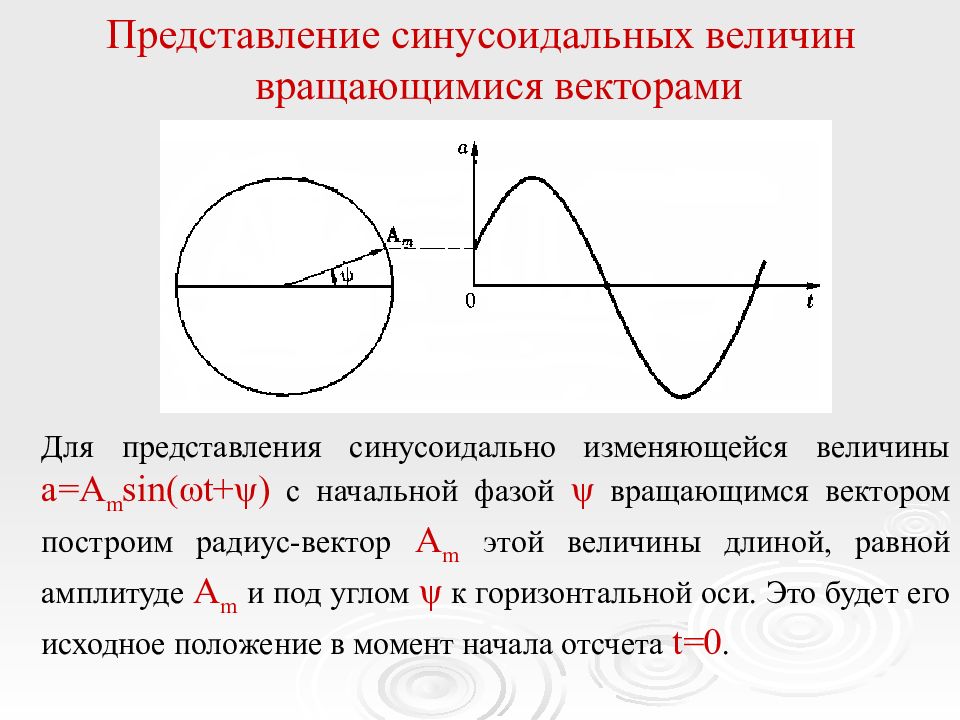
Представление синусоидальных величин вращающимися векторами Для представления синусоидально изменяющейся величины a=A m sin( ω t+ ψ ) с начальной фазой ψ вращающимся вектором построим радиус-вектор A m этой величины длиной, равной амплитуде A m и под углом ψ к горизонтальной оси. Это будет его исходное положение в момент начала отсчета t =0.
Слайд 16
Если радиус-вектор вращать с постоянной угловой скоростью ω против направления движения часовой стрелки, то его проекция на вертикальную ось будет равна A m sin( ω t+ ψ ). Применение вращающихся векторов позволяет компактно представить на одном рисунке совокупность различных синусоидально изменяющихся величин одинаковой частоты.
В резистивном элементе происходит преобразование электрической энергии в тепловую. Элементы, обладающие активным сопротивлением R, нагреваются при прохождении через них тока.
Слайд 18
Если к активному сопротивлению приложено синусоидальное напряжение то и ток изменяется по синусоидальному закону где или в действующих значениях
Слайд 19
Ток в цепи с активным сопротивлением совпадает по фазе с напряжением, т.к. их начальные фазы равны
Слайд 21: Активная мощность
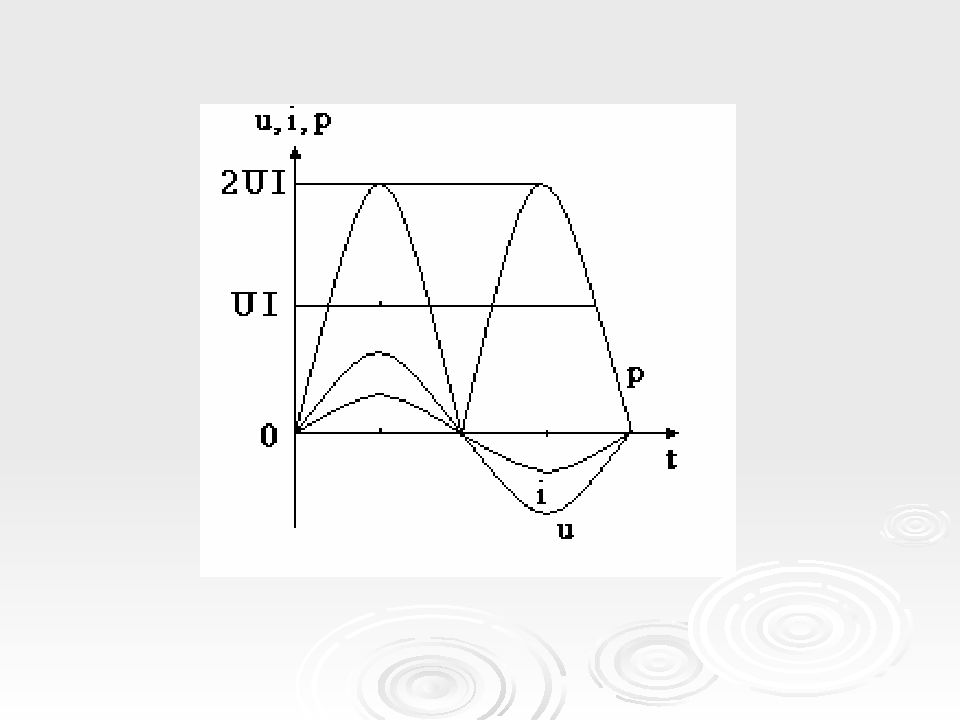
Мощность в цепи с активным сопротивлением изменяется по величине, но не изменяется по направлению. Эта мощность (энергия) необратима. От источника она поступает к потребителю и полностью преобразуется в другие виды мощности (энергии), т.е. потребляется. Такая потребляемая мощность называется активной. Поэтому и сопротивление R, на котором происходит подобное преобразование, называется активным.
Слайд 22
Количественно мощность в цепи с активным сопротивлением определяется Единица активной мощности
Слайд 23
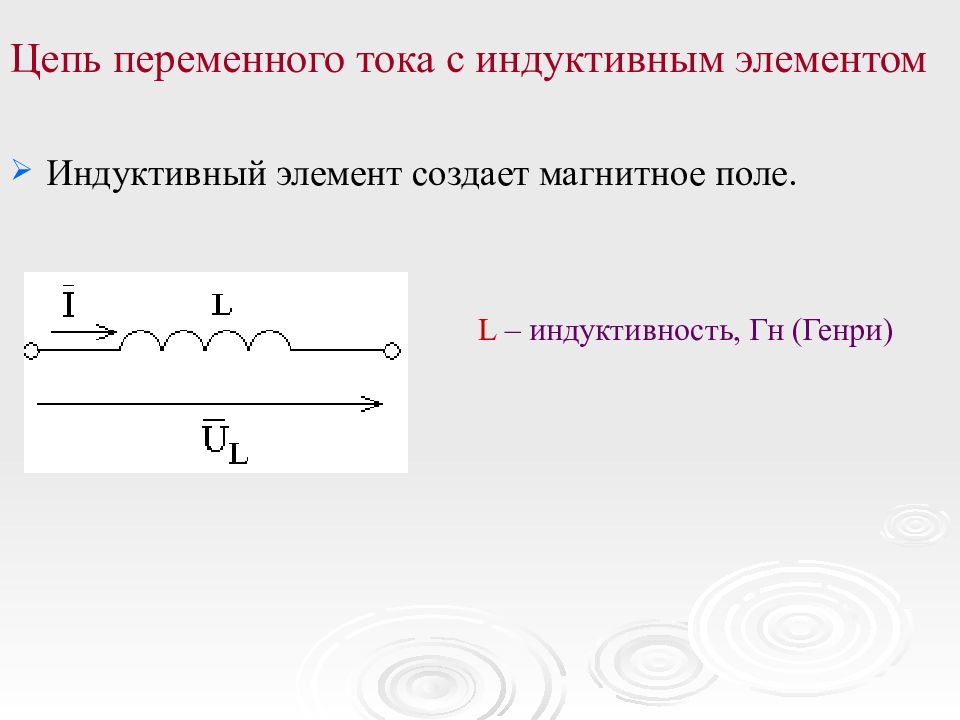
Цепь переменного тока с индуктивным элементом Индуктивный элемент создает магнитное поле. L – индуктивность, Гн (Генри)
Слайд 24
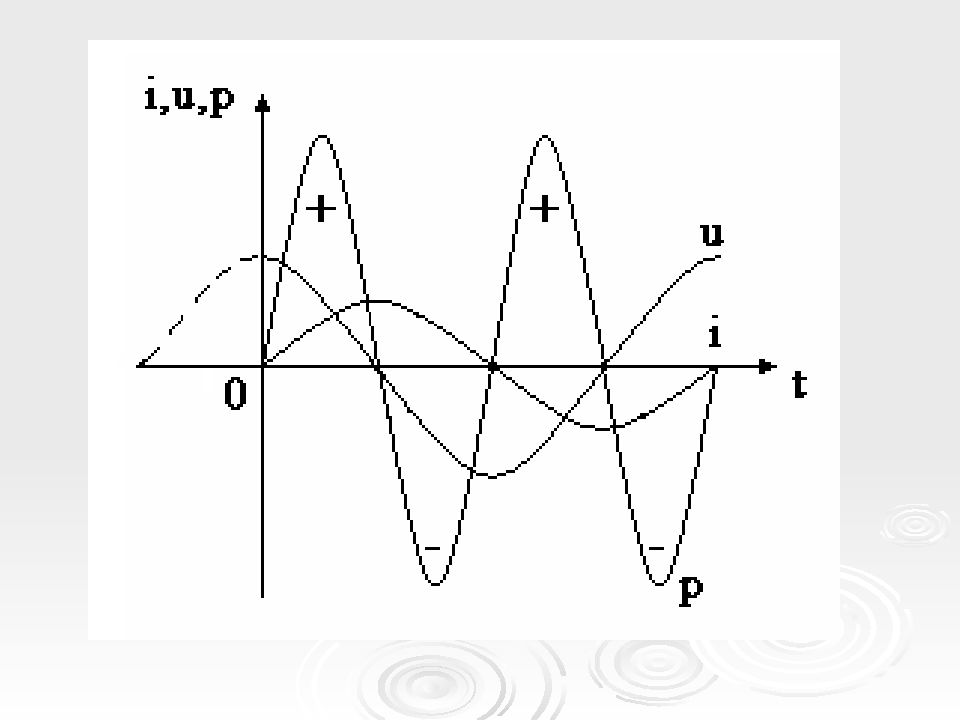
Если ток синусоидальный i = I m sin ω t, то тогда u = U Lm sin ( ω t+ π /2) U Lm = ω L I m Величина Х L = ω L – индуктивное сопротивление, Ом. Напряжение на индуктивном элементе по фазе опережает ток на угол φ = π /2.
Слайд 26: Реактивная мощность в цепи с индуктивностью
Мгновенная мощность для цепи с идеальной катушкой индуктивности определяется Мощность в цепи синусоидального тока с идеальной катушкой индуктивности изменяется по синусоидальному закону с двойной частотой
Слайд 27
Среднее значение этой мощности за период, т.е. активная потребляемая мощность, равно нулю. В 1-ю и 3-ю четверти периода мощность источника накапливается в магнитном поле индуктивности, а во 2-ю и 4-ю – возвращается к источнику. Мощность не потребляется, а колеблется между источником и катушкой индуктивности, загружая источник и провода. Такая колеблющаяся мощность, в отличие от активной, называется реактивной.
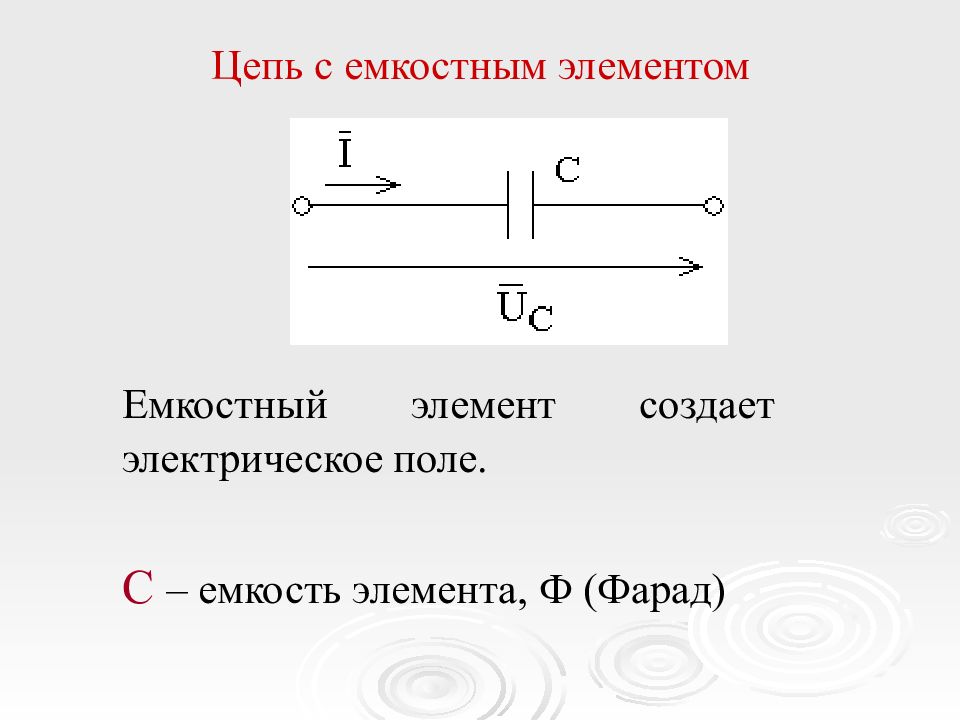
Слайд 28: Цепь с емкостным элементом
Емкостный элемент создает электрическое поле. C – емкость элемента, Ф (Фарад)
Слайд 29
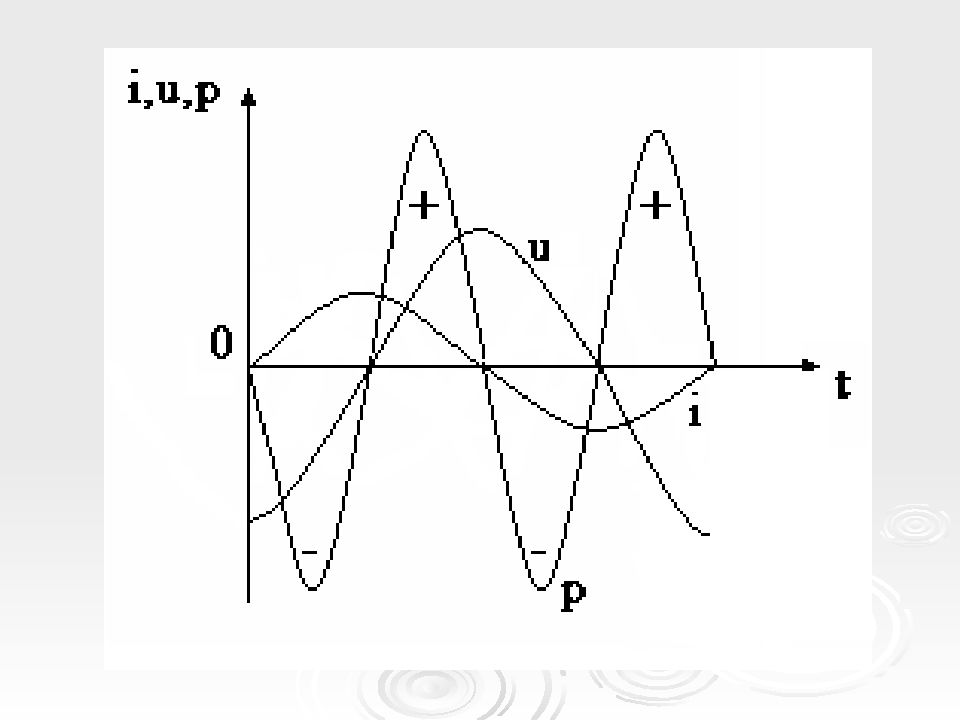
Если в цепи проходит ток i= I m sin ω t, то тогда напряжение то есть напряжение отстает от тока на угол π /2.
Слайд 30
Математическое выражение закона Ома Знаменатель этого выражения является ёмкостным сопротивлением Ёмкостное сопротивление - это противодействие, которое оказывает напряжение заряженного конденсатора напряжению, приложенному к нему. или
Слайд 31: Реактивная мощность в цепи с идеальным конденсатором
Мгновенная мощность в цепи с конденсатором Мощность изменяется по синусоидальному закону с двойной частотой.
Последний слайд презентации: ЭЛЕКТРИЧЕСКИЕ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА
Во 2-ю и 4-ю четверти периода мощность источника накапливается в электрическом поле конденсатора. В 1-ю и 3-ю четверти эта мощность из электрического поля конденсатора возвращается к источнику. Происходит колебание мощности между источником и конденсатором.