ЭЛЕМЕНТЫ АЛГЕБРЫ ЛОГИКИ МАТЕМАТИЧЕСКИЕ ОСНОВЫ ИНФОРМАТИКИ
Ключевые слова алгебра логики высказывание логическая операция конъюнкция дизъюнкция отрицание логическое выражение
Клод Шеннон (1916-2001). Его исследования позволили применить алгебру логики в вычислительной технике Л огик а Аристотель (384-322 до н.э.). Основоположник формальной логики (понятие, суждение, умозаключение). Джордж Буль (1815-1864). Создал новую область науки - Математическую логику (Булеву алгебру или Алгебру высказываний).
Алгебра - наука об общих операциях, аналогичных сложению и умножению, которые могут выполняться над разнообразными математическими объектами – числами, многочленами, векторами и др. Алгебра
Высказывание - это предложение на любом языке, содержание которого можно однозначно определить как истинное или ложное. В русском языке высказывания выражаются повествовательными предложениями: Земля вращается вокруг Солнца. Москва - столица. Побудительные и вопросительные предложения высказываниями не являются. Без стука не входить! Откройте учебники. Ты выучил стихотворение? Высказывание Но не всякое повествовательное предложение является высказыванием: Это высказывание ложное.
Высказывание или нет? Зимой идет дождь. Снегири живут в Крыму. Кто к нам пришел? У треугольника 5 сторон. Как пройти в библиотеку? Переведите число в десятичную систему. Запишите домашнее задание
Алгебра логики определяет правила записи, вычисления значений, упрощения и преобразования высказываний. В алгебре логики высказывания обозначают буквами и называют логическими переменными. Если высказывание истинно, то значение соответствующей ему логической переменной обозначают единицей ( А = 1 ), а если ложно - нулём ( В = 0 ). 0 и 1 называются логическими значениями. Алгебра логики
Простые и сложные высказывания Высказывания бывают простые и сложные. Высказывание называется простым, если никакая его часть сама не является высказыванием. Сложные (составные) высказывания строятся из простых с помощью логических операций. Название логической операции Логическая связка Инверсия (отрицание) «не»; «неверно, что» Конъюнкция «и»; «а»; «но»; «хотя» Дизъюнкция «или»
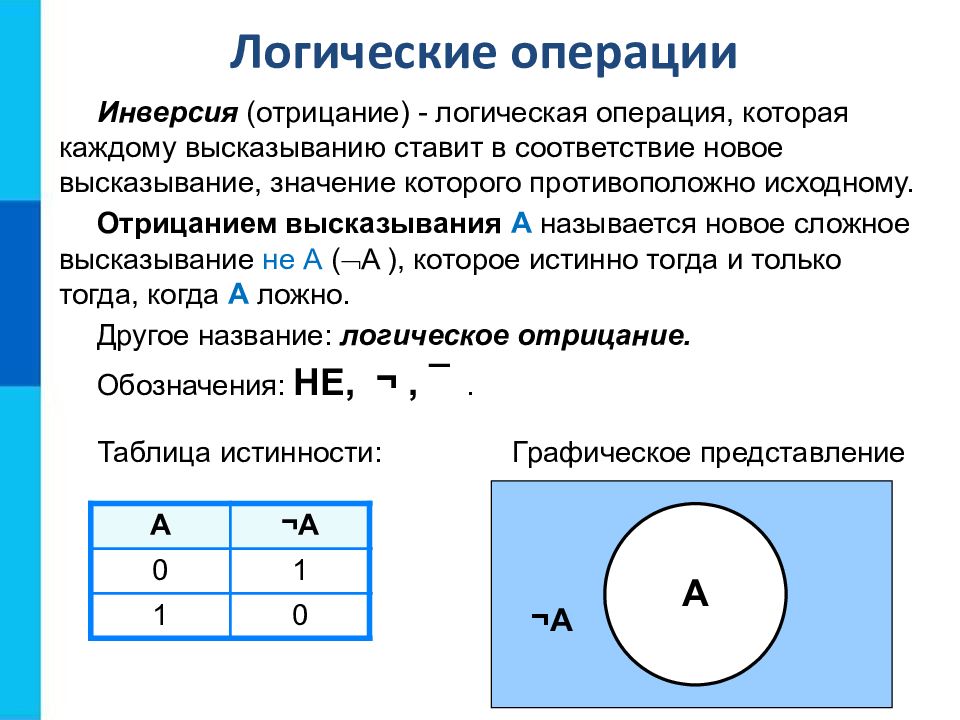
Инверсия (отрицание) - логическая операция, которая каждому высказыванию ставит в соответствие новое высказывание, значение которого противоположно исходному. Отрицанием высказывания A называется новое сложное высказывание не A ( A ), которое истинно тогда и только тогда, когда A ложно. Другое название: логическое отрицание. Обозначения: НЕ, ¬, ¯. А ¬ А 0 1 1 0 Логические операции Таблица истинности: Графическое представление A ¬ А
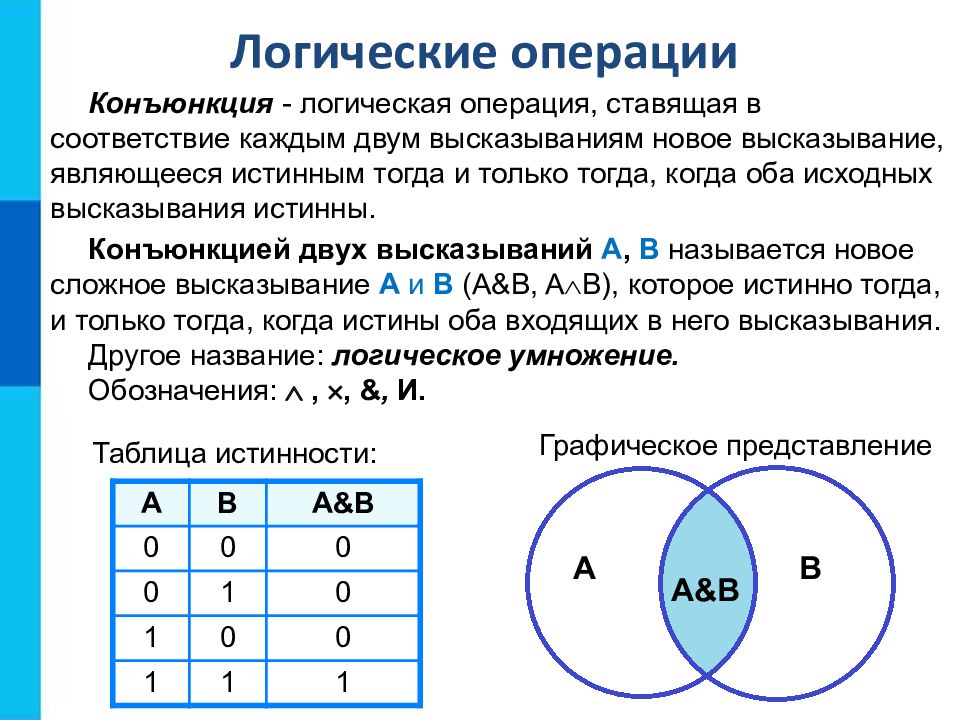
Конъюнкция - логическая операция, ставящая в соответствие каждым двум высказываниям новое высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания истинны. Конъюнкцией двух высказываний A, B называется новое сложное высказывание A и B ( A & B, A B ), которое истинно тогда, и только тогда, когда истины оба входящих в него высказывания. Другое название: логическое умножение. Обозначения: , , &, И. А В А & В 0 0 0 0 1 0 1 0 0 1 1 1 Логические операции Таблица истинности: Графическое представление A B А & В
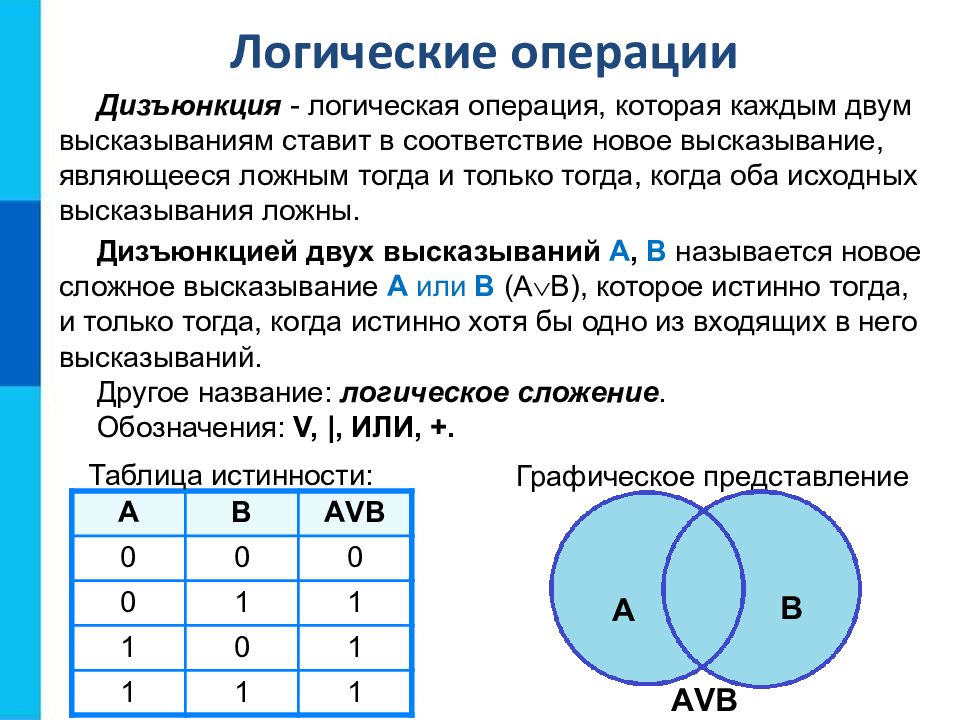
Дизъюнкция - логическая операция, которая каждым двум высказываниям ставит в соответствие новое высказывание, являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны. Дизъюнкцией двух высказываний A, B называется новое сложное высказывание A или B ( A B ), которое истинно тогда, и только тогда, когда истинно хотя бы одно из входящих в него высказываний. Другое название: логическое сложение. Обозначения: V, |, ИЛИ, +. А В А V В 0 0 0 0 1 1 1 0 1 1 1 1 Логические операции Таблица истинности: Графическое представление A B А V В
Логические операции Логические операции имеют следующий приоритет: инверсия, конъюнкция, дизъюнкция.
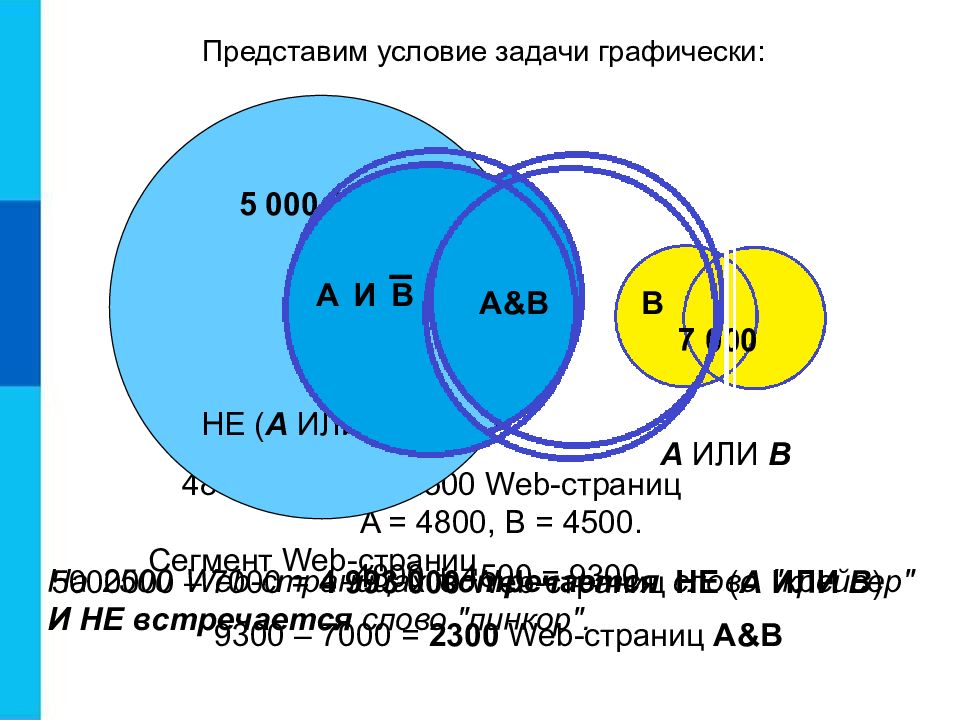
Пусть А = «На Web -странице встречается слово "крейсер"», В = «На Web -странице встречается слово "линкор"». В некотором сегменте сети Интернет 5 000 000 Web -страниц. В нём высказывание А истинно для 4800 страниц, высказывание В - для 4500 страниц, а высказывание А V В - для 7000 страниц. Для какого количества Web -страниц в этом случае будут истинны следующие выражения и высказывание? а) НЕ ( А ИЛИ В ); б) А & B ; в) На Web -странице встречается слово "крейсер" И НЕ встречается слово "линкор". Решаем задачу
5000000 – 7000 = 4 993 000 Web -страниц НЕ ( А ИЛИ В ) A = 4800, B = 4500. 4800 + 4500 = 9300 4800 – 2300 = 2500 Web -страниц Представим условие задачи графически: На 2500 Web-страницах встречается слово "крейсер" И НЕ встречается слово "линкор". 5 000 000 7 000 НЕ ( А ИЛИ В ) Сегмент Web- страниц A B A&B 9300 – 7000 = 2300 Web -страниц A&B A И B А ИЛИ В
Высказывание – это предложение на любом языке, содержание которого можно однозначно определить как истинное или ложное. Основные логические операции, определённые над высказываниями: инверсия, конъюнкция, дизъюнкция. Название логической операции Логическая связка Обозначение Инверсия «не, «неверно, что» ¬, ─ Конъюнкция «и», «а», «но», «хотя» & Дизъюнкция «или» V При вычислении логических выражений сначала выполняются действия в скобках. Приоритет выполнения логических операций: ¬, &, V. Самое главное
Вопросы и задания 1. Объясните, почему следующие предложения не являются высказываниями. 1) Какого цвета этот дом? 2) Число Х не превосходит единицы. 3) 4 Х +3. 4) Посмотрите в окно. 5) Пейте томатный сок! 6) Эта тема скучна. 7) Рикки Мартин - самый популярный певец. 8) Вы были в театре?
Вопросы и задания 2 (№ 77). В следующих высказываниях выделите простые высказывания, обозначив каждое из них буквой. Запишите с помощью букв и знаков логических операций каждое составное высказывание. а) Неверно, что Солнце движется вокруг Земли. б) Число 376 чётное и трёхзначное. в) Новый год мы встретим на даче или на Красной площади. г) Земля имеет форму шара, который из космоса кажется голубым. д) На уроке математики старшеклассники отвечали на вопросы учителя, а также писали самостоятельную работу. е) Зимой мальчики играют в хоккей и не играют в футбол.
Вопросы и задания 3. Постройте отрицания следующих высказываний. 1) Сегодня в театре идёт опера «Евгений Онегин». 2) Каждый охотник желает знать, где сидит фазан. 3) Число 1 есть простое число. 4) Натуральные числа, оканчивающиеся цифрой 0, не являются простыми числами. 5) Неверно, что число 3 не является делителем числа 198. 6) Коля решил все задания контрольной работы. 7) Во всякой школе некоторые ученики интересуются спортом. 8) Некоторые млекопитающие не живут на суше.
Вопросы и задания 4. Пусть А = «Ане нравятся уроки математики», а В = «Ане нравятся уроки химии». Выразите следующие формулы на обычном языке:
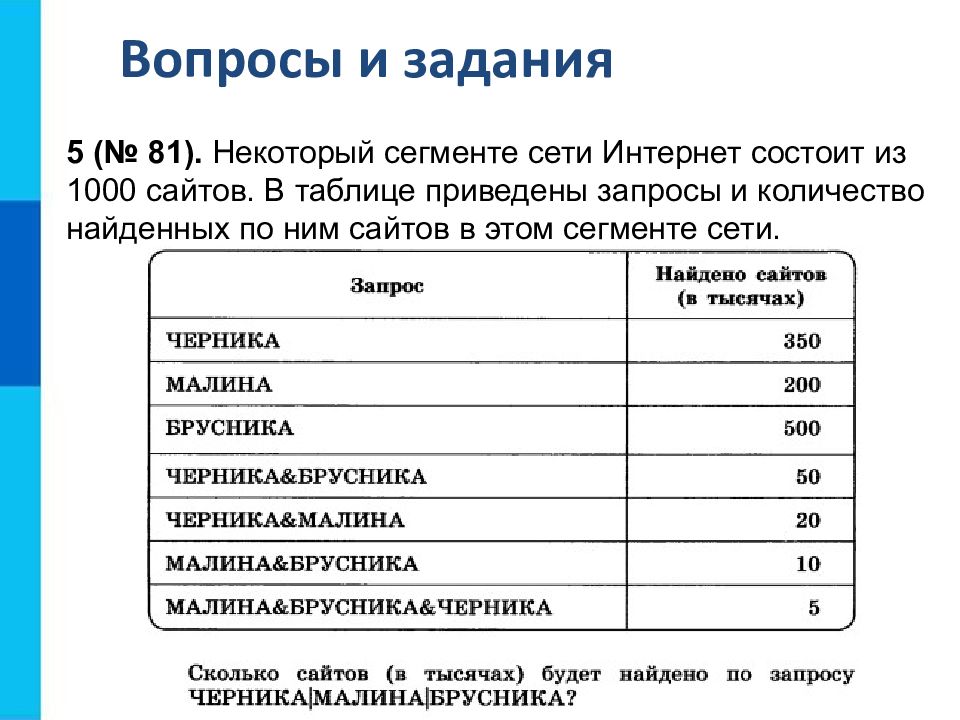
Вопросы и задания 5 (№ 81). Некоторый сегменте сети Интернет состоит из 1000 сайтов. В таблице приведены запросы и количество найденных по ним сайтов в этом сегменте сети.
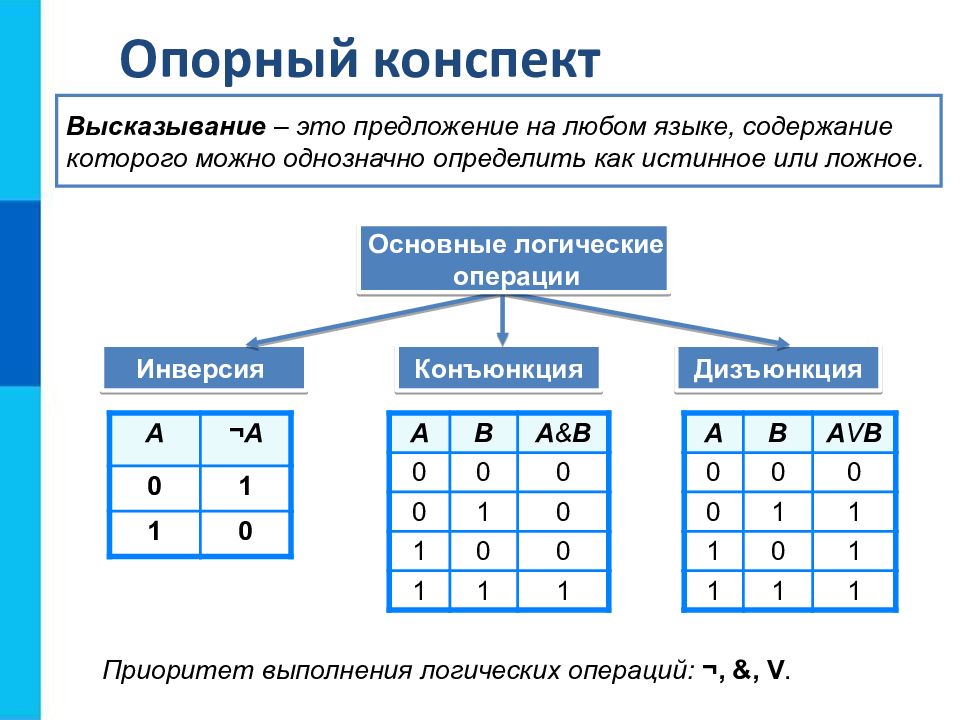
Опорный конспект Инверсия Конъюнкция Дизъюнкция Высказывание – это предложение на любом языке, содержание которого можно однозначно определить как истинное или ложное. А ¬ А 0 1 1 0 A B A & B 0 0 0 0 1 0 1 0 0 1 1 1 A B A V B 0 0 0 0 1 1 1 0 1 1 1 1 Приоритет выполнения логических операций: ¬, &, V. Основные логические операции
Электронные образовательные ресурсы http://school-collection.edu.ru/catalog/res/9e997f40-f285-4369-aa7d-88b892beca45/?interface=catalog&class=51&subject=19 – Элементарные логические операции
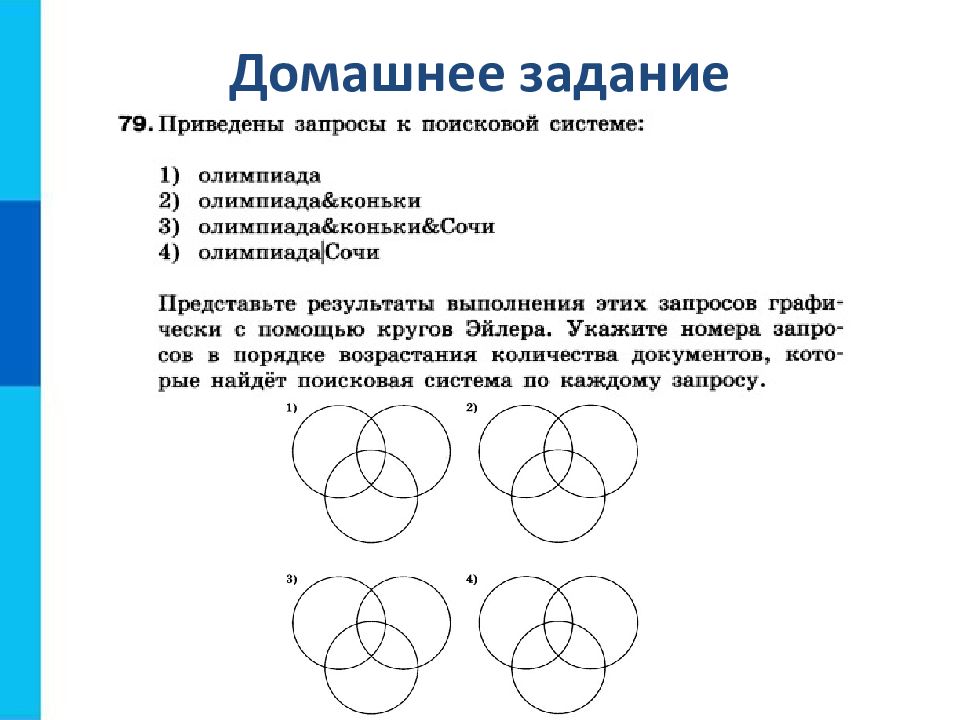
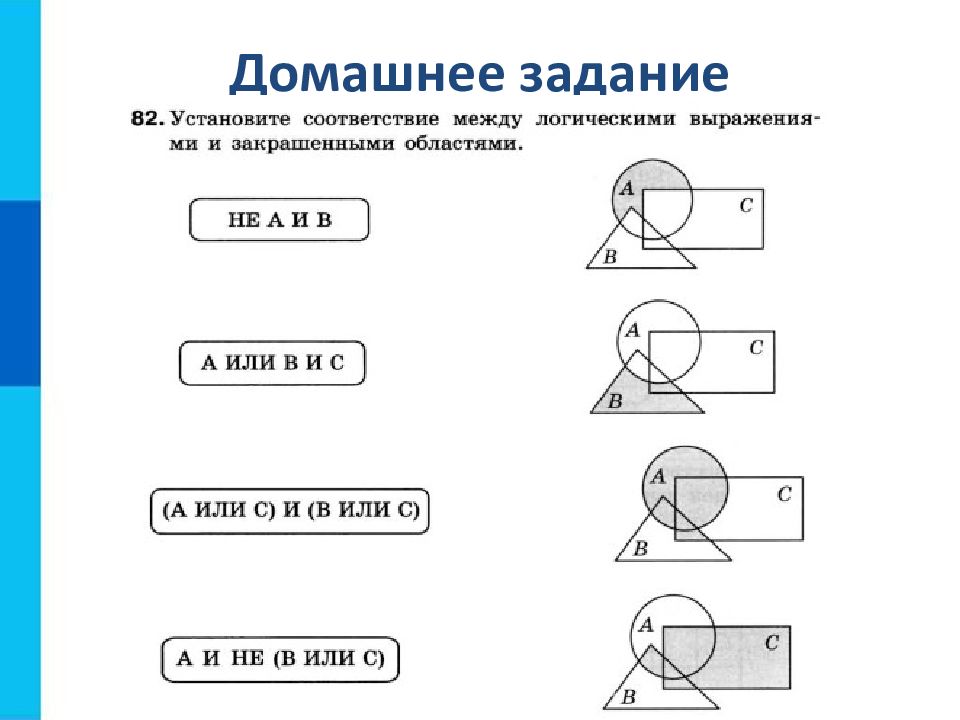
Домашнее задание § 1.3.1, 1.3.2; № 76, 78, 79, 82 в рабочей тетради, выучить таблицы истинности для отрицания, конъюнкции и дизъюнкции.
Домашнее задание
Домашнее задание
Домашнее задание
Домашнее задание
