ЭЛЕМЕНТЫ АЛГЕБРЫ ЛОГИКИ МАТЕМАТИЧЕСКИЕ ОСНОВЫ ИНФОРМАТИКИ
Алгебра - наука об общих операциях, аналогичных сложению и умножению, которые могут выполняться над разнообразными математическими объектами – числами, многочленами, векторами и др. Алгебра
Алгебра логики определяет правила записи, вычисления значений, упрощения и преобразования высказываний. В алгебре логики высказывания обозначают буквами и называют логическими переменными. Если высказывание истинно, то значение соответствующей ему логической переменной обозначают единицей ( А = 1 ), а если ложно - нулём ( В = 0 ). 0 и 1 называются логическими значениями. Алгебра логики
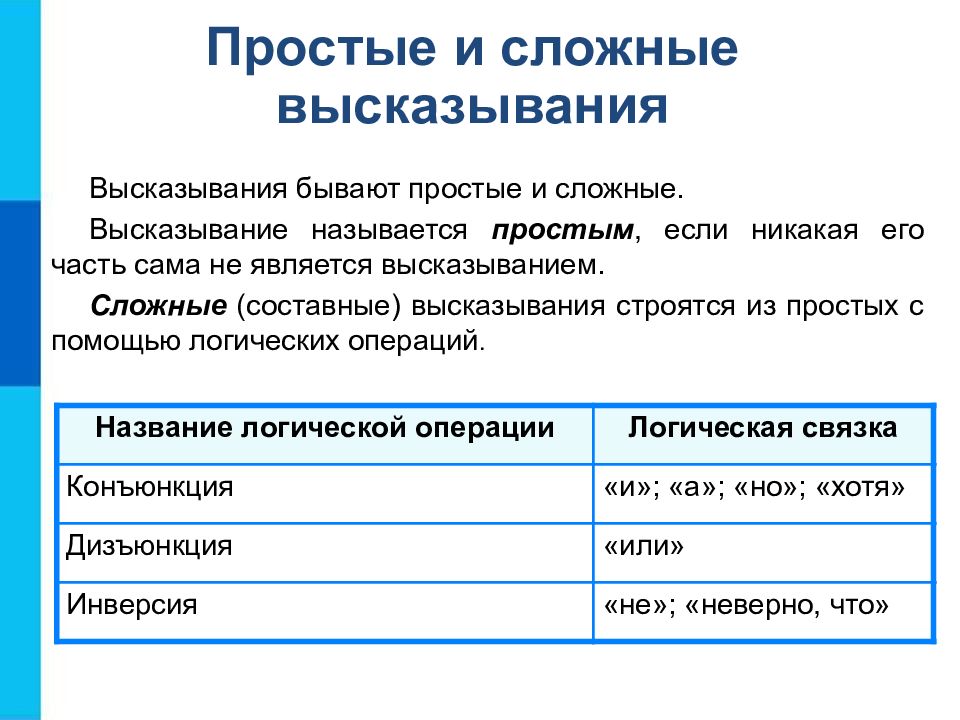
Простые и сложные высказывания Высказывания бывают простые и сложные. Высказывание называется простым, если никакая его часть сама не является высказыванием. Сложные (составные) высказывания строятся из простых с помощью логических операций. Название логической операции Логическая связка Конъюнкция «и»; «а»; «но»; «хотя» Дизъюнкция «или» Инверсия «не»; «неверно, что»
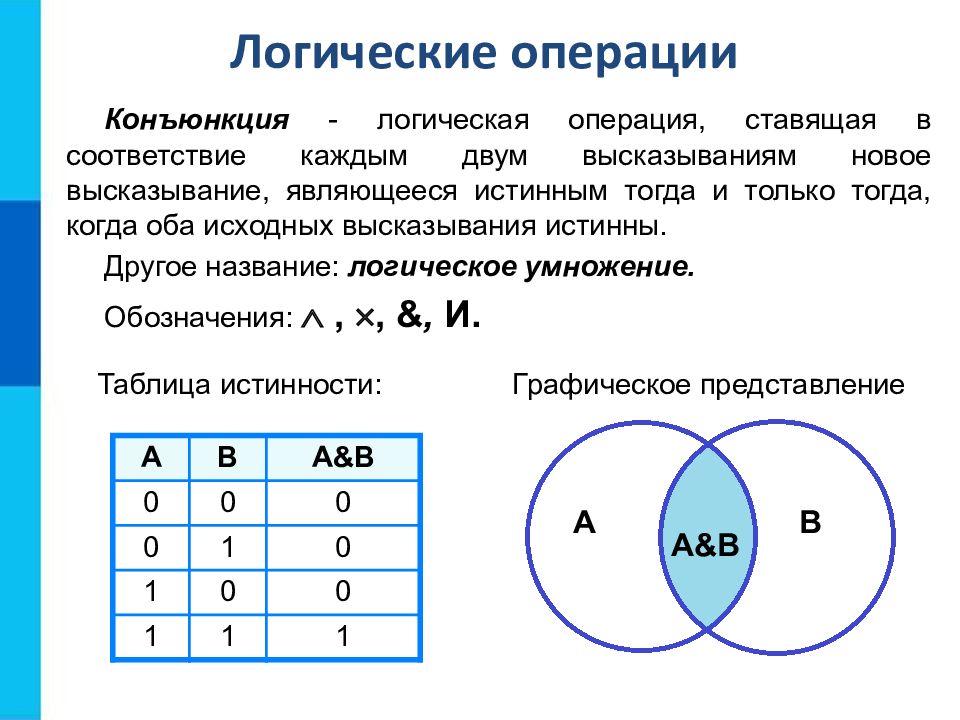
Конъюнкция - логическая операция, ставящая в соответствие каждым двум высказываниям новое высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания истинны. Другое название: логическое умножение. Обозначения: , , &, И. А В А & В 0 0 0 0 1 0 1 0 0 1 1 1 Логические операции Таблица истинности: Графическое представление A B А & В
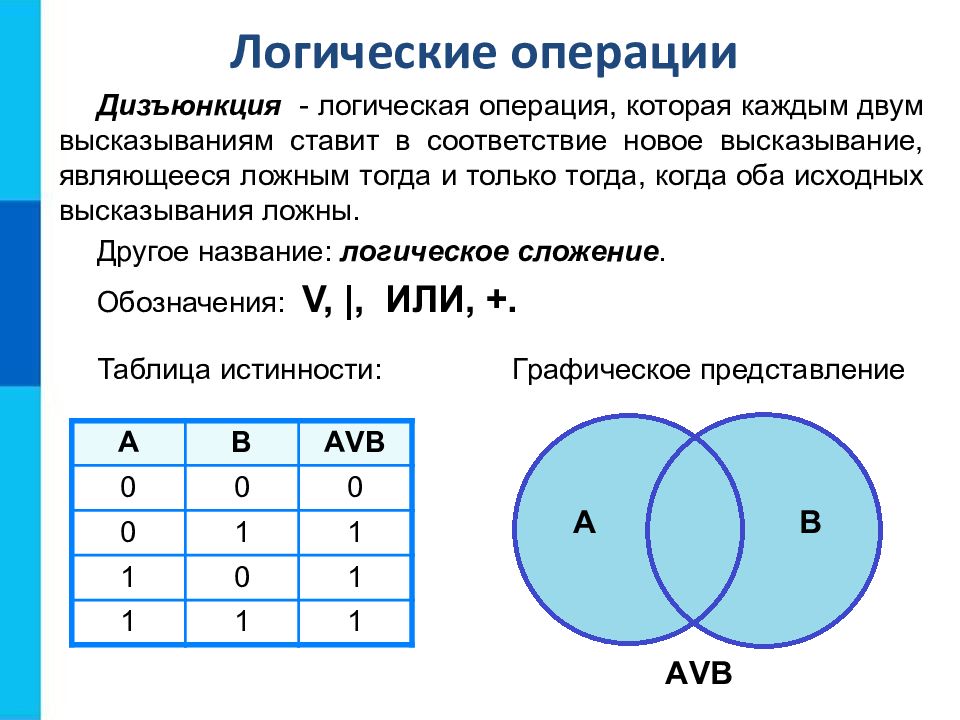
Дизъюнкция - логическая операция, которая каждым двум высказываниям ставит в соответствие новое высказывание, являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны. Другое название: логическое сложение. Обозначения: V, |, ИЛИ, +. А В А V В 0 0 0 0 1 1 1 0 1 1 1 1 Логические операции Таблица истинности: Графическое представление A B А V В
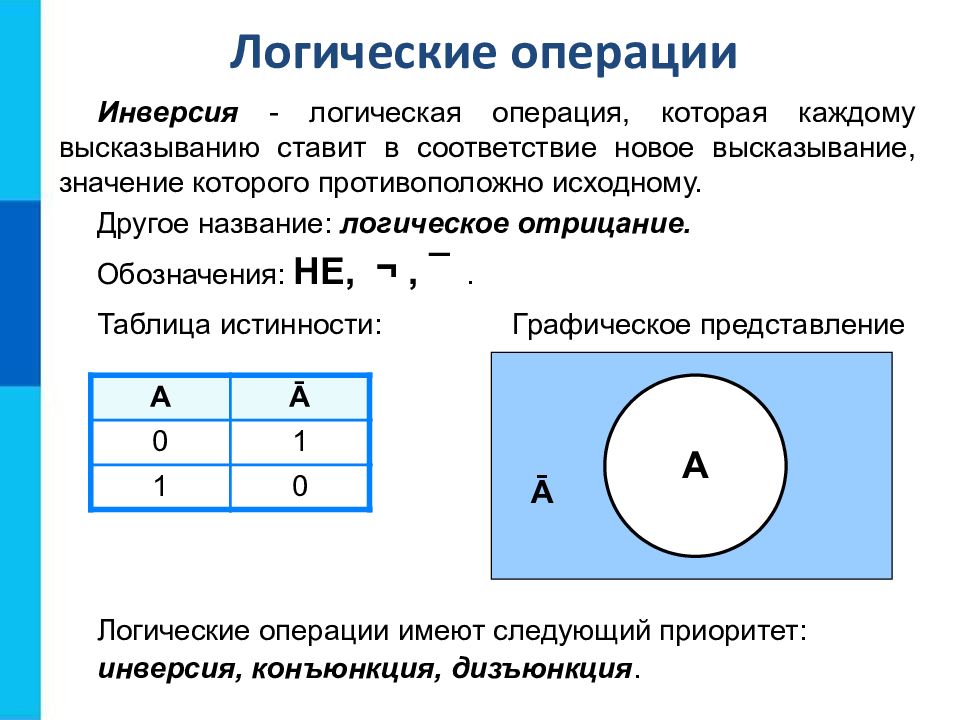
Инверсия - логическая операция, которая каждому высказыванию ставит в соответствие новое высказывание, значение которого противоположно исходному. Другое название: логическое отрицание. Обозначения: НЕ, ¬, ¯. А Ā 0 1 1 0 Логические операции имеют следующий приоритет: инверсия, конъюнкция, дизъюнкция. Логические операции Таблица истинности: Графическое представление A Ā
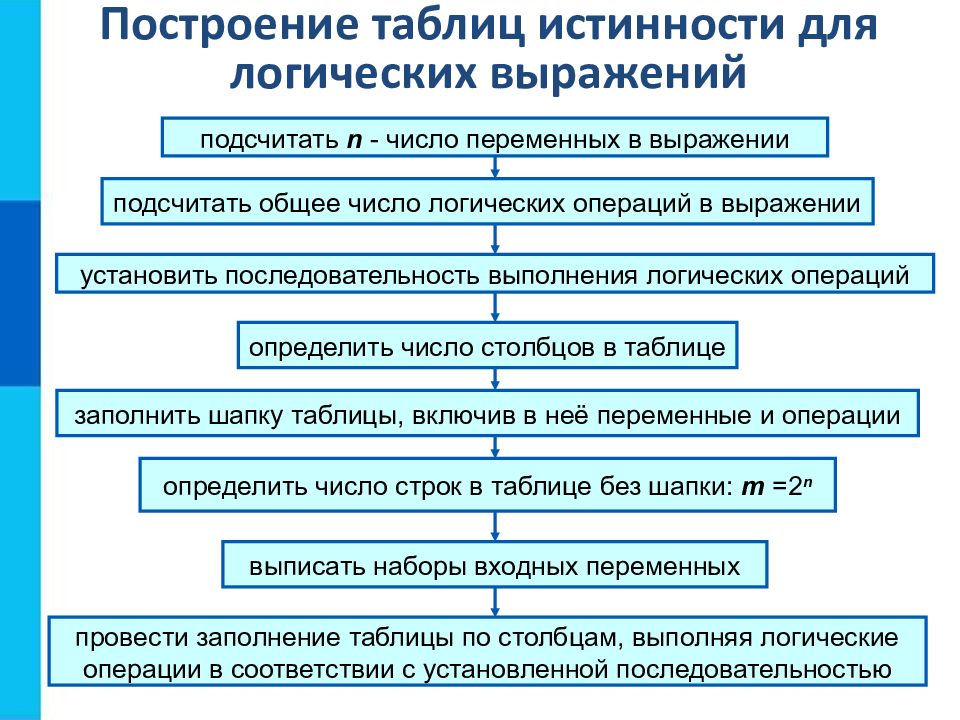
Построение таблиц истинности для логических выражений подсчитать n - число переменных в выражении подсчитать общее число логических операций в выражении установить последовательность выполнения логических операций определить число столбцов в таблице заполнить шапку таблицы, включив в неё переменные и операции определить число строк в таблице без шапки: m =2 n выписать наборы входных переменных провести заполнение таблицы по столбцам, выполняя логические операции в соответствии с установленной последовательностью
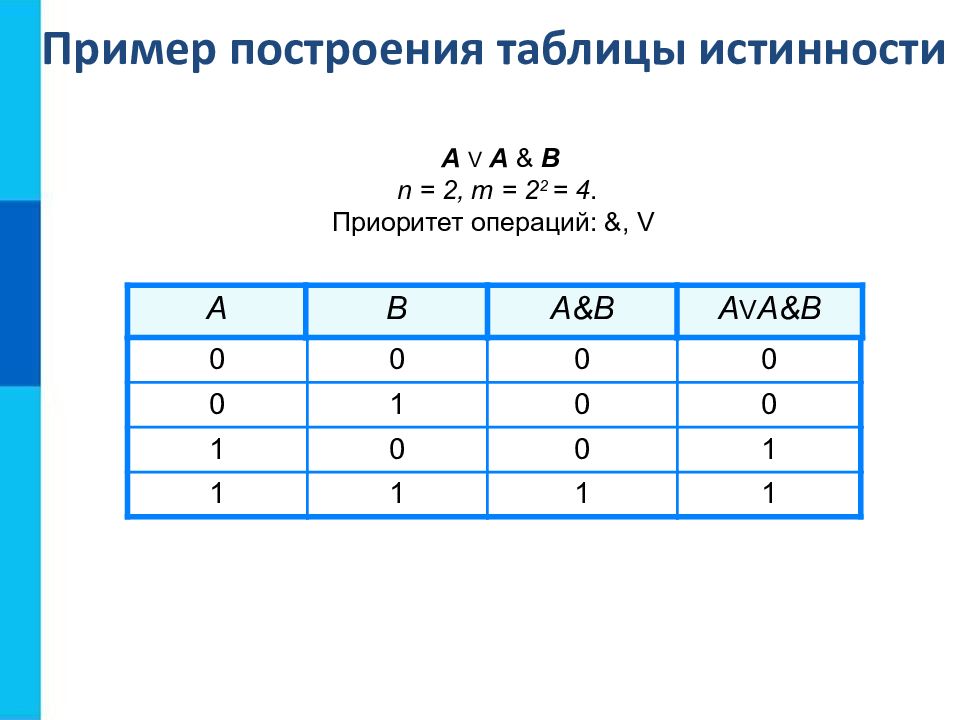
A B A&B A V A&B 0 0 0 0 0 1 0 0 1 0 0 1 1 1 1 1 А V A & B n = 2, m = 2 2 = 4. Приоритет операций: &, V Пример построения таблицы истинности
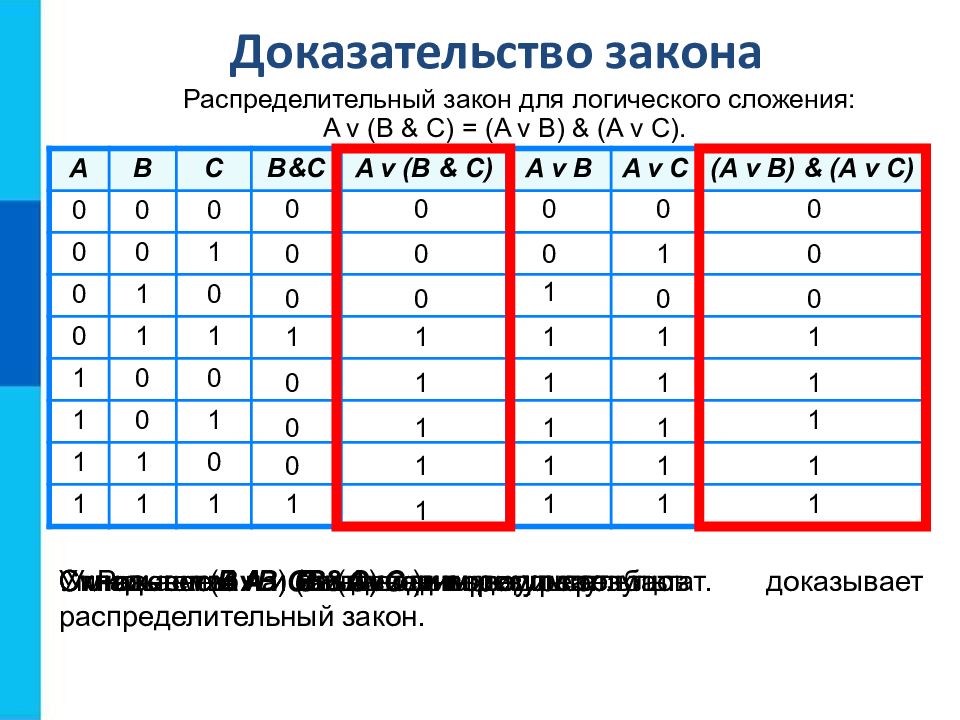
A B C B&C A v (B & C) A v B A v C (A v B) & (A v C) 0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1 Распределительный закон для логического сложения: A v (B & C) = (A v B) & (A v C). Доказательство закона Умножаем В на С и выводим результат. 0 0 0 0 0 0 1 1 Складываем А и В и выводим результат. 0 0 0 1 1 1 1 1 Складываем А и ( В & С ) и выводим результат. 0 0 1 1 1 1 1 1 Складываем А и C и выводим результат. 0 0 1 1 1 1 1 1 Умножаем ( А v B ) на ( A v C ) и выводим результат. 0 0 0 1 1 1 1 1 Равенство выделенных столбцов доказывает распределительный закон.
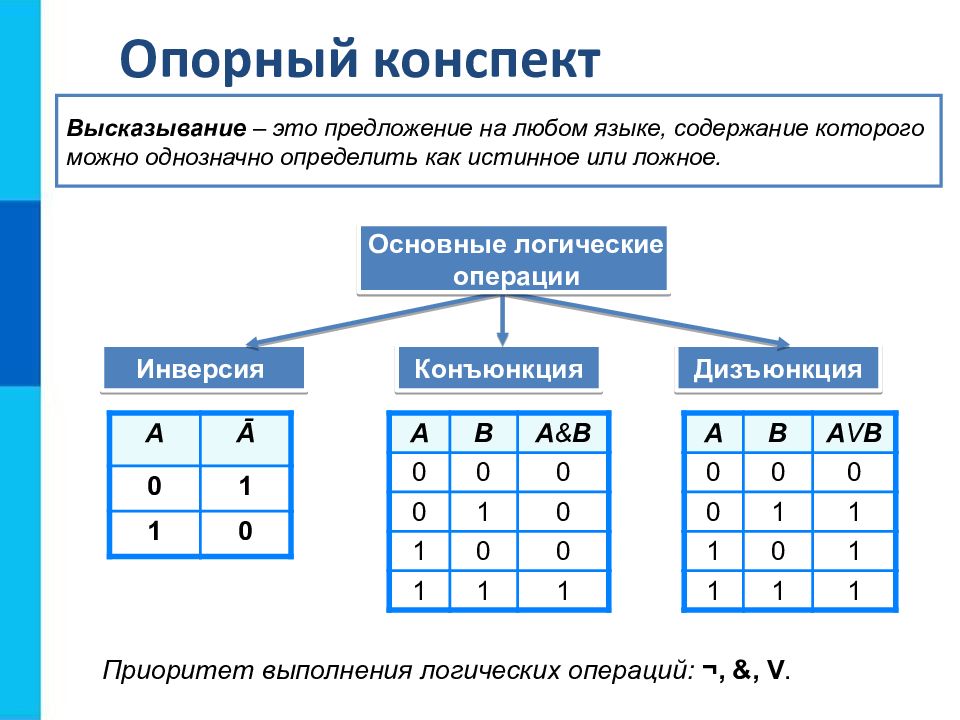
Опорный конспект Инверсия Конъюнкция Дизъюнкция Высказывание – это предложение на любом языке, содержание которого можно однозначно определить как истинное или ложное. А Ā 0 1 1 0 A B A & B 0 0 0 0 1 0 1 0 0 1 1 1 A B A V B 0 0 0 0 1 1 1 0 1 1 1 1 Приоритет выполнения логических операций: ¬, &, V. Основные логические операции
