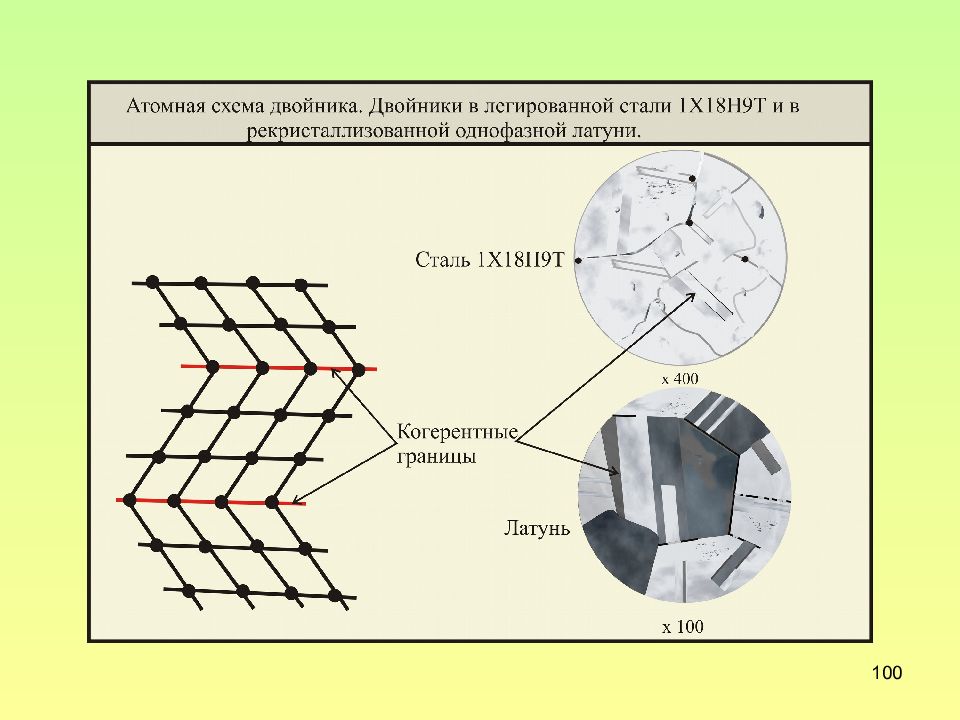
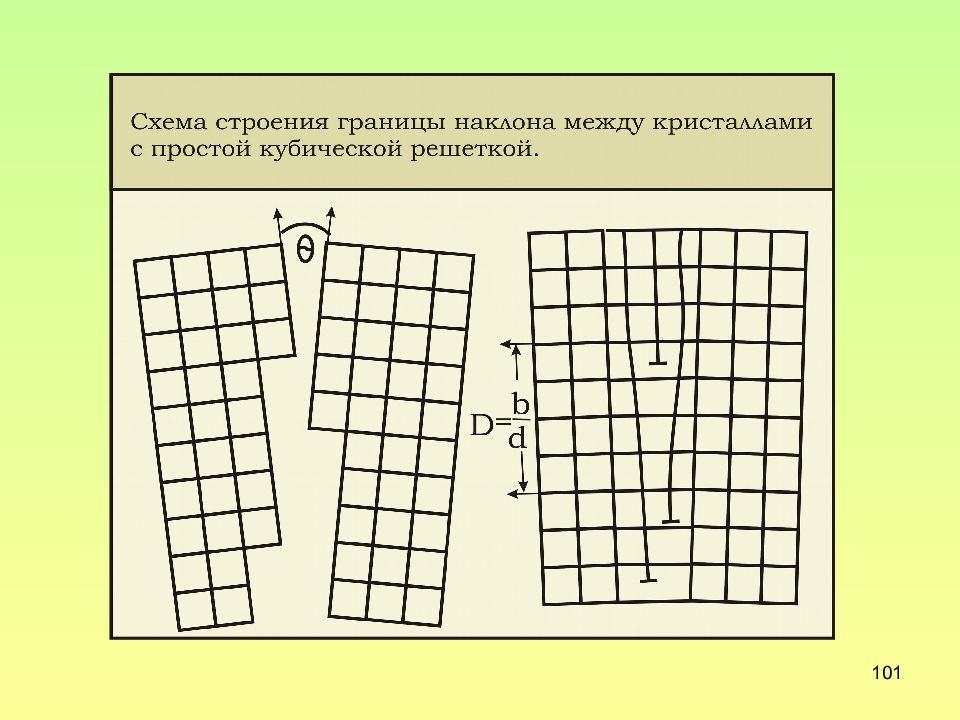
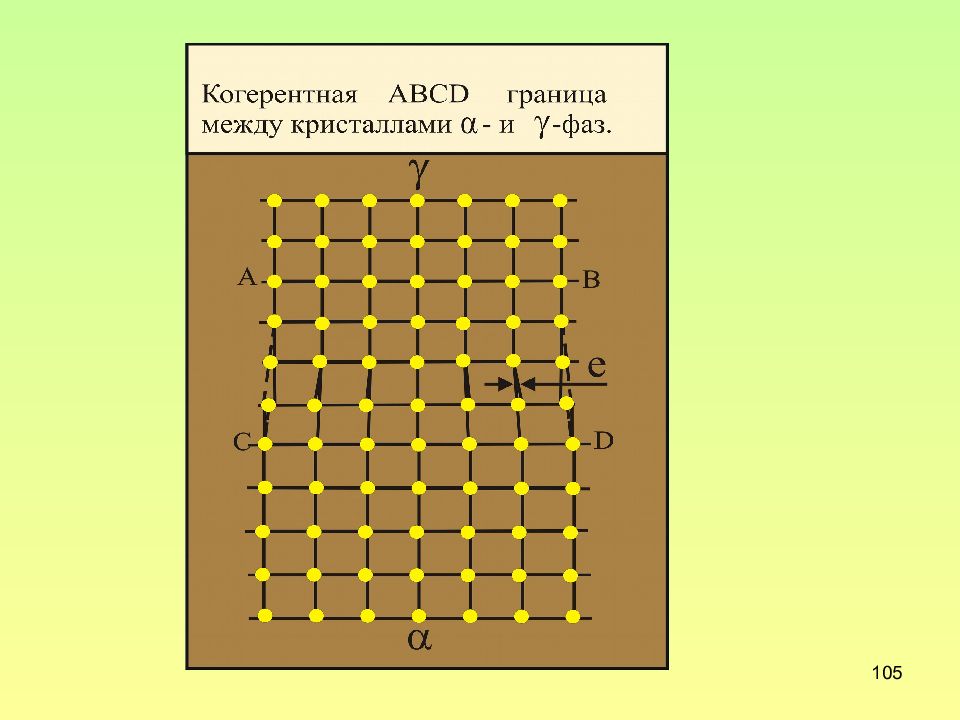
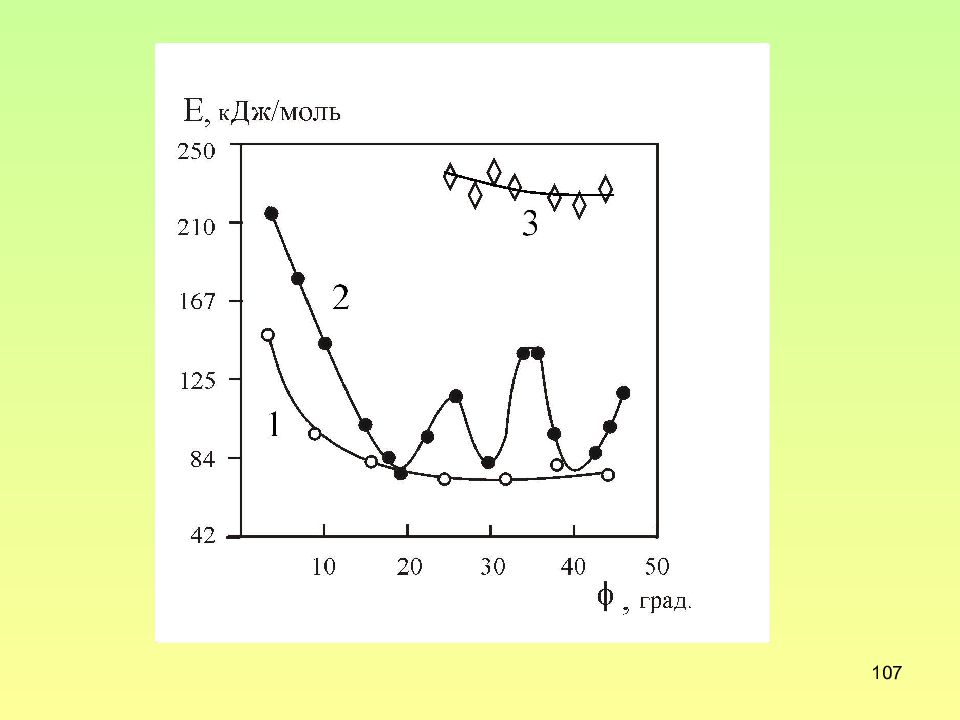
Первый слайд презентации: ФАЗОВЫЕ РАВНОВЕСИЯ И СТРУКТУРООБРАЗОВАНИЕ
1 ФАЗОВЫЕ РАВНОВЕСИЯ И СТРУКТУРООБРАЗОВАНИЕ Лектор: профессор Лилеев А.С. Кафедра физического материаловедения
Слайд 4
4 Материаловедение – наука, изучающая связь между составом, строением и свойствами материалов, закономерностями их изменения при механических, тепловых, химических и других видах воздействия. Фазовое равновесие и структурообразование – основополагающие разделы материаловедения
Слайд 5: СВЯЗЬ МАТЕРИАЛОВЕДЕНИЯ С ДРУГИМИ ПРЕДМЕТАМИ
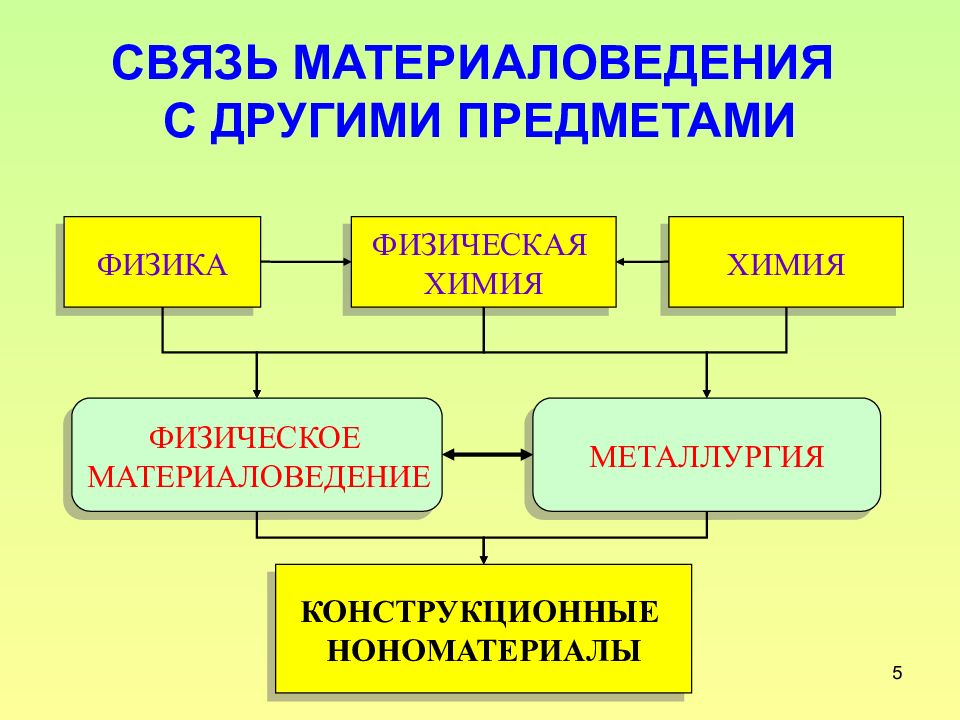
5 СВЯЗЬ МАТЕРИАЛОВЕДЕНИЯ С ДРУГИМИ ПРЕДМЕТАМИ ФИЗИКА ФИЗИЧЕСКАЯ ХИМИЯ ХИМИЯ ФИЗИЧЕСКОЕ МАТЕРИАЛОВЕДЕНИЕ МЕТАЛЛУРГИЯ КОНСТРУКЦИОННЫЕ НОНОМАТЕРИАЛЫ
Слайд 6: Распределение учебного времени
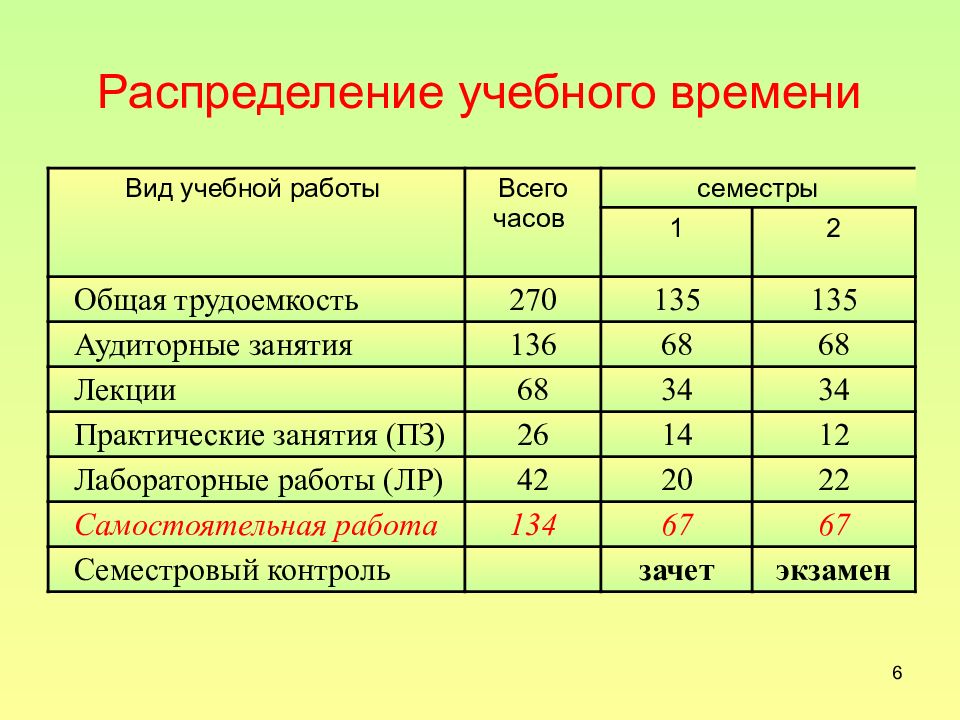
6 Распределение учебного времени Вид учебной работы Всего часов семестры 1 2 Общая трудоемкость 270 135 135 Аудиторные занятия 136 68 68 Лекции 68 34 34 Практические занятия (ПЗ) 26 14 12 Лабораторные работы (ЛР) 42 20 22 Самостоятельная работа 134 67 67 Семестровый контроль зачет экзамен
Слайд 7: Краткое содержание программы
7 Краткое содержание программы Семестр 1. Тема 1. Введение (4 ч) Тема 2. Кристаллическое строение твердого тела и его описание. (8 ч) Тема 3. Кристаллизация. (4 ч) Тема 4. Фазовые равновесия в двойных системах. (6 ч) Тема 5. Превращения в твердом состоянии. (6 ч) Тема 6. Пластическая деформация металлов. (6 ч) ДЗ + коллоквиум по темам 4 и 5
Слайд 8: Краткое содержание программы
8 Краткое содержание программы Семестр 2 Тема 7. Структурообразование в тройных системах. (6 ч) Тема 8. Железо и система железо - углерод. (6 ч) Тема 9. Термическая обработка. (10 ч) Тема 10. Легированные стали. (6 ч) Тема 11. Сплавы на нежелезной основе. (6 ч) ДЗ + контрольная работа по теме 7 ДЗ + коллоквиум по теме 8
Слайд 9: Литература
9 Литература 1. Лившиц Б.Г. Металлография. М.: Металлургия, 1990, ЗЗЗ с. 2.Лилеев А.С., Малютина Е.С. Старикова А.С. «Фазовые равновесия и структуро-образование», Курс лекций, М.:МИСиС, 2010, 88 с.
Слайд 10: К лабораторному практикуму и домашним заданиям
10 К лабораторному практикуму и домашним заданиям Малинина Р.И. и др. Практическая металлография. М., Интермет Инжиниринг, 2002, 233 с. Металлография. Задачник. Часть I. М.: МИСИС, 1996, № 979 Металлография. Задачник. Часть II. М., МИСиС, 1995. № 980. Фазовые равновесия и структурообразование. Сборник задач. М., МИСиС, 2001, № 1650.
Слайд 11: Дополнительная литература
11 Дополнительная литература 1. Лахтин Ю.М. Металловедение и термическая обработка металлов. М.: Металлургия, 1983, 360 с. 2. Металловедение и термическая обработка стали. Справочник. М.: Металлургия, 1983, 367 с.
Слайд 12: Понятие структуры
12 Понятие структуры Структура – ( от лат. строение, порядок, расположение ) – совокупность устойчивых связей объекта, обеспечивающих его целостность и тождественность самому себе. [ Большая Советская Энциклопедия ] Структурирование - способ модельного описания чего- либо, посредством разделения на повторяющиеся структурные части- составляющие, описание которых более просто
Слайд 13: структура металлических тел
13 структура металлических тел 1 Макроструктура – структура, наблюдаемая невооруженным взглядом или при увеличении до 25 раз Фото сечения слитка сплава Pb -50% Sb (по массе) УВЕЛИЧЕНО, высота слитка 2 см
Слайд 14: структура металлических тел
14 структура металлических тел 2 Микроструктура – - структура, наблюдаемая при металлографическом исследовании с помощью светового микроскопа, т.е. при увеличении до 1600 раз; Фото микроструктуры сплава Sb +30% Cu ( по массе) УВЕЛИЧЕНО, D =0.64 мм
Слайд 15: структура металлических тел
15 структура металлических тел 3 Атомно-кристаллическая структура (чаще используют термин строение ) – на изучении этого уровня мы остановимся далее подробнее
Слайд 16: структура металлических тел
16 структура металлических тел 4 Электронная структура – структура, изучающая особенности взаимодействие частиц сравнимых по размеру с электроном в веществе.
Слайд 17
17 Тема 2. Кристаллическое строение твердого тела и его описание. (8 часов)
Слайд 18: Атомно-кристаллическое строение твердых тел
18 Атомно-кристаллическое строение твердых тел При описании атомно-кристаллического строения твердое тело рассматривается как состоящее из атомов, которые уложены в параллелепипеды, которые многократно повторяются в пространстве. Вершины параллелепипедов совпадают с центрами атомов
Слайд 19: ХАРАКТЕРИСТИКИ КРИСТАЛЛИЧЕСКОЙ РЕШЕТКИ
19 ХАРАКТЕРИСТИКИ КРИСТАЛЛИЧЕСКОЙ РЕШЕТКИ Пространственная решетка характеризуется элементарной ячейкой – минимальным по объему параллелепипедом, достаточным для её описания Длины ребер элементарной ячейки называются периодами решетки.
Слайд 20: Геометрические характеристики элементарной ячейки
20 Геометрические характеристики элементарной ячейки Элементарная ячейка в трехмерном пространстве характеризуется тремя периодами решетки – a, b, c и тремя углами : a – между ребрами b и c ; b – между ребрами a и c ; g – между ребрами a и b.
Слайд 21: ТИПЫ КРИСТАЛЛИЧЕСКИХ РЕШЕТОК
21 ТИПЫ КРИСТАЛЛИЧЕСКИХ РЕШЕТОК Пространственные решетки различных металлических материалов можно разделить на семь систем – сингоний, отличающихся соотношением величин сторон и углов Сингония Соотношение сторон Соотношение углов Кубическая а = b = с a=b=g =90 о Гексагональная а = b ¹ с a=b =90 о ; g =120 о Тетрагональная а = b ¹ с a=b=g= 90 о Тригональная (ромбоэдрическая) а=b=с a=b=g¹ 90 о Ромбическая а ¹ b ¹ с a=b=g =90 о Моноклинная а ¹ b ¹ с a=g= 90 о ; b¹ 90 о Триклинная а ¹ b ¹ с a¹b¹g¹ 90 о
Слайд 22: Решетки Браве
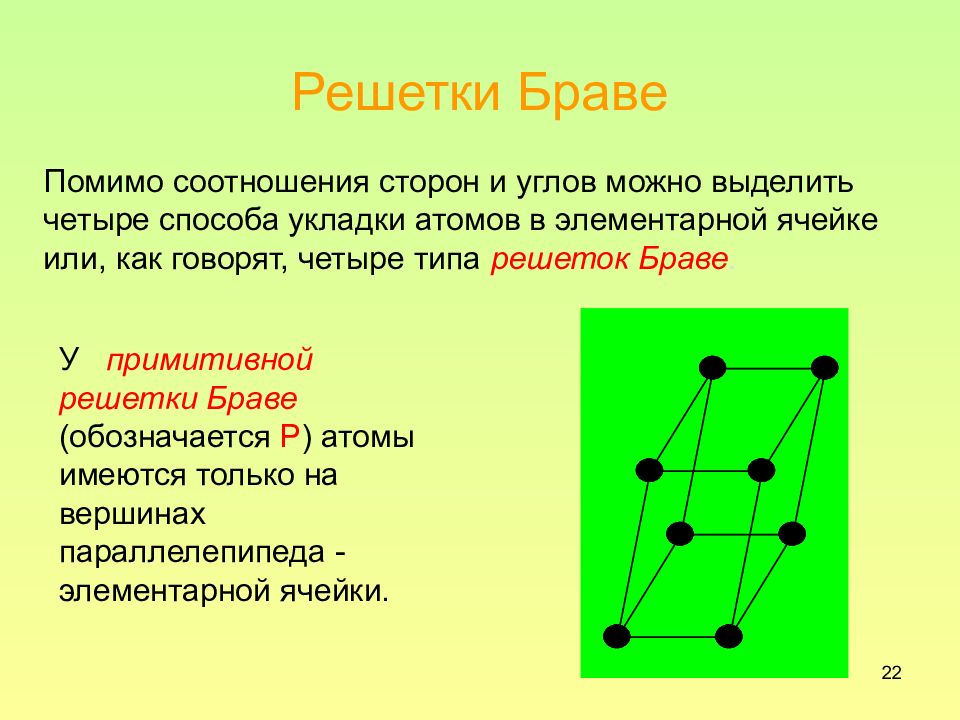
22 Решетки Браве Помимо соотношения сторон и углов можно выделить четыре способа укладки атомов в элементарной ячейке или, как говорят, четыре типа решеток Браве. У примитивной решетки Браве (обозначается Р ) атомы имеются только на вершинах параллелепипеда - элементарной ячейки.
Слайд 23: Решетки Браве
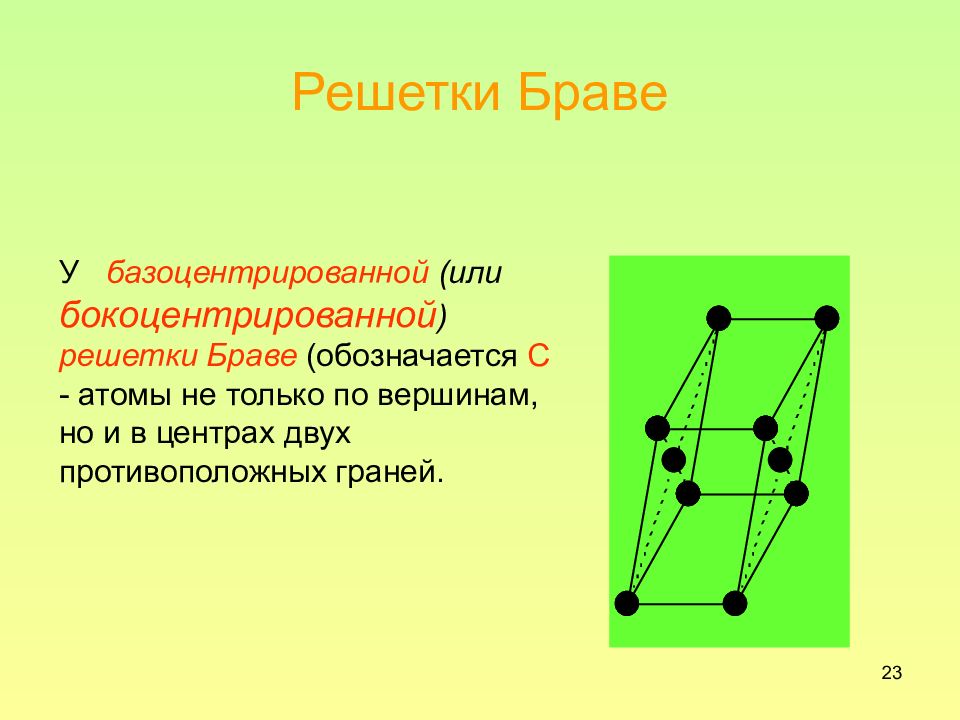
23 Решетки Браве У базоцентрированной (или бокоцентрированной ) решетки Браве (обозначается С - атомы не только по вершинам, но и в центрах двух противоположных граней.
Слайд 24: Решетки Браве
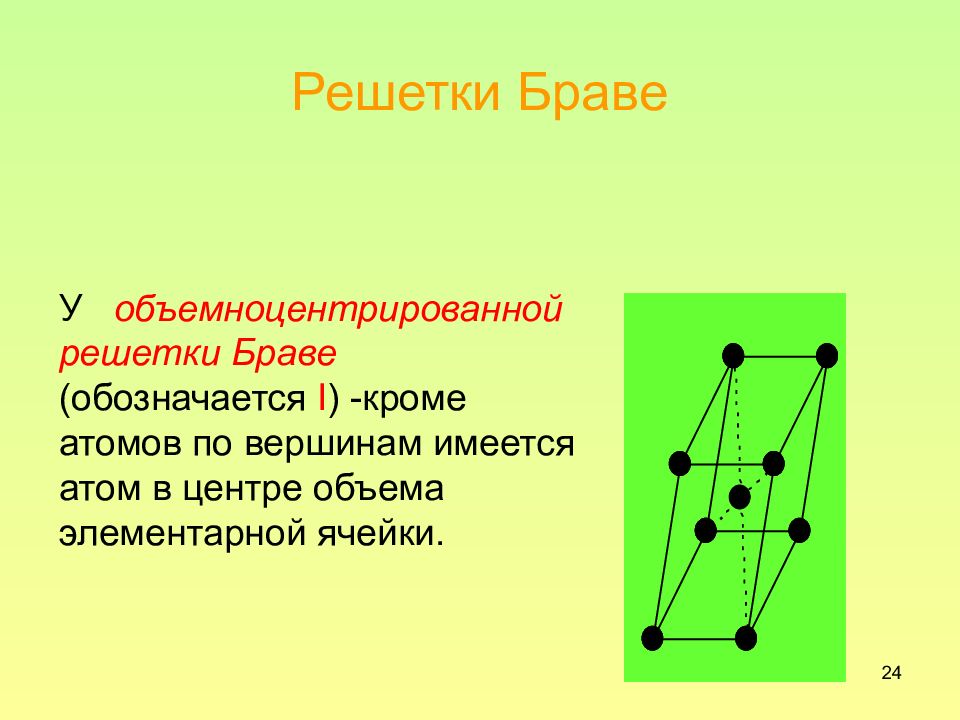
24 Решетки Браве У объемноцентрированной решетки Браве (обозначается I ) - кроме атомов по вершинам имеется атом в центре объема элементарной ячейки.
Слайд 25: Решетки Бравэ
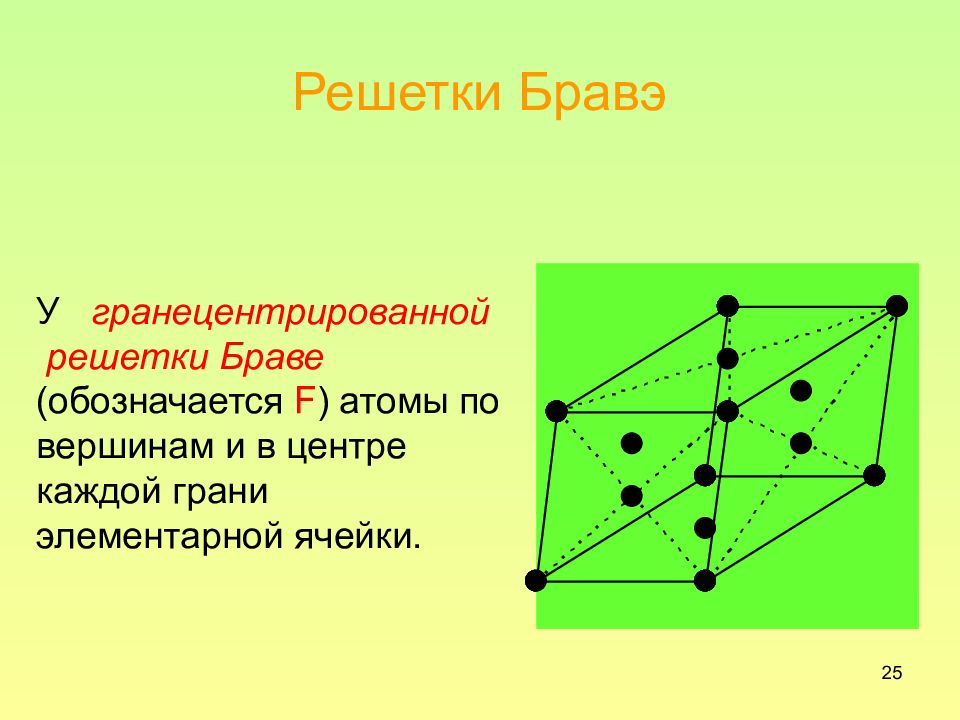
25 Решетки Бравэ У гранецентрированной решетки Браве (обозначается F ) атомы по вершинам и в центре каждой грани элементарной ячейки.
Слайд 26: Решетки Браве в 7 сингониях
26 Решетки Браве в 7 сингониях Сингония Тип решетки Браве Р С I F Кубическая + + + Гексагональная + Тетрагональная + + Тригональная (ромбоэдрическая) + Ромбическая + + + + Моноклинная + + Триклинная + Итого 14 типов элементарной ячейки
Слайд 27: Комментарий :
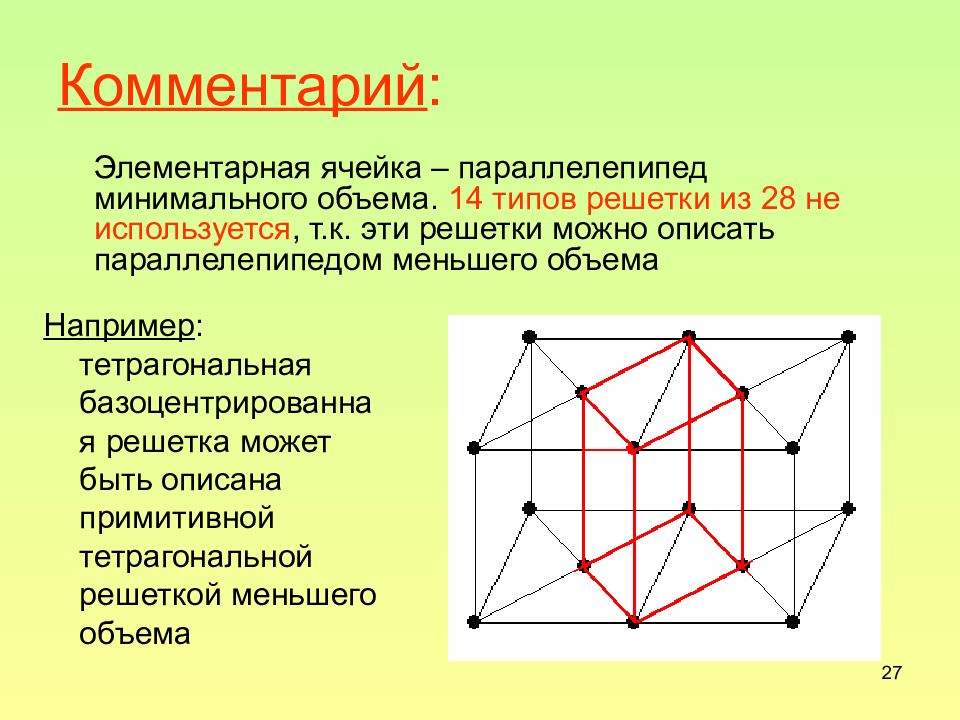
27 Комментарий : Элементарная ячейка – параллелепипед минимального объема. 14 типов решетки из 28 не используется, т.к. эти решетки можно описать параллелепипедом меньшего объема Например : тетрагональная базоцентрированная решетка может быть описана примитивной тетрагональной решеткой меньшего объема
Слайд 28: Другие характеристики элементарной ячейки
28 Другие характеристики элементарной ячейки Кроме геометрических характеристик используются характеристики, отражающие уровень сил связи в решетки и плотность заполнения решетки веществом.
Слайд 29: Координационное число (КЧ)
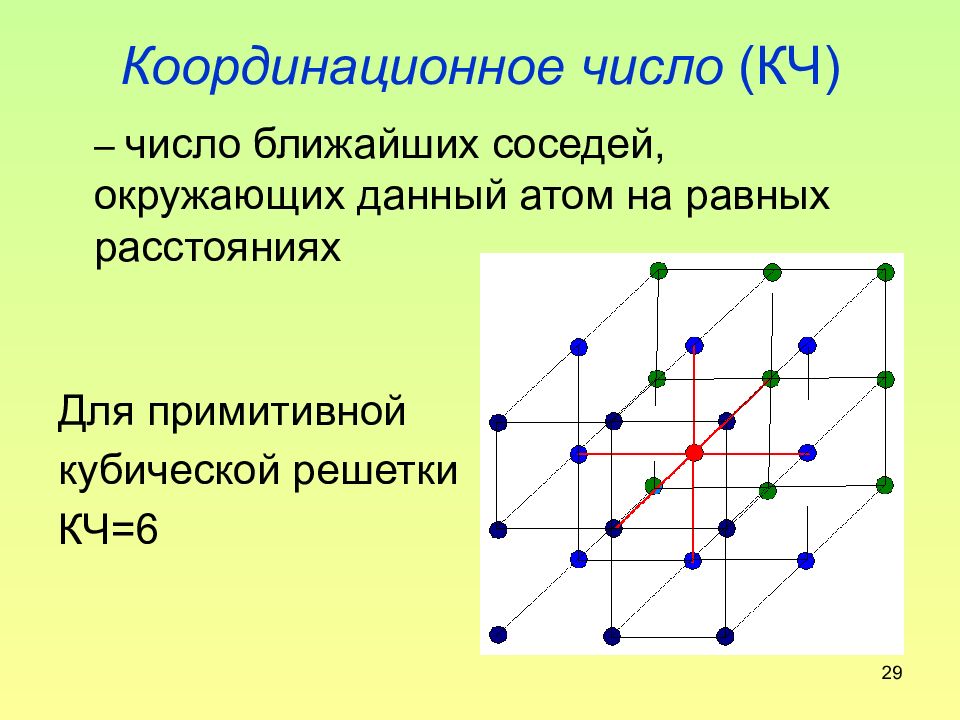
29 Координационное число (КЧ) – число ближайших соседей, окружающих данный атом на равных расстояниях Для примитивной кубической решетки КЧ=6
Слайд 30: Координационное число (КЧ)
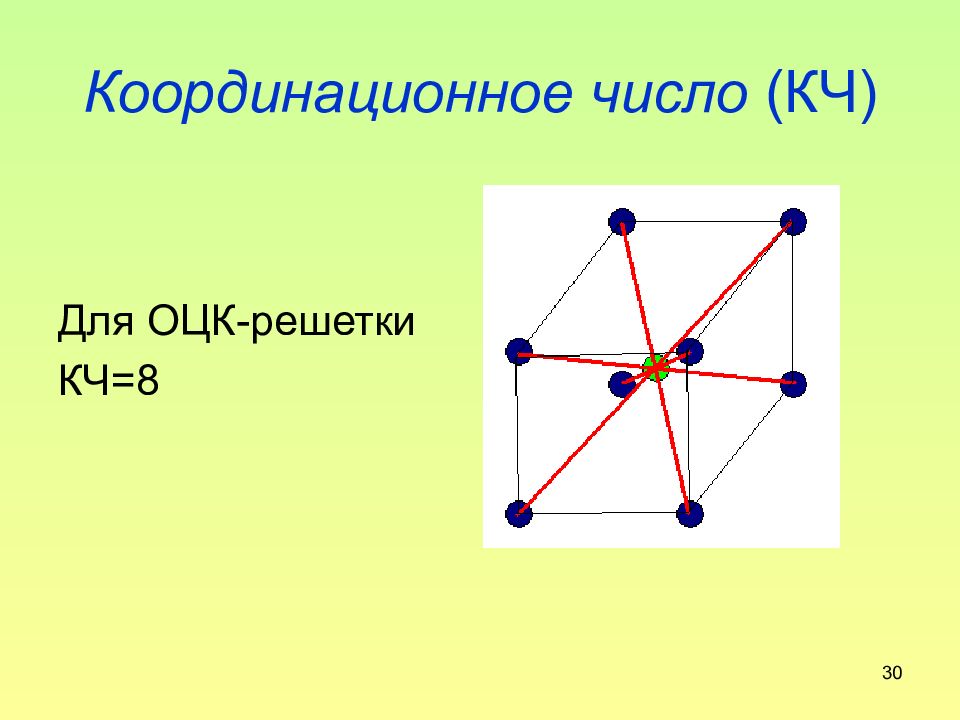
30 Координационное число (КЧ) Для ОЦК-решетки КЧ=8
Слайд 31: Координационное число (КЧ)
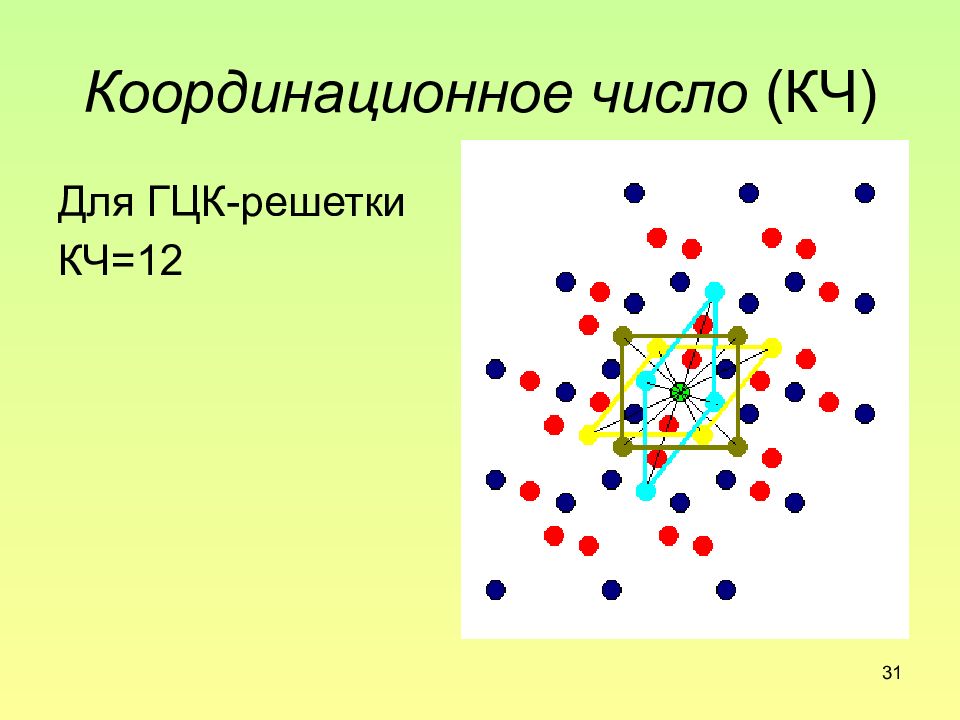
31 Координационное число (КЧ) Для ГЦК-решетки КЧ=12
Слайд 32: Число атомов на ячейку ( n яч )
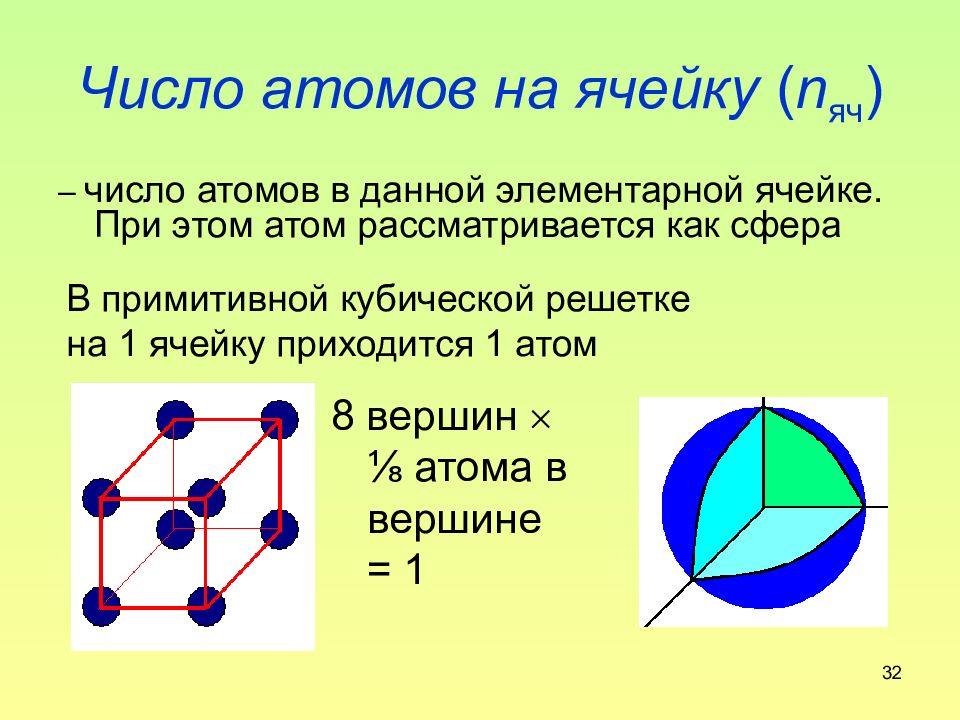
32 Число атомов на ячейку ( n яч ) – число атомов в данной элементарной ячейке. При этом атом рассматривается как сфера В примитивной кубической решетке на 1 ячейку приходится 1 атом 8 вершин ⅛ атома в вершине = 1
Слайд 33: Число атомов на ячейку для ОЦК-решетки
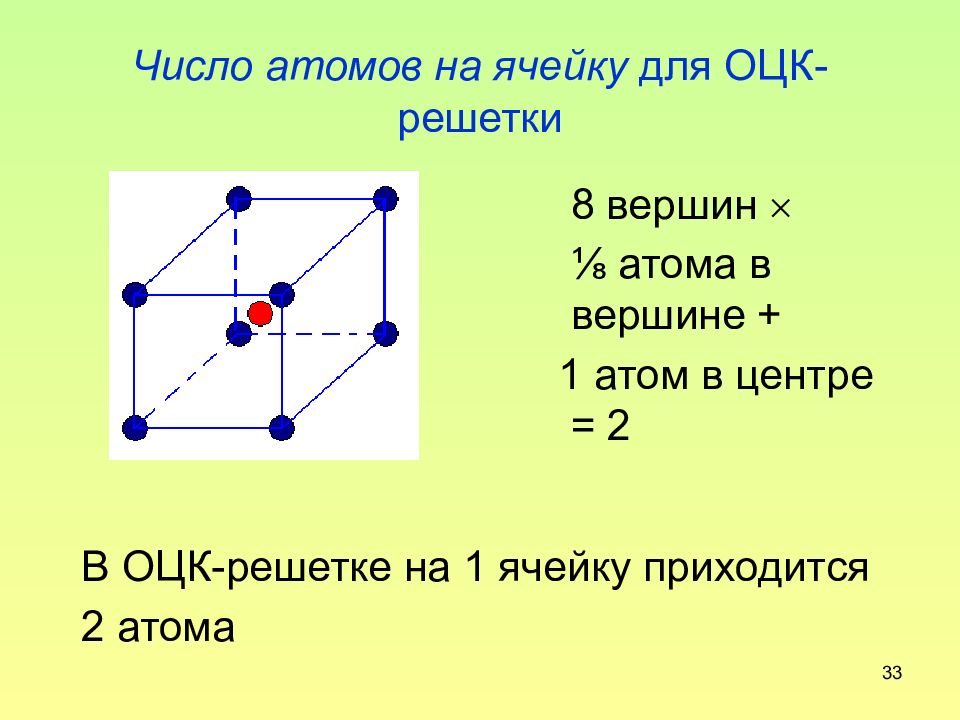
33 Число атомов на ячейку для ОЦК-решетки В ОЦК-решетке на 1 ячейку приходится 2 атома 8 вершин ⅛ атома в вершине + 1 атом в центре = 2
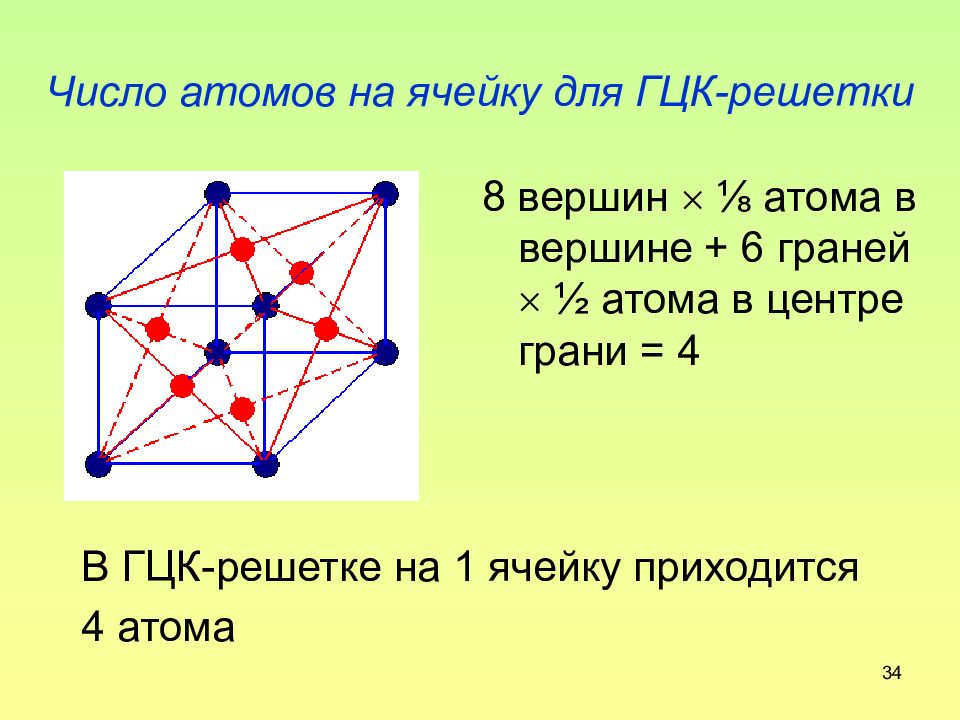
Слайд 34: Число атомов на ячейку для ГЦК-решетки
34 Число атомов на ячейку для ГЦК-решетки В ГЦК-решетке на 1 ячейку приходится 4 атома 8 вершин ⅛ атома в вершине + 6 граней ½ атома в центре грани = 4
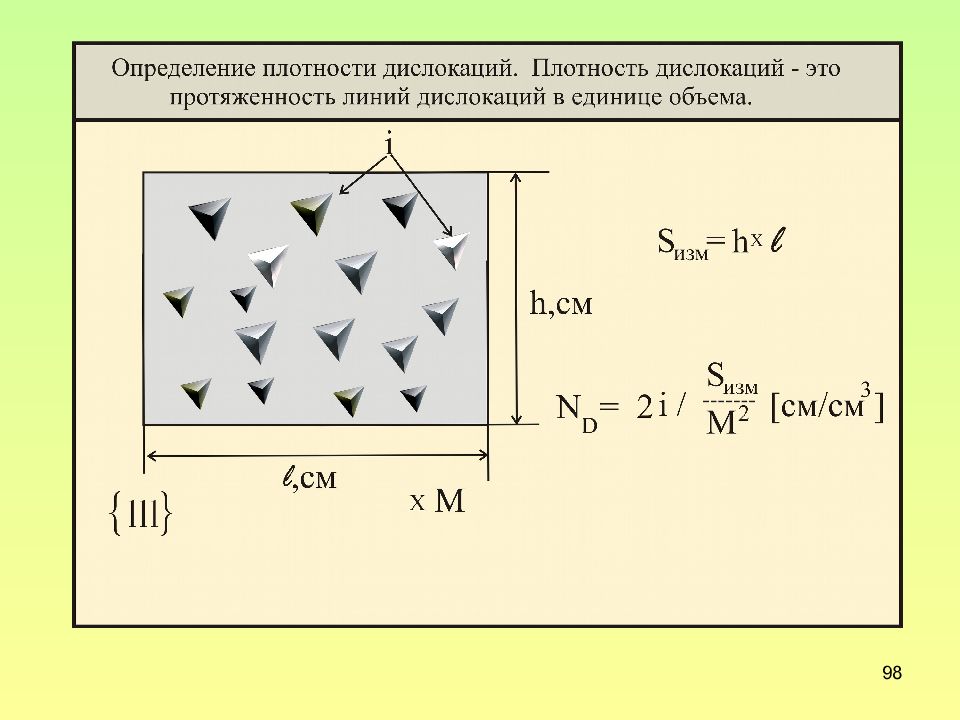
35 Коэффициент заполнения решетки веществом ( h ) – отношение суммарного объема атомов в элементарной ячейке к объему элементарной ячейки, выраженное в процентах =
Слайд 36: Коэффициент заполнения решетки веществом в примитивной кубической решетке
36 Коэффициент заполнения решетки веществом в примитивной кубической решетке В примитивной решетке атомы плотнее всего располагаются по ребрам куба, причем параметр решетки а равен 2 радиусам атома Тогда = =52% a = 2 r
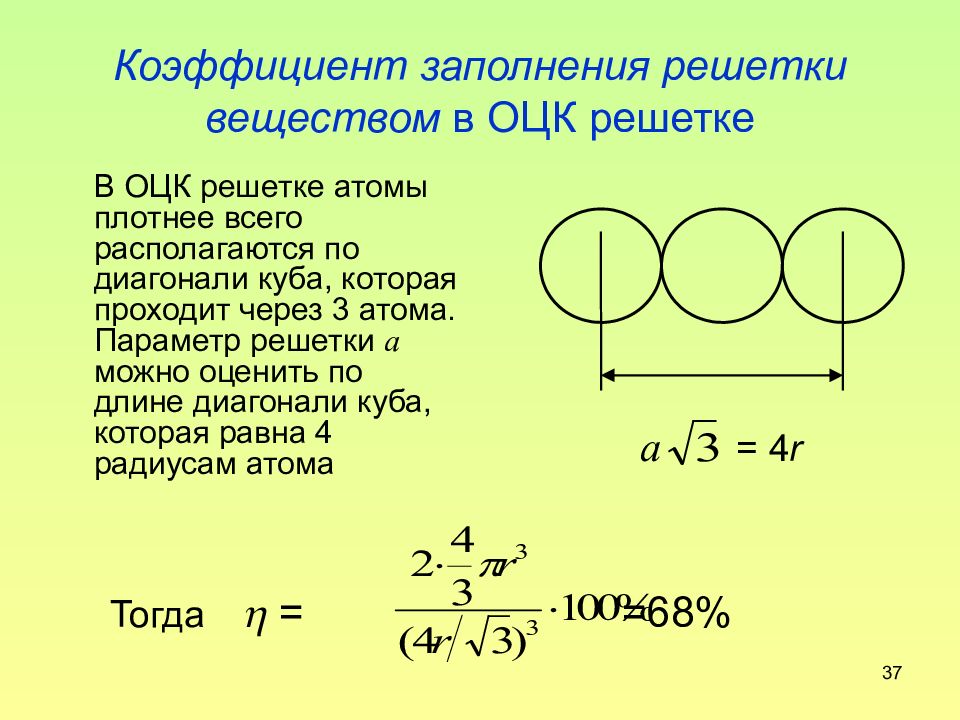
Слайд 37: Коэффициент заполнения решетки веществом в ОЦК решетке
37 Коэффициент заполнения решетки веществом в ОЦК решетке В ОЦК решетке атомы плотнее всего располагаются по диагонали куба, которая проходит через 3 атома. Параметр решетки а можно оценить по длине диагонали куба, которая равна 4 радиусам атома Тогда = =68% a = 4 r
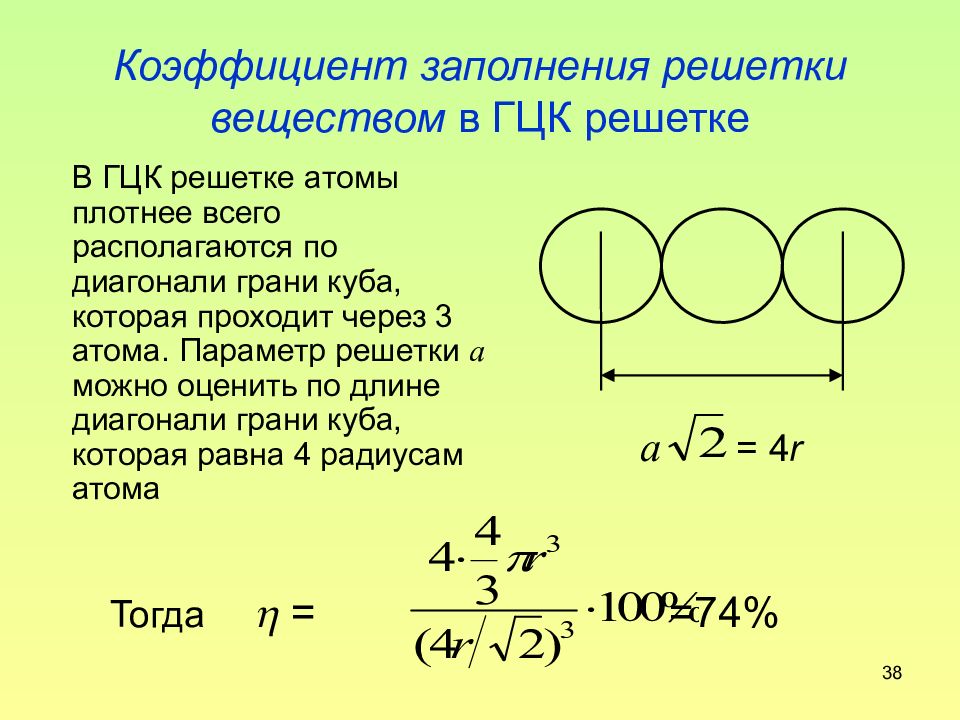
Слайд 38: Коэффициент заполнения решетки веществом в ГЦК решетке
38 Коэффициент заполнения решетки веществом в ГЦК решетке В ГЦК решетке атомы плотнее всего располагаются по диагонали грани куба, которая проходит через 3 атома. Параметр решетки а можно оценить по длине диагонали грани куба, которая равна 4 радиусам атома Тогда = =74% a = 4 r
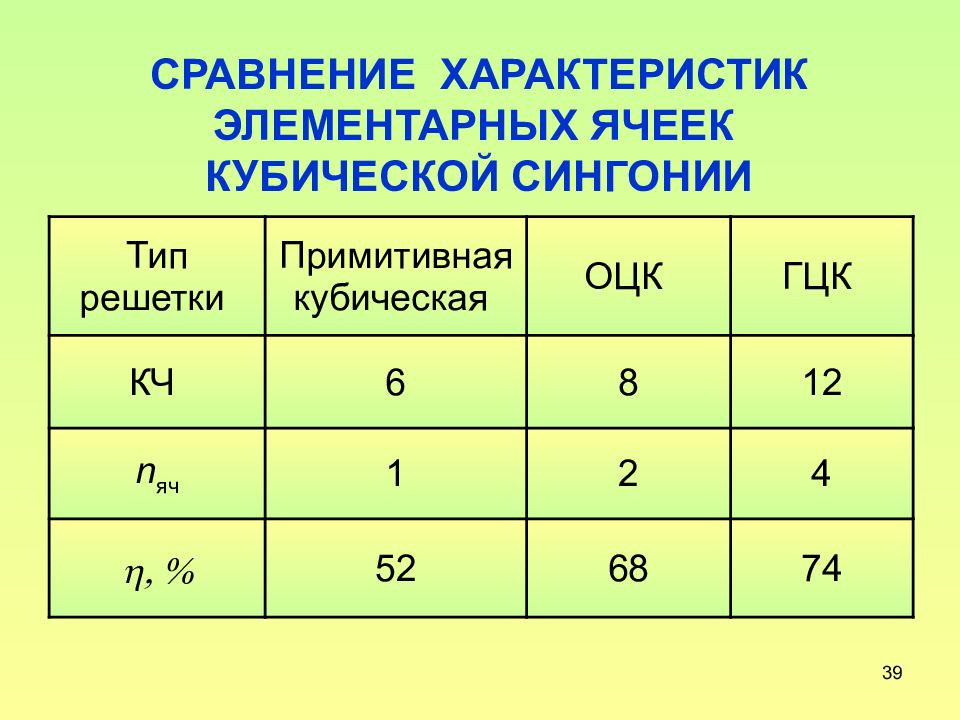
Слайд 39: СРАВНЕНИЕ ХАРАКТЕРИСТИК ЭЛЕМЕНТАРНЫХ ЯЧЕЕК КУБИЧЕСКОЙ СИНГОНИИ
39 СРАВНЕНИЕ ХАРАКТЕРИСТИК ЭЛЕМЕНТАРНЫХ ЯЧЕЕК КУБИЧЕСКОЙ СИНГОНИИ Тип решетки Примитивная кубическая ОЦК ГЦК КЧ 6 8 12 n яч 1 2 4 h, % 52 68 74
Слайд 40: Поры в кристаллической решетке
40 Поры в кристаллической решетке Кристаллическое тело не монолитно - имеет пустоты – поры. Поры играют существенную роль в формировании свойств кристаллического тела: – т.к. являются местом расположения примесных атомов. – движение атомов по порам – один из путей диффузии Различают тетрапоры и октапоры.
Слайд 41: Тетрапора
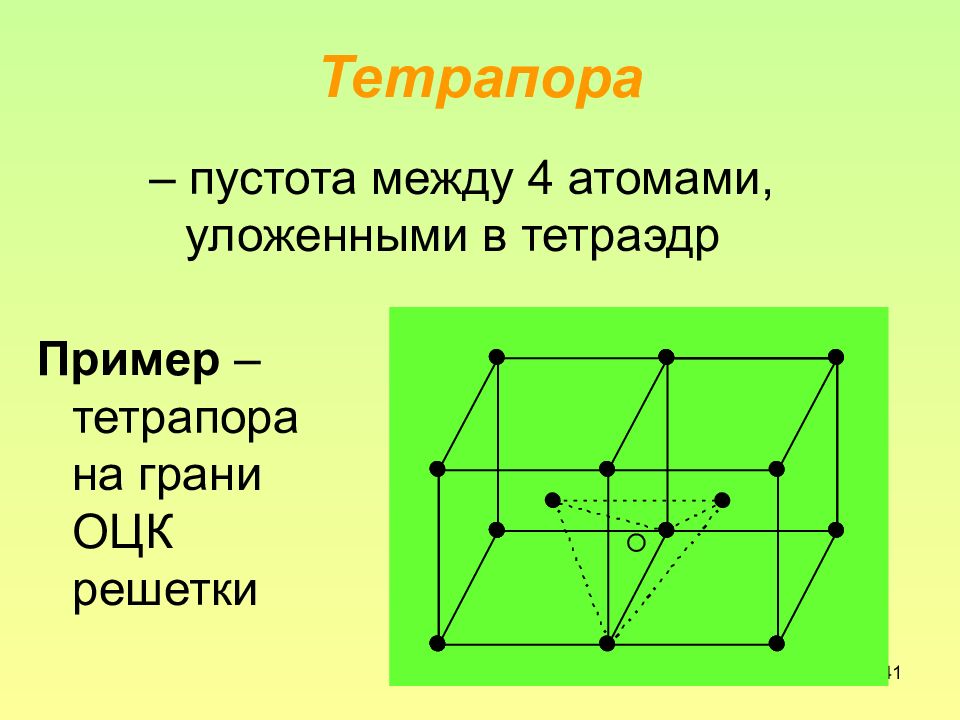
41 Тетрапора – пустота между 4 атомами, уложенными в тетраэдр Пример – тетрапора на грани ОЦК решетки
Слайд 42: Октапора
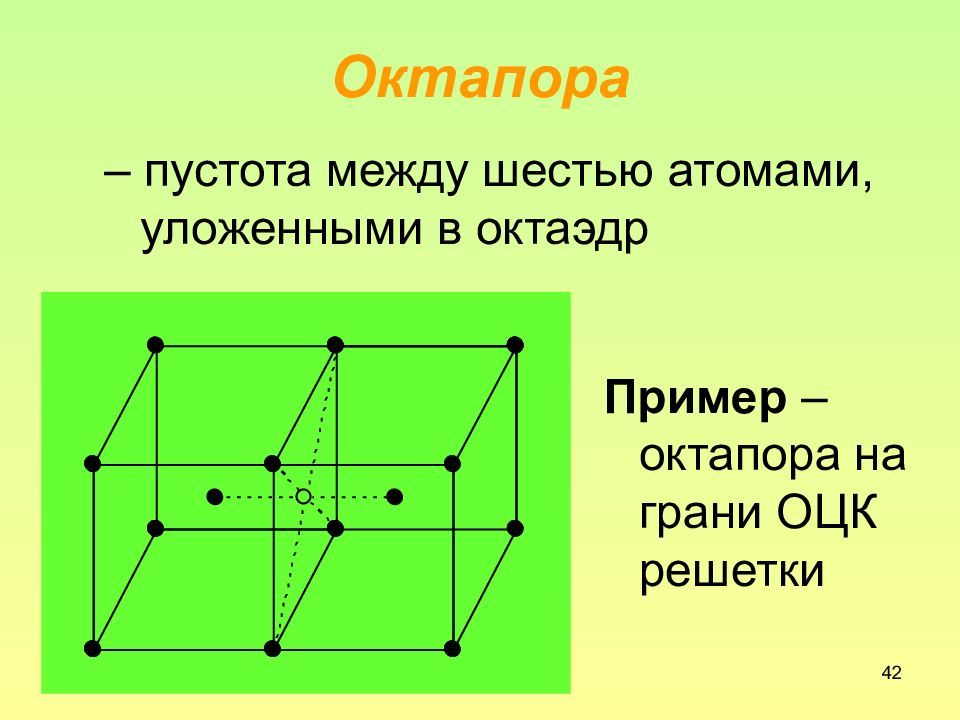
42 Октапора – пустота между шестью атомами, уложенными в октаэдр Пример – октапора на грани ОЦК решетки
Слайд 43: Индицирование
43 Индицирование – наиболее удобный способ описания пространственного расположения плоскостей и направлений путем приписывании им определенных индексов Различают индексы направлений и плоскостей
Слайд 44: Индексы плоскостей
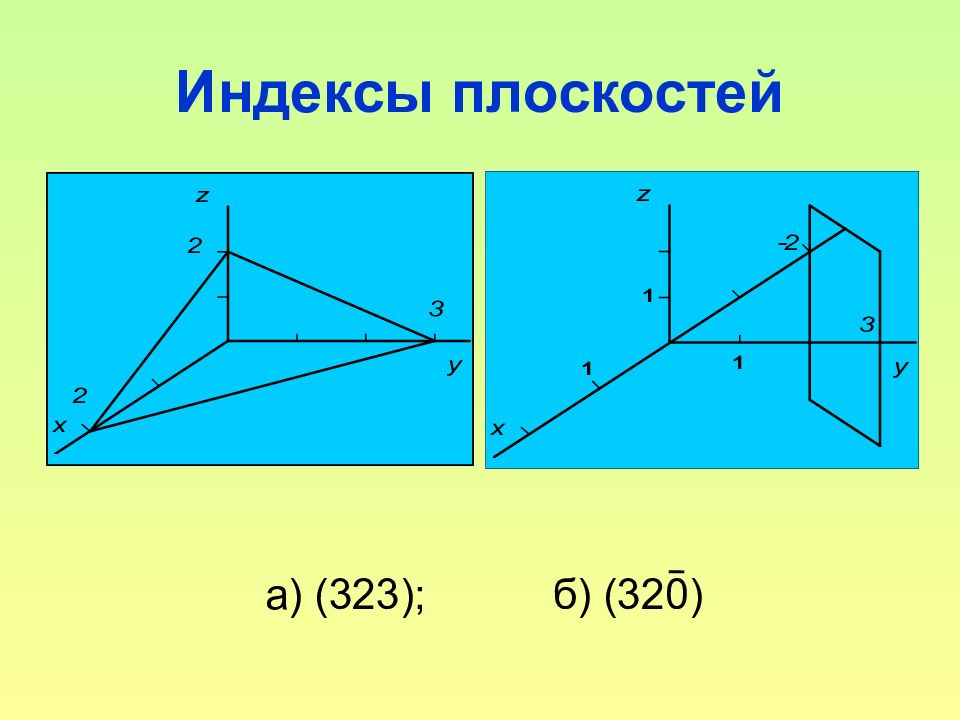
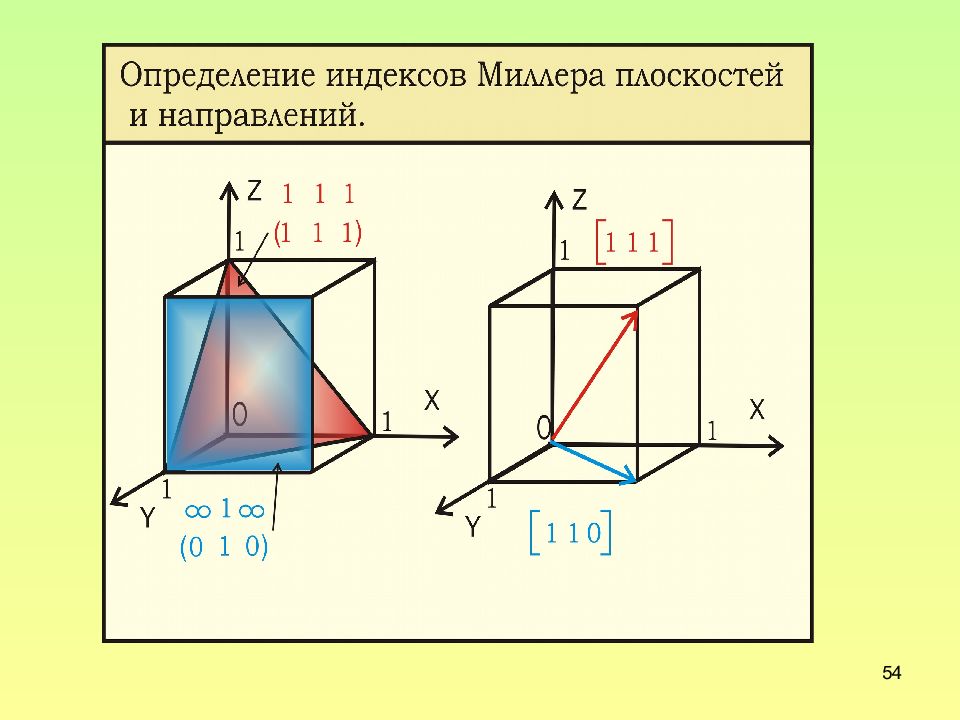
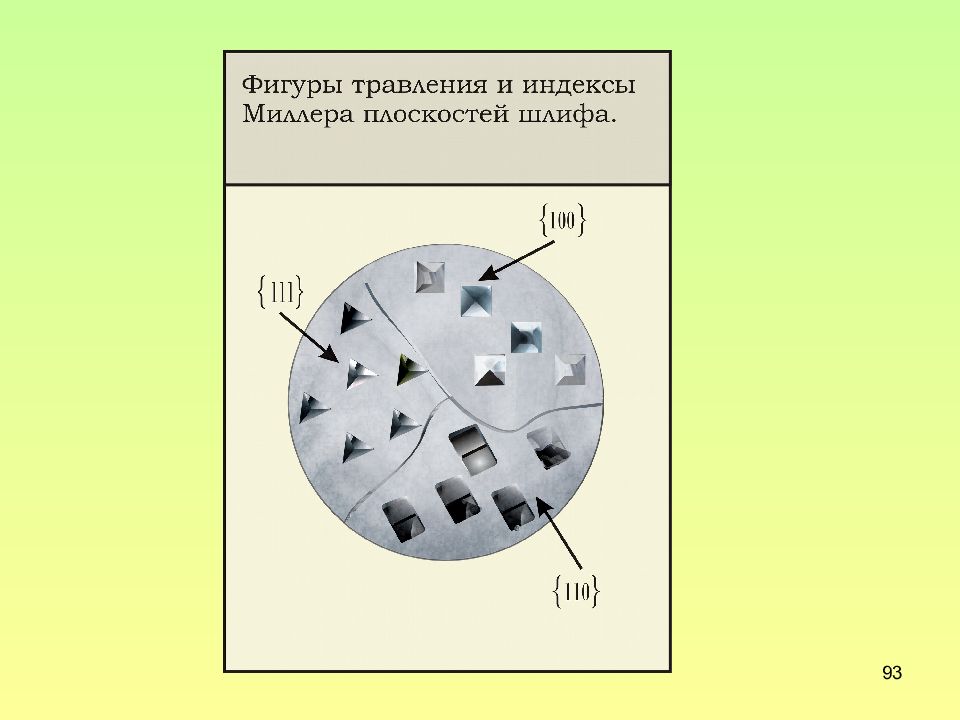
44 Индексы плоскостей В случае плоскости за индексы принимаются три числа h, k, l, равные обратным величинам отрезков, отсекаемых данной плоскостью ( hkl ) на осях x, y, z, умноженные на общий коэффициент, приводящий все числа h, k, l к целым и простым числам Для обозначения плоскостей пользуются обозначением ( hkl ) – для одной плоскости; и { hkl } – для семейства эквивалентных по структуре плоскостей.
Слайд 46: Семейство плоскостей
46 Семейство плоскостей В кристаллах можно выделить несколько непараллельных, но полностью идентичных кристаллографических плоскостей с одинаковым расположением атомов. Совокупность таких плоскостей называют семейством и обозначают { hkl }.
Слайд 47: Семейство плоскостей
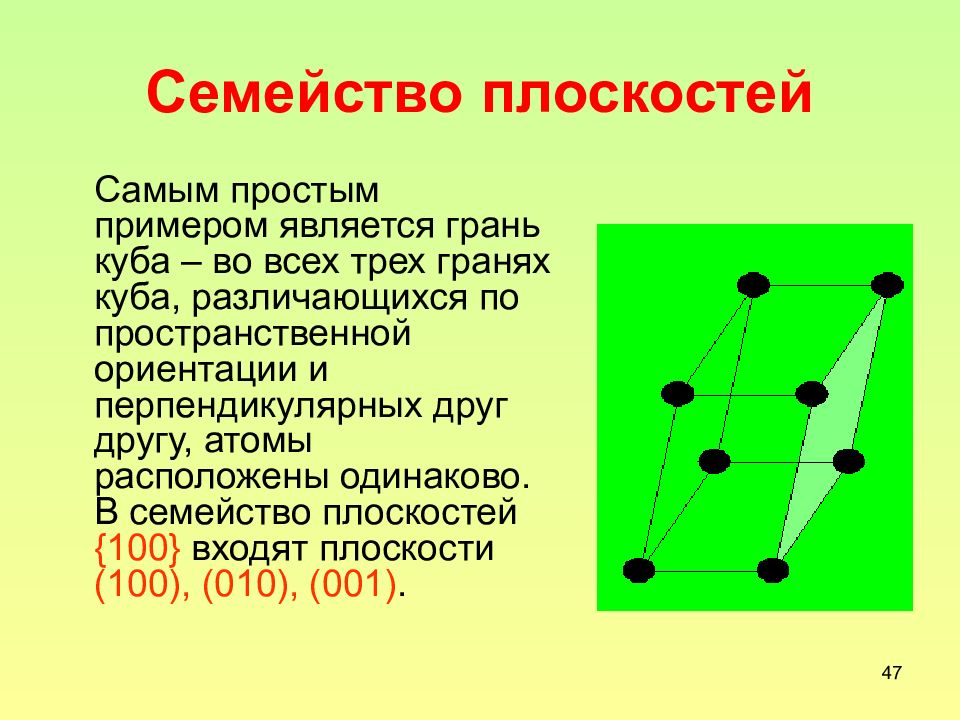
47 Семейство плоскостей Самым простым примером является грань куба – во всех трех гранях куба, различающихся по пространственной ориентации и перпендикулярных друг другу, атомы расположены одинаково. В семейство плоскостей {100} входят плоскости (100), (010), (001).
Слайд 48: Семейство плоскостей
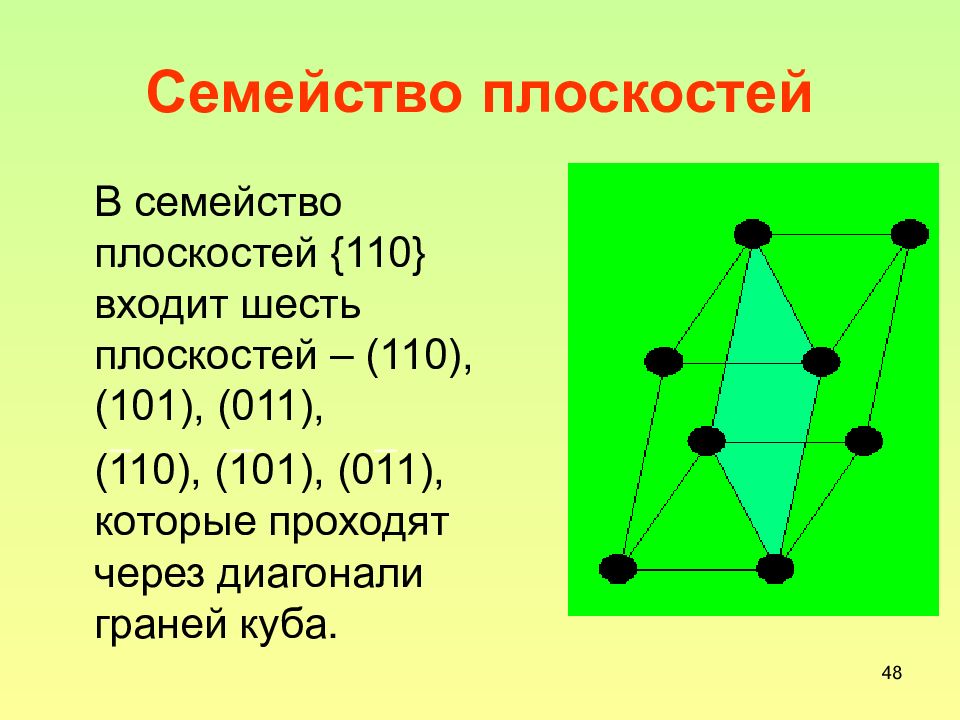
48 Семейство плоскостей В семейство плоскостей {110} входит шесть плоскостей – (110), (101), (011), (110), (101), (011), которые проходят через диагонали граней куба.
Слайд 49: Индексы направлений
49 Индексы направлений За индексы направления [uvw] принимаются координаты атома, через который из начала координат проходит это направление, приведенные к трем наименьшим целым числам делением на общий делитель Аналогично семейству плоскостей существует и семейство направлений – в семейство направлений <uvw> входят все направления [uvw] c одинаковым расположением атомов
Слайд 50: Индексы направлений
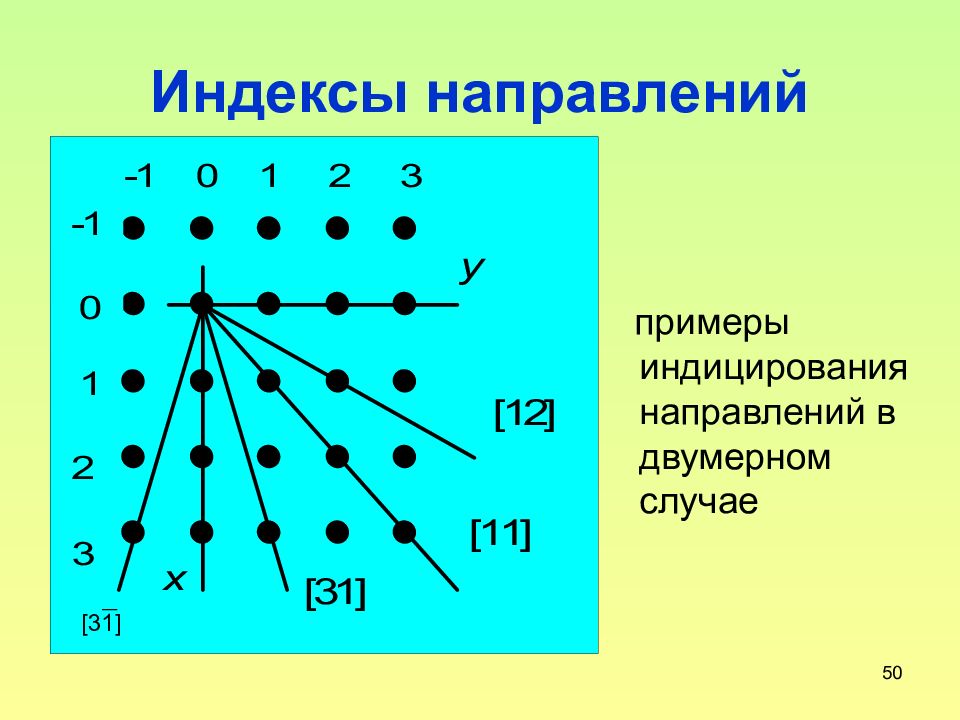
50 Индексы направлений примеры индицирования направлений в двумерном случае [31]
Слайд 51: Семейство направлений
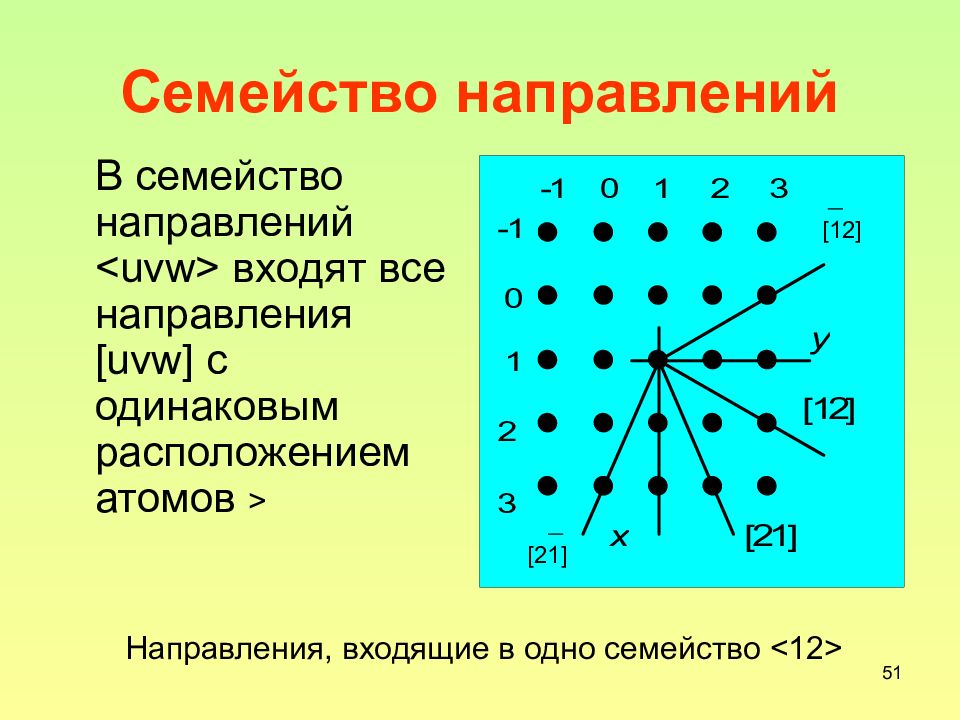
51 Семейство направлений [12] [21] Направления, входящие в одно семейство <12> В семейство направлений <uvw> входят все направления [uvw] c одинаковым расположением атомов >
Слайд 52: Плотноупакованные направления и плоскости
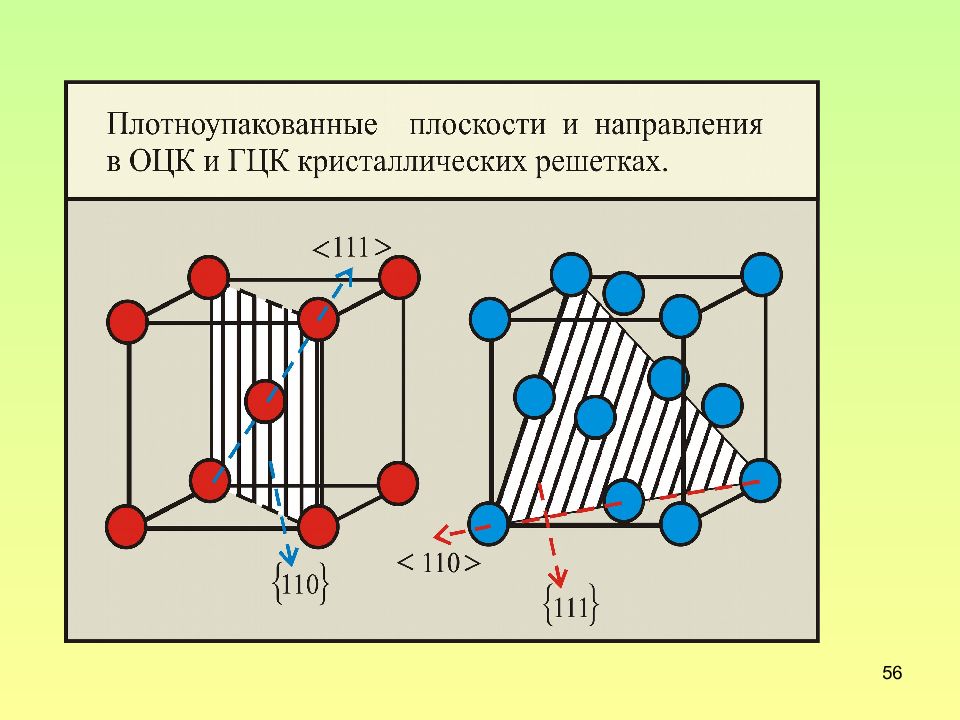
52 Плотноупакованные направления и плоскости Обратим внимание на тот факт, что расстояние между атомами в направлениях, принадлежащих разным семействам, существенно различаются. Так в случае примитивной кубической решетки для направлений <100> оно равно а, для направлений <110> - a, для направлений <111> - a. Расположение атомов в плоскостях с разными индексами различно.
Слайд 53: Плотноупакованные направления и плоскости в кубической сингонии
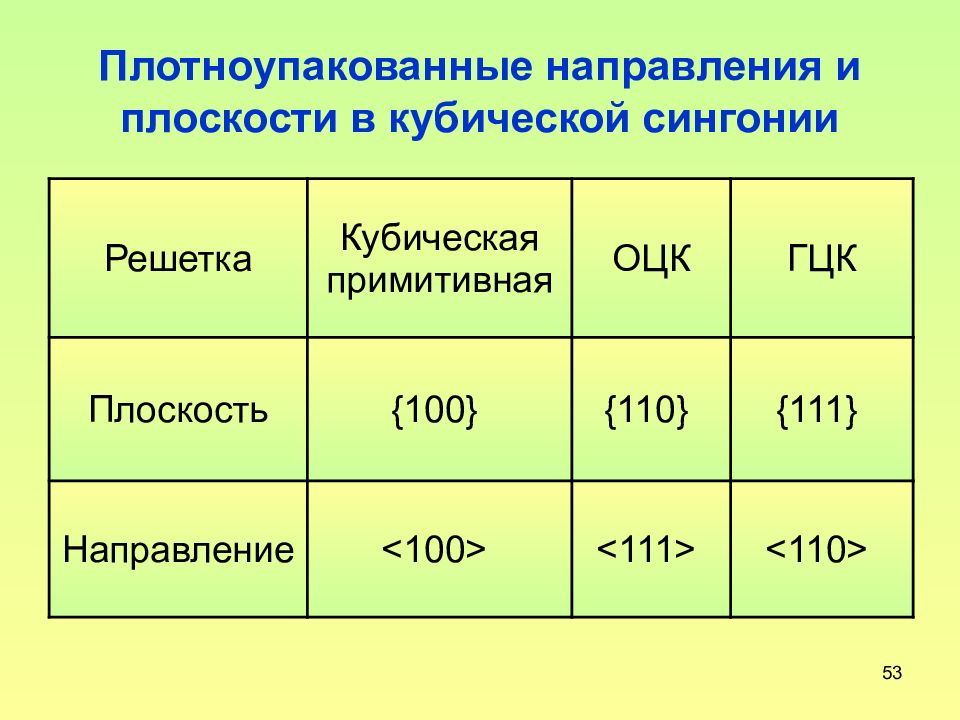
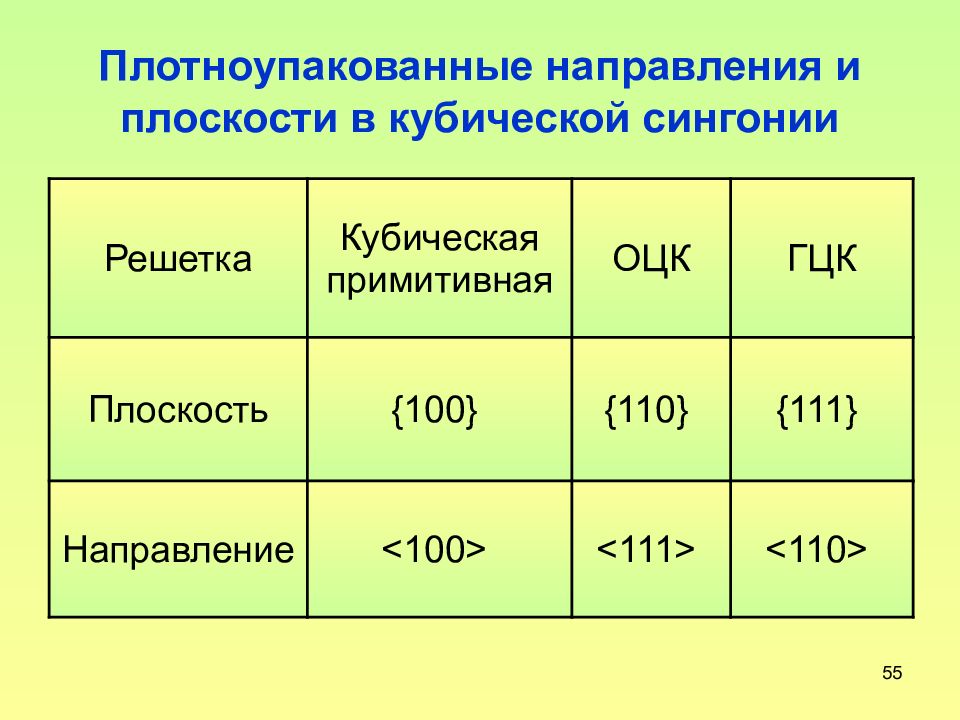
53 Плотноупакованные направления и плоскости в кубической сингонии Решетка Кубическая примитивная ОЦК ГЦК Плоскость {100} {110} {111} Направление <100> <111> <110>
Слайд 55: Плотноупакованные направления и плоскости в кубической сингонии
55 Плотноупакованные направления и плоскости в кубической сингонии Решетка Кубическая примитивная ОЦК ГЦК Плоскость {100} {110} {111} Направление <100> <111> <110>
Слайд 58: Анизотропия свойств металла
58 Анизотропия свойств металла Так как в разных направлениях расстояние между атомами различается, следовательно, различается и уровень сил связей между атомами в различных направлениях. Это означает, что и свойства кристаллического тела вдоль различных направлений (с разным расстоянием между атомами) будут различаться. Это явление различия свойств вдоль различных направлений получило название анизотропии свойств
Слайд 59
59 Дефекты кристаллической решетки линейные (одномерные) - дефекты, размер которых по двум координатным осям сопоставим с размером атома, а в третьем направлении существенно превышает его ( дислокации ); точечные (нульмерные) – дефекты, размер которых по всем трем координатным осям сопоставим с размером атома; поверхностные или плоские (двумерные) – дефекты, размер которых в одном направлении сравним с размером атома, а в двух других существенно превышает его; объемные (трехмерные) – дефекты, размер которых во всех трех направлениях существенно превышает размер атома.
Слайд 60: Точечные дефекты в металлах
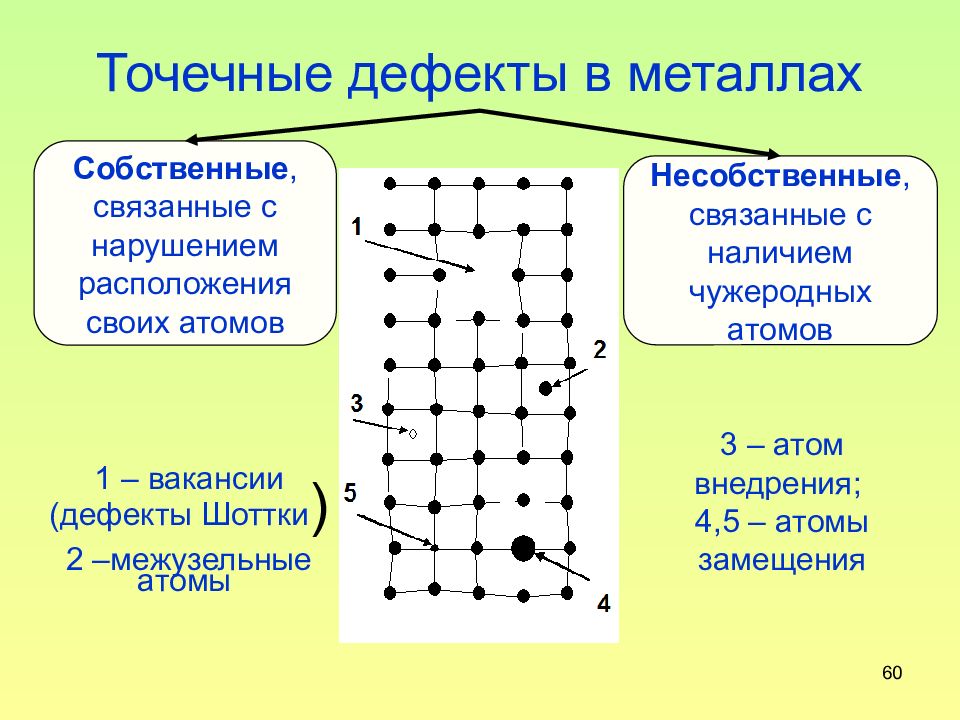
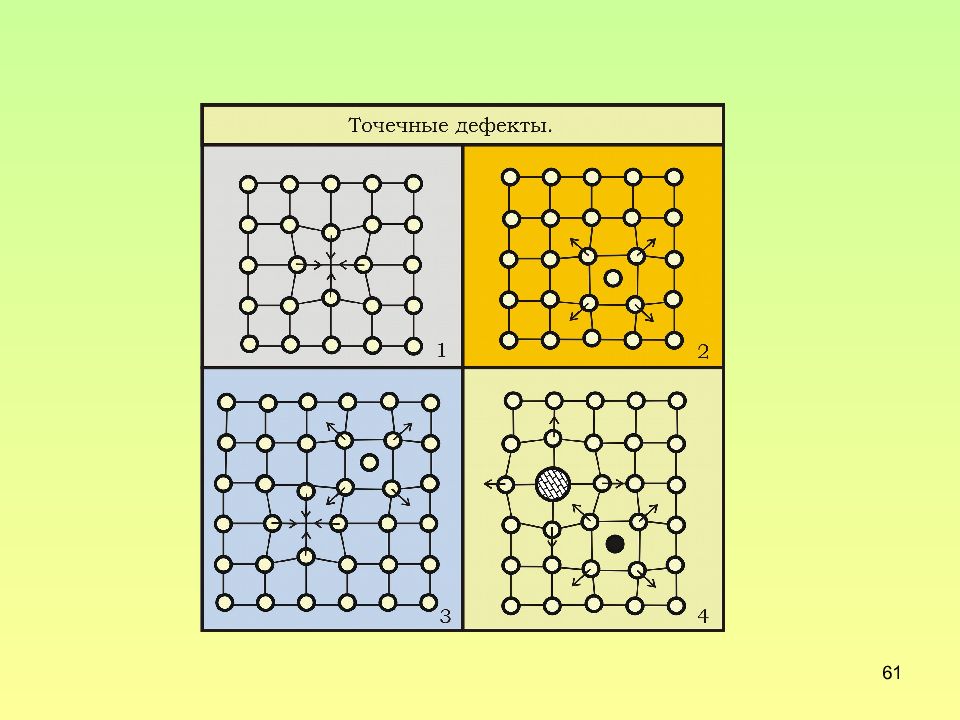
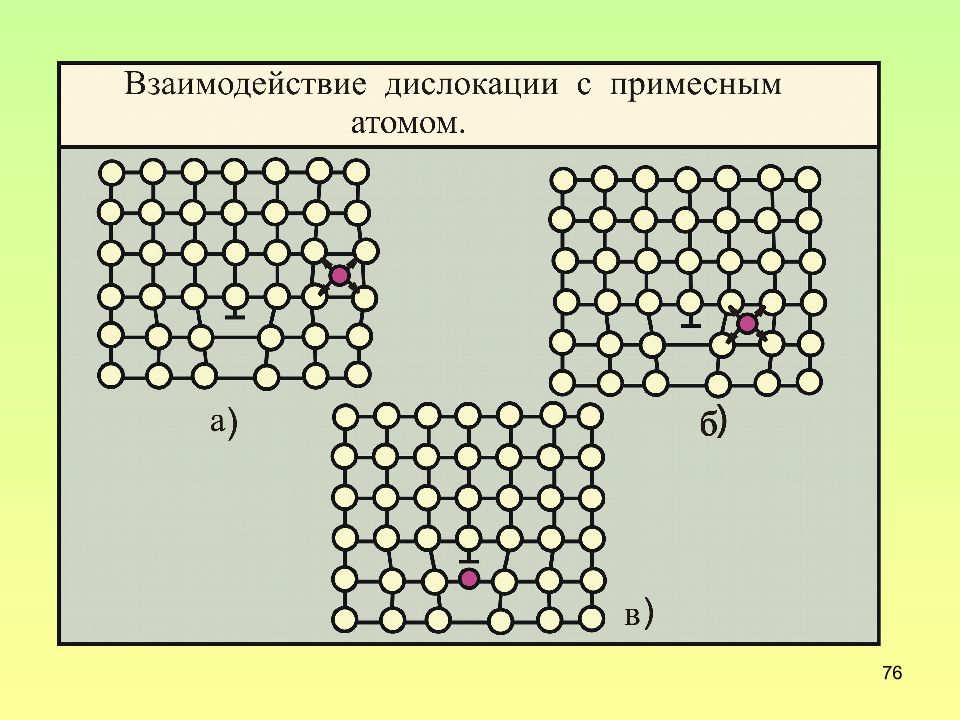
60 Точечные дефекты в металлах Собственные, связанные с нарушением расположения своих атомов Несобственные, связанные с наличием чужеродных атомов 1 – вакансии (дефекты Шоттки ) 2 –межузельные атомы 3 – атом внедрения; 4,5 – атомы замещения
Слайд 62: Влияние точечных дефектов на процессы в материалах
62 Влияние точечных дефектов на процессы в материалах Миграция основных атомов, межузельных атомов и атомов замещения осуществляется по вакансионному механизму – путем обмена местами с вакансией. Миграция атомов внедрения осуществляется быстрее – т.к. вокруг любого узла кристаллической решетки имеется несколько пустот (пор) и внедренный атом может перескакивать из одной пустоты в другую ( по порам ). Поэтому вакансии и атомы внедрения оказывают наиболее значительное влияние на протекание различных процессов в материалах, обусловленных диффузией.
Слайд 63: Влияние точечных дефектов на свойства материалов
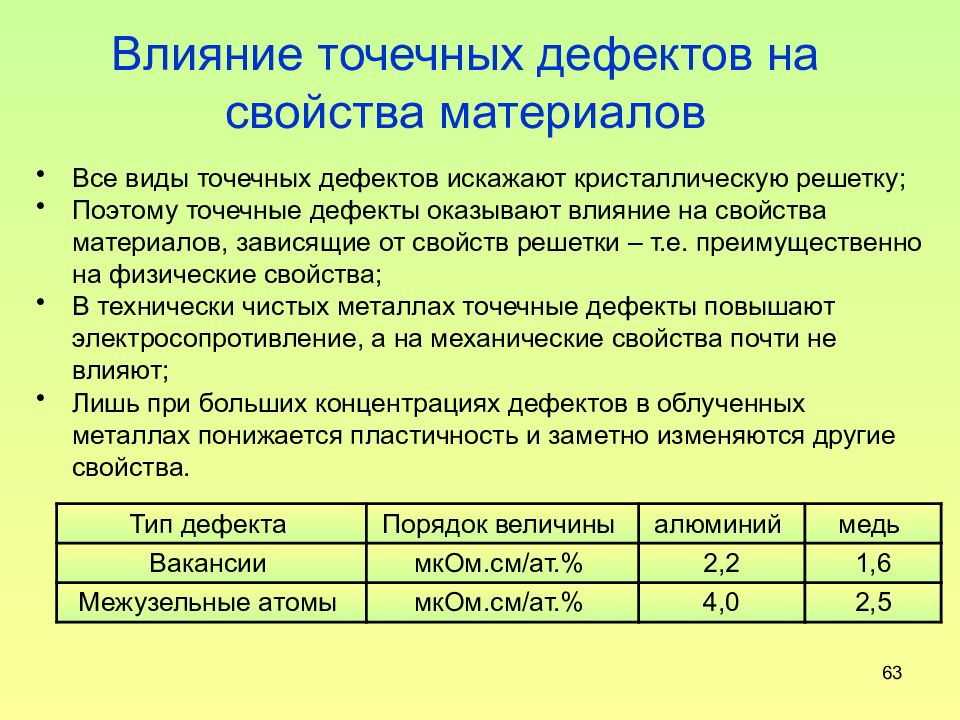
63 Влияние точечных дефектов на свойства материалов Все виды точечных дефектов искажают кристаллическую решетку; Поэтому точечные дефекты оказывают влияние на свойства материалов, зависящие от свойств решетки – т.е. преимущественно на физические свойства; В технически чистых металлах точечные дефекты повышают электросопротивление, а на механические свойства почти не влияют; Лишь при больших концентрациях дефектов в облученных металлах понижается пластичность и заметно изменяются другие свойства. Тип дефекта Порядок величины алюминий медь Вакансии мкОм.см/ат.% 2,2 1,6 Межузельные атомы мкОм.см/ат.% 4,0 2,5
Слайд 64: Строение краевой дислокации
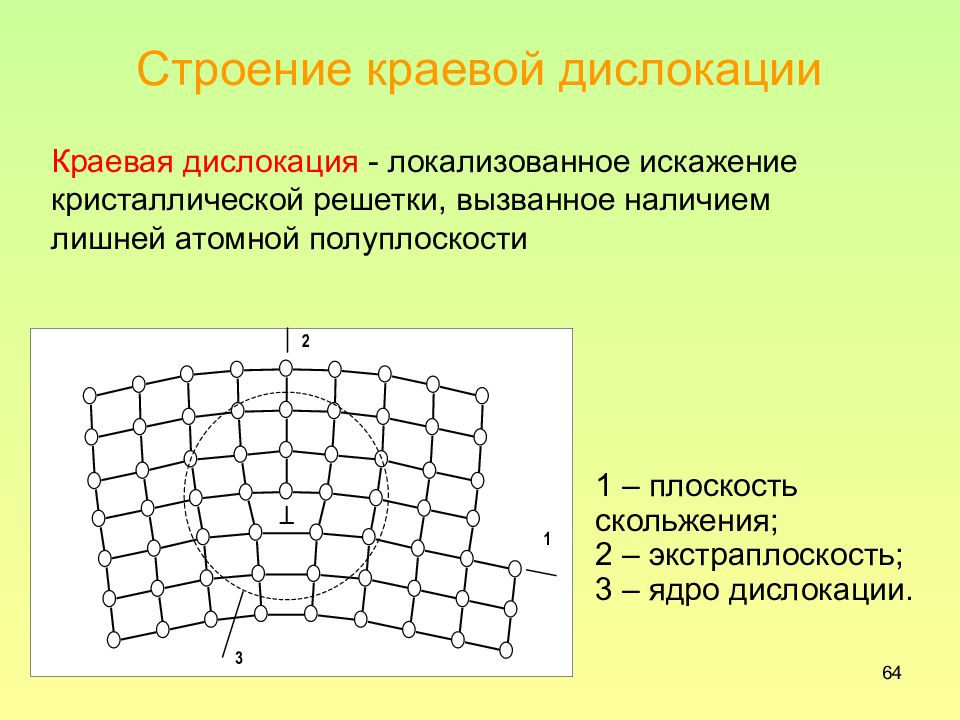
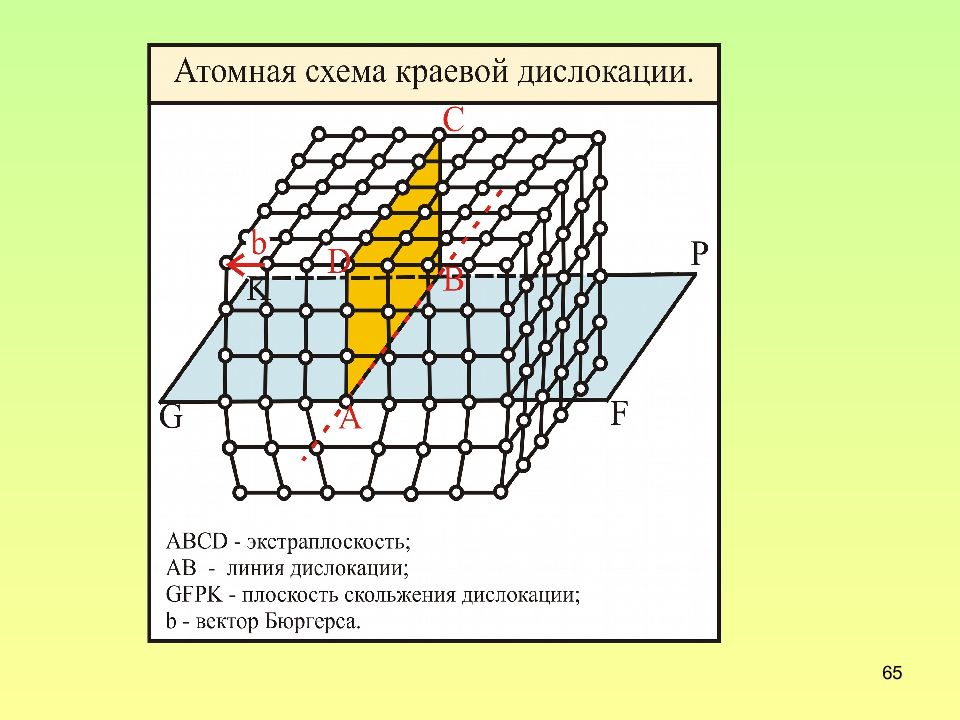
64 Строение краевой дислокации 1 – плоскость скольжения; 2 – экстраплоскость; 3 – ядро дислокации. Краевая дислокация - локализованное искажение кристаллической решетки, вызванное наличием лишней атомной полуплоскости
Слайд 66: Типы краевых дислокаций
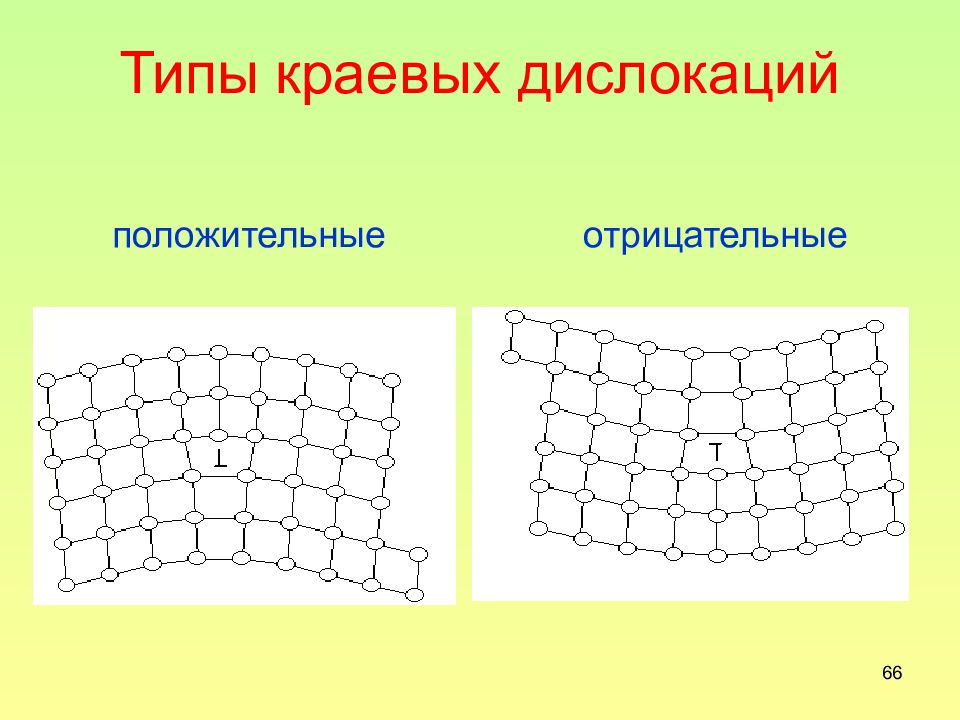
66 Типы краевых дислокаций положительные отрицательные
Слайд 67: Вектор Бюргерса
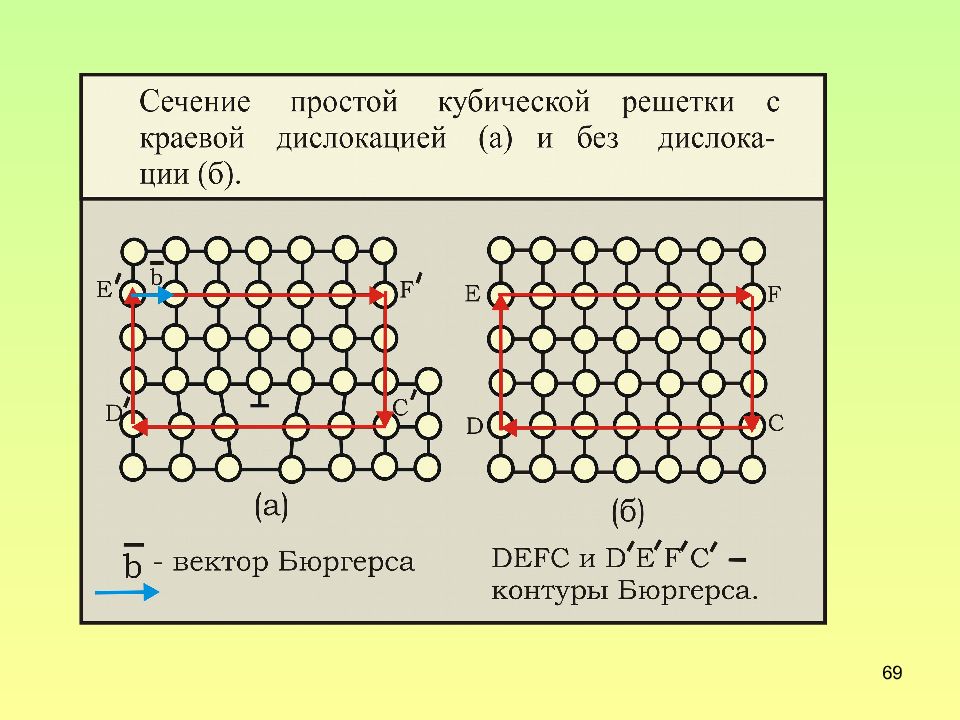
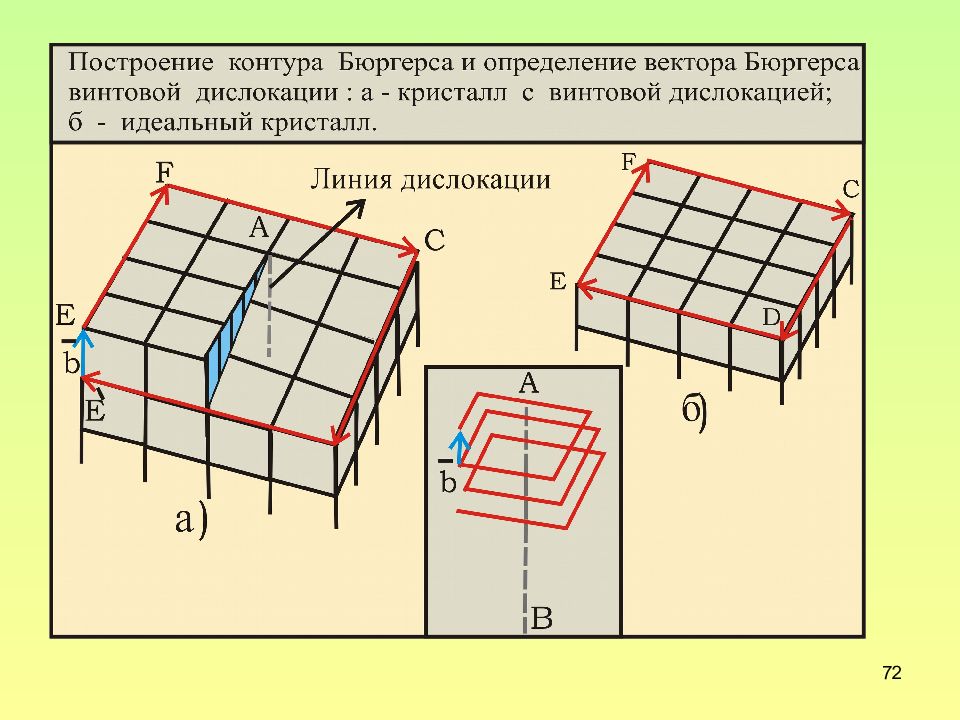
67 Вектор Бюргерса Вектор Бюргерса - главная характеристикой дислокации - мера искаженности кристаллической решетки, обусловленной присутствием в ней дислокации. Вектор Бюргерса определяет энергию дислокации, величину связанного с дислокацией сдвига, позволяет оценить подвижность дислокации. Для определения вектора Бюргерса строят контур Бюргерса.
Слайд 68: Контур Бюргерса
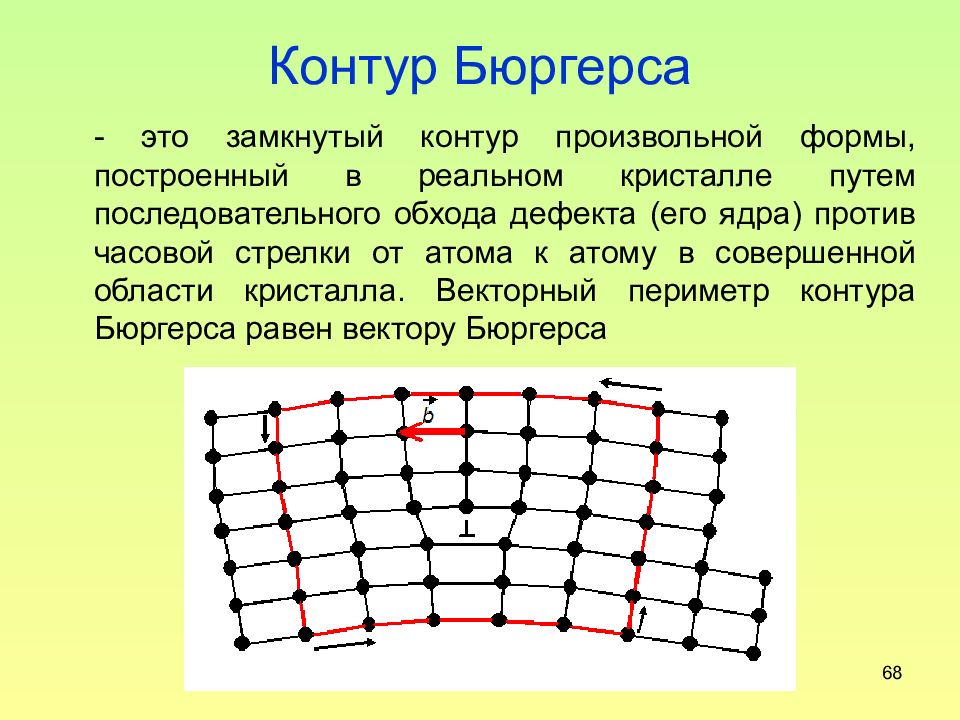
68 Контур Бюргерса - это замкнутый контур произвольной формы, построенный в реальном кристалле путем последовательного обхода дефекта (его ядра) против часовой стрелки от атома к атому в совершенной области кристалла. Векторный периметр контура Бюргерса равен вектору Бюргерса
Слайд 70: Вектор Бюргерса краевой дислокации и её энергия
70 Вектор Бюргерса краевой дислокации и её энергия для краевой дислокации вектор Бюргерса b параллелен плоскости сдвига и перпендикулярен экстраплоскости энергия краевой дислокации где G – модуль сдвига; – коэффициент Пуассона (для металлов ⅓); r o – радиус ядра дислокации (несколько межатомных расстояний) R – расстояние, на которое распространяется упругая деформация от дислокации.
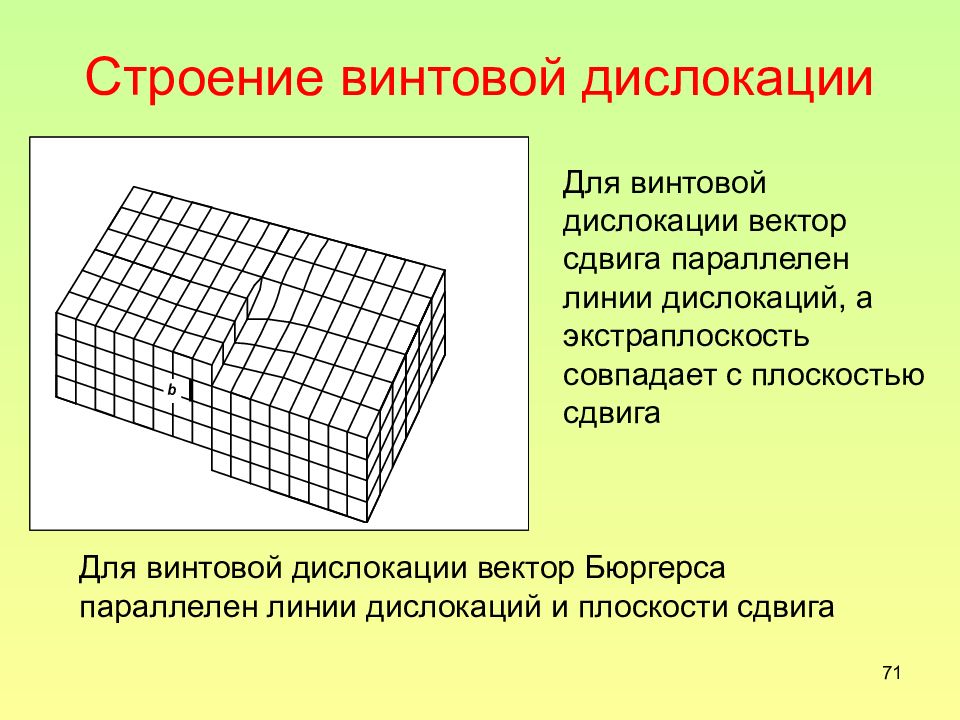
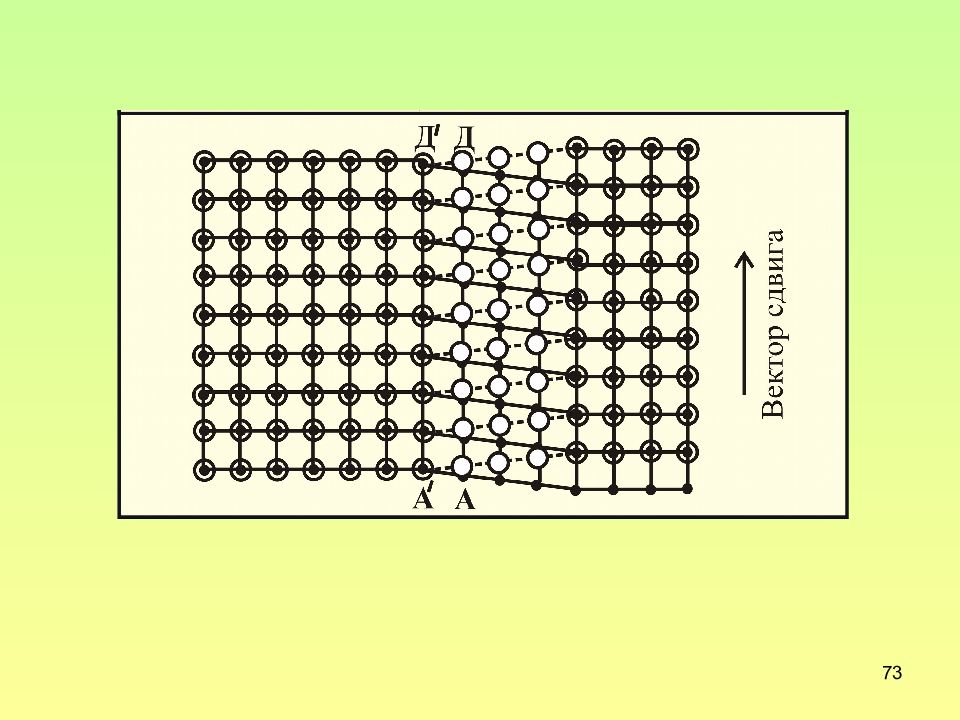
Слайд 71: Строение винтовой дислокации
71 Строение винтовой дислокации Для винтовой дислокации вектор сдвига параллелен линии дислокаций, а экстраплоскость совпадает с плоскостью сдвига Для винтовой дислокации вектор Бюргерса параллелен линии дислокаций и плоскости сдвига
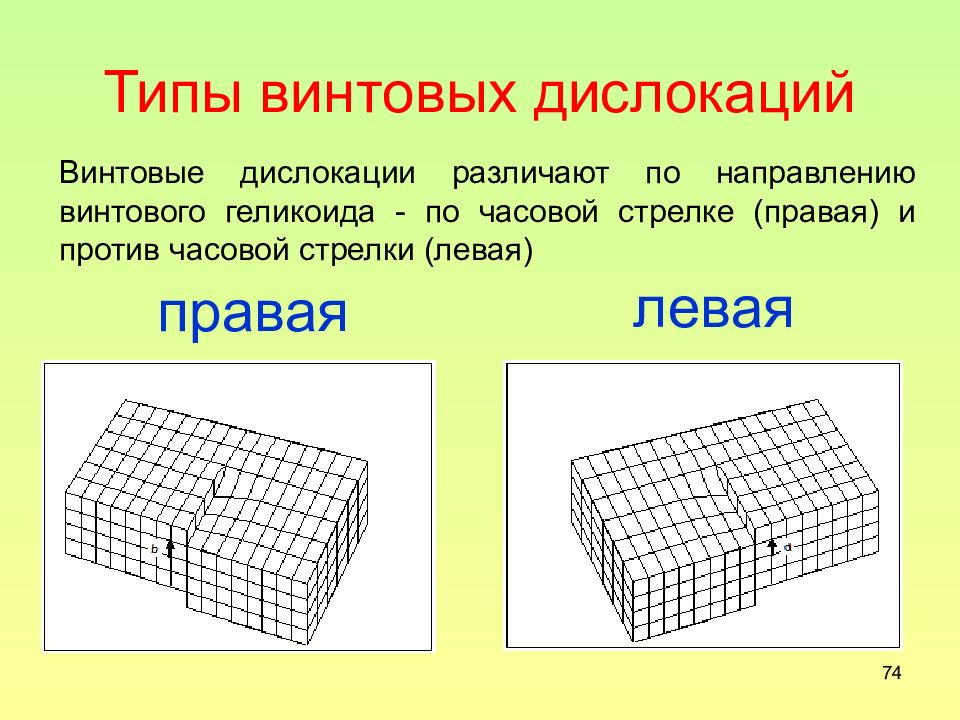
Слайд 74: Типы винтовых дислокаций
74 Типы винтовых дислокаций правая левая Винтовые дислокации различают по направлению винтового геликоида - по часовой стрелке (правая) и против часовой стрелки (левая)
Слайд 75: Энергия винтовой дислокации
75 Энергия винтовой дислокации где G – модуль сдвига; r o – радиус ядра дислокации (несколько межатомных расстояний); R – расстояние, на которое распространяется упругая деформация от дислокации. Сравнив энергии краевой и винтовой дислокаций получим, что энергия краевой дислокации в 1,5 раза больше.
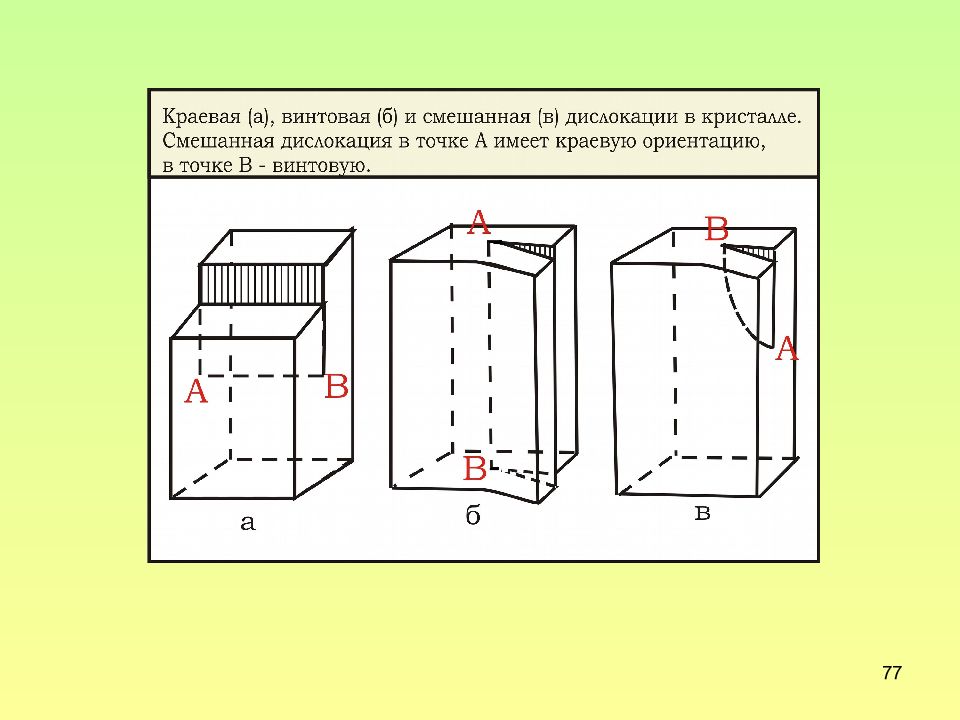
Слайд 78: Смешанные дислокации
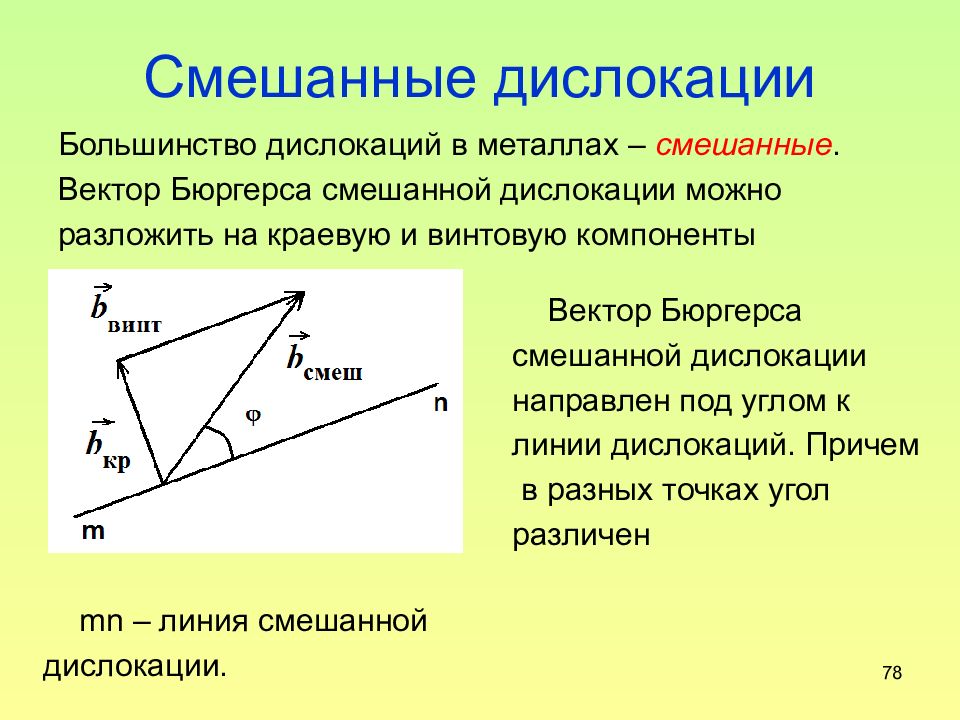
78 Смешанные дислокации Большинство дислокаций в металлах – смешанные. Вектор Бюргерса смешанной дислокации можно разложить на краевую и винтовую компоненты Вектор Бюргерса смешанной дислокации направлен под углом к линии дислокаций. Причем в разных точках угол различен mn – линия смешанной дислокации.
Слайд 79: Скольжение краевой дислокации
79 Скольжение краевой дислокации Это движение края экстраплоскости по плоскости скольжения под действием напряжений. не обусловлено диффузией, поэтому может идти при сколь угодно низких температурах. не связано с переносом массы, поэтому называется консервативным движением. происходит преимущественно по наиболее плотноупакованным плоскостям – по плоскостям {111} в ГЦК-решетке и по плоскостям {110} в ОЦК-решетке. При низких напряжениях со скоростью порядка 10 -7 -10 -8 см/с. Скорость скольжения не может превышать скорость распространения в данном кристалле упругой деформации, т.е. скорости звука в кристалле. При больших напряжениях в кристалле Fe -3,25% Si зафиксирована скорость скольжения дислокаций порядка 10 -2 см/с.
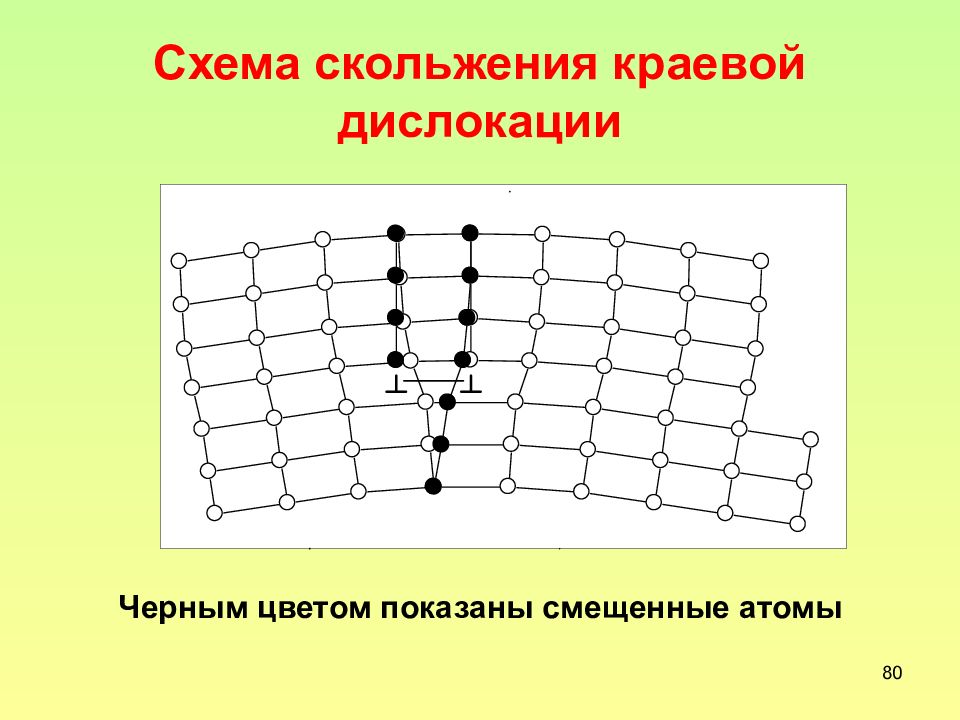
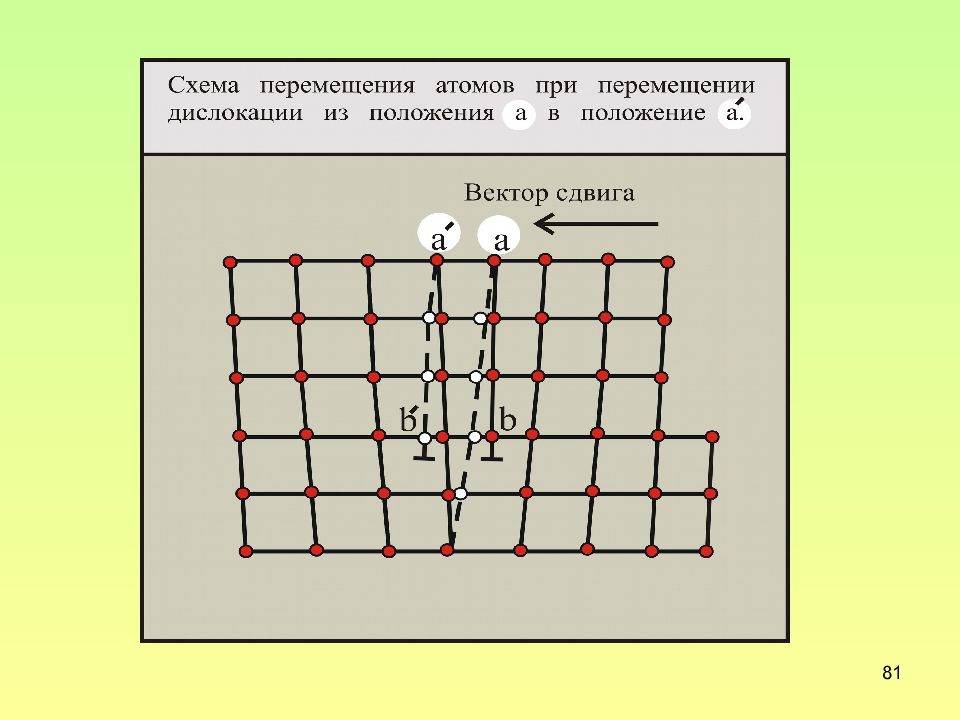
Слайд 80: Схема скольжения краевой дислокации
80 Схема скольжения краевой дислокации Черным цветом показаны смещенные атомы
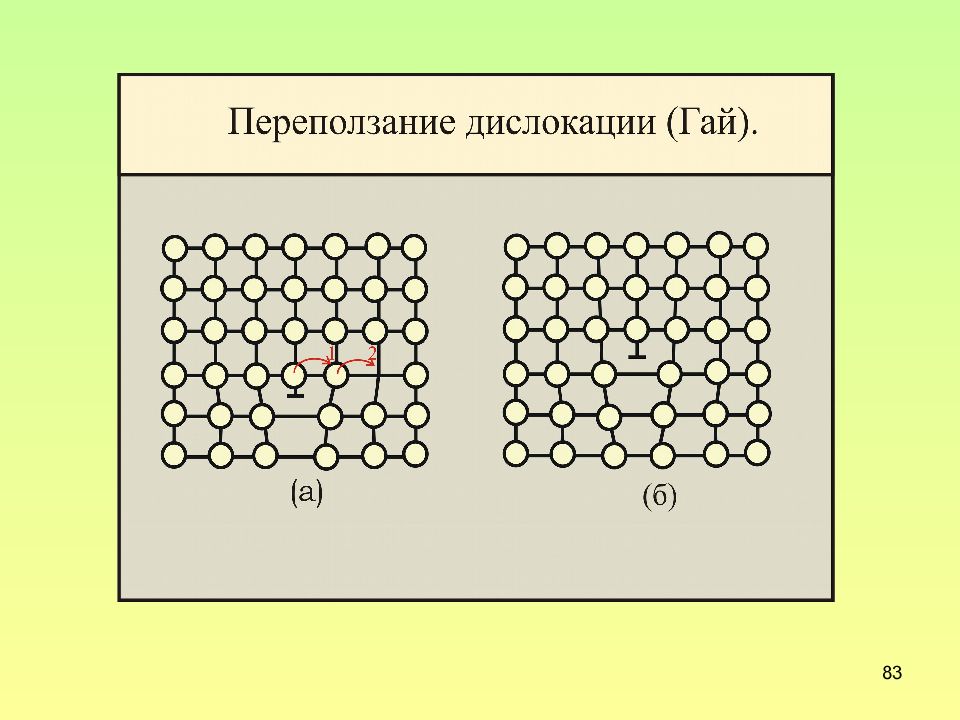
Слайд 82: Переползание краевой дислокации
82 Переползание краевой дислокации Переползание это удлинение или сокращение экстраплоскости краевой дислокации Переползание обусловлено диффузией, т.е. связано с переносом массы (неконсервативное движение). Переползание – термически активируемый процесс, происходит с заметной скоростью лишь при сравнительно высоких температурах.
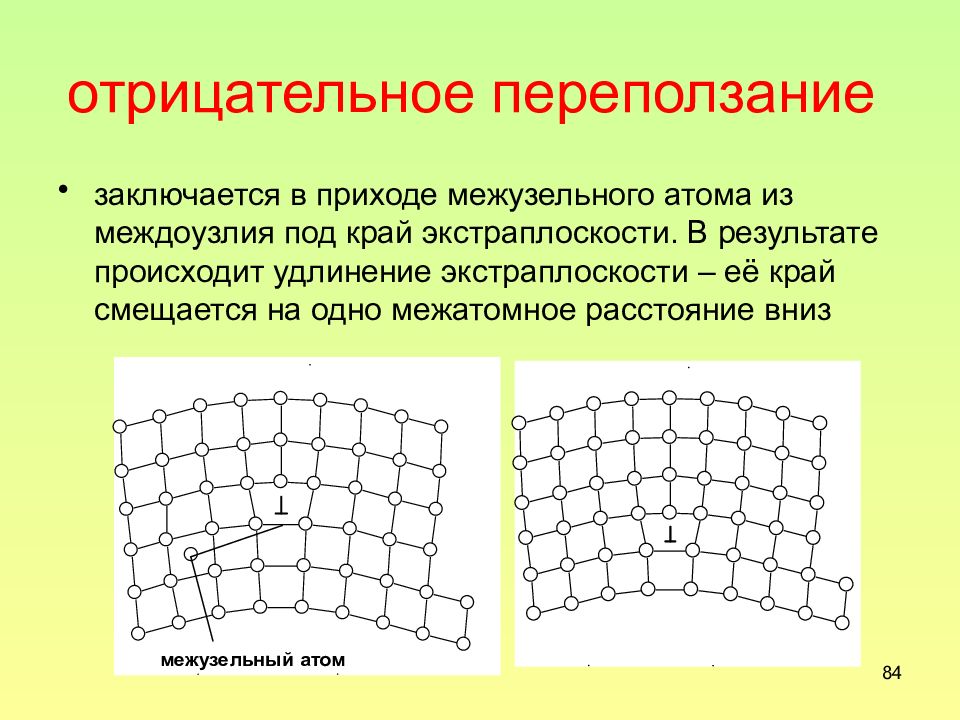
Слайд 84: отрицательное переползание
84 отрицательное переползание заключается в приходе межузельного атома из междоузлия под край экстраплоскости. В результате происходит удлинение экстраплоскости – её край смещается на одно межатомное расстояние вниз
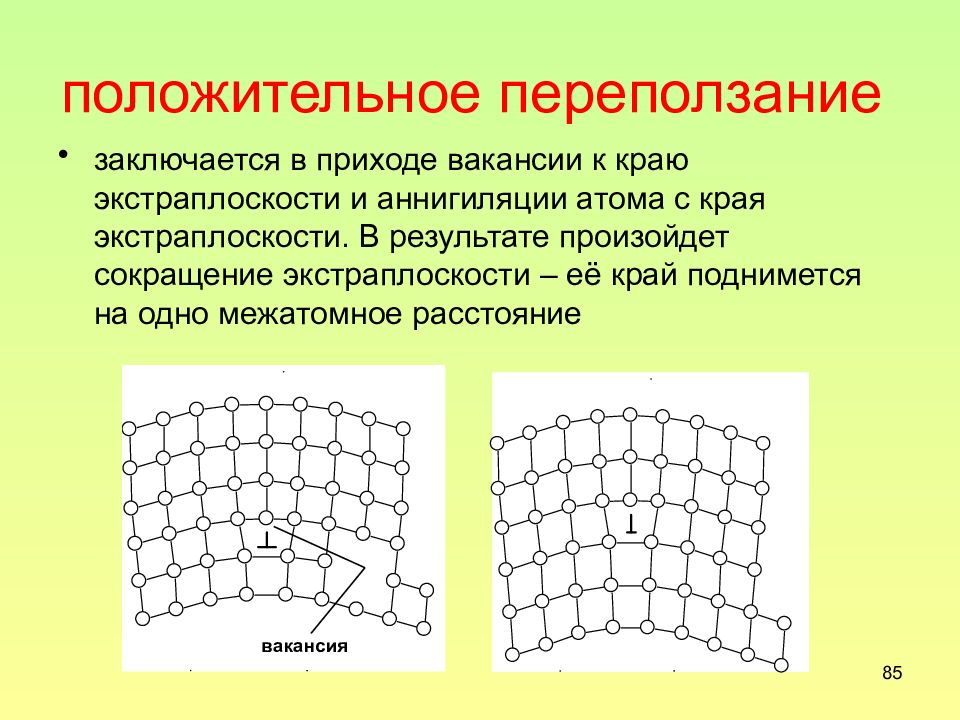
Слайд 85: положительное переползание
85 положительное переползание заключается в приходе вакансии к краю экстраплоскости и аннигиляции атома с края экстраплоскости. В результате произойдет сокращение экстраплоскости – её край поднимется на одно межатомное расстояние
Слайд 86: Движение винтовой дислокации
86 Движение винтовой дислокации В отличие от краевой дислокации винтовая дислокация не может перемещаться с помощью диффузионного механизма. При взаимодействии винтовой дислокации с вакансией образуется другой тип дислокаций – геликоидальный
Слайд 87: Скольжение винтовой дислокации под действием сжимающих напряжений
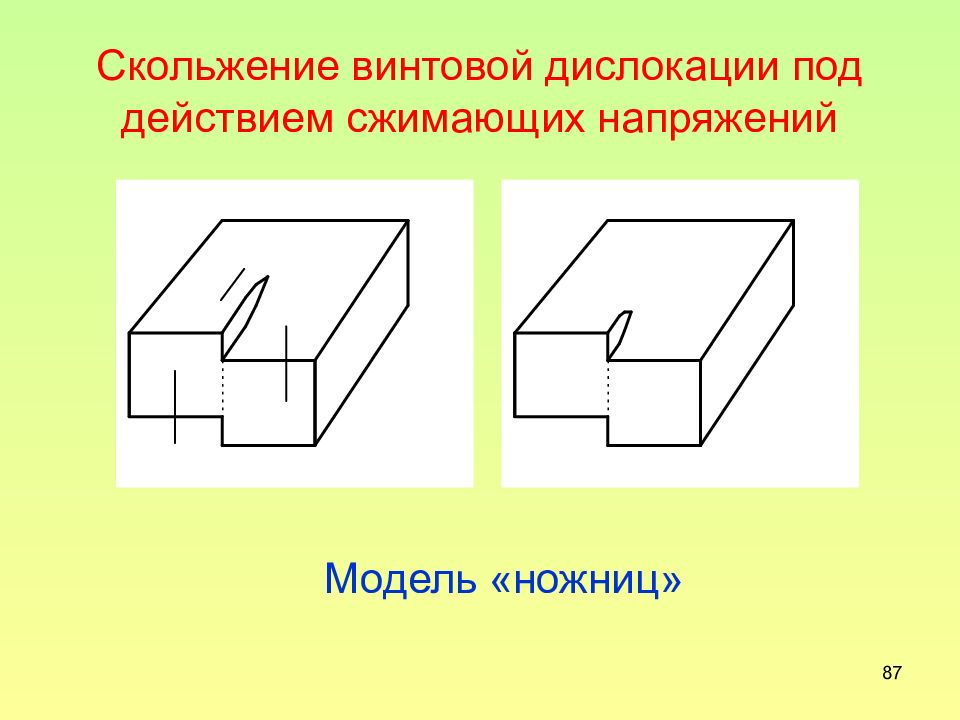
87 Скольжение винтовой дислокации под действием сжимающих напряжений Модель «ножниц»
Слайд 88: Смещение атомов в ядре винтовой дислокации при её скольжении на одно межатомное расстояние
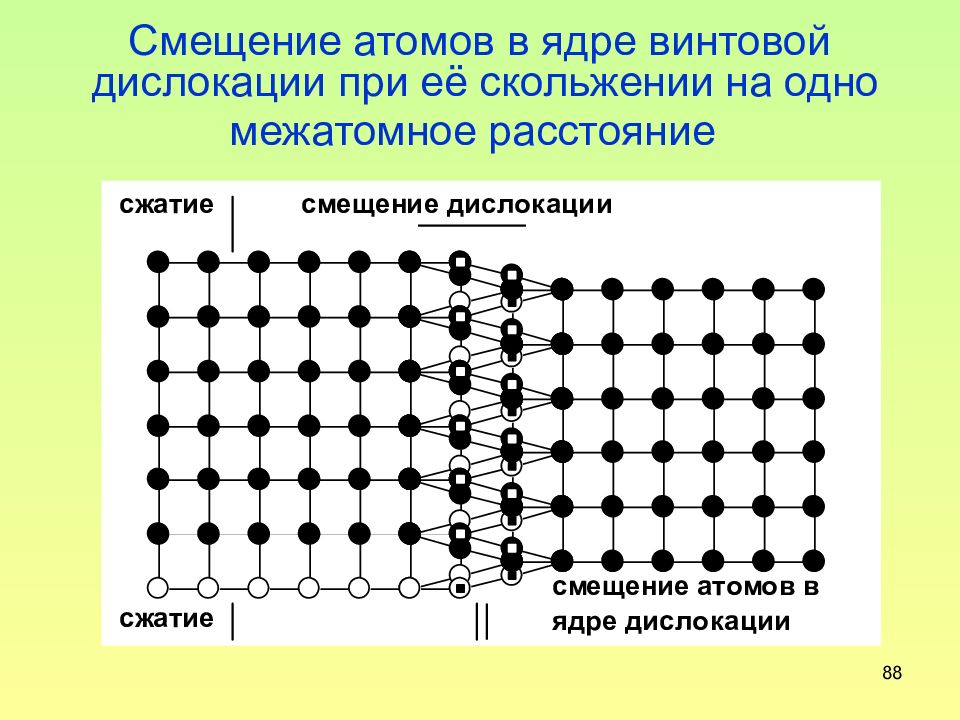
88 Смещение атомов в ядре винтовой дислокации при её скольжении на одно межатомное расстояние
Слайд 90: Особенности скольжения винтовой дислокации
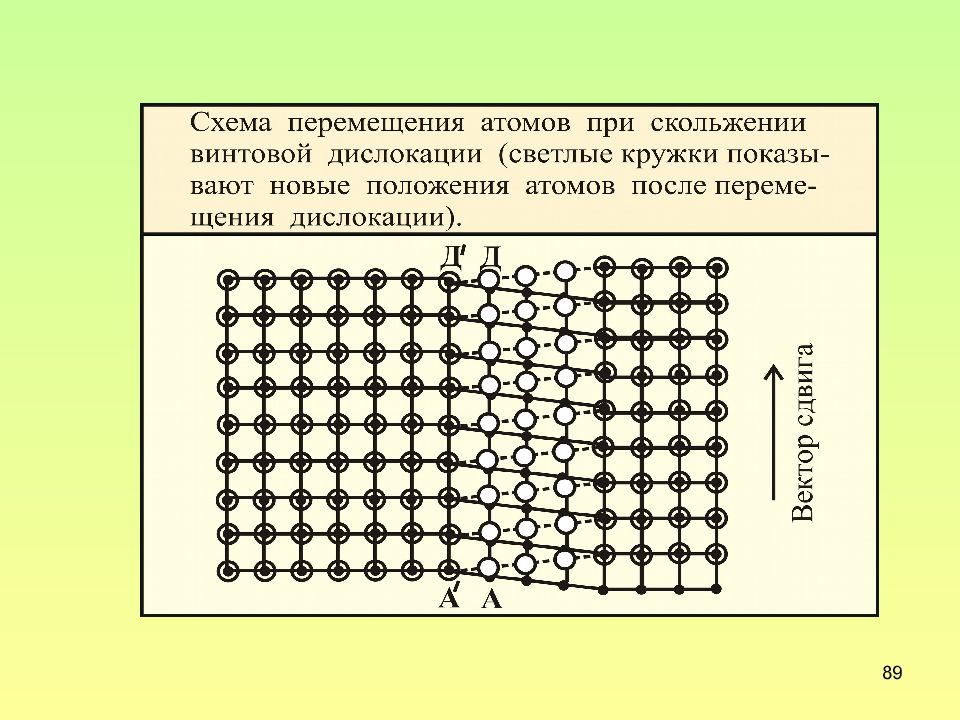
90 Особенности скольжения винтовой дислокации При смещении дислокации на одно межатомное расстояние смещаются только атомы в области несовершенства. Атомы перемещаются только на доли межатомного расстояния. Атомы смещаются в направлении действующих на них сил, а дислокация в направлении перпендикулярном им.
Слайд 91: Двойное поперечное скольжение винтовой дислокации
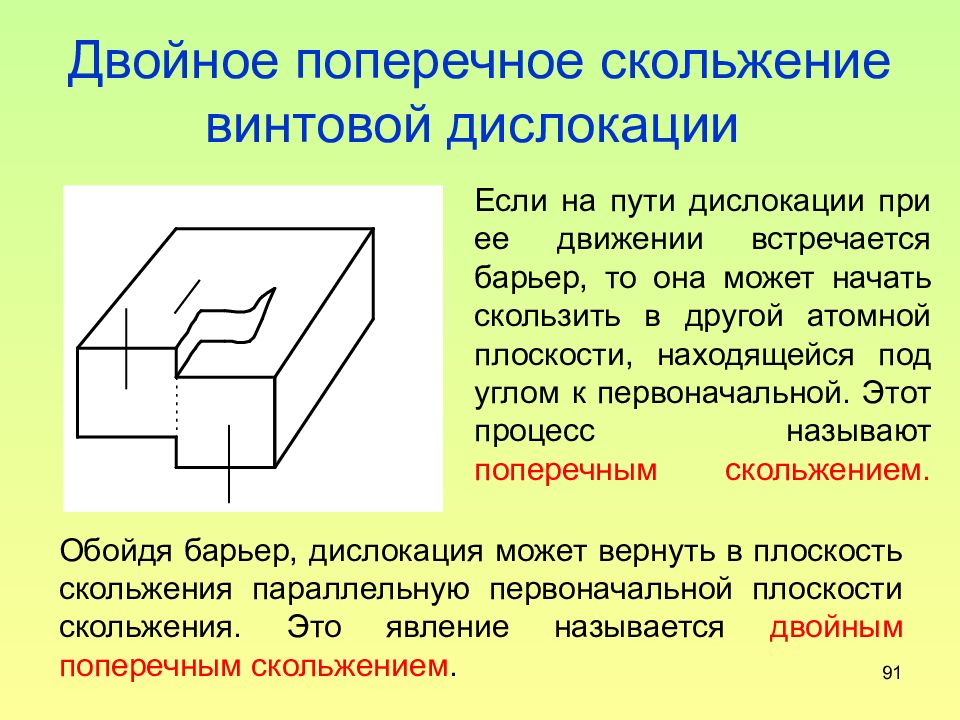
91 Двойное поперечное скольжение винтовой дислокации Если на пути дислокации при ее движении встречается барьер, то она может начать скользить в другой атомной плоскости, находящейся под углом к первоначальной. Этот процесс называют поперечным скольжением. Обойдя барьер, дислокация может вернуть в плоскость скольжения параллельную первоначальной плоскости скольжения. Это явление называется двойным поперечным скольжением.
Слайд 92: Взаимодействие дислокаций
92 Взаимодействие дислокаций Различают два типа взаимодействия двух дислокаций дальнодействие, осуществляемое через поле напряжений; близкодействие - перестройка ядер дислокаций при их соприкосновении.
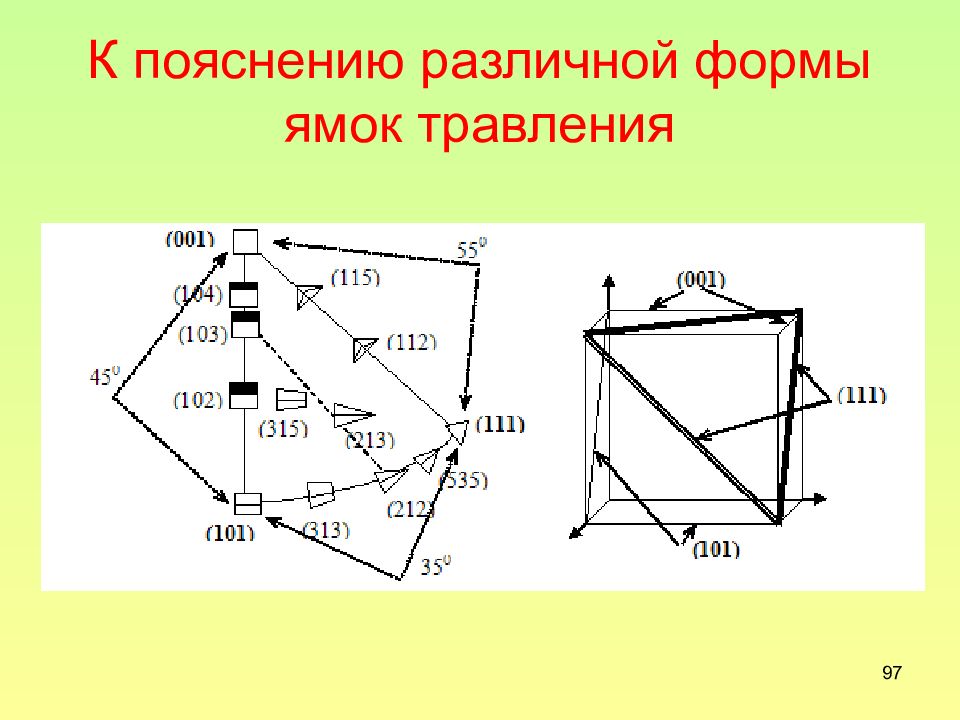
Слайд 97: К пояснению различной формы ямок травления
97 К пояснению различной формы ямок травления
Слайд 102: Поверхностные дефекты
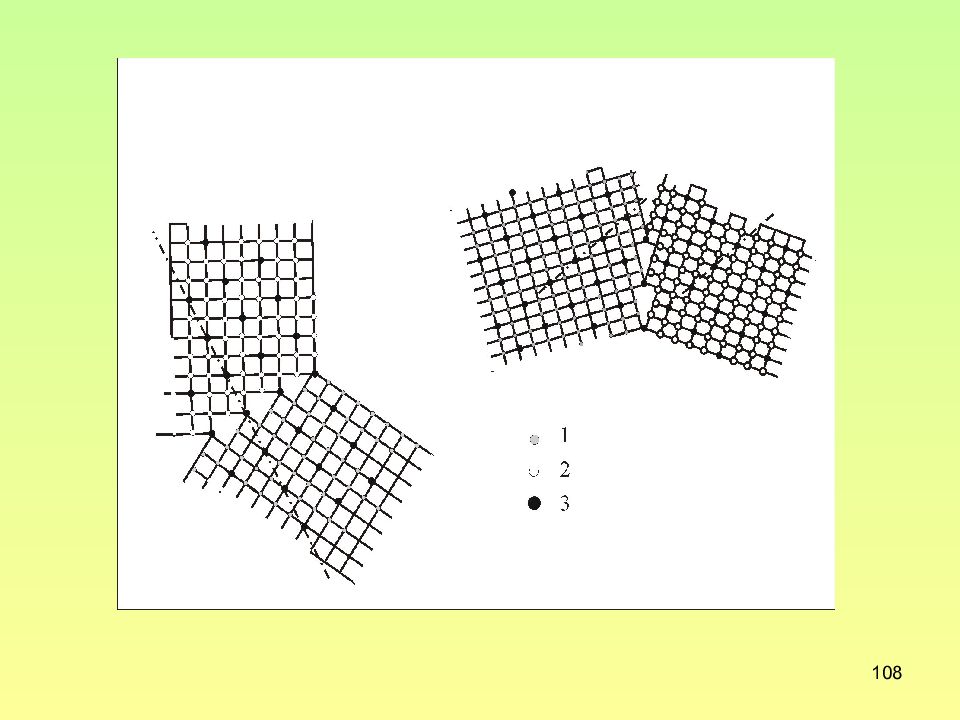
102 Поверхностные дефекты 1.Границы кристалла 2.Границы зерен
Слайд 109: Параметры разориентировки для РСУ с различными ∑ в простой кубической решетки
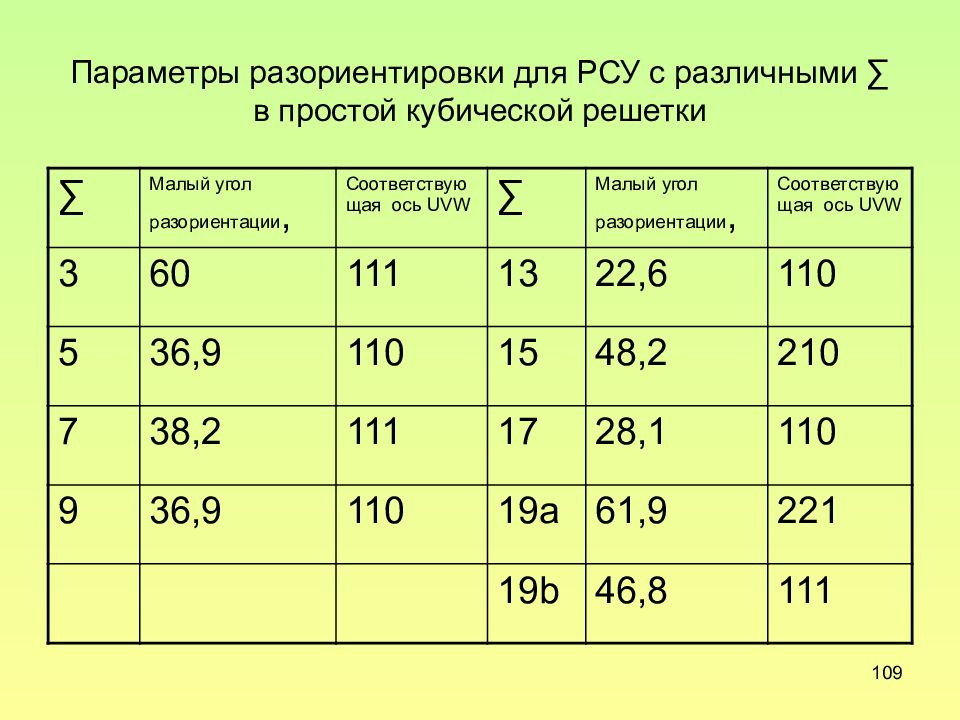
109 Параметры разориентировки для РСУ с различными ∑ в простой кубической решетки ∑ Малый угол разориентации, Соответствующая ось UVW ∑ Малый угол разориентации, Соответствующая ось UVW 3 60 111 13 22,6 110 5 36,9 110 15 48,2 210 7 38,2 111 17 28,1 110 9 36,9 110 19a 61,9 2 21 19b 46,8 111
Слайд 111: Понятие кристаллизации
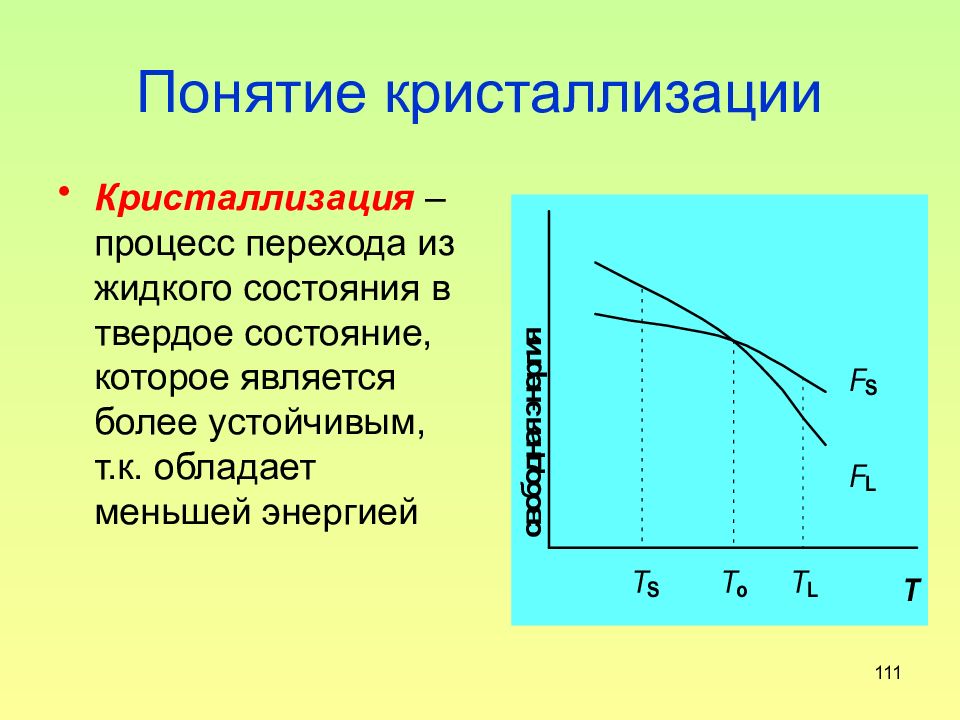
111 Понятие кристаллизации Кристаллизация – процесс перехода из жидкого состояния в твердое состояние, которое является более устойчивым, т.к. обладает меньшей энергией
Слайд 112: Понятие о гомогенной кристаллизации
112 Понятие о гомогенной кристаллизации Гомогенная кристаллизация – флуктуационное образование кристаллов в случайных участках объема жидкости. В реальных веществах такая кристаллизация происходит крайне редко, т.к. всегда имеются готовые твердые поверхности-подложки – стенки литейной формы, взвешенные в расплаве мелкие частицы разной природы.
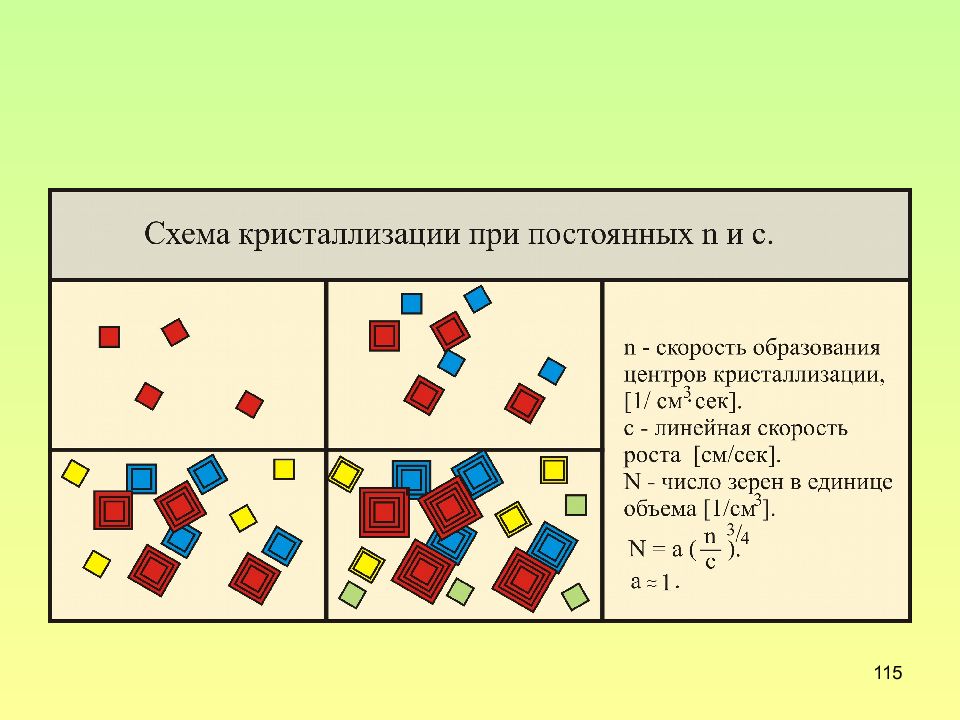
Слайд 113: Элементарные процессы кристаллизации
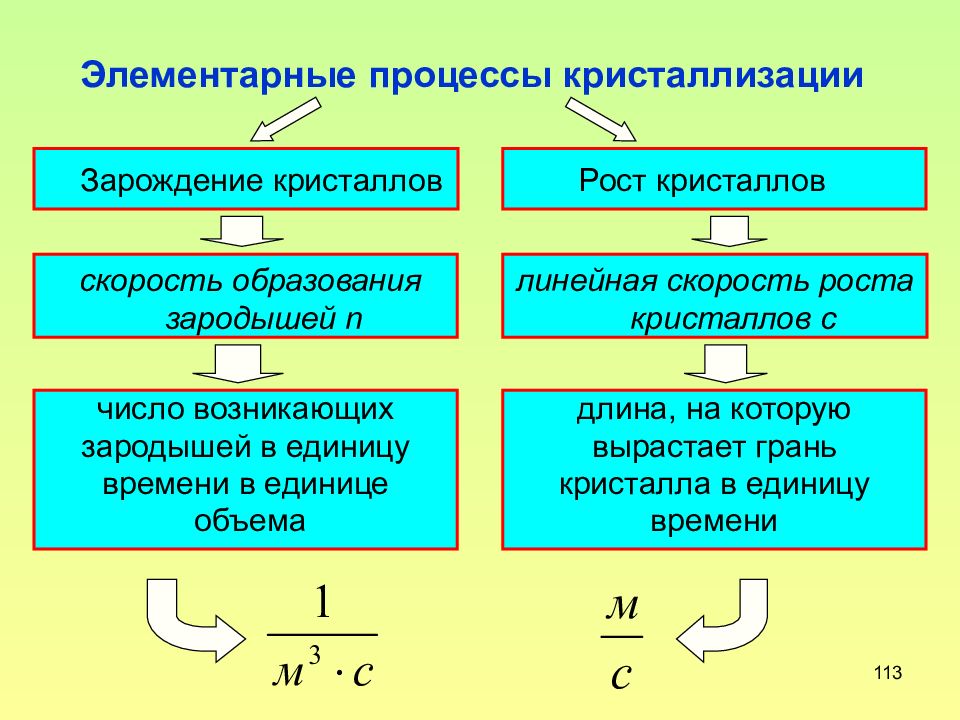
113 Элементарные процессы кристаллизации Зарождение кристаллов Рост кристаллов скорость образования зародышей n длина, на которую вырастает грань кристалла в единицу времени число возникающих зародышей в единицу времени в единице объема линейная скорость роста кристаллов с
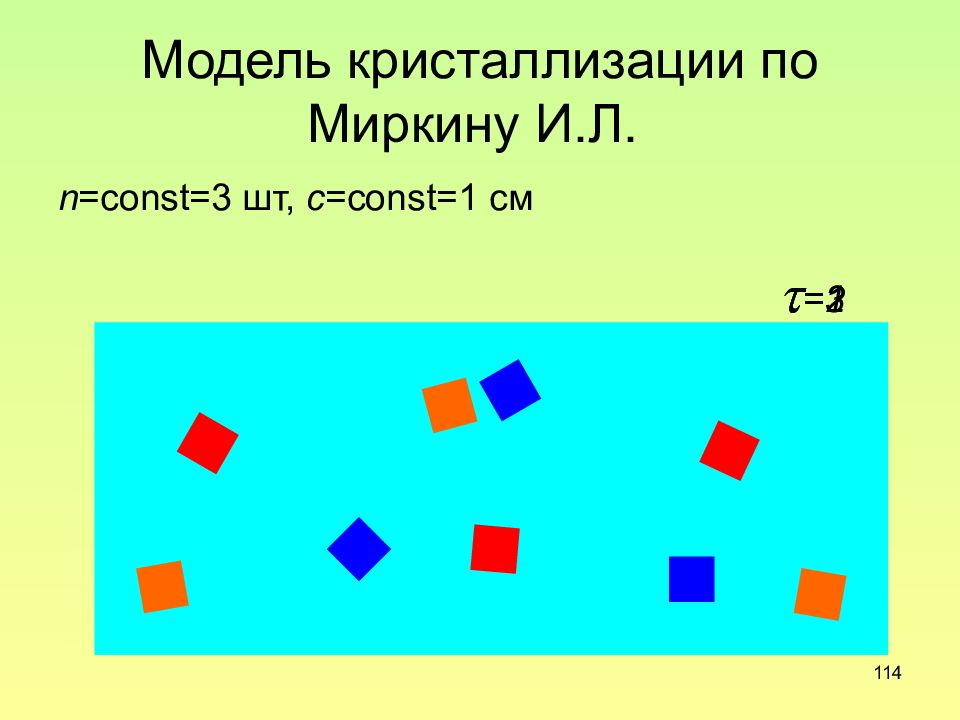
Слайд 114: Модель кристаллизации по Миркину И.Л
114 Модель кристаллизации по Миркину И.Л. n =const=3 шт, c =const=1 c м =1 =2 =3
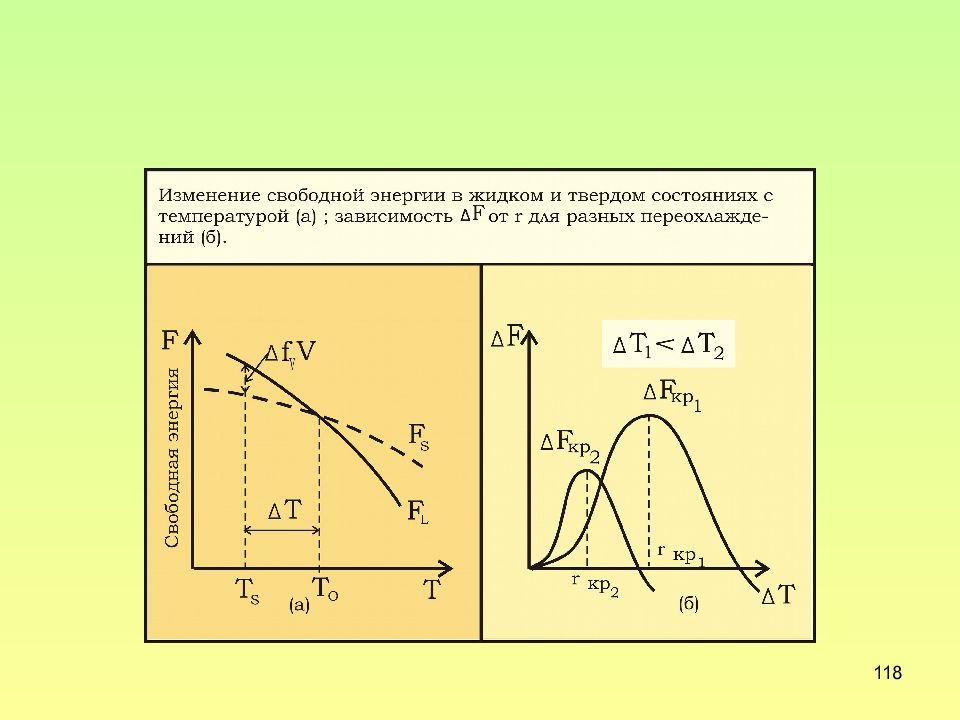
Слайд 117: Размер критического зародыша
117 Размер критического зародыша Изменение свободной энергии F при кристаллизации Для кристалла в форме сферы Условие кристаллизации F <0
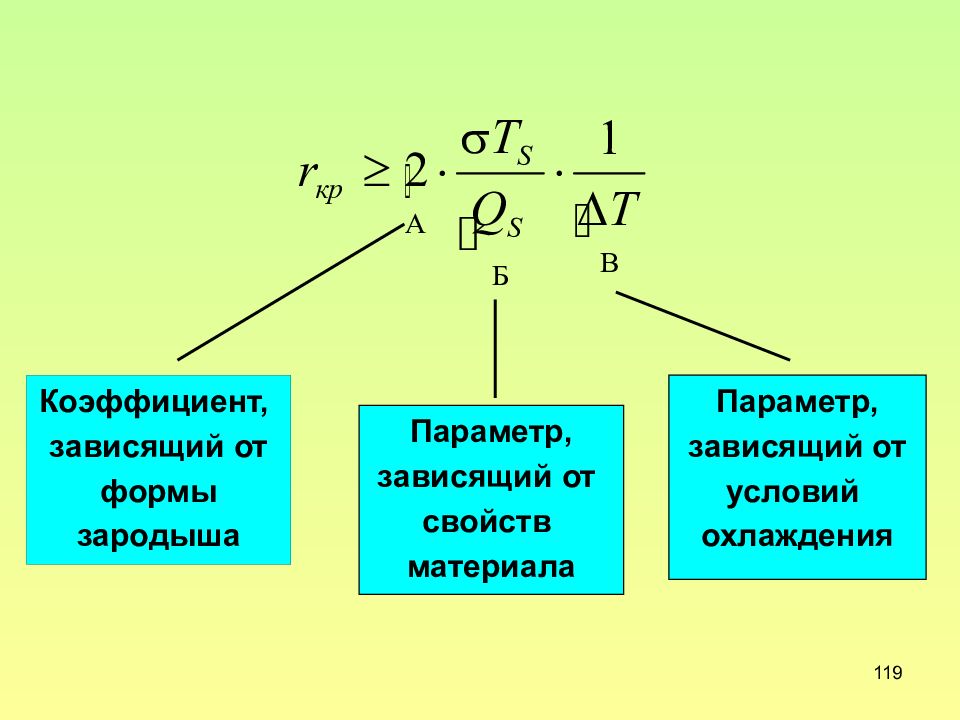
Слайд 119
119 Коэффициент, зависящий от формы зародыша Параметр, зависящий от свойств материала Параметр, зависящий от условий охлаждения
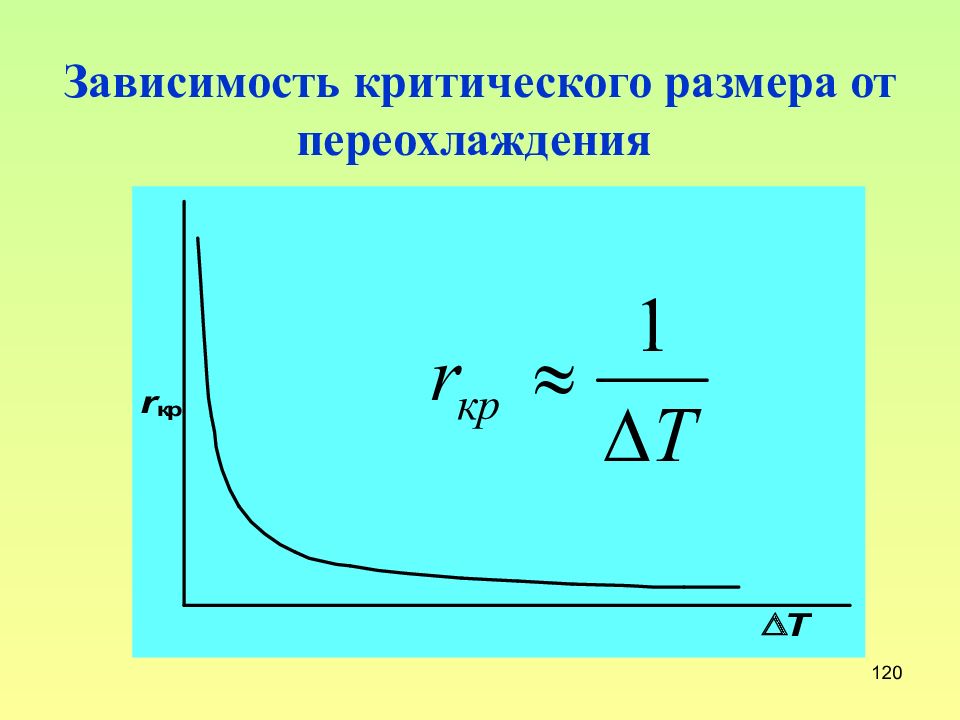
Слайд 120: Зависимость критического размера от переохлаждения
120 Зависимость критического размера от переохлаждения
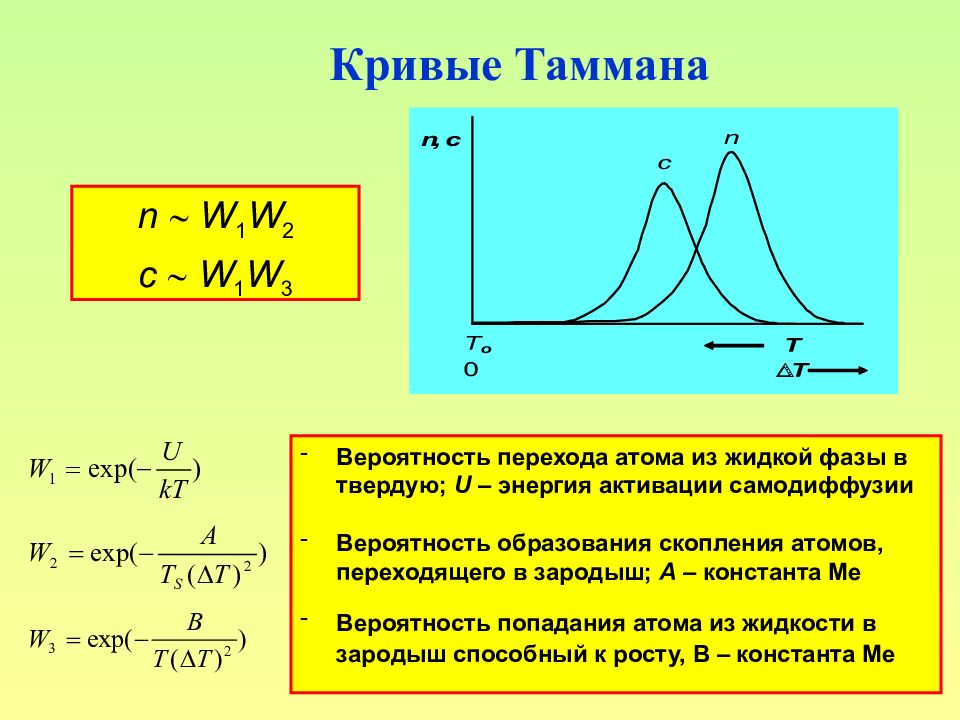
Слайд 122: Кривые Таммана
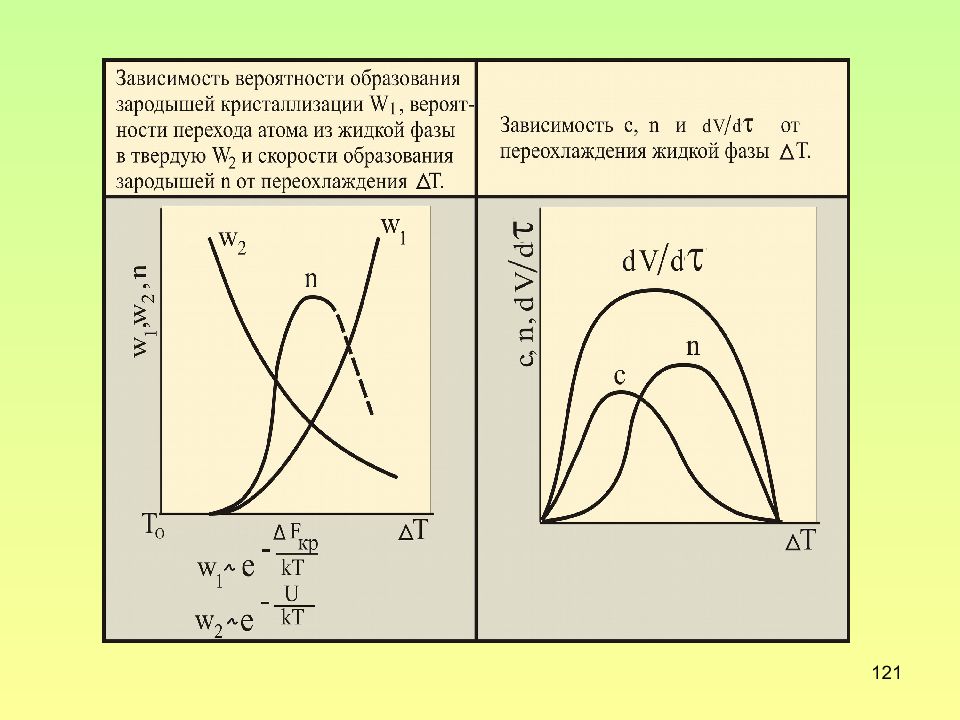
122 Кривые Таммана n W 1 W 2 c W 1 W 3 Вероятность перехода атома из жидкой фазы в твердую; U – энергия активации самодиффузии Вероятность образования скопления атомов, переходящего в зародыш; А – константа Me Вероятность попадания атома из жидкости в зародыш способный к росту, В – константа Me
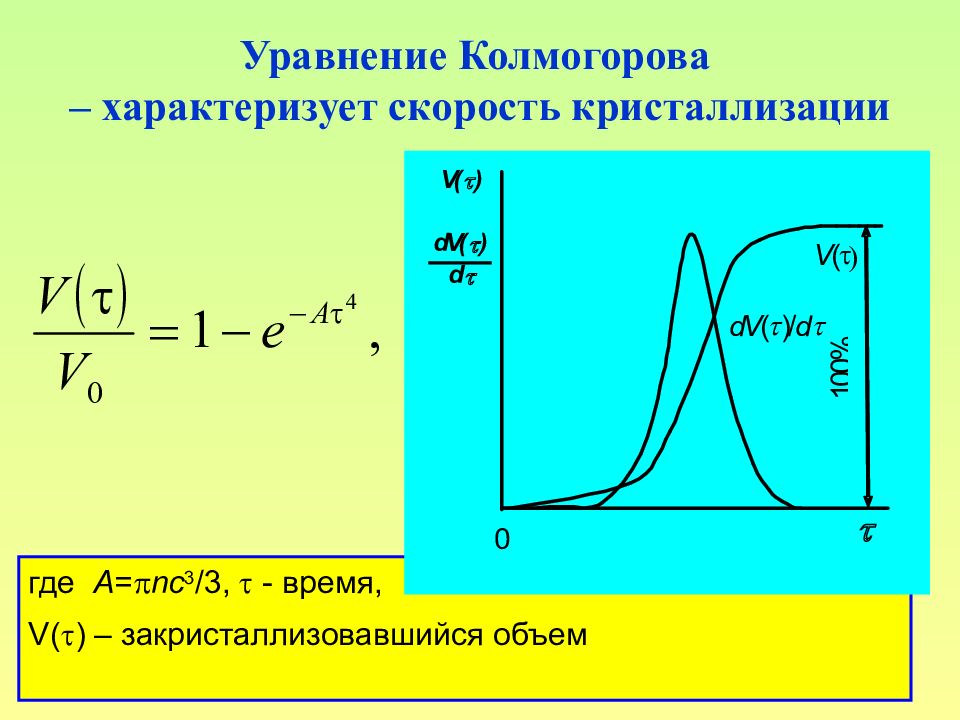
Слайд 123: Уравнение Колмогорова – характеризует скорость кристаллизации
123 Уравнение Колмогорова – характеризует скорость кристаллизации где A = nc 3 /3, - время, V() – закристаллизовавшийся объем
Слайд 124: Гетерогенная кристаллизация
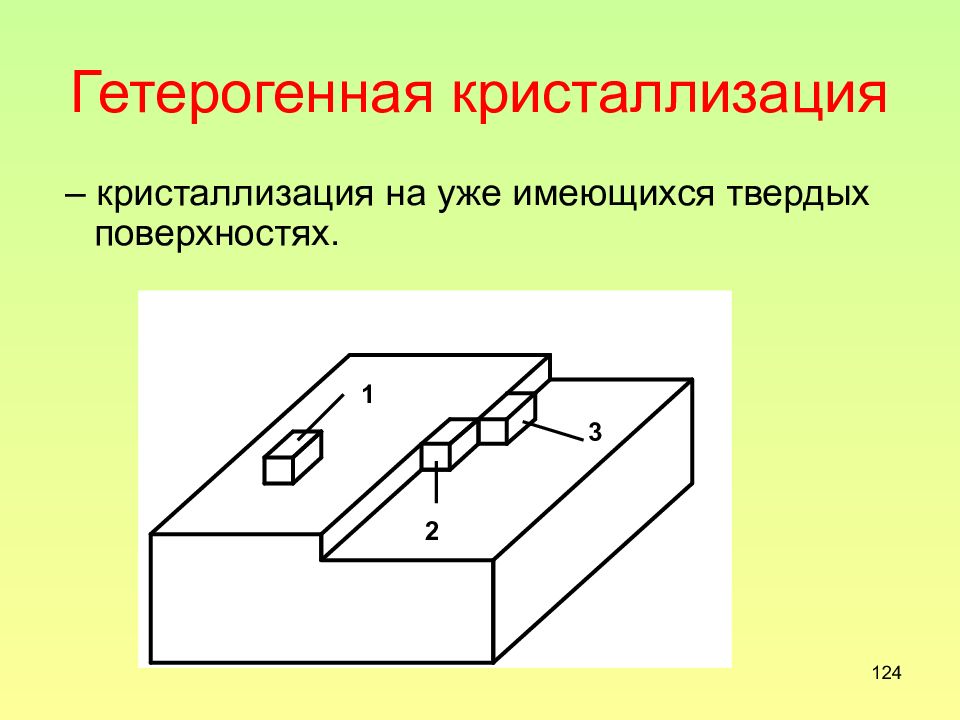
124 Гетерогенная кристаллизация – кристаллизация на уже имеющихся твердых поверхностях.
Слайд 125: Влияние гетерогенности на величину инкубационного периода кристаллизации
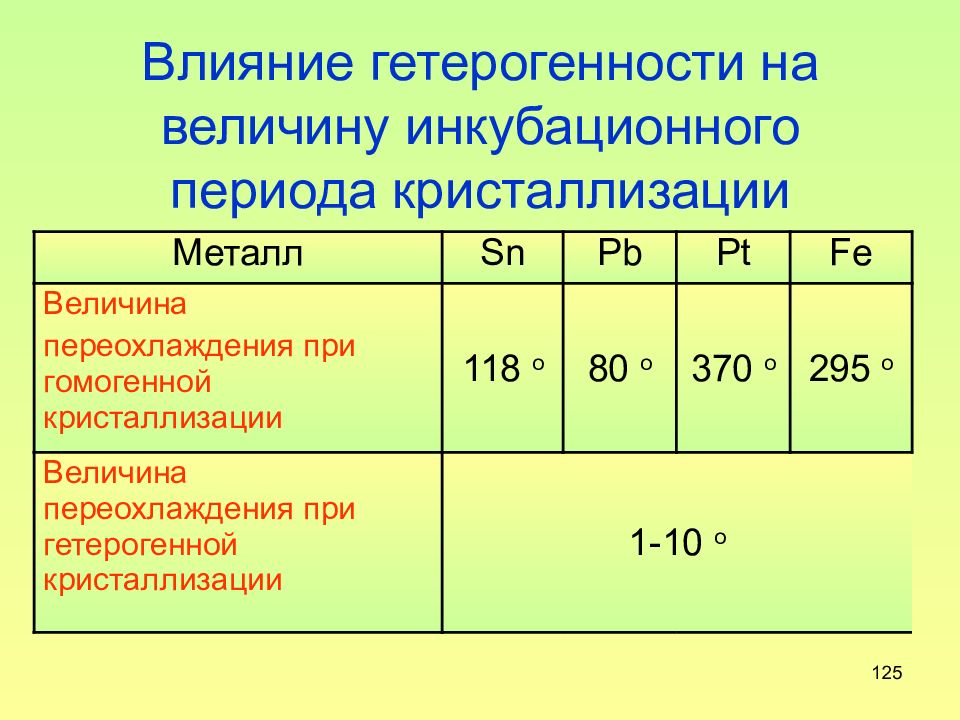
125 Влияние гетерогенности на величину инкубационного периода кристаллизации Металл Sn Pb Pt Fe Величина переохлаждения при гомогенной кристаллизации 118 o 80 o 370 o 295 o Величина переохлаждения при гетерогенной кристаллизации 1-10 o
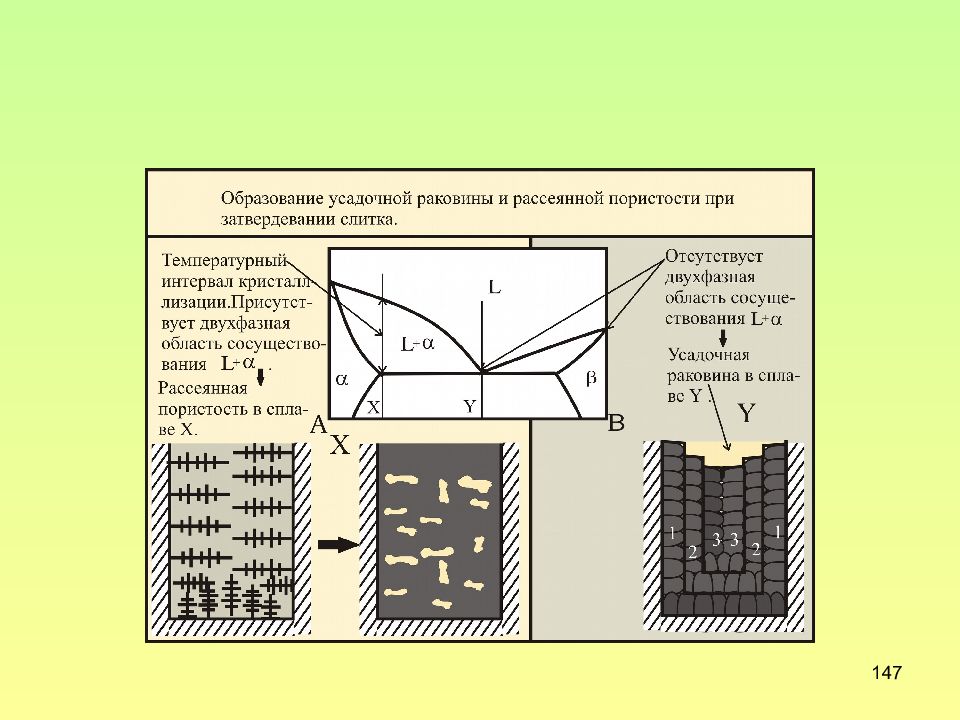
Слайд 126: Структура слитка
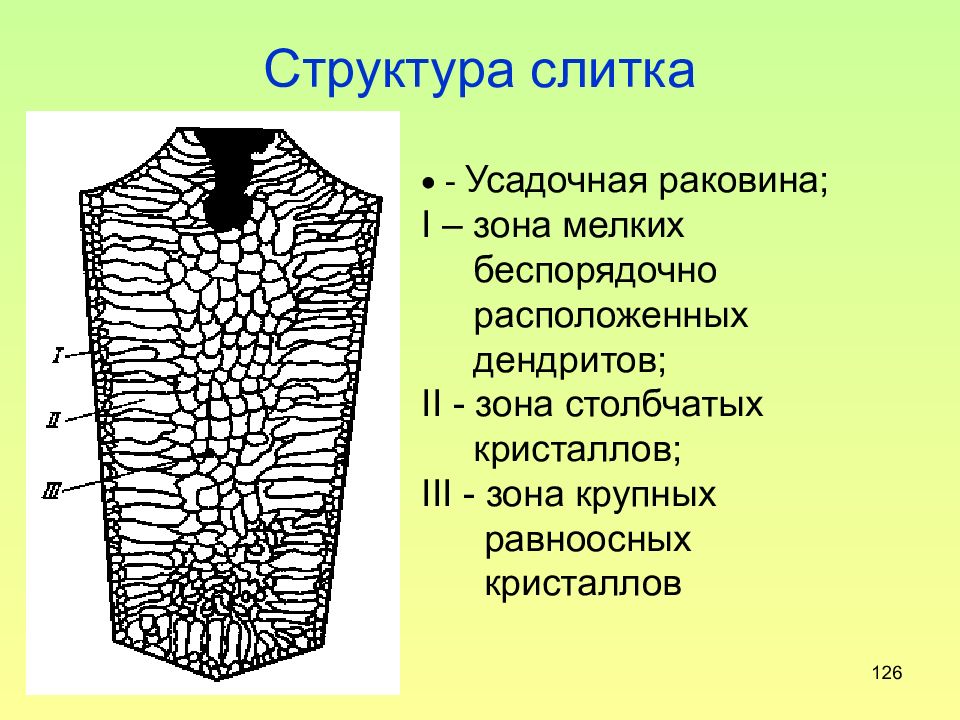
126 Структура слитка - Усадочная раковина; I – зона мелких беспорядочно расположенных дендритов ; II - зона столбчатых кристаллов; III - зона крупных равноосных кристаллов
Слайд 131: Понятие фазы
131 Понятие фазы Фаза - это совокупность тождественных по химическому составу гомогенных частей термодинамической системы, одинаковых по всем свойствам, не зависящим от массы
Слайд 132: Правило фаз Гиббса (1876 г.)
132 Правило фаз Гиббса (1876 г.) где С – число степеней свободы системы или вариантность ; К – число компонентов в системе; 2 – число термодинамических параметров (температура и давление) При постоянном давлении Р= const
Слайд 133: Правило рычага (правило противоположного отрезка)
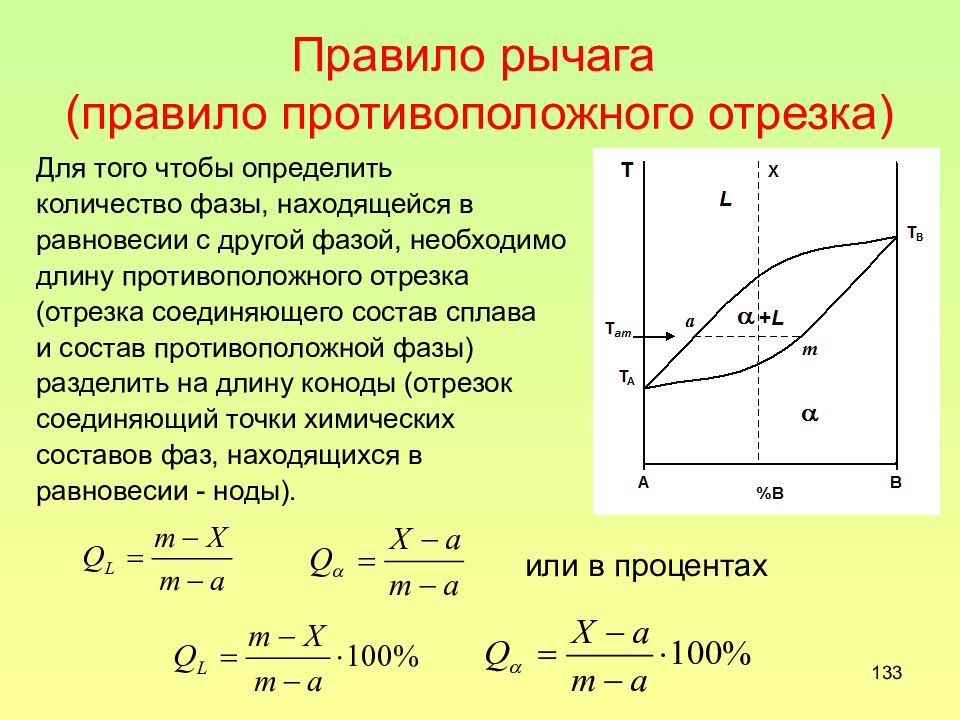
133 Правило рычага (правило противоположного отрезка) Для того чтобы определить количество фазы, находящейся в равновесии с другой фазой, необходимо длину противоположного отрезка (отрезка соединяющего состав сплава и состав противоположной фазы) разделить на длину коноды (отрезок соединяющий точки химических составов фаз, находящихся в равновесии - ноды). или в процентах
Слайд 134: Система с непрерывным рядом твердых растворов (С u — Ni, Fe — Ni, Bi — Sb, Ag —А u, FeO — MnO )
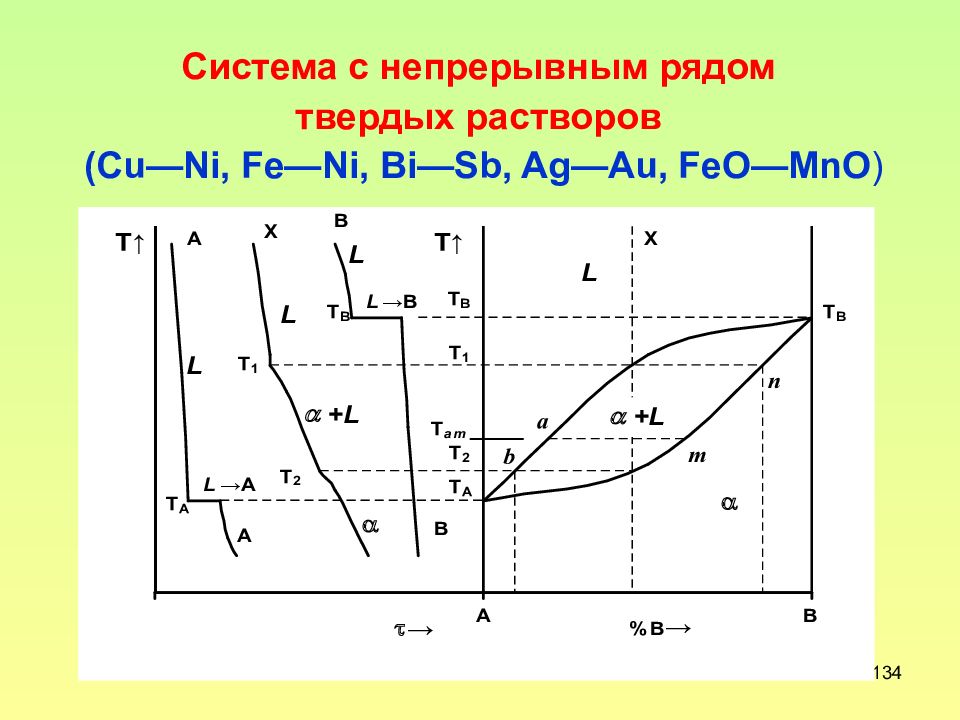
134 Система с непрерывным рядом твердых растворов (С u — Ni, Fe — Ni, Bi — Sb, Ag —А u, FeO — MnO )
Слайд 135: Ликвация
135 Ликвация в процессе кристаллизации из жидкости выделяются кристаллы твердой фазы разного состава; первые кристаллы обогащены тугоплавким компонентом; затвердевшие последними кристаллы обеднены тугоплавким компонентом
Слайд 136: Дендритная ликвация
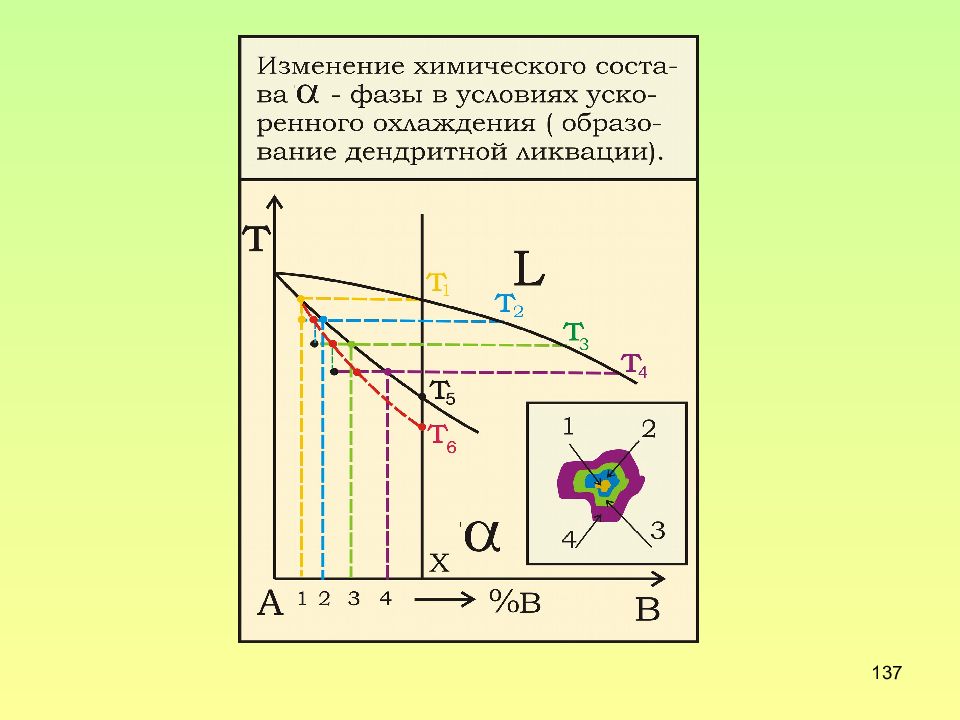
136 Дендритная ликвация главные оси дендритов обогащены тугоплавким компонентом, т.к. затвердевают первыми; межосные пространства обеднены тугоплавким элементов, т.к. затвердевают последними. Для устранения ликвации используют отжиг первого рода, он предназначен для устранения дефекта литья – ликвации, и называется гомогенизирующим или гомогенизацией.
Слайд 141: Диаграмма с эвтектическим превращением (Р b — As, Cd — Bi, А u — Si, KCl — LiCl, CaO — MgO )
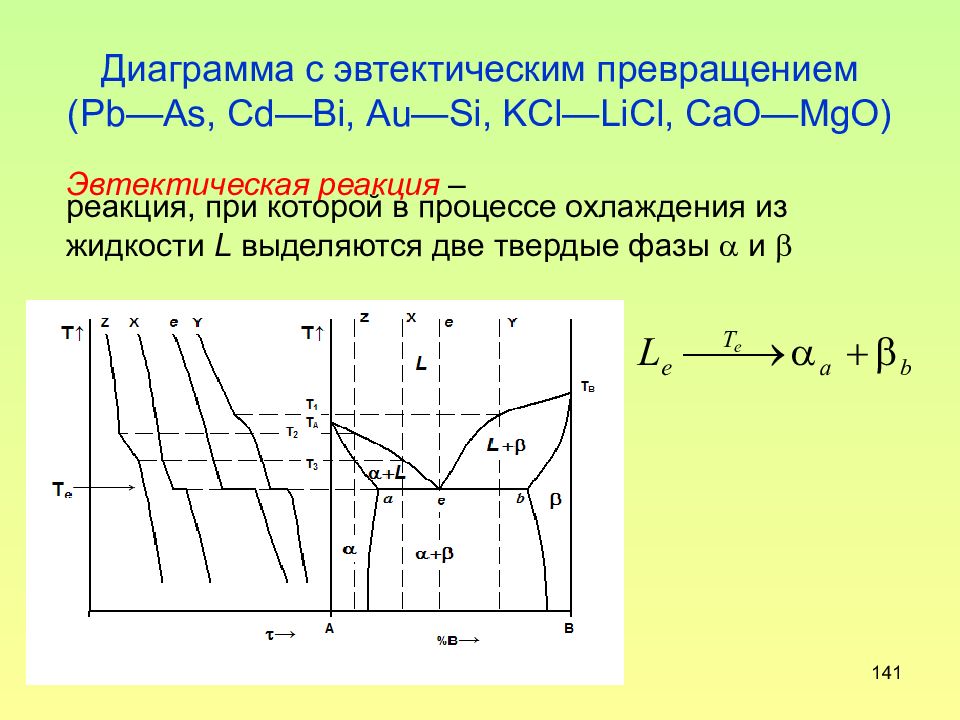
141 Диаграмма с эвтектическим превращением (Р b — As, Cd — Bi, А u — Si, KCl — LiCl, CaO — MgO ) Эвтектическая реакция – реакция, при которой в процессе охлаждения из жидкости L выделяются две твердые фазы и
Слайд 142: Понятие эвтектики
142 Понятие эвтектики Особенностью эвтектических реакций является то, что после них фазовые и структурные составляющие не совпадают – это связано с тем, что в эвтектике только с помощью микроскопа нельзя отождествить фазы – т.е. сказать, где какая. Это связано с тем, что кристаллы фаз в эвтектике очень малы и часто затруднительно определить каких больше. Эвтектическую смесь двух фаз считают одной структурной составляющей, называемой эвтектика. Эвтектику обозначают как механическую смесь двух фаз ( а + b ) e.
Слайд 143: Типы эвтектик
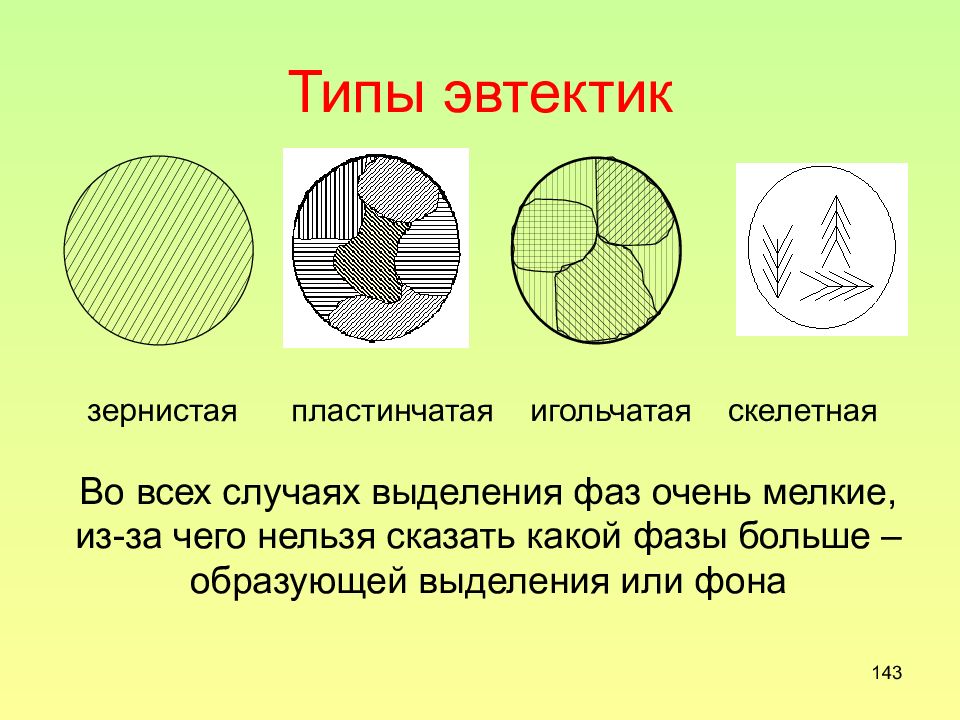
143 Типы эвтектик зернистая пластинчатая игольчатая скелетная Во всех случаях выделения фаз очень мелкие, из-за чего нельзя сказать какой фазы больше – образующей выделения или фона
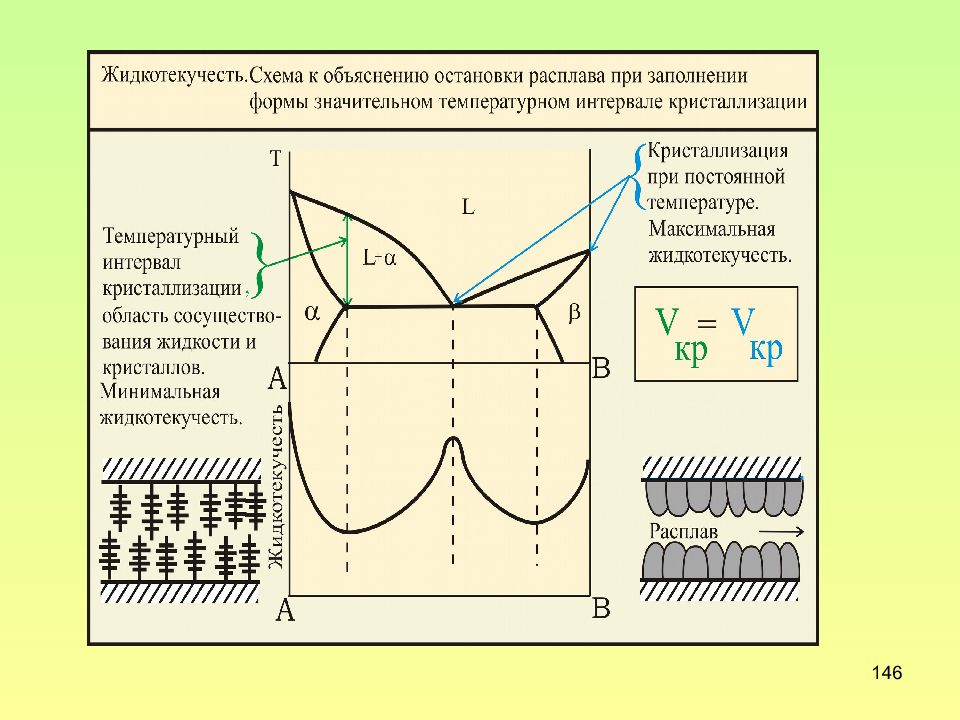
Слайд 144: Кристаллизация доэвтектического сплава
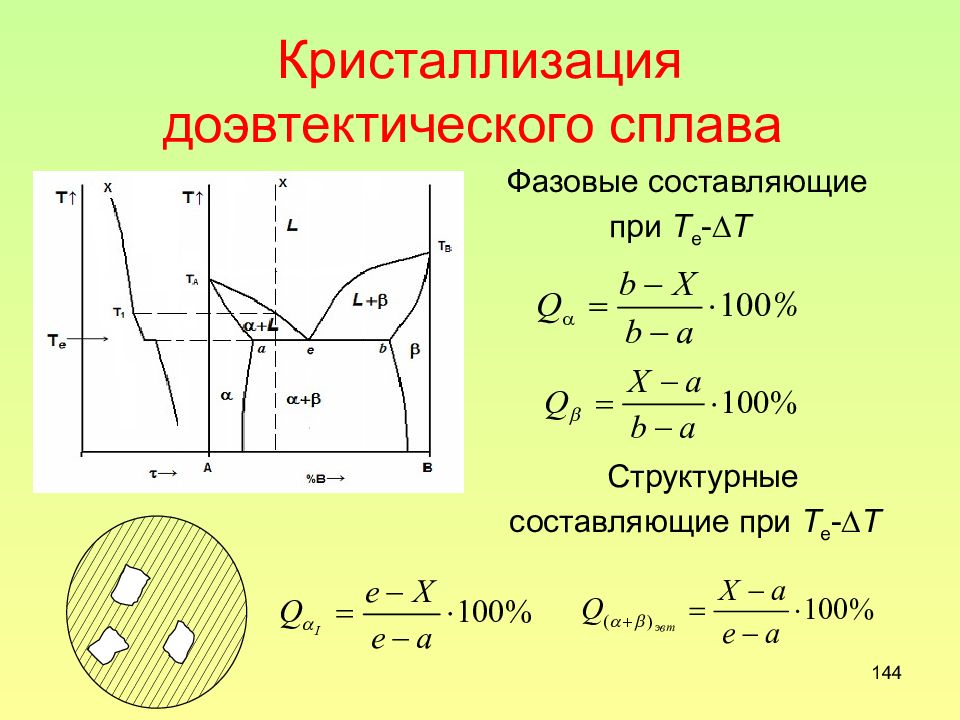
144 Кристаллизация доэвтектического сплава Фазовые составляющие при Т е - Т Структурные составляющие при Т е - Т
Слайд 145: Кристаллизация заэвтектического сплава
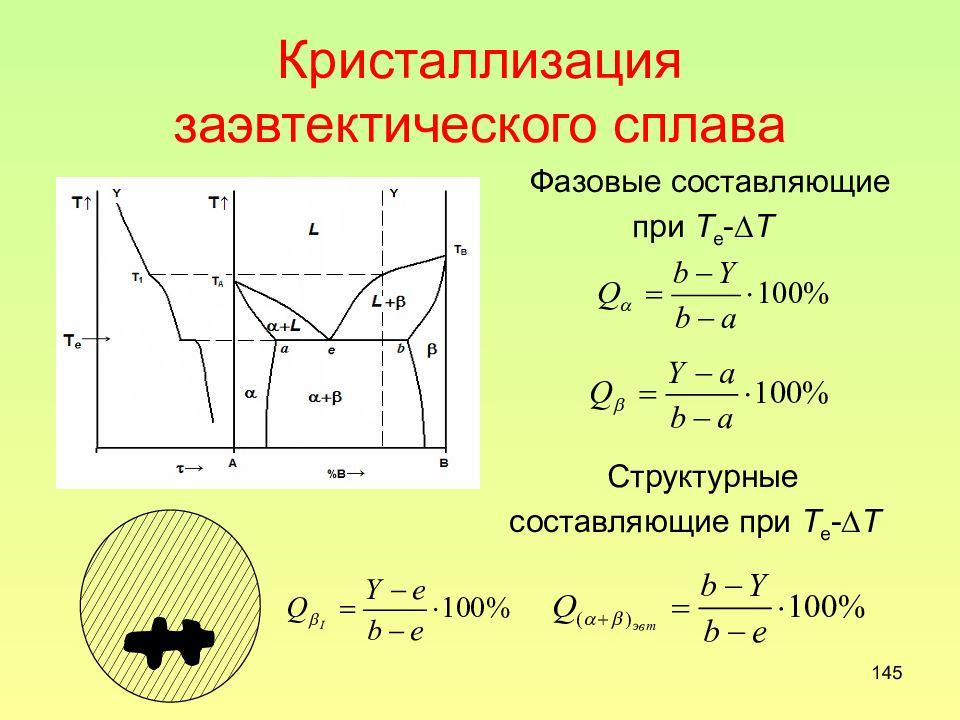
145 Кристаллизация заэвтектического сплава Фазовые составляющие при Т е - Т Структурные составляющие при Т е - Т
Слайд 149: Классификация веществ по магнитным структуре и свойствам
149 Классификация веществ по магнитным структуре и свойствам Все вещества в природе можно разделить на магнитно-неупорядоченные и магнитно-упорядоченные. А. Магнитно-неупорядоченные вещества К ним относятся диамагнетики и парамагнетики. Диамагнетики отталкиваются от магнита, а парамагнетики притягиваются к нему.
Слайд 150
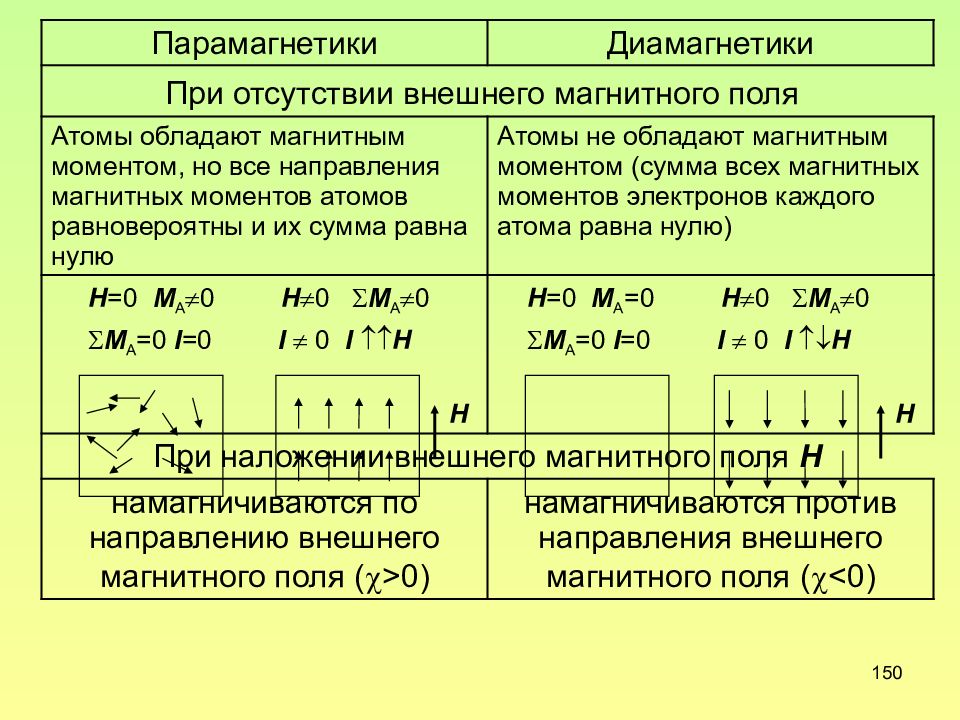
150 Парамагнетики Диамагнетики При отсутствии внешнего магнитного поля Атомы обладают магнитным моментом, но все направления магнитных моментов атомов равновероятны и их сумма равна нулю Атомы не обладают магнитным моментом (сумма всех магнитных моментов электронов каждого атома равна нулю) Н =0 M A 0 Н 0 M A 0 M A =0 I =0 I 0 I H H Н =0 M A =0 Н 0 M A 0 M A =0 I =0 I 0 I H H При наложении внешнего магнитного поля Н намагничиваются по направлению внешнего магнитного поля ( >0) намагничиваются против направления внешнего магнитного поля ( <0)
Слайд 151
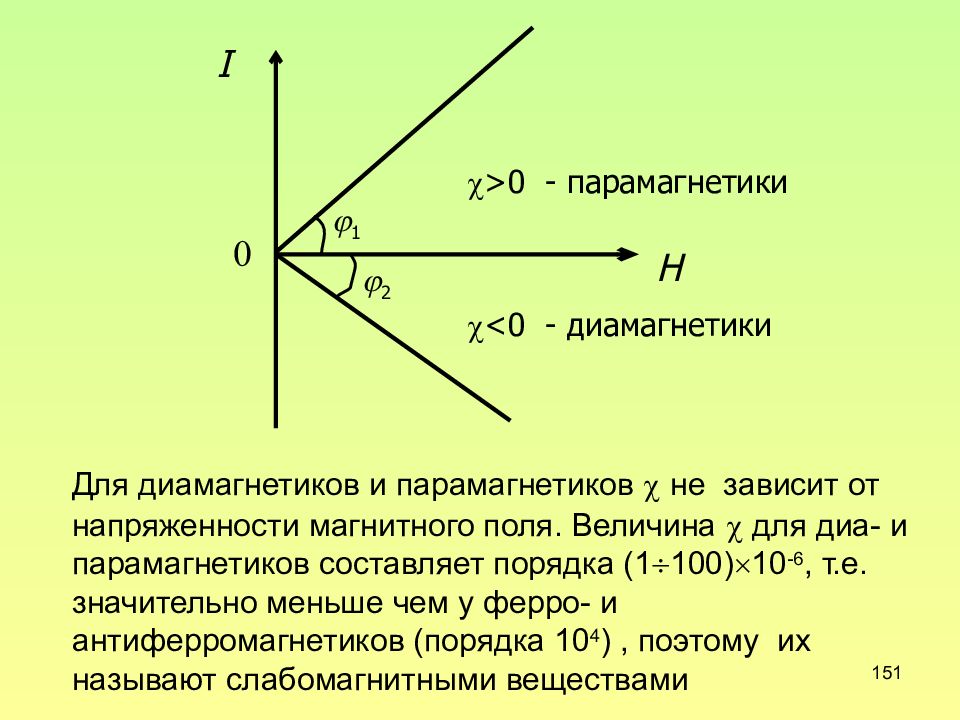
151 H I 1 2 >0 - парамагнетики <0 - диамагнетики Для диамагнетиков и парамагнетиков не зависит от напряженности магнитного поля. Величина для диа- и парамагнетиков составляет порядка (1100)10 -6, т.е. значительно меньше чем у ферро- и антиферромагнетиков (порядка 10 4 ), поэтому их называют слабомагнитными веществами 0
Слайд 152: Б. Магнитно-упорядоченные вещества
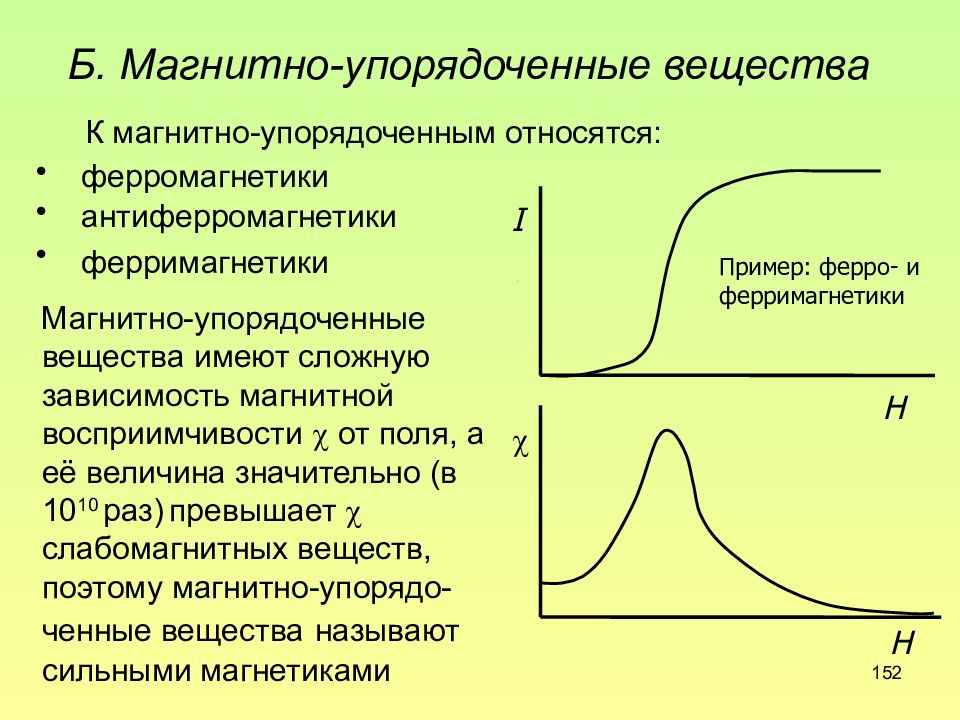
152 Б. Магнитно-упорядоченные вещества К магнитно-упорядоченным относятся: ферромагнетики антиферромагнетики ферримагнетики Магнитно-упорядоченные вещества имеют сложную зависимость магнитной восприимчивости от поля, а её величина значительно (в 10 10 раз) превышает слабомагнитных веществ, поэтому магнитно-упорядо-ченные вещества называют сильными магнетиками I H H Пример: ферро- и ферримагнетики
Слайд 153: Магнитная структура сильных магнетиков
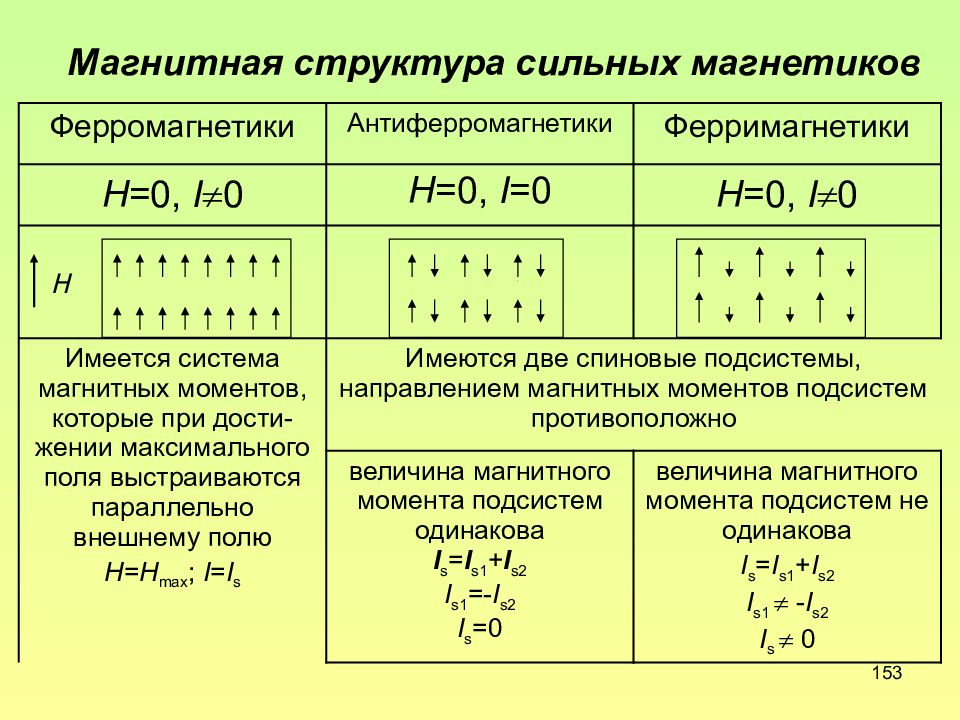
153 Магнитная структура сильных магнетиков Ферромагнетики Антиферромагнетики Ферримагнетики Н =0, I 0 Н =0, I =0 Н =0, I 0 Имеется система магнитных моментов, которые при дости-жении максимального поля выстраиваются параллельно внешнему полю Н=Н max ; I = I s Имеются две спиновые подсистемы, направлением магнитных моментов подсистем противоположно величина магнитного момента подсистем одинакова I s = I s1 + I s2 I s1 =- I s2 I s =0 величина магнитного момента подсистем не одинакова I s = I s1 + I s2 I s1 - I s2 I s 0 H
Слайд 154: Магнетики в таблице Менделеева
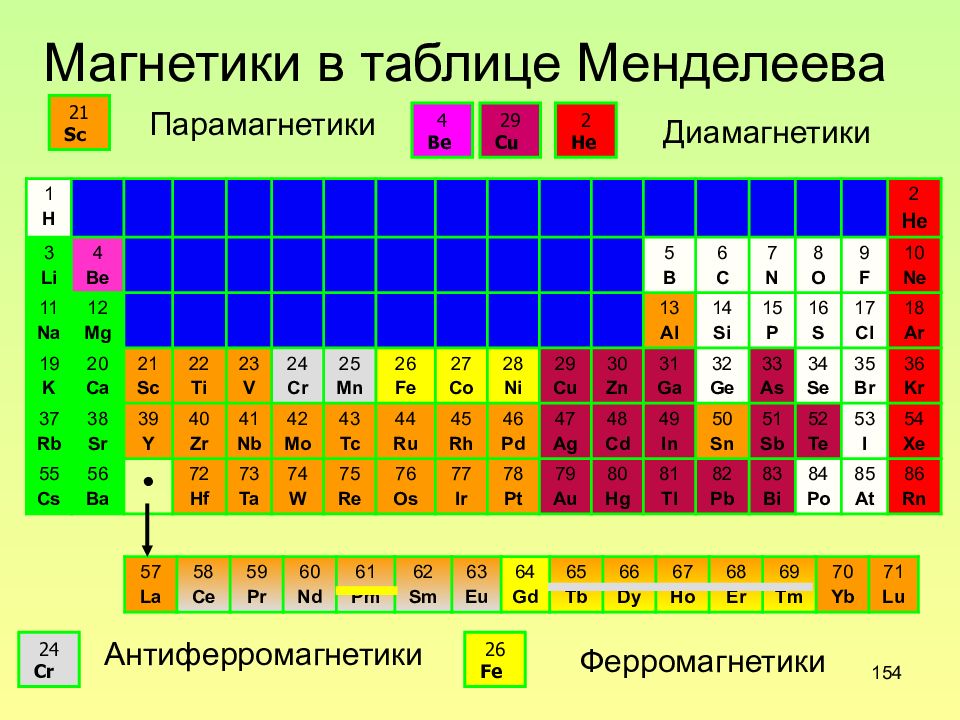
154 Магнетики в таблице Менделеева 57 La 58 Ce 59 Pr 60 Nd 61 Pm 62 Sm 63 Eu 64 Gd 65 Tb 66 Dy 67 Ho 68 Er 69 Tm 70 Yb 71 Lu 1 H 2 He 3 Li 4 Be 5 B 6 C 7 N 8 O 9 F 10 Ne 11 Na 12 Mg 13 Al 14 Si 15 P 16 S 17 Cl 18 Ar 19 K 20 Ca 21 Sc 22 Ti 23 V 24 Cr 25 Mn 26 Fe 27 Co 28 Ni 29 Cu 30 Zn 31 Ga 32 Ge 33 As 34 Se 35 Br 36 Kr 37 Rb 38 Sr 39 Y 40 Zr 41 Nb 42 Mo 43 Tc 44 Ru 45 Rh 46 Pd 47 Ag 48 Cd 49 In 50 Sn 51 Sb 52 Te 53 I 54 Xe 55 Cs 56 Ba • 72 Hf 73 Ta 74 W 75 Re 76 Os 77 Ir 78 Pt 79 Au 80 Hg 81 Tl 82 Pb 83 Bi 84 Po 85 At 86 Rn 24 Cr Антиферромагнетики 26 Fe Ферромагнетики 21 Sc Парамагнетики 4 Be Диамагнетики 29 Cu 2 He
Слайд 156: Основные механизмы магнитного гистерезиса
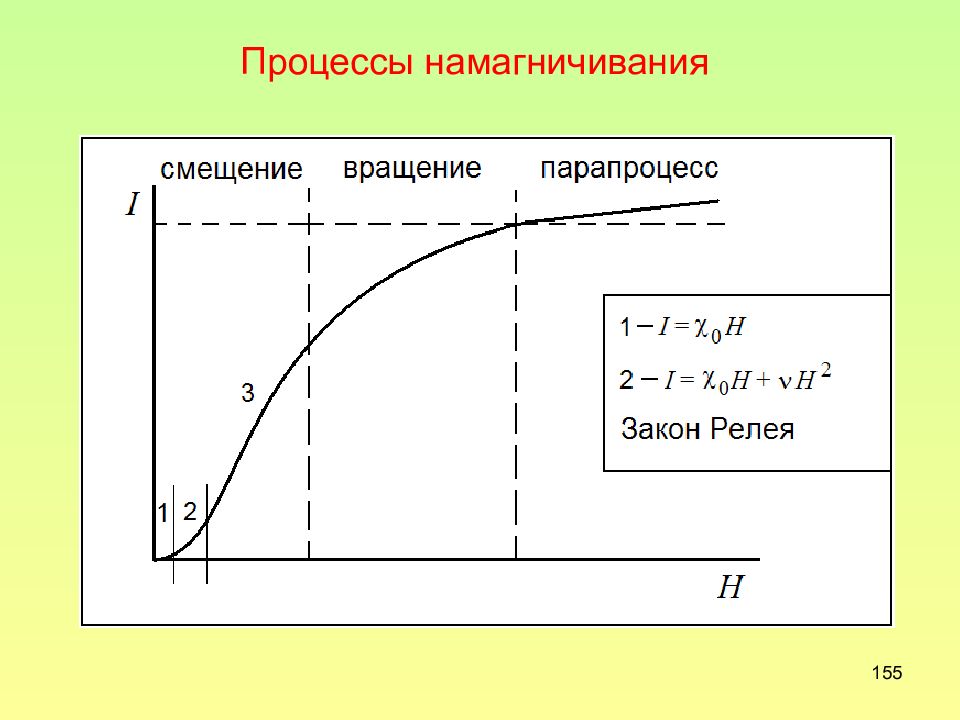
156 Основные механизмы магнитного гистерезиса Задержка смещения границ между доменами Задержка образования и роста зародышей перемагничивания Задержка вращения вектора намагниченности
Слайд 158: Механизмы пластической деформации
158 Механизмы пластической деформации скольжение дислокаций двойникование диффузионный массоперенос зернограничное скольжение сдвиговые диффузионные
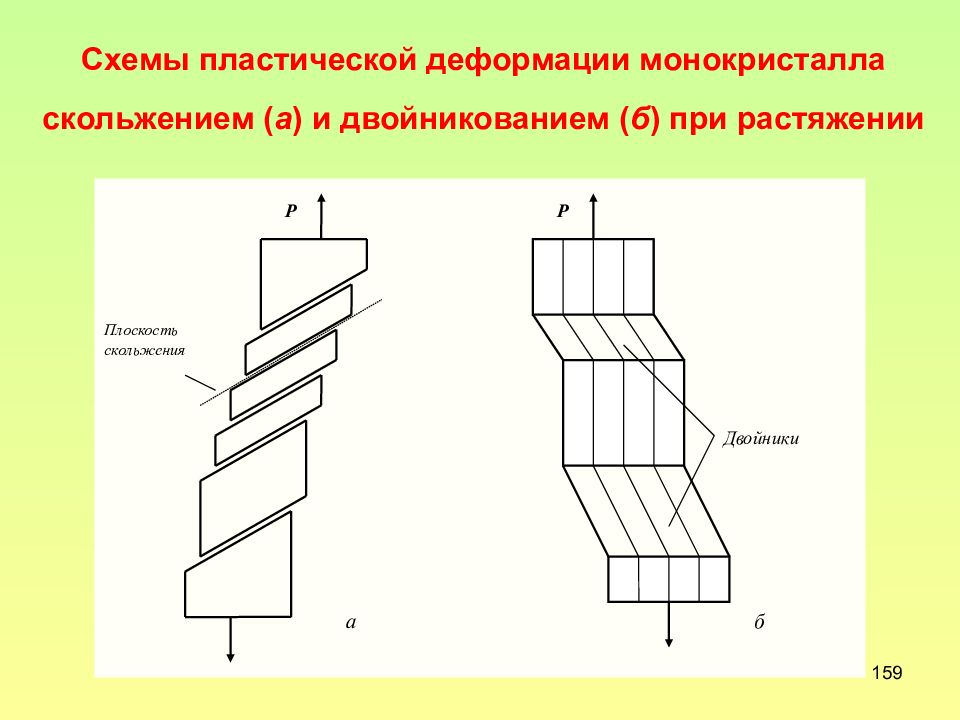
Слайд 159: Схемы пластической деформации монокристалла скольжением ( а ) и двойникованием ( б ) при растяжении
159 Схемы пластической деформации монокристалла скольжением ( а ) и двойникованием ( б ) при растяжении Двойники б а Плоскость скольжения Р Р
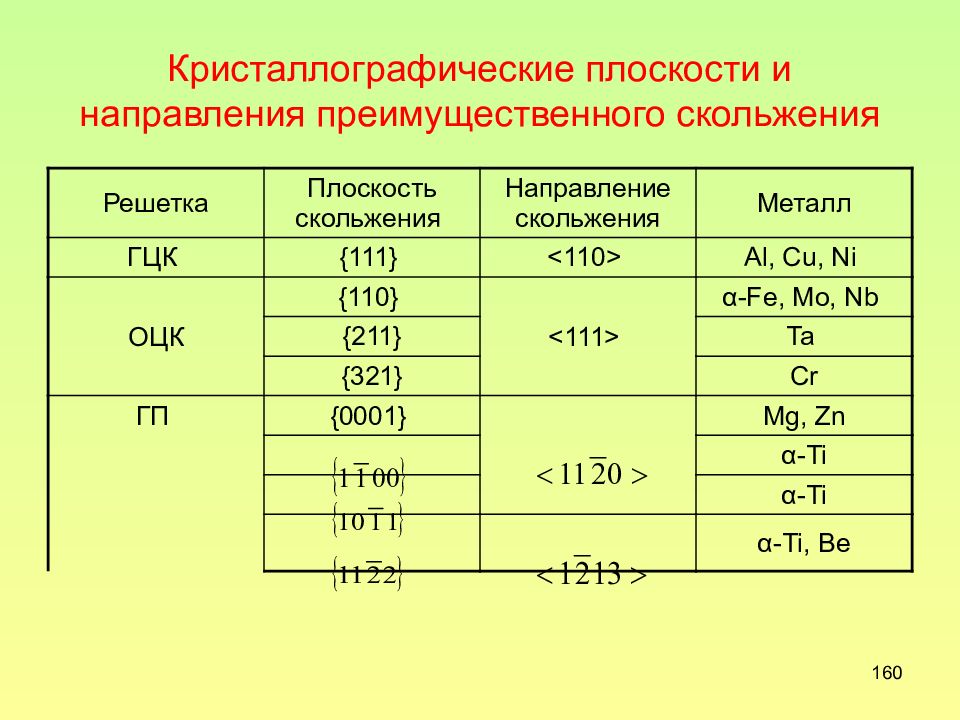
Слайд 160: Кристаллографические плоскости и направления преимущественного скольжения
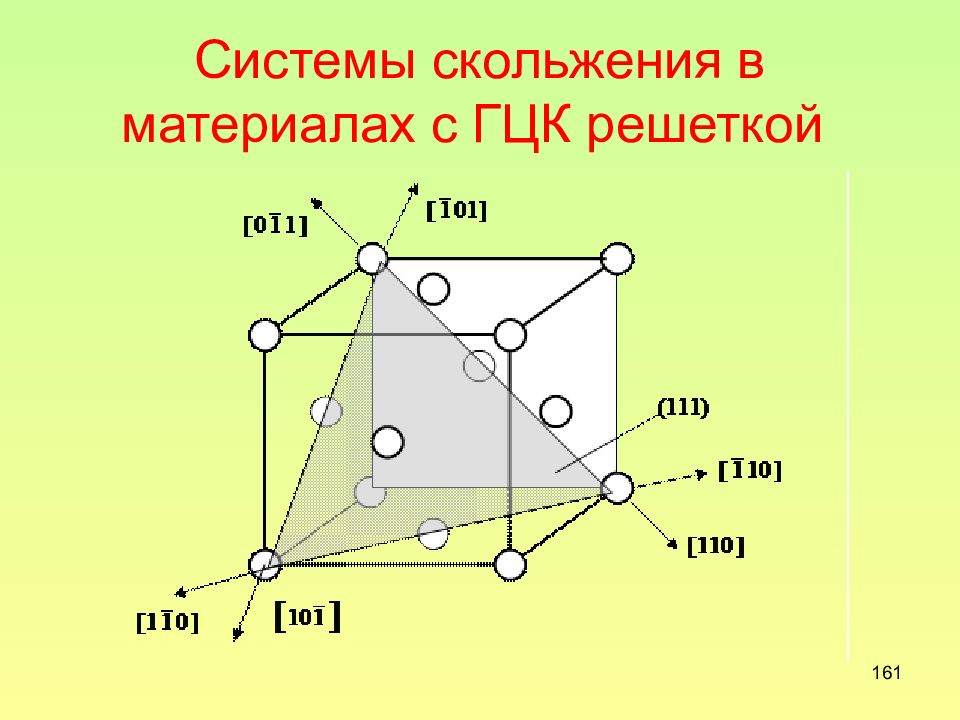
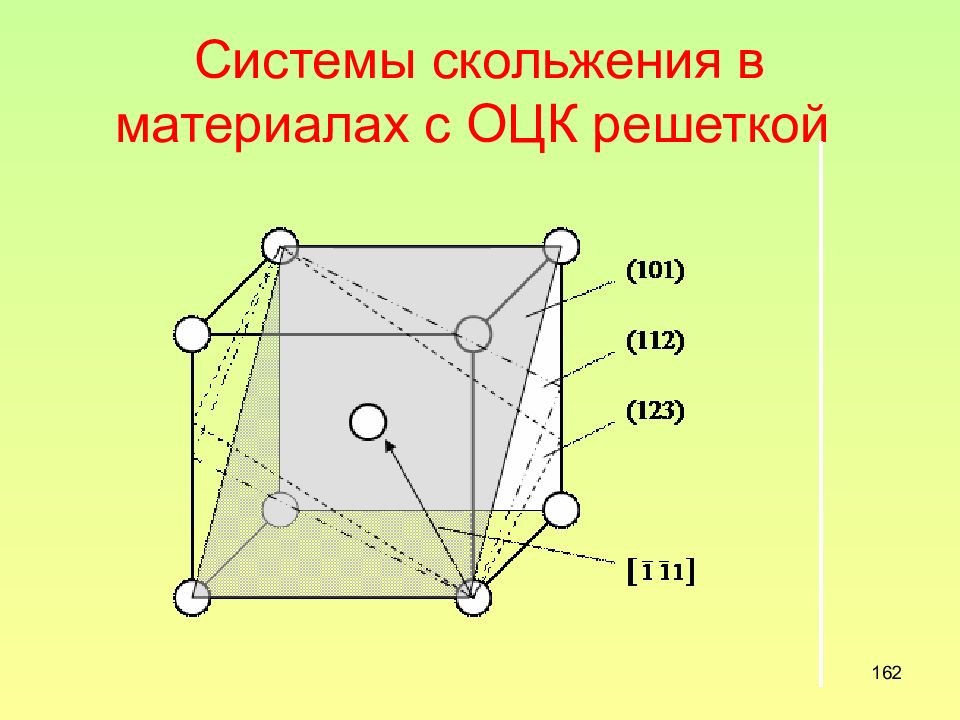
160 Кристаллографические плоскости и направления преимущественного скольжения Решетка Плоскость скольжения Направление скольжения Металл ГЦК {111} <110> Al, Cu, Ni ОЦК {110} <111> α-Fe, Mo, Nb {211} Ta {321} Cr ГП {0001} Mg, Zn α-Ti α-Ti α-Ti, Be
Слайд 161: Системы скольжения в материалах с ГЦК решеткой
161 Системы скольжения в материалах с ГЦК решеткой
Слайд 162: Системы скольжения в материалах с ОЦК решеткой
162 Системы скольжения в материалах с ОЦК решеткой
Слайд 163: Изменение структуры металла при ХПД
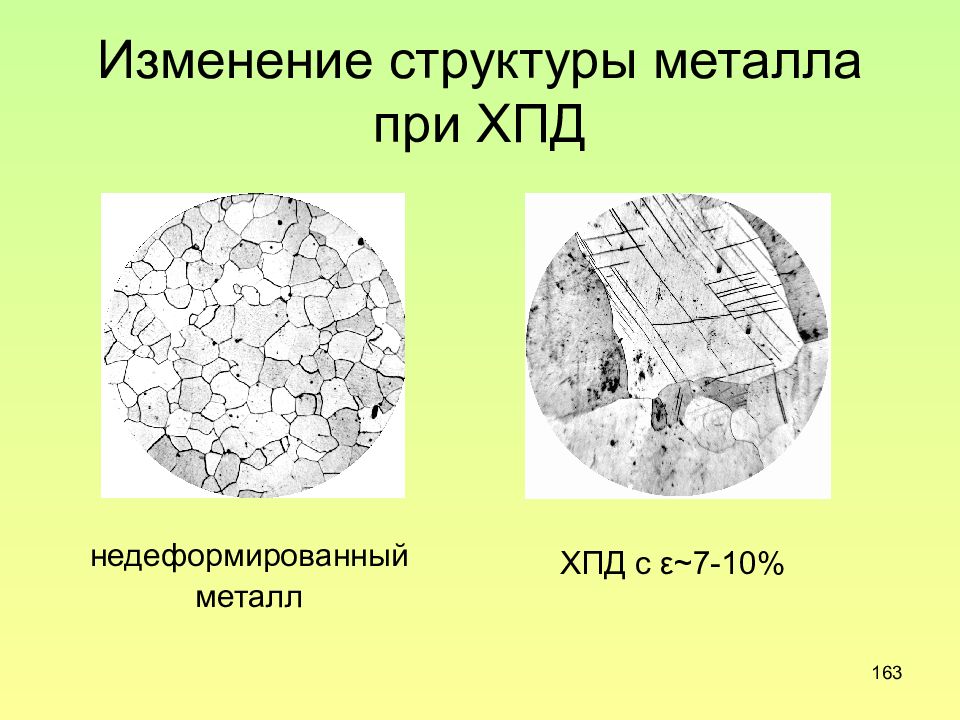
163 Изменение структуры металла при ХПД недеформированный металл ХПД с ε ~ 7-10%
Слайд 164: Изменение структуры металла при ХПД
164 Изменение структуры металла при ХПД ХПД с ε ~ 30-40% ХПД с ε ~ 70-80%
Слайд 165: Упрочнение в результате пластической деформации (наклеп или нагартовка)
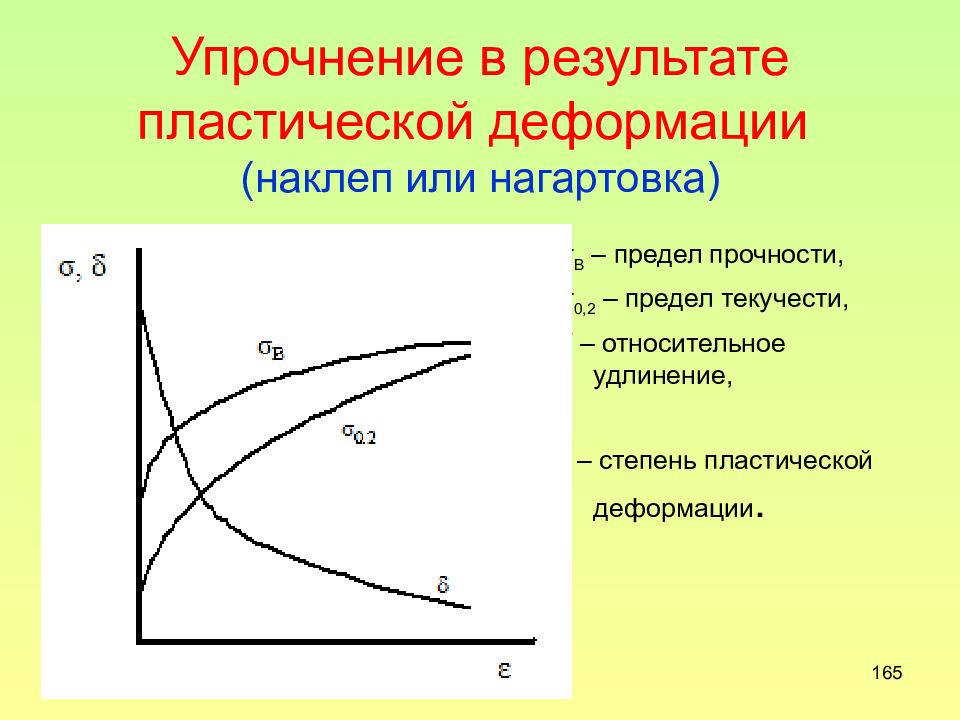
165 Упрочнение в результате пластической деформации (наклеп или нагартовка) σ В – предел прочности, σ 0,2 – предел текучести, δ – относительное удлинение, ε – степень пластической деформации.
Слайд 166: Возврат
166 Возврат - процессы уменьшения количества и перераспределения дефектов кристаллической решетки, не сопровождающиеся движением границ зерен. Другими словами, возврат – это изменения тонкой структуры, которые происходят без изменения размеров и формы зерен.
Слайд 167: Отдых
167 Отдых это стадия возврата, при которой уменьшается количество точечных дефектов, в основном вакансий, и происходит аннигиляция дислокаций разных знаков уменьшаются твердость и прочность металла (обычно не больше, чем на 10–15 %) снижается удельное электрическое сопротивление и повышается сопротивление коррозии металла
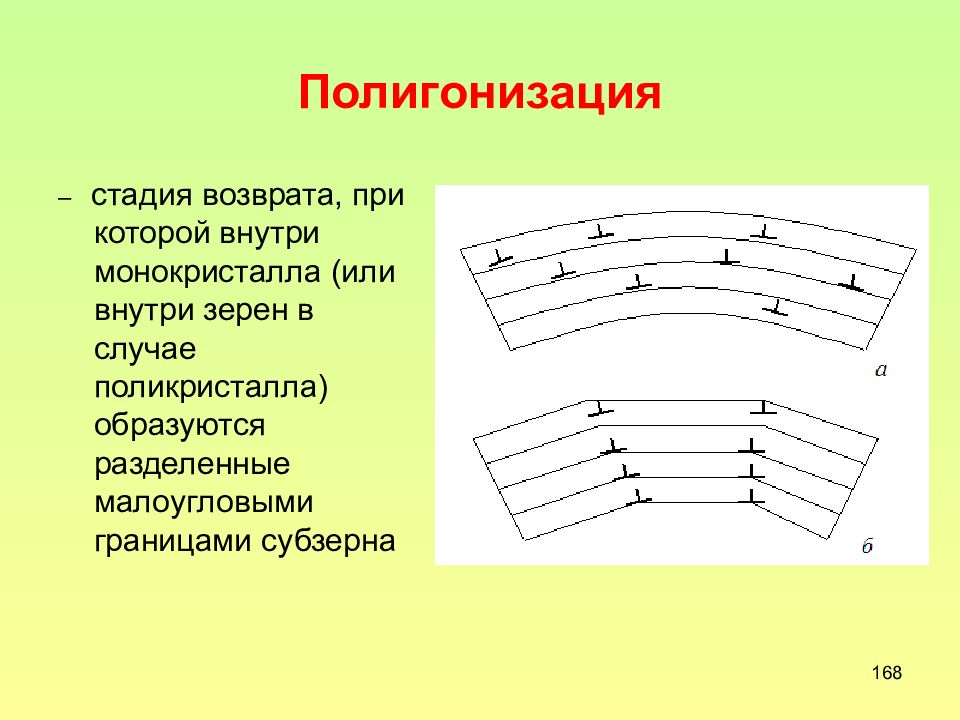
Слайд 168: Полигонизация
168 Полигонизация – стадия возврата, при которой внутри монокристалла (или внутри зерен в случае поликристалла) образуются разделенные малоугловыми границами субзерна
Слайд 169: Первичная рекристаллизация Т п.р = 0,4·Т пл
169 Первичная рекристаллизация Т п.р = 0,4·Т пл Начало первичной рекристаллизации После первичной рекристаллизации
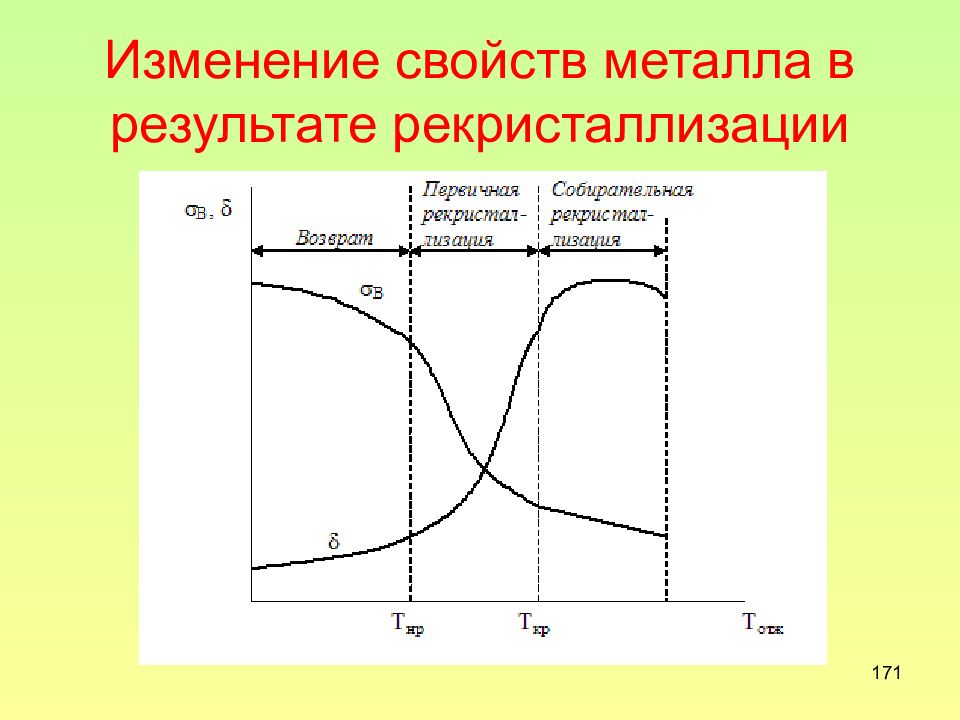
Слайд 170: собирательная рекристаллизация 0,6-0,7 Т пл
170 собирательная рекристаллизация 0,6-0,7 Т пл до собирательной рекристаллизации после собирательной рекристаллизации