Первый слайд презентации: Функция и её свойства
9 класс Урок повторения и обобщения изученного материала
Слайд 2: Содержание
Цели урока Определение Виды функций Свойства функций Задание 1 Задание 2 Тест
Слайд 3: Цели урока
Закрепление свойств функции Развитие умений исследования графиков функции Выполнение упражнений и построение графиков функций
Слайд 4: Определение
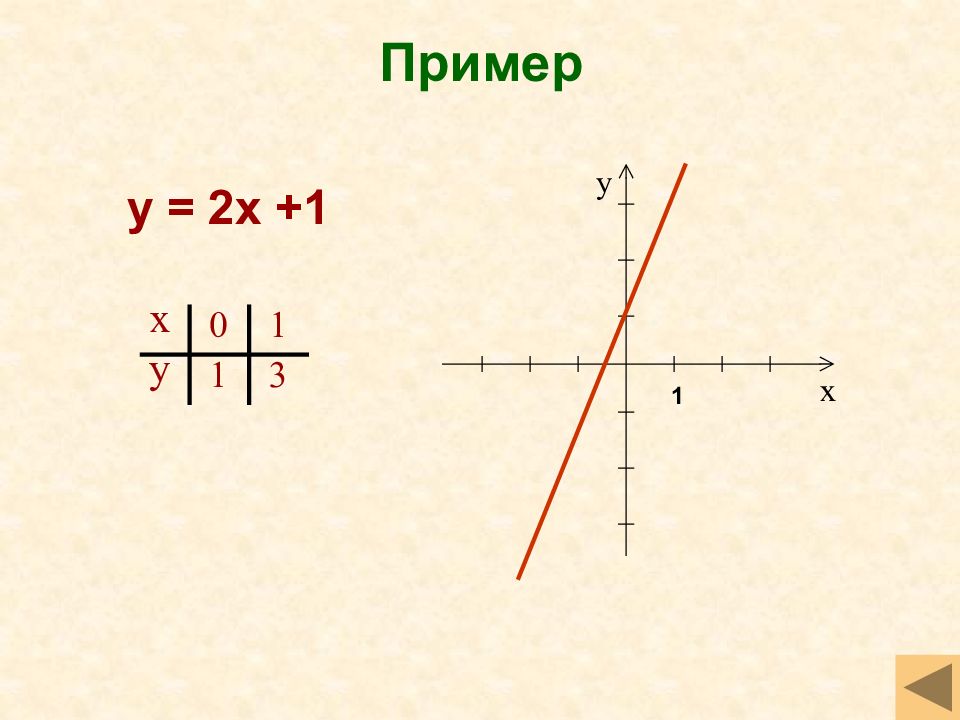
Функция – зависимость одной переменной от другой, причем для любых значений х соответствует единственное значение функции y. График функции – множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты соответствующим значениям функции. Определение
Слайд 5: Виды функций
Линейная Прямая пропорциональность Обратная пропорциональность Квадратичная Квадратный корень Модуль Другие функции
Слайд 6: Свойства функций
Область определения функции Множество значений функции Монотонность Четность Ограниченность Наибольшее, наименьшее значение Точки экстремума Выпуклость Пересечение с осями координат Промежутки знакопостоянства
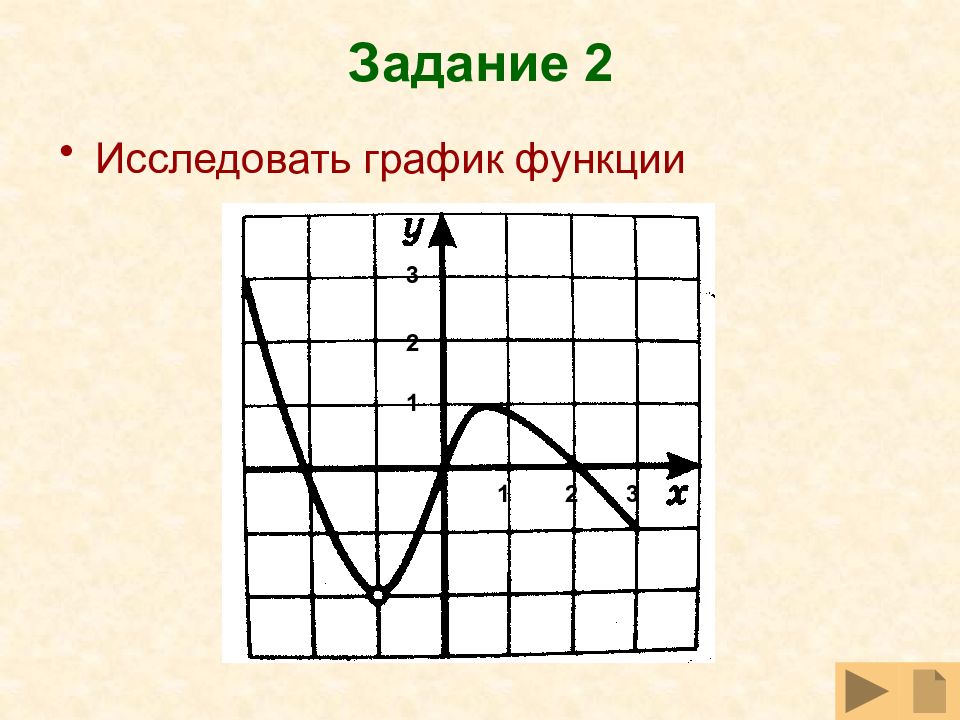
Слайд 16
2. Исследуйте на ограниченность функцию а) ограничена сверху б) ограничена снизу в) ограничена снизу и сверху г) не ограничена ни снизу, ни сверху
Слайд 17
3. Среди заданных функций укажите возрастающие а) 2, 4 б) 1, 2, 4 в) 3 г) 1, 2
Слайд 19
5. Среди заданных функций укажите четные а) 1, 3 б) 1, 2 в) 3, 4 г) 1, 4
Слайд 20: 6. Среди заданных функций укажите нечетные
а) 1, 3 б) 2, 4 в) 2, 3 г) 3, 4
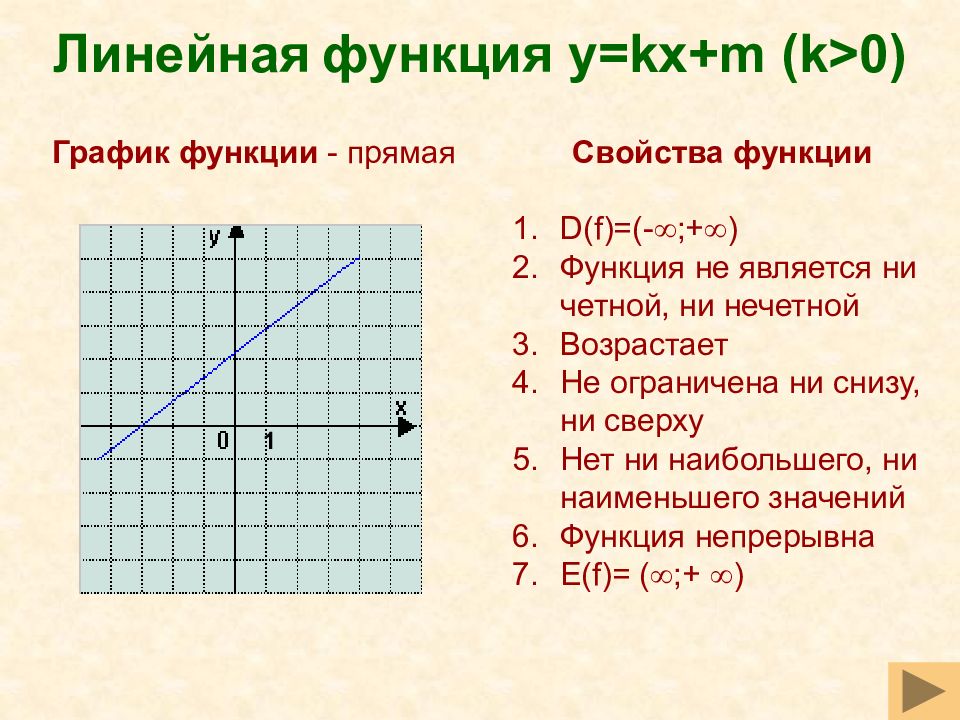
Слайд 24: Линейная функция y = k х+ m ( k>0)
Свойства функции D(f)=(- ;+ ) Функция не является ни четной, ни нечетной Возрастает Не ограничена ни снизу, ни сверху Нет ни наибольшего, ни наименьшего значений Функция непрерывна Е( f)= ( ;+ ) График функции - прямая 1
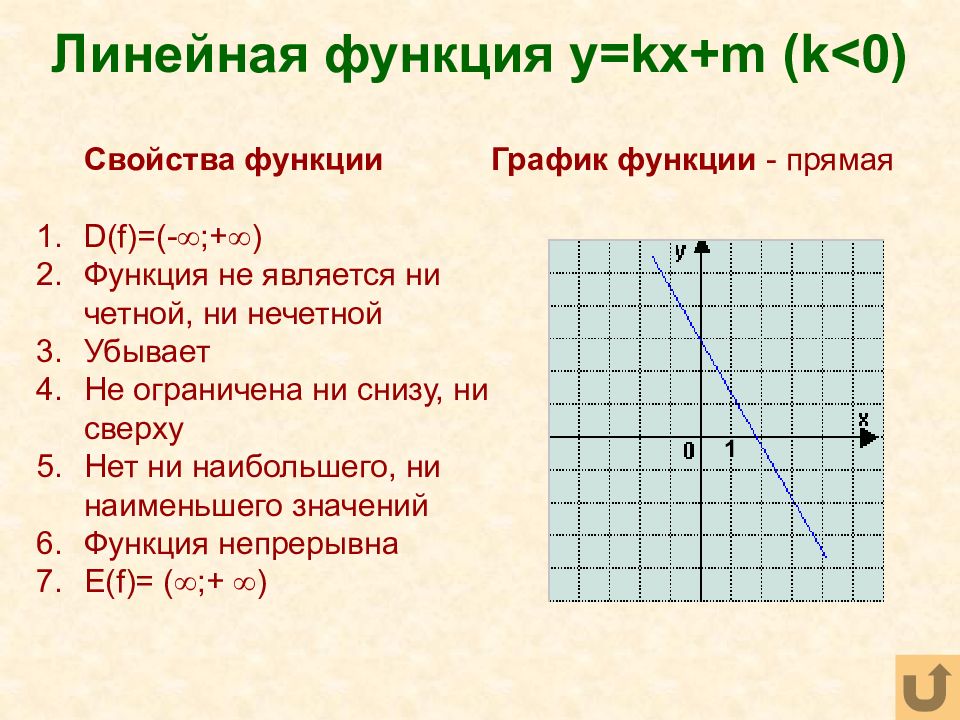
Слайд 25: Линейная функция y=kx+m (k<0)
Свойства функции D(f)=(- ;+ ) Функция не является ни четной, ни нечетной Убывает Не ограничена ни снизу, ни сверху Нет ни наибольшего, ни наименьшего значений Функция непрерывна Е( f)= ( ;+ ) График функции - прямая 1
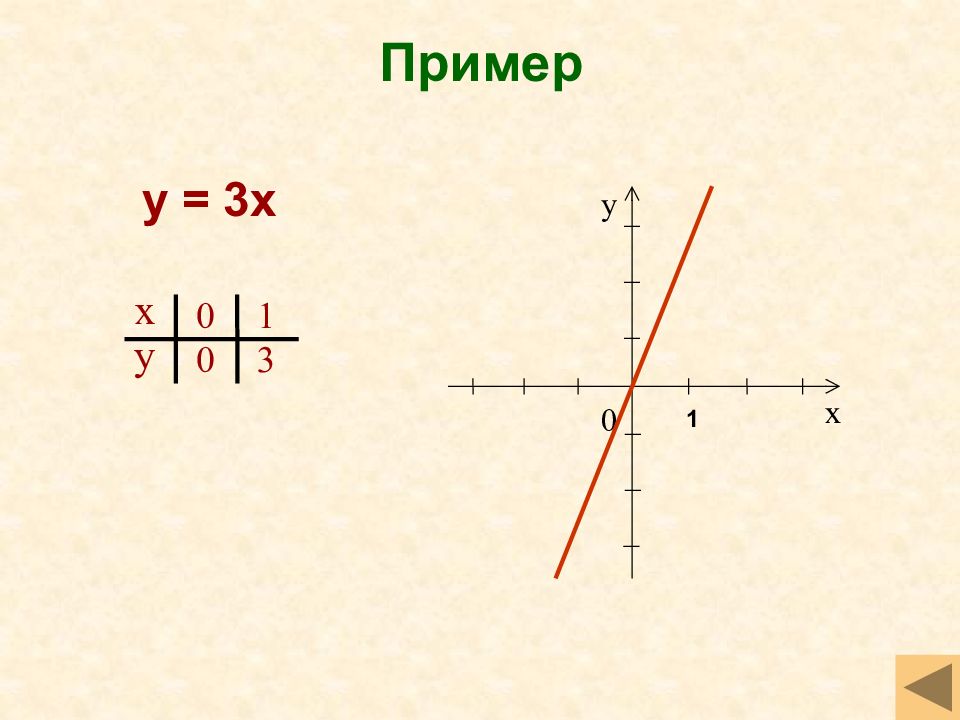
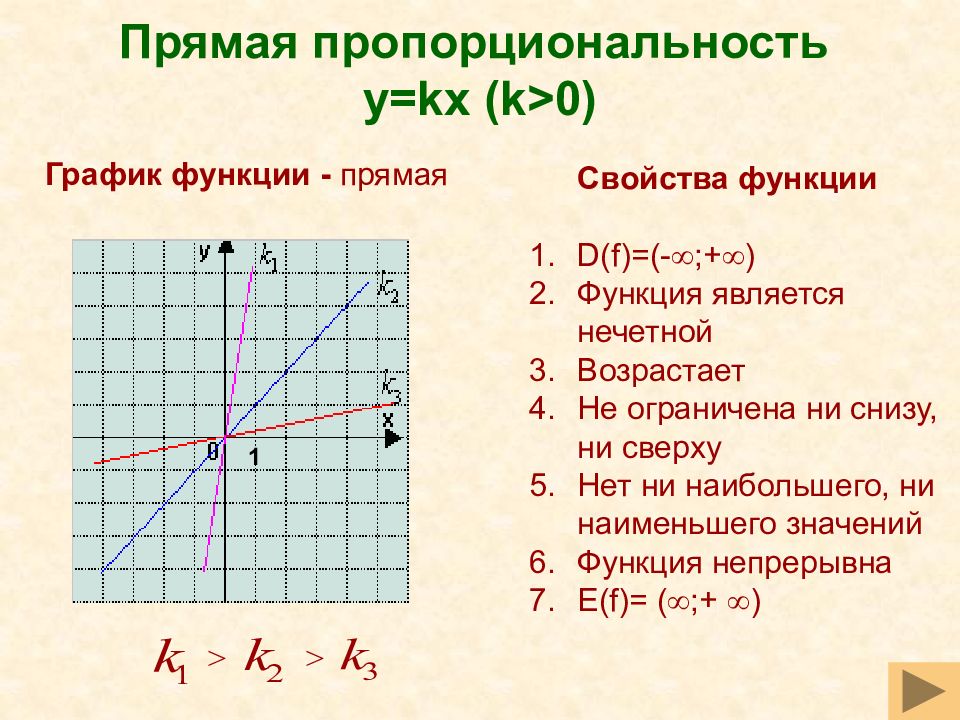
Слайд 26: Прямая пропорциональность y=kx (k>0)
Свойства функции D(f)=(- ;+ ) Функция является нечетной Возрастает Не ограничена ни снизу, ни сверху Нет ни наибольшего, ни наименьшего значений Функция непрерывна Е( f)= ( ;+ ) > > График функции - прямая 1
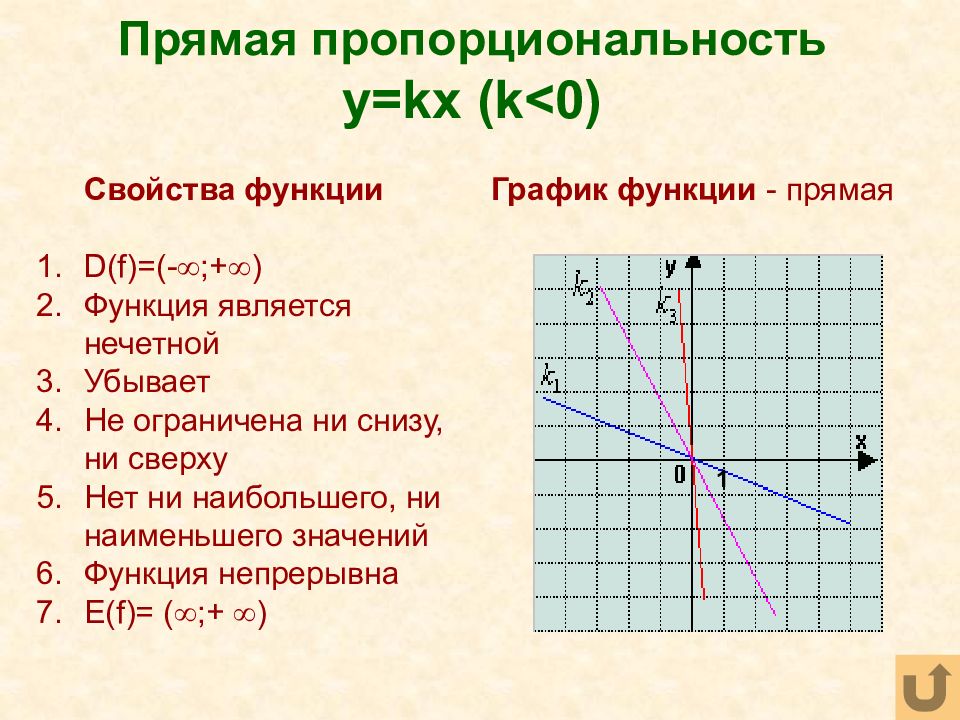
Слайд 27: Прямая пропорциональность y=kx (k<0)
Свойства функции D(f)=(- ;+ ) Функция является нечетной Убывает Не ограничена ни снизу, ни сверху Нет ни наибольшего, ни наименьшего значений Функция непрерывна Е( f)= ( ;+ ) График функции - прямая 1
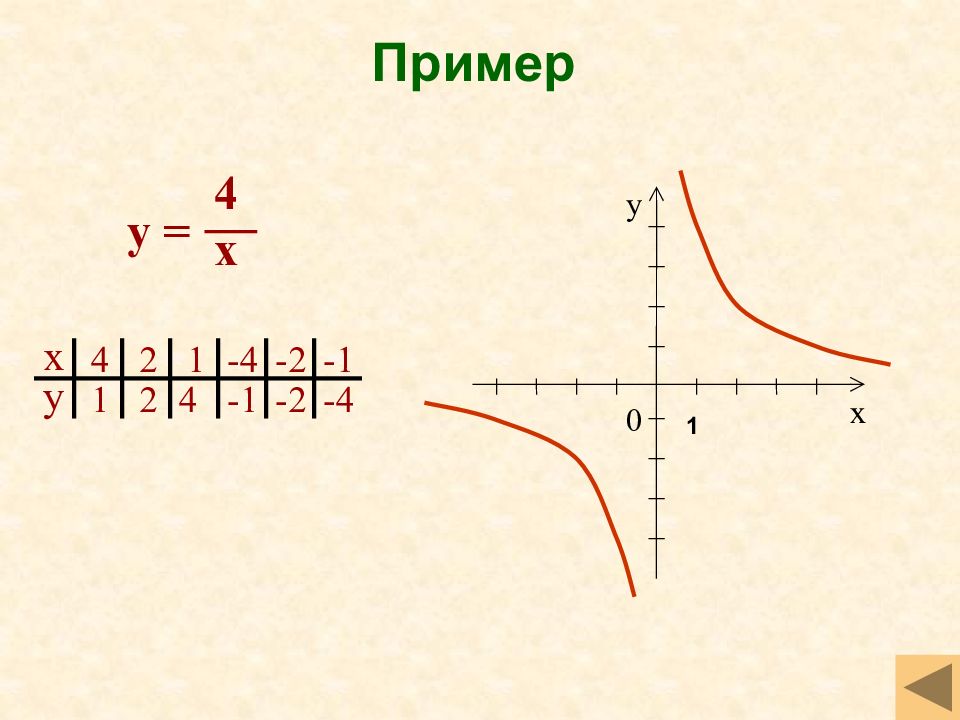
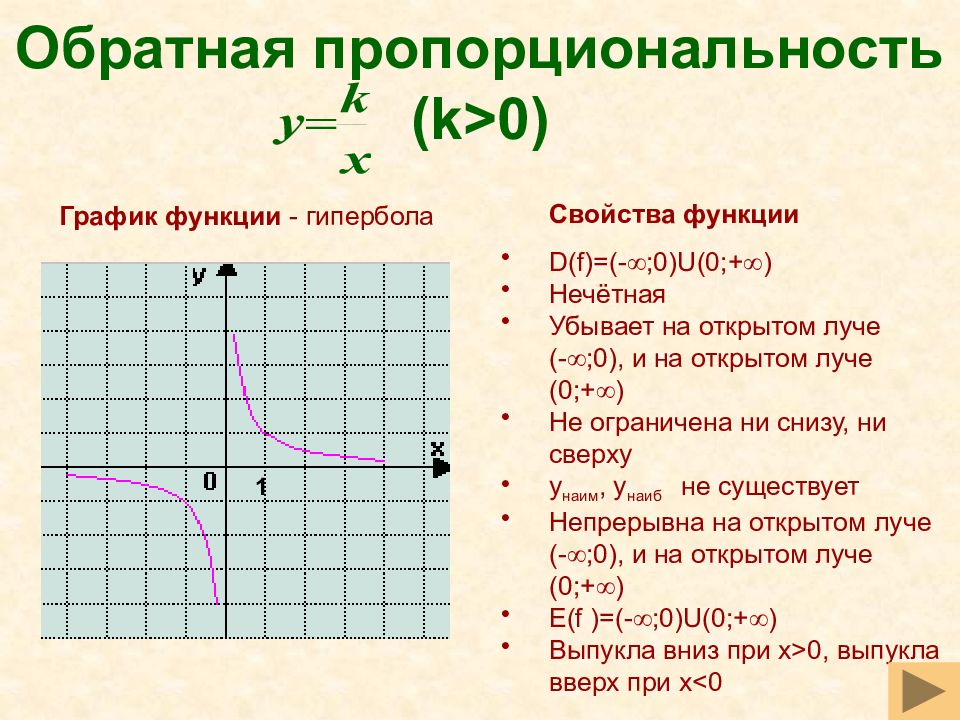
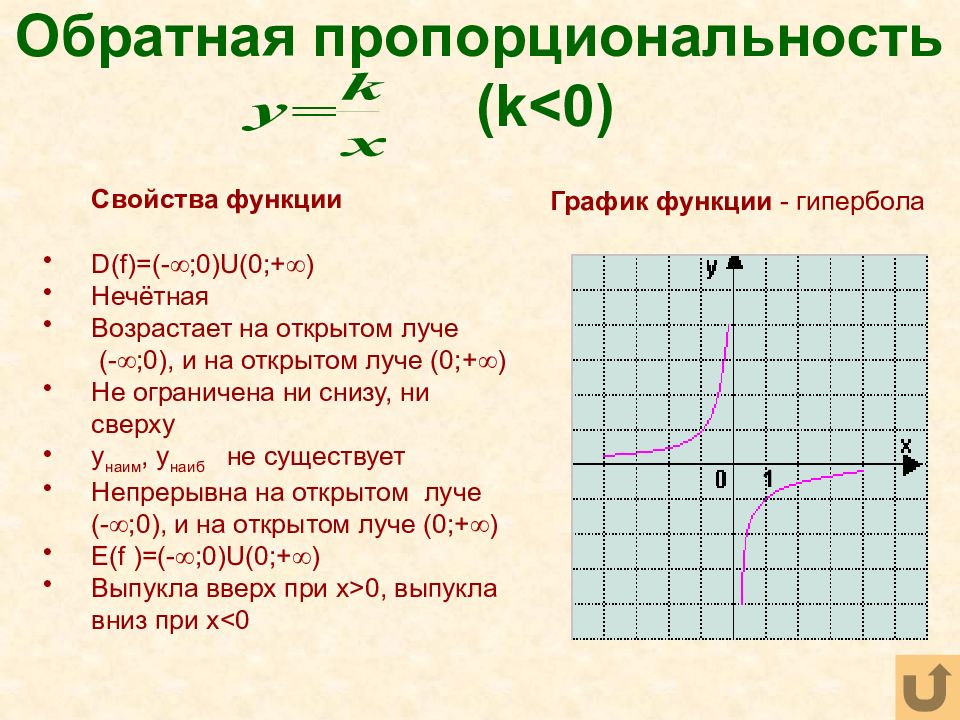
Слайд 28: Обратная пропорциональность ( k>0)
Свойства функции D(f)=(- ;0) U (0;+ ) Нечётная Убывает на открытом луче (- ;0), и на открытом луче ( 0 ;+ ) Не ограничена ни снизу, ни сверху y наим, y наиб не существует Непрерывна на открытом луче (- ;0), и на открытом луче ( 0 ;+ ) E(f )=(- ;0) U (0;+ ) Выпукла вниз при x>0, выпукла вверх при x<0 График функции - гипербола 1
Слайд 29: Обратная пропорциональность ( k<0)
Свойства функции D(f)=(- ;0) U (0;+ ) Нечётная Возрастает на открытом луче (- ;0), и на открытом луче ( 0 ;+ ) Не ограничена ни снизу, ни сверху y наим, y наиб не существует Непрерывна на открытом луче ( - ;0), и на открытом луче ( 0 ;+ ) E(f )=(- ;0) U (0;+ ) Выпукла вверх при x>0, выпукла вниз при x<0 График функции - гипербола 1
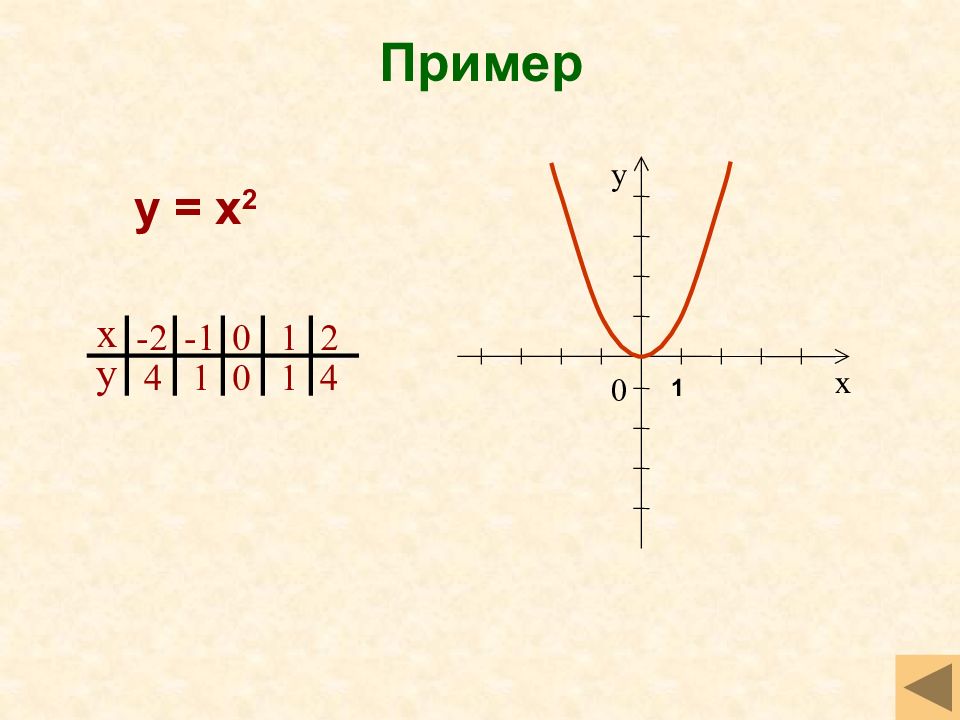
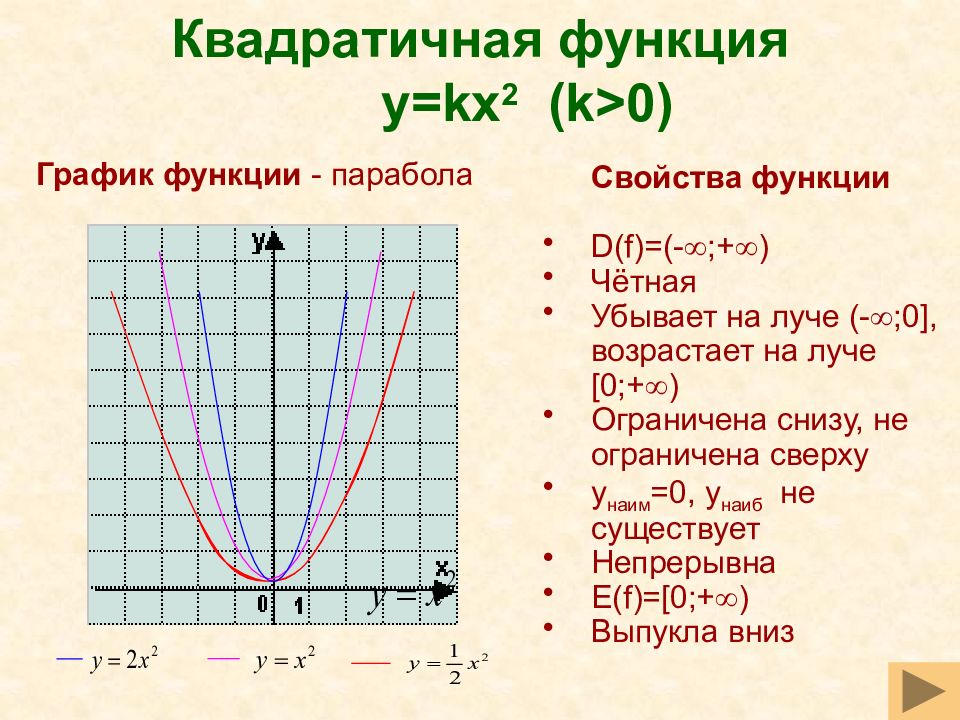
Слайд 30: Квадратичная функция y=kx 2 (k>0)
Свойства функции D(f)=(- ;+ ) Чётная Убывает на луче (- ;0 ], возрастает на луче [0 ;+ ) Ограничена снизу, не ограничена сверху y наим =0, y наиб не существует Непрерывна E(f)=[0; + ) Выпукла вниз График функции - парабола
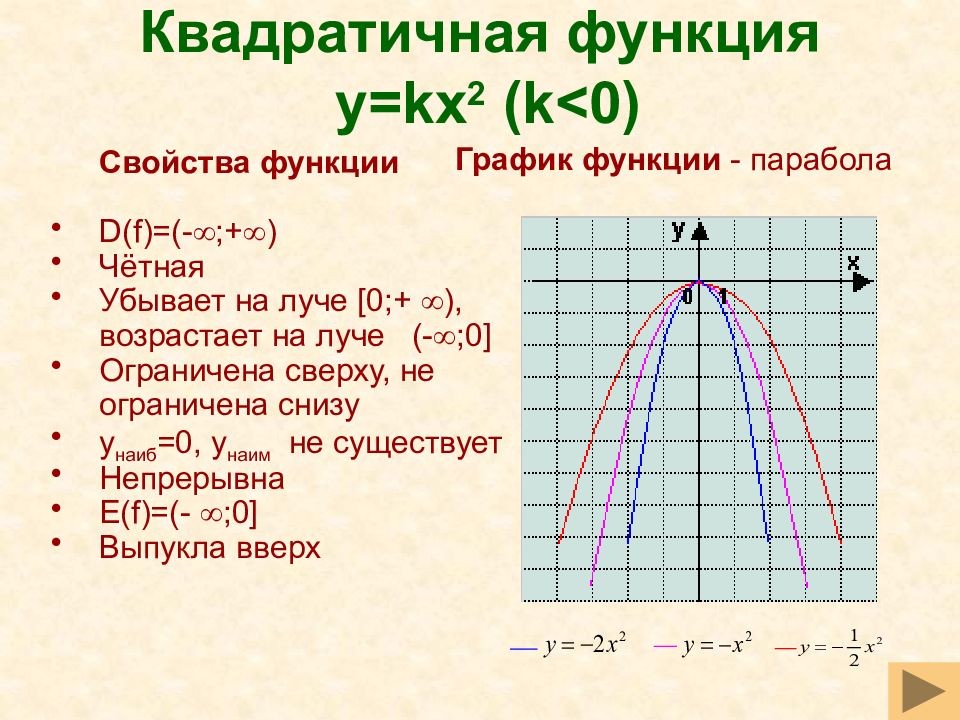
Слайд 31: Квадратичная функция y=kx 2 (k<0)
Свойства функции D(f)=(- ;+ ) Чётная Убывает на луче [0;+ ), возрастает на луче ( - ;0] Ограничена сверху, не ограничена снизу y наиб =0, y наим не существует Непрерывна E(f)= (- ;0] Выпукла вверх График функции - парабола
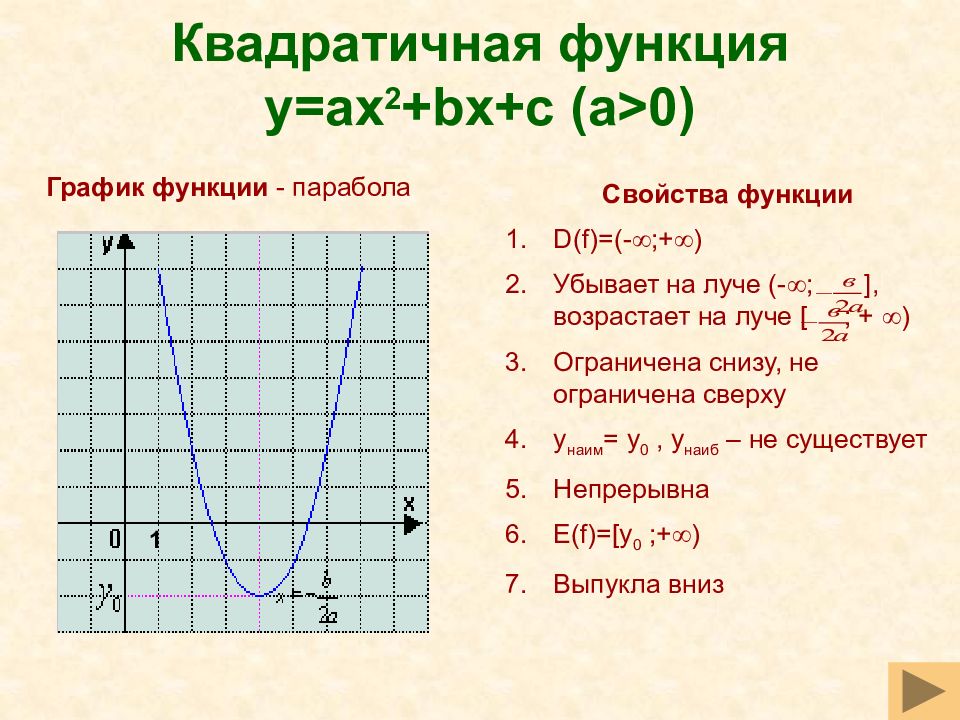
Слайд 32: Квадратичная функция y=ax 2 +bx+c (a>0)
Свойства функции D(f)=(- ;+ ) Убывает на луче (- ; ], возрастает на луче [ ; + ) Ограничена снизу, не ограничена сверху y наим = y 0, y наиб – не существует Непрерывна E(f)=[y 0 ; + ) Выпукла вниз График функции - парабола 1
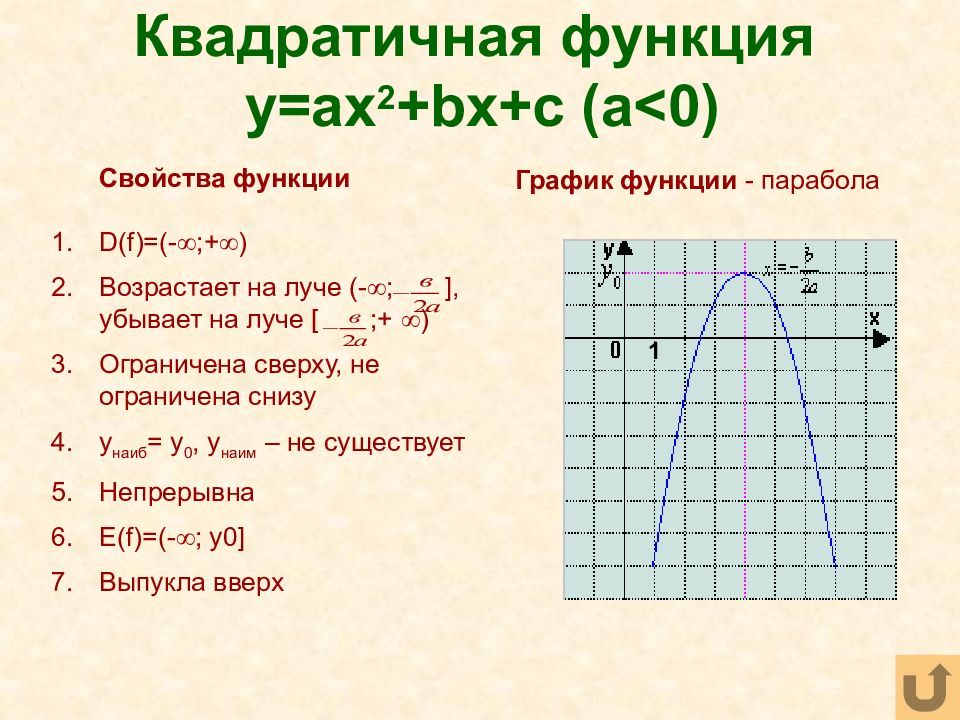
Слайд 33: Квадратичная функция y=ax 2 +bx+c (a<0)
Свойства функции D(f)=(- ;+ ) Возрастает на луче (- ; ], убывает на луче [ ;+ ) Ограничена сверху, не ограничена снизу y наиб = y 0, y наим – не существует Непрерывна E(f)= (- ; y 0 ] Выпукла вверх График функции - парабола 1
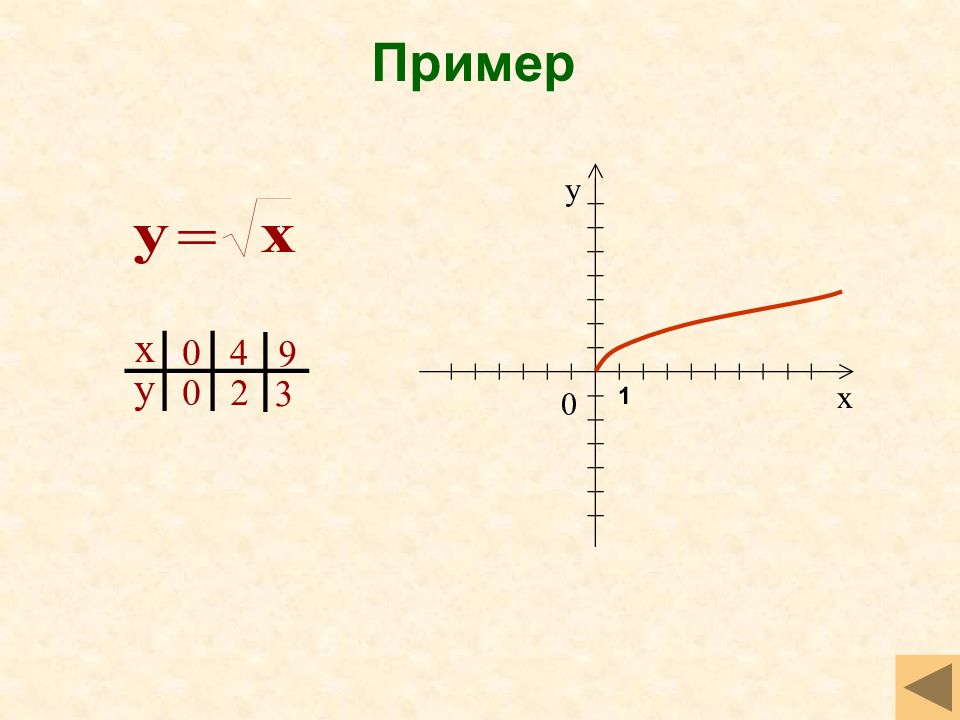
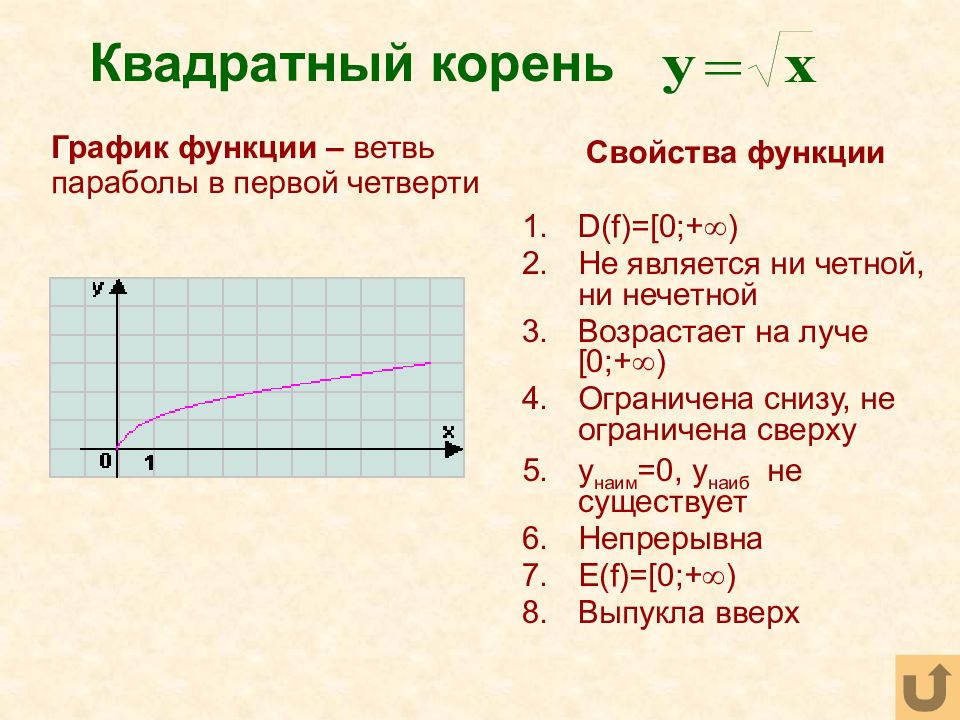
Слайд 34: Квадратный корень
Свойства функции D(f)=[0 ;+ ) Не является ни четной, ни нечетной Возрастает на луче [0 ;+ ) Ограничена снизу, не ограничена сверху y наим =0, y наиб не существует Непрерывна E(f)=[0; + ) Выпукла вверх График функции – ветвь параболы в первой четверти
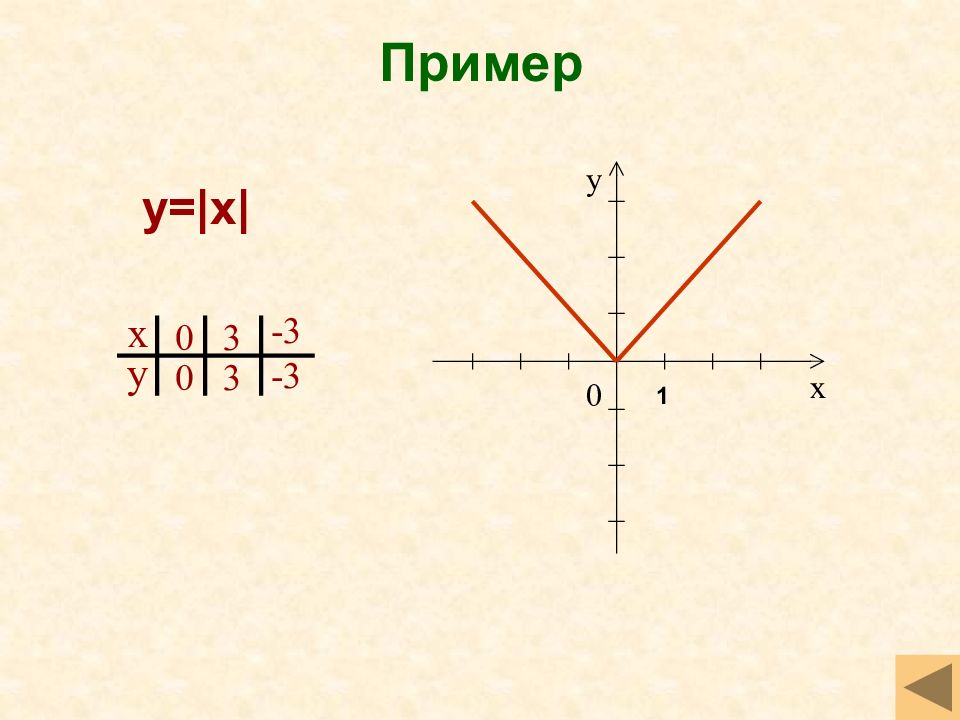
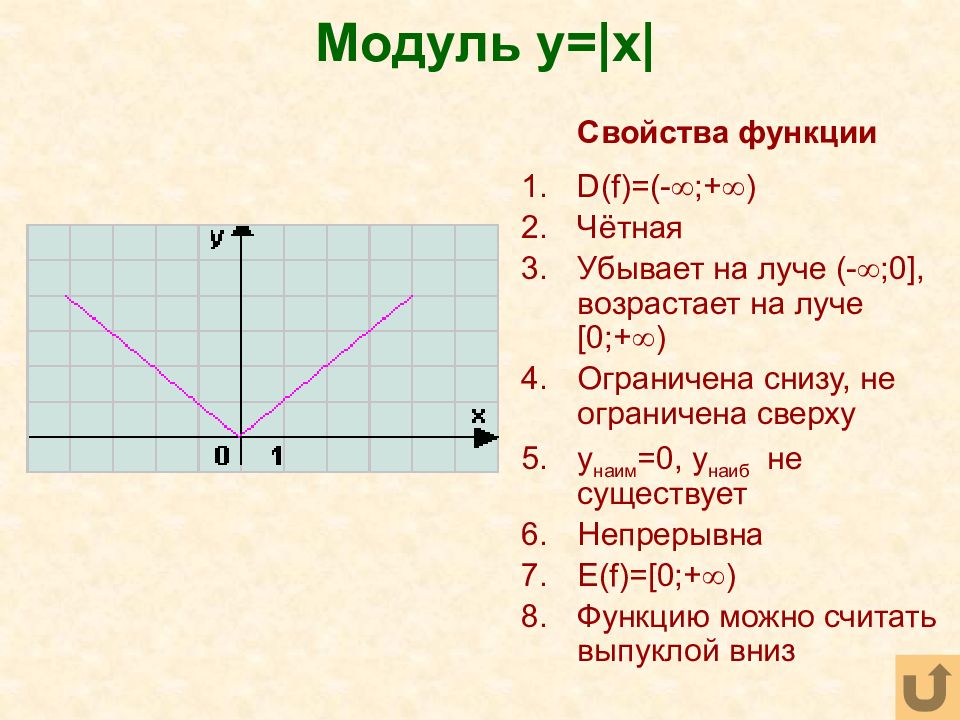
Слайд 35: Модуль y=|x|
Свойства функции D(f)=(- ;+ ) Чётная Убывает на луче (- ;0 ], возрастает на луче [0 ;+ ) Ограничена снизу, не ограничена сверху y наим =0, y наиб не существует Непрерывна E(f)=[0; + ) Функцию можно считать выпуклой вниз
Слайд 36: Функция y=x 2n+1 (n N)
Свойства функции D(f)=(- ;+ ) Нечётная Возрастает Не ограничена ни снизу, ни сверху y наим, y наиб не существует Непрерывна E(f )=(- ;+ ) Выпукла вверх при x<0 Выпукла вниз при x>0 График функции - кубическая парабола
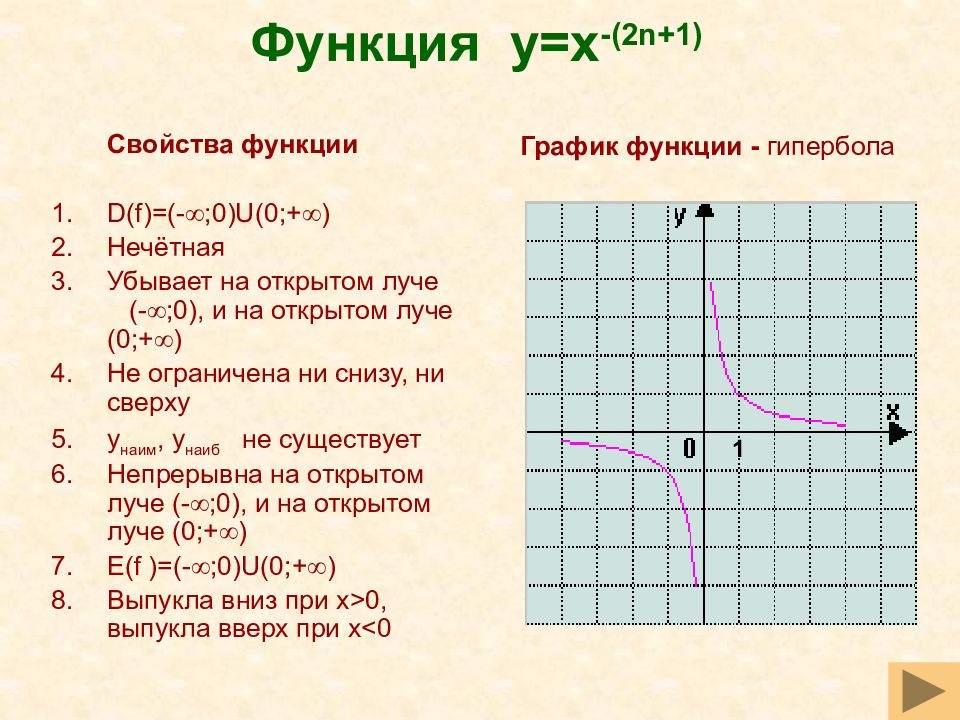
Слайд 37: Функция y=x -(2n+1)
Свойства функции D(f)=(- ;0) U (0;+ ) Нечётная Убывает на открытом луче (- ;0), и на открытом луче ( 0 ;+ ) Не ограничена ни снизу, ни сверху y наим, y наиб не существует Непрерывна на открытом луче (- ;0), и на открытом луче ( 0 ;+ ) E(f )=(- ;0) U (0;+ ) Выпукла вниз при x>0, выпукла вверх при x<0 График функции - гипербола 1
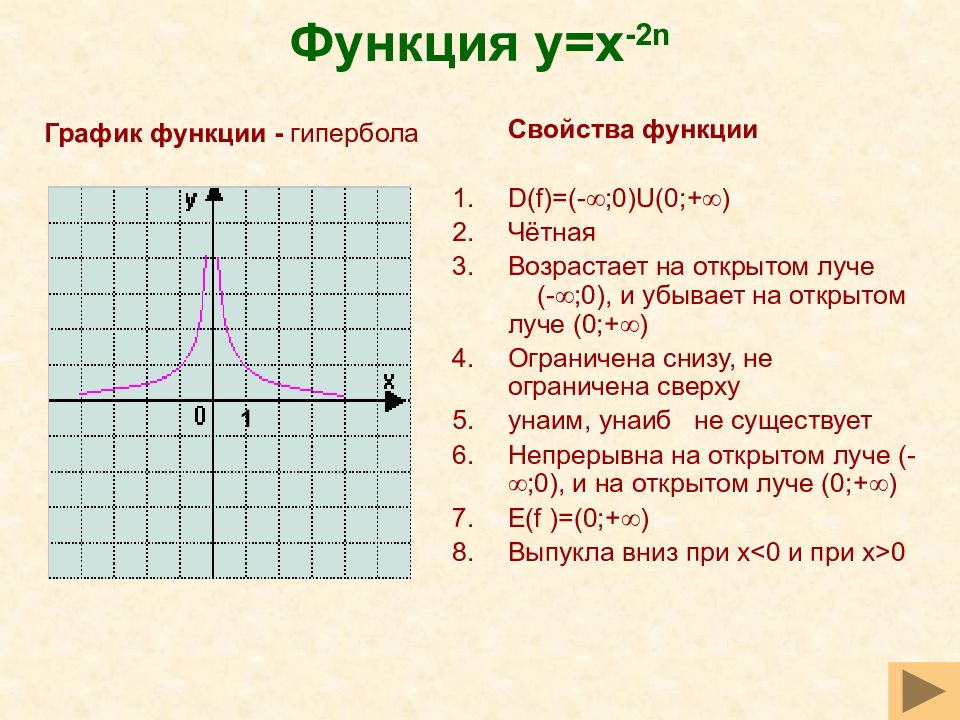
Слайд 38: Функция y=x -2n
Свойства функции D(f)=(- ;0) U (0;+ ) Чётная Возрастает на открытом луче (- ;0), и убывает на открытом луче ( 0 ;+ ) Ограничена снизу, не ограничена сверху y наим, y наиб не существует Непрерывна на открытом луче (- ;0), и на открытом луче ( 0 ;+ ) E(f )= (0;+ ) Выпукла вниз при x<0 и при x>0 График функции - гипербола 1
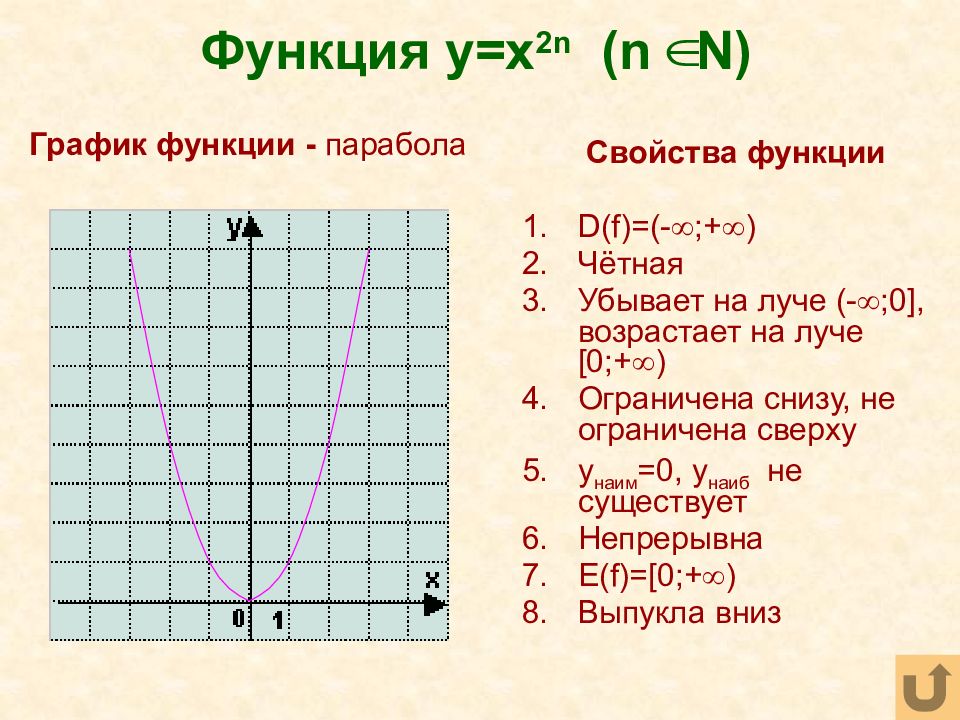
Последний слайд презентации: Функция и её свойства: Функция y=x 2n (n N)
Свойства функции D(f)=(- ;+ ) Чётная Убывает на луче (- ;0 ], возрастает на луче [0 ;+ ) Ограничена снизу, не ограничена сверху y наим =0, y наиб не существует Непрерывна E(f)=[0; + ) Выпукла вниз График функции - парабола