Решите показательные уравнения с помощью выражения переменной х через переменную у
Слайд 4
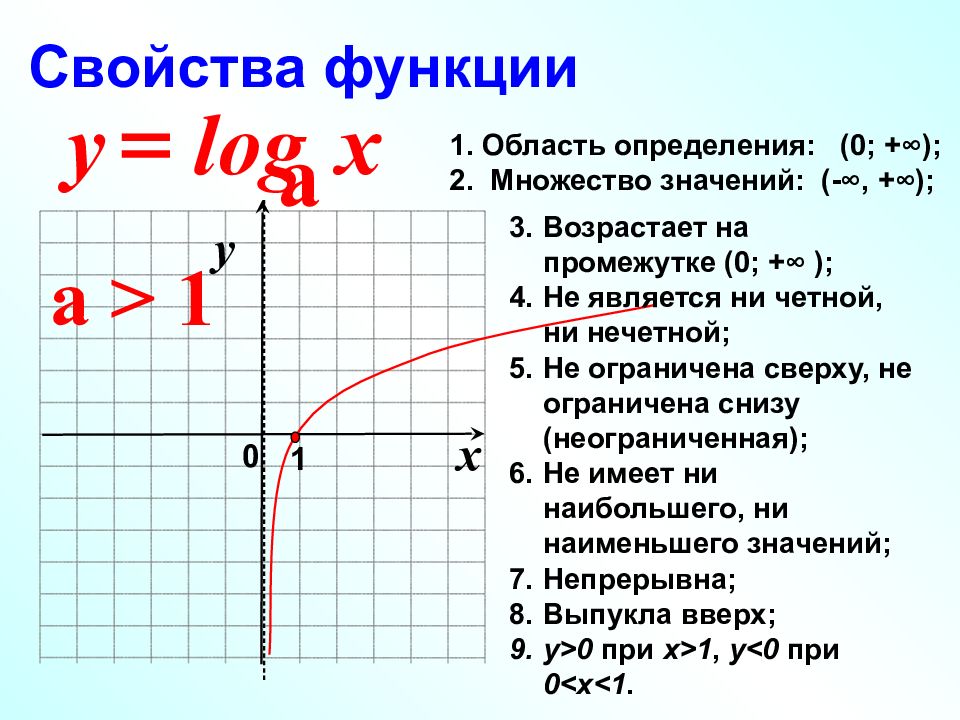
x 0 y 1 log а = x y a > 1 Область определения: (0; +∞); Множество значений: (-∞, +∞); Возрастает на промежутке (0; +∞ ); Не является ни четной, ни нечетной; Не ограничена сверху, не ограничена снизу (неограниченная); Не имеет ни наибольшего, ни наименьшего значений; Непрерывна; Выпукла вверх; у>0 при х>1, у<0 при 0<х<1. Свойства функции
Слайд 5
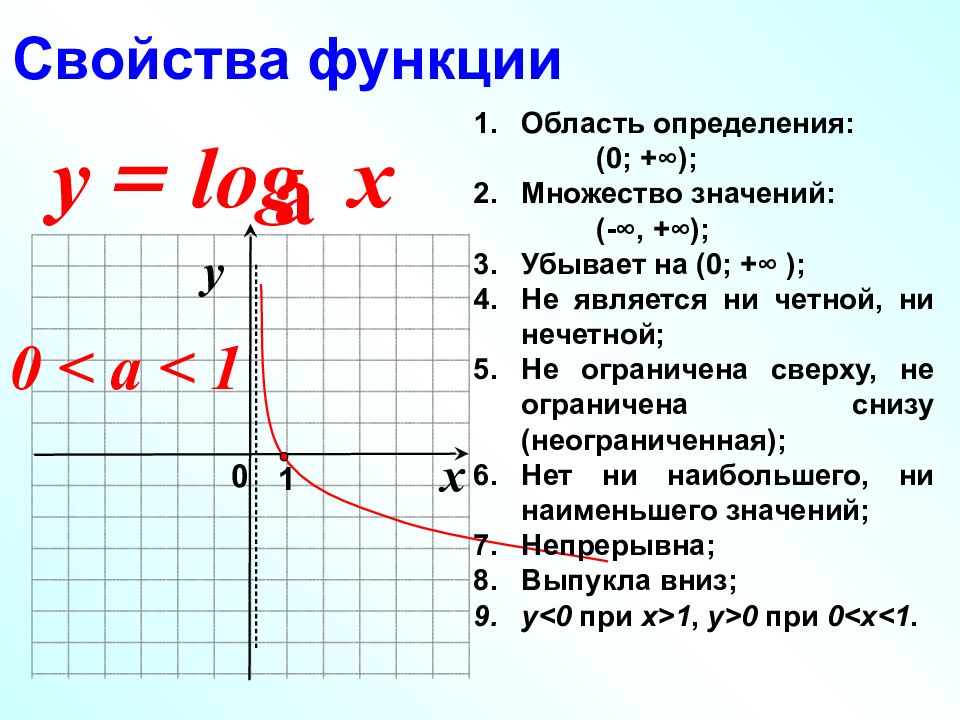
x 0 y 1 log а = x y Свойства функции 0 < a < 1 Область определения: (0; +∞); Множество значений: (-∞, +∞); Убывает на (0; +∞ ); Не является ни четной, ни нечетной; Не ограничена сверху, не ограничена снизу (неограниченная); Нет ни наибольшего, ни наименьшего значений; Непрерывна; Выпукла вниз; у<0 при х>1, у>0 при 0<х<1.
Слайд 6
№ a > 1 0 < a < 1 1 Область определения х = (0, + ∞) 2 Множество значений у = (- ∞, + ∞) ; 3 возрастает на (0, + ∞) убывает на (0, + ∞) 4 не ограничена сверху, не ограничена снизу 5 не имеет ни наибольшего, ни наименьшего значений 6 непрерывна 7 не является ни чётной, ни нечётной; 8 выпукла вверх выпукла вниз Основные свойства логарифмической функции
Слайд 7
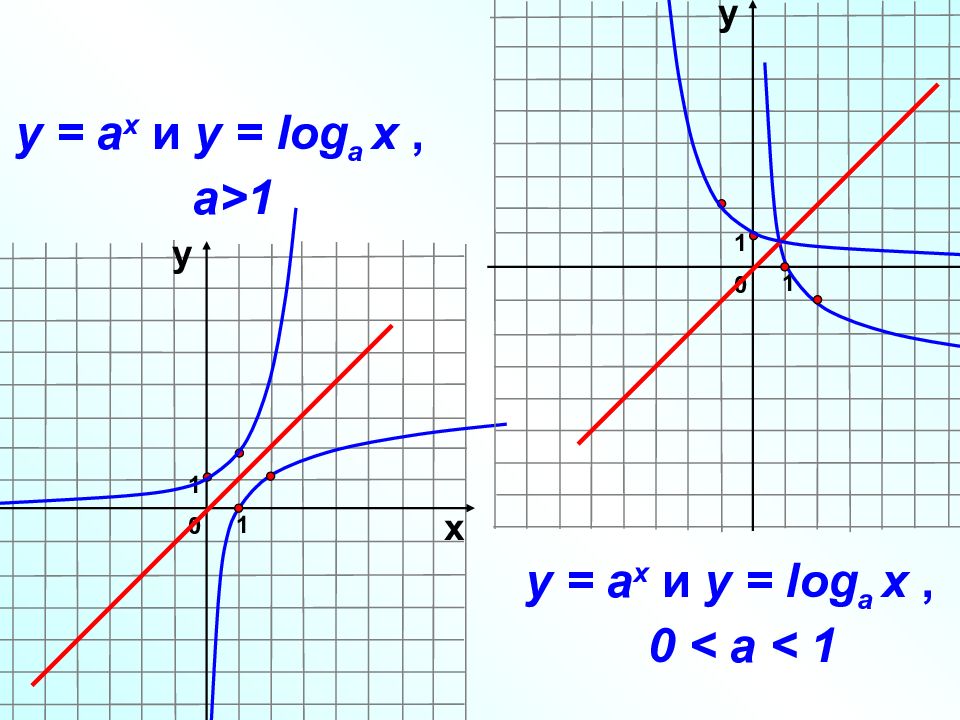
1 0 х у 1 1 0 х у 1 у = а x и у = log a х, a>1 у = а x и у = log a х, 0 < a < 1
1) у = log 0,3 х 2) у = log 2 (х-1) 3) у = log 3 (3-х) Ответы (0; +∞) (1;+∞) (-∞; 3)
1) у = log 3 х 2 2) у = log 5 (- х ) 3) у = lg │ х│ х≠0 х≠0 x <0
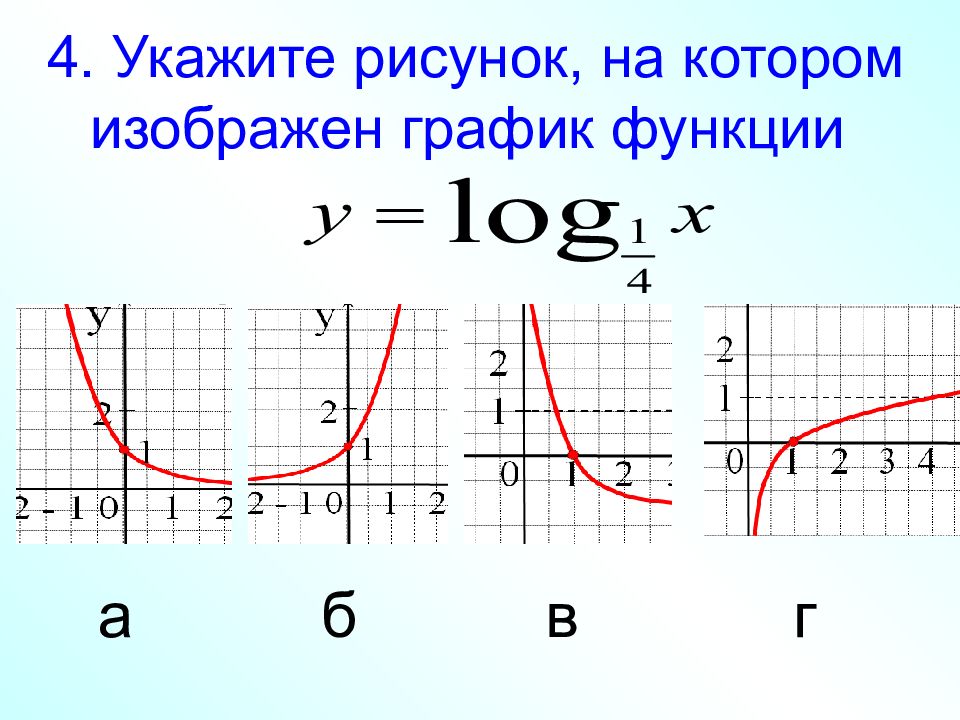
Слайд 10: 3. Какие из функций являются возрастающими?
а) у = log 5 х в) у = log π х б) г)
Последний слайд презентации: Логарифмическая функция, её свойства и график: Рефлексия
О чем вы не имели представления до сегодняшнего урока, и что теперь вам стало ясно? Что нового вы узнали о логарифмической функции и ее приложениях? С какими трудностями вы столкнулись при выполнении заданий? Выделите тот вопрос, который для вас оказался менее понятным. Какая информация вас заинтересовала? Составьте синквейн «логарифмическая функция» Оцените работу своей группы