Функция y = tg x её свойства и график Автор: Брызгалова Наталья Юрьевна Преподаватель Архангельского техникума строительства и экономики
Цель : Изучить функцию y = tg x Задачи: 1. Изучить свойства функции у = tg x. 2. Уметь применять свойства функции у = tg x и читать график. 3. Формировать практические навыки построения графика функции у = tg x на основе изученного теоретического материала. 4. Закрепить понятия с помощью выполнения заданий.
Функция y=tgx определена при x ≠ π/2+πn, n∈Z, является нечётной и периодической с периодом Т=π Поэтому достаточно построить её график на промежутке [0;π/2). Используя периодичность, строим график функции y=tg x на всей области определения. Затем, отобразив её симметрично относительно начала координат, получим график на интервале (−π/2;π/2).
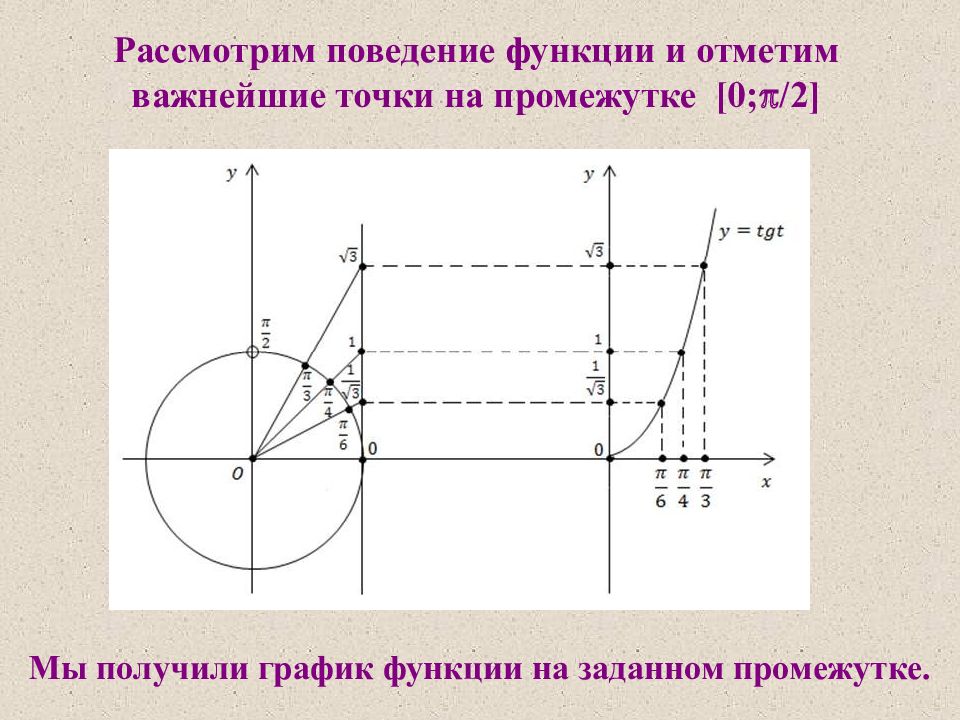
Рассмотрим поведение функции и отметим важнейшие точки на промежутке [0; /2 ] Мы получили график функции на заданном промежутке.
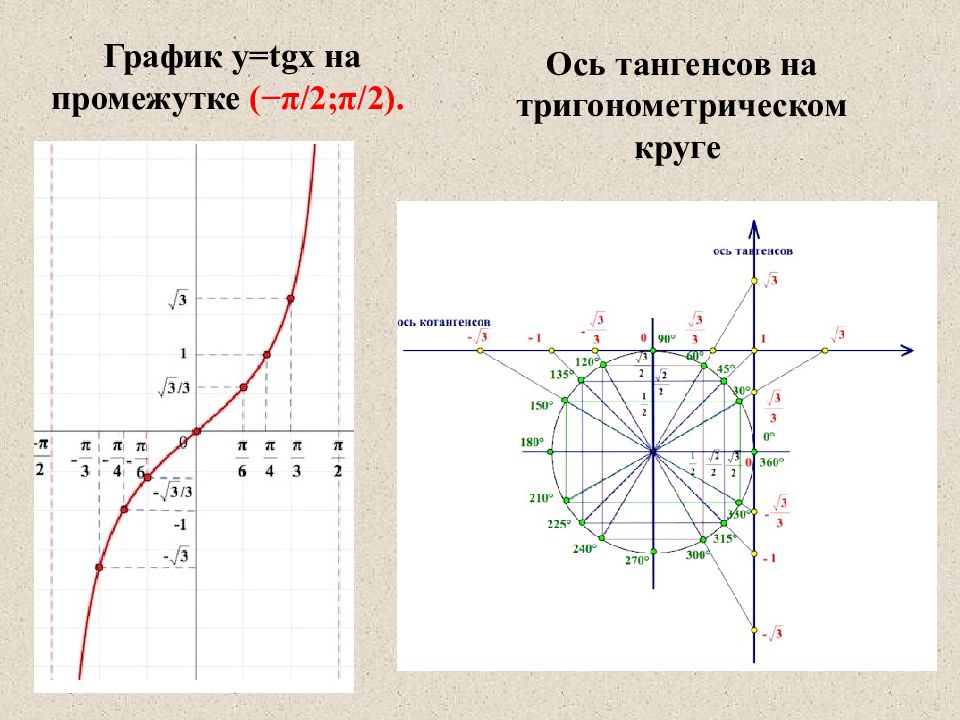
Ось тангенсов на тригонометрическом круге График y=tgx на промежутке (−π/2;π/2).
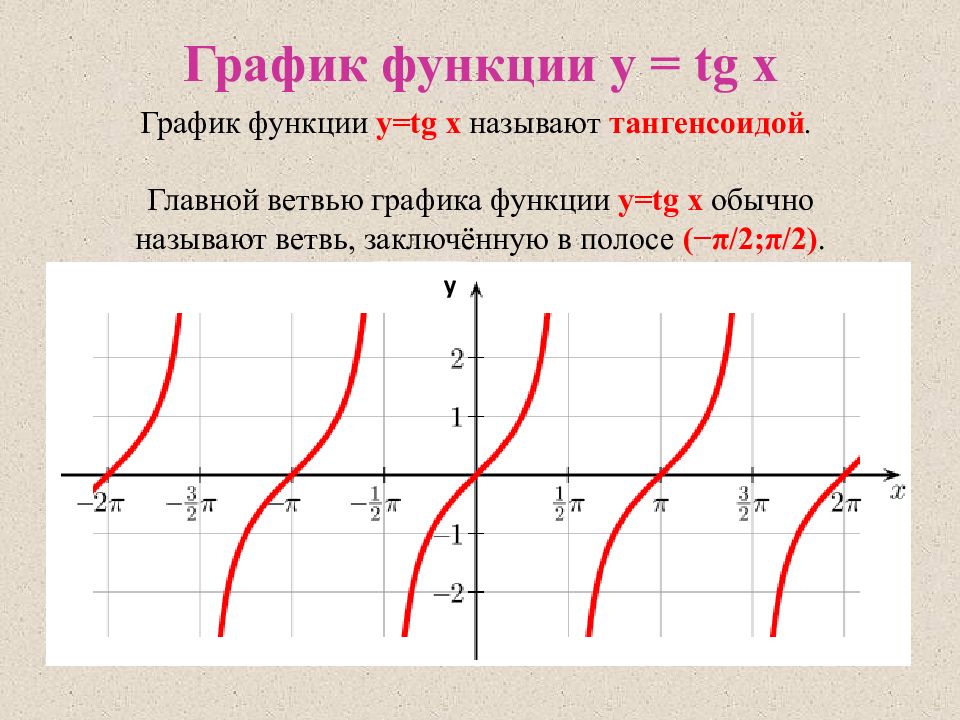
График функции y=tg x называют тангенсоидой. Главной ветвью графика функции y=tg x обычно называют ветвь, заключённую в полосе (−π/2;π/2). у График функции y = tg x
Свойства функции y = tg x 1. Область определения — множество R всех действительных чисел. D(y) = (-∞ ; + ∞ ), кроме x ≠ π/2+πn, n∈Z. 2. Множество значений Е(у) = R 3. Функция периодическая с периодом T= π 4. Функция нечётная tg (-x) = - tg x (график симметричен относительно начала координат ). 5. Функция не ограничена и сверху, и снизу. 6. Функция y= tg x принимает: - значение, равное 0, при x=πn, n∈Z; 7. Функция не имеет максимального и минимального значения
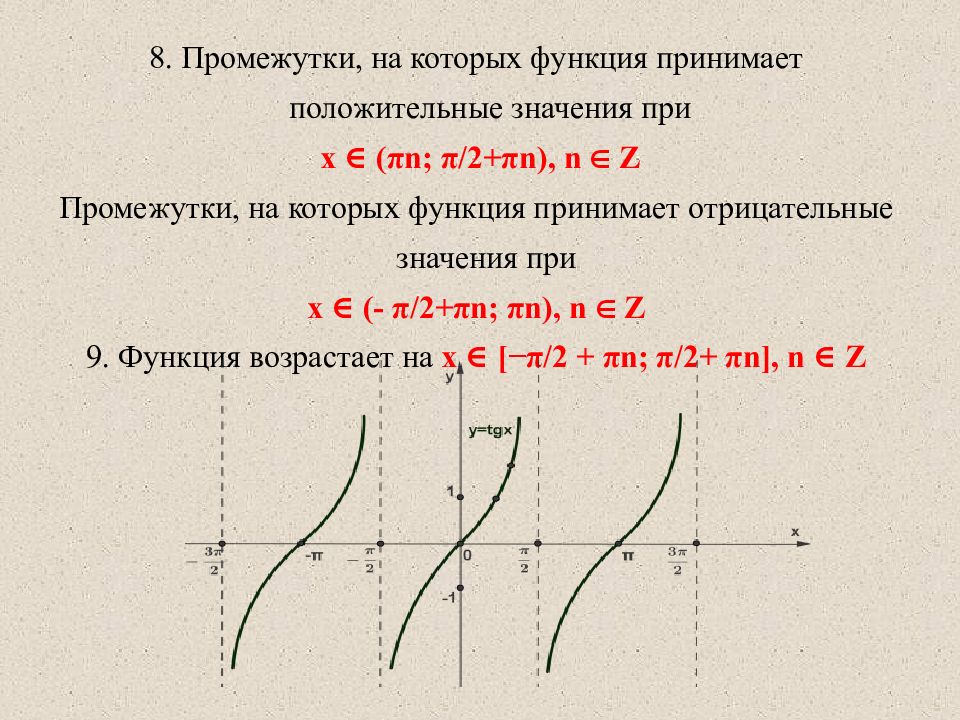
8. Промежутки, на которых функция принимает положительные значения при x ∈ ( π n; π /2+ π n), n ∈ Z Промежутки, на которых функция принимает отрицательные значения при x ∈ (- π /2+ π n; π n), n ∈ Z 9. Функция возрастает на x ∈ [−π/2 + π n ; π/2 + π n ], n ∈ Z
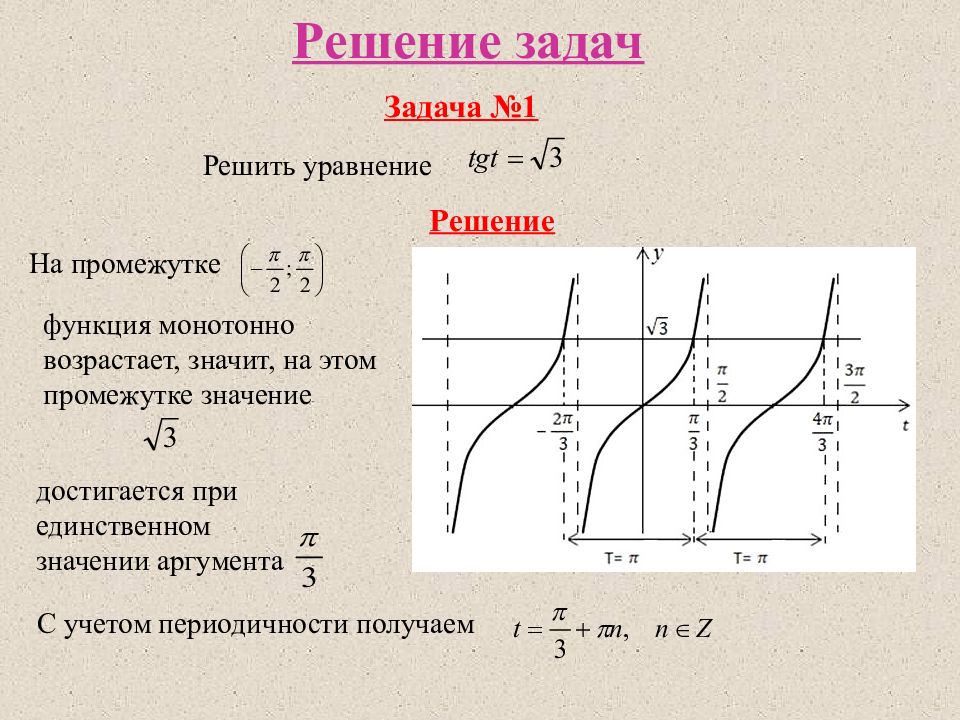
Решение задач Решить уравнение Задача №1 Решение На промежутке функция монотонно возрастает, значит, на этом промежутке значение достигается при единственном значении аргумента С учетом периодичности получаем
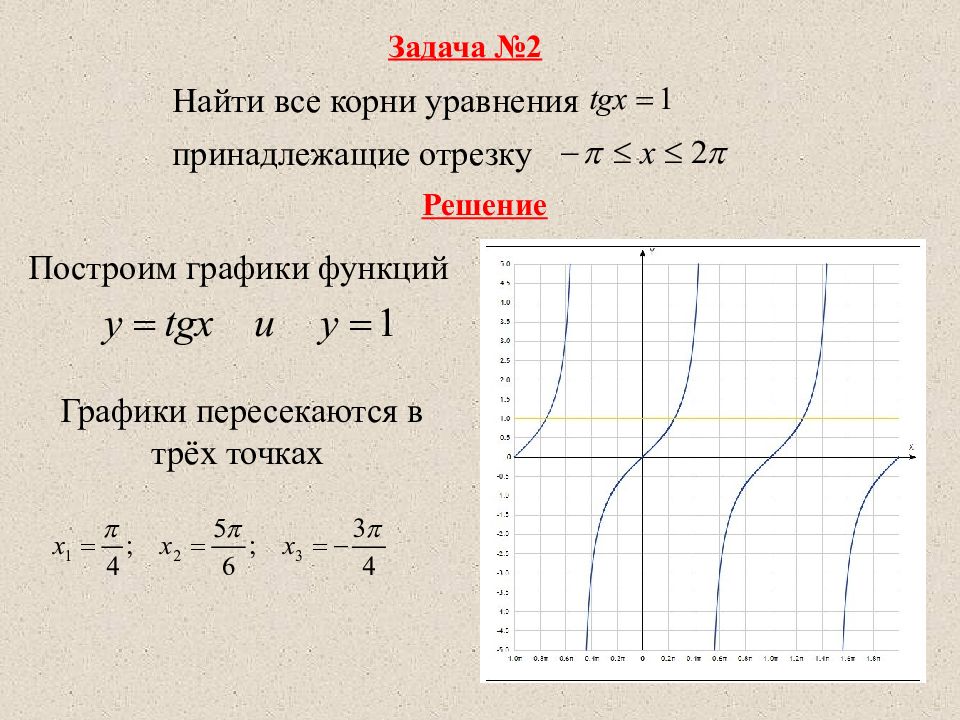
Задача №2 Найти все корни уравнения принадлежащие отрезку Решение Построим графики функций Графики пересекаются в трёх точках
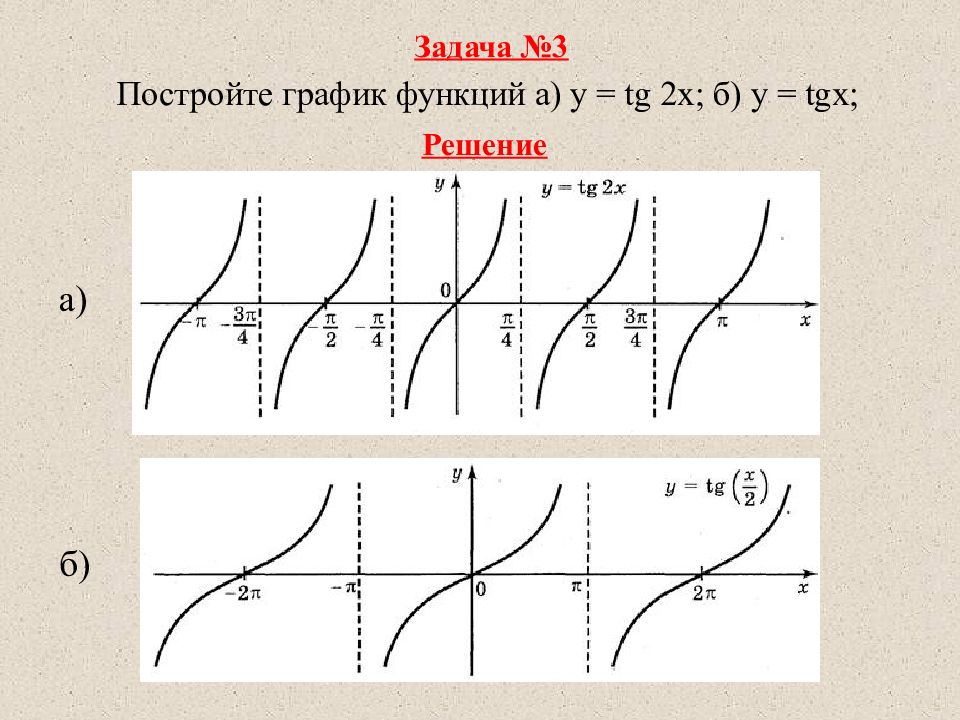
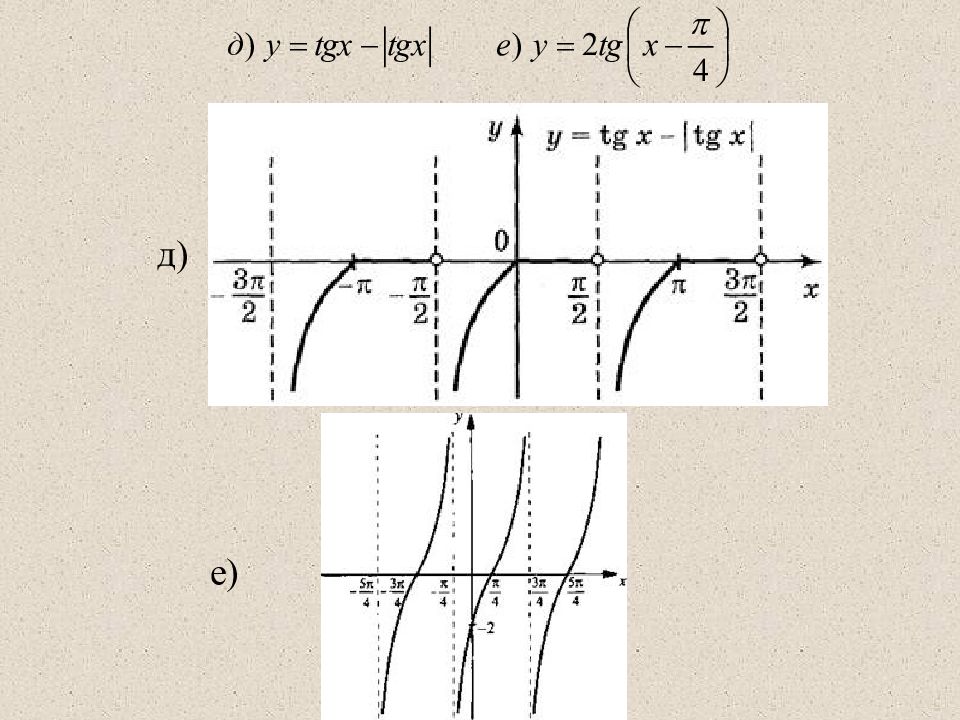
Задача №3 Постройте график функций а) у = tg 2х; б) у = t g x ; Решение а) б)
в) у = tg x + 2; г) у = tg (-x). Решение в) г)
е) д)
Задача №4 Установить чётность или нечётность функции Решение Так как выполнено равенство y(-x) = у(х), то функция у(х) по определению четная.
Задания для самостоятельного решения 1) Постройте графики функций а) у = tg(x+ π /3) ; б) у = 3-tgx ; в) у = tg (x + π /2) г ) у = tg (x – π /3) д) у= tgx+5
2 ) Определить чётность или нечётность функции:
3) Решить графически уравнения:
4 ) Используя свойства функции у = tg x, сравните числа: 5 ) Используя свойства функции у = tg x, сравните числа:
Заключение. Мы рассмотрели график функции y = tg x, изучили особенности ее поведения, использовали их и свойства функции при решении задач.
