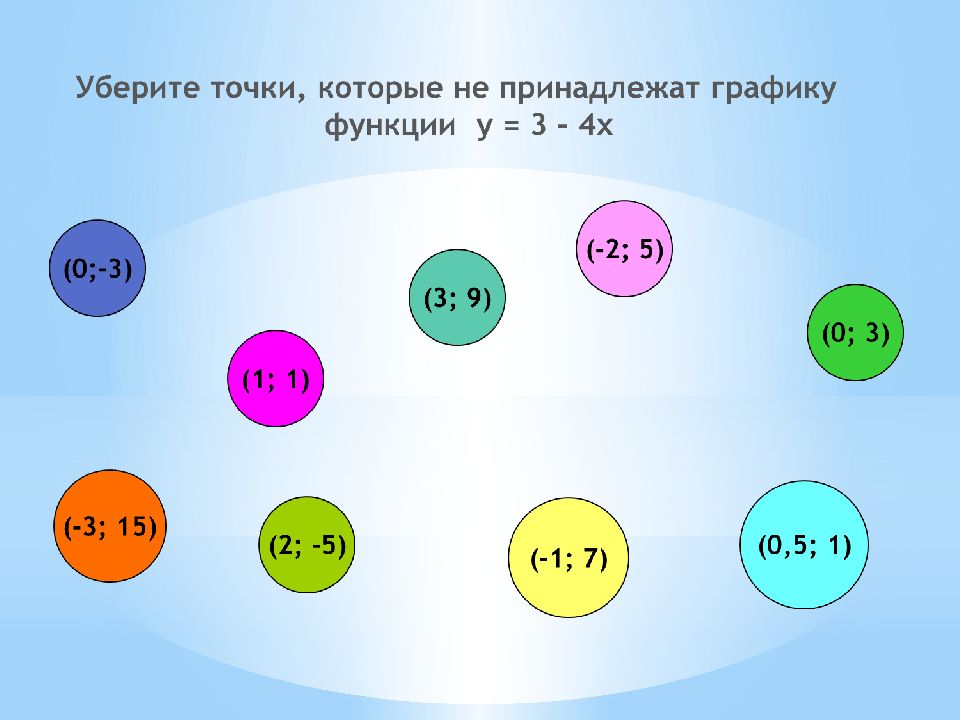
Слайд 2: Укажите линейные уравнения :
1) 5y = x 2) 3y = 0 3) y 2 + 16x 2 = 0 4) + y = 4 5) x + y =4 6) y = -x + 11 7) + 0.5x – 2 = 0 8) 25d – 2m + 1 = 0 9) y = 3 – 2x 5
Слайд 3
Функция вида у = kx + b называется линейной. Графиком функции вида у = kx +b является прямая. Для построения прямой необходимы только две точки, так как через две точки проходит единственная прямая.
Слайд 4
Найти уравнения линейных функций y =-x+0,2; y= 1 2, 4x-5,7 ; y =- 9 x- 1 8; y= 5,04x; y =- 5,04x; y=1 26,35+ 8,75x; y=x -0, 2; y=x :8; y=0, 00 5x; y=13 3,13 3 13 3 x; y= 3 - 1 0, 01x ; y=2 : x ; y =-0, 004 9; y= х:6 2.
Слайд 5
y = kx + b – линейная функция х – аргумент (независимая переменная) у – функция (зависимая переменная) k, b – числа (коэффициенты) к ≠ 0
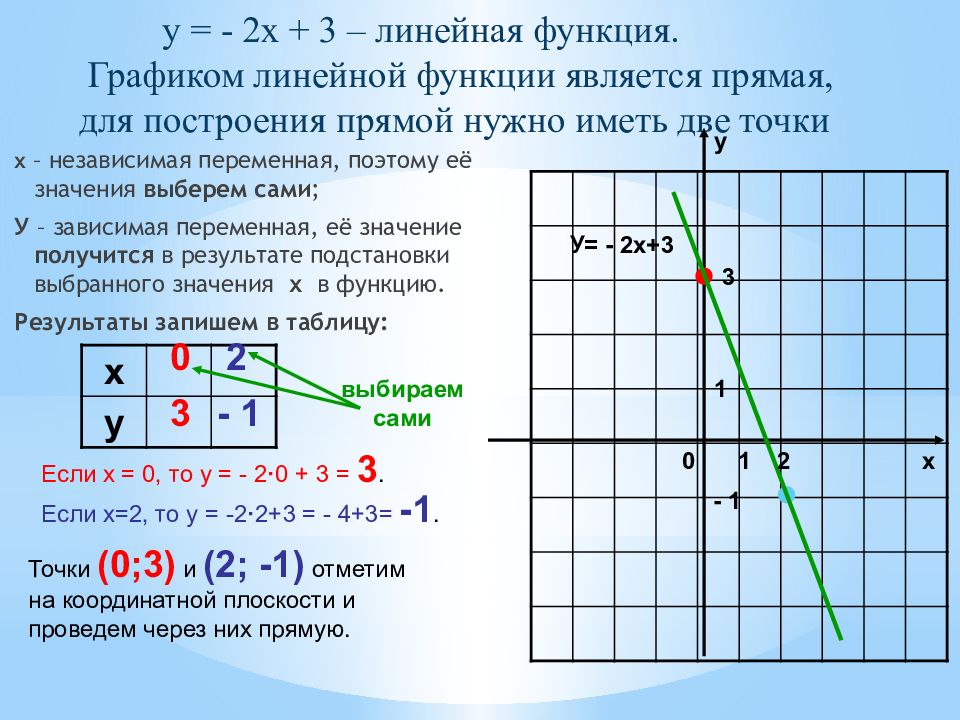
х – независимая переменная, поэтому её значения выберем сами ; У – зависимая переменная, её значение получится в результате подстановки выбранного значения х в функцию. Результаты запишем в таблицу: х у 0 2 Если х = 0, то у = - 2 · 0 + 3 = 3. 3 Если х=2, то у = -2 · 2+3 = - 4+3= -1. - 1 Точки (0;3) и (2; -1) отметим на координатной плоскости и проведем через них прямую. х у 0 1 1 У= - 2х+3 3 2 - 1 выбираем сами
Слайд 8
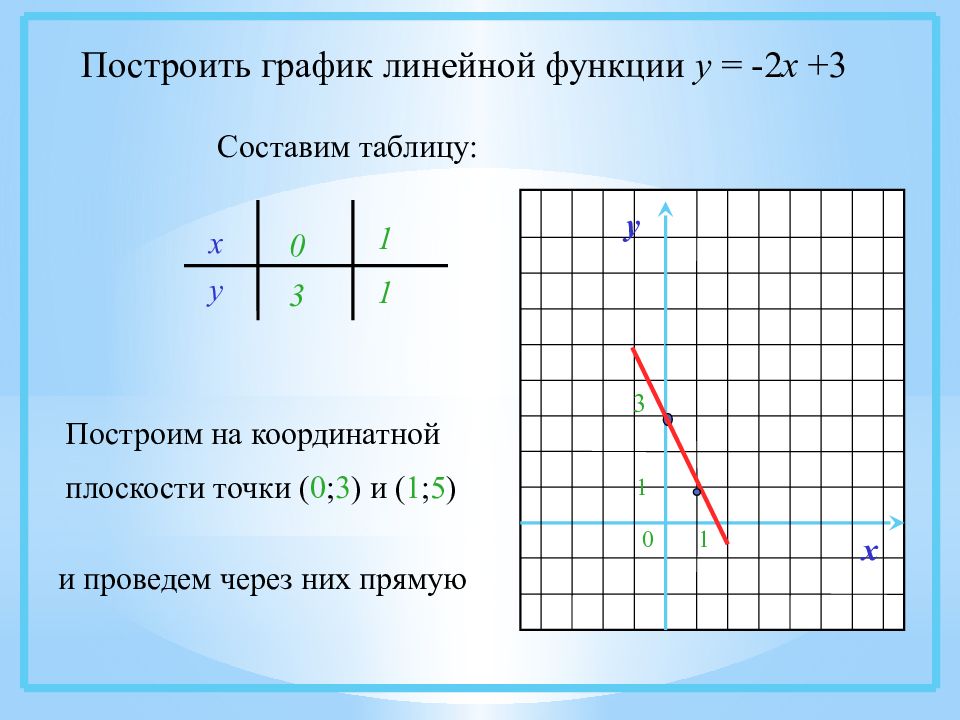
Построить график линейной функции у = - 2 х +3 Составим таблицу: х у 03 1 1 Построим на координатной плоскости точки ( 0 ; 3 ) и ( 1 ; 5 ) и проведем через них прямую х 1 0 1 3 у
Слайд 9: Построить график линейной функции
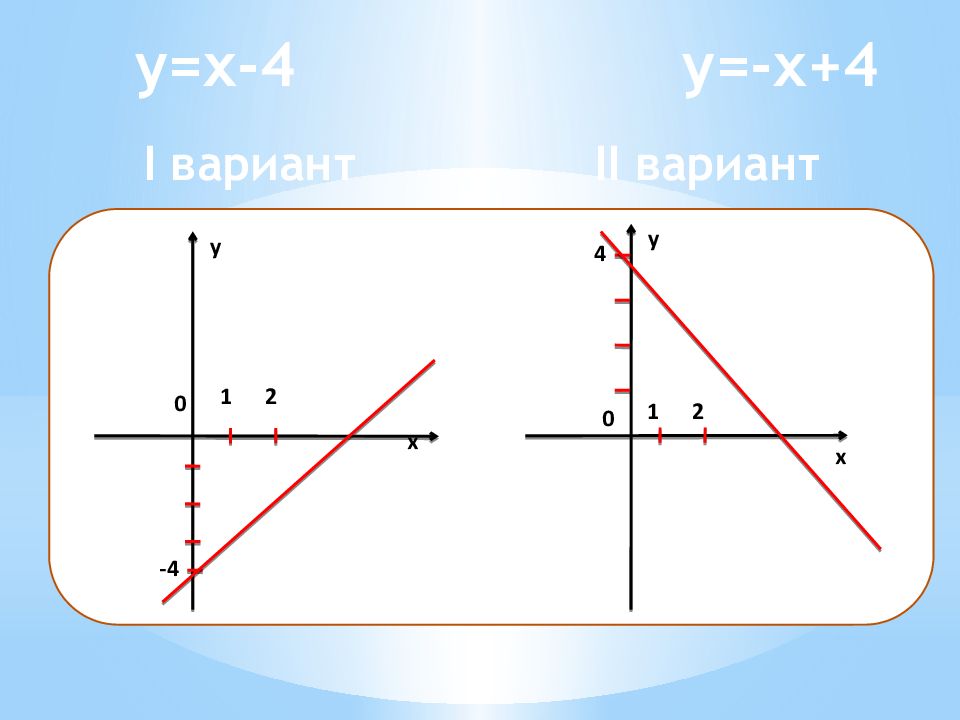
I вариант II вариант y=x-4 y =- x+4 Определить взаимосвязь коэффициентов k и b и расположения прямых Построить график линейной функции
Слайд 11
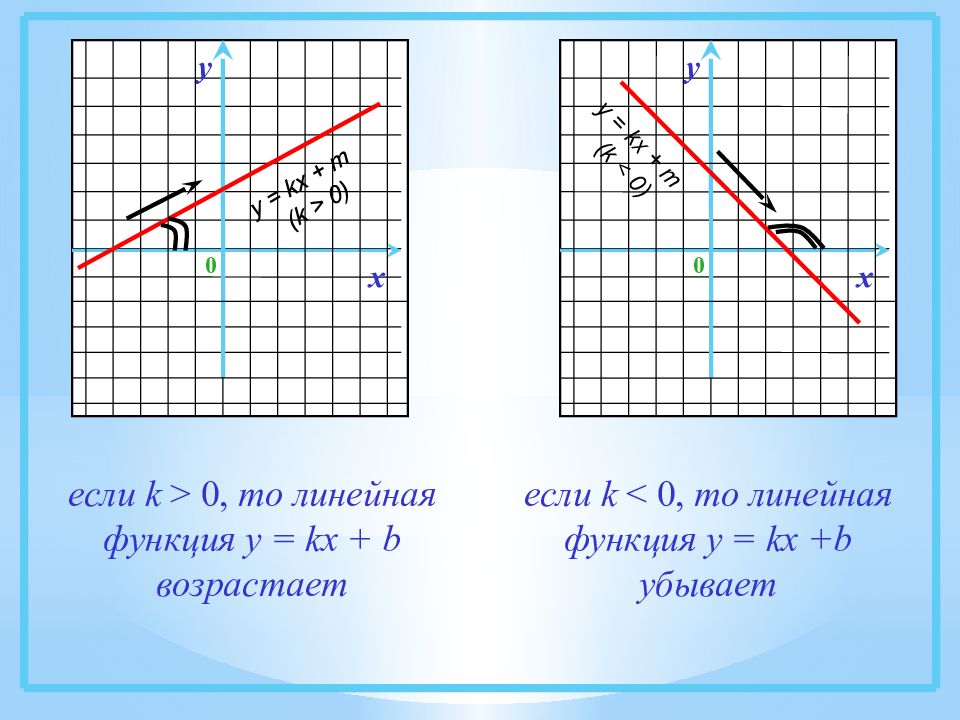
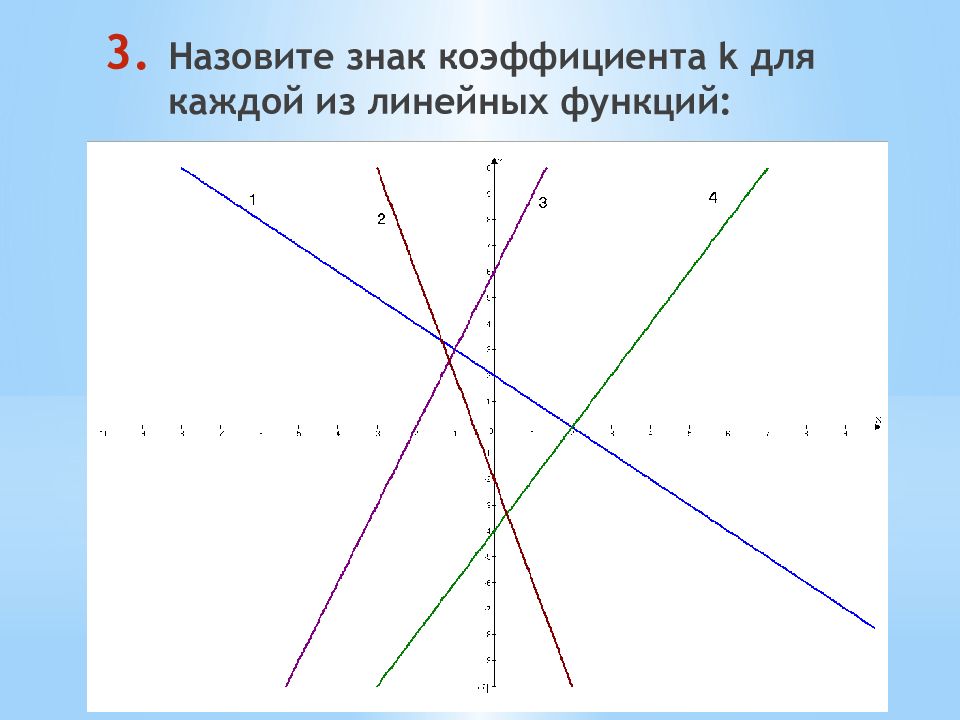
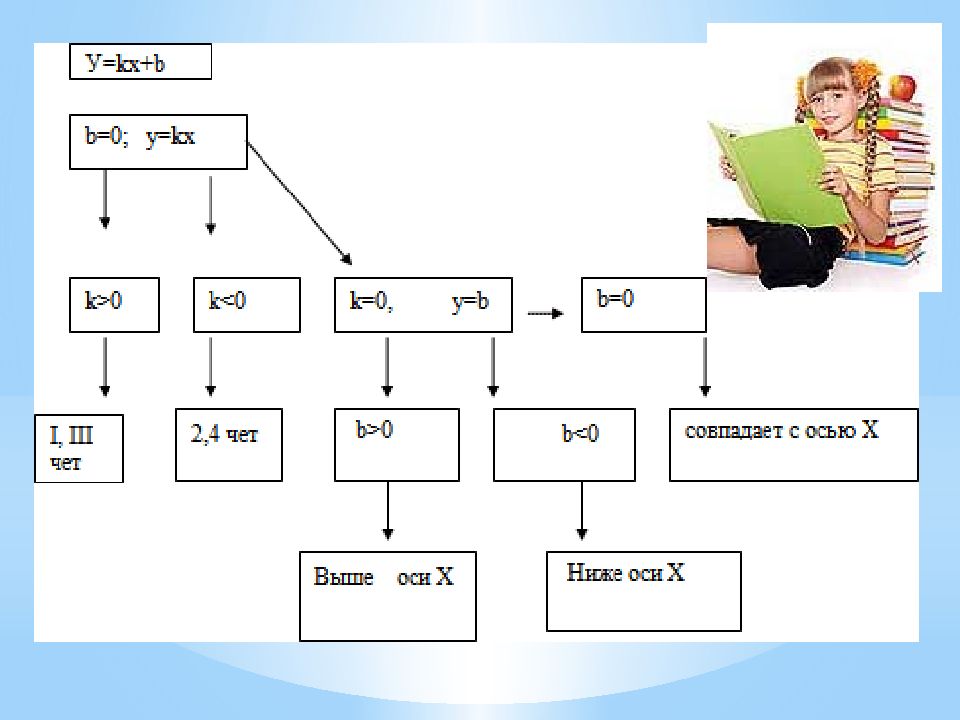
х 0 у y = kx + m (k > 0) х 0 у y = kx + m (k < 0) если k > 0, то линейная функция у = kx + b возрастает если k < 0, то линейная функция у = kx + b убывает
Слайд 12
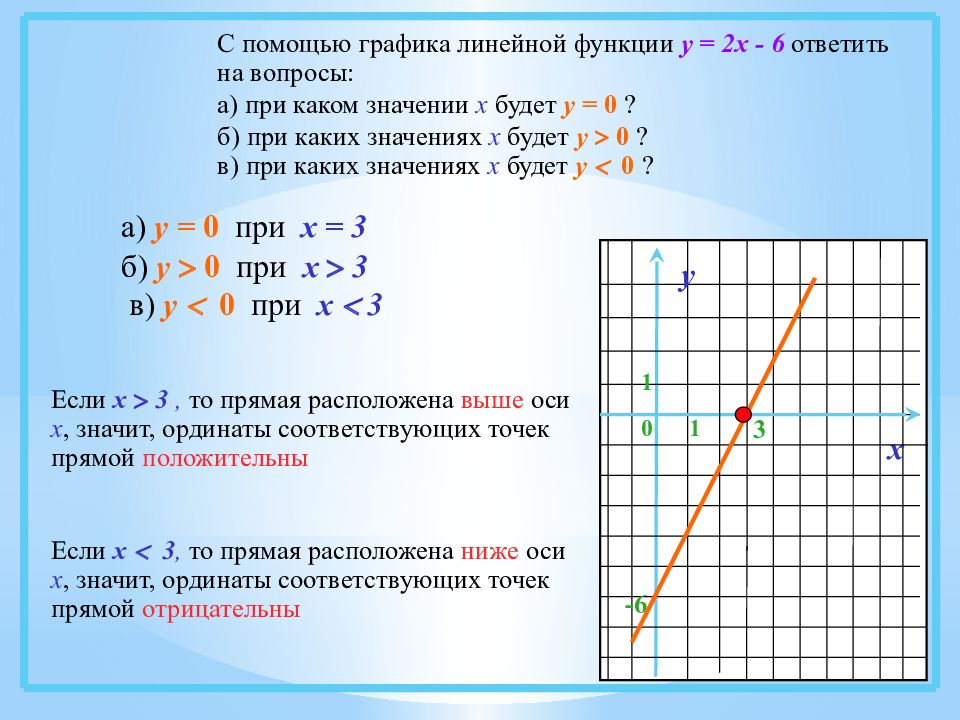
С помощью графика линейной функции у = 2х - 6 ответить на вопросы: а) при каком значении х будет у = 0 ? б) при каких значениях х будет у 0 ? в) при каких значениях х будет у 0 ? 1 0 3 у 1 х -6 а) у = 0 при х = 3 б) у 0 при х 3 Если х 3, то прямая расположена выше оси х, значит, ординаты соответствующих точек прямой положительны в) у 0 при х 3 Если х 3, то прямая расположена ниже оси х, значит, ординаты соответствующих точек прямой отрицательны
Слайд 13
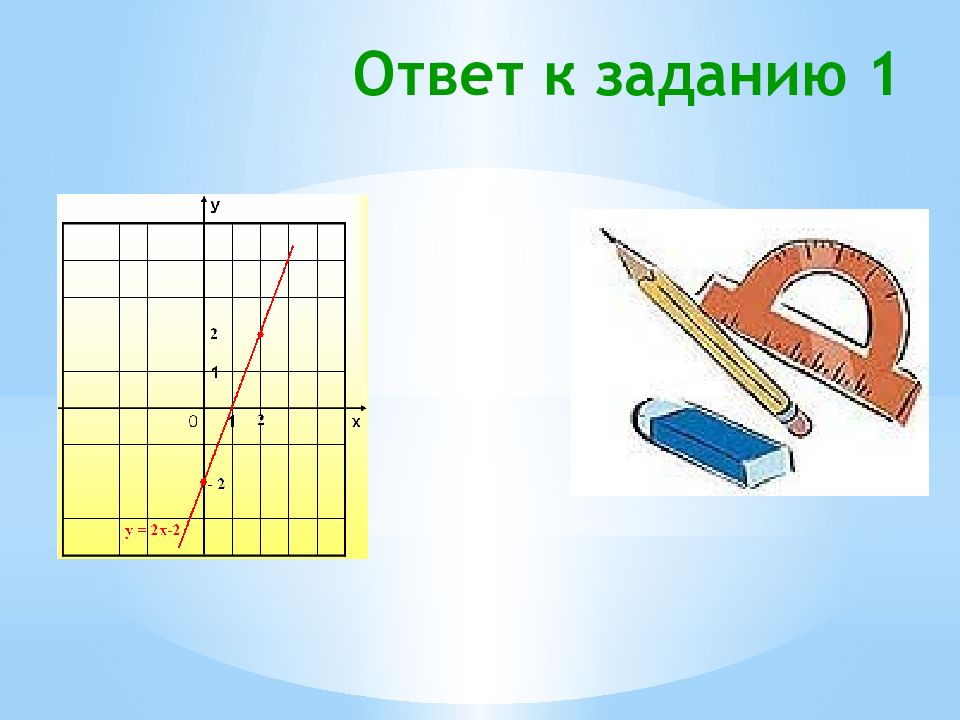
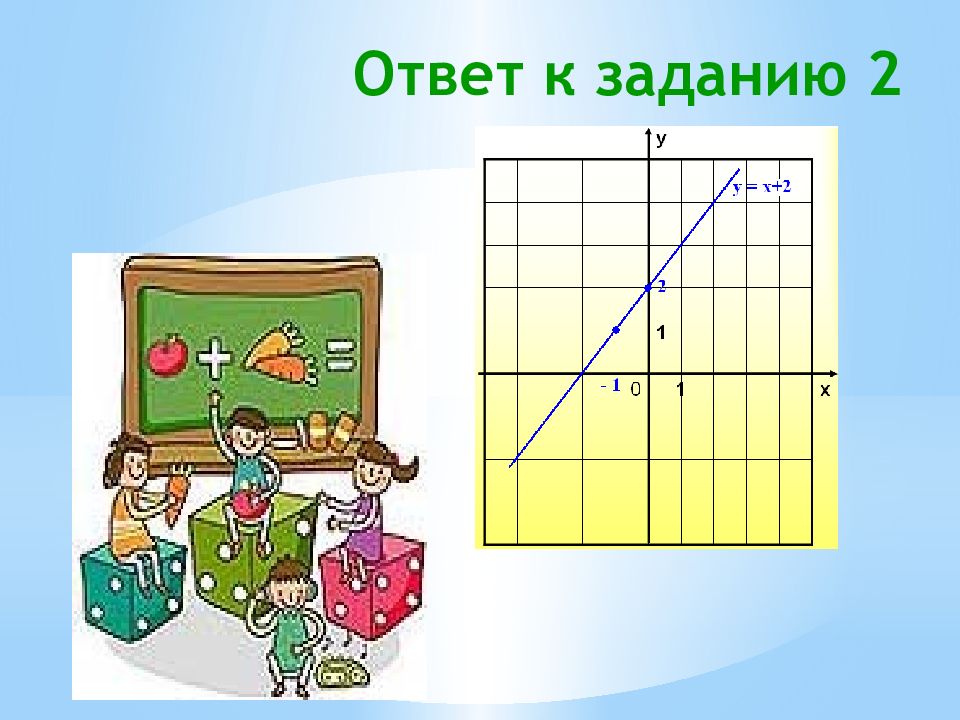
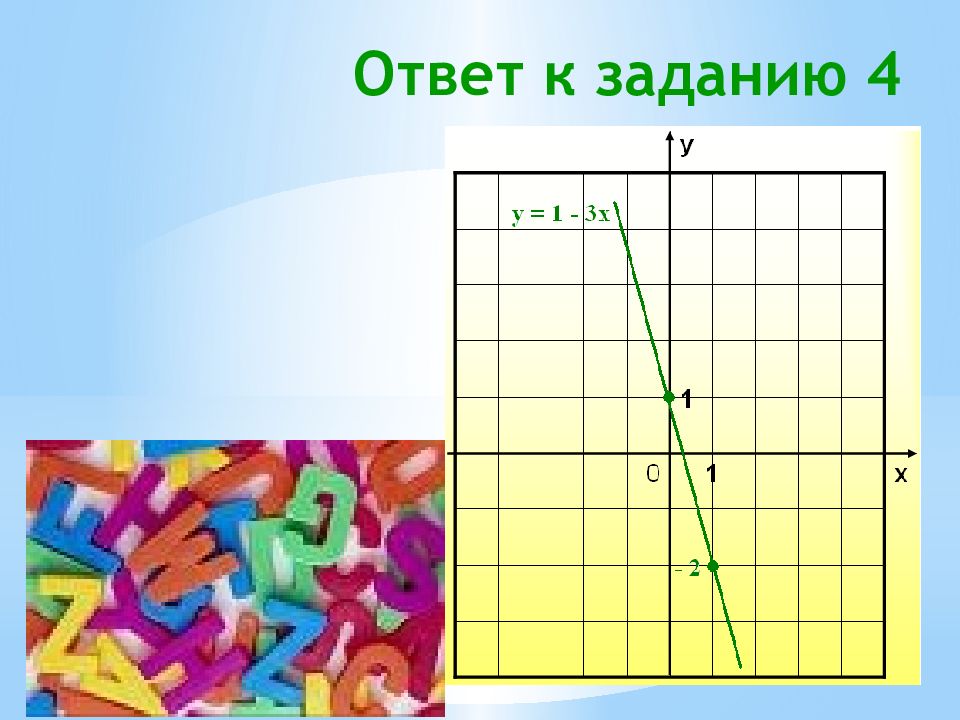
Задания для самостоятельного решения: построить графики функций (выполнять в тетради) 1. у = 2х – 2 2. у = х + 2 3. у = 4 – х 4. у = 1 – 3х О братите внимание: точки, выбранные вами для построения прямой, могут быть другими, но расположение графиков обязательно должно совпадать
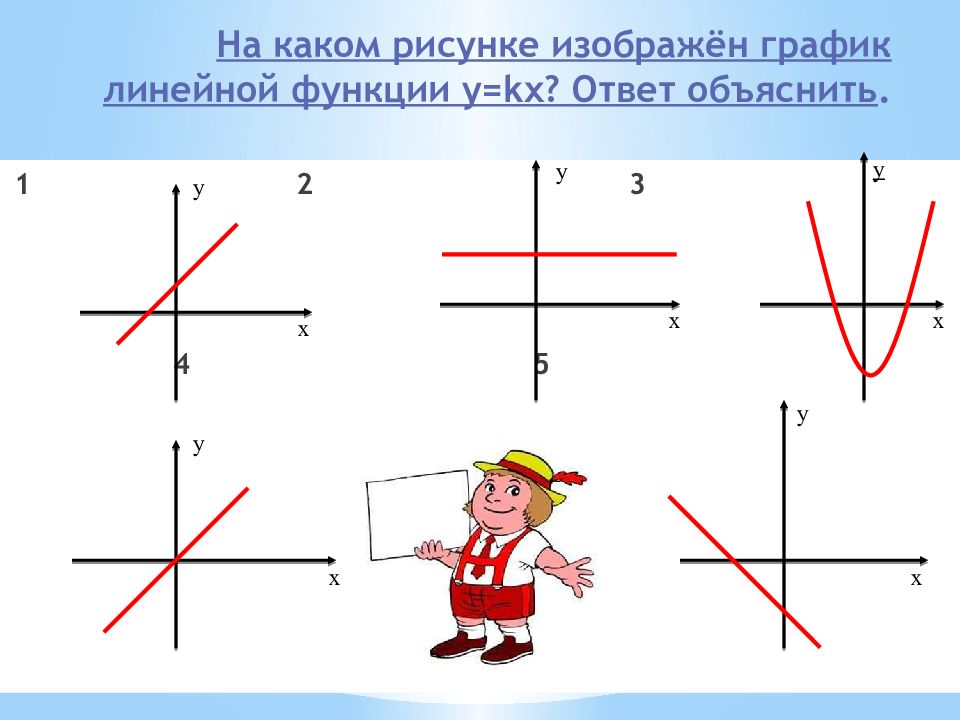
1 2 3 4 5 x y x y x y x y x y
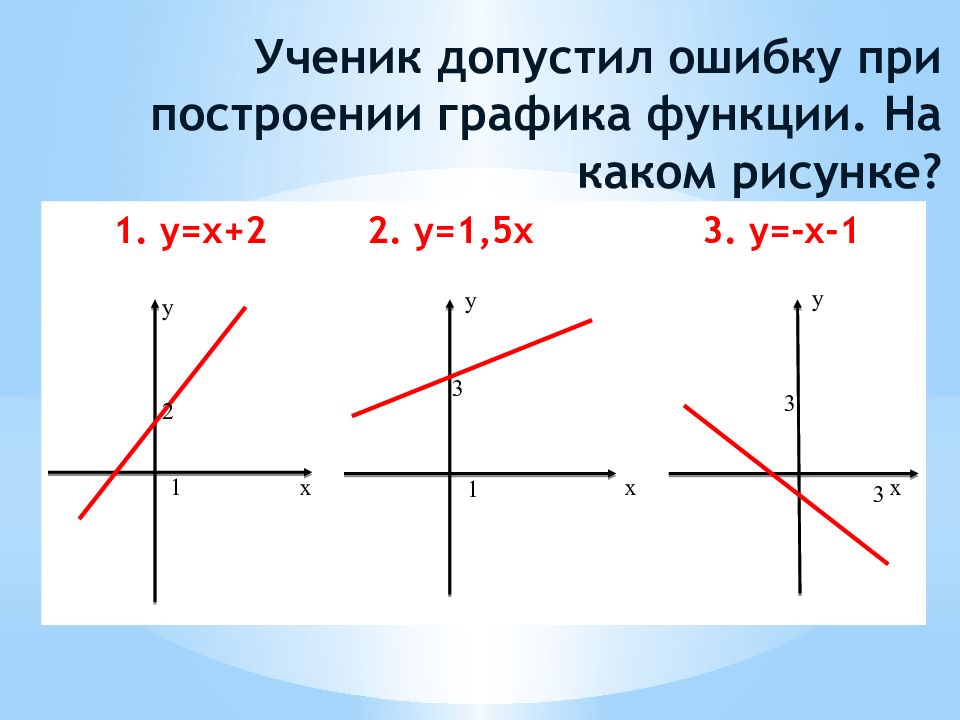
Слайд 20: Ученик допустил ошибку при построении графика функции. На каком рисунке?
1. y =х+2 2. y =1,5х 3. y =-х-1 x y 2 1 x y 3 1 x y 3 3
Слайд 21
1 2 3 4 5 x y x y y x y x y На каком рисунке коэффициент k отрицателен? x
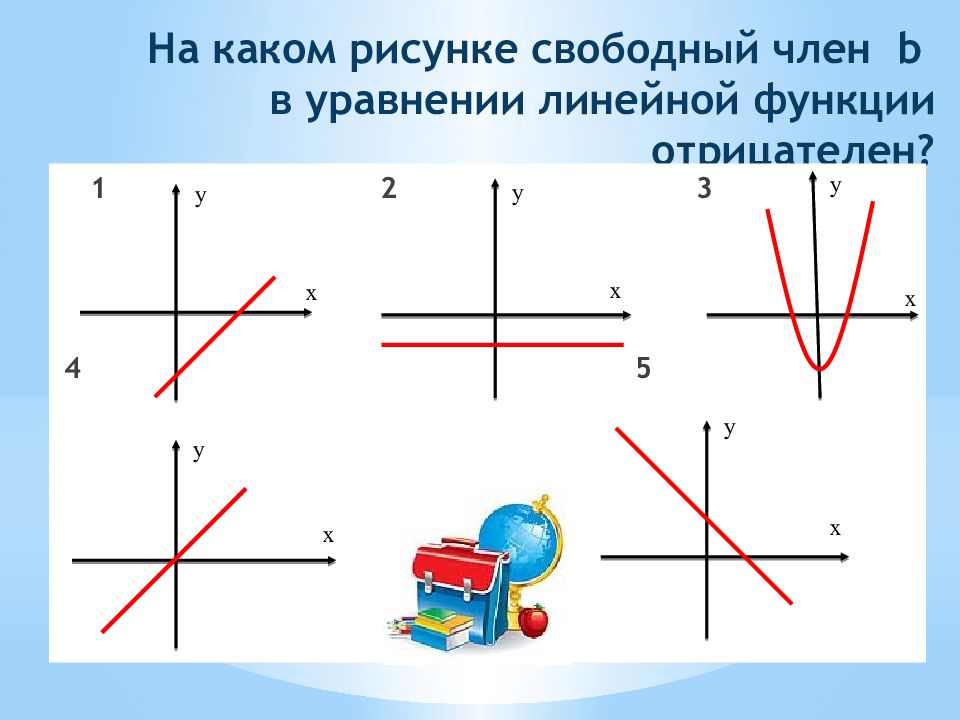
Слайд 23: На каком рисунке свободный член b в уравнении линейной функции отрицателен?
1 2 3 4 5 х y x y x y x y x y
Слайд 24
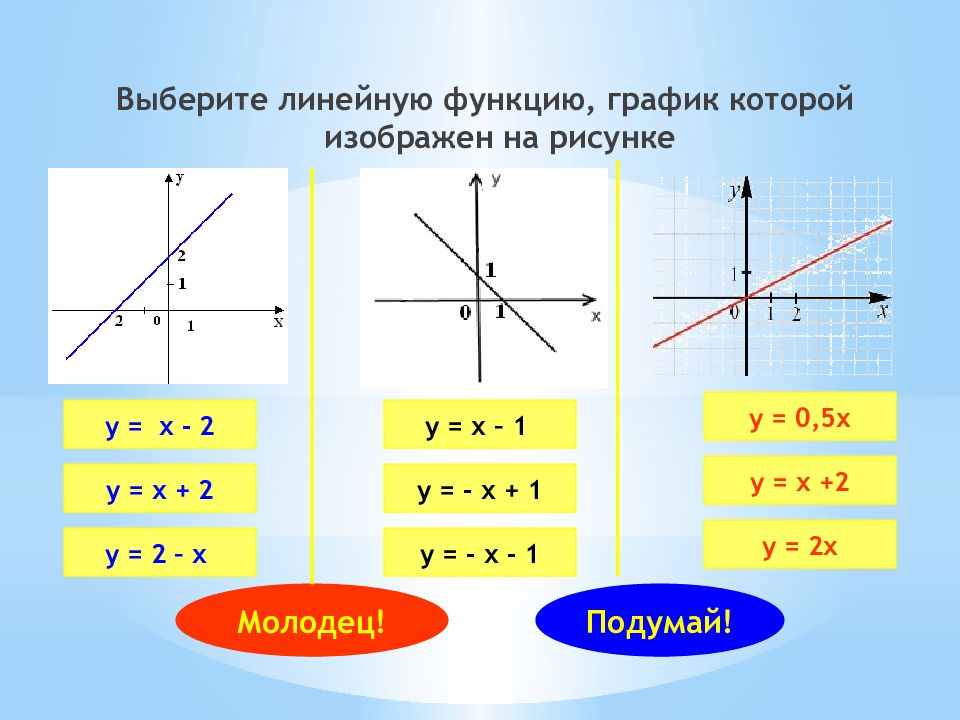
Выберите линейную функцию, график которой изображен на рисунке у = х - 2 у = х + 2 у = 2 – х у = х – 1 у = - х + 1 у = - х - 1 у = 0,5х у = х +2 у = 2х Молодец! Подумай!
Слайд 25
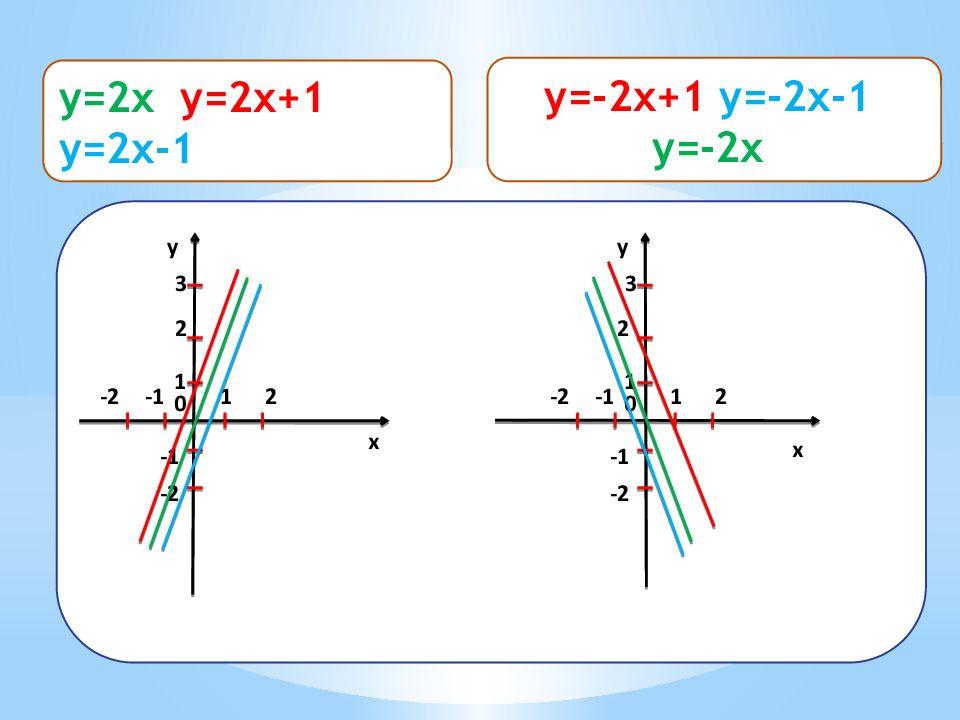
x y 1 2 0 1 2 3 -1 -2 -1 -2 x y 1 2 0 1 2 3 -1 -2 -1 -2 y=2x y=2x+ 1 y=2x- 1 y=-2x+ 1 y = -2x- 1 y =-2x
Слайд 26
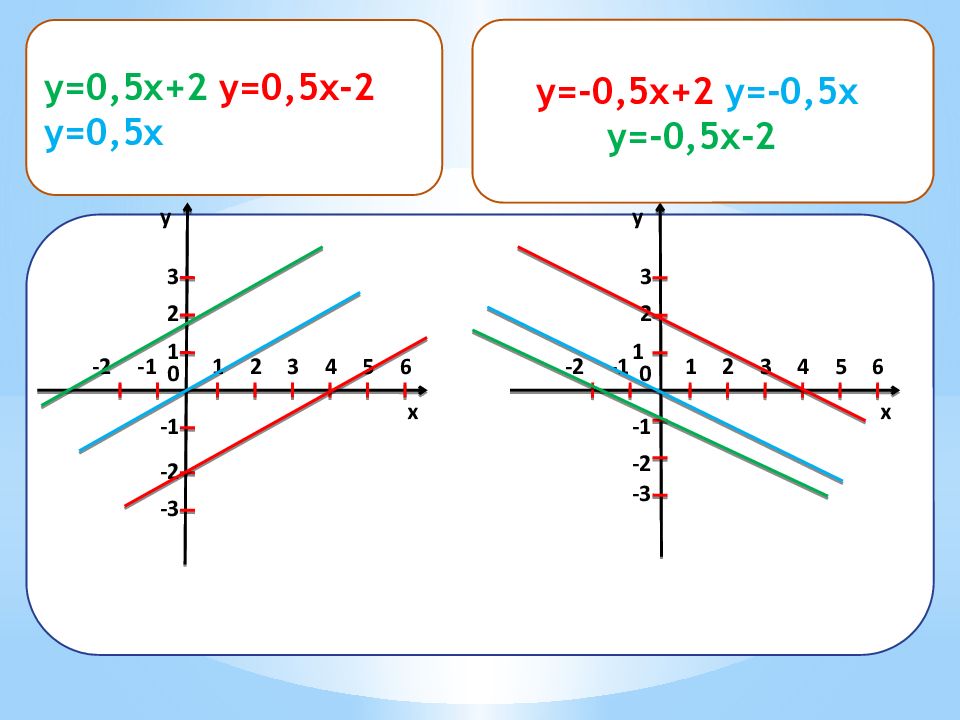
y=-0,5x+ 2, y=-0,5x, y=-0,5x- 2 x y 1 2 0 1 2 3 -1 -2 -1 -2 3 4 5 6 -3 x y 1 2 0 2 3 -1 -2 -1 -2 3 4 5 6 -3 1 y=0,5x+ 2 y=0,5x- 2 y=0,5x y=-0,5x+ 2 y=-0,5x y =-0,5x- 2
Слайд 27
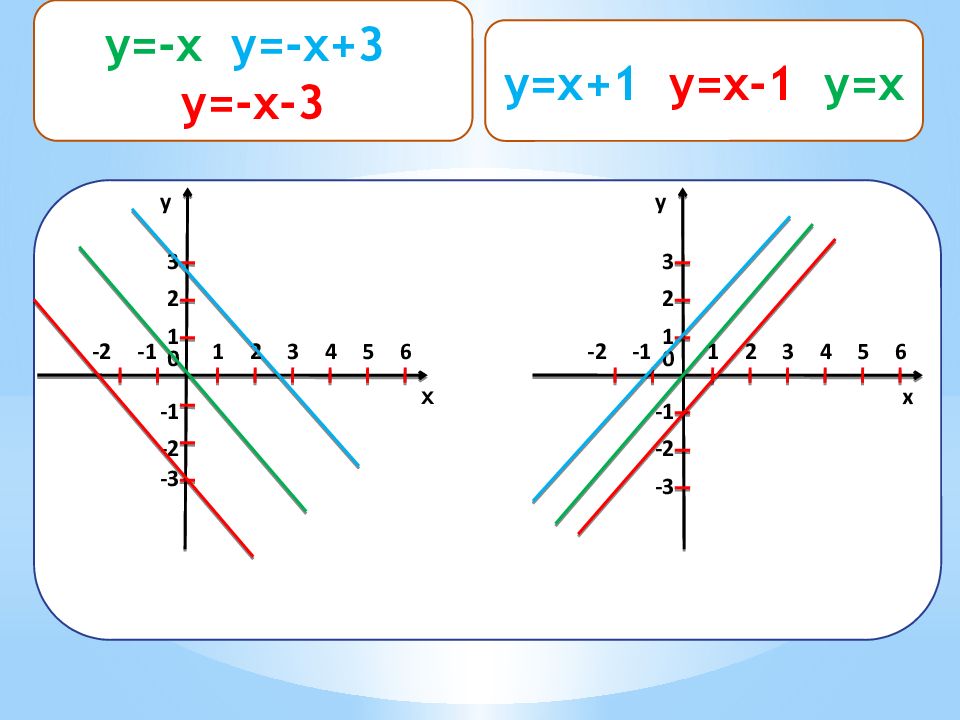
y=x+ 1 y=x- 1, y=x y 1 2 0 1 2 3 -1 -2 -1 -2 3 4 5 6 -3 x y 1 2 0 1 2 3 -1 -2 -1 -2 3 4 5 6 -3 x y=-x y=-x+ 3 y =-x- 3 y=x+ 1 y=x- 1 y=x
Слайд 30: Мы узнали: *Функция вида у = kx + b называется линейной. * Графиком функции вида у = kx + b является прямая. *Для построения прямой необходимы только две точки, так как через две точки проходит единственная прямая. *Коэффициент k показывает возрастает или убывает прямая. *Коэффициент b показывает, в какой точке прямая пересекает ось OY. *Условие параллельности двух прямых
Выводы записать в тетрадь Мы узнали: *Функция вида у = kx + b называется линейной. * Графиком функции вида у = kx + b является прямая. *Для построения прямой необходимы только две точки, так как через две точки проходит единственная прямая. *Коэффициент k показывает возрастает или убывает прямая. *Коэффициент b показывает, в какой точке прямая пересекает ось OY. *Условие параллельности двух прямых.
Слайд 33: Алгебра – это слово произошло от названия сочинения Мухаммеда Аль-Хорезми «Аль- джебр и Аль- мукабала », в котором алгебра излагалась как самостоятельный предмет
Слайд 34
Роберт Рекорд – это английский математик, который в 1556г. ввёл знак равенства и объяснил свой выбор тем, что ничто не может быть более равным, чем два параллельных отрезка.
Слайд 35: Готфрид Лейбниц – немецкий математик (1646 – 1716г.г.), который первым ввёл термин «абсцисса» - в 1695г., «ордината» - в 1684г., «координаты» - в 1692г
Слайд 36: Рене Декарт – французский философ и математик (1596 – 1650г.г.), который первым ввёл понятие «функция»
Последний слайд презентации: Линейная функция, её график, свойства
Использованная литература 1.МордковичА.Г. и др. Алгебра: учебник для 7 класса общеобразовательных учреждений – М.: Просвещение,2010. 2.Звавич Л.И. и др. Дидактические материалы по алгебре для 7 класса - М.: Просвещение,2010. 3.Алгебра 7 класс, под редакцией Макарычев Ю.Н. и др., Просвещение, 2010 г. 4.Интернетресурсы: www.symbolsbook.ru/Article.aspx %...id%3D222