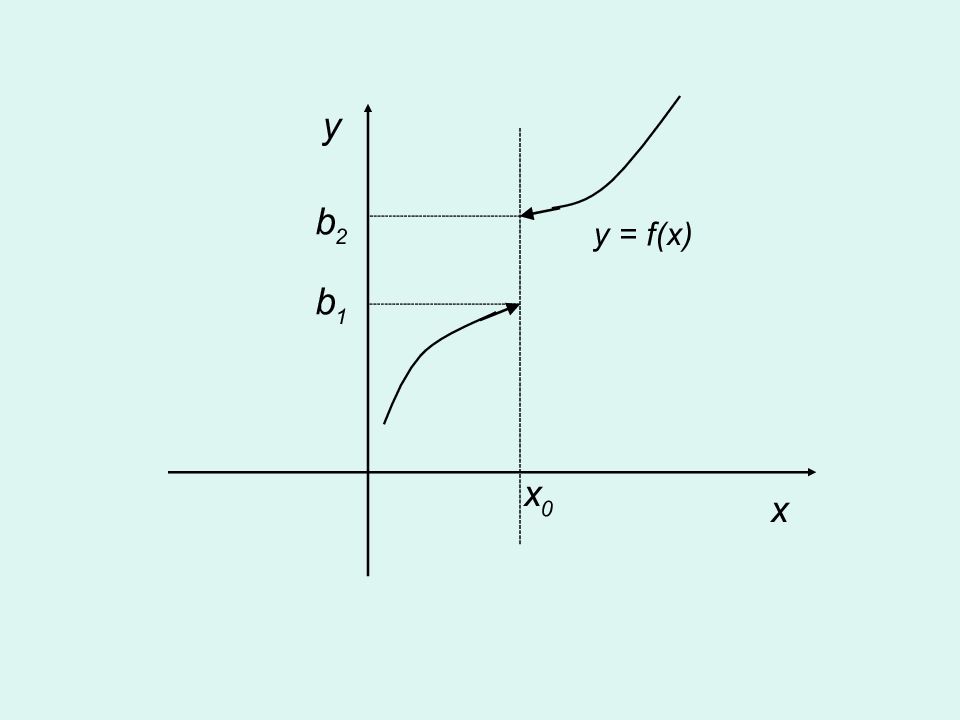Основополагающие понятия и представления о функции одного переменного. Основные свойства функций и их графики. Предел функции. Основные теоремы о пределах. Исследование функций. Раздел N 1 Введение в математический анализ. Лекция N1
Литература для подготовки Основная : 1. Основы высшей математики и математической статистики : Учебник / И.В. Павлушков 2. Основы высшей математики и статистики : Учебник / Ю. В. Морозов Дополнительная : Курс дифференциального и интегрального исчисления (3 Тома). Г.М. Фихтенгольц Теория вероятностей и математическая статистика. В.Е. Гмурман
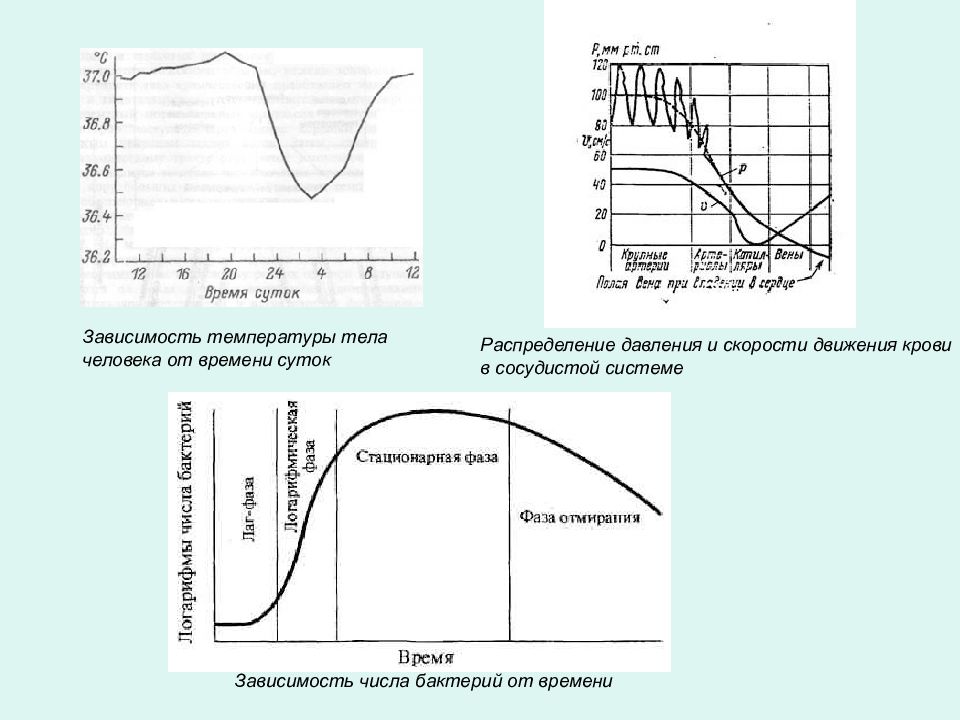
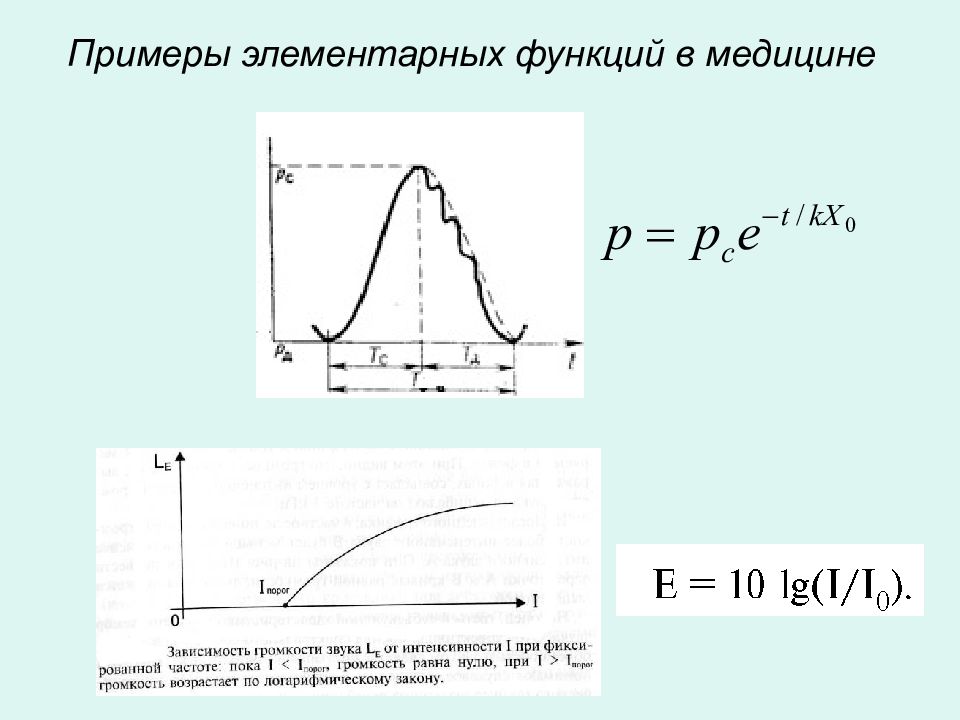
Зависимость температуры тела человека от времени суток Зависимость числа бактерий от времени Распределение давления и скорости движения крови в сосудистой системе
Множество x всех значений, которые может принимать данная переменная величина, называется областью изменения этой переменной величины Переменная величина считается заданной, если задана область её изменения
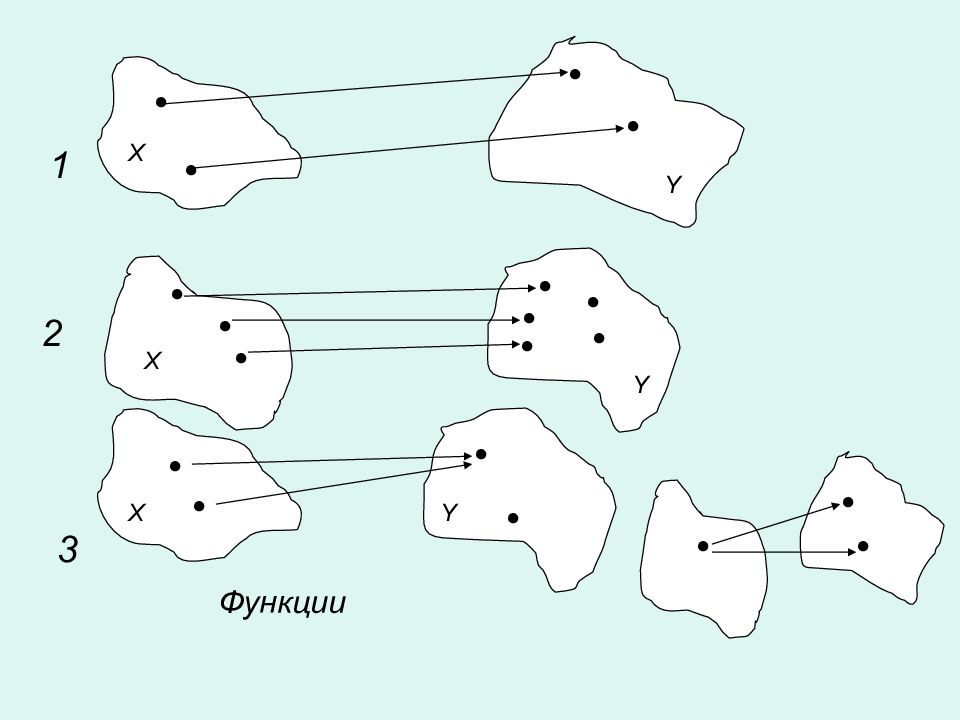
Определение Функции. Пусть даны некоторые множества X и Y, элементами которых являются некоторые числа. Если каждому числу x принадлежащему X по некоторому закону или правилу f ставится в соответствие одно число y, принадлежащее Y, то говорят, что на множестве X задана числовая функция f и записывают эту функциональную зависимость формулой y = f(x). X → Y f x - независимая переменная или аргумент. y - зависимая переменная (от x ) или функция. множество X - область изменения аргумента, или Область определения функции. Множество Y – область изменения функции ( Область значений функции.)
● ● ● ● X Y Функции ● ● ● ● ● ● ● ● ● ● ● ● X Y X Y ● ● ● 1 2 3
Аналитический. (Задание функции с помощью формул) Например : y = sinx. y = x 2 + 1 при x < 2 x – 4 при x ≥ 2 2. Табличный. (Задание таблиц) Пример : тригонометрические таблицы, таблицы логарифмов таблица зависимости температуры от времени и т д. 3. Графический. Пример : кардиограмма, осциллограмма
1. Возрастание (убывание) функций Нули функции Четность функции Периодичность функции Ограниченность функции 6. Сложная и обратная функции
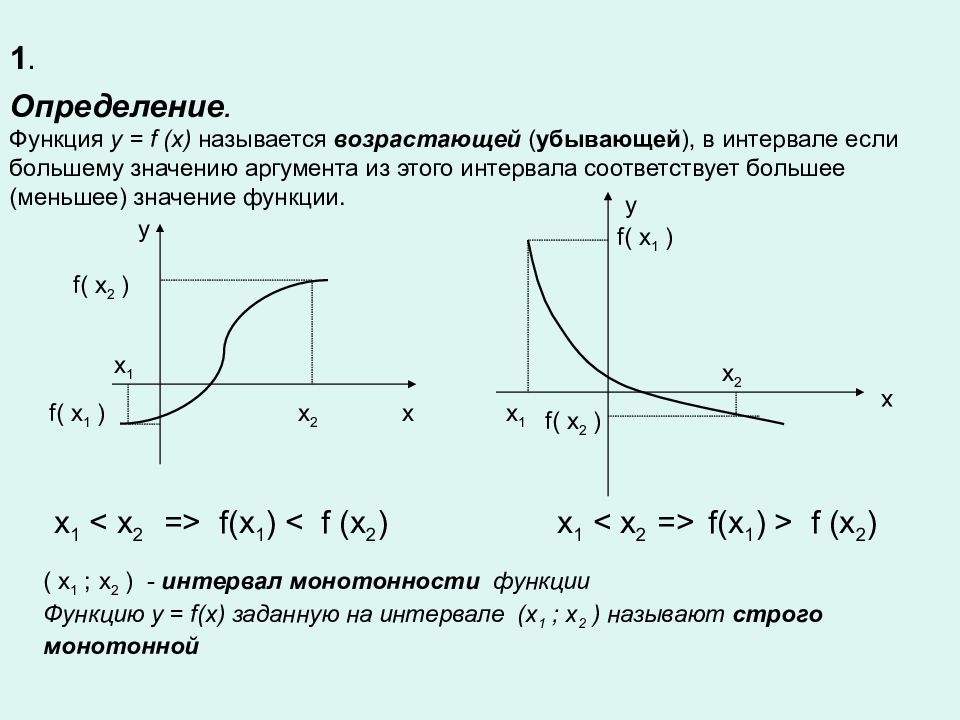
Определение. Функция y = f (x) называется возрастающей ( убывающей ), в интервале если большему значению аргумента из этого интервала соответствует большее (меньшее) значение функции. 1. x 2 y x 1 x f( x 2 ) f( x 1 ) x y x 2 x 1 f( x 1 ) f( x 2 ) x 1 < x 2 => f(x 1 ) < f (x 2 ) x 1 < x 2 => f(x 1 ) > f (x 2 ) ( x 1 ; x 2 ) - интервал монотонности функции Функцию y = f(x) заданную на интервале ( x 1 ; x 2 ) называют строго монотонной
2. Определение. Значение аргумента, при котором функция обращается в нуль, называется нулем функции. пример : f ( x ) = 3x + 1 Для нахождения нуля функции необходимо решить уравнение f(x) = 0 3x + 1 =0 x = -1/3 3. Определение. Функция, определенная на множестве X называется четной, если для всех значений аргумента x принадлежащих этому множеству выполняется условие f(-x) = f(x) Примеры : 1) y = x n, n - четное число, 2) y = Ι x Ι Функция называется нечетной, если для всех значений аргумента x, принадлежащих множеству X выполняется условие f(- x) = - f (x) 1) y = sin x, 2) y = arctg x Примеры : √х – функция не четная, не нечетная (функция общего вида)
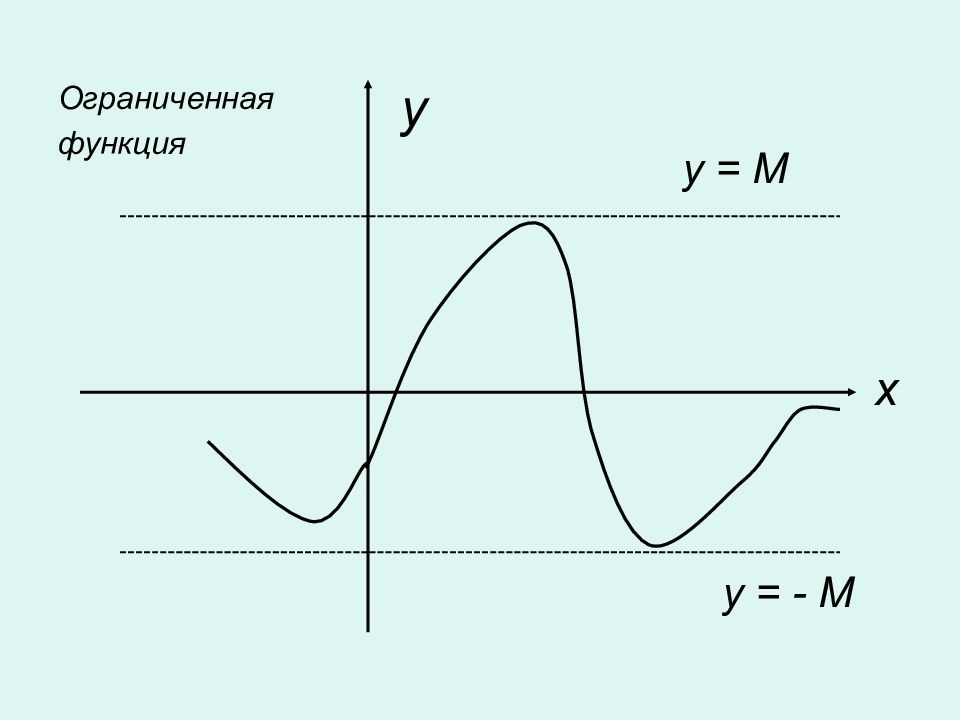
4. Определение. Функция y = f(x) с областью определения X называется периодической, если существует хотя бы одно число T > 0, такое, при котором выполняются два условия : Для любого числа x, принадлежащего X, x +T, x – T тоже принадлежат X. 2. Для каждого числа x, принадлежащего X, имеет место соотношение f (x) = f (x + T) = f (x - T) 5. Определение. Функция y = f(x) определенная на множестве X называется ограниченной, если существует число М > 0, что для всех x, принадлежащих X выполняется неравенство : │ f(x) │≤ М Отсюда следует, что график функции лежит между прямыми y = - M y = M
Ограниченная функция y x y = M y = - M
6. Определение. Функция F (x) называется сложной, аргумент которой также является функцией, т.е F (x) = f ( φ (x) ) X U Y φ f Переменную u = φ (x) называют промежуточным аргументом сложной функции Примеры сложных функций y = sin 2x, y = sin u, u = 2x. y = arctg (1/x), y = arctg u, u = 1/x y = log sin x
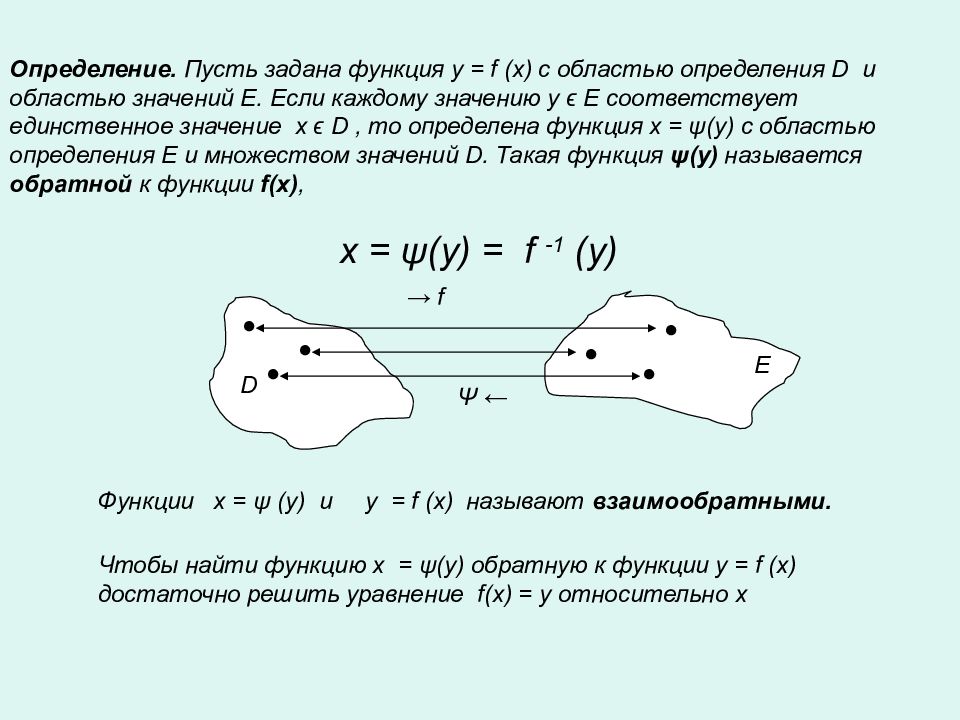
Определение. Пусть задана функция y = f (x) с областью определения D и областью значений E. Если каждому значению y ϵ E соответствует единственное значение x ϵ D, то определена функция x = ψ (y) с областью определения Е и множеством значений D. Такая функция ψ (y) называется обратной к функции f(x), x = ψ (y) = f -1 (y) D E → f Ψ ← Функции x = ψ (y) и y = f (x) называют взаимообратными. Чтобы найти функцию x = ψ (y) обратную к функции y = f (x) достаточно решить уравнение f(x) = y относительно х ● ● ● ● ● ●
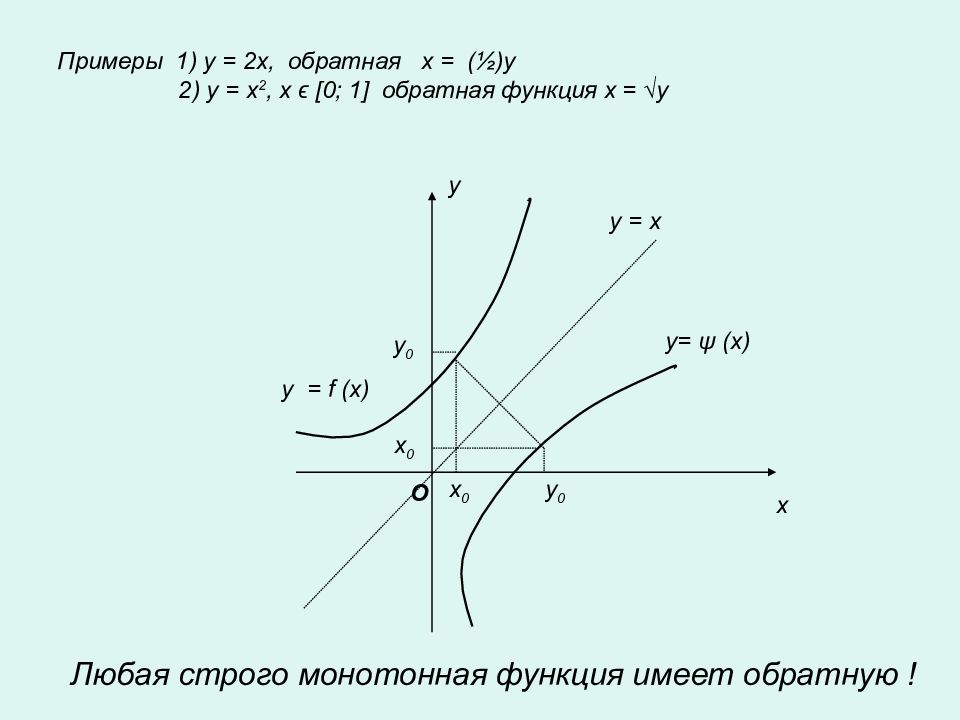
Примеры 1) y = 2x, обратная x = (½)y 2) y = x 2, x ϵ [0; 1] обратная функция x = √y y = x y = f (x) y= ψ (x) O x y x 0 x 0 y 0 y 0 Любая строго монотонная функция имеет обратную !
1. Целая и дробная рациональные функции y = a 0 x n + a 1 x n – 1 + …. a n-1 x + a n дробная рациональная функция y = a 0 x n + a 1 x n – 1 + …. a n-1 x + a n b 0 x n + b 1 x n – 1 + …. b n-1 x + b n 2. C тепенная функция 3. Показательная функция y = x α y = a x 4. Логарифмическая функция y = log a x 5. Тригонометрические функции y = sin x ; y = cos x; y = tgx; y = ctg x 6. Обратные тригонометрические функции y = arcsin x ; y = arccos x; y = arctgx; y = arcctg x α ϵ R a > 0, a ≠ 1 a > 0, a ≠ 1
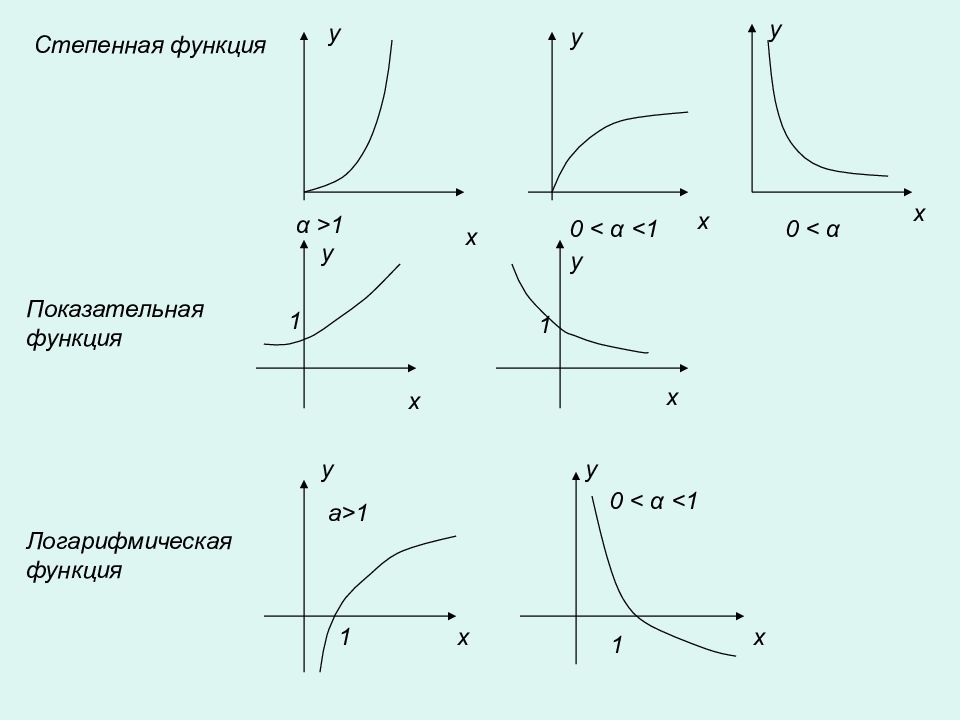
C тепенная функция α >1 0 < α <1 0 < α Показательная функция 1 1 x x x x x y y y y y Логарифмическая функция 1 1 a>1 0 < α <1 y y x x
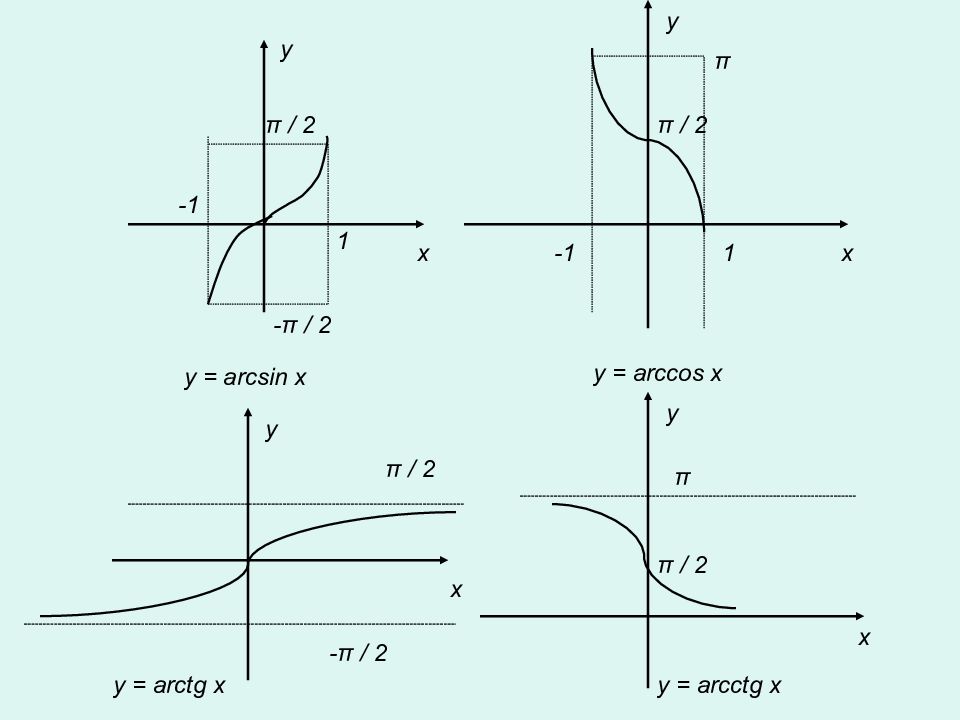
1 π / 2 - π / 2 y x x y -1 1 -1 π / 2 π y = arcsin x y = arccos x x y π / 2 - π / 2 y = arctg x π π / 2 x y y = arcctg x
Примеры элементарных функций в медицине
Примеры неэлементарных функций y = sign x = 1, x > 0, 0, x = 0, -1, x < 0 y = x 2 + 1, x ≤ 0 x, x > 0
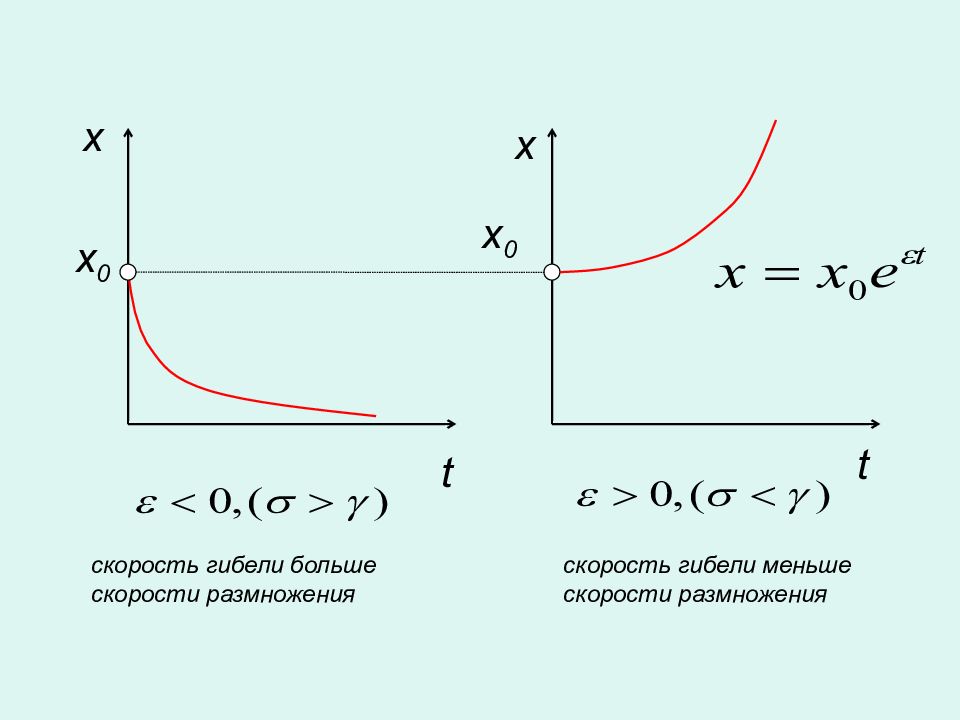
Понятие предела функции Модель естественного роста численности популяции (модель Мальтуса) Имеется реальная система (бактерии, зайцы и т.д.) Постановка задачи. (Найти законы изменения численности популяции во времени. ) Основные допущения. 1. Имеются только естественные процессы размножения и гибели, скорости которых пропорциональны численности популяций. 2. Нет борьбы между особями за место обитания, пищу и т.д. 3. Рассматривают только одну популяцию, нет хищников x – численность популяции в момент времени t R – скорость размножения, γ – коэффициент размножения S – скорость естественной гибели, σ – коэффициент естественной гибели - скорость изменения численности популяции, ε – коэффициент роста
Тогда,
x 0 x 0 t t скорость гибели больше скорости размножения скорость гибели меньше скорости размножения x x
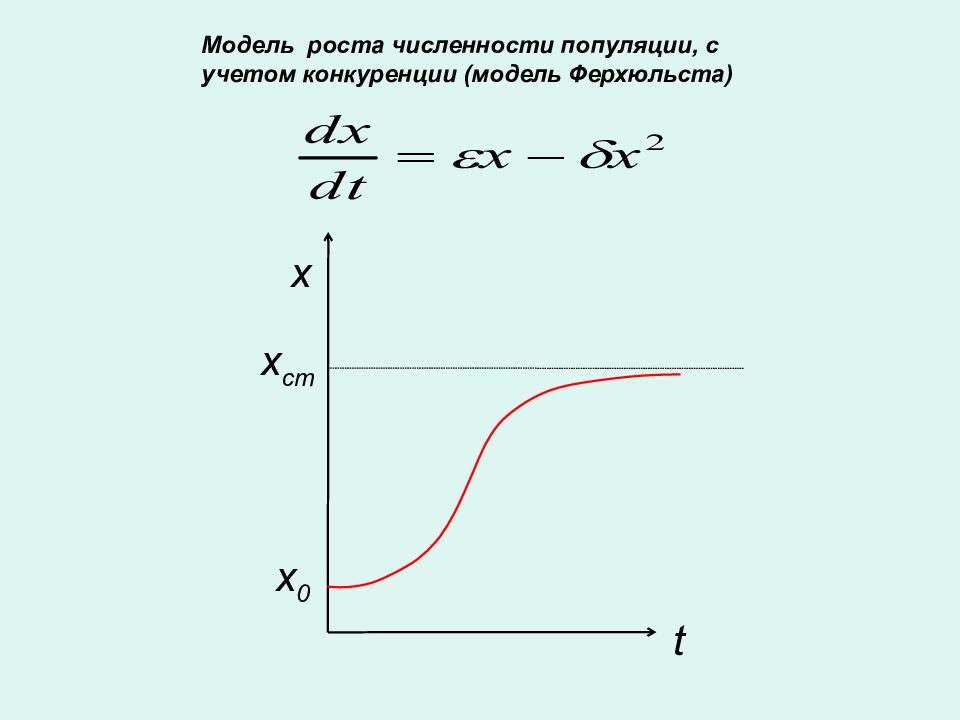
x 0 t Модель роста численности популяции, с учетом конкуренции (модель Ферхюльста) x ст x
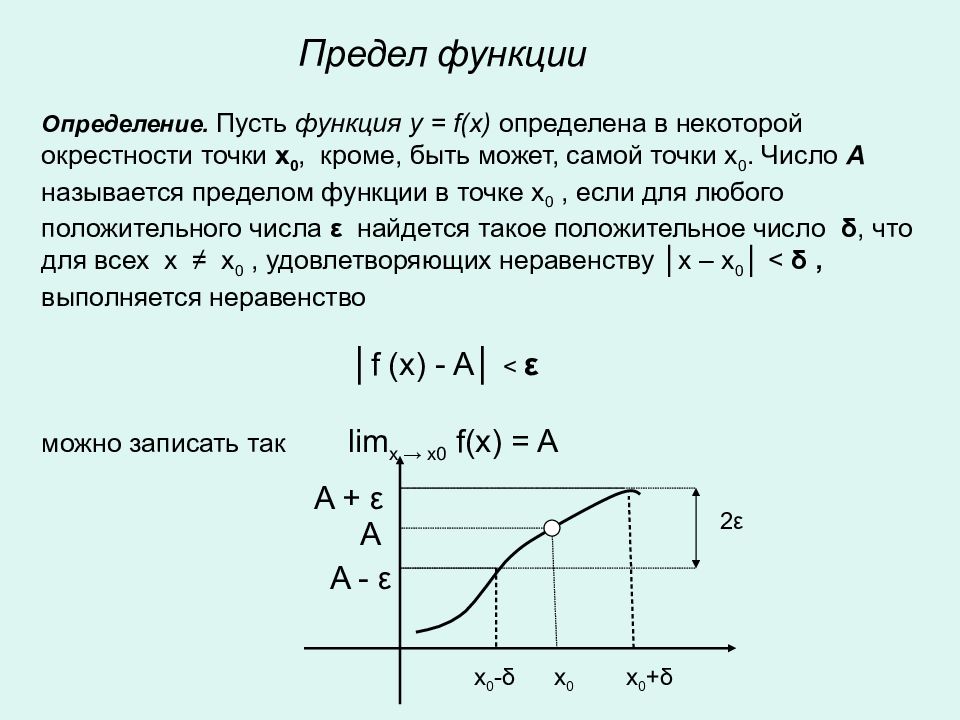
Предел функции Определение. Пусть функция y = f(x) определена в некоторой окрестности точки x 0, кроме, быть может, самой точки x 0. Число А называется пределом функции в точке x 0, если для любого положительного числа ε найдется такое положительное число δ, что для всех x ≠ x 0, удовлетворяющих неравенству │ x – x 0 │ < δ, выполняется неравенство │ f (x) - A │ < ε можно записать так lim x → x0 f(x) = A x 0 - δ x 0 + δ x 0 2 ε A A - ε A + ε
Пример 1. Доказать, что lim x →3 ( 2x - 1 ) = 5 Возьмем произвольное число ε > 0, найдем такое число δ > 0, что для всех x, удовлетворяющих неравенству Ι x - 3 Ι < δ, выполняется неравенство Ι (2х - 1) – 5 Ι < ε, т.е Ι x - 3 Ι < ε /2 Взяв δ = ε / 2, видим, что для всех x, удовлетворяющих неравенству Ι x - 3 Ι < δ = ε / 2 выполняется неравенство Ι (2х - 1) – 5 Ι < ε, следовательно lim x→3 ( 2x - 1 ) = 5 Пример 2. Найти предел lim x →4 5x + 2 2x + 3 Числитель стремится к числу 5*4 + 2 = 22 Знаменатель стремится к числу 2*4 + 3 = 11 Искомый предел равен 22/11 = 2
Определение. Число b 1, называется пределом слева, если для любого положительного числа ε найдется такое положительное число δ, что для всех x принадлежащих интервалу ( x 0 – δ, x 0 ), выполняется неравенство │ f (x) – b 1 │ < ε Определение. Число b 2, называется пределом справа, если для любого положительного числа ε найдется такое положительное число δ, что для всех x принадлежащих интервалу ( x 0, x 0 + δ ), выполняется неравенство │ f (x) – b 2 │ < ε Пределы функции слева и справа называют односторонними пределами. Если существует предел lim f (x) = A, то существуют оба односторонних предела, причем b 1 = b 2 = A, справедливо и обратное утверждение : если существуют левый и правый пределы и они равны, то существует предел lim x → x0 f(x) = А Если же b 1 ≠ b 2, то А = lim x →x0 f(x) не существует
x 0 x y b 1 b 2 y = f(x)
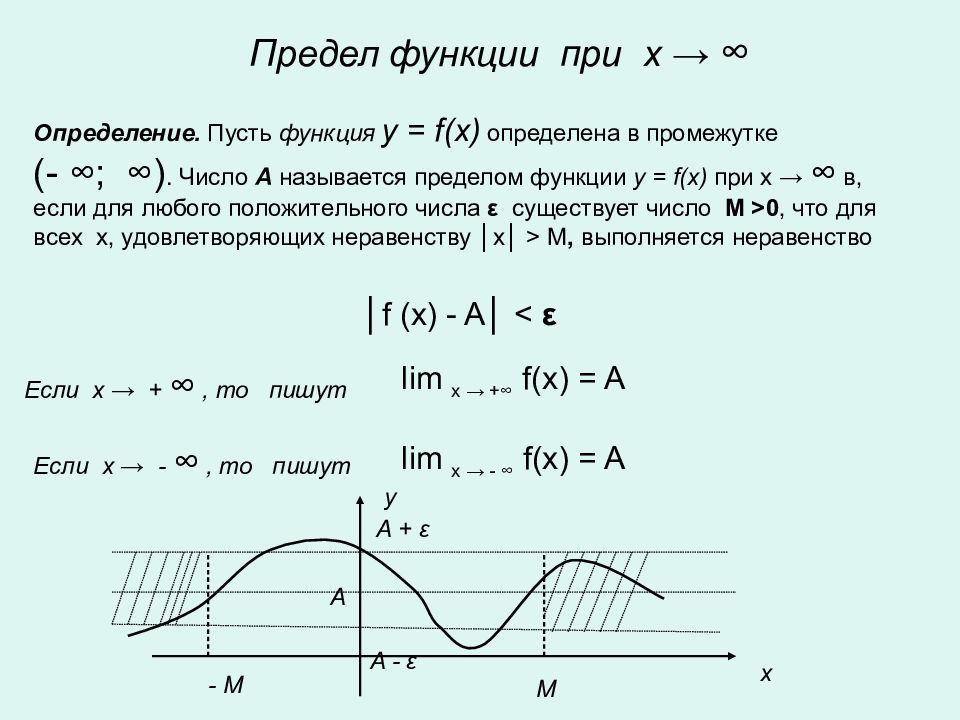
Предел функции при x → ∞ Определение. Пусть функция y = f(x) определена в промежутке (- ∞ ; ∞ ). Число А называется пределом функции y = f(x) при x → ∞ в, если для любого положительного числа ε c уществует число M >0, что для всех x, удовлетворяющих неравенству │ x │ > M, выполняется неравенство │ f (x) - A │ < ε lim x → + ∞ f(x) = A Если x → + ∞, то пишут Если x → - ∞, то пишут lim x → - ∞ f(x) = A М - М х y A + ε A - ε A
Бесконечно большие и бесконечно малые функции. Функция f(x) называется бесконечно большой, если предел lim x → a f (x) = ± ∞, где а = х 0 или a → ± ∞ Функция f(x) называется бесконечно малой, если предел lim x → a f (x) = 0, где а = х 0 или a → ± ∞ Пример : y = 1 / ( x - 2 ) бесконечно большая при x → 2 Бесконечно малые функции называют бесконечно малыми величинами и обозначают греческими буквами α, β, γ Примеры : 1) y = x - 2 бесконечно малая при x → 2 2) y = x 2, бесконечно малая при x → 0 3) y = 1/x бесконечно малая при x → ∞
Связь между функцией, её пределом и бесконечно малой функцией. Теорема 1.1. Если функция f(x) имеет предел, равный А, то её можно представить как сумму числа А и бесконечно малой функции α (х), т.е если lim x→x0 f(x) = A, f (x) = A + α (х) Доказательство : Пусть lim x→x0 f(x) = A, следовательно, для любого ε > 0, существует δ >0, что для любых x, Ι x - x 0 Ι < δ следует Ι f(x) – A Ι < ε, т.е Ι f(x) – A - 0 Ι < ε Это означает, что функция f(x ) - A имеет предел, равный 0, т.е является бесконечно малой величиной, которую обозначим через α (х) : f(x) – A = α (х). Отсюда f(x) = A + α (х)
Пример использования бесконечно малых величин. Найти предел lim x →∞ 3x +5 2x+ 7 При непосредственной подстановке получим неопределенность вида ∞ ∞ Разделим числитель и знаменатель на x, получим lim x→∞ 3 + 5/ x = 3 /2 2 + 7/x
Основные теоремы о пределах Пусть даны две функции f(x) и g(x), которые имеют общую область определения X и точку в х 0, принадлежащую этой области определения. Теорема 1.2. Предел суммы двух функций равен сумме пределов функций. lim x → x0 (f (x) + g(x)) = lim x → x0 f (x) + lim x → x0 g(x) Доказательство Пусть lim x → x0 f (x) = A, lim x → x0 g(x) = B. По теореме 1 можно записать f(x) = A + α (x), g (x) = B + β (x). Следовательно f(x) + g(x) = A + B +( α (x) + β (x)) lim (f(x) + g(x)) = A + B. Теорема 1.3. Предел произведения двух функций равен произведению пределов функций. lim x → x0 (f (x) * g(x)) = lim x → x0 f (x) * lim x → x0 g(x) Пусть lim x → x0 f (x) = A, lim x → x0 g(x) = B. f(x) = A + α (x), g (x) = B + β (x). Следовательно f(x) * g(x) = A * B + B* α (x) + A* β (x) + α (x)* β (x) Поэтому lim x → x0 f (x) * g(x) = A*B
Следствие. Постоянный множитель можно выносить за знак предела. lim x → x0 ( с* f (x) ) = с * lim x → x0 f (x) Теорема 1.4. Предел отношения двух функций равен отношению пределов функций. lim x → x0 (f (x) / g(x)) = lim x → x0 f (x) lim x → x0 g(x) Пусть lim x → x0 f (x) = A, lim x → x0 g(x) = B. f(x) = A + α (x), g (x) = B + β (x) Следовательно f(x) / g(x) = A + α (х) = A +( A + α (x) – A ) = B + β (x) B B + β (x) B = A / B + ( B* α (x) – A * β (x)) / (B 2 + B* β (x)) – второе слагаемое б.м.ф Поэтому lim x → x0 f (x) / g(x) = A / B
Теорема 1.5. Если функция h (x) заключена между двумя другими функциями f (x) и g (x) и пределы f (x) и g(x) при x → x 0 равны между собой, то предел h(x) существует и совпадает с ними. Теорема 1.6. Если функция h (x) монотонна и ограниченна на интервале, содержащем точку x 0, то она имеет в этой точке односторонние пределы (левый и правый).
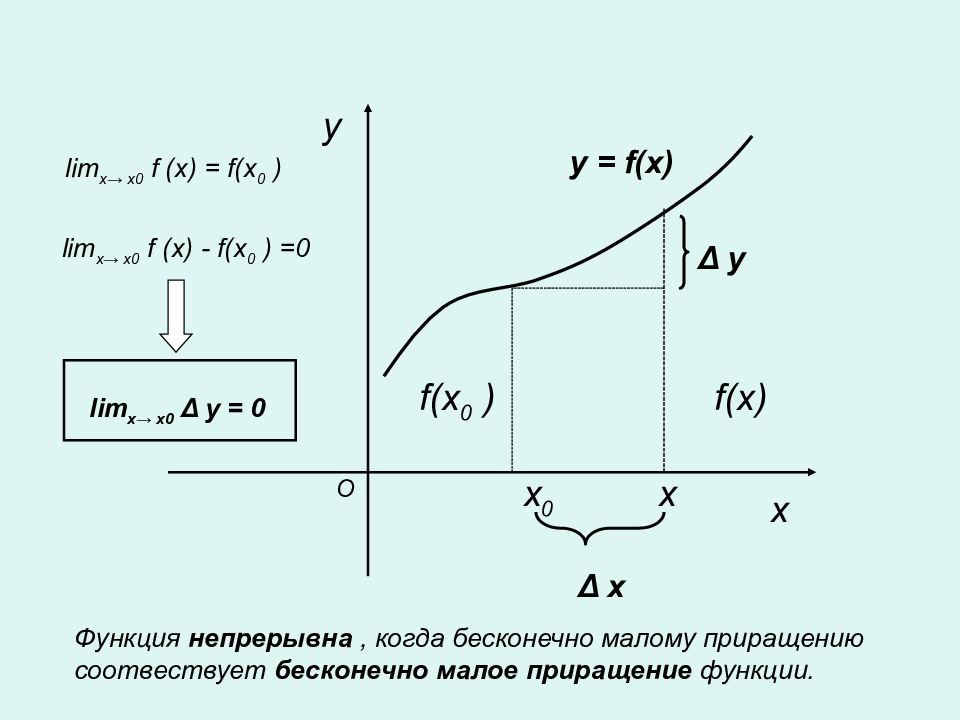
Непрерывность функций Непрерывность функции в точке Определение Пусть функция y = f(x) определена в точке x 0 и в некоторой окрестности этой точки. Функция y = f(x) называется непрерывной в точке х 0, если существует предел функции в этой точке и он равен значению функции в этой точке, т.е. lim x → х0 f (x) = f(x 0 ) 1) функция f(x) определена в точке x 0 и в её окрестности ; 2) функция f(x) имеет предел при x→ х 0 ; 3) предел функции в точке x 0 равен значению функции в этой точке.
x 0 x y f(x 0 ) y = f(x) x f(x) Δ x Δ y O lim x → х0 f (x) = f(x 0 ) lim x → х0 f (x) - f(x 0 ) =0 lim x → х0 Δ y = 0 Функция непрерывна, когда бесконечно малому приращению соотвествует бесконечно малое приращение функции.
Специальные пределы sin x x = lim x →0 1 1 2 lim x →∞ ( 1 + 1/x ) x = e lim α →0 ( 1 + α ) 1/ α = e Первый замечательный предел Второй замечательный предел 3 lim x →0 ln ( 1 + x ) = x 1 lim x →0 a x - 1 = ln a x 4
