Первый слайд презентации: Исследование фазовых равновесий
1 Исследование фазовых равновесий Фазовые переходы Физико-химический анализ Равновесие в однокомпонентных системах Равновесие в двухкомпонентных системах Фазовые диаграммы I типа Фазовые диаграммы I I типа Фазовые диаграммы I II типа Фазовые диаграммы I V типа Фазовые диаграммы V типа Фазовые диаграммы V I типа Сводная таблица типов диаграмм Равновесие в трехкомпонентных системах Методы изображения многокомпонентных систем Методы исследования фазовых равновесий ТА, ДТА, ТГ и ДТГ Исследования вязкости Исследования поверхностного натяжения Кондуктометрия
Слайд 2: Фазовые переходы
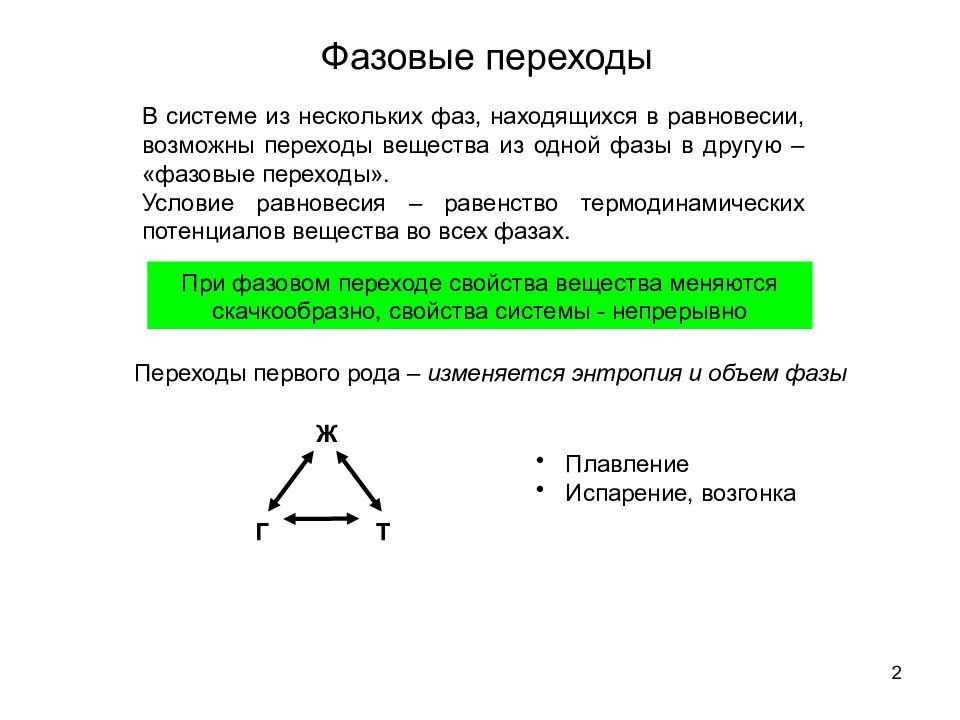
2 Фазовые переходы В системе из нескольких фаз, находящихся в равновесии, возможны переходы вещества из одной фазы в другую – «фазовые переходы». Условие равновесия – равенство термодинамических потенциалов вещества во всех фазах. При фазовом переходе свойства вещества меняются скачкообразно, свойства системы - непрерывно Переходы первого рода – изменяется энтропия и объем фазы Ж Г Т Плавление Испарение, возгонка
Слайд 3
3 Переходы второго рода – изменяется вторая производная по температуре для термодинамического потенциала, энтропии и т.п. Имеет смысл теплоемкости, сжимаемости, и т.п.
Слайд 4
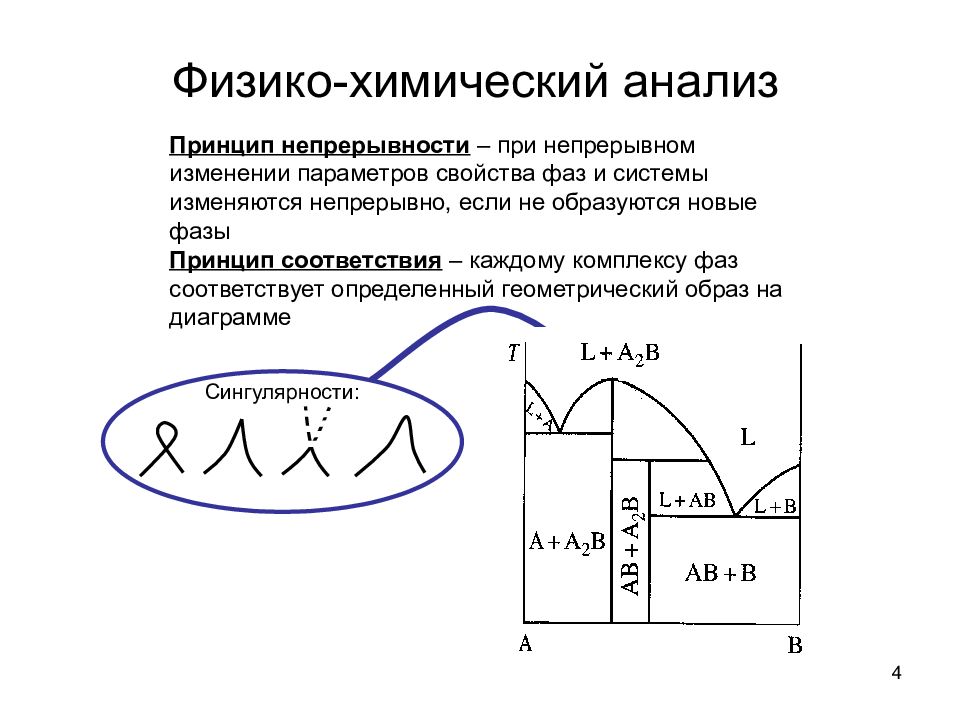
4 Физико-химический анализ Принцип непрерывности – при непрерывном изменении параметров свойства фаз и системы изменяются непрерывно, если не образуются новые фазы Принцип соответствия – каждому комплексу фаз соответствует определенный геометрический образ на диаграмме a b c Сингулярности:
Слайд 5
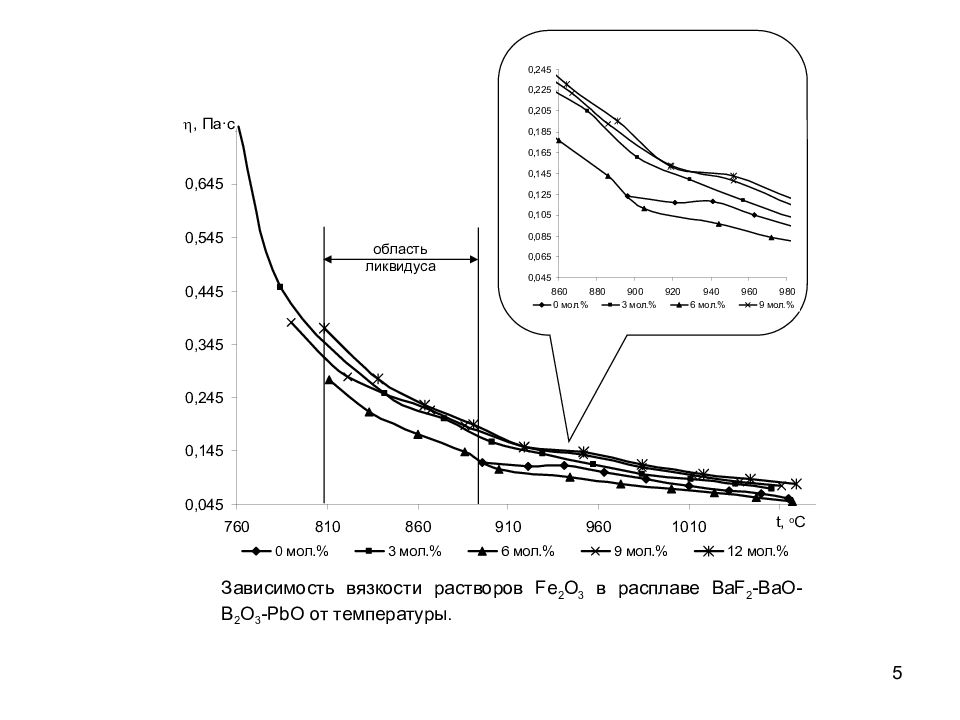
5 h, Па∙с t, o C область ликвидуса Зависимость вязкости растворов Fe 2 O 3 в расплаве BaF 2 - BaO - B 2 O 3 - PbO от температуры.
Слайд 6
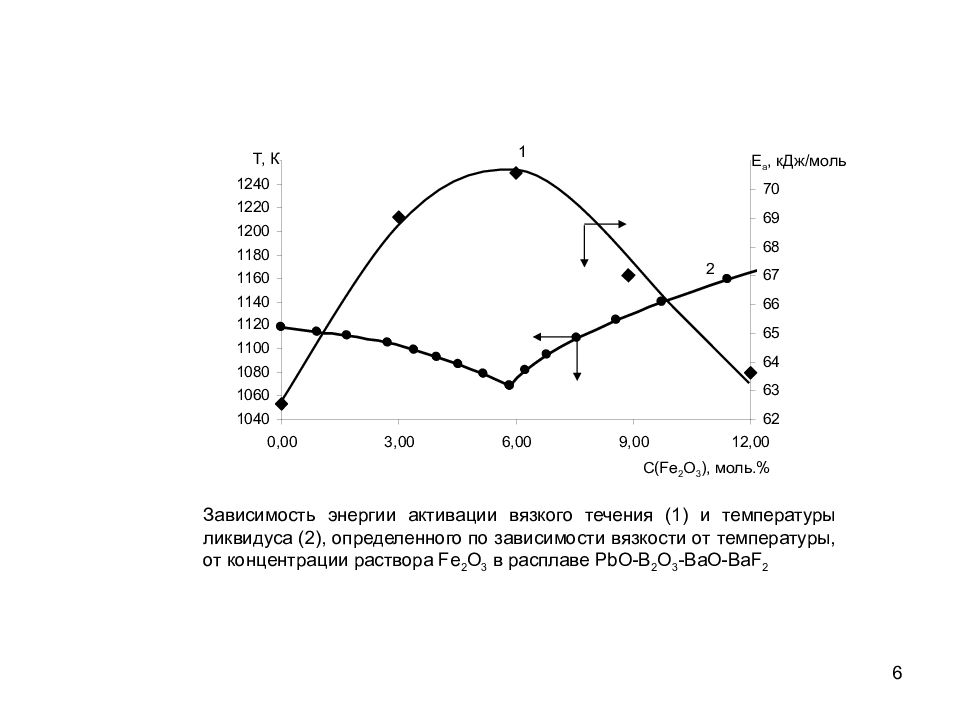
6 Т, К C(Fe 2 O 3 ), моль.% Е а, кДж/моль Зависимость энергии активации вязкого течения (1) и температуры ликвидуса (2), определенного по зависимости вязкости от температуры, от концентрации раствора Fe 2 O 3 в расплаве PbO-B 2 O 3 -BaO-BaF 2 1 2
Слайд 7
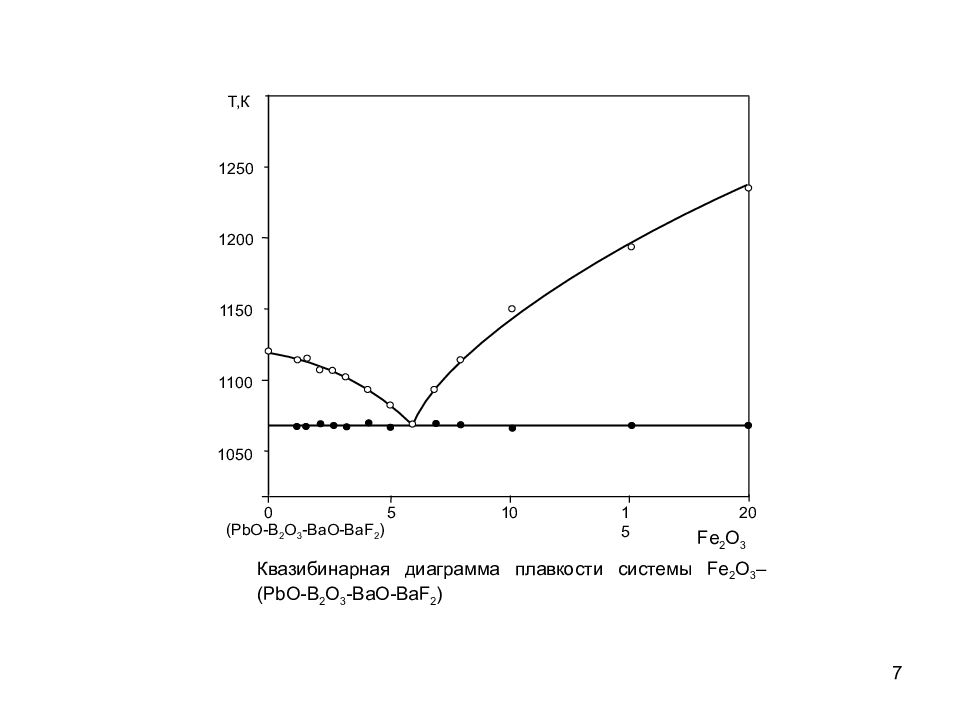
7 Квазибинарная диаграмма плавкости системы Fe 2 O 3 –(PbO-B 2 O 3 -BaO-BaF 2 ) (PbO-B 2 O 3 -BaO-BaF 2 ) 0 5 10 15 20 1100 1200 Т,К 1250 1050 1150 Fe 2 O 3
Слайд 8
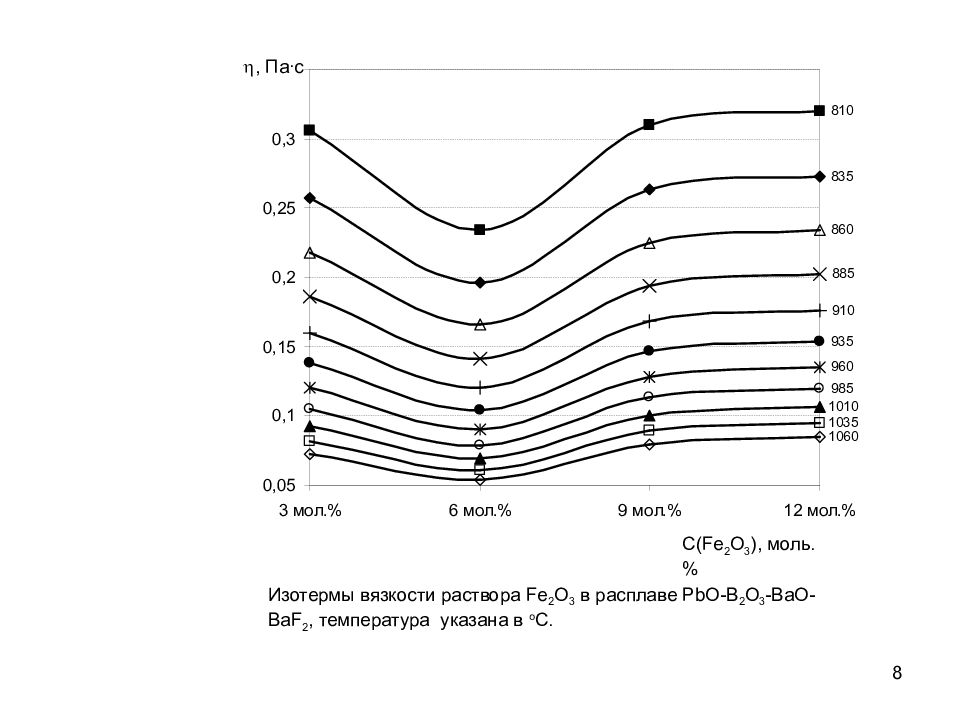
8 C(Fe 2 O 3 ), моль.% Изотермы вязкости раствора Fe 2 O 3 в расплаве PbO-B 2 O 3 -BaO-BaF 2, температура указана в о С. h, Па∙с
Слайд 9
9 -2,0 -1,5 -1,0 -0,5 0,0 0,5 1,0 1,5 2,0 7,2 7,4 7,6 7,8 8,0 8,2 8,4 8,6 1 ln 3 2 1 Звисимость логарифма удельной электропроводности от обратной температуры в расплаве ІАГ-B 2 O 3 –BaO–BaF 2 –PbO при 15 моль.% PbO: 1 – 4.27 моль.% ІАГ; 2 – 4.54 моль.% ІАГ; 3 – 4.75 моль.% ІАГ. 1/Т*10 4
Слайд 17
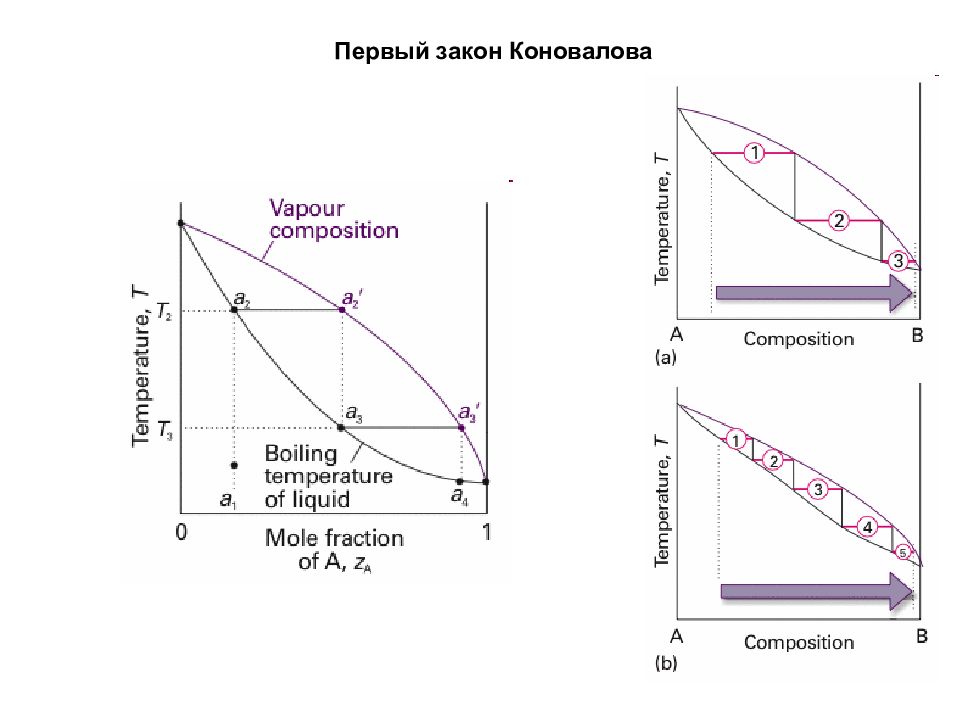
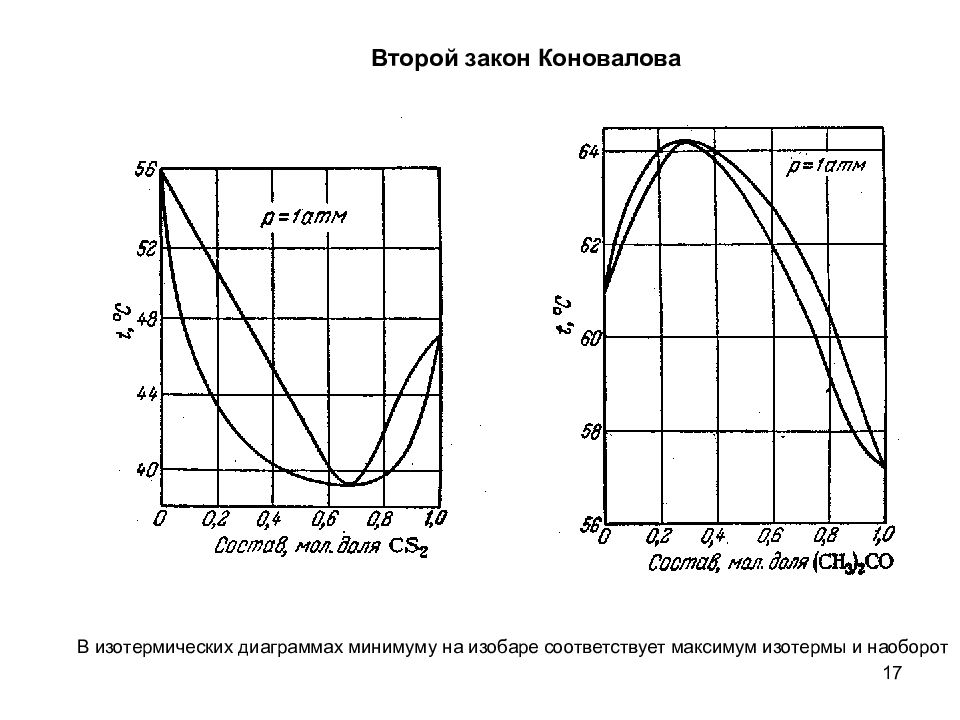
17 Второй закон Коновалова В изотермических диаграммах минимуму на изобаре соответствует максимум изотермы и наоборот
Слайд 18
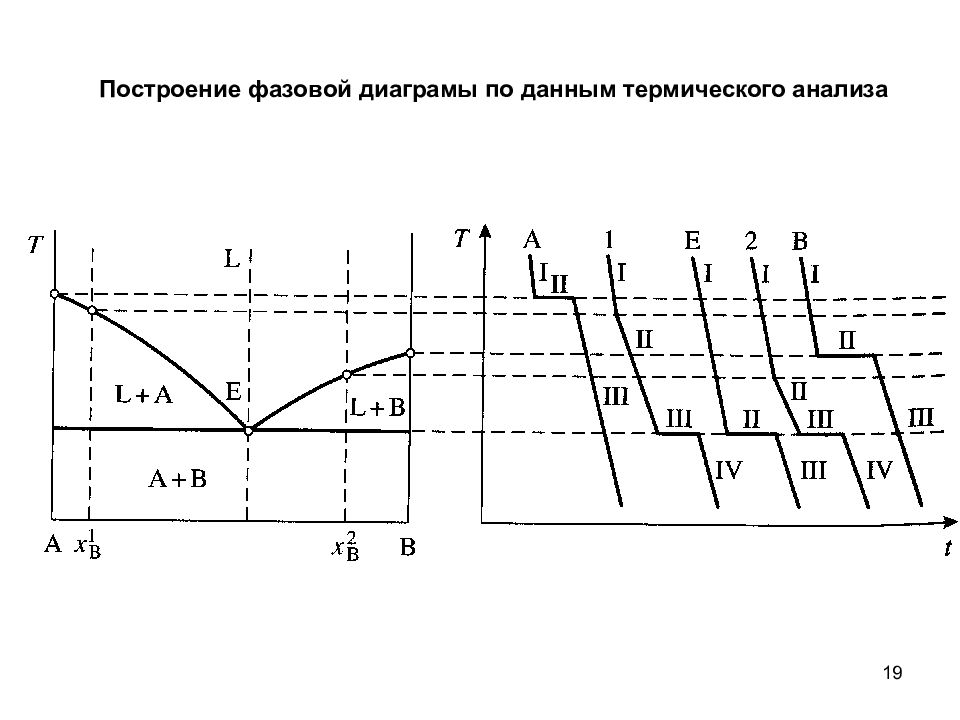
18 Фазовые диаграммы I типа При бесконечной растворимости компонентов в жидкой фазе и отсутствии растворимости в твердой Пример: Cd - Bi
Слайд 20
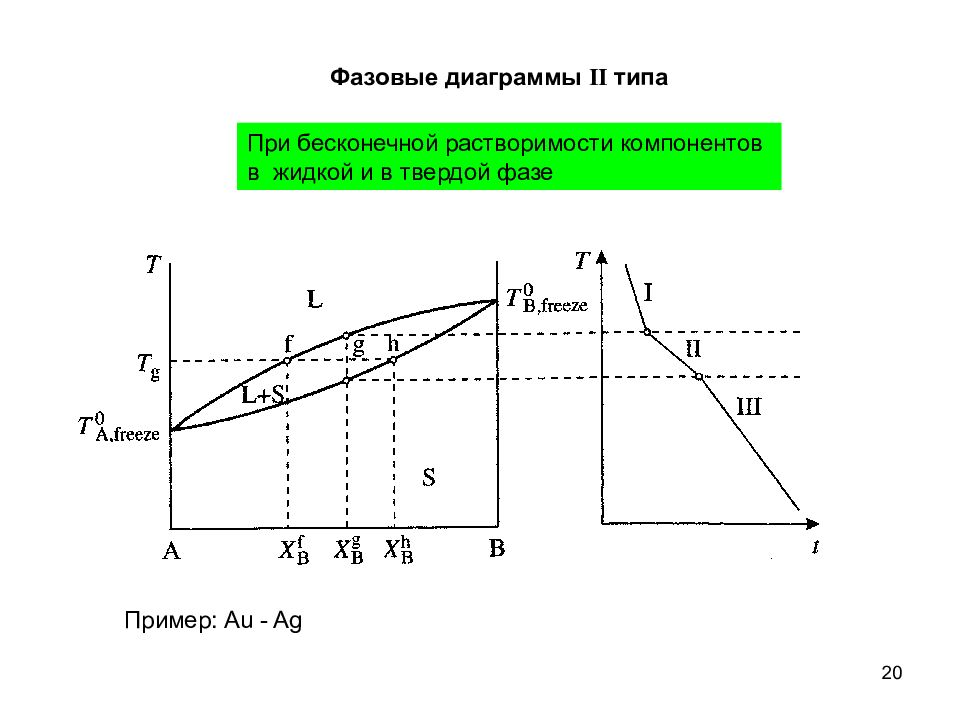
20 Фазовые диаграммы II типа При бесконечной растворимости компонентов в жидкой и в твердой фазе Пример: Au - Ag
Слайд 21
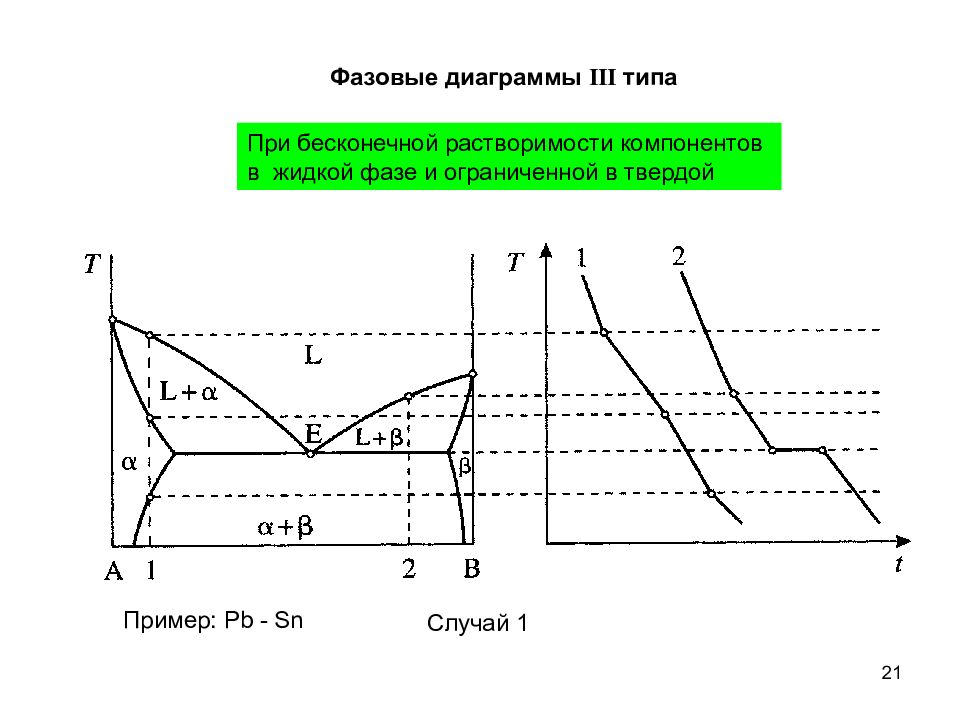
21 Фазовые диаграммы III типа При бесконечной растворимости компонентов в жидкой фазе и ограниченной в твердой Случай 1 Пример: Pb - Sn
Слайд 22
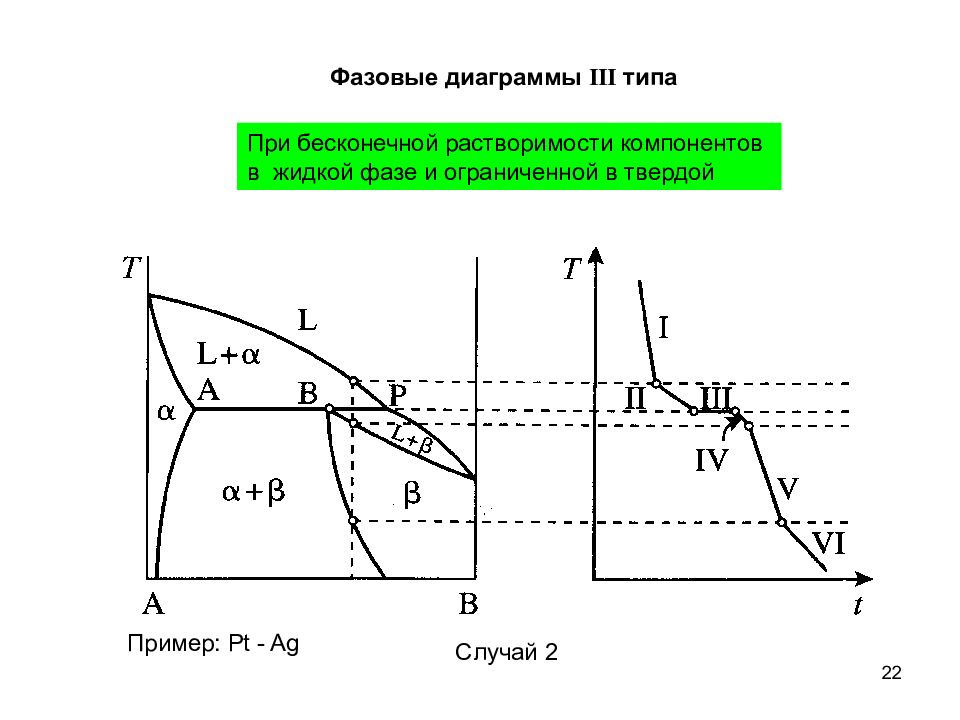
22 Фазовые диаграммы III типа При бесконечной растворимости компонентов в жидкой фазе и ограниченной в твердой Случай 2 Пример: Pt - Ag
Слайд 23
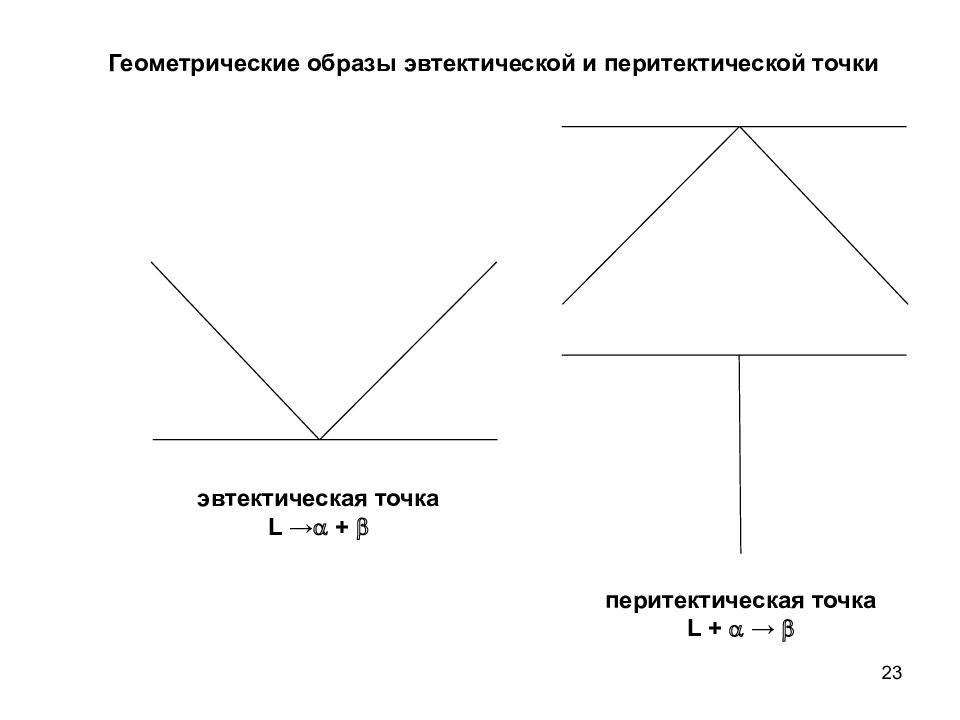
23 Геометрические образы эвтектической и перитектической точки эвтектическая точка L → + перитектическая точка L + →
Слайд 24
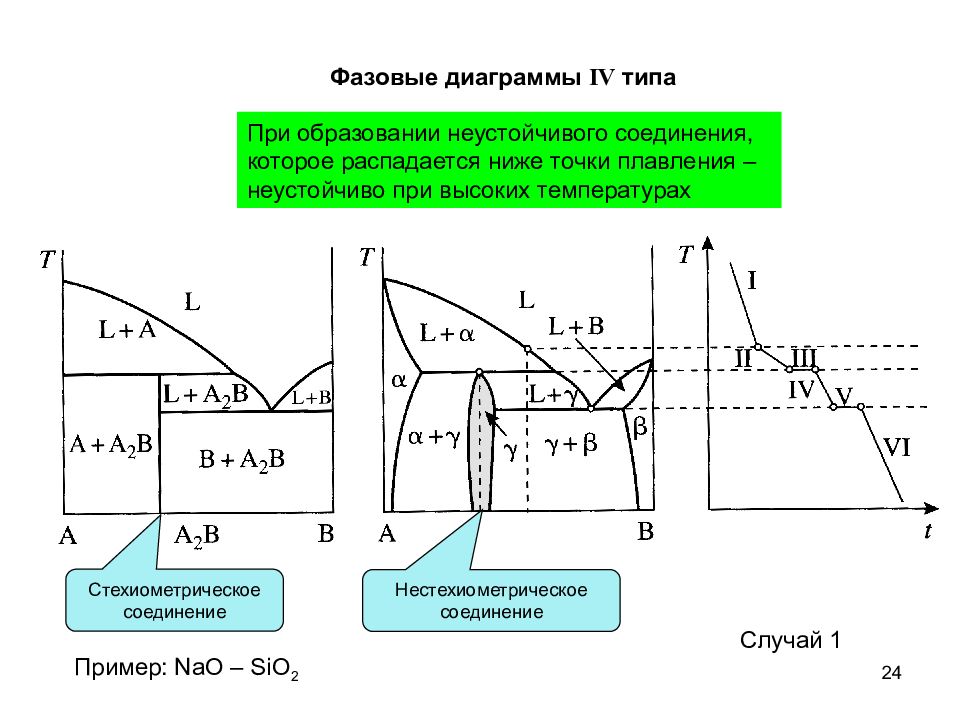
24 Фазовые диаграммы IV типа При образовании неустойчивого соединения, которое распадается ниже точки плавления – неустойчиво при высоких температурах Стехиометрическое соединение Нестехиометрическое соединение Случай 1 Пример: NaO – SiO 2
Слайд 25
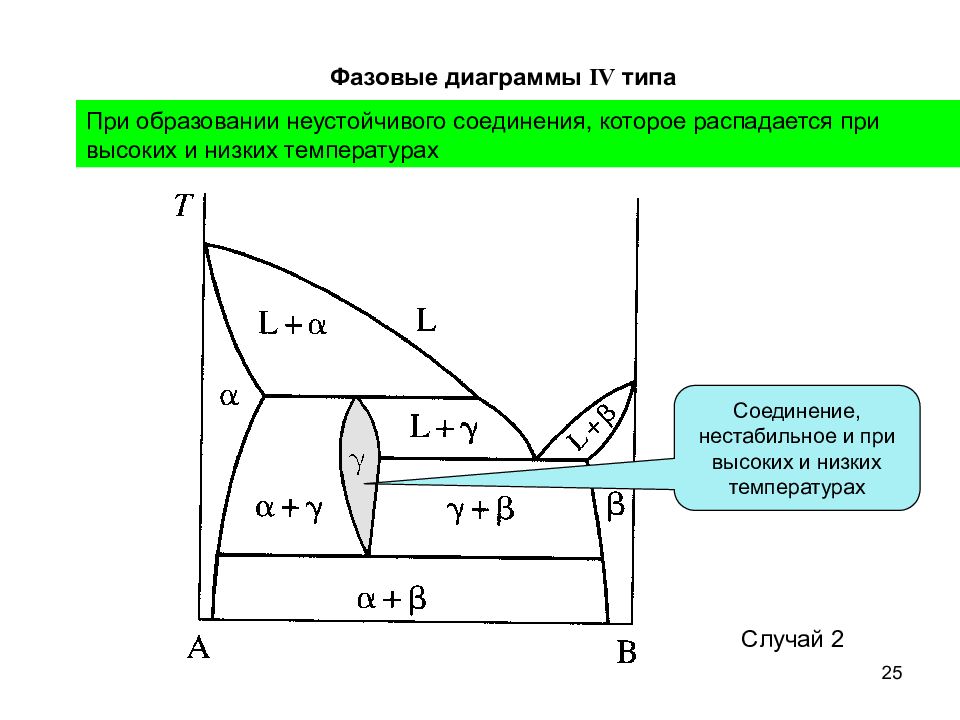
25 Фазовые диаграммы IV типа При образовании неустойчивого соединения, которое распадается при высоких и низких температурах Соединение, нестабильное и при высоких и низких температурах Случай 2
Слайд 26
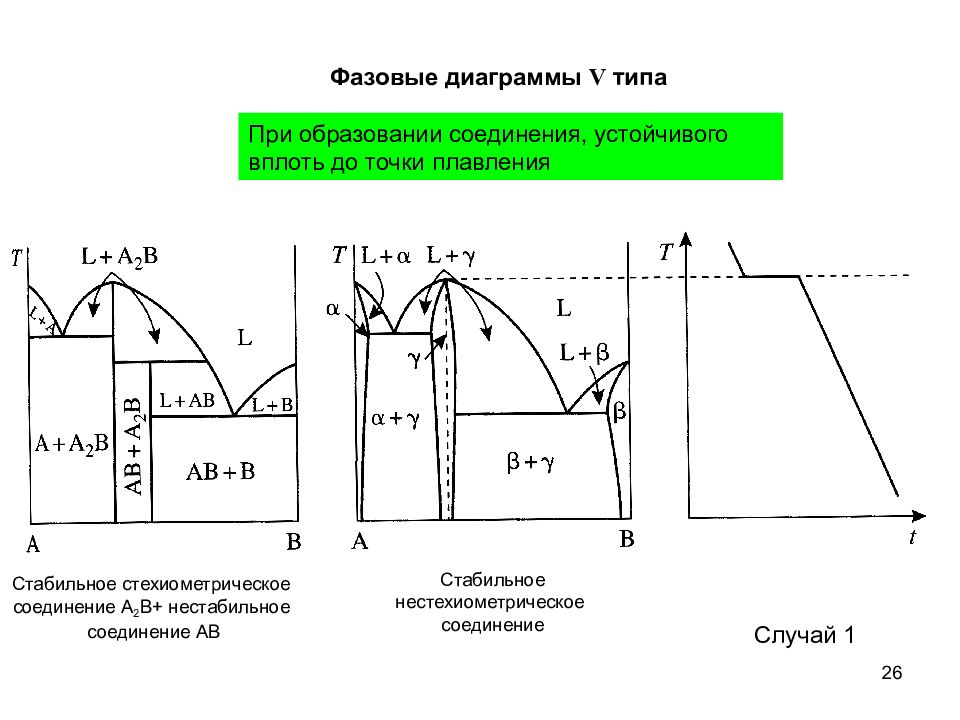
26 Фазовые диаграммы V типа При образовании соединения, устойчивого вплоть до точки плавления Стабильное стехиометрическое соединение А 2 В+ нестабильное соединение АВ Стабильное нестехиометрическое соединение Случай 1
Слайд 27
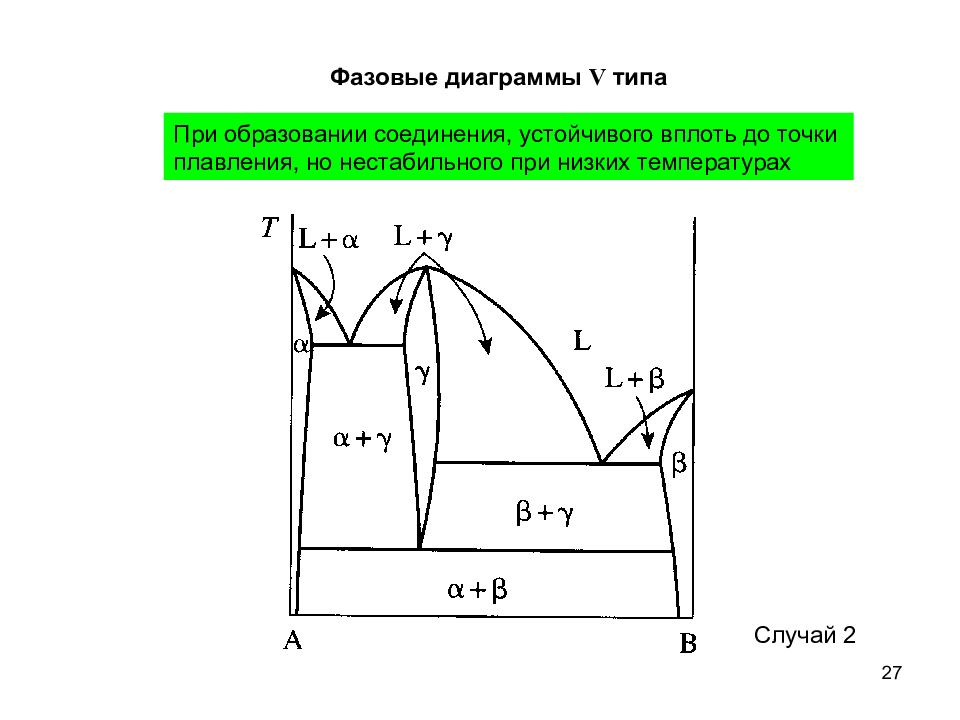
27 Случай 2 Фазовые диаграммы V типа При образовании соединения, устойчивого вплоть до точки плавления, но нестабильного при низких температурах
Слайд 28
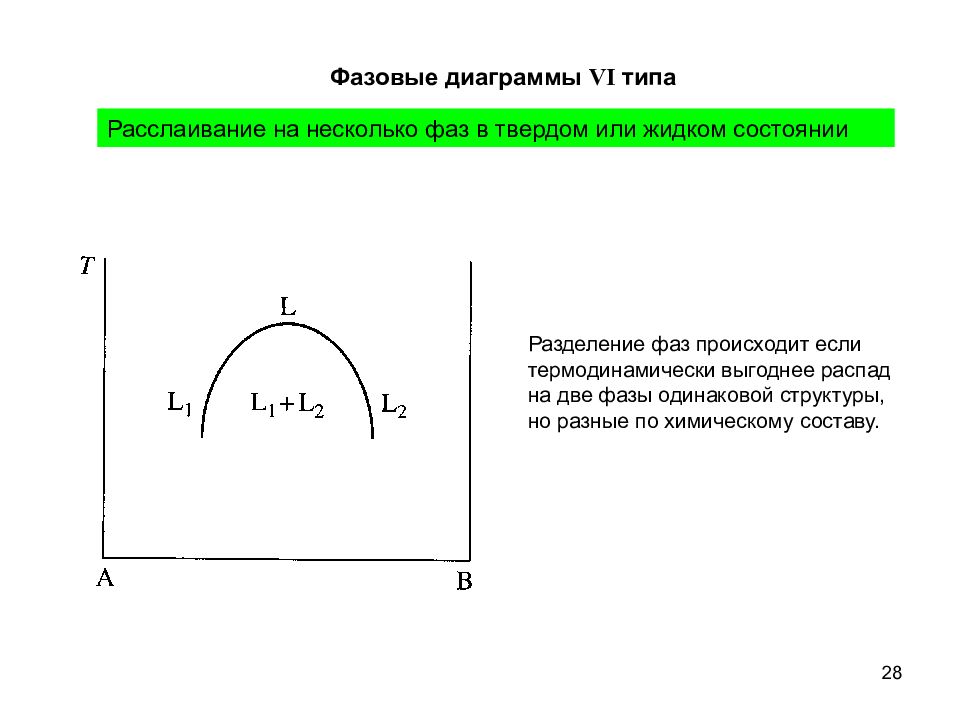
28 Фазовые диаграммы VI типа Расслаивание на несколько фаз в твердом или жидком состоянии Разделение фаз происходит если термодинамически выгоднее распад на две фазы одинаковой структуры, но разные по химическому составу.
Слайд 30
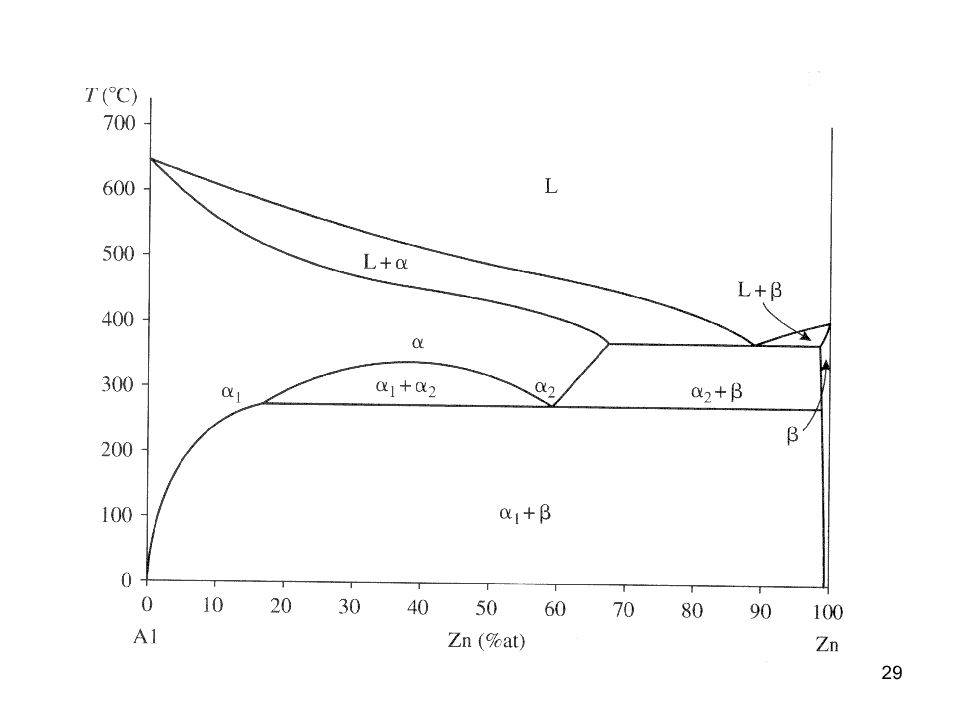
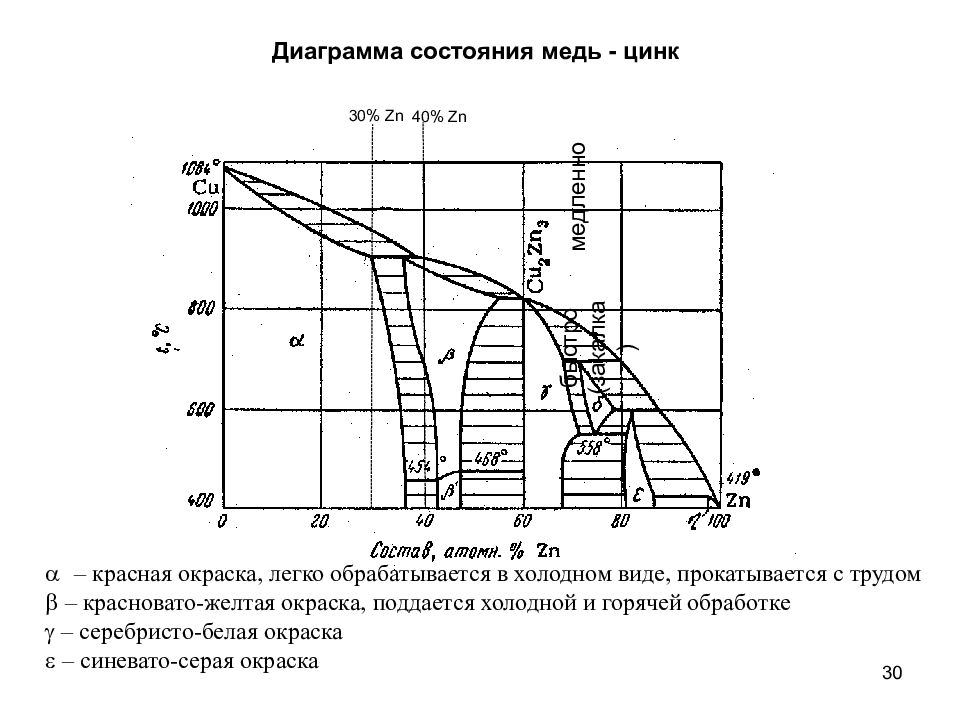
30 Диаграмма состояния медь - цинк – красная окраска, легко обрабатывается в холодном виде, прокатывается с трудом b – красновато-желтая окраска, поддается холодной и горячей обработке g – серебристо-белая окраска e – синевато-серая окраска медленно быстро (закалка) 30% Zn 40 % Zn
Слайд 31
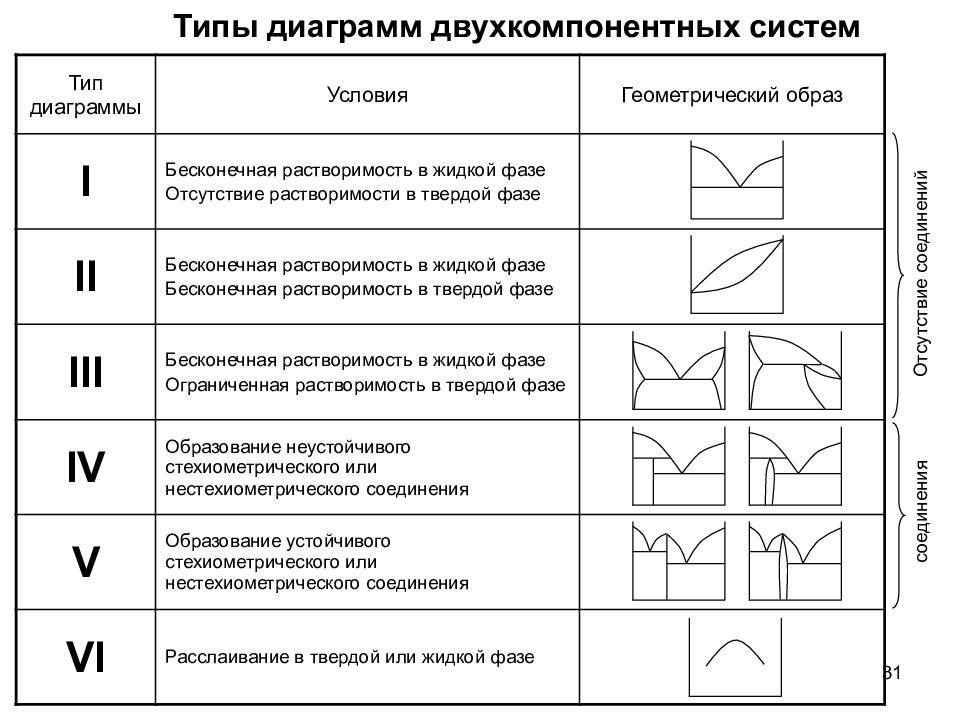
31 Тип диаграммы Условия Геометрический образ I Бесконечная растворимость в жидкой фазе Отсутствие растворимости в твердой фазе II Бесконечная растворимость в жидкой фазе Бесконечная растворимость в твердой фазе III Бесконечная растворимость в жидкой фазе Ограниченная растворимость в твердой фазе IV Образование неустойчивого стехиометрического или нестехиометрического соединения V Образование устойчивого стехиометрического или нестехиометрического соединения VI Расслаивание в твердой или жидкой фазе Типы диаграмм двухкомпонентных систем Отсутствие соединений соединения
Слайд 34
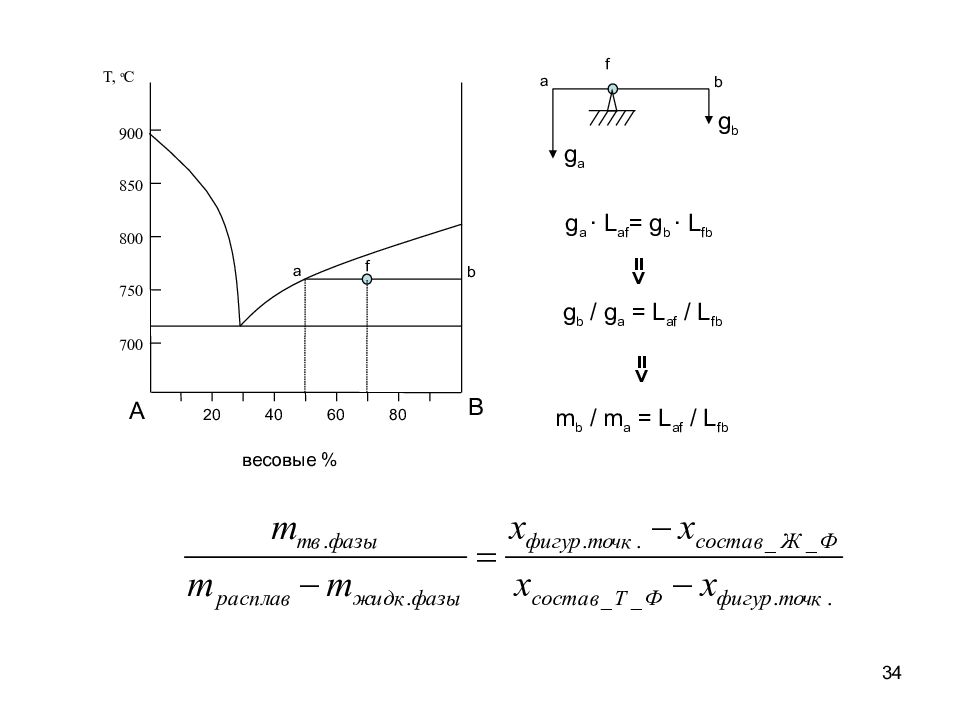
34 f 700 T, o C 750 800 850 900 A B 20 40 60 80 a b весовые % a b f g a g b g a ∙ L af = g b ∙ L fb g b / g a = L af / L fb => => m b / m a = L af / L fb
Слайд 35
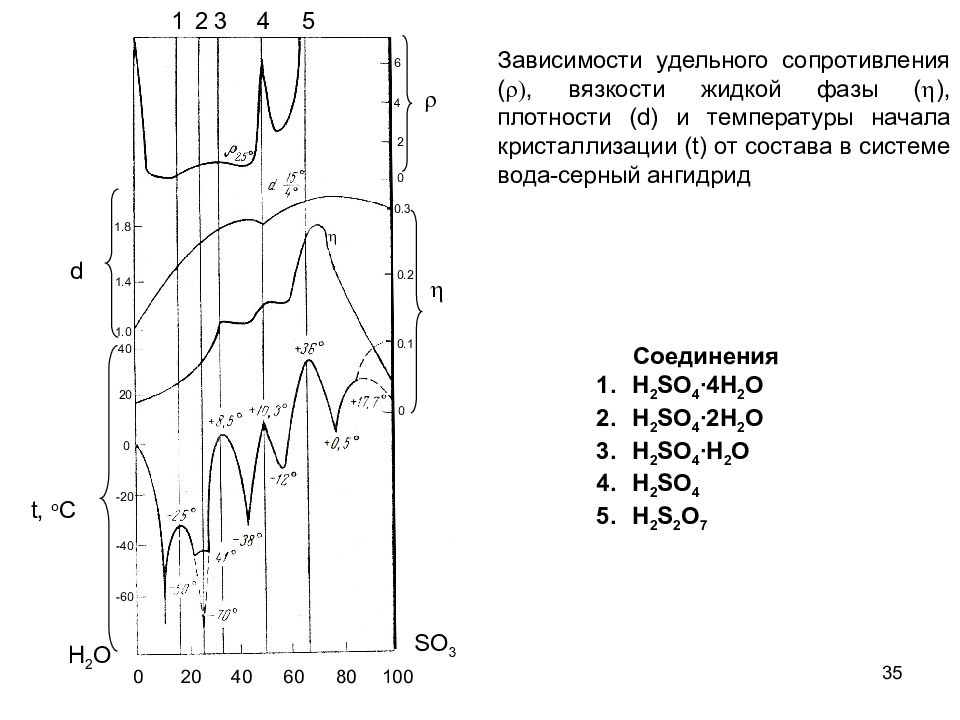
35 Соединения H 2 SO 4 ∙4H 2 O H 2 SO 4 ∙2H 2 O H 2 SO 4 ∙H 2 O H 2 SO 4 H 2 S 2 O 7 Зависимости удельного сопротивления ( r ), вязкости жидкой фазы ( h ), плотности (d) и температуры начала кристаллизации (t) от состава в системе вода-серный ангидрид r h d t, o C 0 20 40 60 80 100 H 2 O SO 3 1 2 3 4 5 1.8 1.4 1.0 40 20 0 -20 -40 -60 6 4 2 0 h 0 0.1 0.2 0.3
Слайд 38
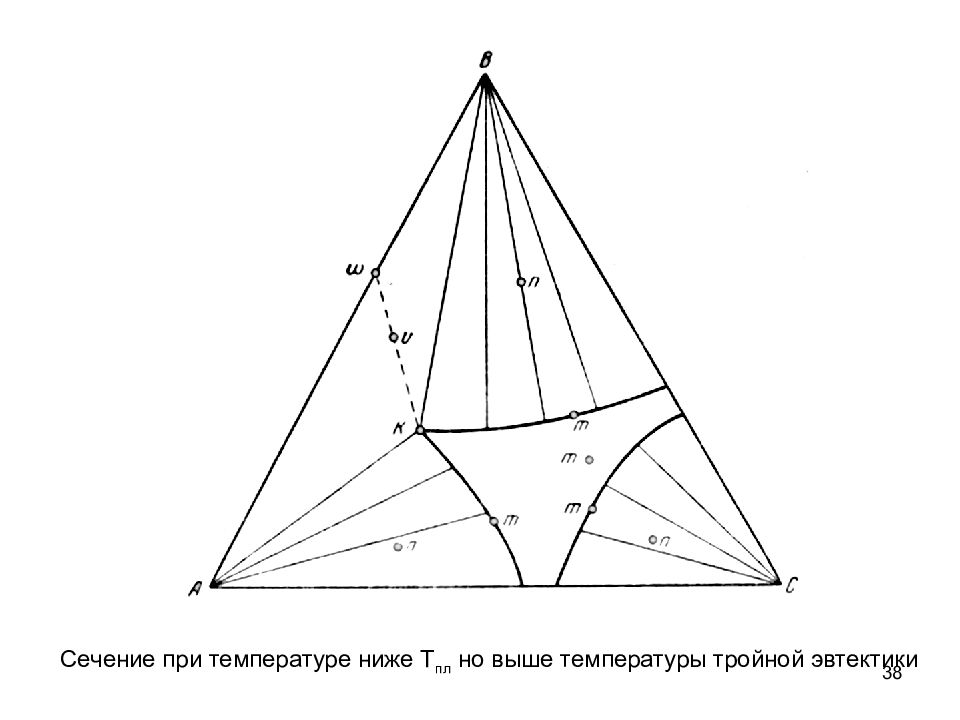
38 C ечение при температуре ниже Т пл но выше температуры тройной эвтектики
Слайд 39
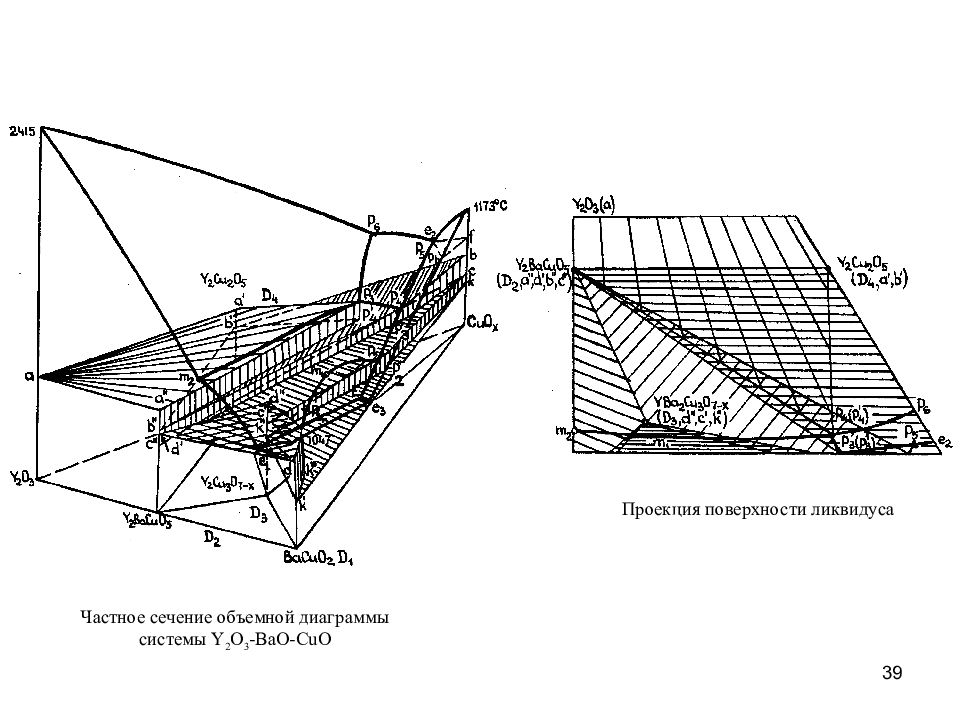
39 Частное сечение объемной диаграммы системы Y 2 O 3 -BaO-CuO Проекция поверхности ликвидуса
Слайд 40
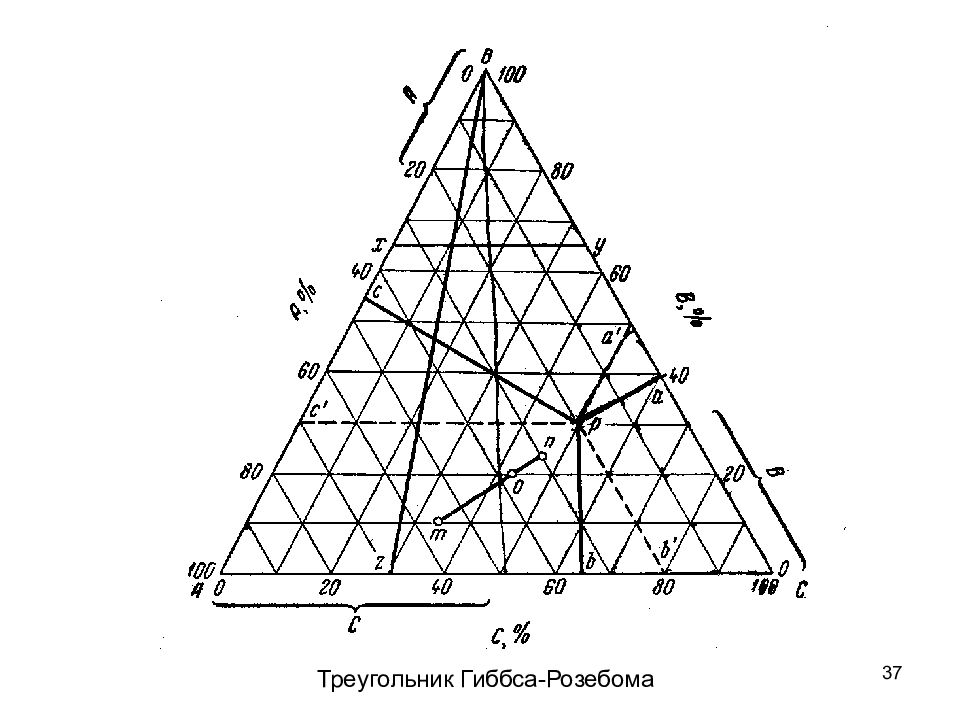
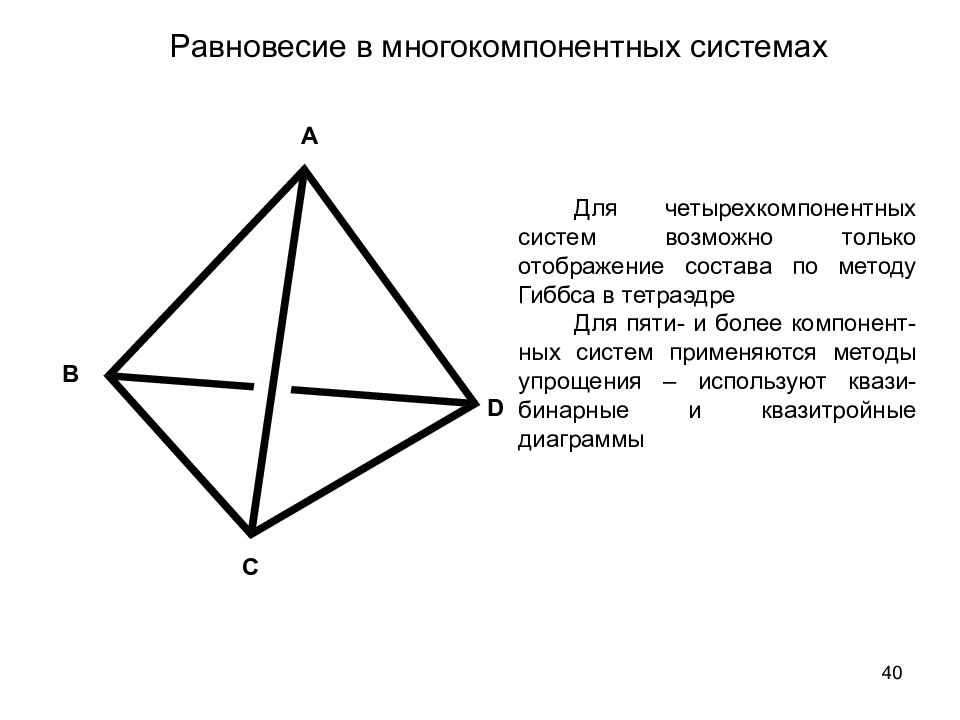
40 Равновесие в многокомпонентных системах A B C D Для четырехкомпонентных систем возможно только отображение состава по методу Гиббса в тетраэдре Для пяти- и более компонент-ных систем применяются методы упрощения – используют квази-бинарные и квазитройные диаграммы
Слайд 41
41 Квазибинарная диаграмма плавкости системы Fe 2 O 3 –(PbO-B 2 O 3 -BaO-BaF 2 ) (PbO-B 2 O 3 -BaO-BaF 2 ) 0 5 10 15 20 1100 1200 Т,К 1250 1050 1150 Fe 2 O 3
Слайд 42
42 Методы исследования фазовых равновесий Термический и дифференциальный термический анализ Термогравиметрический анализ Исследования зависимостей состав - свойство вязкость поверхностное натяжение плотность электропроводность спектральные и акустические методы анализа
Слайд 43
43 механические – плотность, вязкость; поверхностные – поверхностное натяжение; оптические – показатель преломления; спектральные – оптическая плотность или интегральная интенсивность полос поглощения в различных областях спектра (ИК, видимая, УФ), поглощение в области радиочастот (резонансная спектроскопия); акустические – скорость распространения звука (адиабатическая сжимаемость); тепловые – теплоты смешения, теплопроводность; электрические и магнитные – электропроводность, доли переноса тока, электропотенциалы, магнитная восприимчивость, диэлектрическая проницаемость. все физико-химические свойства разделить на 3 группы: свойства смеси аддитивно слагаются из свойств компонентов (при определенном способе выражения состава); cвойства смеси в более или менее явной форме рассчитываются, исходя из свойств компонентов; свойства смеси не находятся в какой-либо связи с величинами свойств компонентов, либо свойство имеет физический смысл лишь в применении к смеси, но не к отдельному компоненту. К первой группе относятся: плотность, показательное преломление, оптическая плотность, магнитная восприимчивость и др. Ко второй группе относятся: вязкость, диэлектрическая проницаемость. К третьей группе относятся: электропроводность, теплота смешения.
Слайд 44
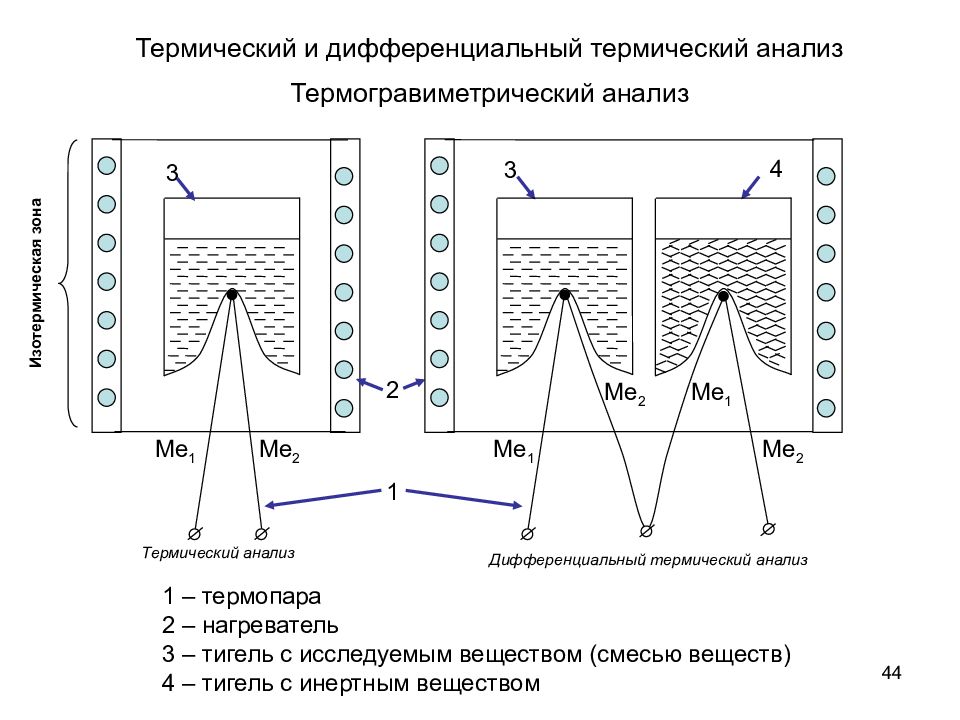
44 Термический и дифференциальный термический анализ Термогравиметрический анализ Ме 1 Ме 2 Термический анализ Ме 1 Ме 2 Изотермическая зона Дифференциальный термический анализ 1 2 3 3 4 1 – термопара 2 – нагреватель 3 – тигель с исследуемым веществом (смесью веществ) 4 – тигель с инертным веществом Ме 2 Ме 1
Слайд 45
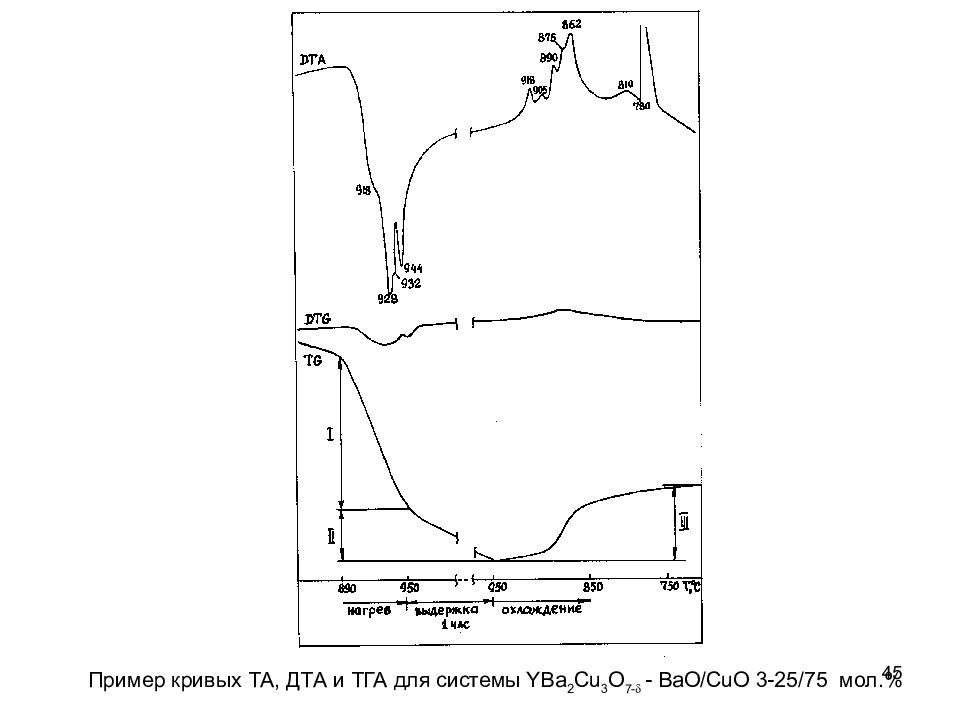
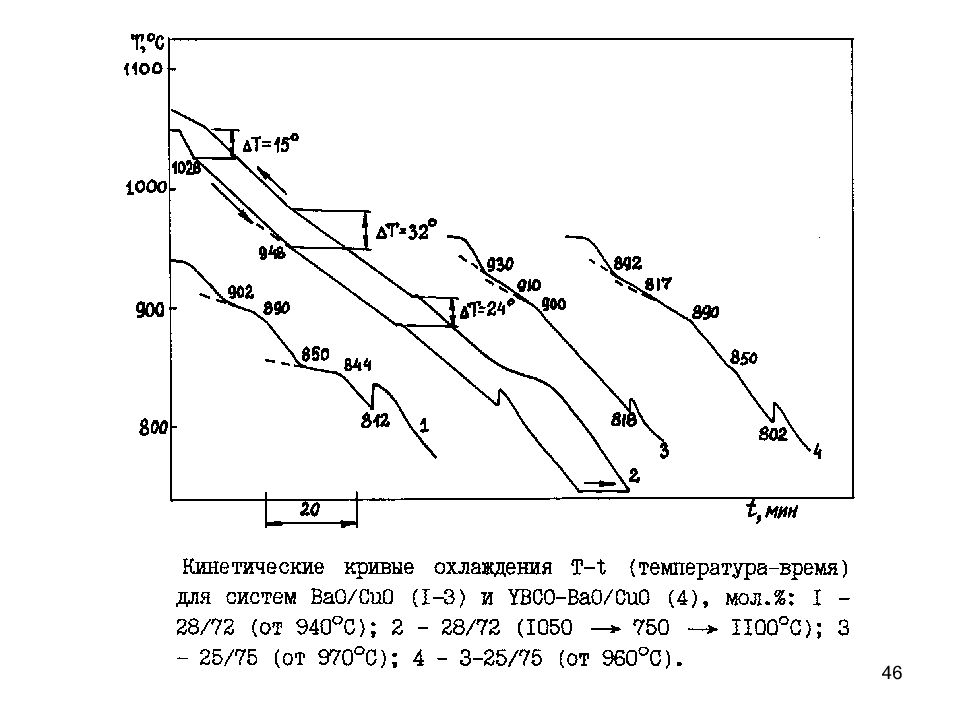
45 Пример кривых ТА, ДТА и ТГА для системы YB a 2 C u 3 O 7- d - BaO/CuO 3-25/75 мол.%
Слайд 47
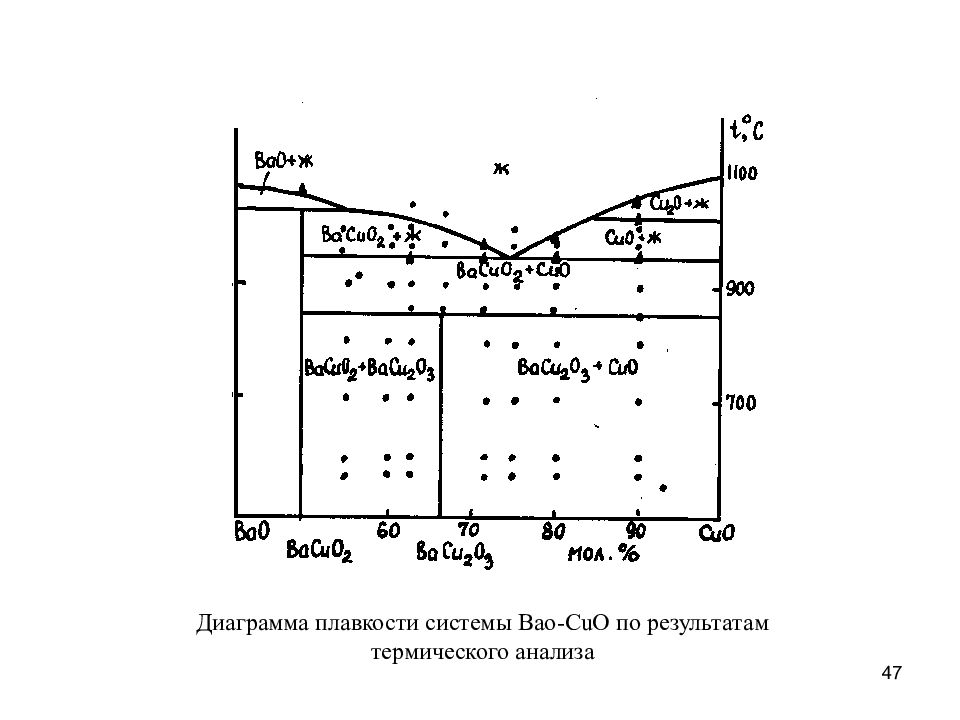
47 Диаграмма плавкости системы Bao-CuO по результатам термического анализа
Слайд 48
48 Исследования вязкости Вязкость – свойство жидкости или газа оказывать сопротивление перемещению одной части относительно другой при сдвиге, растяжениии других деформациях Если в жидкости существует поле скоростей, причем скорость w каждого объема направлена параллельно оси х, то на площадку ds, перпендикулярную оси z действует вязкая сила dF, действующая со стороны жидкости: , где h – динамическая вязкость Динамическая вязкость определяет характер течения в стационарных условиях (скорость в каждой точке пространства не зависит от времени). В нестационарных условиях течение определяется кинематической вязкостью n = h/r
Слайд 49
49 Методы измерения вязкости жидкостей основаны на регистрации в процессе измерения параметров, функционально связанных с вязкостью. Связь между параметрами и динамической или кинематической вязкостью обосновывается в математических теориях методов. При выводе расчетных формул принимают следующие положения: скольжение на поверхности соприкосновения жидкость - твердое тело плотность отсутствует, т. е. имеет место полное смачивание; движение жидкости с достаточной степенью точности описывается уравнением Навье-Стокса для несжимаемой жидкости; система рассматривается при стационарном, размерном движении жидкости или твердого тела в жидкости.
Слайд 50
50 МЕТОДЫ ИЗМЕРЕНИЯ ВЯЗКОСТИ Методы измерения вязкости делятся на стационарные капиллярного истечения падающего тела ротационные (вращающихся цилиндров) метод стационарных колебаний ( вибрационный); нестационарные основанные на наблюдениях крутильных колебаний основанные на наблюдениях продольных колебаний
Слайд 51
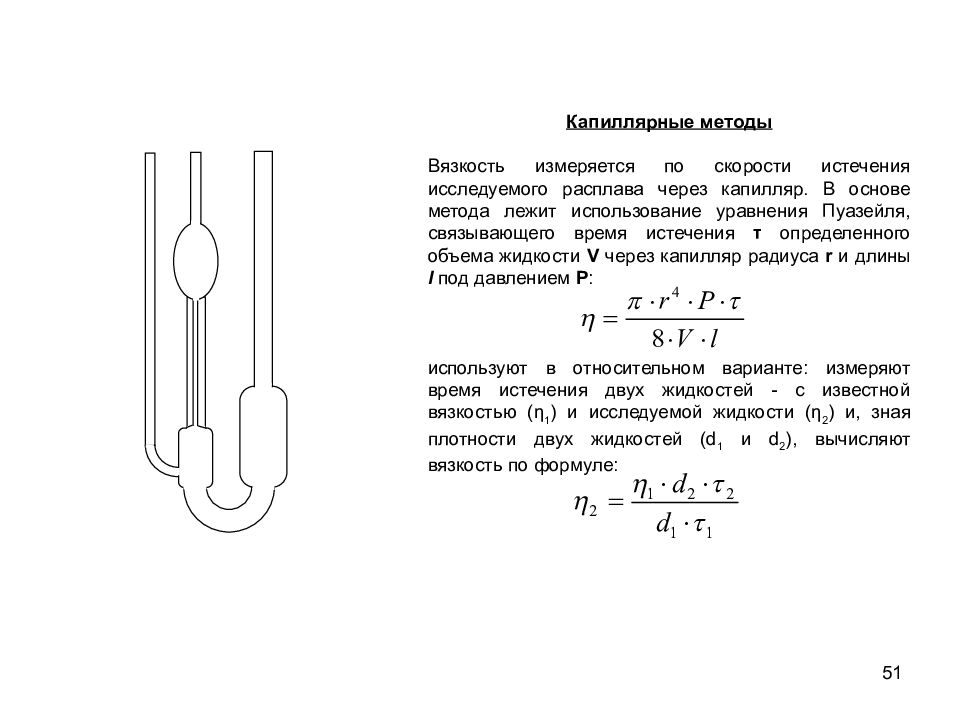
51 Капиллярные методы Вязкость измеряется по скорости истечения исследуемого расплава через капилляр. В основе метода лежит использование уравнения Пуазейля, связывающего время истечения τ определенного объема жидкости V через капилляр радиуса r и длины l под давлением Р : используют в относительном варианте: измеряют время истечения двух жидкостей - с известной вязкостью (η 1 ) и исследуемой жидкости (η 2 ) и, зная плотности двух жидкостей (d 1 и d 2 ), вычисляют вязкость по формуле:
Слайд 52
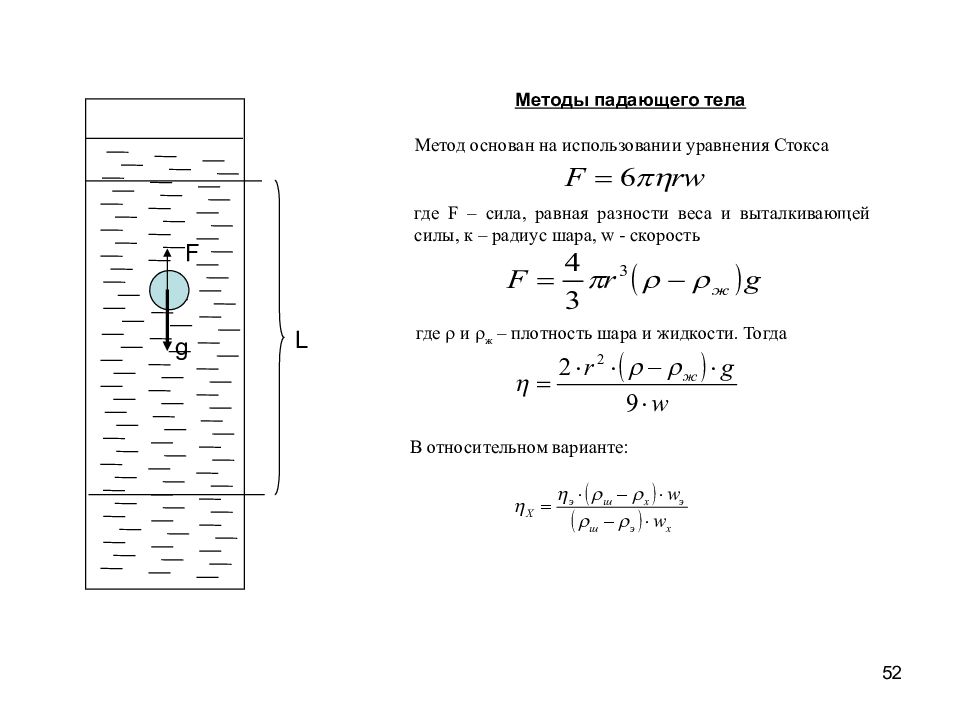
52 Методы падающего тела Метод основан на использовании уравнения Стокса g F L где F – сила, равная разности веса и выталкивающей силы, к – радиус шара, w - скорость где r и r ж – плотность шара и жидкости. Тогда В относительном варианте:
Слайд 53
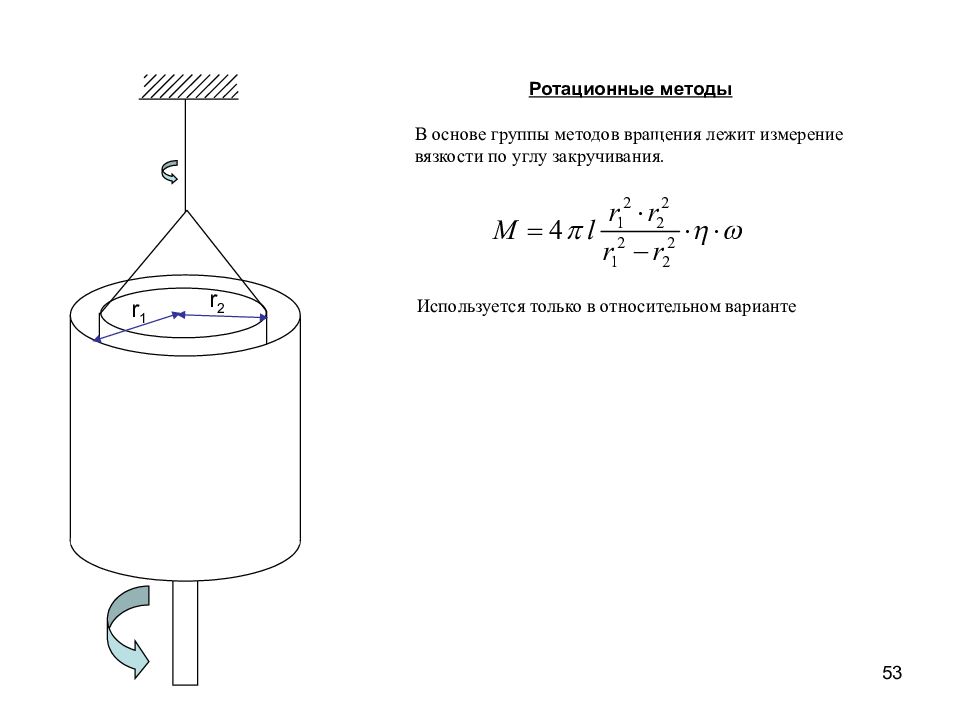
53 Ротационные методы В основе группы методов вращения лежит измерение вязкости по углу закручивания. r 2 r 1 Используется только в относительном варианте
Слайд 54
54 Осцилляционные методы Вязкость определяется по затуханию колебаний жесткой системы погруженной в жидкость или содержащей в себе жидкость метод крутильных колебаний помещенному в расплав телу вращения, подвешенному на упругой нити, придаются крутильные колебания. Силы вязкого трения расплава тормозят вращение маятника, период и амплитуда затухающих колебаний зависят от вязкости и плотности исследуемого расплава. Амплитуда колебаний А описывается уравнением: где t — время измерения, τ — период полного колебания, δ — логарифмический декремент затухания, А 0 — константа прибора 3 1 2 6 4 5 Схема установки для измерения вязкости расплава по вибрационному методу: 1-раствор-расплав; 2-платиновый датчик; 3-держатель датчика (алундовый шток); 4-пружина; 5-массивная площадка; 6-магниты; 7-индукционная катушка. 7 вибрационный метод
Слайд 55
55 Методы стационарных колебаний Вязкость определяется по резонансной амплитуде или сдвигу фаз колебаний жесткой системы погруженной в жидкость Для вязких жидкостей Определяют частоту вынужденных колебаний, при которой сдвиг фаз между силой и смещением равен p /2. Тогда Для маловязких жидкостей Определяют частоту, при которой амплитуда максимальна, тогда
Слайд 56
56 ТЕМПЕРАТУРНАЯ ЗАВИСИМОСТЬ ВЯЗКОСТИ В соответствии с активационной моделью жидкости, развитой Френкелем, вязкость выражается формулой Время релаксации можно представить как время связи атома (иона) с данным положением равновесия в квазирешетке. В этом случае вероятность преодоления потенциального барьера любым атомом (ионом) будет пропорциональна величине Поскольку время пребывания частицы жидкости около данного положения равновесия обратно пропорционально вероятности его перехода в новое положение равновесия, то где G — модуль сдвига, τ — время релаксации. Это уравнение позволяет определить Е h :
Слайд 57
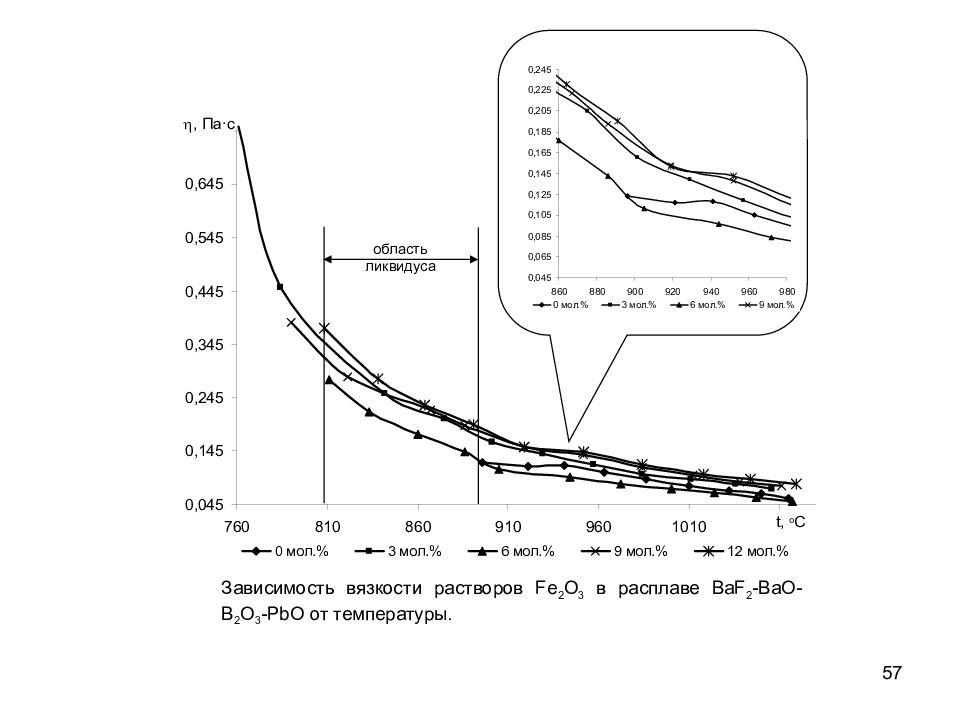
57 h, Па∙с t, o C область ликвидуса Зависимость вязкости растворов Fe 2 O 3 в расплаве BaF 2 - BaO - B 2 O 3 - PbO от температуры.
Слайд 58
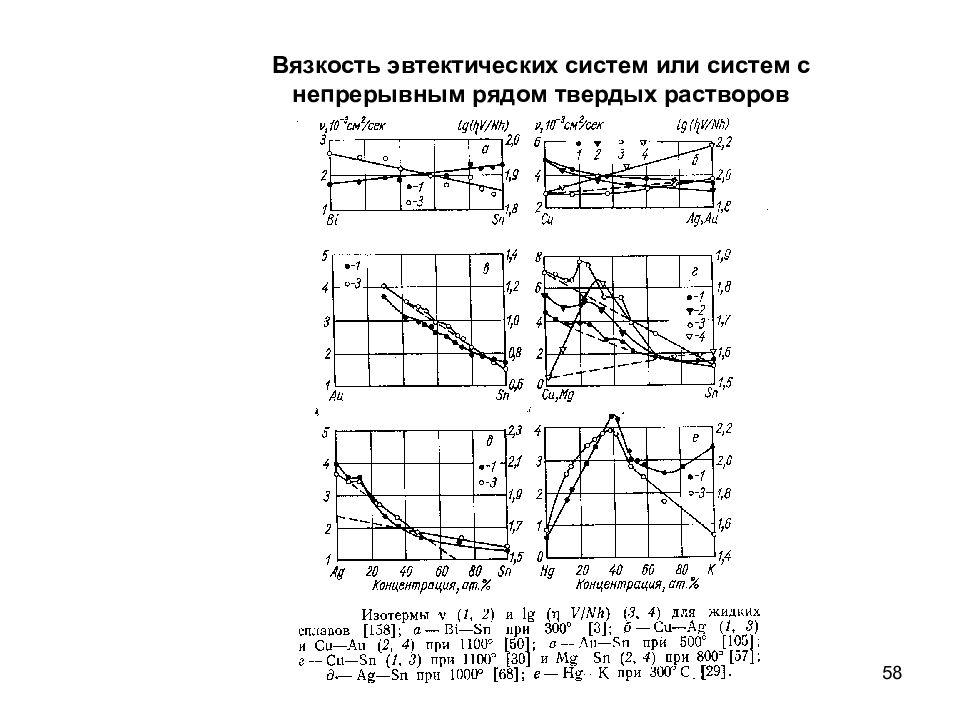
58 Вязкость эвтектических систем или систем с непрерывным рядом твердых растворов
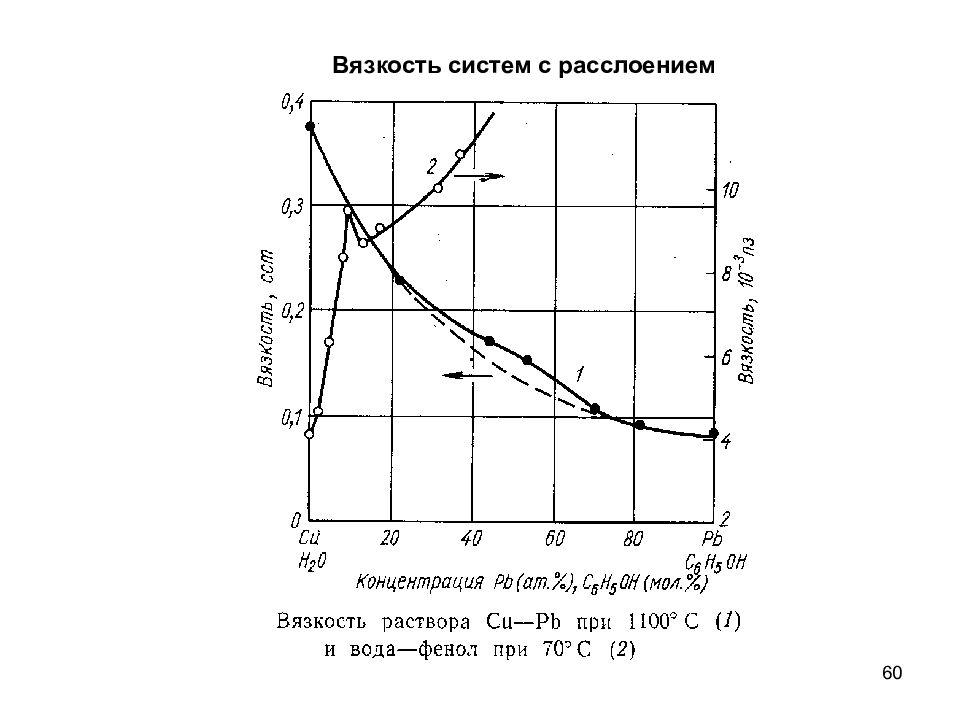
Слайд 61
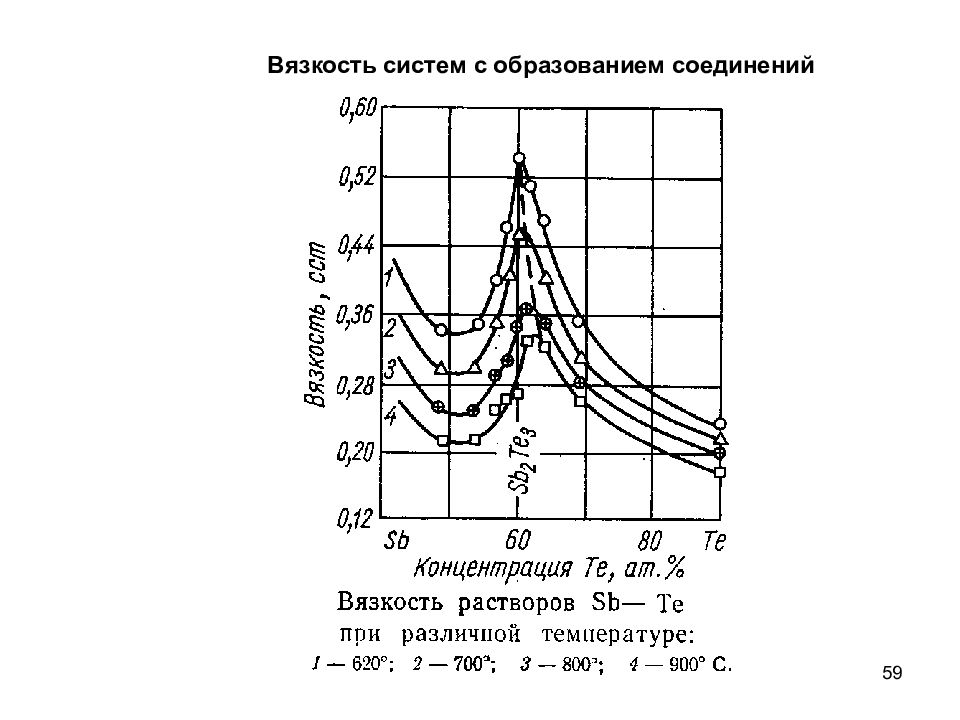
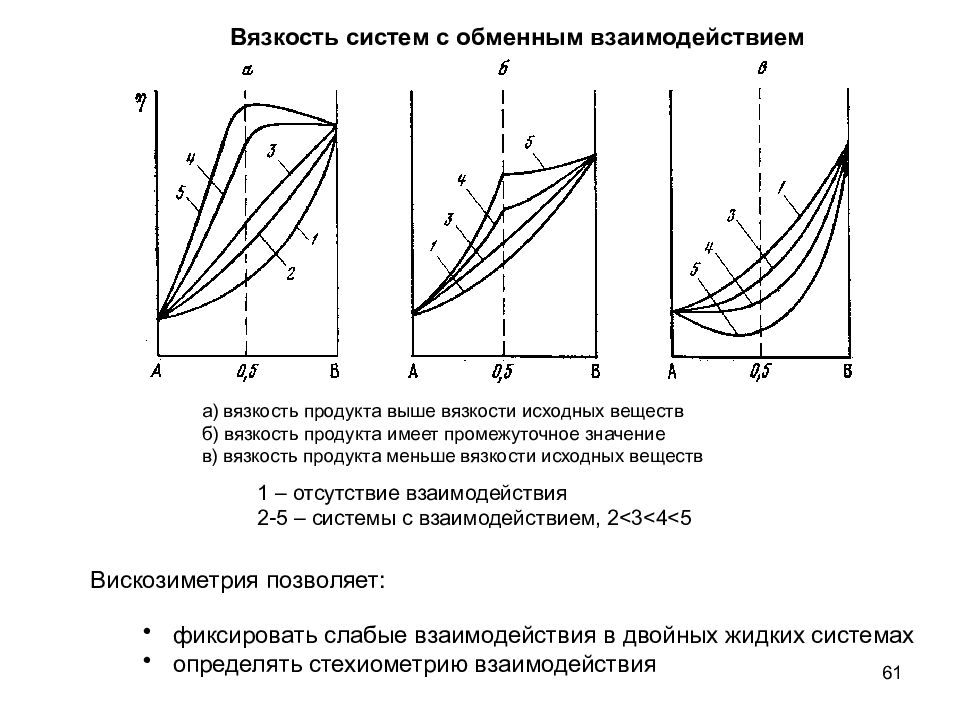
61 Вязкость систем с обменным взаимодействием а) вязкость продукта выше вязкости исходных веществ б) вязкость продукта имеет промежуточное значение в) вязкость продукта меньше вязкости исходных веществ 1 – отсутствие взаимодействия 2-5 – системы с взаимодействием, 2<3<4<5 фиксировать слабые взаимодействия в двойных жидких системах определять стехиометрию взаимодействия Вискозиметрия позволяет :
Слайд 62: Плотность
62 Плотность Скалярная физическая величина, которая определяется как отношение массы тела к занимаемому этим телом объёму. Исходя из определения плотности, её размерность кг/м³ и г/см³. Плотность находится по формуле:
Слайд 63
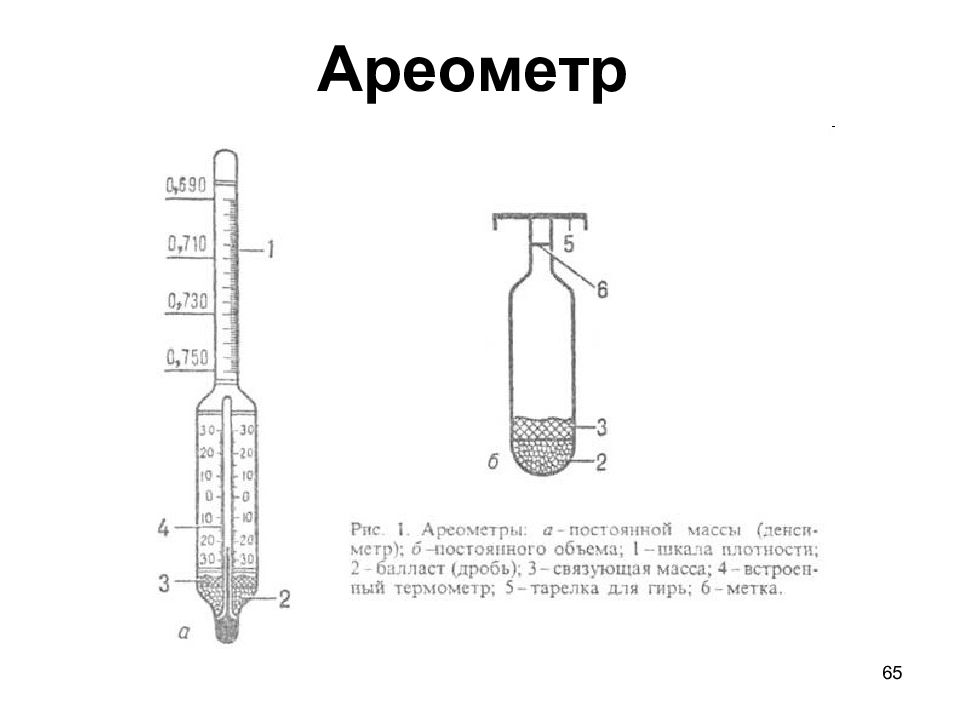
63 Приборы для измерения плотности жидкостей: Пикнометр – прибор для измерения истинной плотности. Ареометр (денсиметр, плотномер) – измеритель плотности жидкостей. Поплавковые плотномеры Массовые плотномеры Гидростатические плотномеры Радиоизотопные плотномеры Вибрационные плотномеры Ультразвуковые плотномеры Методы измерения плотности твердых тел: Гидростатическое взвешивание волюметрия
Слайд 66: Поплавковые приборы
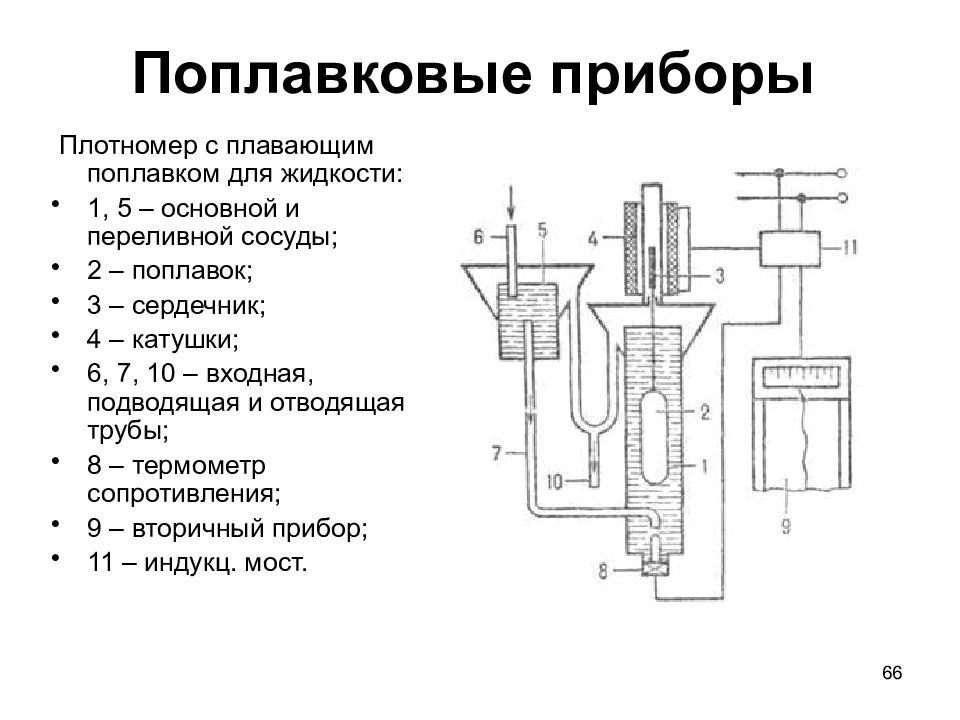
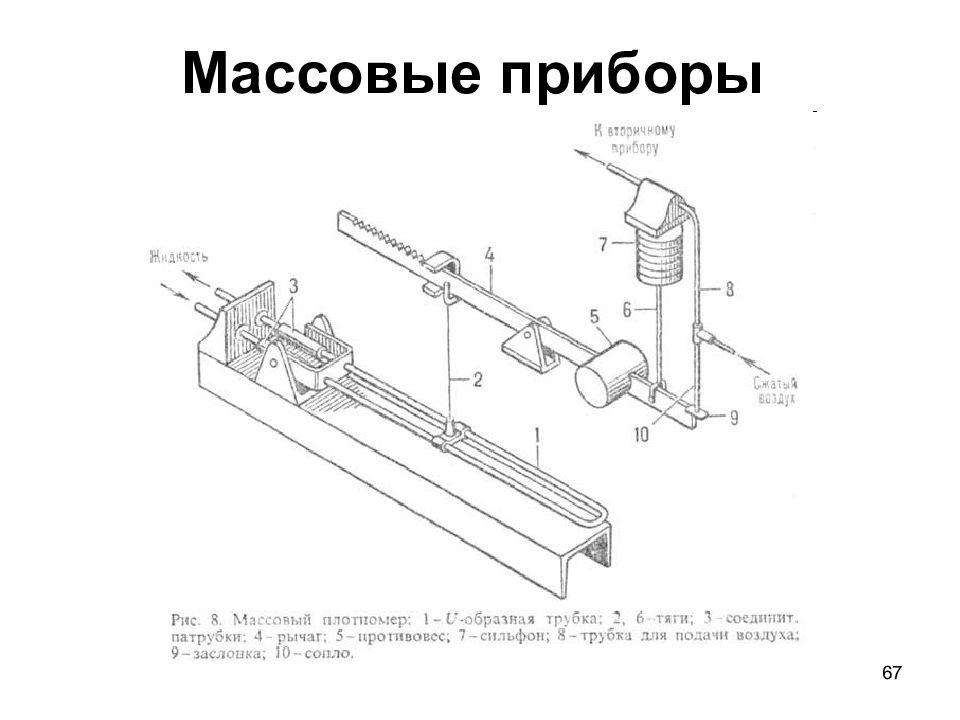
66 Поплавковые приборы Плотномер с плавающим поплавком для жидкости: 1, 5 – основной и переливной сосуды; 2 – поплавок; 3 – сердечник; 4 – катушки; 6, 7, 10 – входная, подводящая и отводящая трубы; 8 – термометр сопротивления; 9 – вторичный прибор; 11 – индукц. мост.
Слайд 68
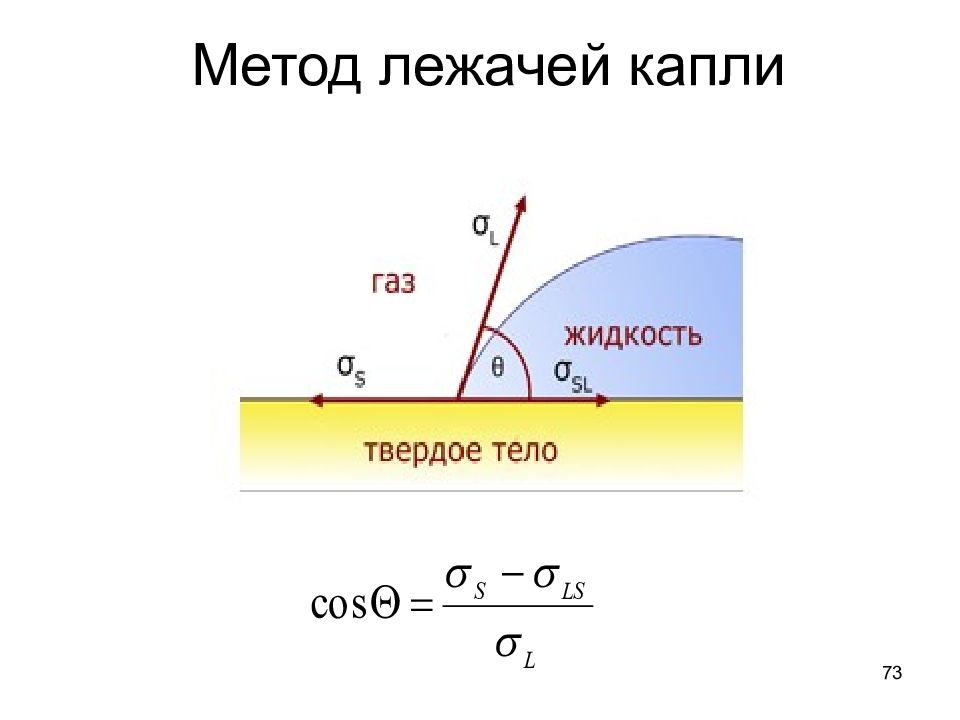
68 Поверхностное натяжение Поверхностное натяжение s – мера нескомпенсированости межмолекулярных сил у границы раздела фаз, определяется как работа обратимого изотермического образования единицы площади поверхности раздела фаз где U (s) – полная поверхностная энергия слоя, S (s) – поверхностная э н тропия слоя, n i (s) – избыток компонента i в поверхностном слое
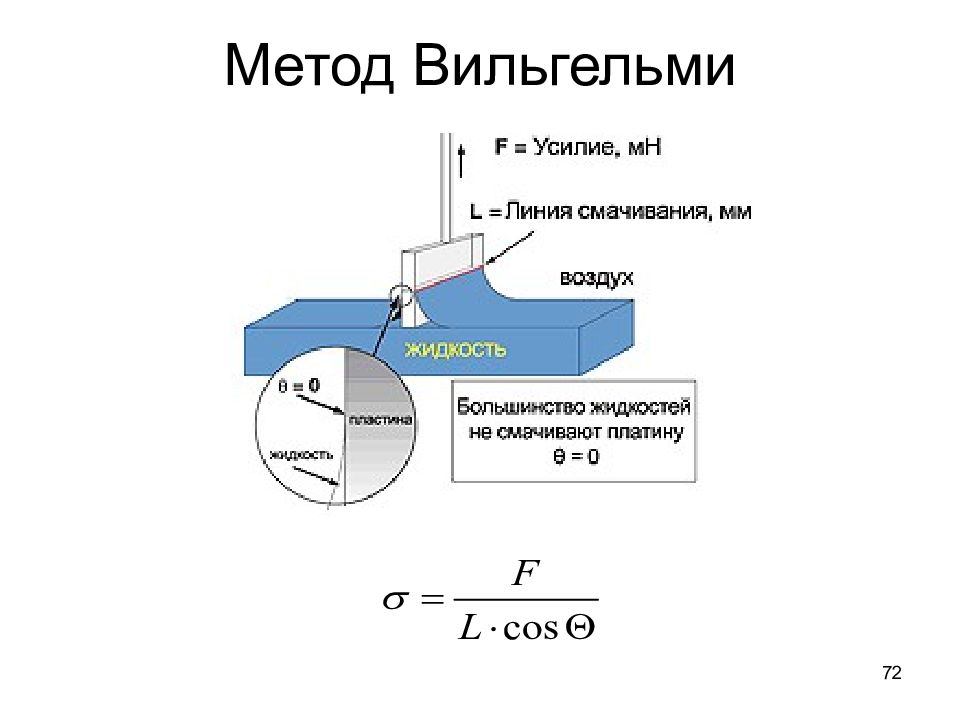
69 Методы измерения поверхностного натяжения жидкости Статические методы: Метод поднятия в капилляре Метод Вильгельми Метод лежачей капли Метод определения по форме висячей капли Метод вращающейся капли Динамические методы: Метод дю Нуи (метод отрыва кольца) Сталагмометрический, или метод счета капель Метод максимального давления пузырька Метод осциллирующей струи Метод стоячих волн Метод бегущих волн
Слайд 70: Метод вращающейся капли
70 Метод вращающейся капли Схема вращающегося капилляра с каплей жидкости(а) и капля жидкости (б).
Слайд 71: Метод дю Нуи (метод отрыва кольца )
71 Метод дю Нуи (метод отрыва кольца )
Слайд 74
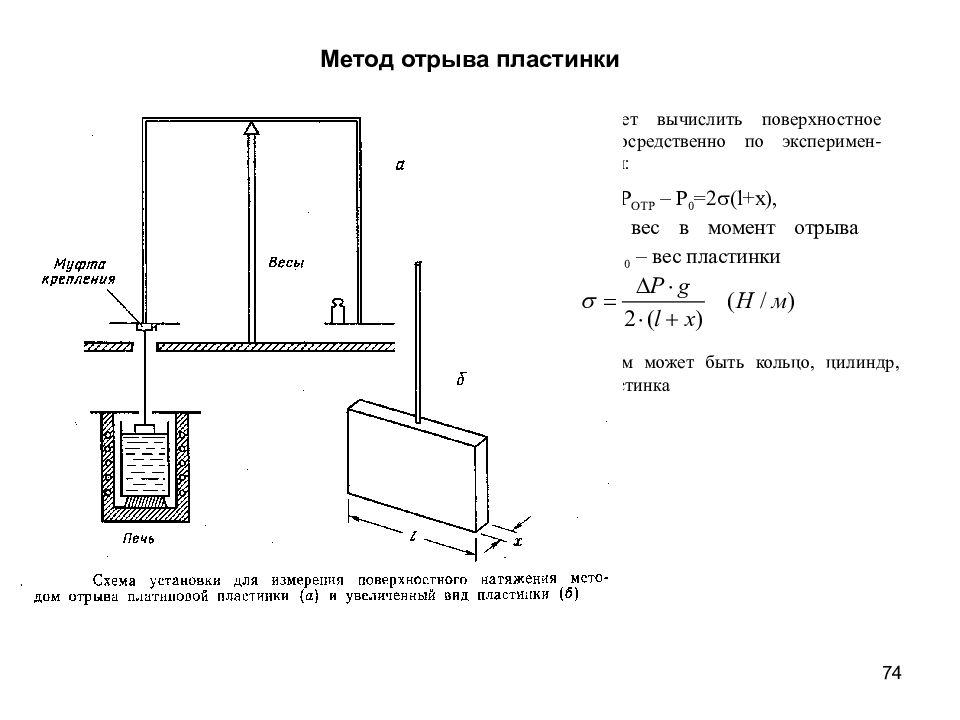
74 Метод отрыва пластинки Рабочим телом может быть кольцо, цилиндр, стержень, пластинка Метод позволяет вычислить поверхностное натяжение непосредственно по эксперимен-тальным данным: D P=P OTP – P 0 =2 s (l+x), где Р отр – вес в момент отрыва пластинки, Р 0 – вес пластинки
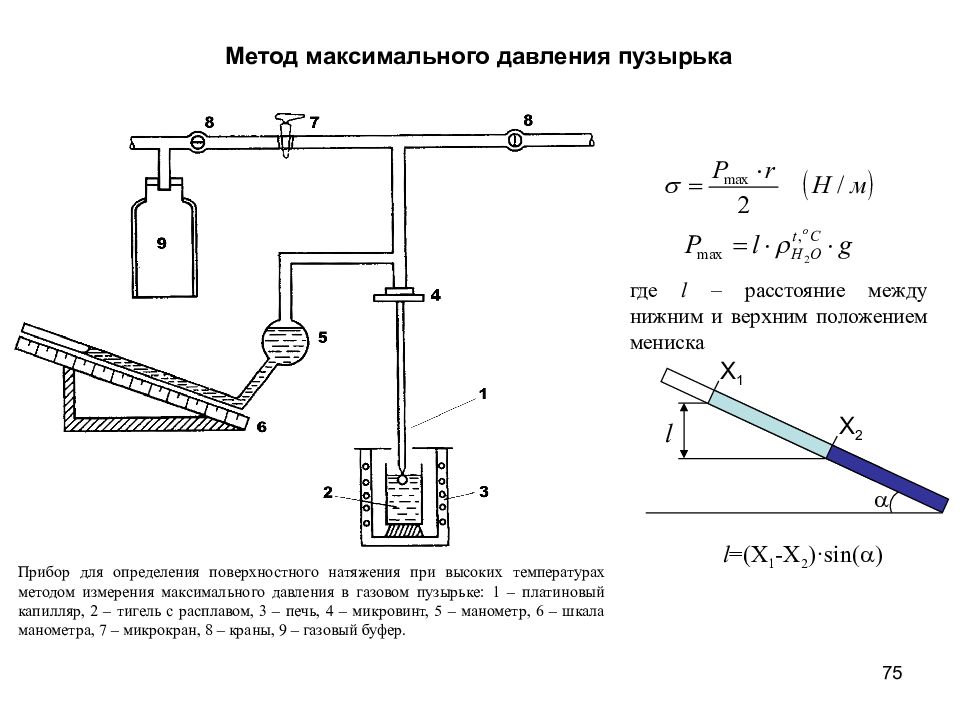
Слайд 75
75 Прибор для определения поверхностного натяжения при высоких температурах методом измерения максимального давления в газовом пузырьке: 1 – платиновый капилляр, 2 – тигель с расплавом, 3 – печь, 4 – микровинт, 5 – манометр, 6 – шкала манометра, 7 – микрокран, 8 – краны, 9 – газовый буфер. Метод максимального давления пузырька где l – расстояние между нижним и верхним положением мениска l a X 1 X 2 l =(X 1 -X 2 ) ·sin (a)
Слайд 76
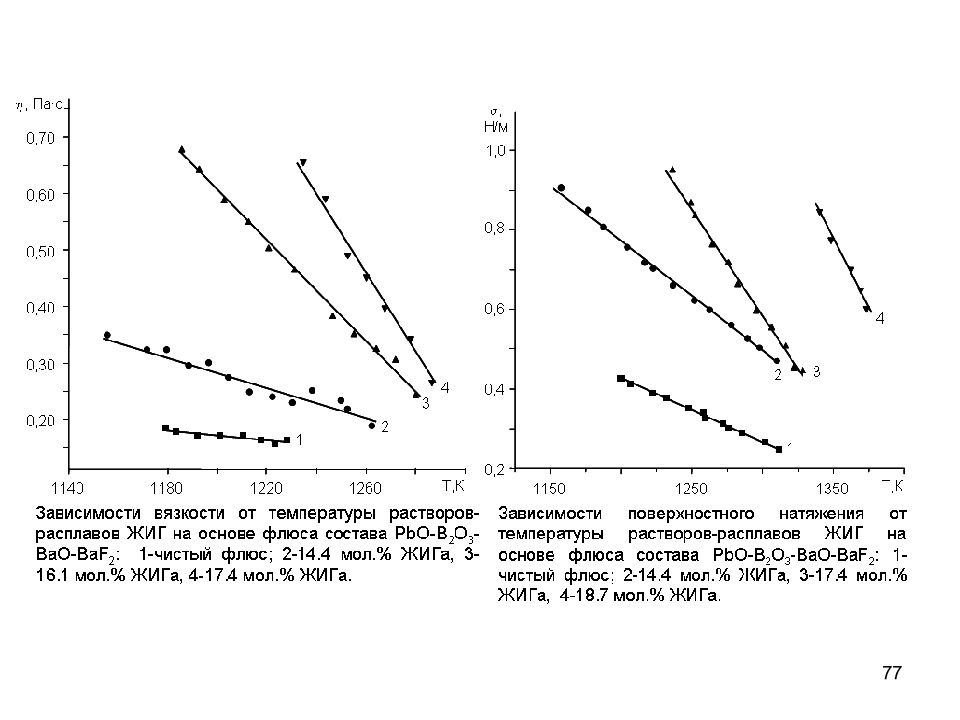
76 Температурная зависимость поверхностного натяжения Зависимость поверхностного натяжения от температуры в различных растворителях Зависимости поверхностного натяжения расплавов от температуры описываются уравнениями прямой: = a – b T Изломы на линиях коррелируют с изломами на зависимостях вязкости от температуры Согласно кинетической теории жидкостей поверхностное натяжение связано с энергией активации вязкого течения: E h =4 · p · r 2 · s · N A что позволяет определить объем единицы течения
Слайд 78
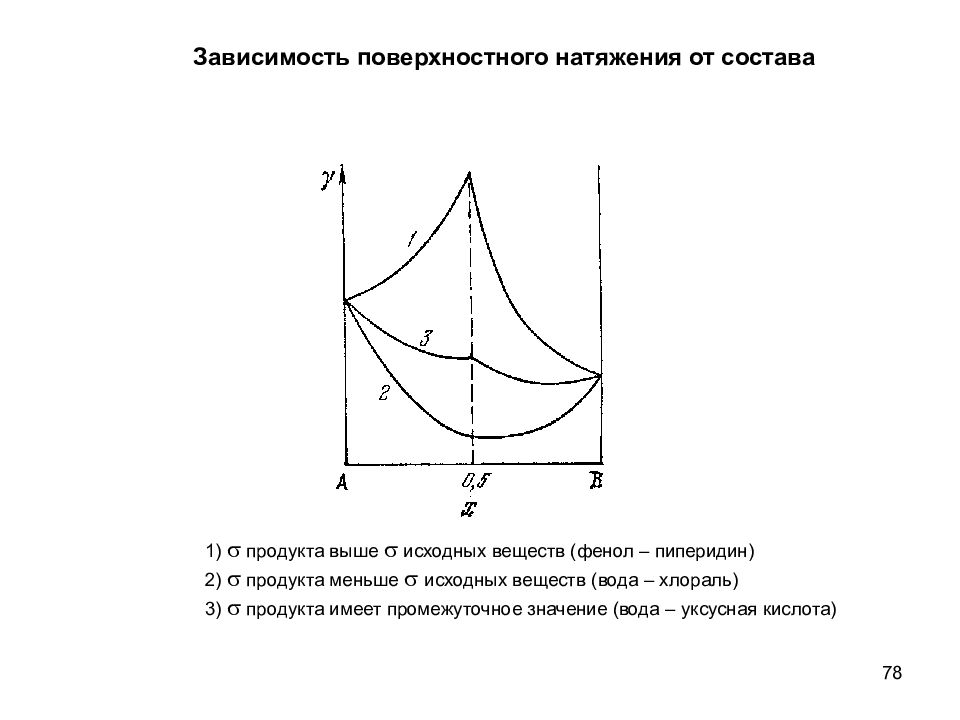
78 1) s продукта выше s исходных веществ ( фенол – пиперидин) 2) s продукта меньше s исходных веществ (вода – хлораль) 3) s продукта имеет промежуточное значение (вода – уксусная кислота) s Зависимость поверхностного натяжения от состава
Слайд 79
79 Электропроводность Электропроводность – способность вещества проводить электрический ток; величина, обратная сопротивлению Электропроводность не может быть ни в явной, ни в неявной форме связана с величинами свойств компонентов, поскольку большая часть электропроводных жидких систем образована непроводящими ток компонентами. Принято пользоваться диаграммами «удельная электропроводность —состав». Поскольку электропроводность относится к заведомо неаддитивным свойствам, способ выражения концентрации при этом может быть произвольным, однако для наглядности чаще всего выбирают мольные доли.
Слайд 80
80 ИЗМЕРЕНИЕ ЭЛЕКТРОПРОВОДНОСТИ a b c d e f R 0 ~ G Четырехточечный метод измерения электропроводности : R=(V/V 0 )R 0
Слайд 81
81 Температурная зависимость электропроводности Поскольку жидкости – проводники второго рода, а носители заряда в них – ионы, электропроводность растет при нагревании с увеличением подвижности -4,0 1/T 10 4, K -1 -3,5 -3,0 -2,5 Зависимости удельной электропроводности расплава растворителя PbO-В 2 O 3 -BaO-BaF 2 от температуры при различном содержании оксида свинца: 1 – 15 моль.% PbO; 2 – 20 моль.% PbO; 3 – 25 моль.% PbO. ln 8,0 8,5 9,0 1 2 3 Зависимость линейна в координатах ln k – 1/T h n · l = const Для ионных расплавов
Слайд 82
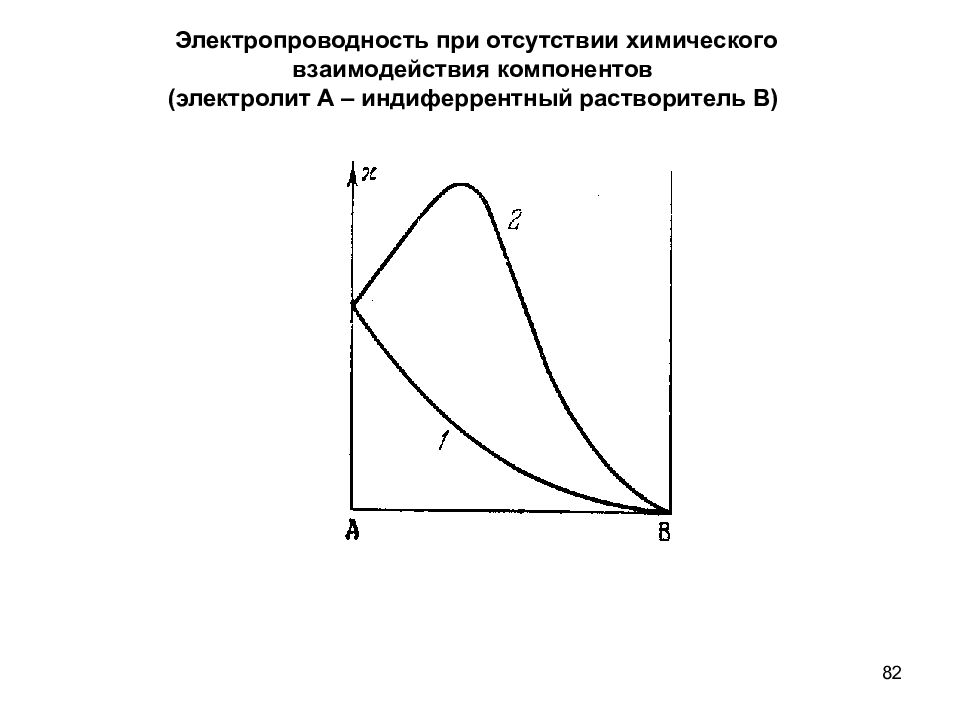
82 Электропроводность при отсутствии химического взаимодействия компонентов (электролит А – индиферрентный растворитель В)