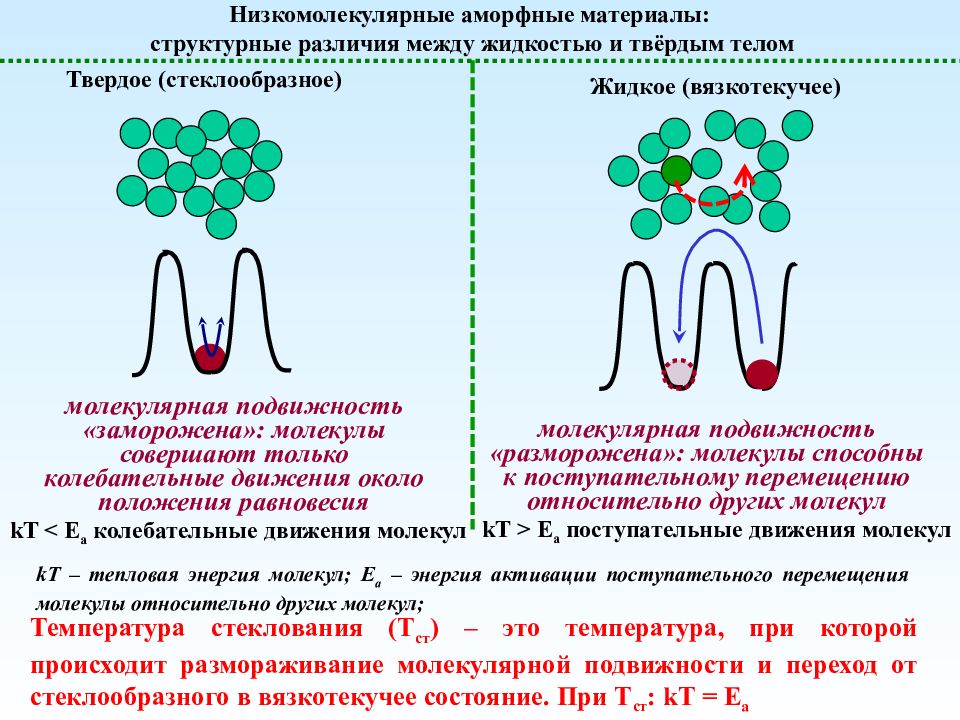
Первый слайд презентации
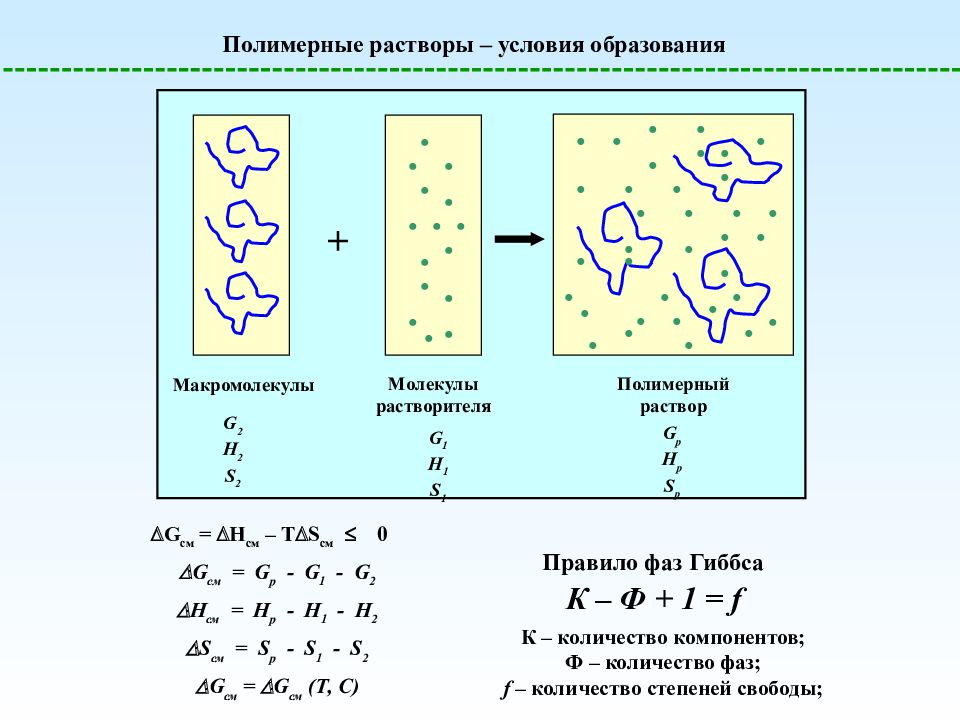
Полимерные растворы – условия образования Макромолекулы G 2 H 2 S 2 + Молекулы растворителя Полимерный раствор G 1 H 1 S 1 G р H р S р G см = H см – T S см 0 G см = G р - G 1 - G 2 H см = H р - H 1 - H 2 S см = S р - S 1 - S 2 G см = G см (Т, С) К – Ф + 1 = f Правило фаз Гиббса К – количество компонентов; Ф – количество фаз; f – количество степеней свободы;
Слайд 2
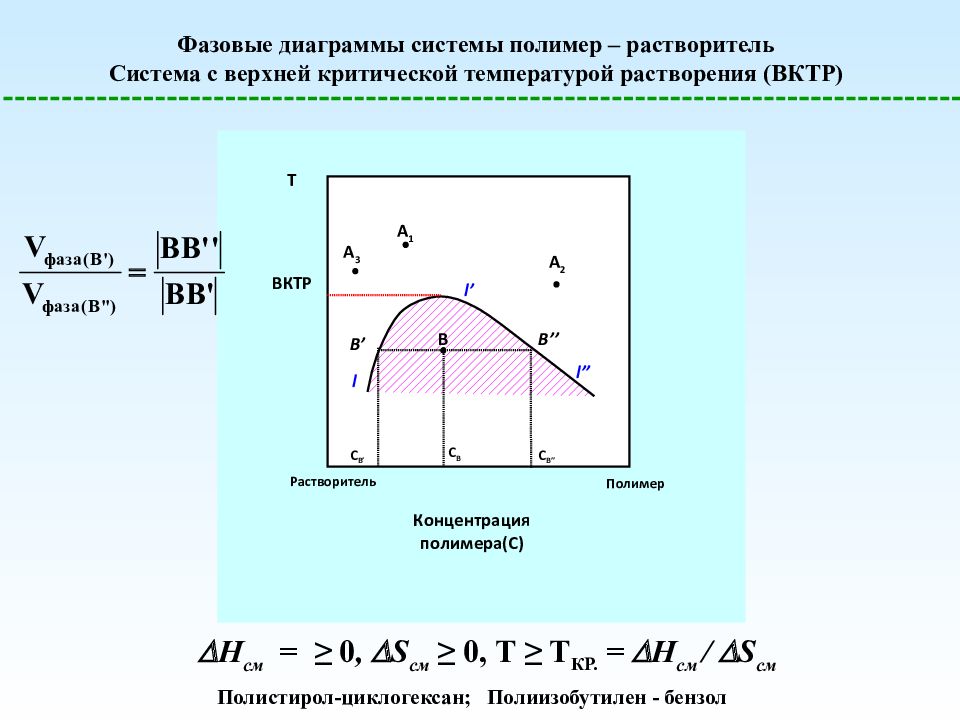
Фазовые диаграммы системы полимер – растворитель Система с верхней критической температурой растворения (ВКТР) ВКТР T Концентрация полимера(С) A 1 A 2 A 3 B B’’ B’ Растворитель С B’’ С B’ l l’ l’’ С B Полимер H см = ≥ 0, S см ≥ 0, T ≥ T КР. = H см / S см Полистирол-циклогексан; Полиизобутилен - бензол
Слайд 3
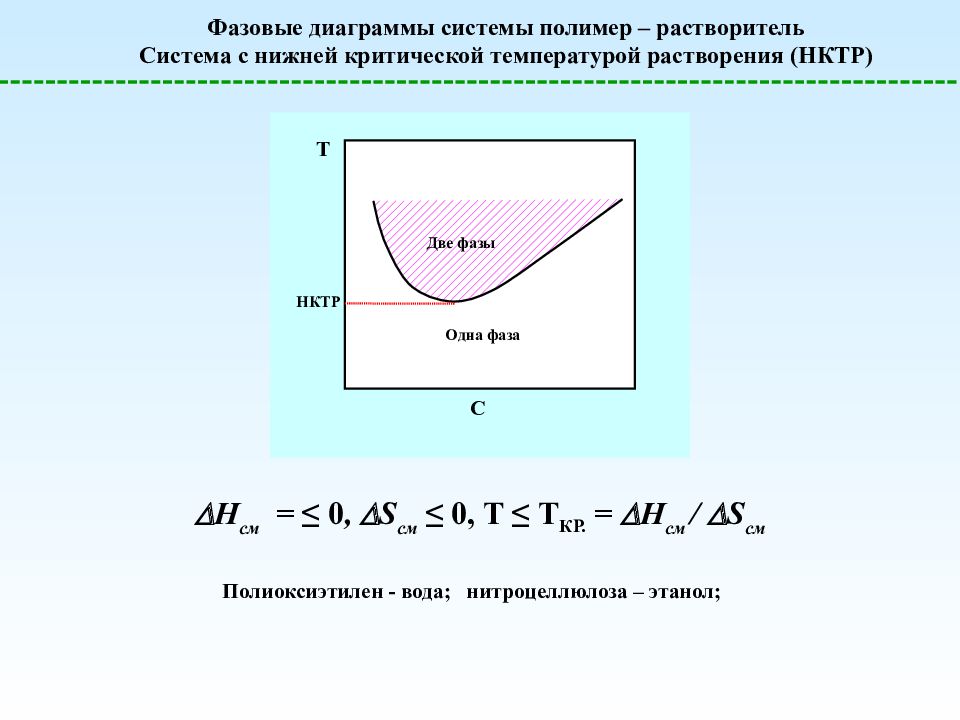
Фазовые диаграммы системы полимер – растворитель Система с нижней критической температурой растворения (НКТР) T С НКТР Две фазы Одна фаза H см = ≤ 0, S см ≤ 0, T ≤ T КР. = H см / S см Полиоксиэтилен - вода; нитроцеллюлоза – этанол;
Слайд 4
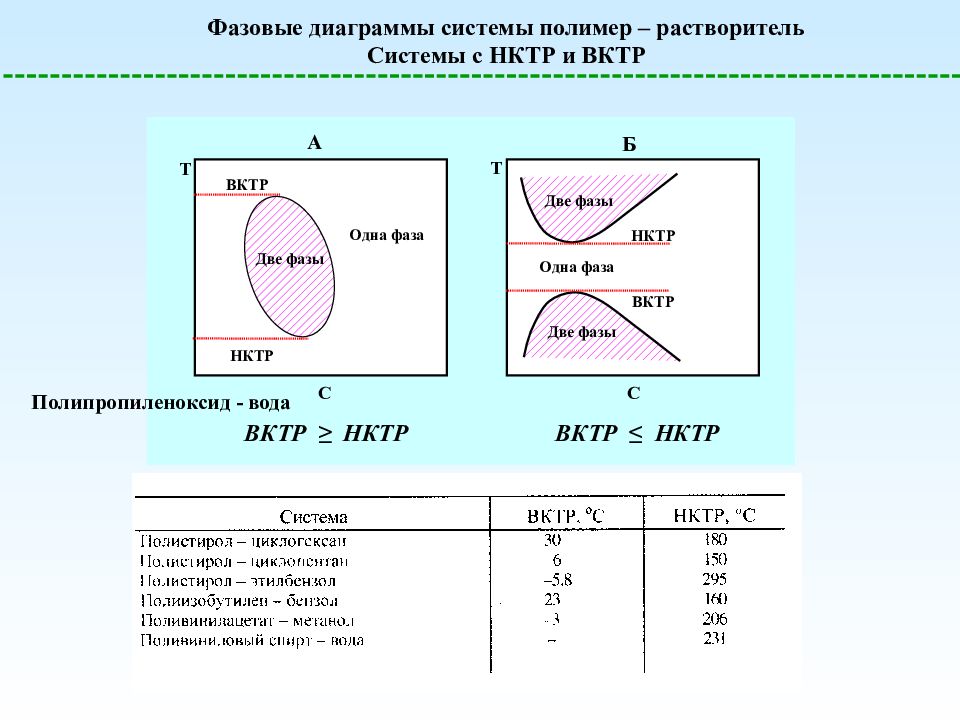
Фазовые диаграммы системы полимер – растворитель Системы с НКТР и ВКТР T С НКТР Одна фаза Две фазы ВКТР A Одна фаза Две фазы Две фазы T С НКТР ВКТР Б ВКТР ≤ НКТР ВКТР ≥ НКТР Полипропиленоксид - вода
Слайд 5
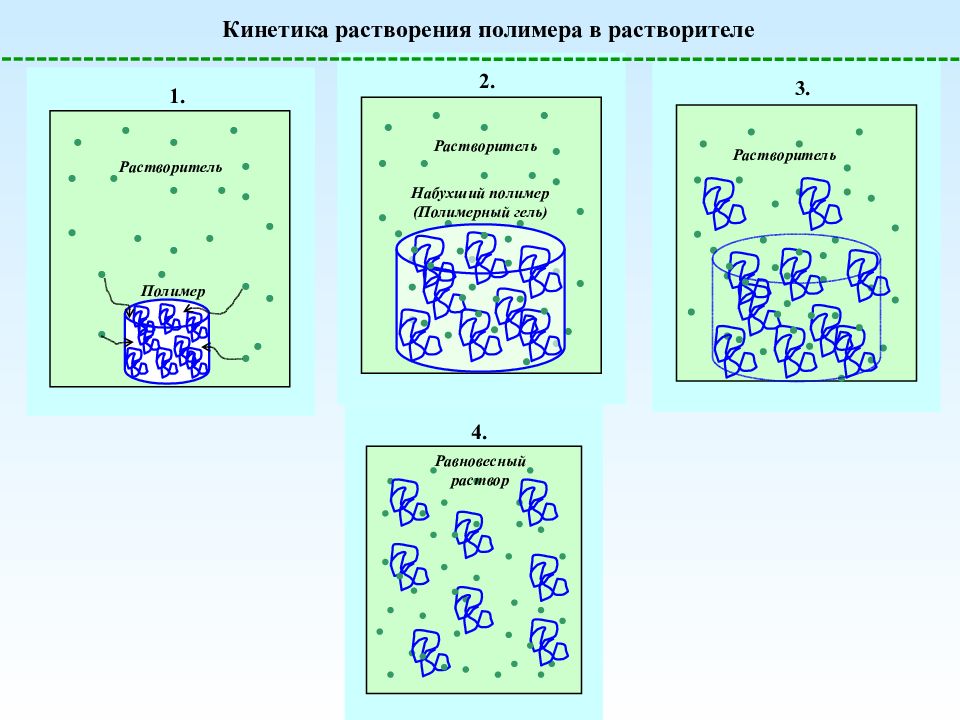
Кинетика растворения полимера в растворителе Полимер 1. Растворитель 2. Набухший полимер ( Полимерный гель ) Растворитель 3. Растворитель 4. Равновесный раствор ;
Слайд 6
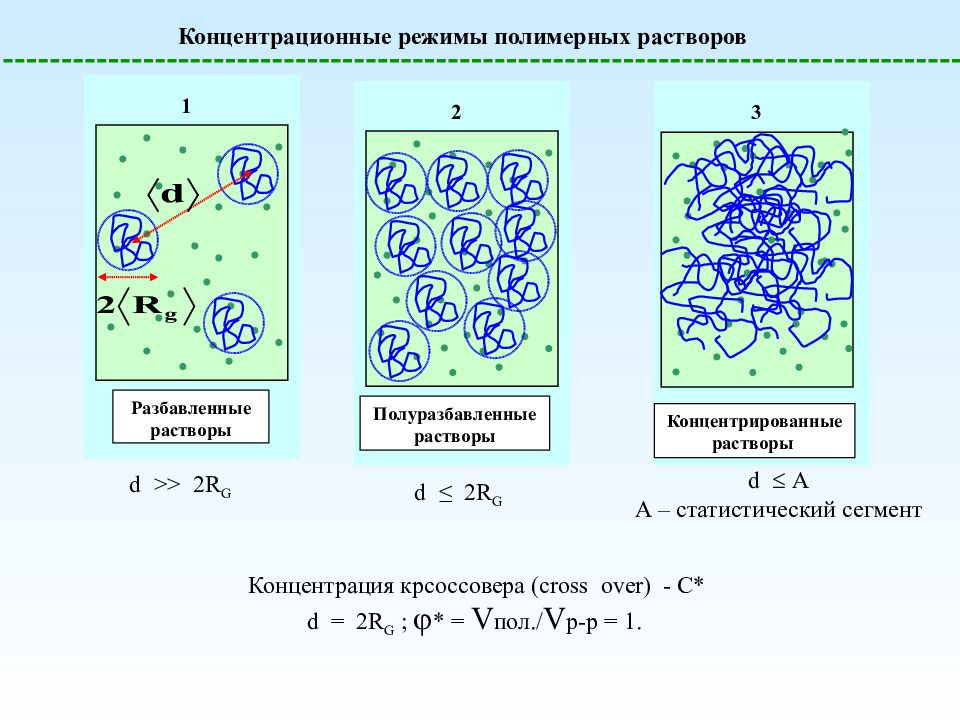
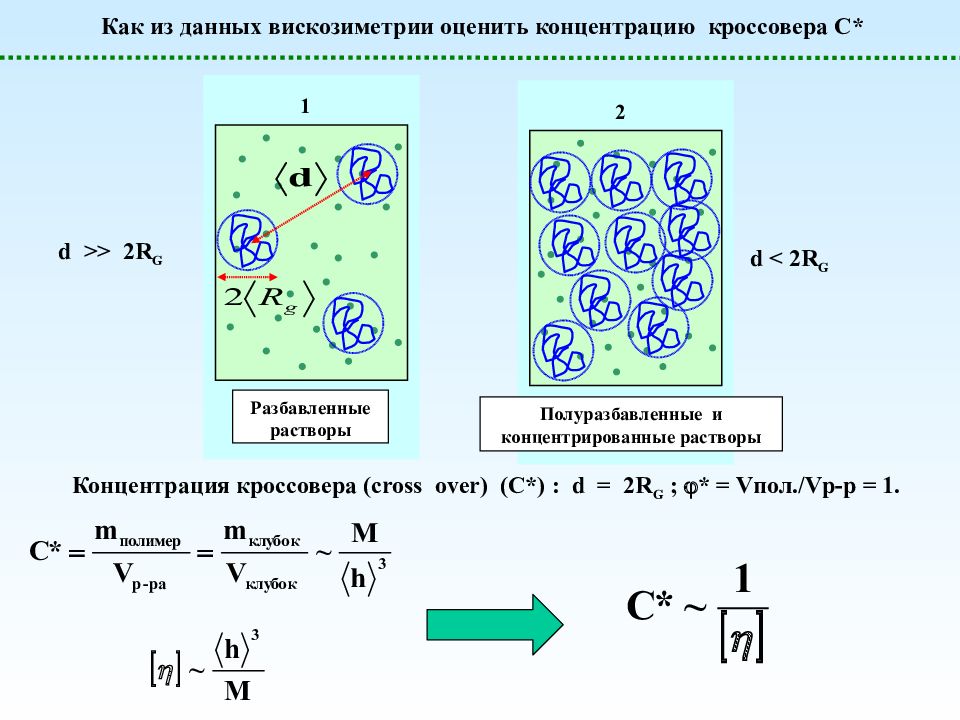
Концентрационные режимы полимерных растворов 1 Разбавленные растворы 2 Полуразбавленные растворы 3 Концентрированные растворы d >> 2R G d ≤ 2R G d А А – статистический сегмент Концентрация крсоссовера ( cross over) - C* d = 2R G ; * = V пол./ V р-р = 1.
Слайд 7
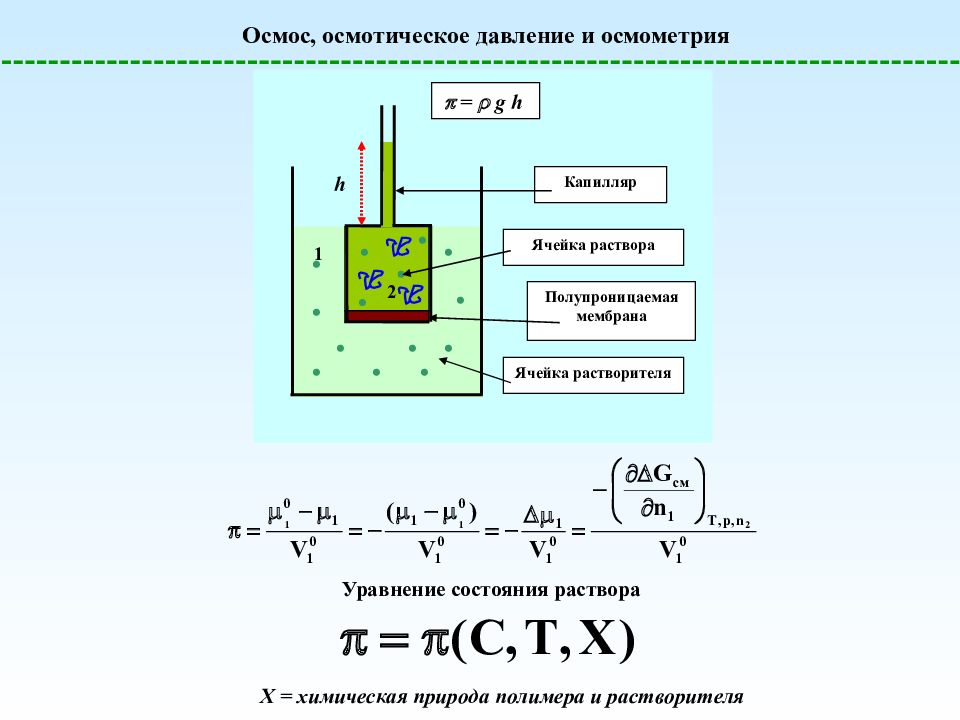
Осмос, осмотическое давление и осмометрия Ячейка растворителя h Ячейка раствора Полупроницаемая мембрана 1 2 Капилляр = g h Уравнение состояния раствора Х = химическая природа полимера и растворителя
Слайд 8
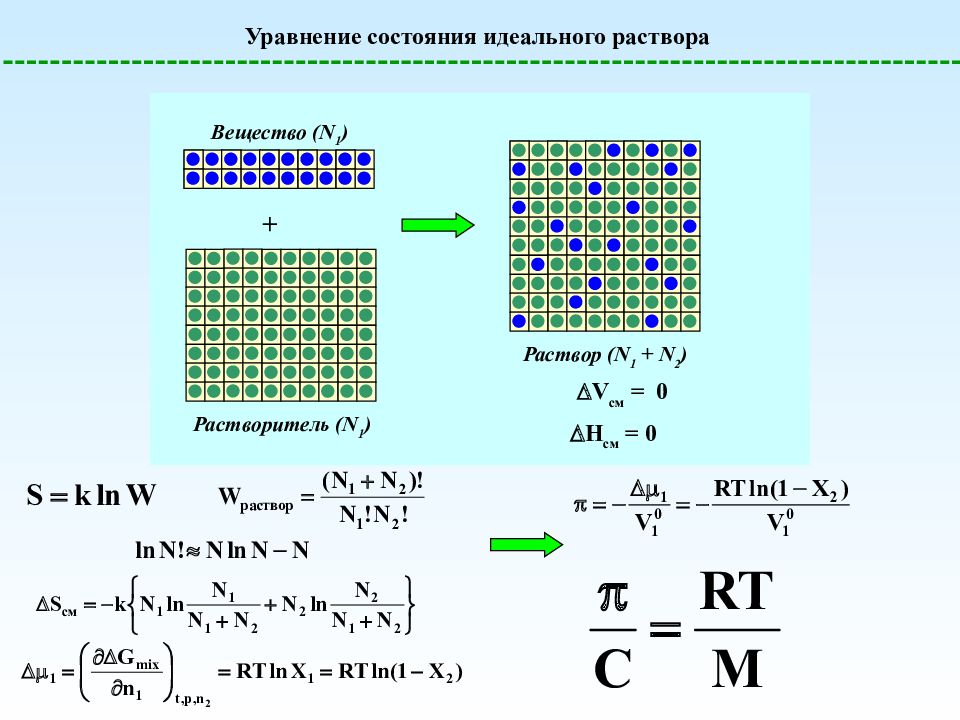
Уравнение состояния идеального раствора + Раствор (N 1 + N 2 ) Вещество (N 1 ) Растворитель (N 1 ) V см = 0 H см = 0
Слайд 9
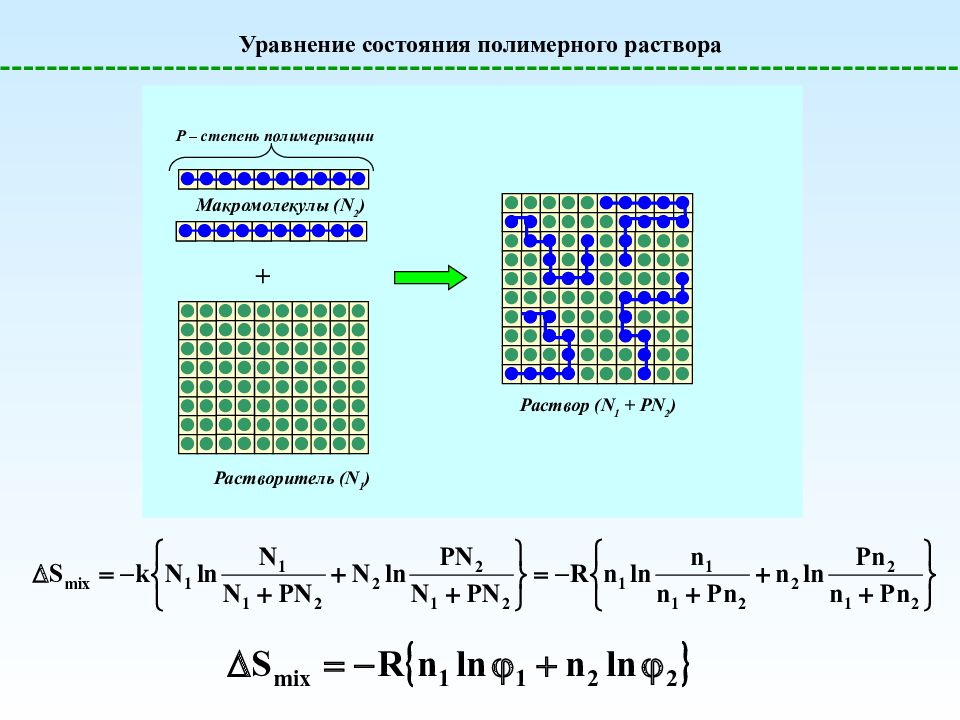
Уравнение состояния полимерного раствора Растворитель (N 1 ) + Макромолекулы (N 2 ) Раствор (N 1 + PN 2 ) P – степень полимеризации
Слайд 10
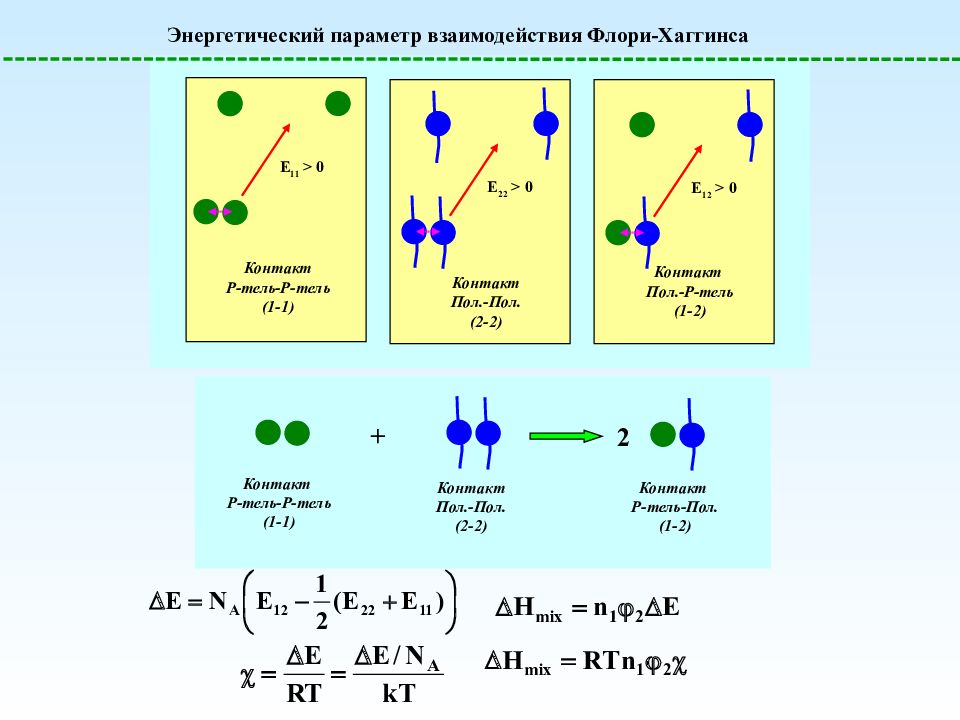
Энергетический параметр взаимодействия Флори-Хаггинса E 11 > 0 Контакт Р-тель-Р-тель (1-1) E 22 > 0 Контакт Пол.-Пол. (2-2) E 12 > 0 Контакт Пол.-Р-тель (1-2) Контакт Р-тель-Пол. (1-2) Контакт Р-тель-Р-тель (1-1) + Контакт Пол.-Пол. (2-2) 2
Слайд 13
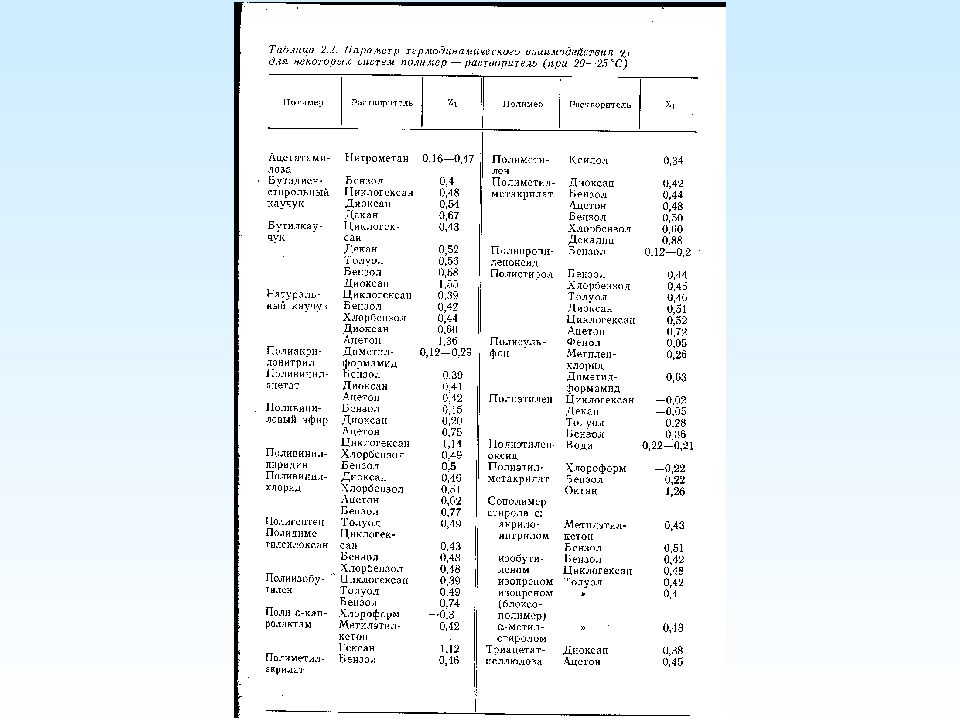
Определения -температуры для данной системы полимер - растворитель I II III -температура - т емпература, при которой раствор полимера формально подчиняется законам идеальных растворов (законы Рауля, Вант-Гоффа и др.) -температура - к ритическая температура растворения полимера с бесконечно большой молекулярной массой. -температура - т емпература, при которой исключенный объём клубка (u) равен нулю. Исключенный объем – область пространства, в которую данный клубок исключает проникновение других клубков. В - условиях клубок принимает такие размеры, какие он принял бы, если бы растворителя не было совсем.
Слайд 15
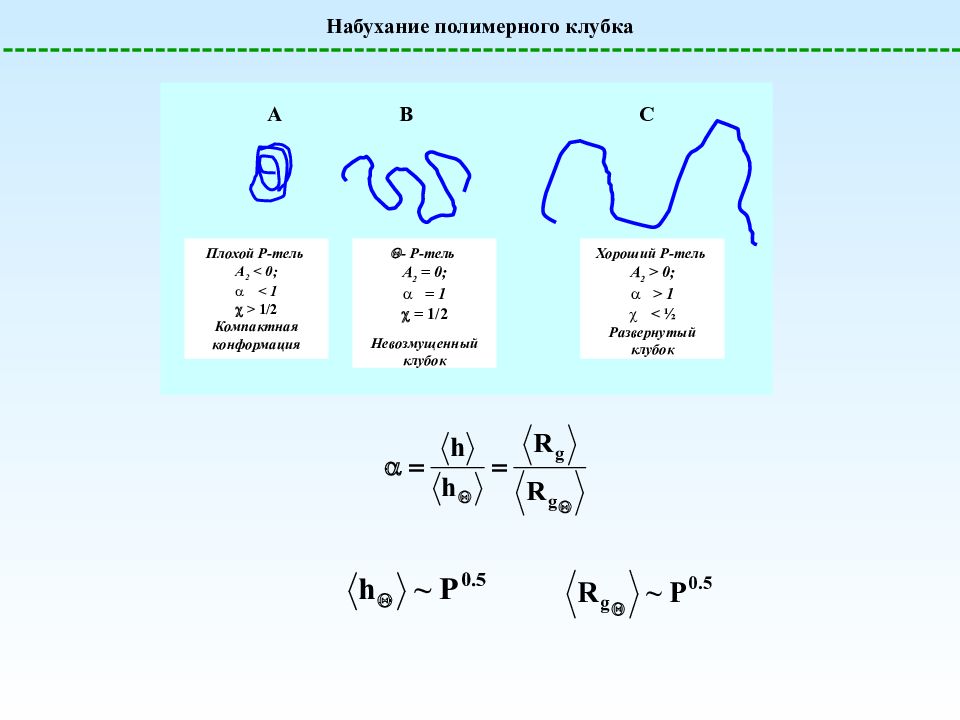
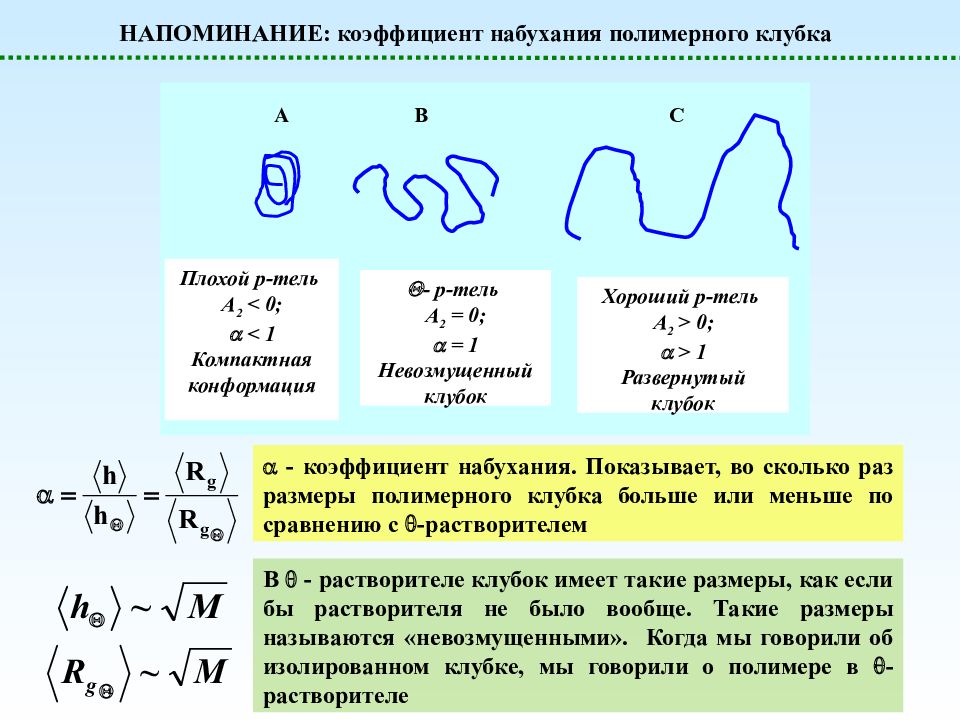
Набухание полимерного клубка Плохой Р-тель A 2 < 0; < 1 > 1/2 Компактная конформация A B C - Р-тель A 2 = 0; = 1 = 1/2 Невозмущенный клубок Хороший Р-тель A 2 > 0; > 1 < ½ Развернутый клубок
Слайд 16
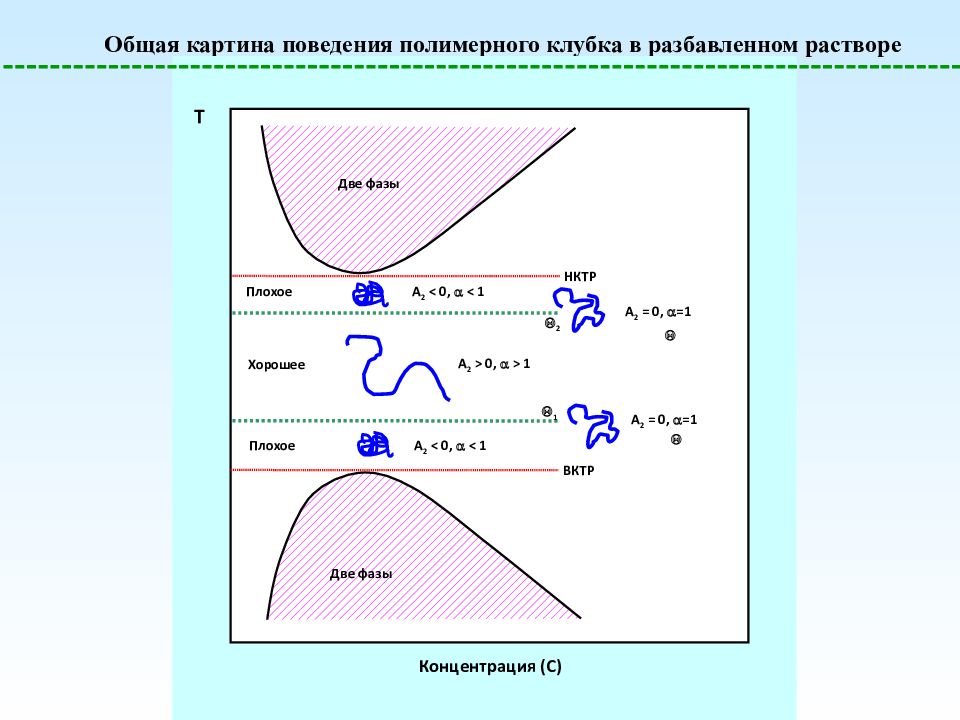
Общая картина поведения полимерного клубка в разбавленном растворе T Две фазы Две фазы Концентрация (C) НКТР ВКТР 2 1 A 2 = 0, =1 A 2 = 0, =1 A 2 < 0, < 1 A 2 < 0, < 1 A 2 > 0, > 1 Хорошее Плохое Плохое
Слайд 17
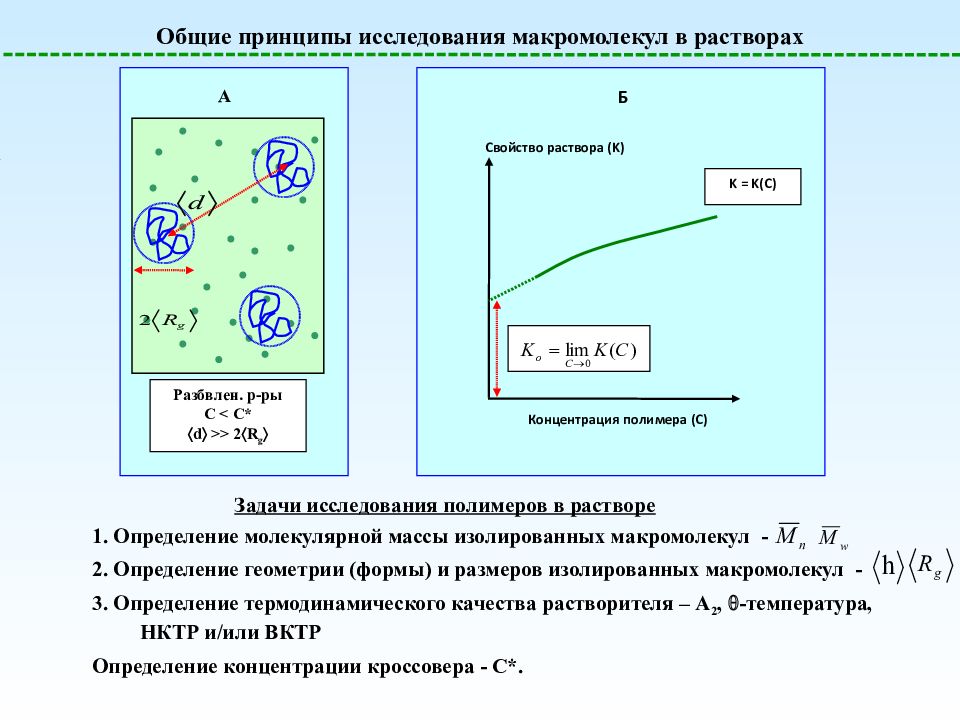
Общие принципы исследования макромолекул в растворах Разбвлен. р-ры C < C * d >> 2 R g A Свойство раствора ( K ) Концентрация полимера ( C ) K = K(C) Б Задачи исследования полимеров в растворе 1. Определение молекулярной массы изолированных макромолекул - 2. Определение геометрии (формы) и размеров изолированных макромолекул - 3. Определение термодинамического качества растворителя – A 2, -температура, НКТР и/или ВКТР Определение концентрации кроссовера - С*.
Слайд 18
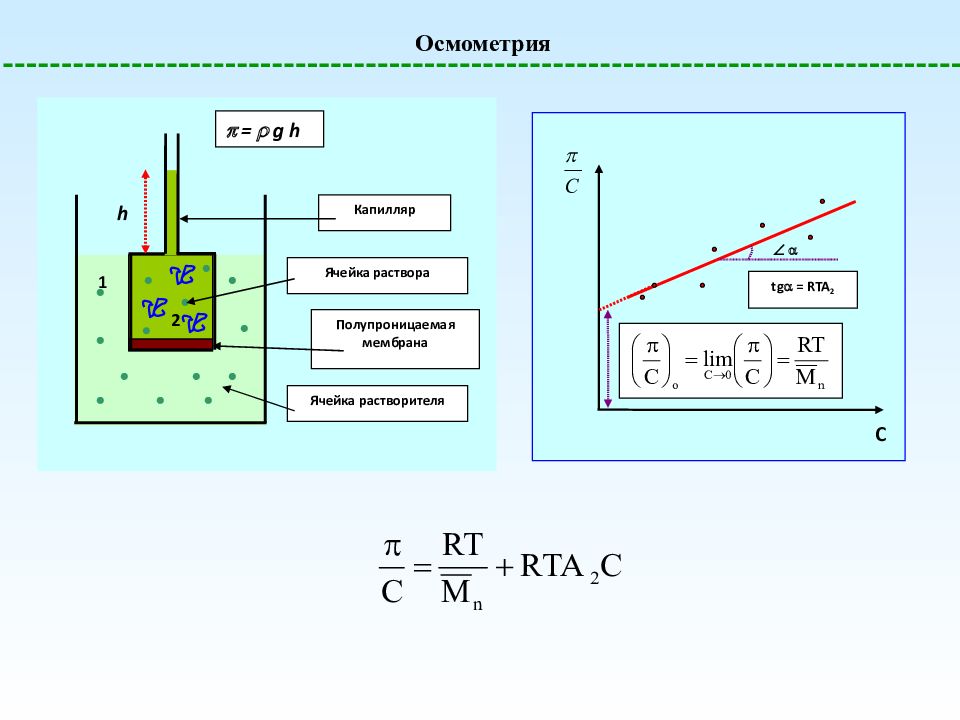
Осмометрия Ячейка растворителя h Ячейка раствора Полупроницаемая мембрана 1 2 Капилляр = g h C tg = RTA 2
Слайд 19
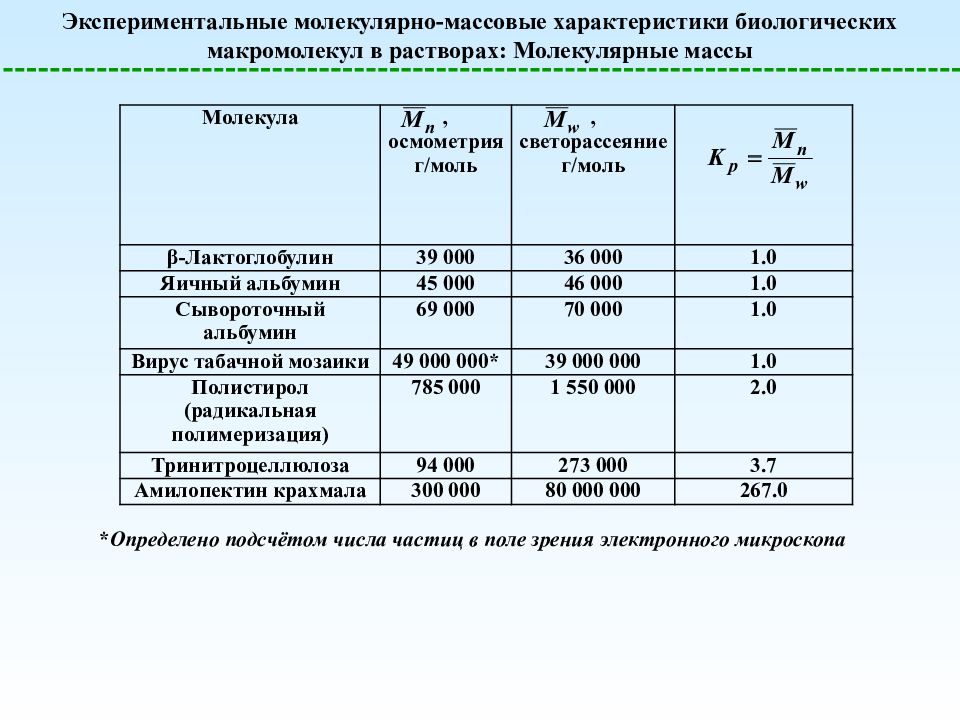
Экспериментальные молекулярно-массовые характеристики биологических макромолекул в растворах: Молекулярные массы Молекула , осмометрия г/моль , светорассеяние г/моль β-Лактоглобулин 39 000 36 000 1.0 Яичный альбумин 45 000 46 000 1.0 Сывороточный альбумин 69 000 70 000 1.0 Вирус табачной мозаики 49 000 000* 39 000 000 1.0 Полистирол (радикальная полимеризация) 785 000 1 550 000 2.0 Тринитроцеллюлоза 94 000 273 000 3.7 Амилопектин крахмала 300 000 80 000 000 267.0 * Определено подсчётом числа частиц в поле зрения электронного микроскопа
Слайд 20
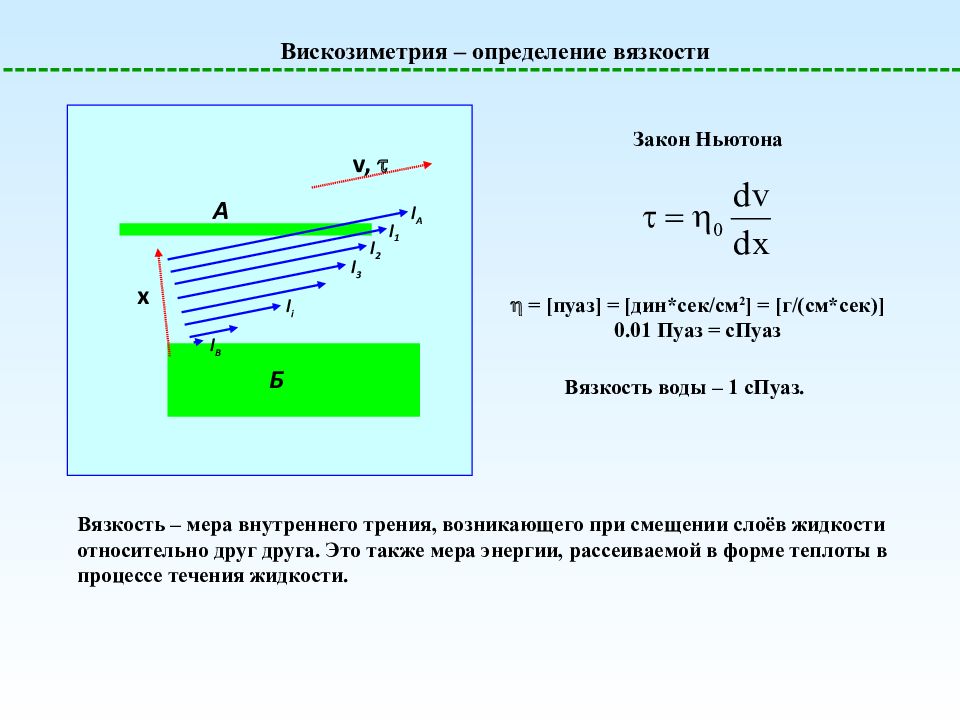
Вискозиметрия – определение вязкости A Б v, x l A l B l 1 l 2 l 3 l i Закон Ньютона = [пуаз] = [дин*сек/см 2 ] = [г/(см*сек)] 0.01 Пуаз = сПуаз Вязкость воды – 1 сПуаз. Вязкость – мера внутреннего трения, возникающего при смещении слоёв жидкости относительно друг друга. Это также мера энергии, рассеиваемой в форме теплоты в процессе течения жидкости.
Слайд 21
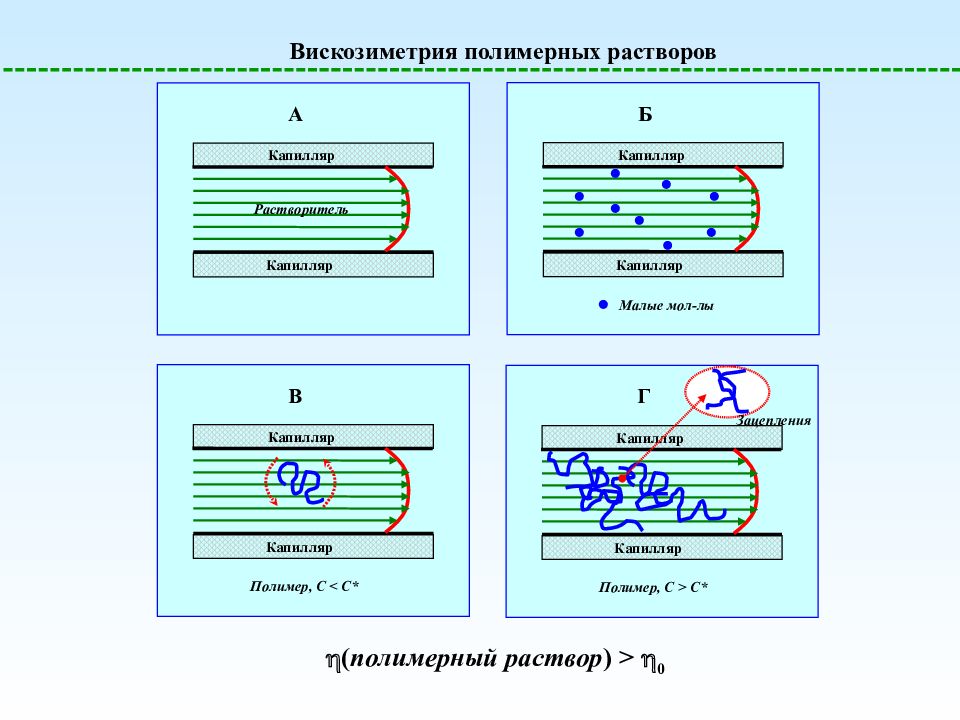
Вискозиметрия полимерных растворов A Капилляр Капилляр Растворитель Б Капилляр Капилляр Малые мол-лы В Капилляр Капилляр Полимер, C < C * Г Капилляр Капилляр Полимер, C > C * Зацепления ( полимерный раствор ) > 0
Слайд 22
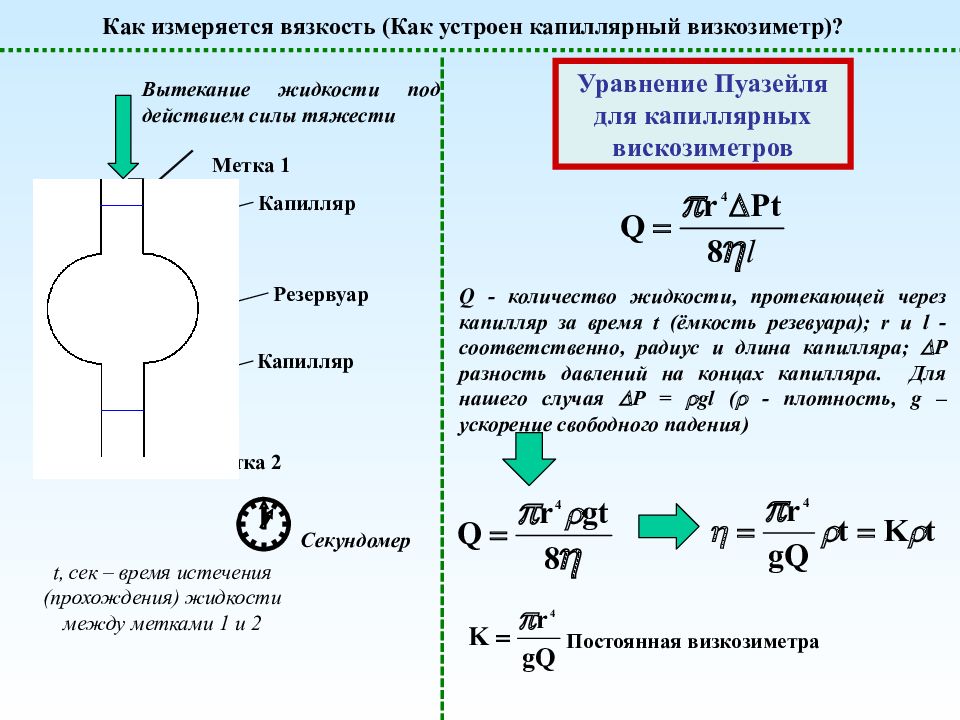
Как измеряется вязкость (Как устроен капиллярный визкозиметр)? Резервуар Капилляр Капилляр Вытекание жидкости под действием силы тяжести Метка 2 Секундомер Метка 1 t, сек – время истечения (прохождения) жидкости между метками 1 и 2 Уравнение Пуазейля для капиллярных вискозиметров Q - количество жидкости, протекающей через капилляр за время t (ёмкость резевуара); r и l - соответственно, радиус и длина капилляра; Р разность давлений на концах капилляра. Для нашего случая Р = gl ( - плотность, g – ускорение свободного падения) Постоянная визкозиметра
Слайд 23
Что такое удельная, приведенная и характеристическая вязкость? Как их определить экспериментально? Каковы единицы их измерения? Зачем нужны эти понятия? Удельная вязкость : Допущение: для разбавленных растворов: o (плотность раствора равна плотности растворителя t – время истечения раствора полимера, t 0 – время истечения чистого растворителя Единицы измерения – безразмерная; Физический смысл – относительный прирост вязкости за счёт введения полимера (исключает влияние вязкости растворителя на прирост вязкости раствора приведенная вязкость : С – весовая концентрация полимера в г/дл или г/см 3 Единицы измерения – дл/г или см 3 /г; Физический смысл – исключает концентрационный вклад в прирост вязкости Характеристическая вязкость [ ] : Единицы измерения – дл/г или см 3 /г; Характеристическая вязкость – это приведенная вязкость при бесконечном разбавлении. Физический смысл – характеризует молекулярные свойства отдельных клубков.
Слайд 24
Уравнение Хаггинса (эмпирическое) для разбавленных растворов незаряженных полимеров: С, г/дл tg =[ ] 2 K h пр. [ ] K h - Константа Хаггинса - для гибкоцепных полимеров качественно характеризует термодинамическое качество растворителя: K h = 0.2 0.3 - термодинамически хорошие растворители; K h > 0.5 - термодинамически плохие раст в орители; Как экспериментально определить характеристическую вязкость?
Слайд 25
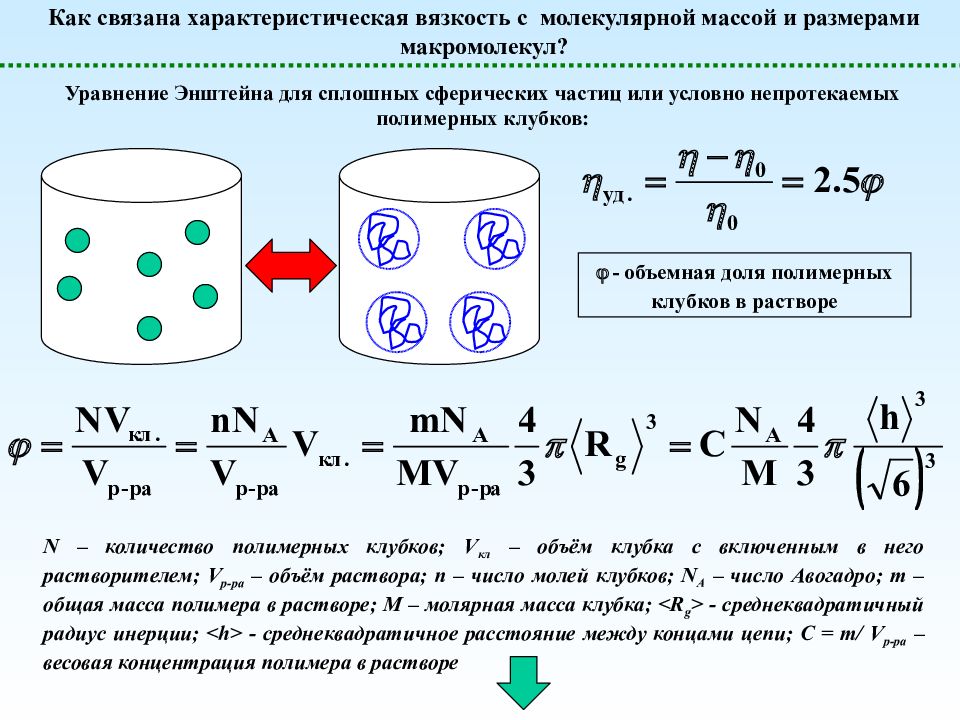
- объемная доля полимерных клубков в растворе Уравнение Энштейна для сплошных сферических частиц или условно непротекаемых полимерных клубков: Как связана характеристическая вязкость с молекулярной массой и размерами макромолекул? N – количество полимерных клубков ; V кл – объём клубка с включенным в него растворителем ; V р-ра – объём раствора; n – число молей клубков ; N A – число Авогадро ; m – общая масса полимера в растворе ; M – молярная масса клубка ; <R g > - среднеквадратичный радиус инерции; <h> - среднеквадратичное расстояние между концами цепи; С = m/ V р-ра – весовая концентрация полимера в растворе
Слайд 26
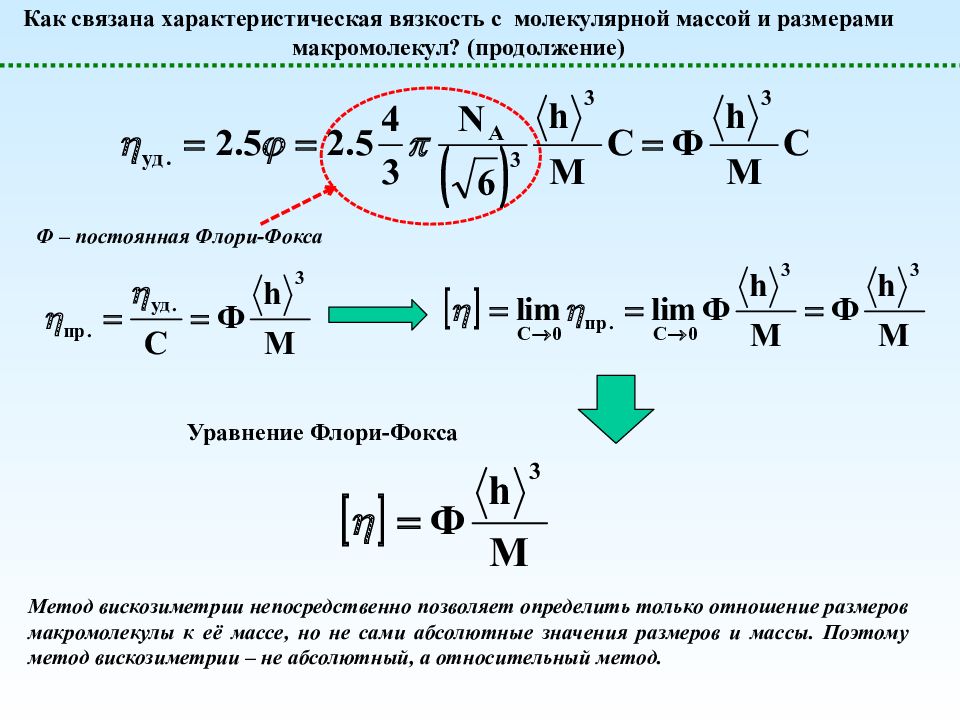
Как связана характеристическая вязкость с молекулярной массой и размерами макромолекул? (продолжение) Ф – постоянная Флори-Фокса Уравнение Флори-Фокса Метод вискозиметрии непосредственно позволяет определить только отношение размеров макромолекулы к её массе, но не сами абсолютные значения размеров и массы. Поэтому метод вискозиметрии – не абсолютный, а относительный метод.
Слайд 27
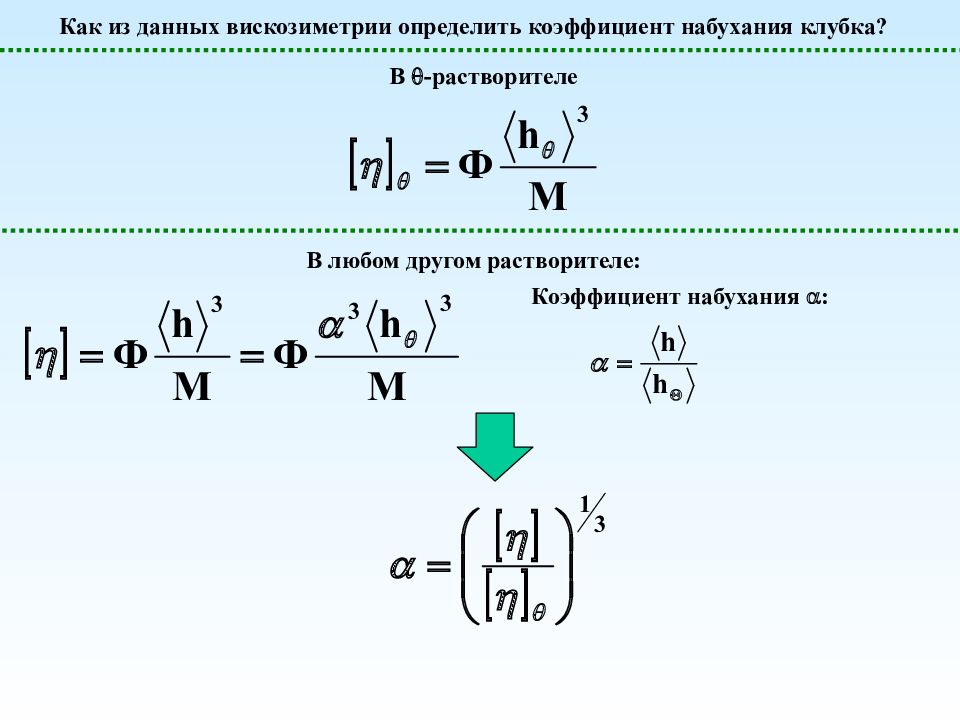
Как из данных вискозиметрии определить коэффициент набухания клубка? В -растворителе В любом другом растворителе: Коэффициент набухания :
Слайд 28
НАПОМИНАНИЕ: коэффициент набухания полимерного клубка Плохой р -тель A 2 < 0; < 1 Компактная конформация A B C - р -тель A 2 = 0; = 1 Невозмущенный клубок Хороший р -тель A 2 > 0; > 1 Развернутый клубок - к оэффициент набухания. Показывает, во сколько раз размеры полимерного клубка больше или меньше по сравнению с -растворителем В - растворителе клубок имеет такие размеры, как если бы растворителя не было вообще. Такие размеры называются «невозмущенными». Когда мы говорили об изолированном клубке, мы говорили о полимере в -растворителе
Слайд 29
1 Разбавленные растворы 2 Полуразбавленные и концентрированные растворы d >> 2R G d < 2R G Концентрация кроссовера ( cross over) ( C* ) : d = 2R G ; * = V пол./ V р-р = 1. Как из данных вискозиметрии оценить концентрацию кроссовера С*
Слайд 30
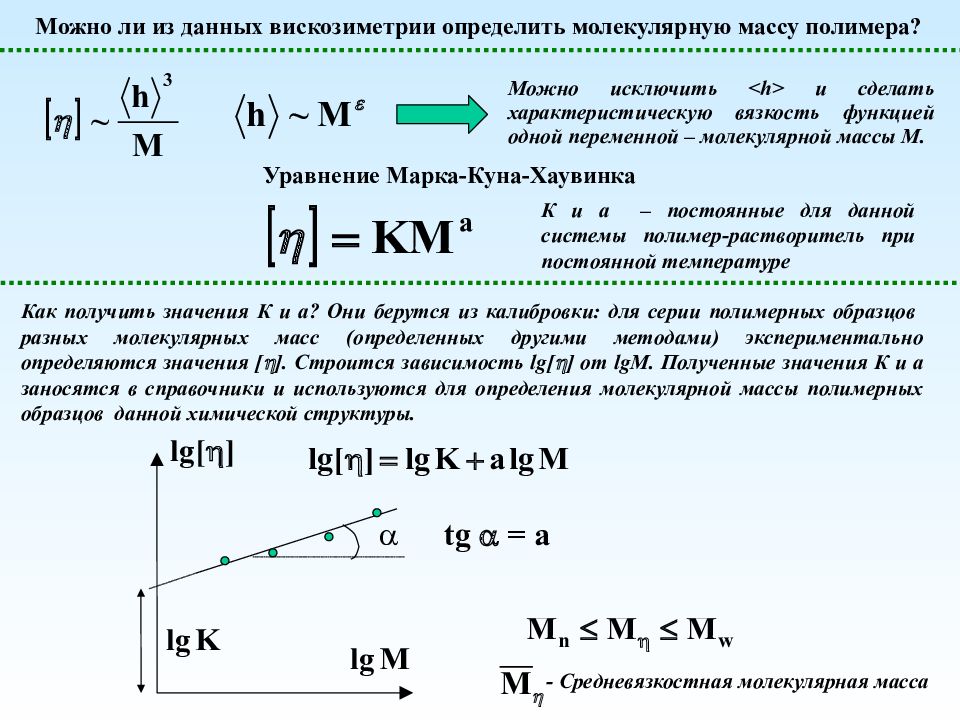
Можно ли из данных вискозиметрии определить молекулярную массу полимера? Можно исключить <h> и сделать характеристическую вязкость функцией одной переменной – молекулярной массы М. Уравнение Марка-Куна-Хаувинка К и а – постоянные для данной системы полимер-растворитель при постоянной температуре tg = a Как получить значения К и а? Они берутся из калибровки: для серии полимерных образцов разных молекулярных масс (определенных другими методами) экспериментально определяются значения [ ]. Строится зависимость lg[ ] от lgM. Полученные значения К и а заносятся в справочники и используются для определения молекулярной массы полимерных образцов данной химической структуры. - Средневязкостная молекулярная масса
Слайд 31
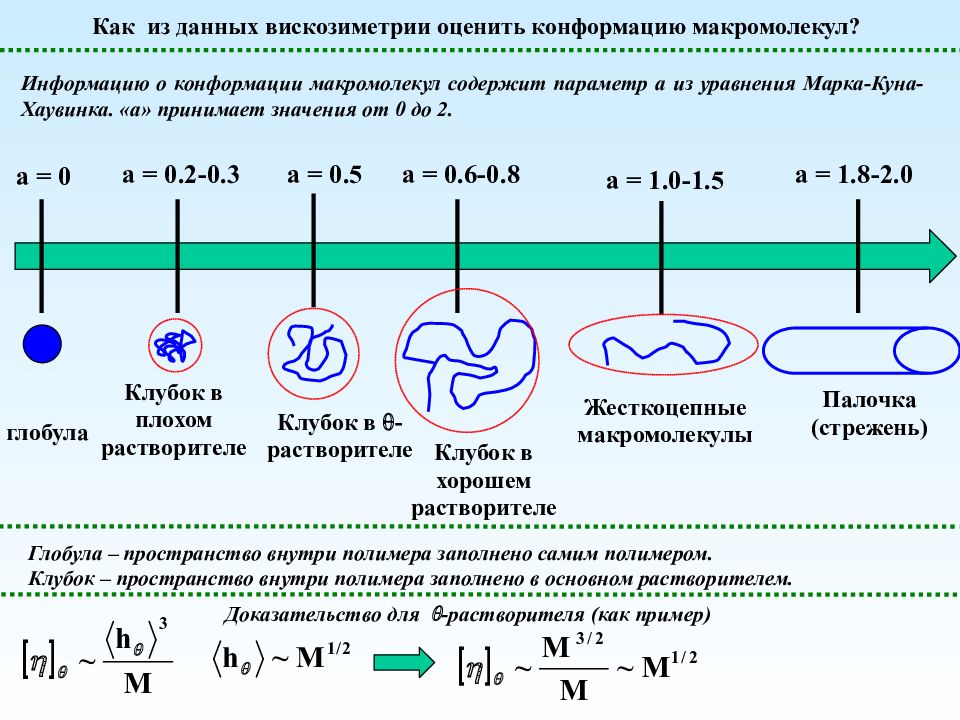
Как из данных вискозиметрии оценить конформацию макромолекул? Информацию о конформации макромолекул содержит параметр а из уравнения Марка-Куна-Хаувинка. «а» принимает значения от 0 до 2. а = 0 глобула а = 0.5 а = 0.2-0.3 а = 0.6-0.8 а = 1.0-1.5 а = 1.8-2.0 Клубок в плохом растворителе Клубок в - растворителе Клубок в хорошем растворителе Жесткоцепные макромолекулы Палочка (стрежень) Глобула – пространство внутри полимера заполнено самим полимером. Клубок – пространство внутри полимера заполнено в основном растворителем. Доказательство для -растворителя (как пример)
Слайд 32
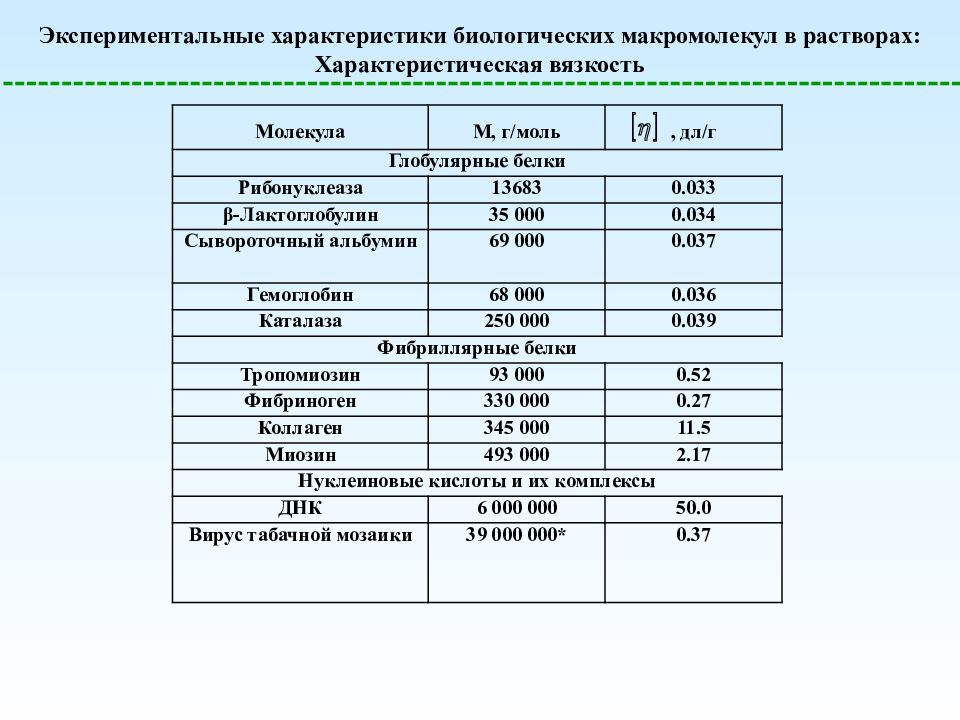
Экспериментальные характеристики биологических макромолекул в растворах: Характеристическая вязкость Молекула М, г/моль , дл/г Глобулярные белки Рибонуклеаза 13683 0.033 β-Лактоглобулин 35 000 0.034 Сывороточный альбумин 69 000 0.037 Гемоглобин 68 000 0.036 Каталаза 250 000 0.039 Фибриллярные белки Тропомиозин 93 000 0.52 Фибриноген 330 000 0.27 Коллаген 345 000 11.5 Миозин 493 000 2.17 Нуклеиновые кислоты и их комплексы ДНК 6 000 000 50.0 Вирус табачной мозаики 39 000 000* 0.37
Слайд 33
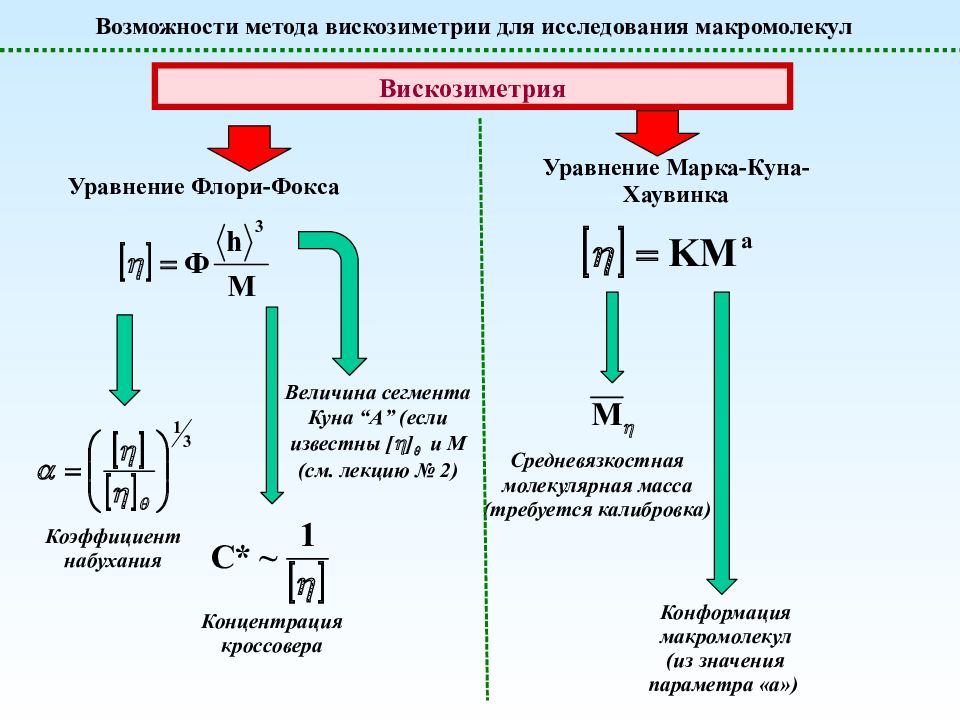
Возможности метода вискозиметрии для исследования макромолекул Вискозиметрия Уравнение Флори-Фокса Уравнение Марка-Куна-Хаувинка Коэффициент набухания Средневязкостная молекулярная масса (требуется калибровка) Конформация макромолекул (из значения параметра «а») Концентрация кроссовера Величина сегмента Куна “A” (если известны [ ] и M ( см. лекцию № 2)
Слайд 34
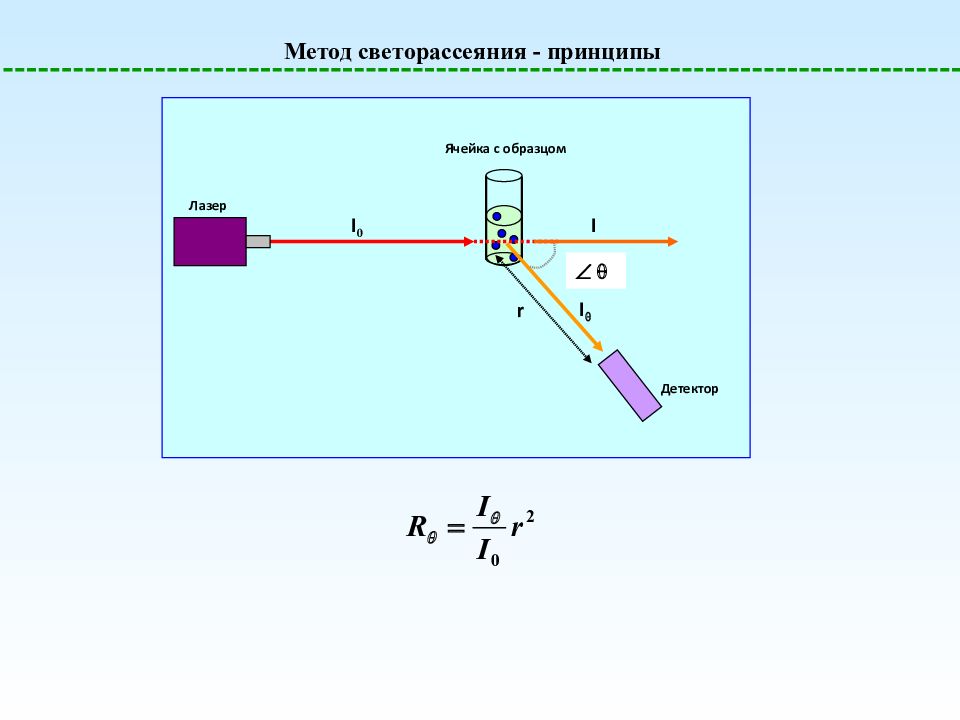
Метод светорассеяния - принципы Детектор Ячейка с образцом Лазер I 0 I I r
Слайд 35
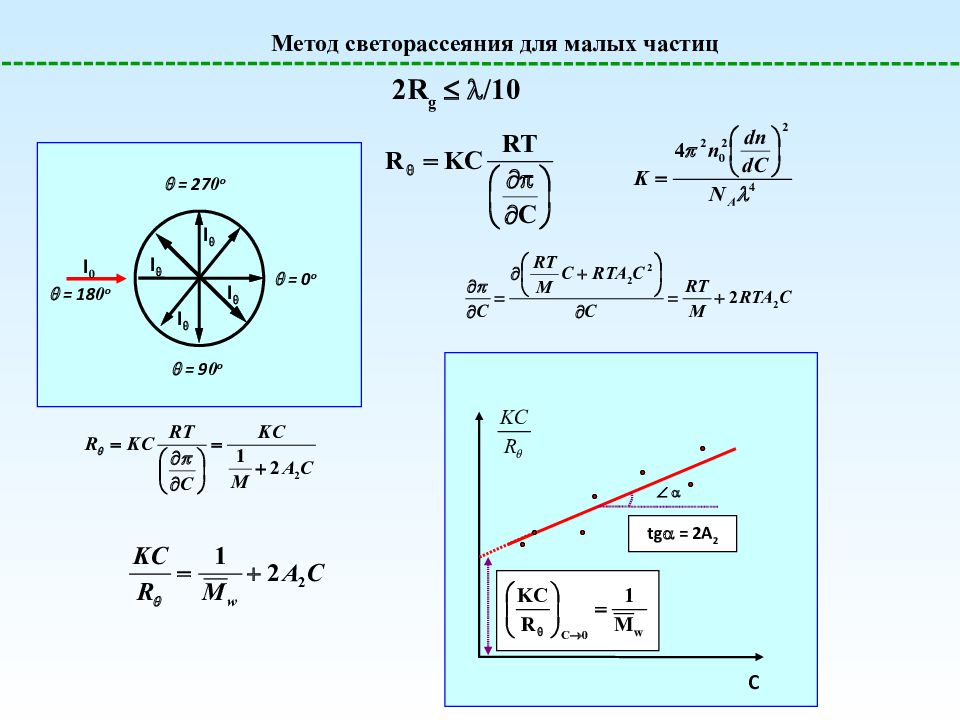
Метод светорассеяния для малых частиц 2R g /10 I 0 I I I I = 0 o = 9 0 o = 18 0 o = 27 0 o C tg = 2A 2
Последний слайд презентации: Полимерные растворы – условия образования Макромолекулы G 2 H 2 S 2 + Молекулы
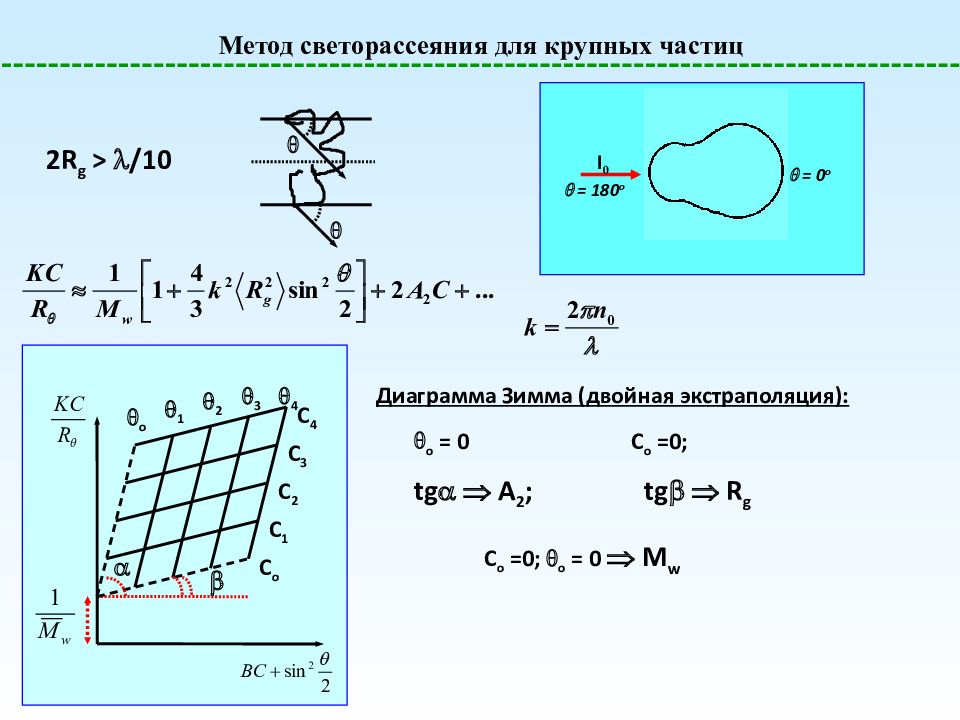
Метод светорассеяния для крупных частиц I 0 I I I I = 0 o = 90 o = 180 o = 270 o 2R g > /10 Диаграмма Зимма (двойная экстраполяция): 3 4 C 4 C 3 C 2 C 1 C o 2 1 o о = 0 tg A 2 ; С о =0; tg R g С о =0; о = 0 M w