Сложение и вычитание векторов Л.С. Атанасян "Геометрия 7-9" Савченко Е.М., учитель математики, МОУ гимназия №, г. Полярные Зори, Мурманской обл.
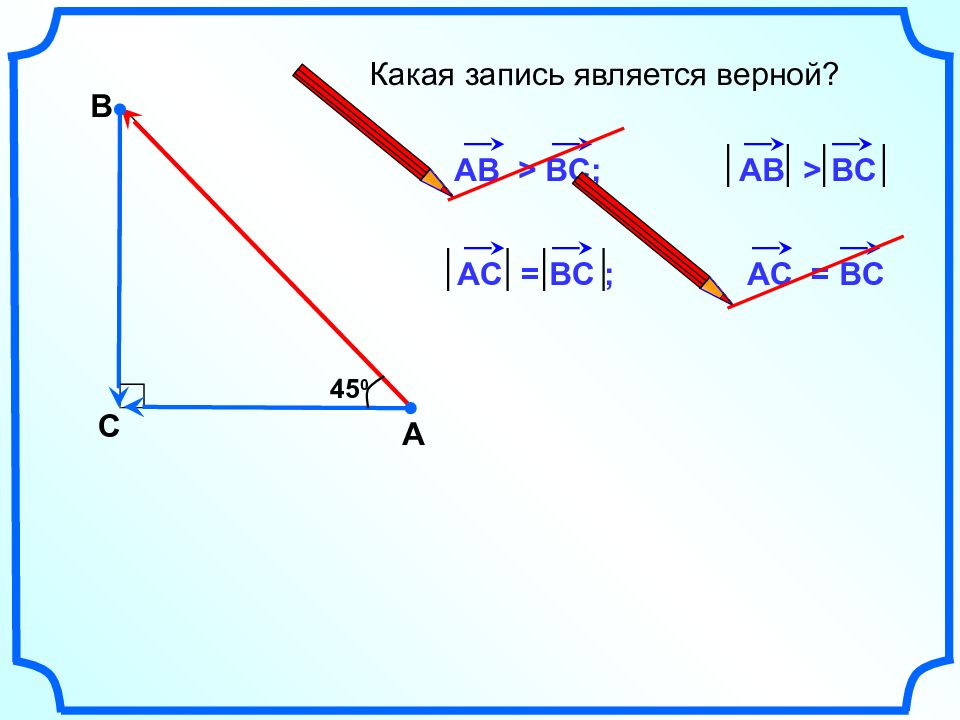
А В С Какая запись является верной? 45 0 A В > BC ; A В > BC AC = BC ; AC = BC
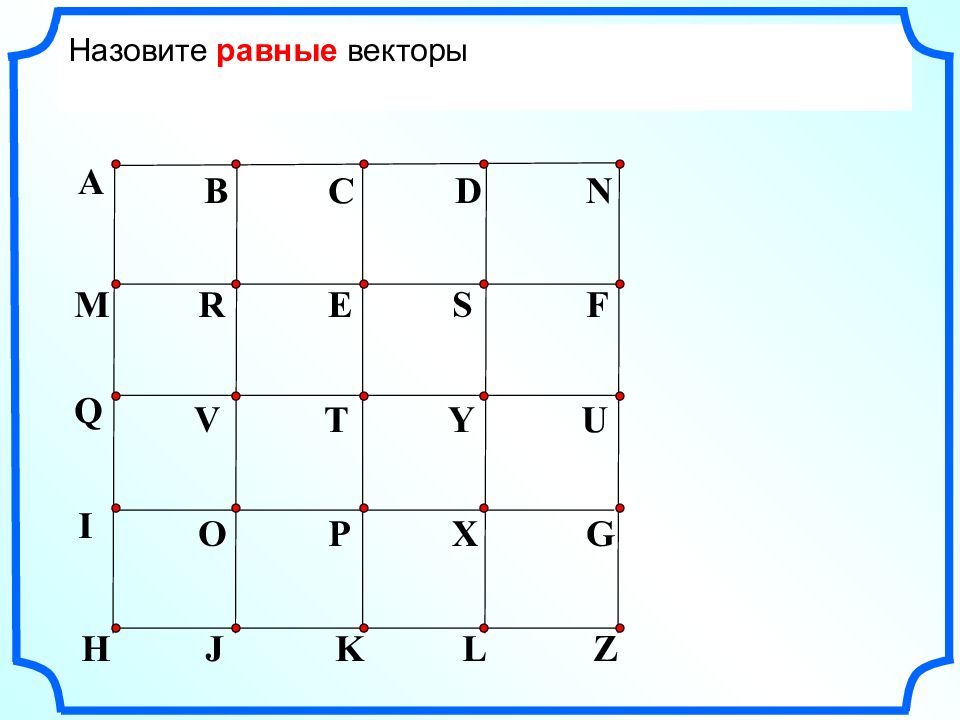
Назовите коллинеарные сонаправленные векторы Назовите коллинеарные противоположнонаправленные векторы A B C D N M R E S F H J K L Z I O P X G Q V T Y U Назовите равные векторы
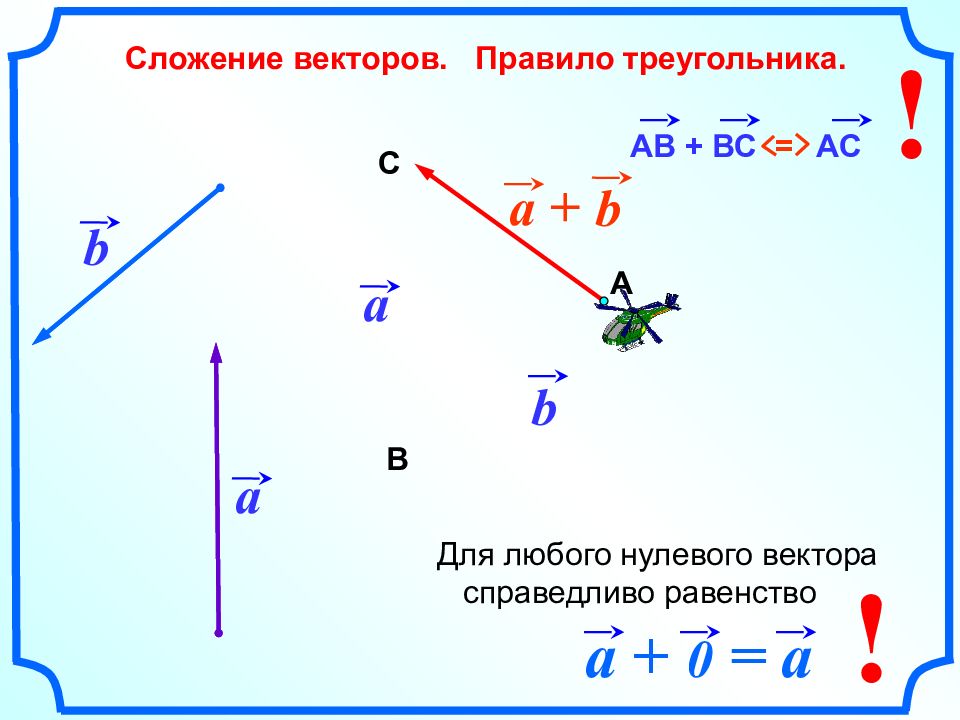
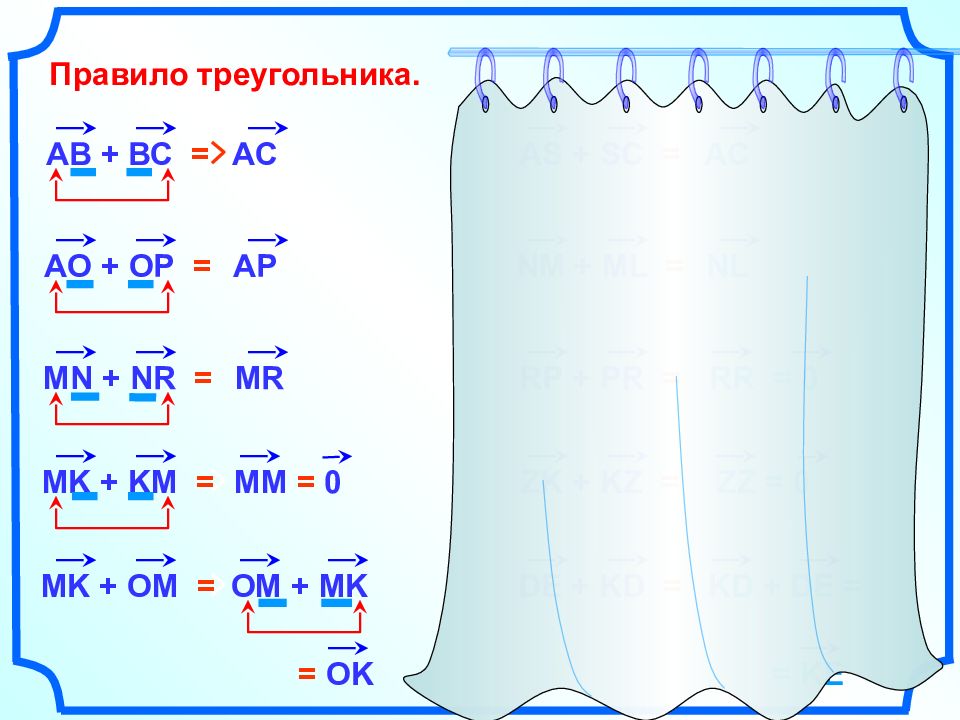
Сложение векторов. Правило треугольника. a a b b a + b А В С АВ + ВС = АС a + 0 = a ! ! Для любого нулевого вектора справедливо равенство
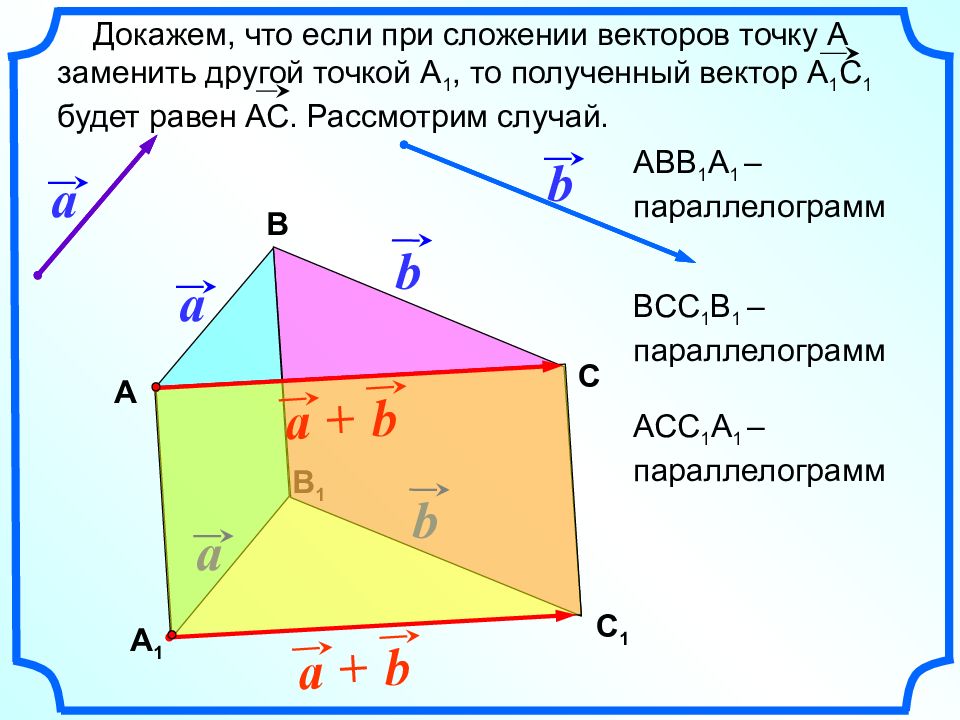
В 1 Докажем, что если при сложении векторов точку А заменить другой точкой А 1, то полученный вектор А 1 С 1 будет равен АС. Рассмотрим случай. a b В b a b a b a + А С b a + С 1 А 1 АВВ 1 А 1 – параллелограмм ВСС 1 В 1 – параллелограмм АСС 1 А 1 – параллелограмм
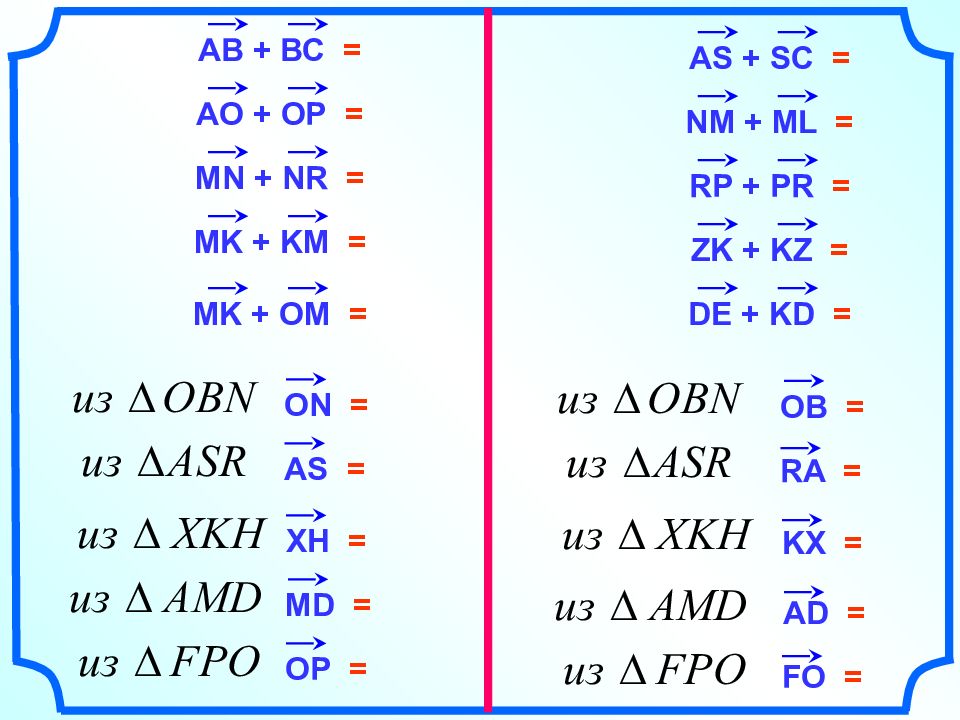
= OK АВ + ВС = Правило треугольника. АС АО + ОР = АР MN + NR = MR MK + KM = MM = 0 MK + OM = OM + MK = KE А S + S С = АС NM + ML = NL RP + PR = RR = 0 ZK + KZ = ZZ = 0 DE + KD = KD + DE =
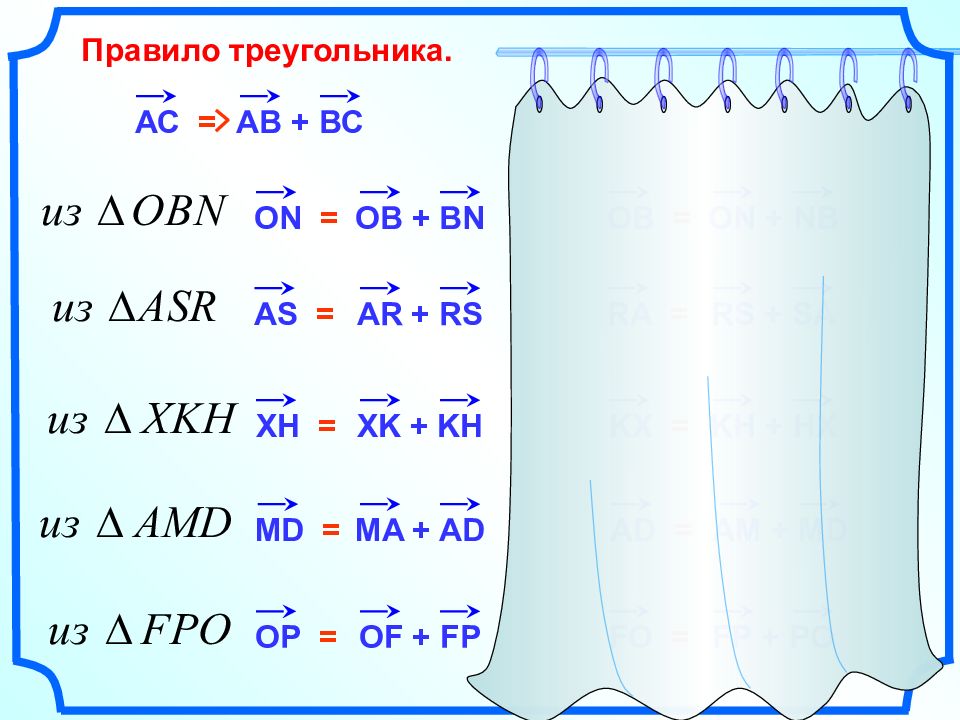
Правило треугольника. АС = АВ + ВС OB + В N ON = AR + RS AS = XK + KH XH = MA + AD MD = OF + FP OP = ON + N В OB = RS + SA RA = KH + HX KX = AM + MD AD = FP + PO FO =
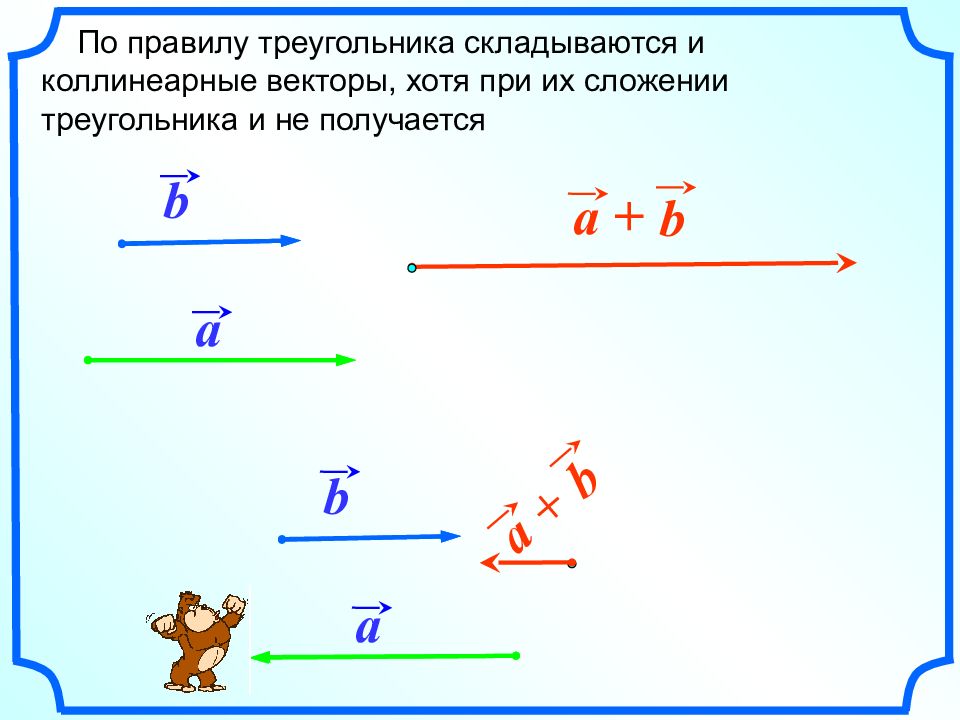
По правилу треугольника складываются и коллинеарные векторы, хотя при их сложении треугольника и не получается a b a + b a b a + b
a b a + b c f c + f
Законы сложения векторов Для любых векторов справедливы равенства: a, b, c 1 2 a + b = b + a переместительный закон сочетательный закон ( a + b ) + c = a + (b + c) ! ! Теорема
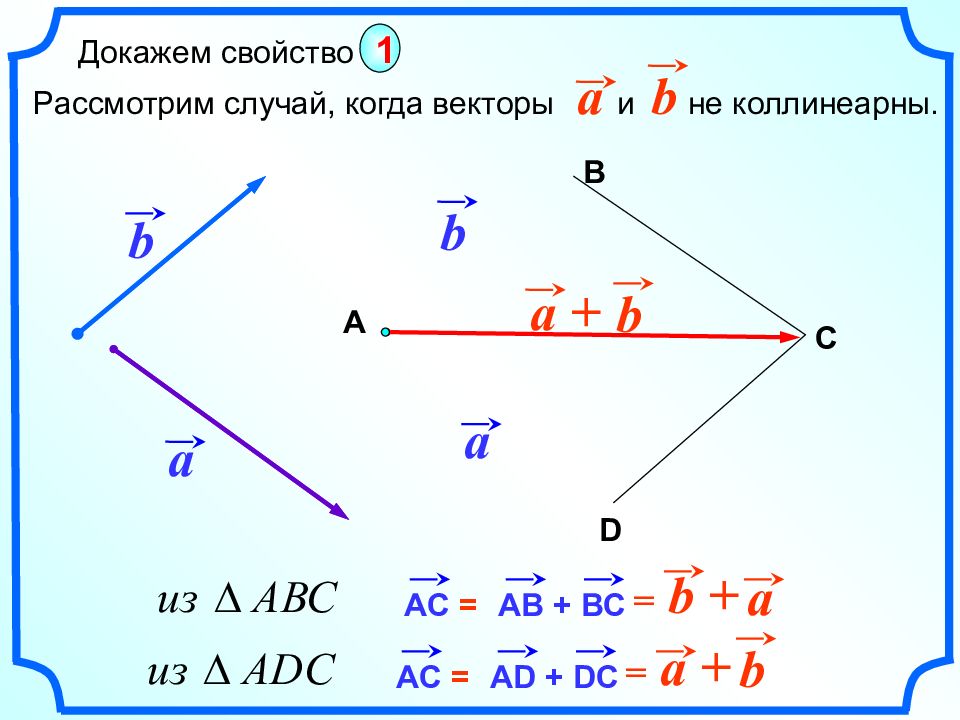
a a b b a + b А В D C АС = АВ + ВС a = b + АС = А D + D С b = a + Докажем свойство Рассмотрим случай, когда векторы и не коллинеарны. b a 1
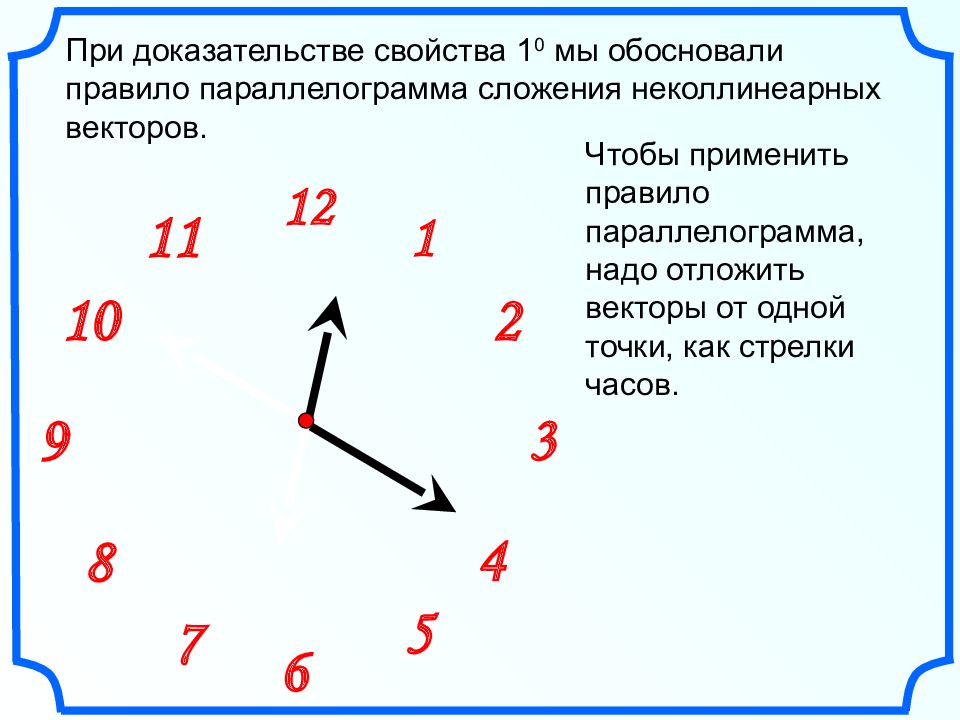
1 2 9 6 12 11 10 8 7 4 5 3 При доказательстве свойства 1 0 мы обосновали правило параллелограмма сложения неколлинеарных векторов. Чтобы применить правило параллелограмма, надо отложить векторы от одной точки, как стрелки часов.
Сложение векторов. Правило параллелограмма. 1 2 9 6 12 11 10 8 7 4 5 3 a b a+b a b
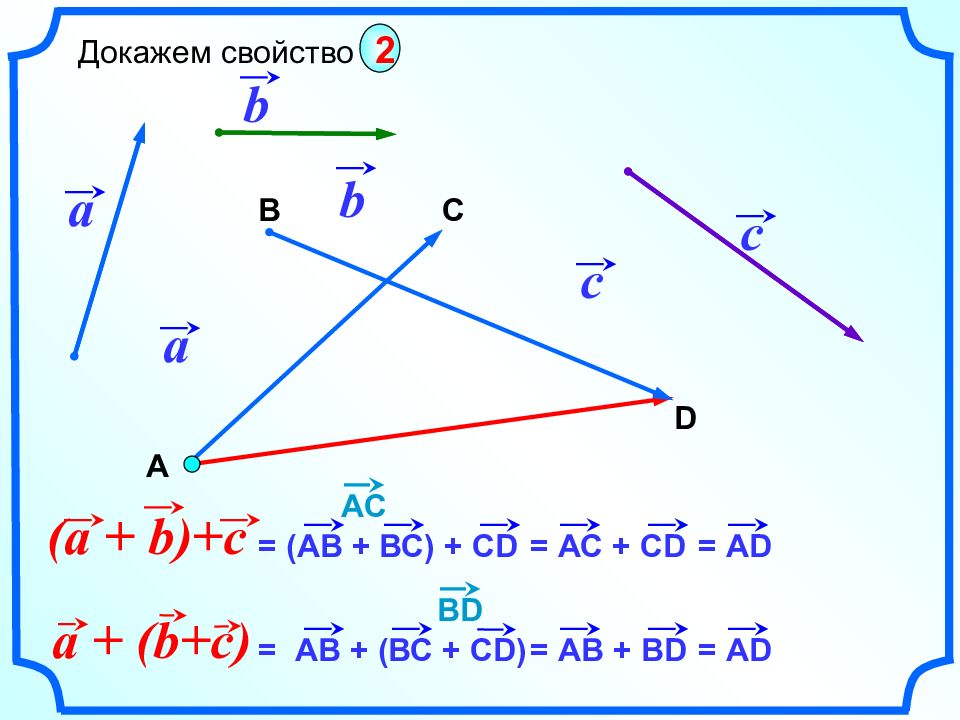
a a b b В D C (a + b)+c Докажем свойство 2 c c = ( АВ + ВС ) + CD А = АС + CD = А D А C a + (b+c) = АВ + ( ВС + CD) = А B + BD = А D BD
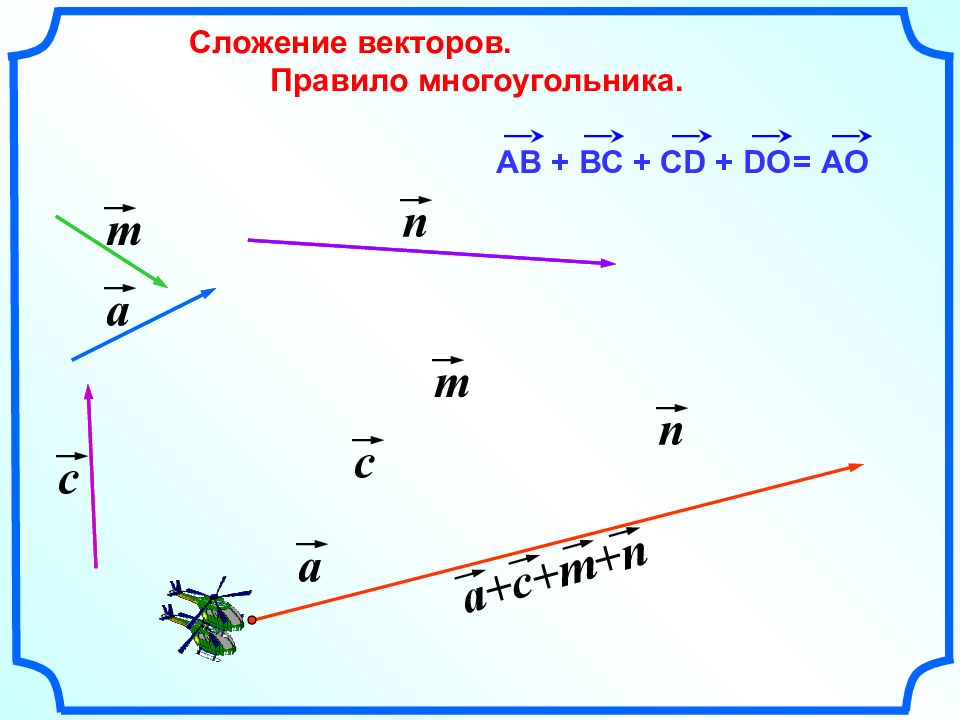
Сложение векторов. Правило многоугольника. = А O АВ + ВС + С D + DO a c n m c m n a+c+m+n a
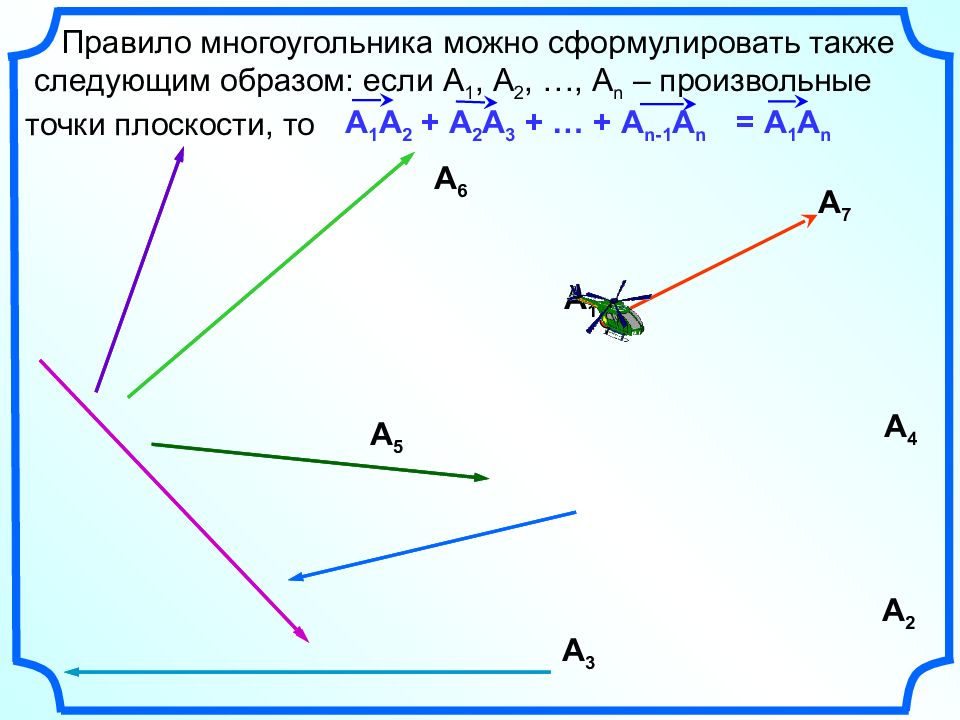
Правило многоугольника можно сформулировать также следующим образом: если А 1, А 2, …, А n – произвольные точки плоскости, то = А 1 A n А 1 А 2 + А 2 А 3 + … + А n-1 A n А 2 А 3 А 4 А 5 А 6 А 7 А 1
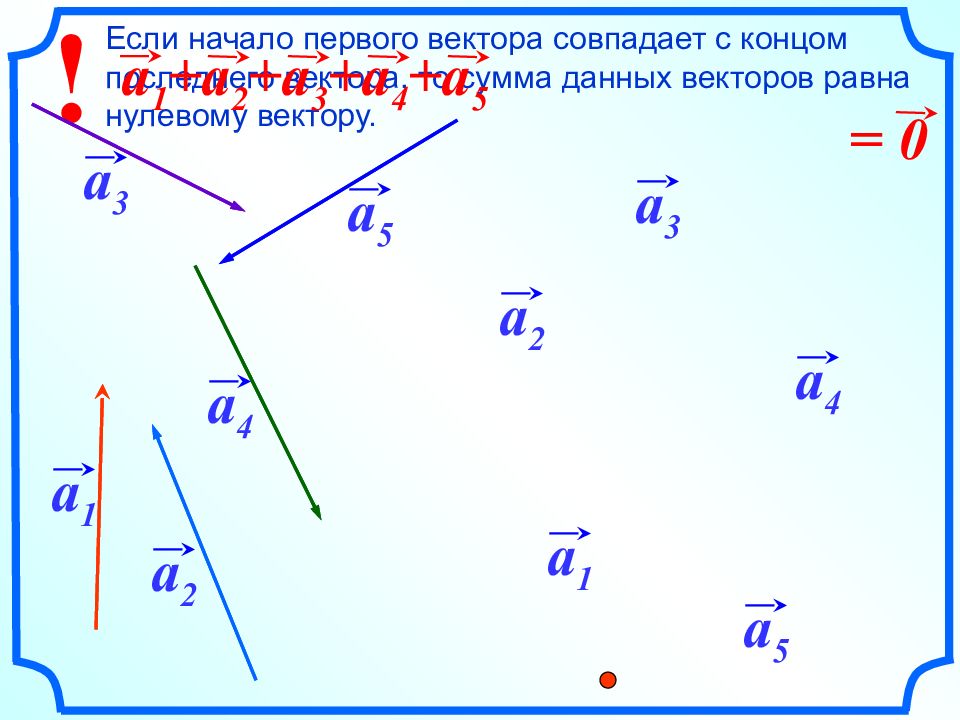
! Если начало первого вектора совпадает с концом последнего вектора, то сумма данных векторов равна нулевому вектору. a 1 +a 2 +a 3 +a 4 +a 5 = 0 a 1 a 1 a 2 a 2 a 3 a 4 a 5 a 3 a 4 a 5
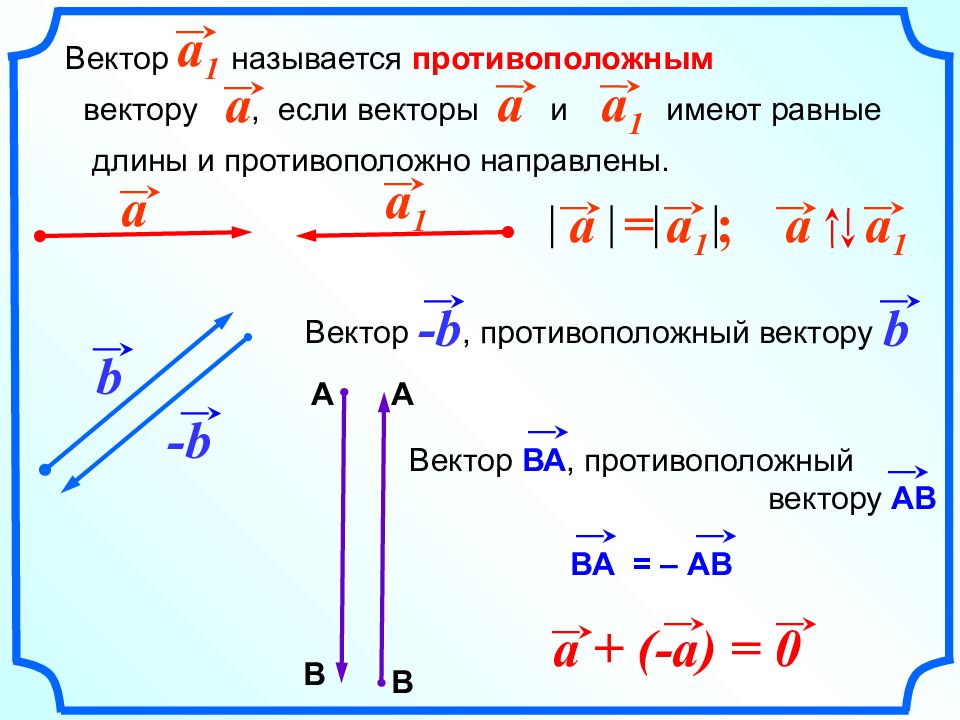
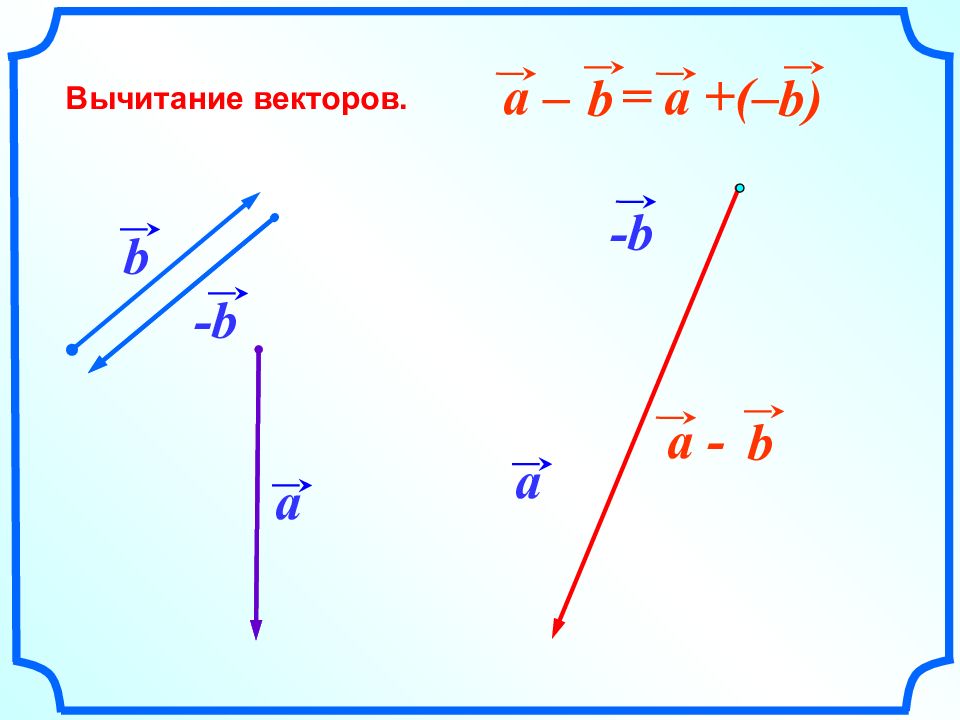
Вектор называется противоположным вектору, если векторы и имеют равные длины и противоположно направлены. a 1 b - b a a a 1 - b b Вектор, противоположный вектору А В А В Вектор ВА, противоположный вектору АВ a + (-a) = 0 ВА = – АВ a a 1 a = a 1 ; a a 1
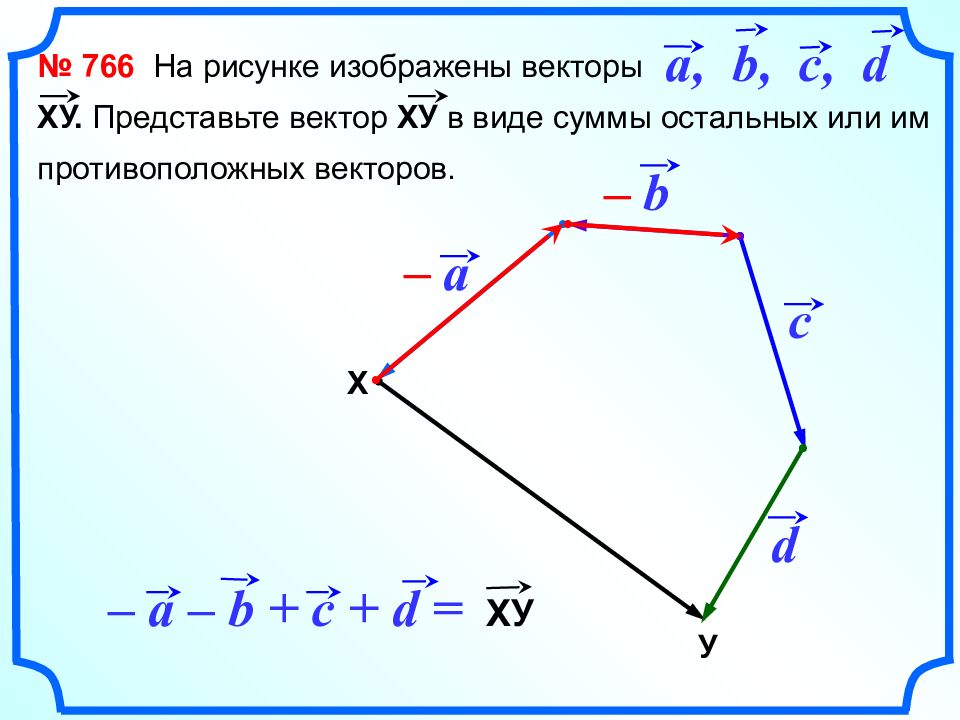
a b № 766 На рисунке изображены векторы ХУ. Представьте вектор ХУ в виде суммы остальных или им противоположных векторов. a, b, c, d c d У Х – a – b + c + d = ХУ – –
Вычитание векторов. a a - b b a - b b a – = a +(– b ) - b
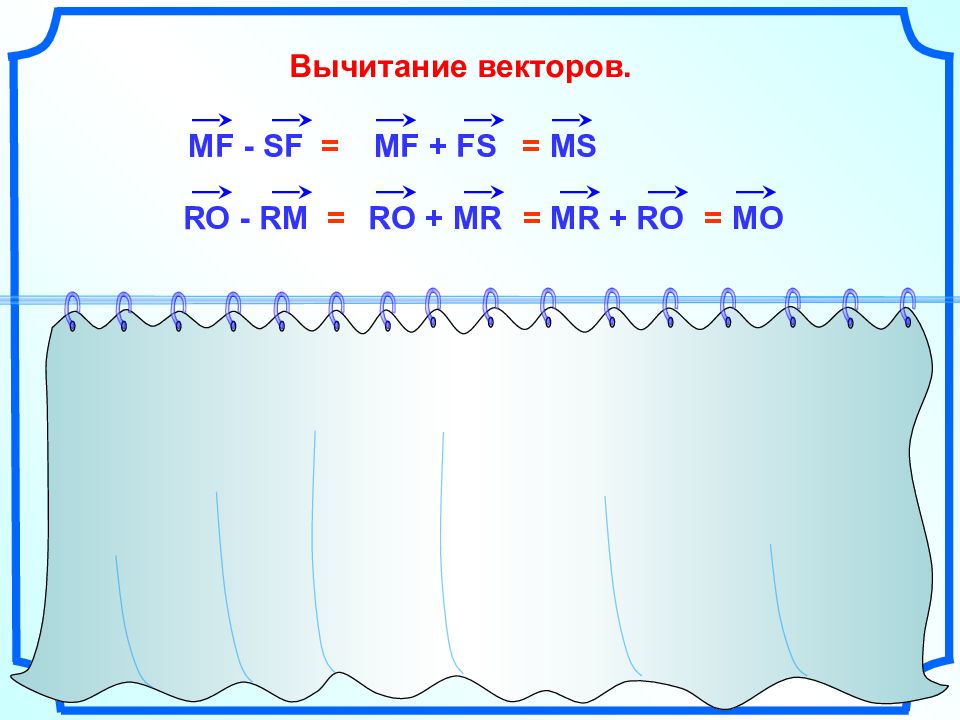
Вычитание векторов. MF - SF = MF + FS = MS RO - RM = RO + MR = MR + RO MD - SD = MD + DS = MS - OS - ST = SO + TS = TS + SO RO - AO = RO + OA = RA RO - RO = RO + OR = RR = 0 = TO = MO
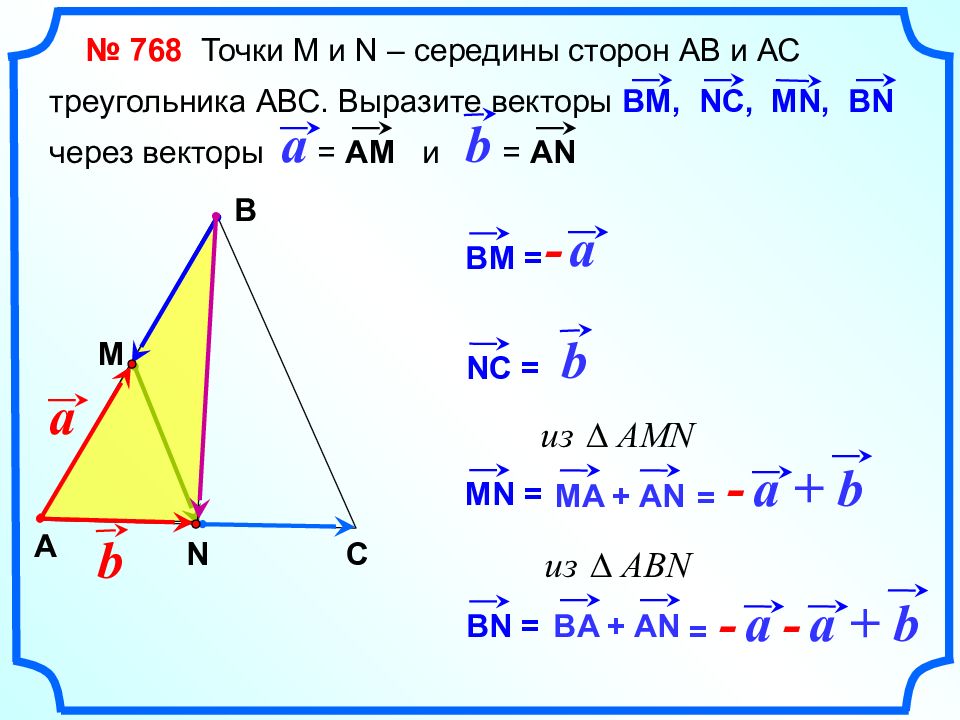
№ 768 Точки М и N – середины сторон АВ и АС треугольника АВС. Выразите векторы ВМ, NC, MN, BN через векторы = АМ и = А N a b С ВМ = a - NC = MN = b MA + AN - = a + b BN = BA + AN = - a + b - a В А М N a b
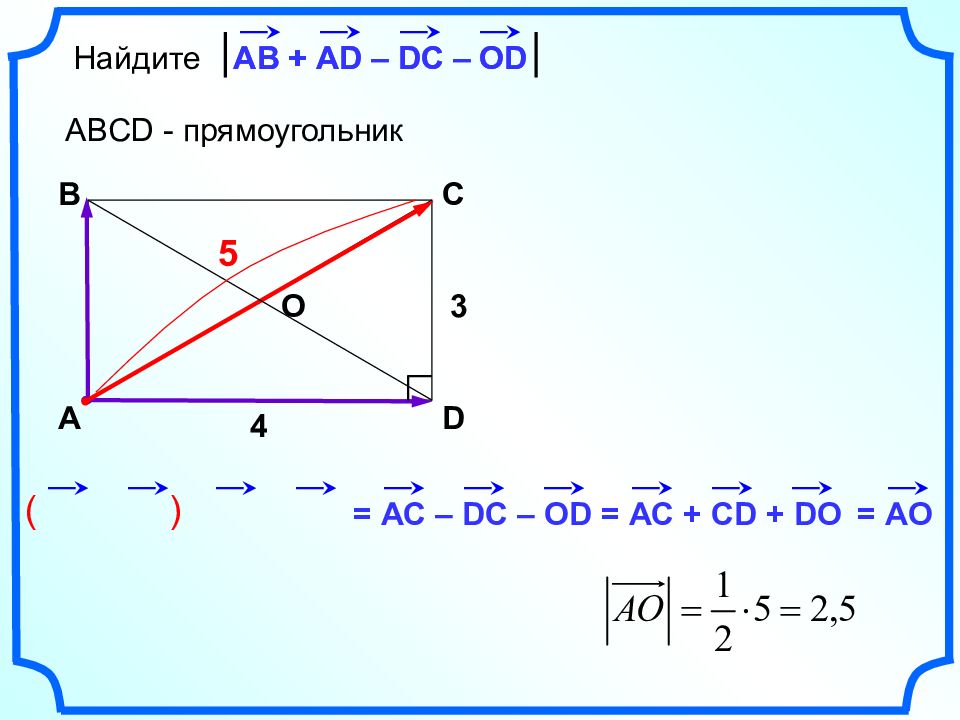
( ) Найдите АВ + AD – DC – OD ABCD - прямоугольник А B C D АВ + AD – DC – OD = АС – DC – OD = АС + CD + DO = АО О 3 4 5
АВ + ВС = АО + ОР = MN + NR = MK + KM = MK + OM = А S + S С = NM + ML = RP + PR = ZK + KZ = DE + KD = ON = AS = XH = MD = OP = OB = RA = KX = AD = FO =
