Слайд 2: Сопряженные диаметры
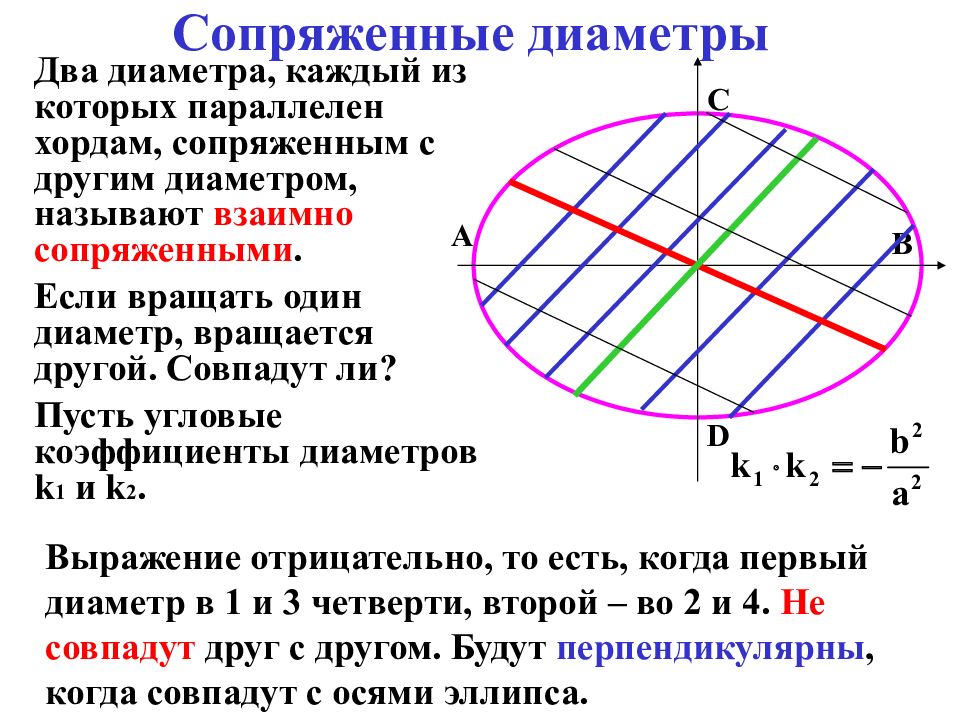
A B C D Два диаметра, каждый из которых параллелен хордам, сопряженным с другим диаметром, называют взаимно сопряженными. Если вращать один диаметр, вращается другой. Совпадут ли? Пусть угловые коэффициенты диаметров k 1 и k 2. Выражение отрицательно, то есть, когда первый диаметр в 1 и 3 четверти, второй – во 2 и 4. Не совпадут друг с другом. Будут перпендикулярны, когда совпадут с осями эллипса.
Слайд 3: Касательная к эллипсу
Касательной к кривой второго порядка называют предельное положение секущей М 0 М 1, когда М 1 совпадает с М 0. М 0 (х 0 ;у 0 ) М 1 (х 1 ;у 1 ) Будем искать уравнение прямой в виде y -у 0 = k(x-x 0 ). 2. Угловой коэффициент касательной равен угловому коэффициенту хорд, сопряженных диаметру, проведенному в точку касания.
Слайд 5: Оптическое свойство эллипса
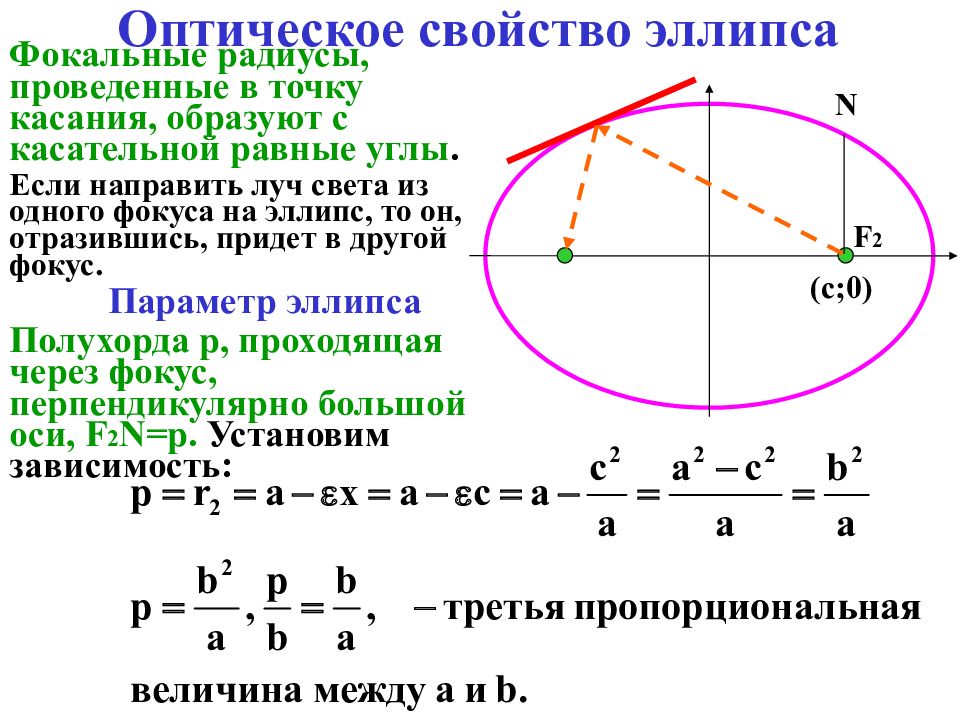
Фокальные радиусы, проведенные в точку касания, образуют с касательной равные углы. Если направить луч света из одного фокуса на эллипс, то он, отразившись, придет в другой фокус. Параметр эллипса Полухорда p, проходящая через фокус, перпендикулярно большой оси, F 2 N=p. Установим зависимость: N F 2 (c;0)
Слайд 6: Построение эллипса и параметрические уравнения
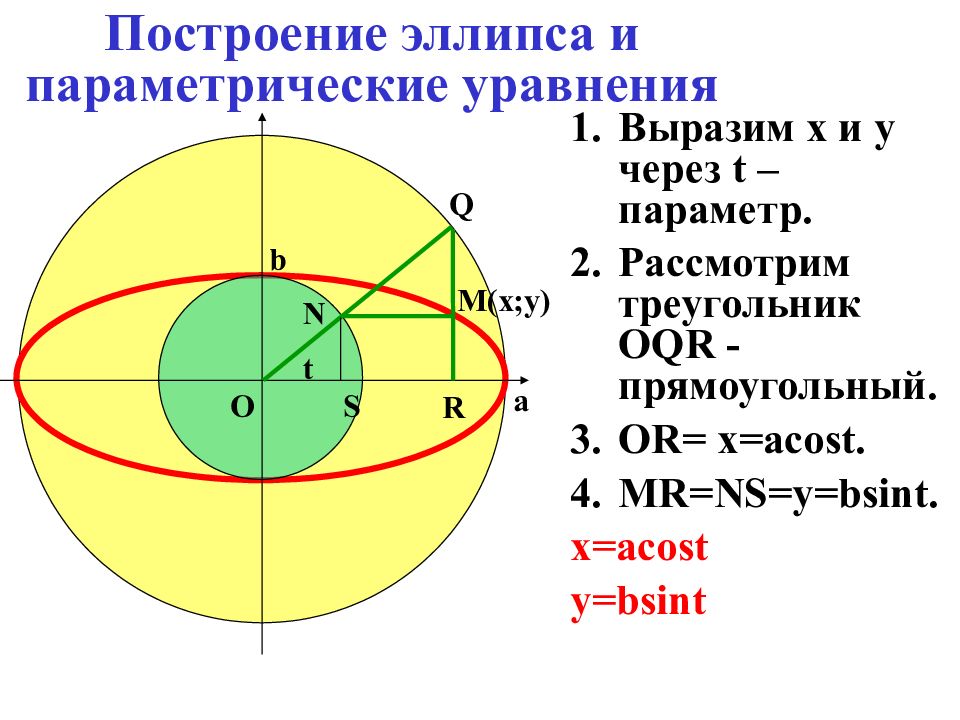
Выразим х и у через t – параметр. Рассмотрим треугольник OQR - прямоугольный. OR= x = acost. MR=NS=y=bsint. x = acost y=bsint Q N R M(x;y) t a b O S
Слайд 7: Уравнение эллипса в полярных координатах
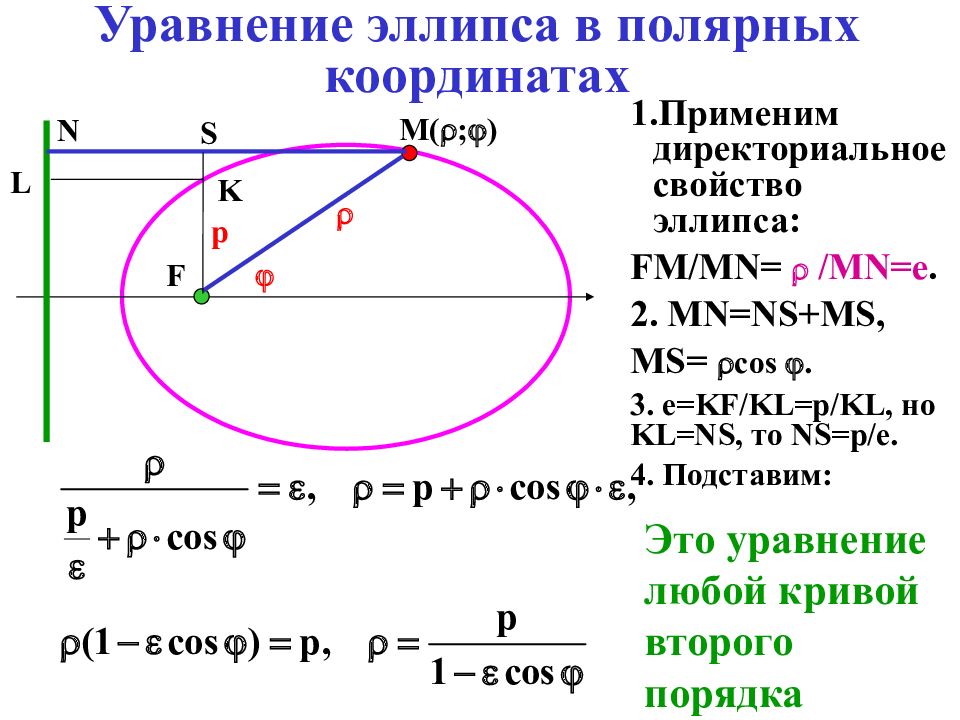
Применим директориальное свойство эллипса: FM/MN= /MN=e. 2. MN=NS+MS, MS= cos . 3. e=KF/KL = p/KL, но KL=NS, то NS=p/e. 4. Подставим: М( ;) F р N L K S Это уравнение любой кривой второго порядка
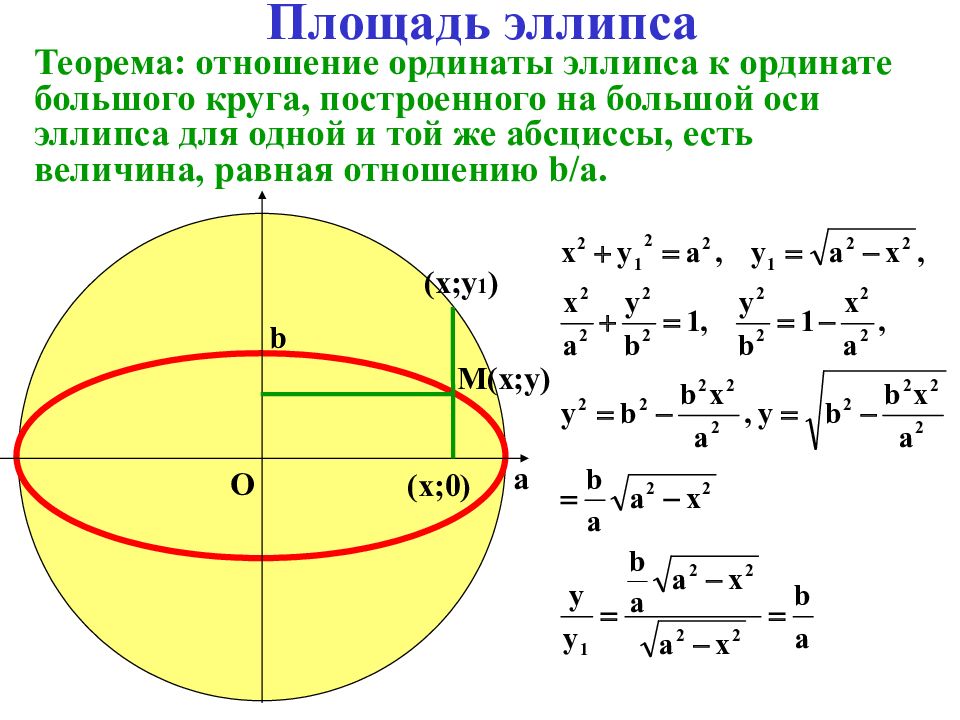
Слайд 8: Площадь эллипса
Теорема: отношение ординаты эллипса к ординате большого круга, построенного на большой оси эллипса для одной и той же абсциссы, есть величина, равная отношению b/a. (х;у 1 ) (х;0) M(x;y) a b O
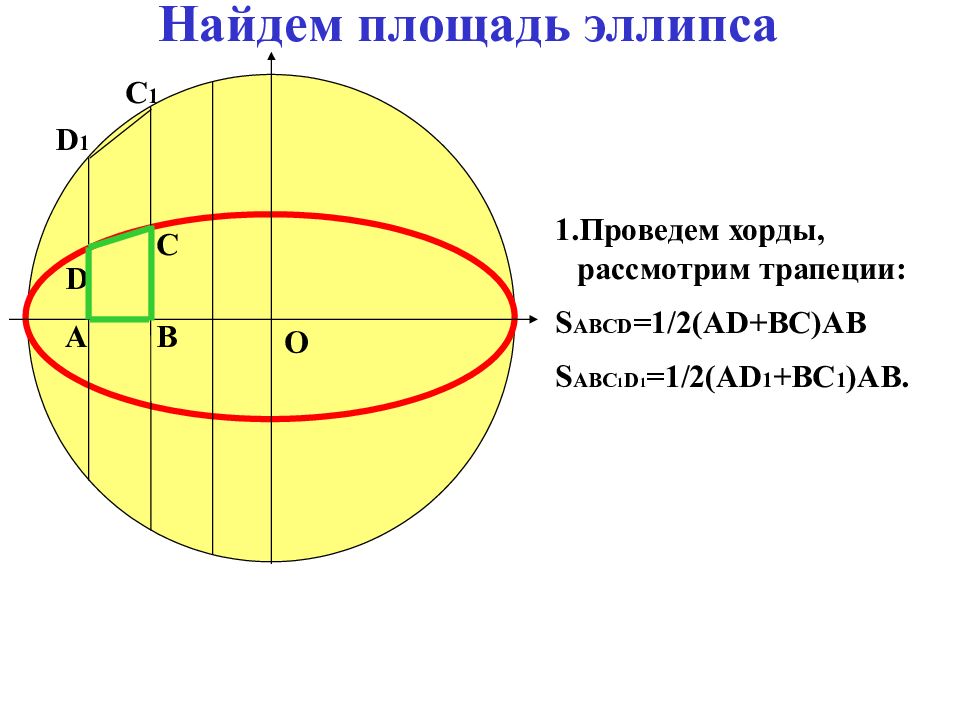
Слайд 9: Найдем площадь эллипса
O А В С D D 1 С 1 Проведем хорды, рассмотрим трапеции: S ABCD =1/2(AD+BC)AB S ABC 1 D 1 =1/2(AD 1 +BC 1 )AB.
Последний слайд презентации: Лекция №6 Линии второго порядка. Эллипс: Приведение уравнения общего вида кривой второго порядка к каноническому виду
Алгоритм Преобразование уравнения на базе формул переноса системы координат. Вычисляем х0 и у0, приравнивая нулю коэффициенты при х ’ и y’. Подставляем в уравнение и вычисляем свободный член. Вычисление угла, на который надо повернуть систему координат, чтобы ее оси были параллельны осям кривой. Составление формул поворота системы координат с учетом вычисленного угла. Преобразование уравнения на базе формул поворота системы координат. Расположение членов уравнения по степеням Х,У. Переносим в правую часть свободный член и делим на это число и левую и правую часть.