Первый слайд презентации: Плоскость в пространстве
Общее уравнение плоскости Уравнение плоскости в отрезках Уравнение плоскости, проходящей через три точки Угол между двумя плоскостями Расстояние от точки до плоскости
Слайд 2: Общее уравнение плоскости
Если в пространстве фиксирована произвольная декартова система координат Oxyz, то всякое уравнение первой степени с тремя переменными x y z определяет относительно этой системы плоскость. A; B; C; D – некоторые постоянные, причем из чисел A; B; C хотя бы одно отлично от нуля. (1) Общее уравнение плоскости Пусть точка М 0 ( x 0 ; y 0 ; z 0 ) принадлежит плоскости: (2) Вычтем из уравнения (1) тождество (2): ( 3 ) Общее уравнение плоскости
Слайд 3: Общее уравнение плоскости
Произвольная точка М( x; y; z) лежит на плоскости, если ее координаты удовлетворяют уравнению (3): М 0 М Уравнение (3) является условием перпендикулярности двух векторов: и Таким образом, точка М лежит в плоскости, если Значит перпендикулярен любому вектору, лежащему в плоскости и, следовательно, самой плоскости. Нормальный вектор плоскости Общее уравнение плоскости называется полным, если все коэффициенты А; B; C; D отличны от нуля. В противном случае уравнение называется неполным.
Слайд 4: Общее уравнение плоскости
1) Виды неполных уравнений : 2) 3) 4) 5) Плоскость проходит через точку О. y z 0 x 6) 7) 8) 9) 10)
Слайд 5: Уравнение плоскости в отрезках
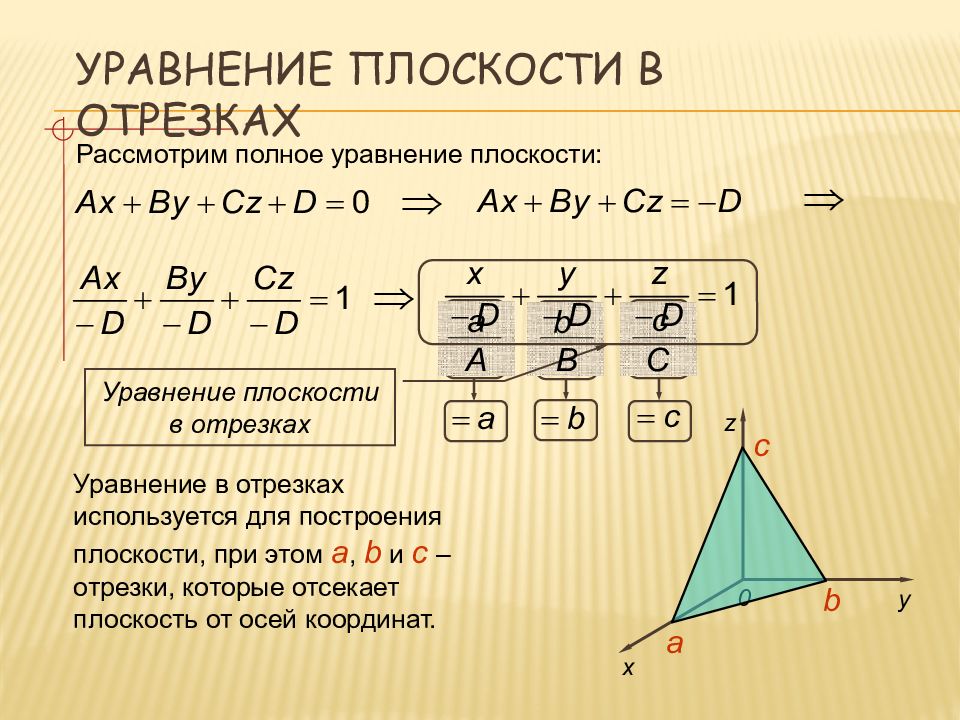
Рассмотрим полное уравнение плоскости: Уравнение в отрезках используется для построения плоскости, при этом a, b и с – отрезки, которые отсекает плоскость от осей координат. Уравнение плоскости в отрезках y z 0 x a b с
Слайд 6: Уравнение плоскости, проходящей через три точки
Пусть точки М 1 (х 1 ; у 1 ; z 1 ), М 2 (х 2 ; у 2 ; z 2 ) и М 3 (х 3 ; у 3 ; z 3 ) не лежат на одной прямой. Тогда векторы: и не коллинеарны. М 1 М 2 М 3 М Точка М(х ; у ; z ) лежит в одной плоскости с точками М 1, М 2 и М 3 только в том случае, если векторы: и компланарны. Уравнение плоскости, проходящей через 3 точки
Слайд 7: Угол между двумя плоскостями
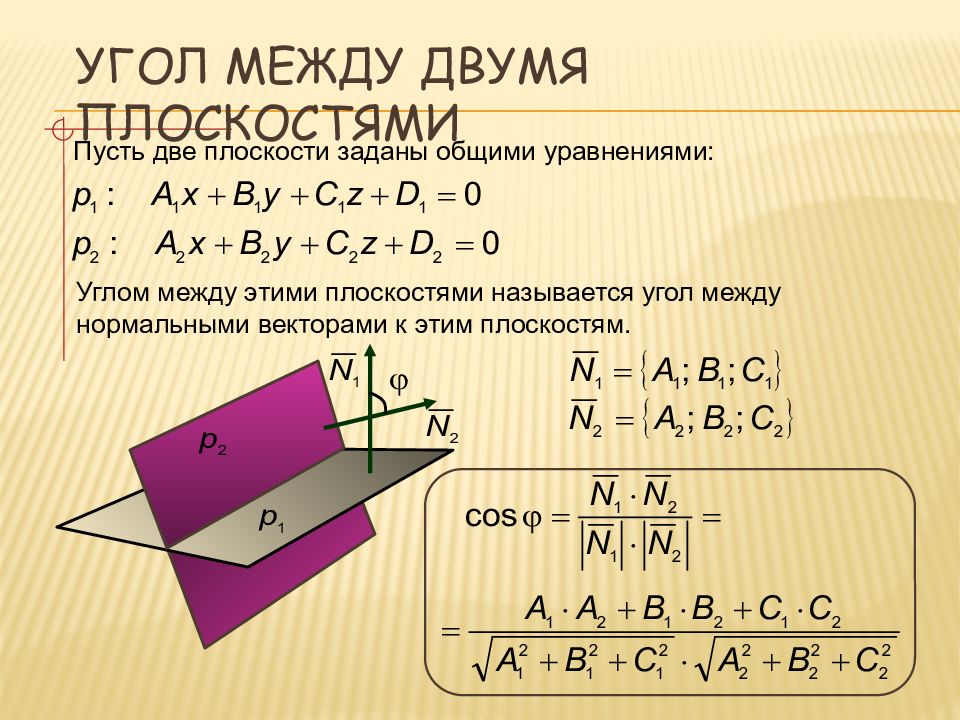
Пусть две плоскости заданы общими уравнениями: Углом между этими плоскостями называется угол между нормальными векторами к этим плоскостям.
Слайд 8: Угол между двумя плоскостями
Условия параллельности и перпендикулярности плоскостей аналогичны условию параллельности и перпендикулярности нормальных векторов:
Слайд 9: Расстояние от точки до плоскости
Пусть точка М 1 ( x 1 ; y 1 ; z 1 ) – основание перпендикуляра, опущенного из точки М 0 ( x 0 ; y 0 ; z 0 ) на плоскость М 1 М 0
Слайд 10: Пример
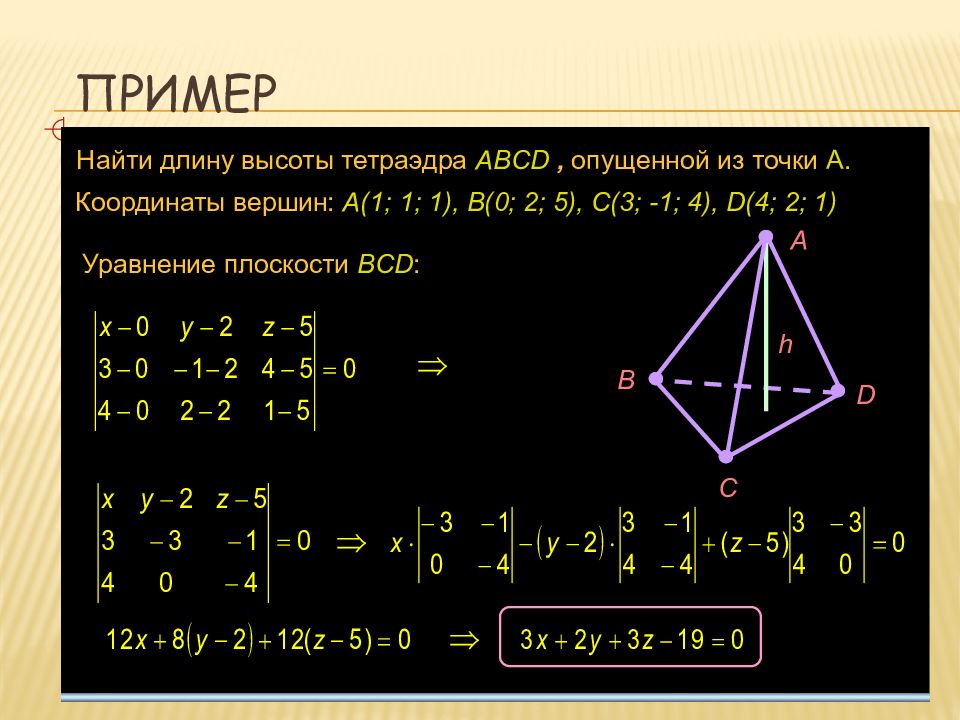
Найти длину высоты тетраэдра ABCD, опущенной из точки A. Координаты вершин: A(1; 1; 1), B(0; 2; 5), C(3; -1; 4), D (4 ; 2 ; 1 ) Уравнение плоскости BCD : A B С D h
Слайд 12: Прямая в пространстве
Каноническое уравнение прямой Параметрическое уравнение прямой Уравнение прямой, как линии пересечения двух плоскостей Угол между двумя прямыми Угол между прямой и плоскостью Условие принадлежности двух прямых одной плоскости Точка пересечения прямой и плоскости
Слайд 13: Каноническое уравнение прямой
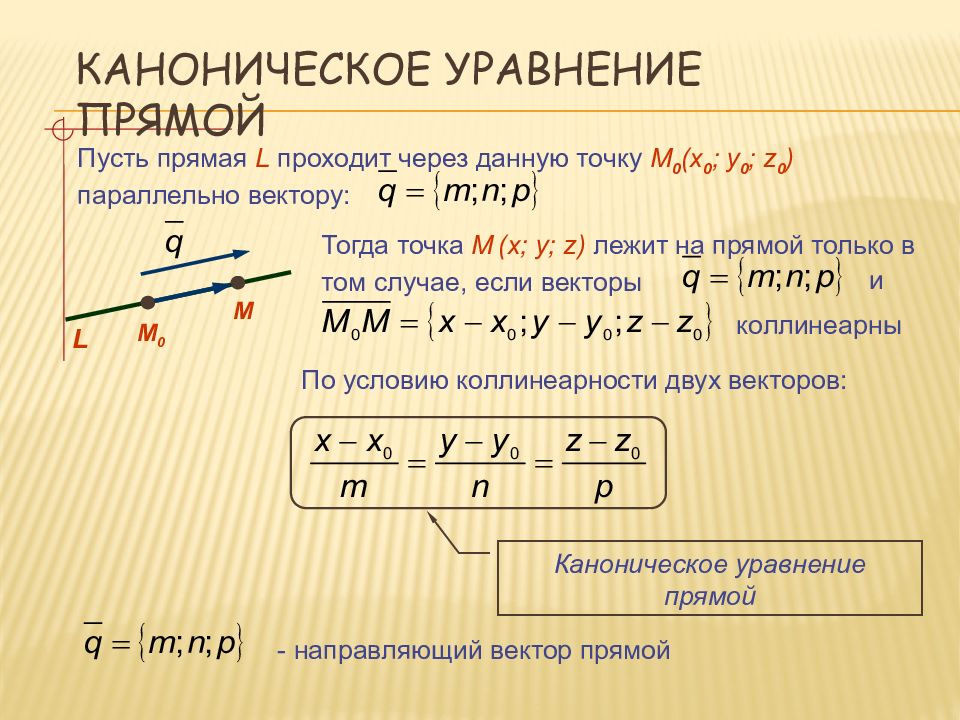
Пусть прямая L проходит через данную точку М 0 ( x 0 ; y 0 ; z 0 ) параллельно вектору: Каноническое уравнение прямой М 0 L М Тогда точка М ( x; y; z) лежит на прямой только в том случае, если векторы и коллинеарны По условию коллинеарности двух векторов: - направляющий вектор прямой
Слайд 14: Каноническое уравнение прямой
Пусть прямая проходит через две заданные и отличные друг от друга точки: М 1 (х 1 ; у 1 ; z 1 ) и М 2 (х 2 ; у 2 ; z 2 ). М 1 М 2 Тогда в качестве направляющего вектора в каноническом уравнении можно взять вектор: Уравнение прямой, проходящей через две заданные точки L
Слайд 15: Параметрическое уравнение прямой
При решении многих практических задач используют параметрическое уравнение прямой, которое получается из канонического уравнения: Параметрическое уравнение прямой
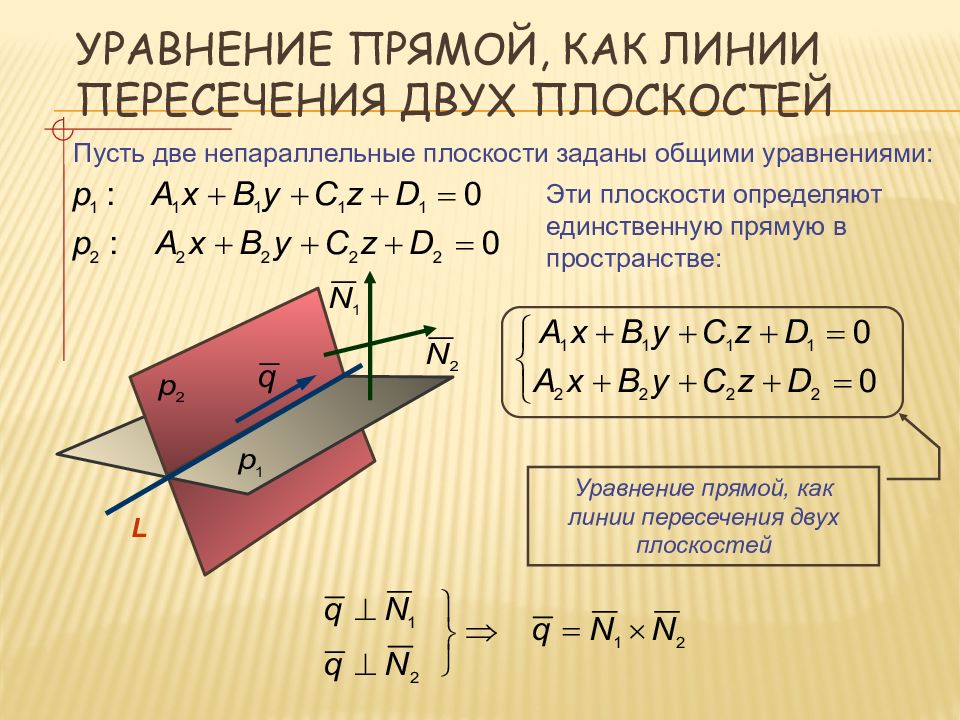
Слайд 16: Уравнение прямой, как линии пересечения двух плоскостей
Пусть две непараллельные плоскости заданы общими уравнениями: Эти плоскости определяют единственную прямую в пространстве: L Уравнение прямой, как линии пересечения двух плоскостей
Слайд 17: Пример
Написать каноническое уравнение прямой: Найдем точку, принадлежащую прямой, то есть удовлетворяющую системе уравнений. Пологая z равному любому числу, например, z = 0, получим: Точка M 0 (11; -8; 0) – принадлежит прямой Найдем координаты направляющего вектора прямой:
Слайд 18: Угол между прямыми
Пусть две прямые заданы каноническими уравнениями: Углом между этими прямыми называется угол между направляющими векторами к этим прямым. L 1 L 2
Слайд 19: Угол между прямой и плоскостью
Пусть прямая L задана каноническим уравнением: Плоскость p задана общим уравнением: Углом между прямой и плоскостью называется угол между прямой и проекцией этой прямой на плоскость. L р
Слайд 20: Условие принадлежности двух прямых одной плоскости
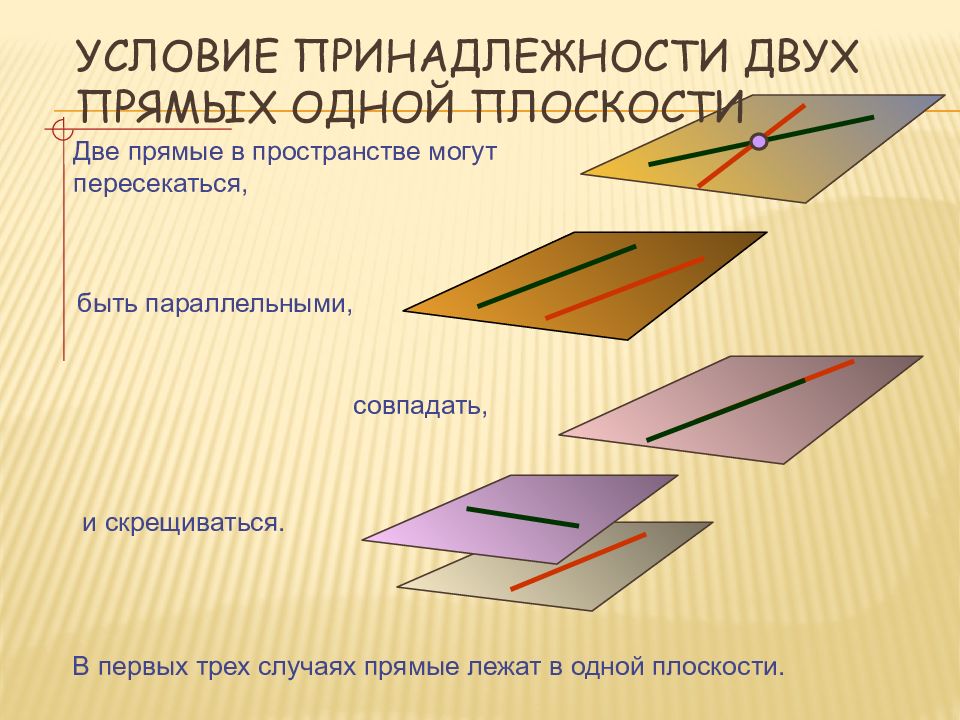
Две прямые в пространстве могут пересекаться, быть параллельными, и скрещиваться. совпадать, В первых трех случаях прямые лежат в одной плоскости.
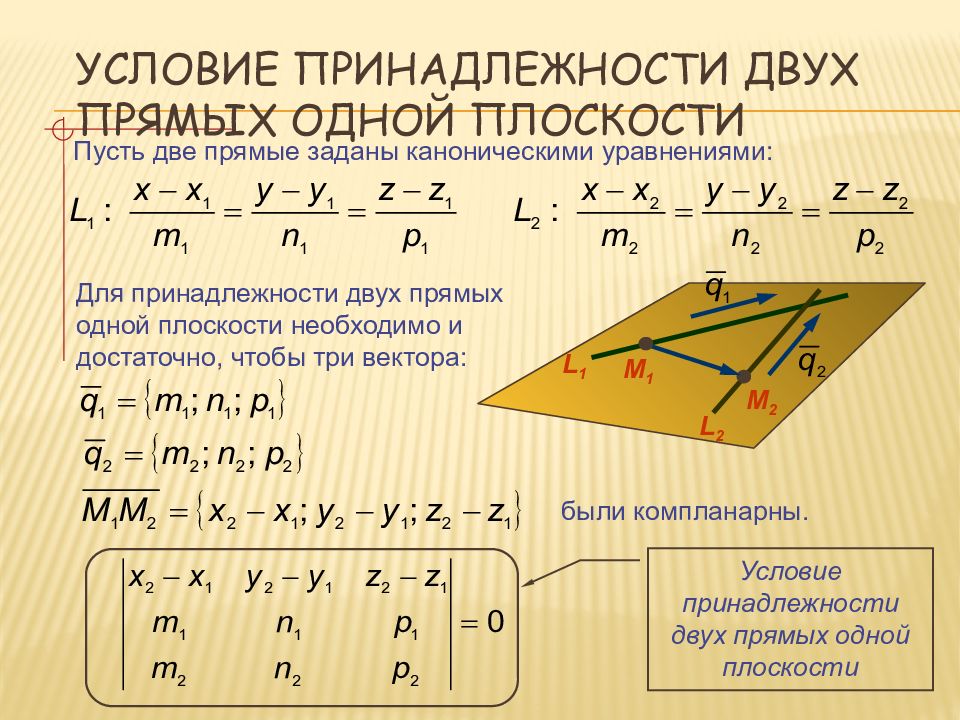
Слайд 21: Условие принадлежности двух прямых одной плоскости
Пусть две прямые заданы каноническими уравнениями: Для принадлежности двух прямых одной плоскости необходимо и достаточно, чтобы три вектора: М 1 М 2 L 1 L 2 были компланарны. Условие принадлежности двух прямых одной плоскости
Слайд 22: Точка пересечения прямой и плоскости
При вычислении координат точки пересечения прямой и плоскости следует совместно решить систему уравнений: К При этом необходимо: Записать уравнение прямой в параметрическом виде:
Слайд 23: Точка пересечения прямой и плоскости
Подставить t 0 в параметрическое уравнение прямой: Подставить в уравнение плоскости вместо x; y; z : Решить полученное уравнение относительно t :