Первый слайд презентации: Лекция 4
Методы преобразования плоскостей проекций. Общие положения Замена плоскостей проекций.
Слайд 2: Общие положения
Методы преобразования плоскостей проекций применяются для облегчения решения какой-либо поставленной задачи. В пространстве с объектом ничего не происходит. Все преобразования выполняются только на комплексных чертежах.
Слайд 3: Общие положения
Все методы можно разделить на две группы: 1) Объект жестко зафиксирован в пространстве. Вокруг него меняется исходный базис (плоскости проекций П1 и П2) на новый базис так, чтобы объект отразился в удобном для решения задачи положении (метод замены плоскостей проекций). 2) Исходный базис (П1 иП2) жестко зафиксирован в пространстве. Объект перемещается (вращается) так, чтобы он отразился на исходные плоскости П1 и П2 в удобном для решения задачи положении (методы: вращения и плоско- параллельного перемещения).
Слайд 4: Общие положения
Независимо от метода преобразования, в задаче выделяется главный элемент, с которым и выполняются преобразования. Все остальные элементы (объекты) задачи являются зависимыми от главного и преобразуются вместе с ним. Главным элементом может быть прямая или плоскость
Слайд 5: Общие положения
Типовые задачи: Главный элемент – прямая Прямую общего положения преобразовать в линию уровня L→ L‘ ‖ П 2) Прямую общего положения преобразовать в проецирующую L→ L‘‘┴ П
Слайд 6: Общие положения
Главный элемент – плоскость 3) Плоскость общего положения преобразовать в проецирующую α → α ‘ ┴ П 4) Плоскость общего положения преобразовать в плоскость уровня α → α ‘‘ ‖ П
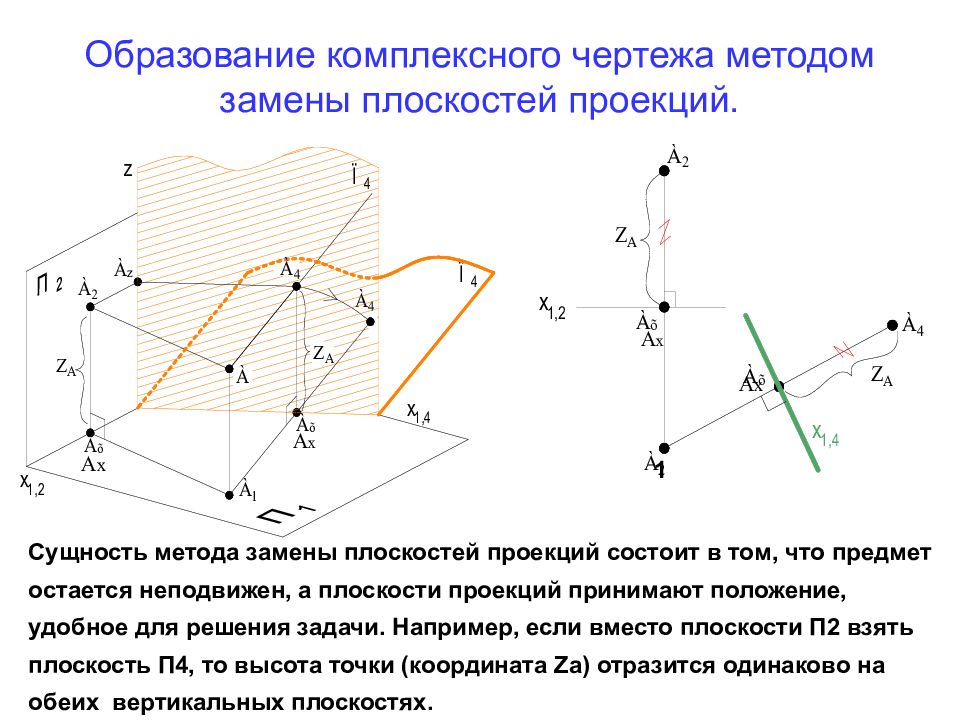
А х А х А х А х Сущность метода замены плоскостей проекций состоит в том, что предмет остается неподвижен, а плоскости проекций принимают положение, удобное для решения задачи. Например, если вместо плоскости П2 взять плоскость П4, то высота точки (координата Z а) отразится одинаково на обеих вертикальных плоскостях. 1
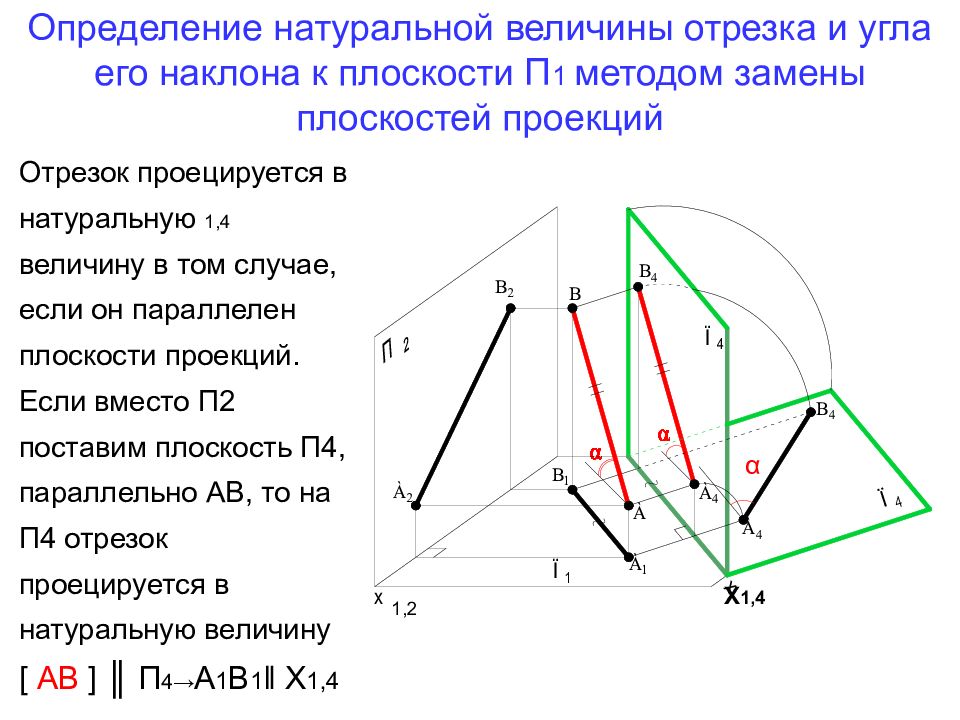
Отрезок проецируется в натуральную 1,4 величину в том случае, если он параллелен плоскости проекций. Если вместо П2 поставим плоскость П4, параллельно АВ, то на П4 отрезок проецируется в натуральную величину [ АВ ] ║ П 4→ А 1 В 1 ‖ Х 1,4 α 1,2 Х 1,4
Слайд 9: Определение натуральной величины отрезка и угла его наклона к плоскости П 1
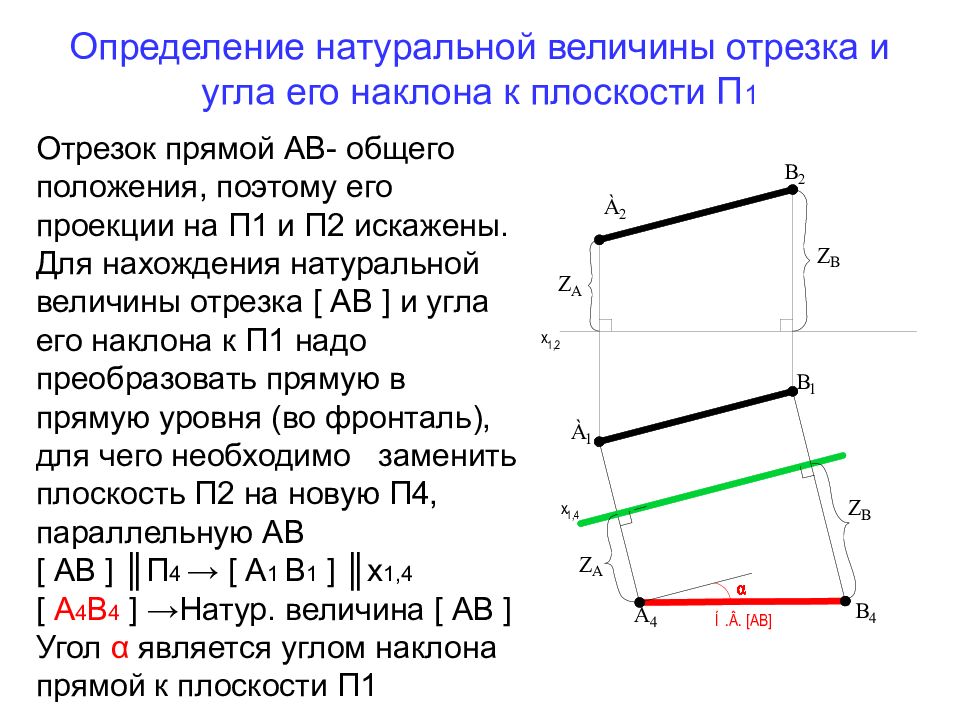
Отрезок прямой АВ- общего положения, поэтому его проекции на П1 и П2 искажены. Для нахождения натуральной величины отрезка [ АВ ] и угла его наклона к П1 надо преобразовать прямую в прямую уровня (во фронталь), для чего необходимо заменить плоскость П2 на новую П4, параллельную АВ [ АВ ] ║П 4 → [ А 1 В 1 ] ║х 1,4 [ А 4 В 4 ] →Натур. величина [ АВ ] Угол α является углом наклона прямой к плоскости П1
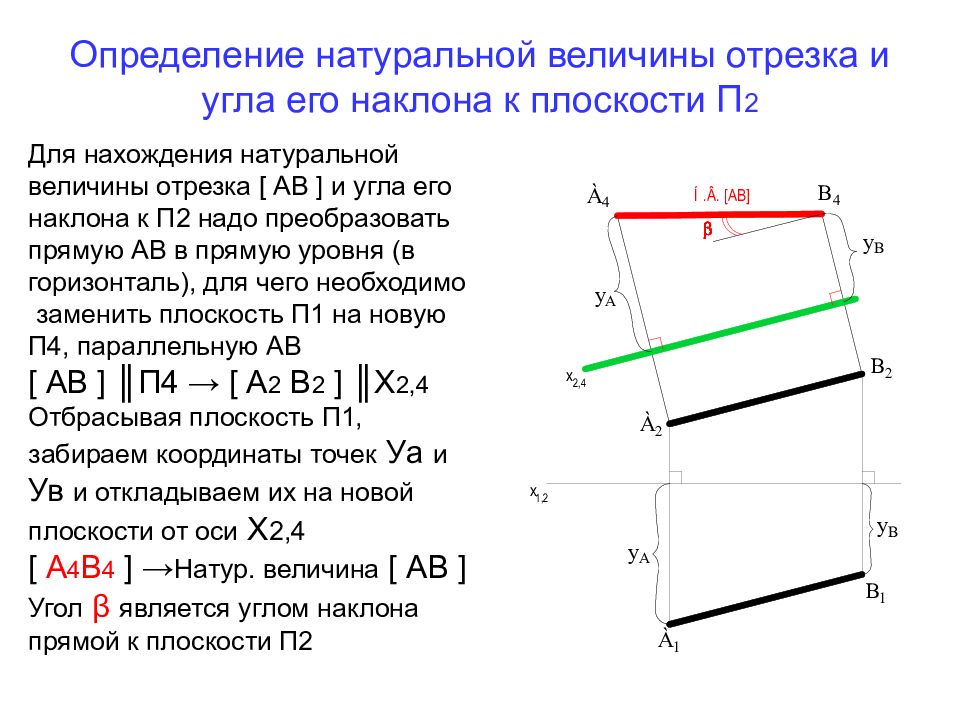
Слайд 10: Определение натуральной величины отрезка и угла его наклона к плоскости П 2
Для нахождения натуральной величины отрезка [ АВ ] и угла его наклона к П2 надо преобразовать прямую АВ в прямую уровня (в горизонталь), для чего необходимо заменить плоскость П1 на новую П4, параллельную АВ [ АВ ] ║П4 → [ А 2 В 2 ] ║Х 2,4 Отбрасывая плоскость П1, забираем координаты точек Уа и Ув и откладываем их на новой плоскости от оси Х 2,4 [ А 4 В 4 ] → Натур. величина [ АВ ] Угол β является углом наклона прямой к плоскости П2
Слайд 11: Задача 6.1 (стр.30): Определить расстояние от точки А до прямой ВС методом замены плоскостей проекций
Расстояние от точки А до прямой ВС = перпендикуляру, опущенному из точки А к прямой ВС. Решение: Главный элемент – прямая. Необходимо прямую преобразовать в проецирующую (2 типовая задача).
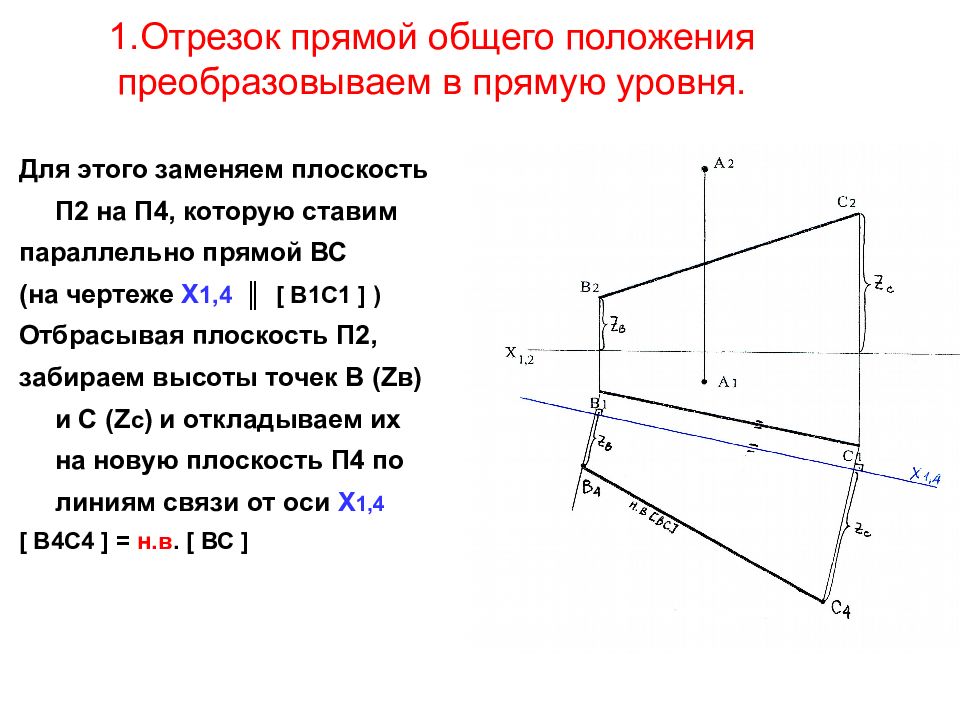
Слайд 12: 1.Отрезок прямой общего положения преобразовываем в прямую уровня
Для этого заменяем плоскость П2 на П4, которую ставим параллельно прямой ВС (на чертеже Х 1,4 ║ [ В1С1 ] ) Отбрасывая плоскость П2, забираем высоты точек В ( Z в) и С ( Z с ) и откладываем их на новую плоскость П4 по линиям связи от оси Х 1,4 [ В4С4 ] = н.в. [ ВС ]
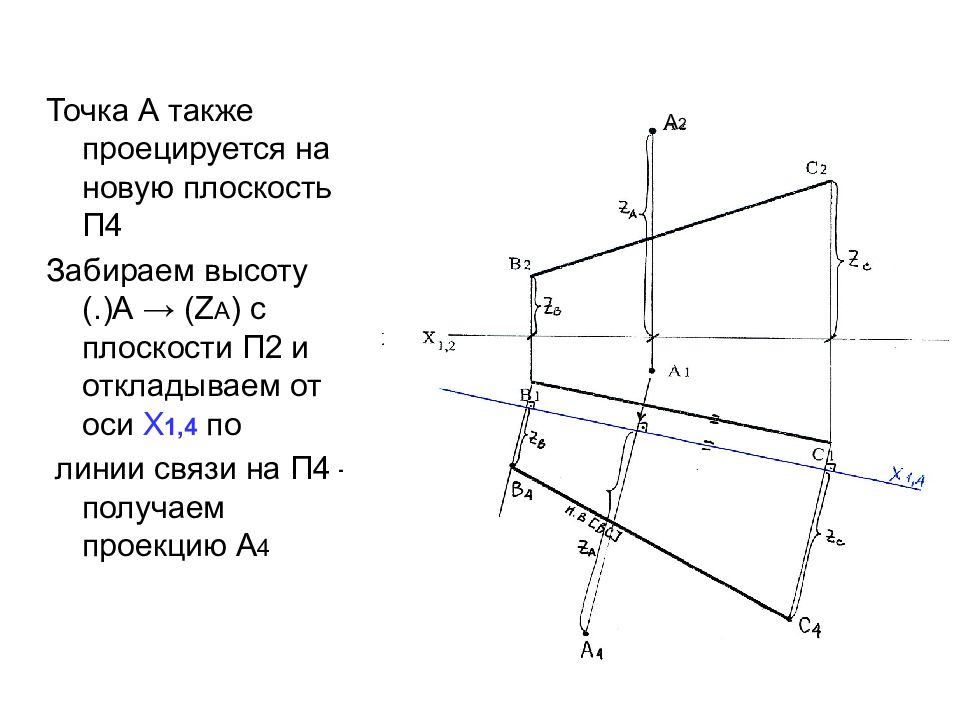
Слайд 13
Точка А также проецируется на новую плоскость П4 Забираем высоту (.)А → ( Z А ) с плоскости П2 и откладываем от оси Х 1,4 по линии связи на П4 – получаем проекцию А 4 А 2 А 2
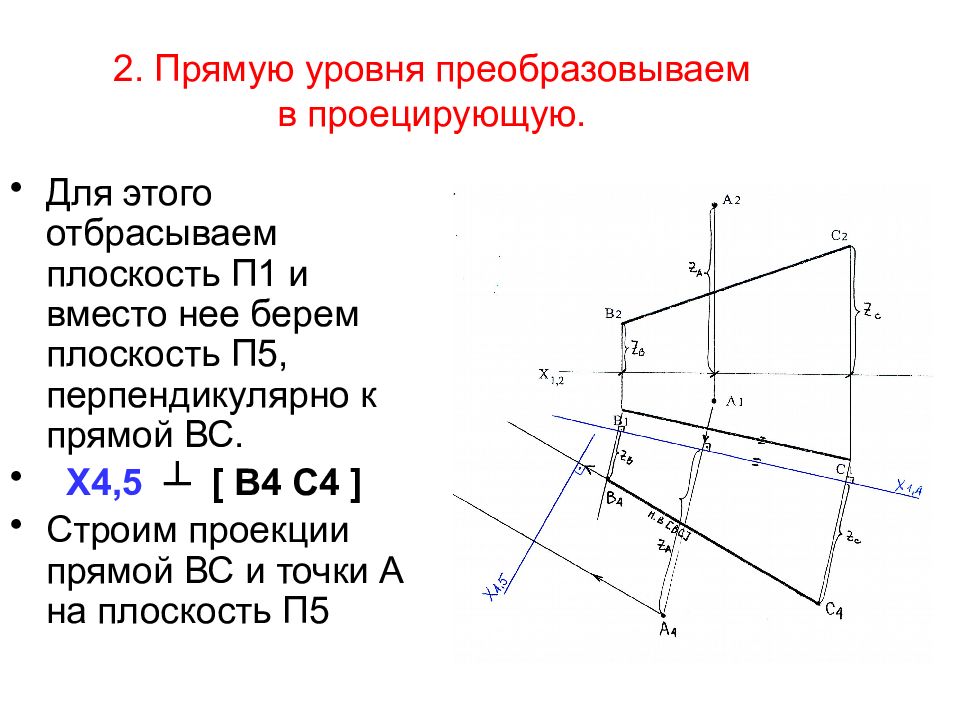
Слайд 14: 2. Прямую уровня преобразовываем в проецирующую
Для этого отбрасываем плоскость П1 и вместо нее берем плоскость П5, перпендикулярно к прямой ВС. Х4,5 ┴ [ В4 С4 ] Строим проекции прямой ВС и точки А на плоскость П5
Слайд 15
Так как отбрасываем плоскость П1, забираем с нее информацию о удалении точек. Измеряем расстояния от В1, А1, С1 до оси Х1,4 и откладываем их на плоскости П5 от оси Х4,5, получаем соответственно проекции В5 ≡ С5, А5 (расстояния выделены желтым цветом)
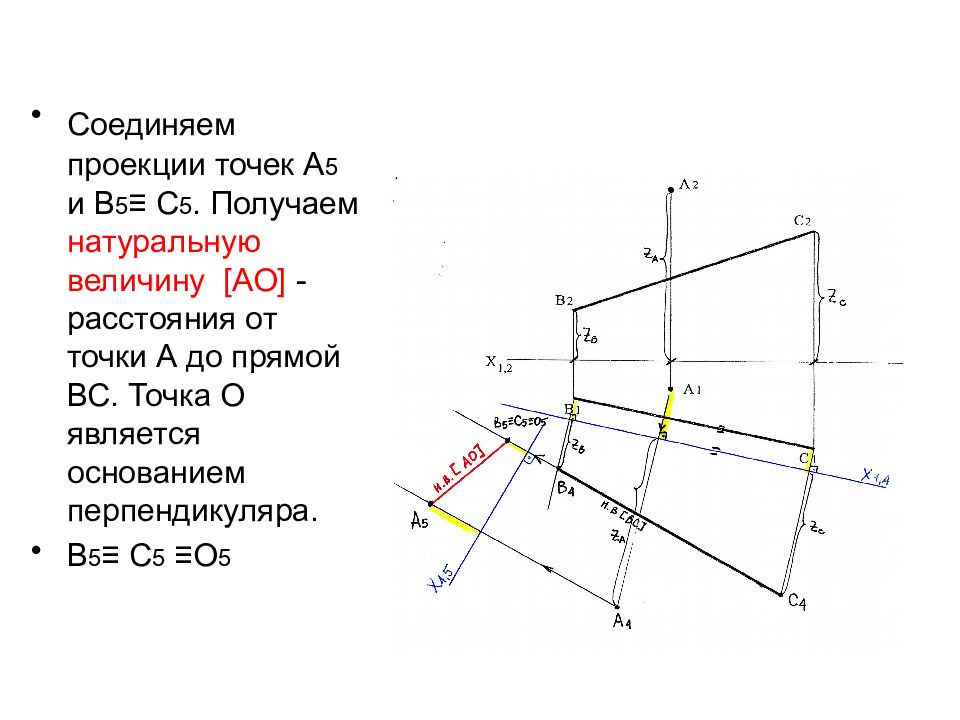
Слайд 16
Соединяем проекции точек А 5 и В 5 ≡ С 5. Получаем натуральную величину [ АО ] -расстояния от точки А до прямой ВС. Точка О является основанием перпендикуляра. В 5 ≡ С 5 ≡О 5
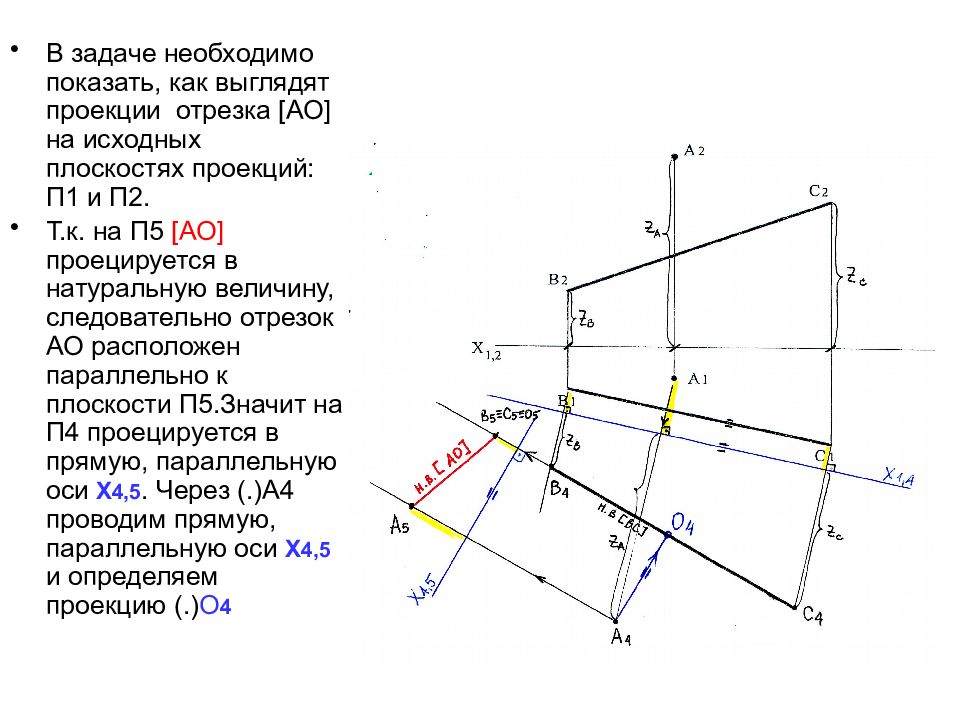
Слайд 17
В задаче необходимо показать, как выглядят проекции отрезка [ АО ] на исходных плоскостях проекций: П1 и П2. Т.к. на П5 [ АО ] проецируется в натуральную величину, следовательно отрезок АО расположен параллельно к плоскости П5.Значит на П4 проецируется в прямую, параллельную оси Х 4,5. Через (.)А4 проводим прямую, параллельную оси Х 4,5 и определяем проекцию (.) О 4
Слайд 18: Далее по линиям связи, перпендикулярно к оси Х1,4 определяем положение проекции О 1 и, соединив А 1 и О 1, получим [ А 1 О 1 ]
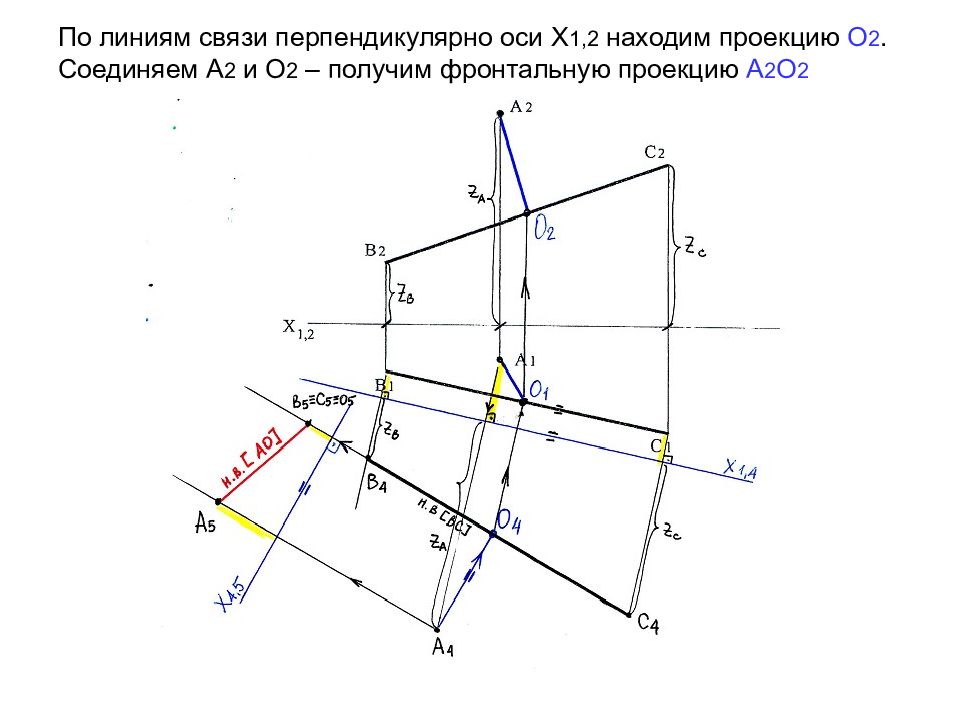
Слайд 19: По линиям связи перпендикулярно оси Х 1,2 находим проекцию О 2. Соединяем А 2 и О 2 – получим фронтальную проекцию А 2 О 2
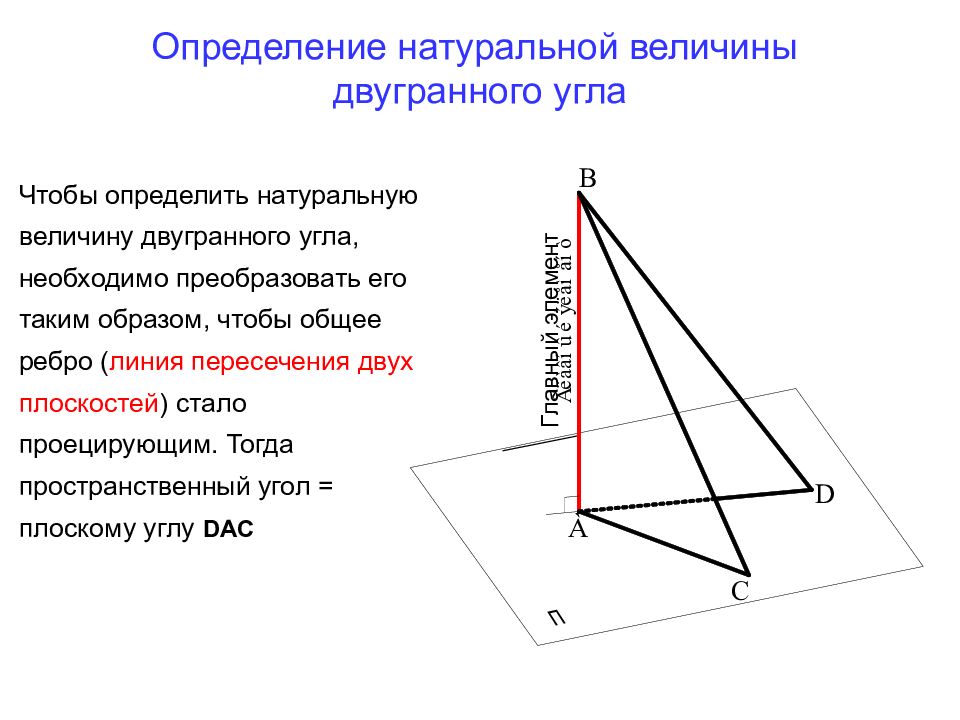
Слайд 20: Определение натуральной величины двугранного угла
Главный элемент Чтобы определить натуральную величину двугранного угла, необходимо преобразовать его таким образом, чтобы общее ребро ( линия пересечения двух плоскостей ) стало проецирующим. Тогда пространственный угол = плоскому углу DAC
Слайд 21: Задача 6.6 (стр.33) Определить натуральную величину двугранного угла
В том случае, если общее ребро ВС двугранного угла – прямая общего положения, задача решается в два действия (вторая типовая: прямую общего положения преобразовать в проецирующую).
Слайд 22
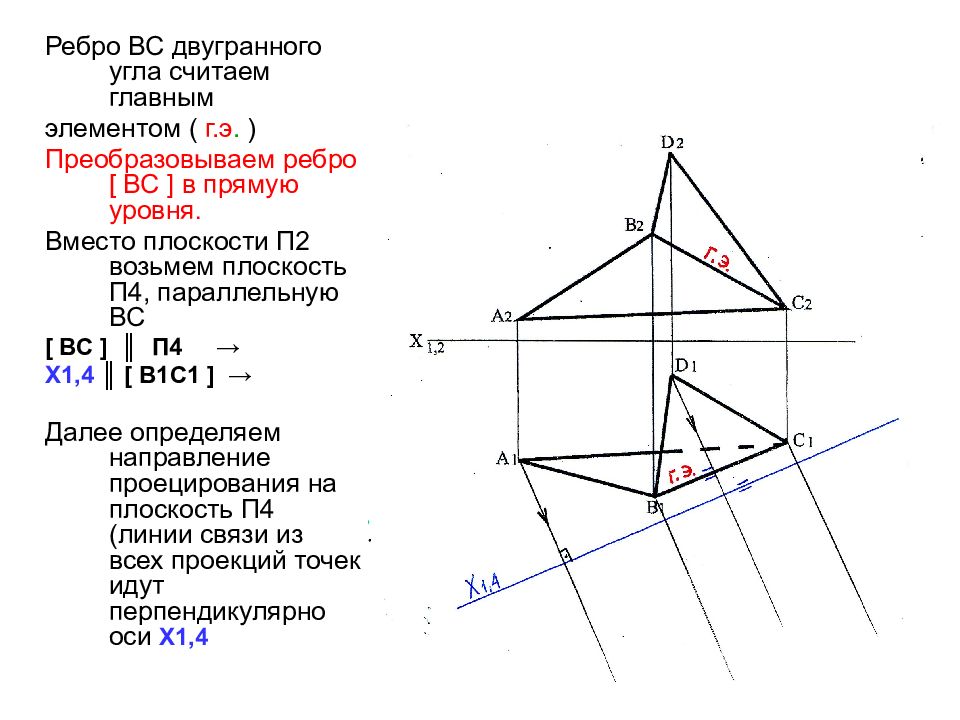
Ребро ВС двугранного угла считаем главным элементом ( г.э. ) Преобразовываем ребро [ ВС ] в прямую уровня. Вместо плоскости П2 возьмем плоскость П4, параллельную ВС [ ВС ] ║ П4 → Х1,4 ║ [ В1С1 ] → Далее определяем направление проецирования на плоскость П4 (линии связи из всех проекций точек идут перпендикулярно оси Х1,4
Слайд 23
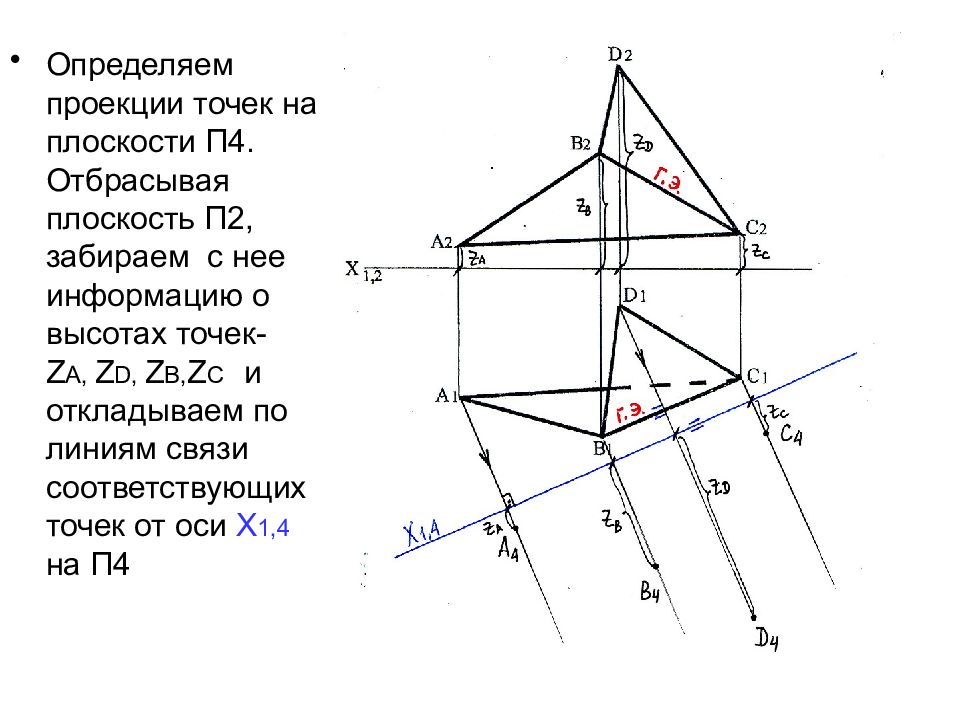
Определяем проекции точек на плоскости П4. Отбрасывая плоскость П2, забираем с нее информацию о высотах точек- Z А, Z D, Z В, Z С и откладываем по линиям связи соответствующих точек от оси Х 1,4 на П4
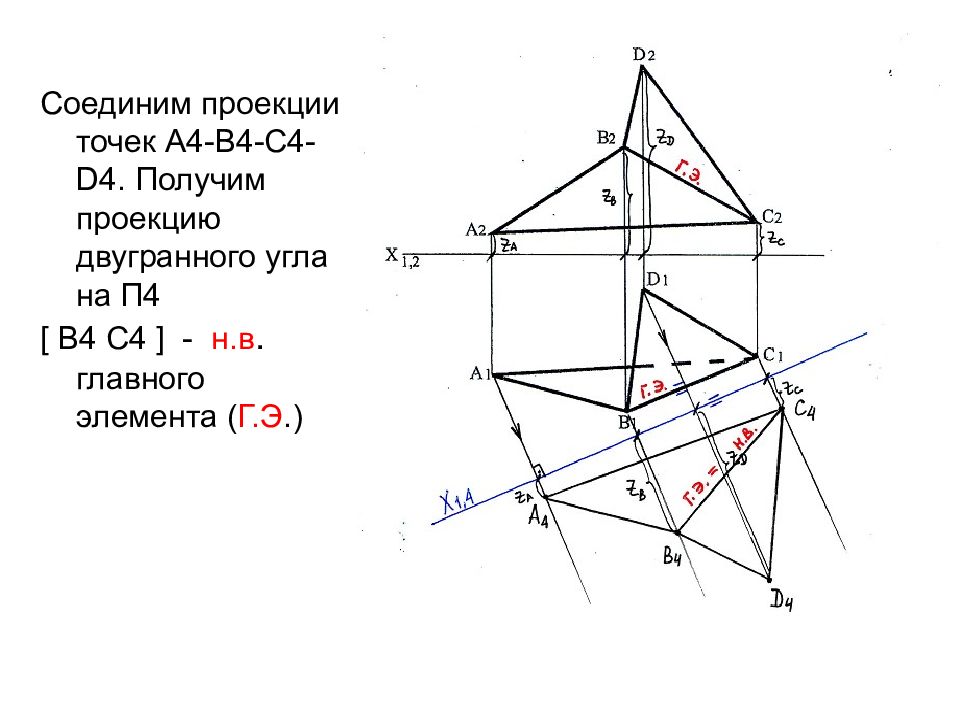
Слайд 24
Соединим проекции точек А4-В4-С4- D4. Получим проекцию двугранного угла на П4 [ В4 С4 ] - н.в. главного элемента ( Г.Э.)
Слайд 25: Прямую ВС преобразуем в проецирующую
Вместо плоскости П1 возьмем плоскость П5 ┴ ВС. На чертеже новая ось Х4,5 ┴В4С4
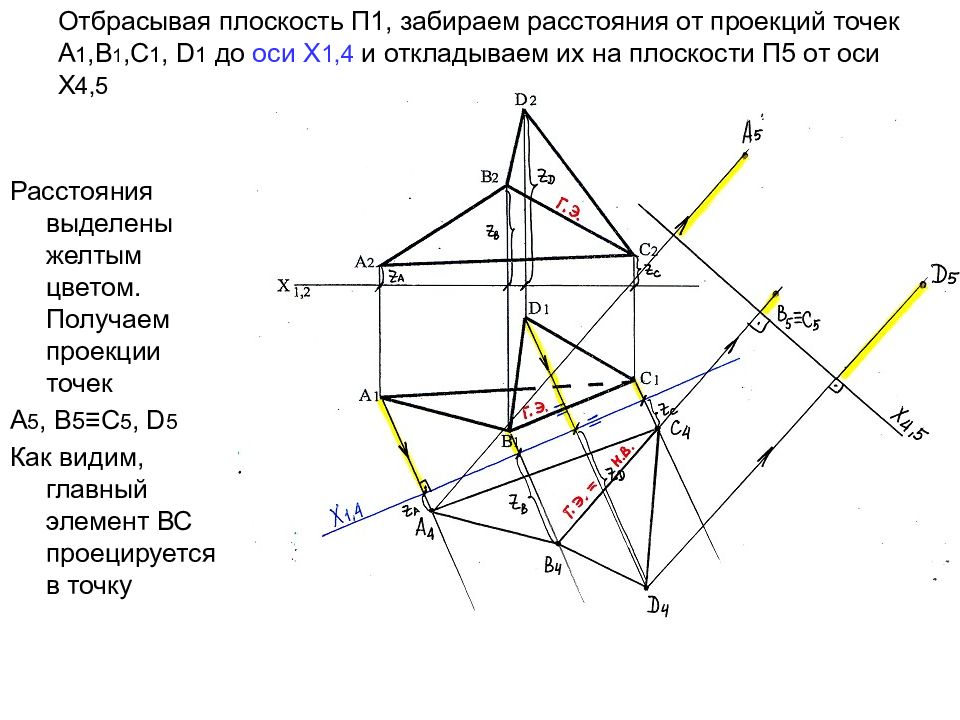
Слайд 26: Отбрасывая плоскость П1, забираем расстояния от проекций точек А 1,В 1,С 1, D 1 до оси Х 1,4 и откладываем их на плоскости П5 от оси Х 4,5
Расстояния выделены желтым цветом. Получаем проекции точек А 5, В 5 ≡ С 5, D 5 Как видим, главный элемент ВС проецируется в точку
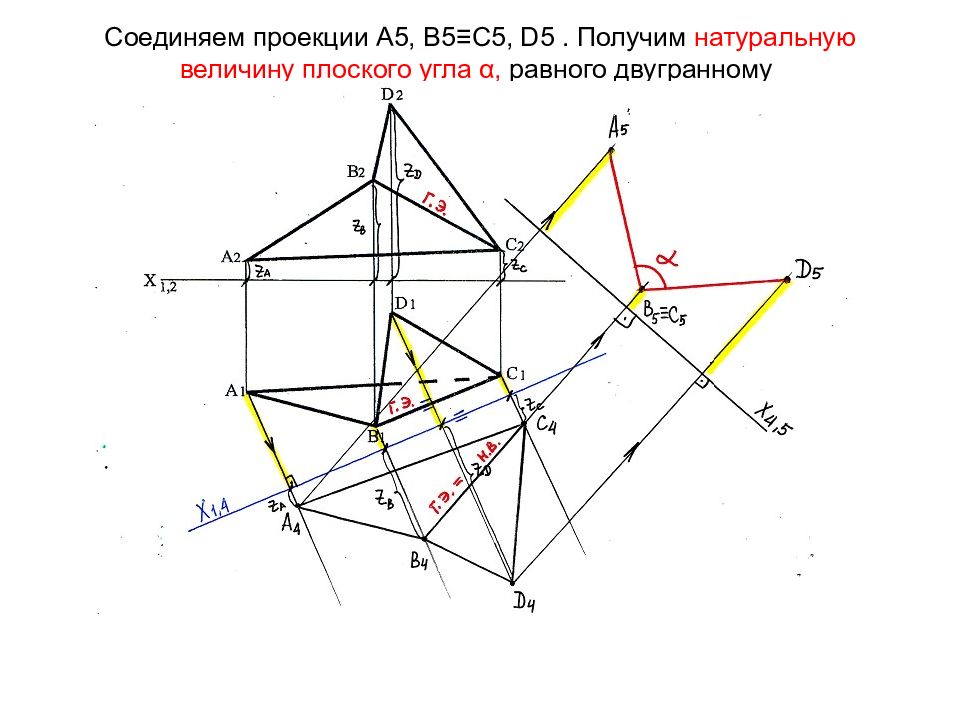
Слайд 27: Соединяем проекции А5, В5 ≡С5, D5. Получим натуральную величину плоского угла α, равного двугранному
Слайд 28: Преобразование плоскости общего положения в проецирующую
Чтобы определить угол наклона плоскости общего положения к плоскости проекций, необходимо преобразовать эту плоскость в проецирующую (3 типовая задача). Плоскость перпендикулярна другой плоскости, в том числе плоскости проекций в том случае, если она содержит в себе прямую, перпендикулярную этой плоскости.
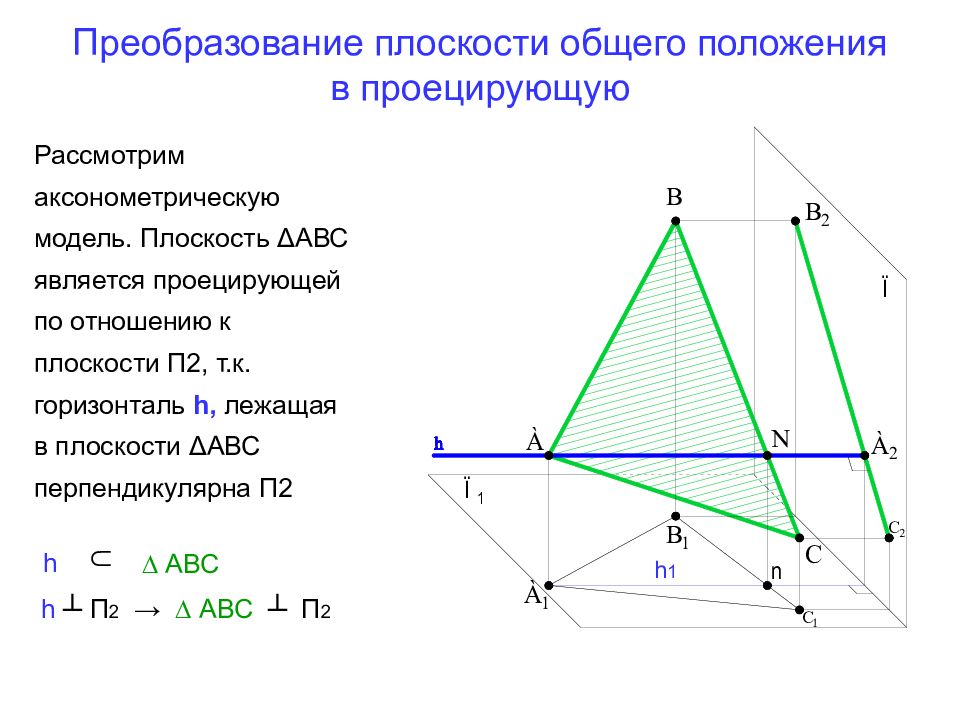
Слайд 29: Преобразование плоскости общего положения в проецирующую
Рассмотрим аксонометрическую модель. Плоскость Δ АВС является проецирующей по отношению к плоскости П2, т.к. горизонталь h, лежащая в плоскости Δ АВС перпендикулярна П2 h ∩ ∆ АВС h ┴ П 2 → ∆ АВС ┴ П 2 h 1
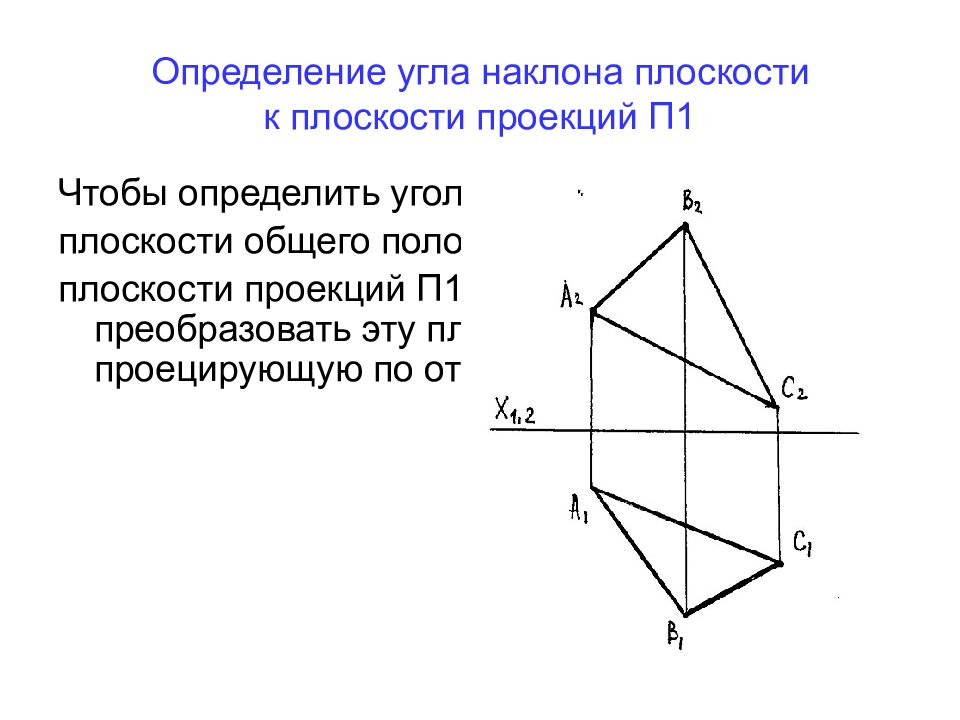
Слайд 30: Определение угла наклона плоскости к плоскости проекций П1
Чтобы определить угол наклона плоскости общего положения к плоскости проекций П1, необходимо преобразовать эту плоскость в проецирующую по отношению к П2.
Слайд 31: Определение угла наклона плоскости к плоскости проекций П1
Задаем в плоскости Δ АВС горизонталь на любой высоте, например через (.) А. h 2 ‖ Х 1,2 → h 1 строим по признаку принадлежности прямой плоскости (как проходящую через (.)А и (.)1)
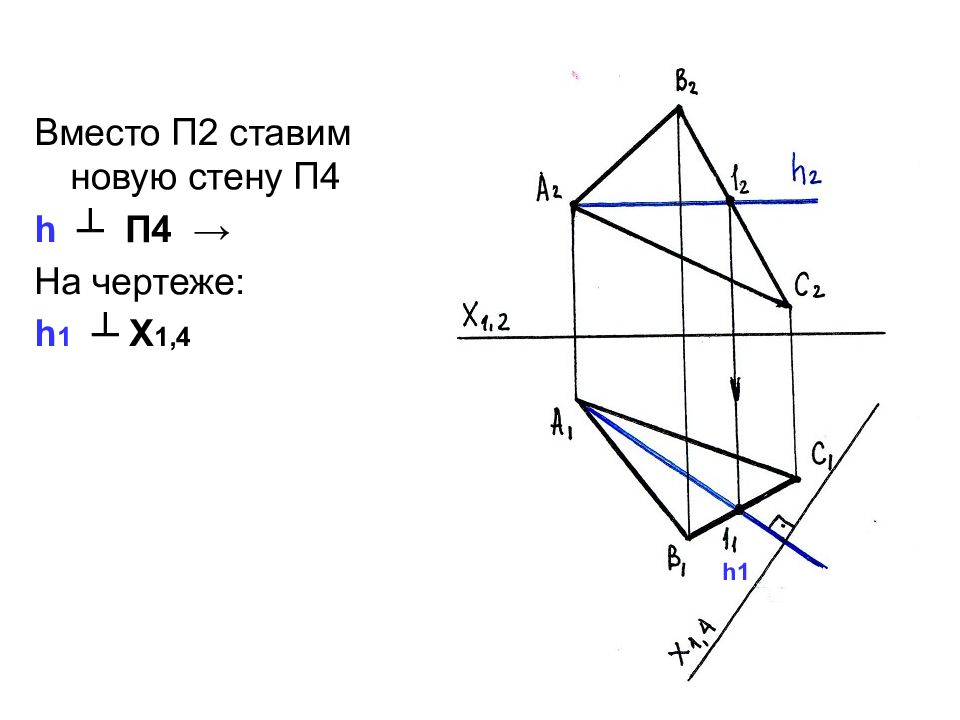
Слайд 33
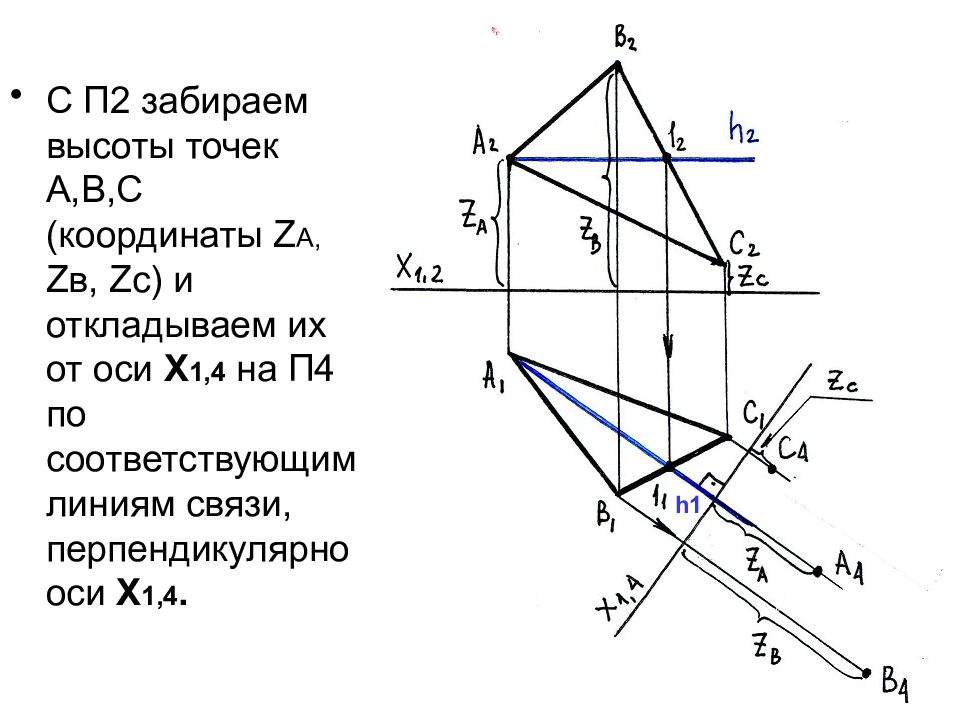
С П2 забираем высоты точек А,В,С (координаты Z А, Z в, Z с) и откладываем их от оси Х 1,4 на П4 по соответствующим линиям связи, перпендикулярно оси Х 1,4. h1
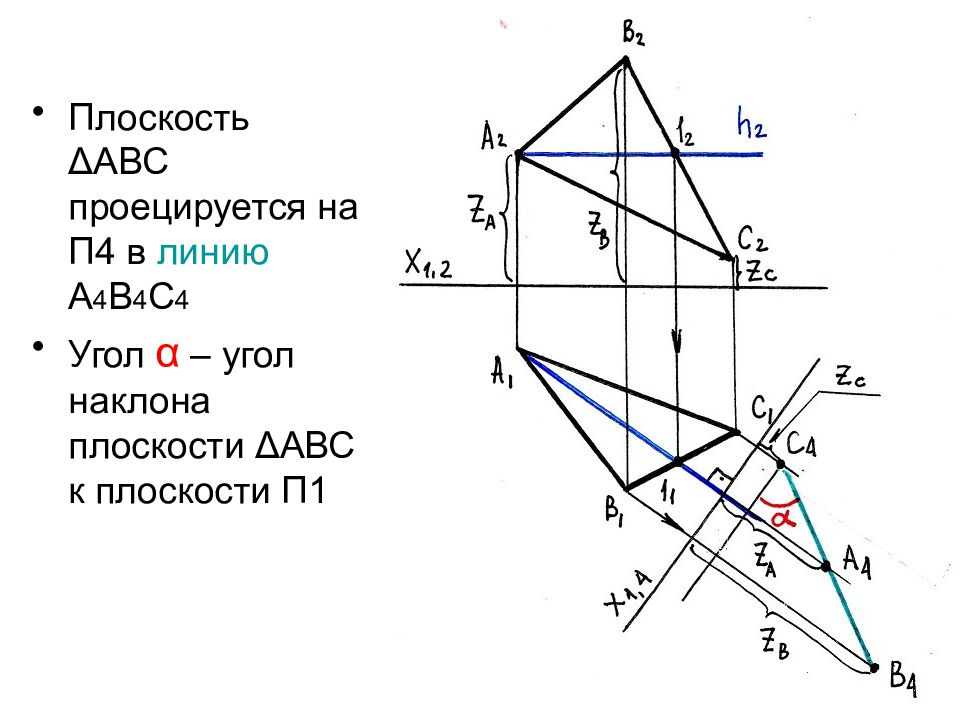
Слайд 34
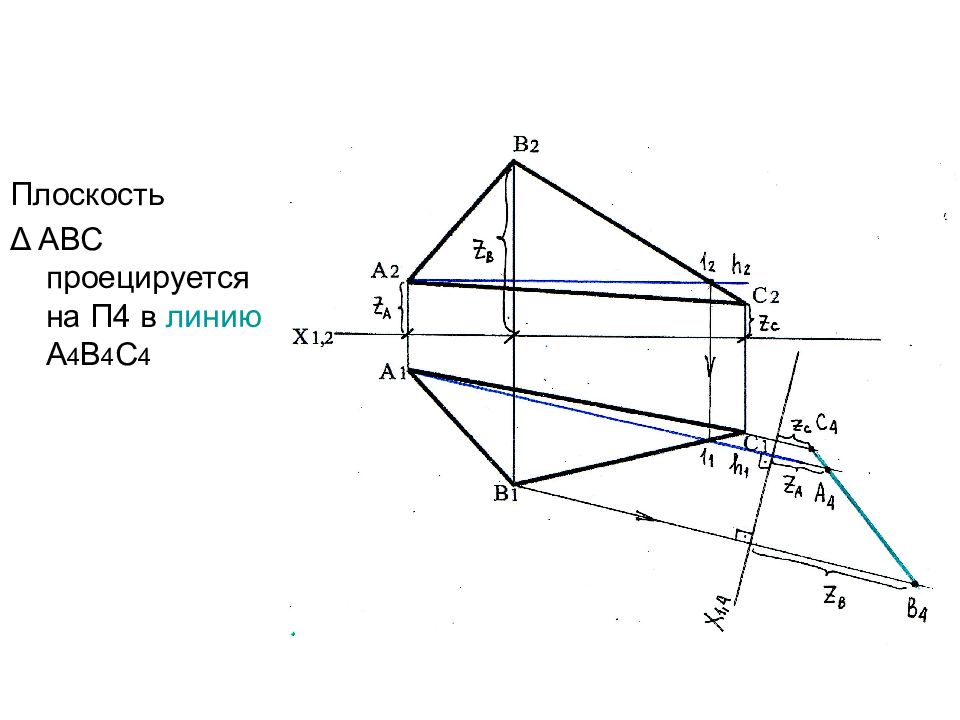
Плоскость Δ АВС проецируется на П4 в линию А 4 В 4 С 4 Угол α – угол наклона плоскости Δ АВС к плоскости П1
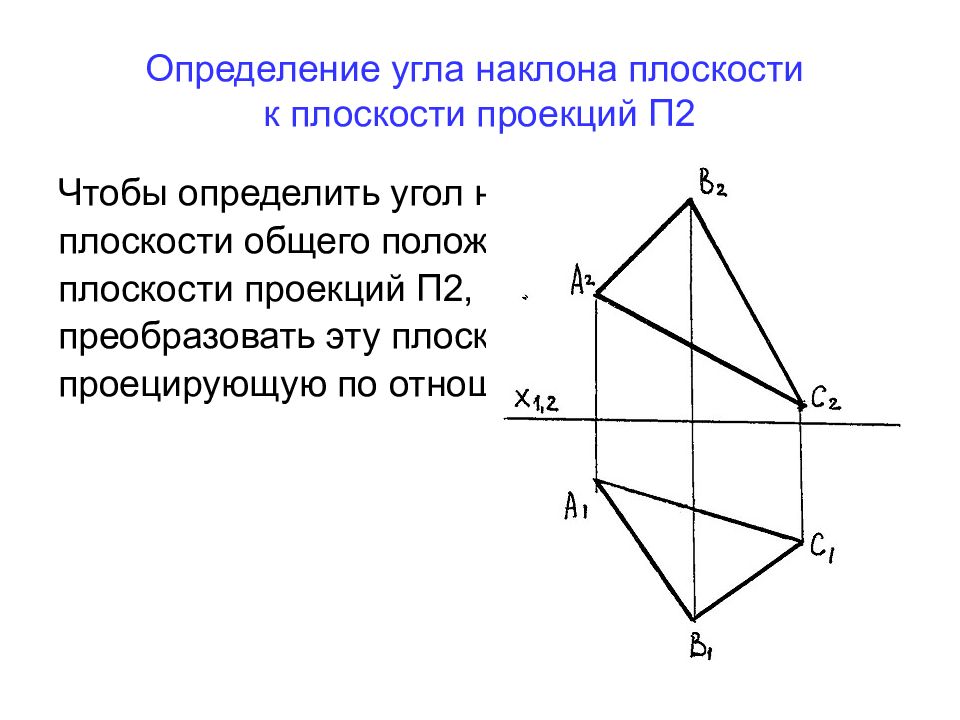
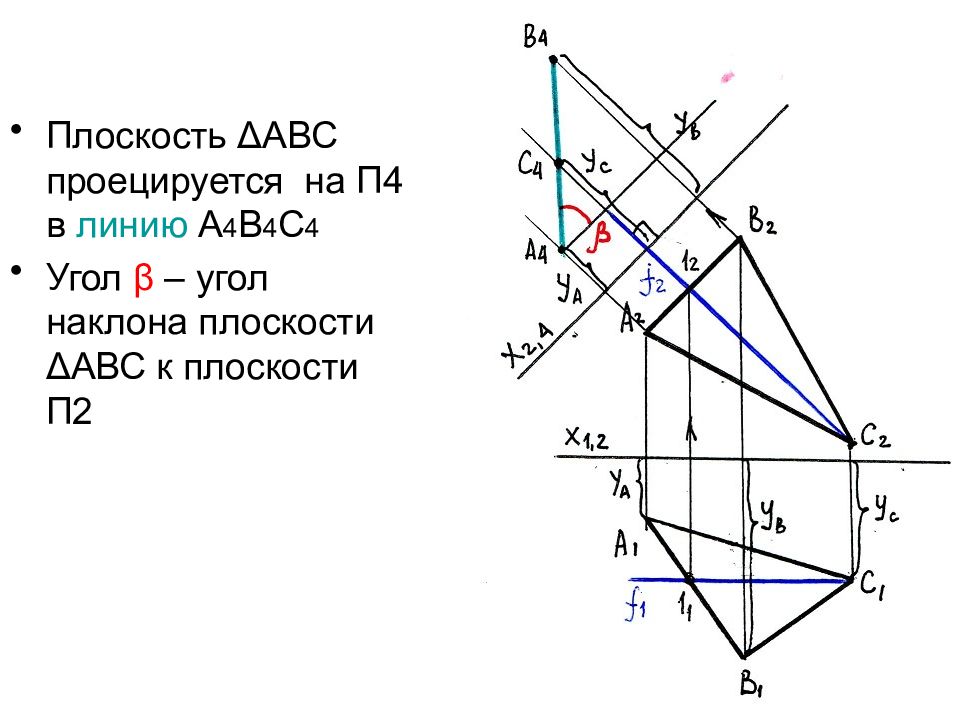
Слайд 35: Определение угла наклона плоскости к плоскости проекций П2
Чтобы определить угол наклона плоскости общего положения к плоскости проекций П2, необходимо преобразовать эту плоскость в проецирующую по отношению к П1.
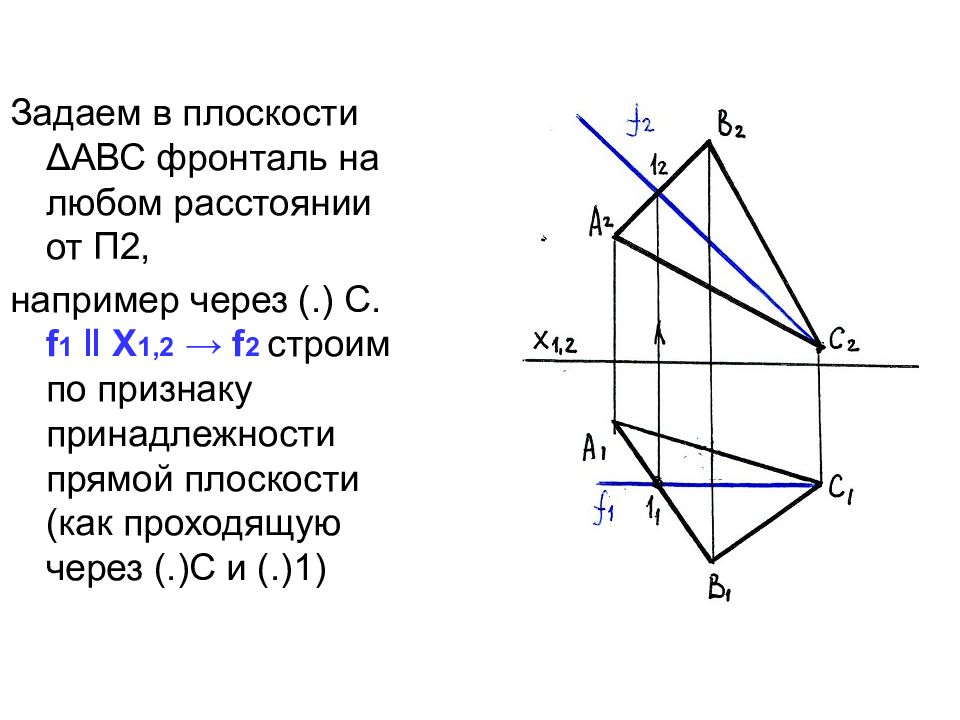
Слайд 36
Задаем в плоскости Δ АВС фронталь на любом расстоянии от П2, например через (.) С. f 1 ‖ Х 1,2 → f 2 строим по признаку принадлежности прямой плоскости (как проходящую через (.)С и (.)1)
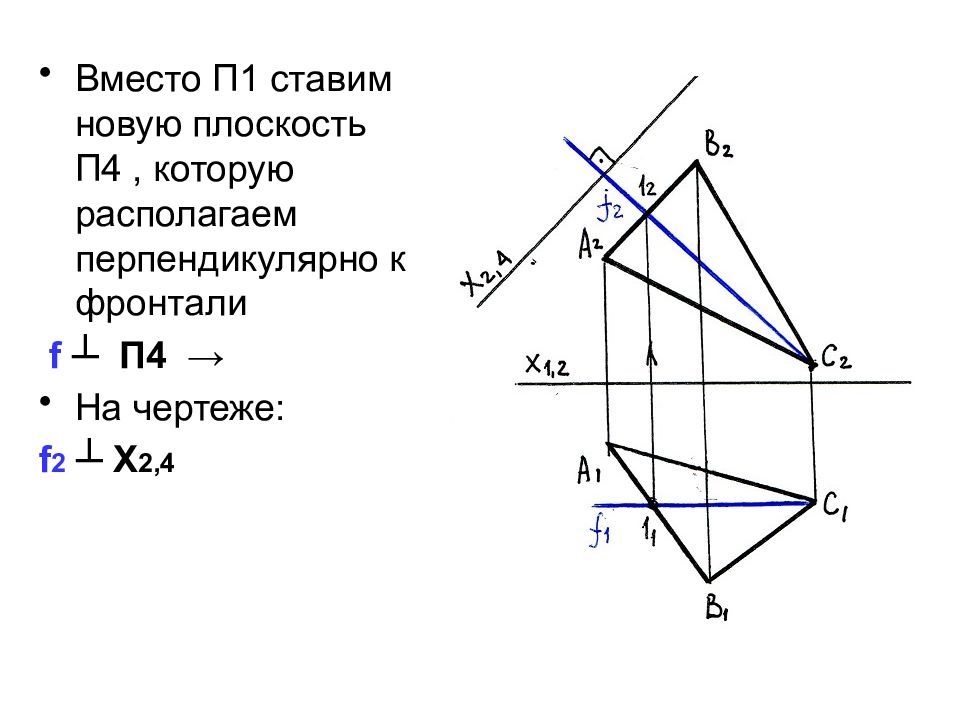
Слайд 37
Вместо П1 ставим новую плоскость П4, которую располагаем перпендикулярно к фронтали f ┴ П4 → На чертеже: f 2 ┴ Х 2,4
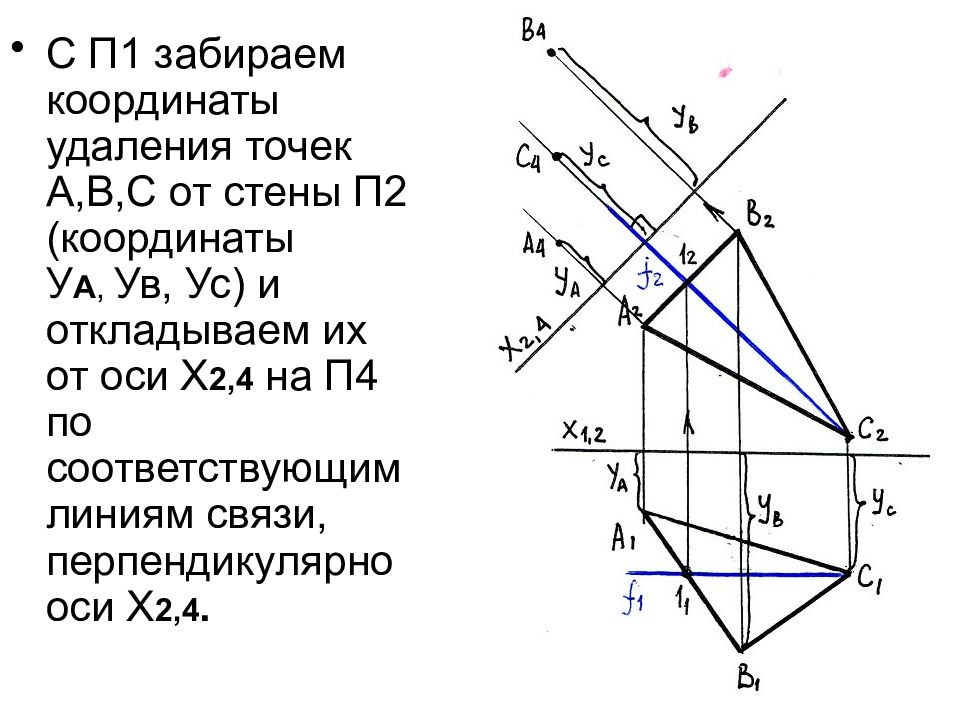
Слайд 38
С П1 забираем координаты удаления точек А,В,С от стены П2 (координаты У А, Ув, Ус) и откладываем их от оси Х 2,4 на П4 по соответствующим линиям связи, перпендикулярно оси Х 2,4.
Слайд 39
Плоскость Δ АВС проецируется на П4 в линию А 4 В 4 С 4 Угол β – угол наклона плоскости Δ АВС к плоскости П2
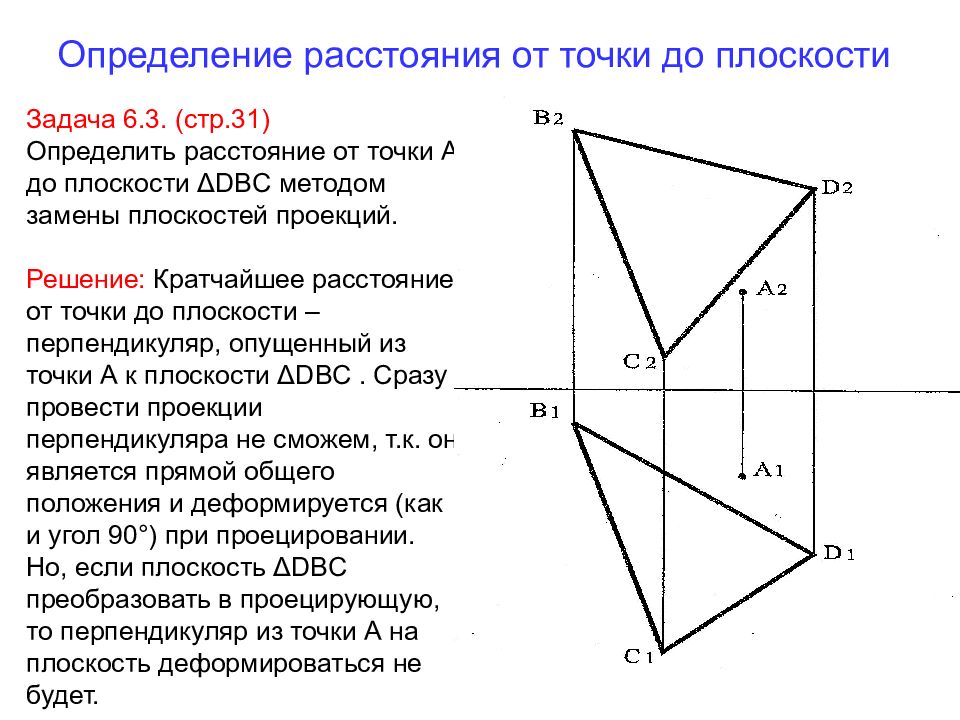
Слайд 40: Определение расстояния от точки до плоскости
Задача 6.3. (стр.31) Определить расстояние от точки А до плоскости Δ DBC методом замены плоскостей проекций. Решение: Кратчайшее расстояние от точки до плоскости – перпендикуляр, опущенный из точки А к плоскости Δ DBC. Сразу провести проекции перпендикуляра не сможем, т.к. он является прямой общего положения и деформируется (как и угол 90 ° ) при проецировании. Но, если плоскость Δ DBC преобразовать в проецирующую, то перпендикуляр из точки А на плоскость деформироваться не будет.
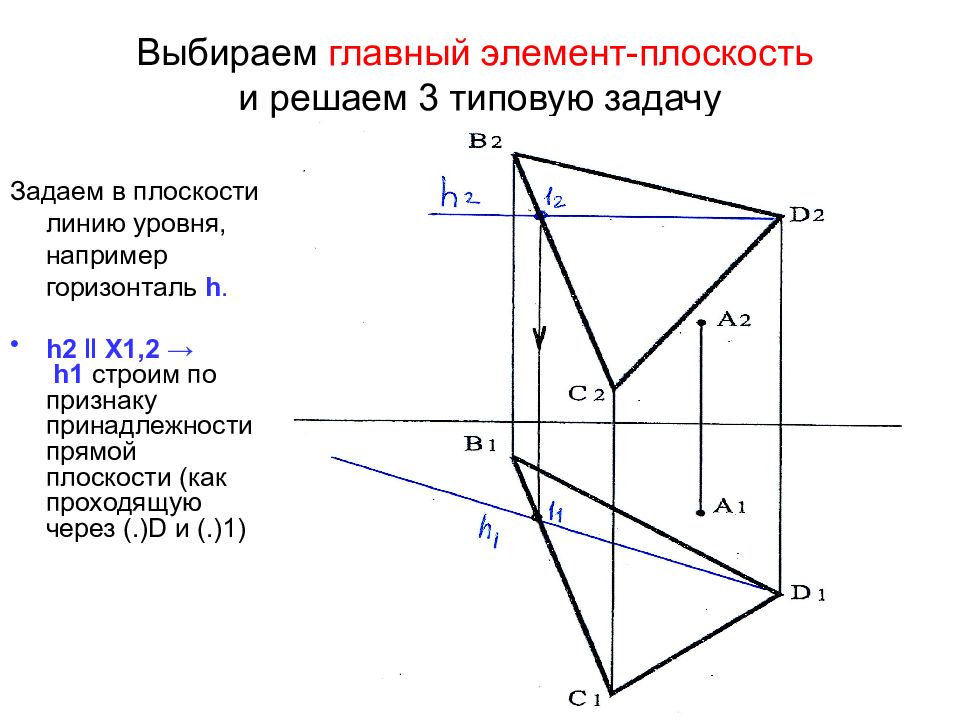
Слайд 41: Выбираем главный элемент-плоскость и решаем 3 типовую задачу
Задаем в плоскости линию уровня, например горизонталь h. h 2 ‖ Х1,2 → h 1 строим по признаку принадлежности прямой плоскости (как проходящую через (.) D и (.)1)
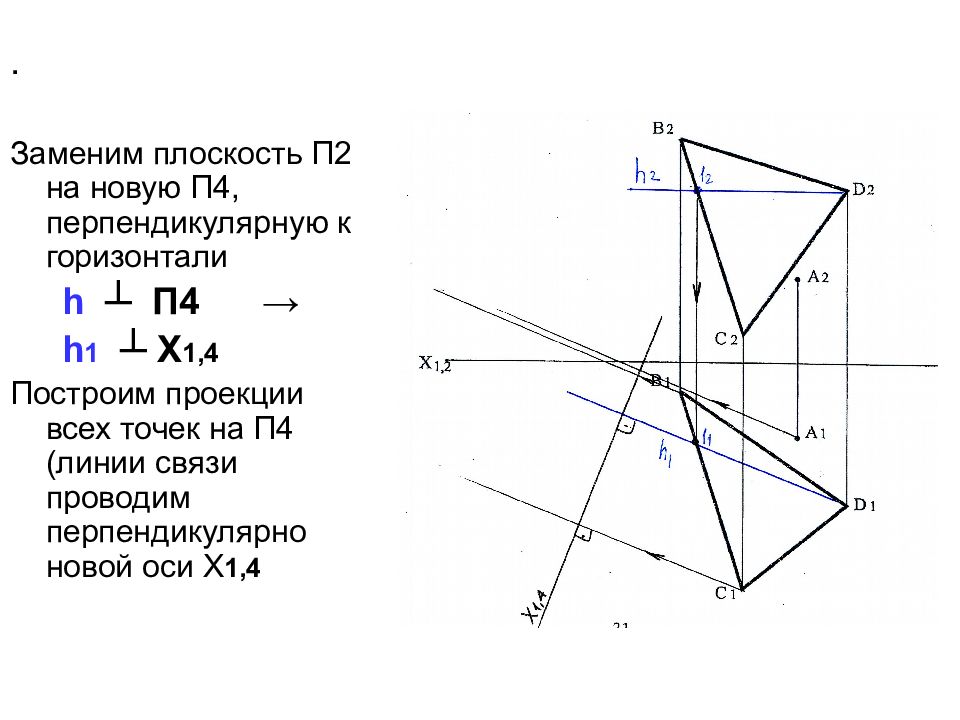
Слайд 42
. Заменим плоскость П2 на новую П4, перпендикулярную к горизонтали h ┴ П4 → h 1 ┴ Х 1,4 Построим проекции всех точек на П4 (линии связи проводим перпендикулярно новой оси Х 1,4
Слайд 43
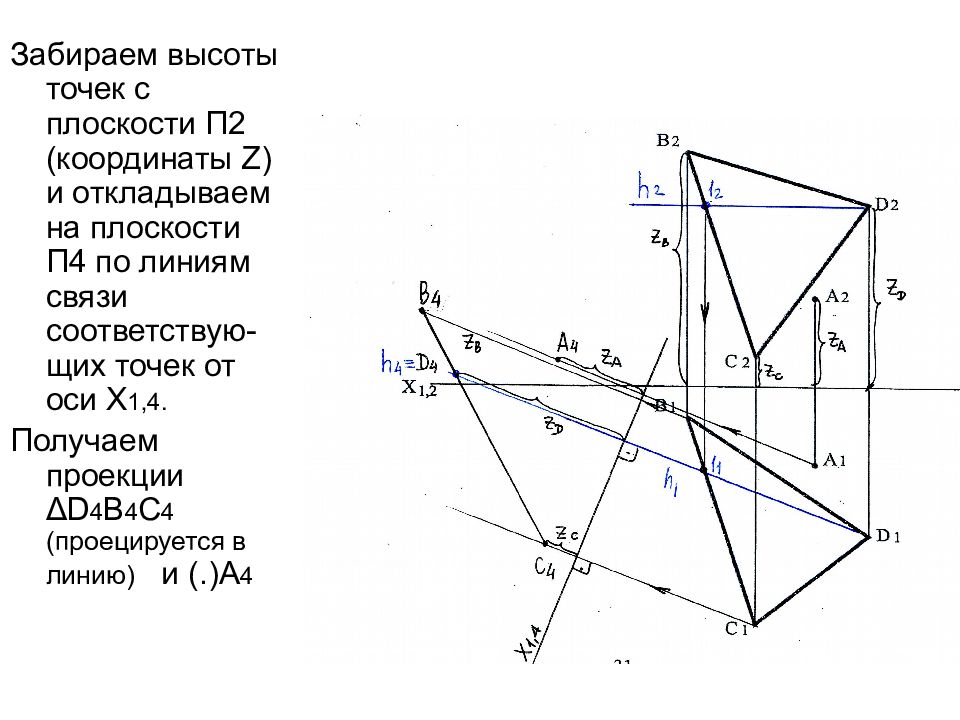
Забираем высоты точек с плоскости П2 (координаты Z ) и откладываем на плоскости П4 по линиям связи соответствую-щих точек от оси Х 1,4. Получаем проекции Δ D 4 B 4 C 4 (проецируется в линию) и (.)А 4
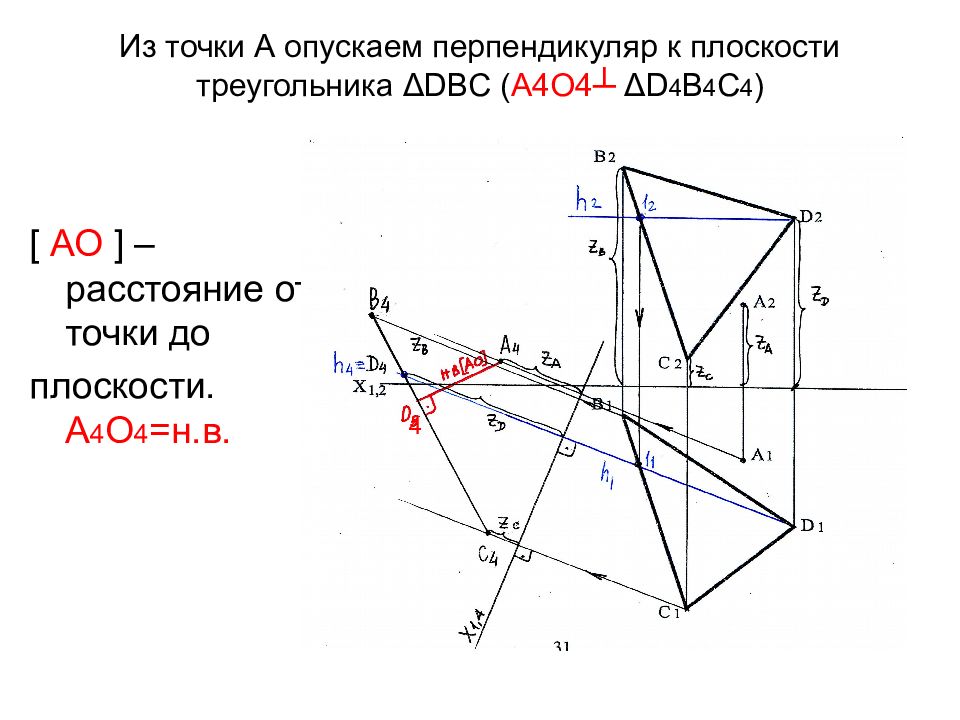
Слайд 44: Из точки А опускаем перпендикуляр к плоскости треугольника Δ DBC ( А4О4 ┴ Δ D 4 B 4 C 4 )
[ АО ] – расстояние от точки до плоскости. А 4 О 4 =н.в. 4
Слайд 45
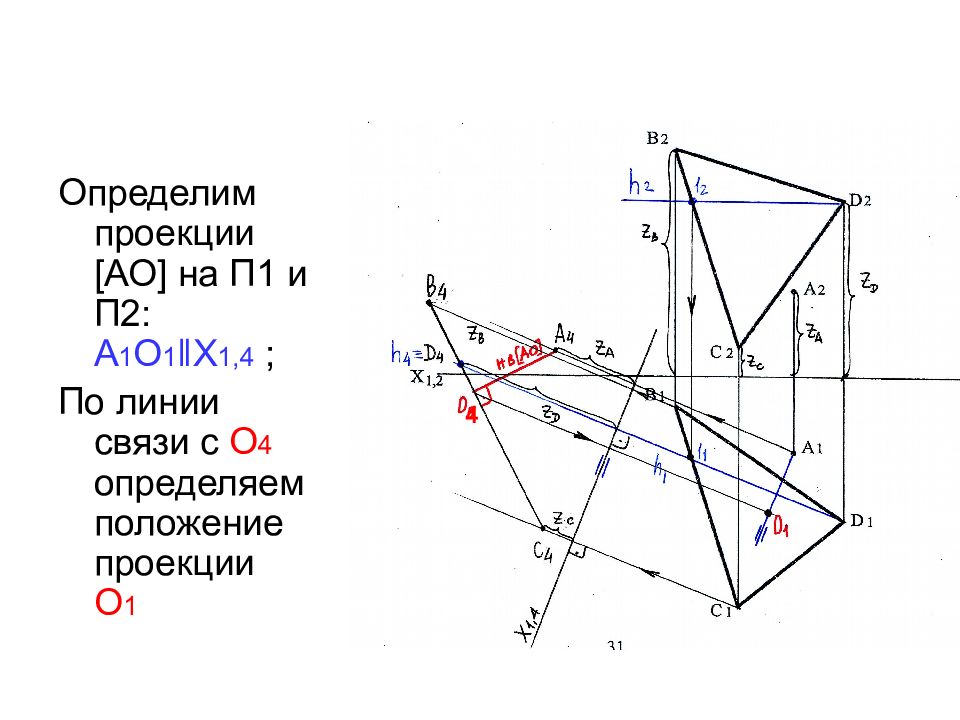
Операцию по замене плоскости П2 на П4 мы сделали для облегчения решения задачи. Необходимо показать, как выглядит расстояние в исходных проекциях (на П1 и П2). Т.к. на плоскость П4 отрезок [ АО ] проецируется в натуральную величину, значит он параллелен этой плоскости. Следовательно на П1 его проекция отразится параллельно оси Х 1,4 4
Слайд 46
Определим проекции [ АО ] на П1 и П2: А 1 О 1 ‖Х 1,4 ; По линии связи с О 4 определяем положение проекции О 1 4
Слайд 47
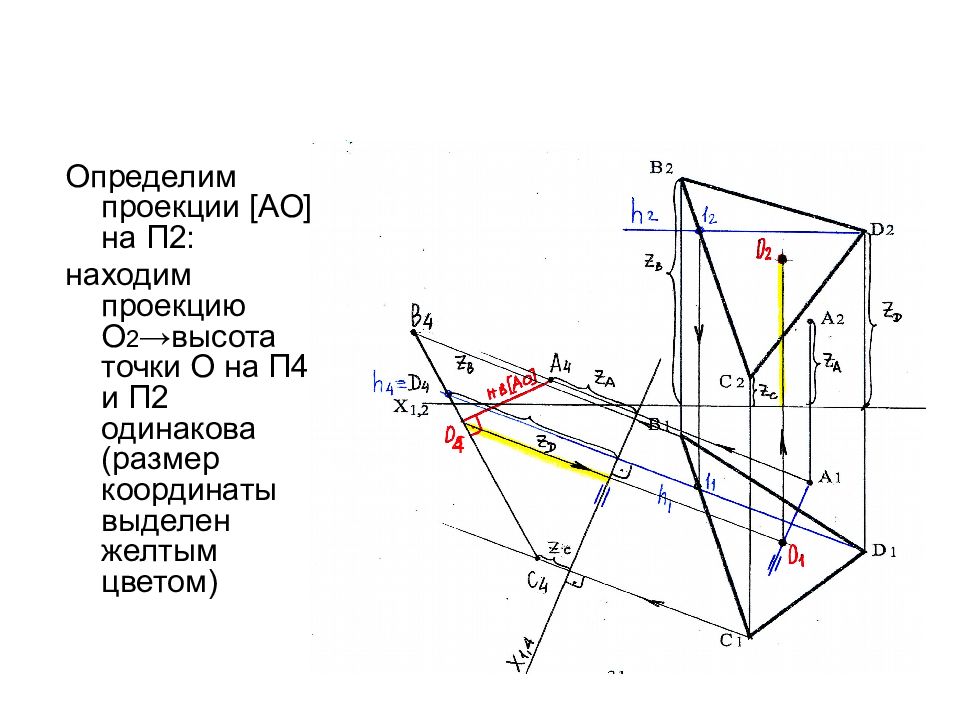
Определим проекции [ АО ] на П2: находим проекцию О 2 →высота точки О на П4 и П2 одинакова (размер координаты выделен желтым цветом) 4
Слайд 48
Соединяем фронтальные проекции точек О 2 и А 2 – получим проекцию расстояния от точки до плоскости треугольника на П2 ( О 2 А 2 ) 4
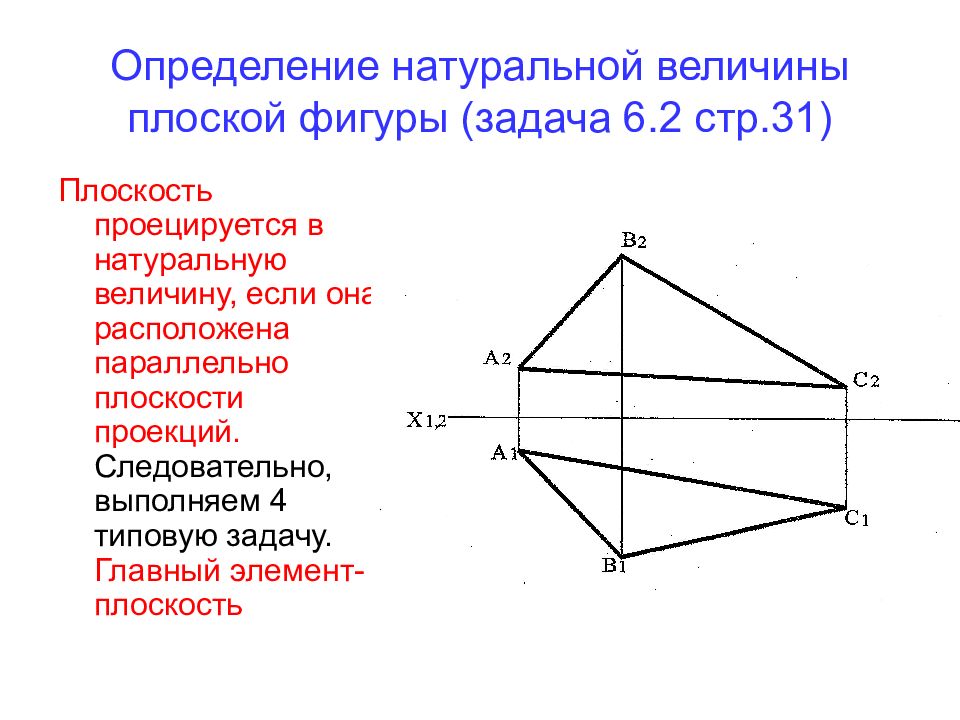
Слайд 49: Определение натуральной величины плоской фигуры (задача 6.2 стр.31)
Плоскость проецируется в натуральную величину, если она расположена параллельно плоскости проекций. Следовательно, выполняем 4 типовую задачу. Главный элемент- плоскость
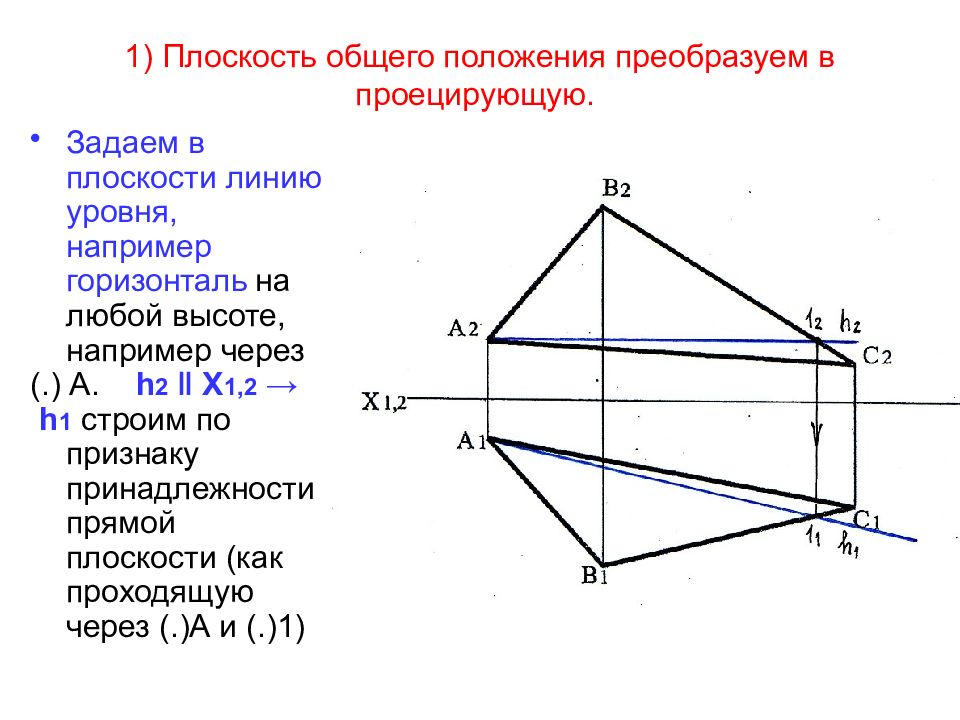
Слайд 50: 1) Плоскость общего положения преобразуем в проецирующую
Задаем в плоскости линию уровня, например горизонталь на любой высоте, например через (.) А. h 2 ‖ Х 1,2 → h 1 строим по признаку принадлежности прямой плоскости (как проходящую через (.)А и (.)1)
Слайд 52
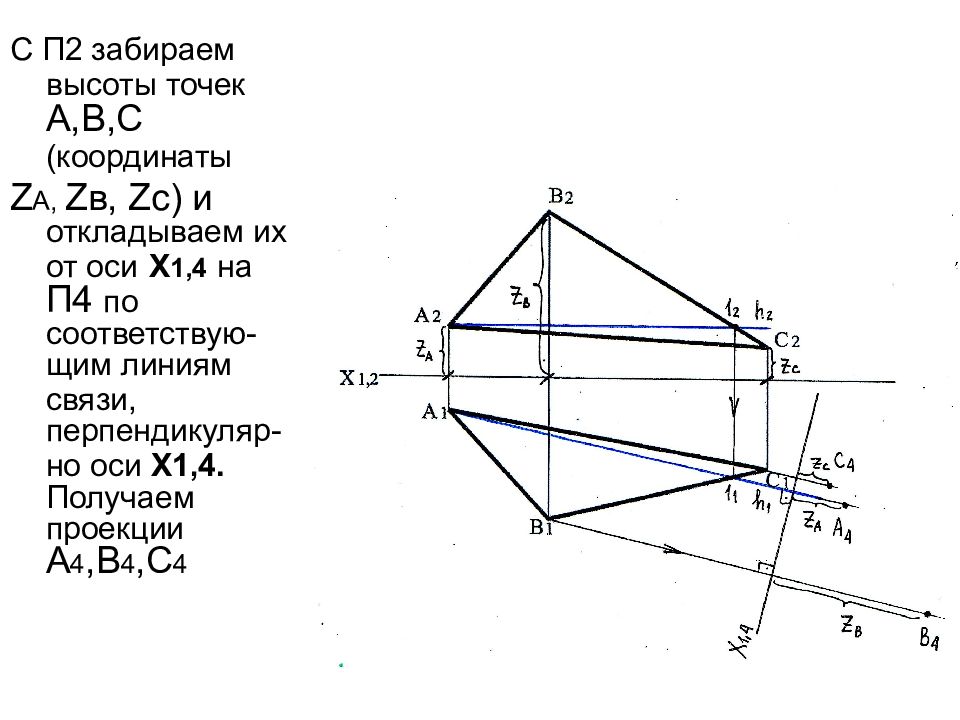
С П2 забираем высоты точек А,В,С (координаты Z А, Z в, Z с) и откладываем их от оси Х 1,4 на П4 по соответствую-щим линиям связи, перпендикуляр-но оси Х1,4. Получаем проекции А 4,В 4,С 4
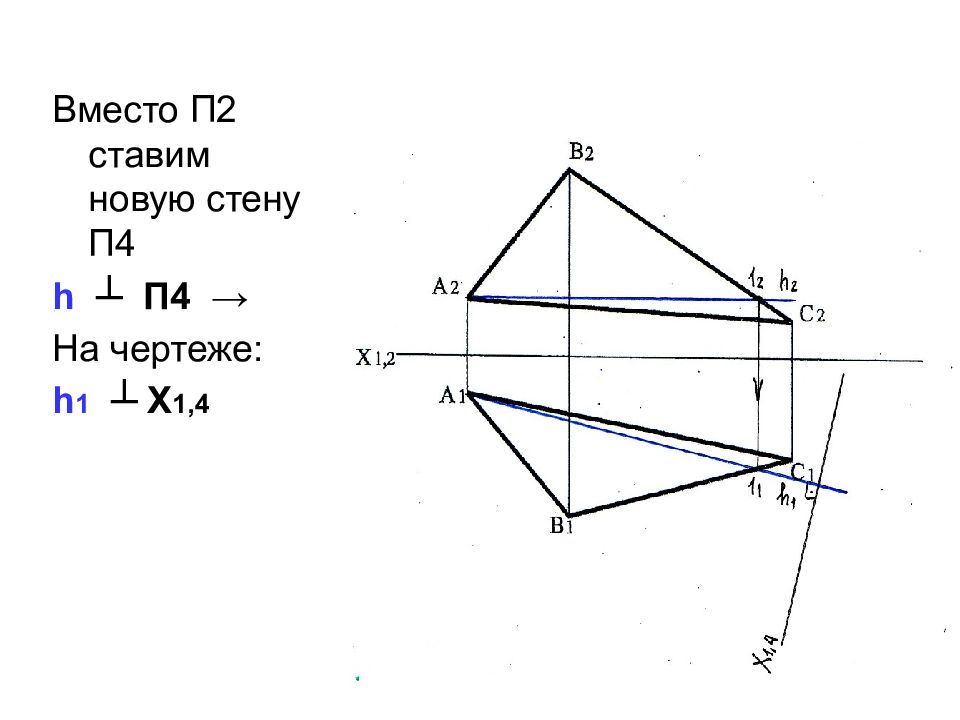
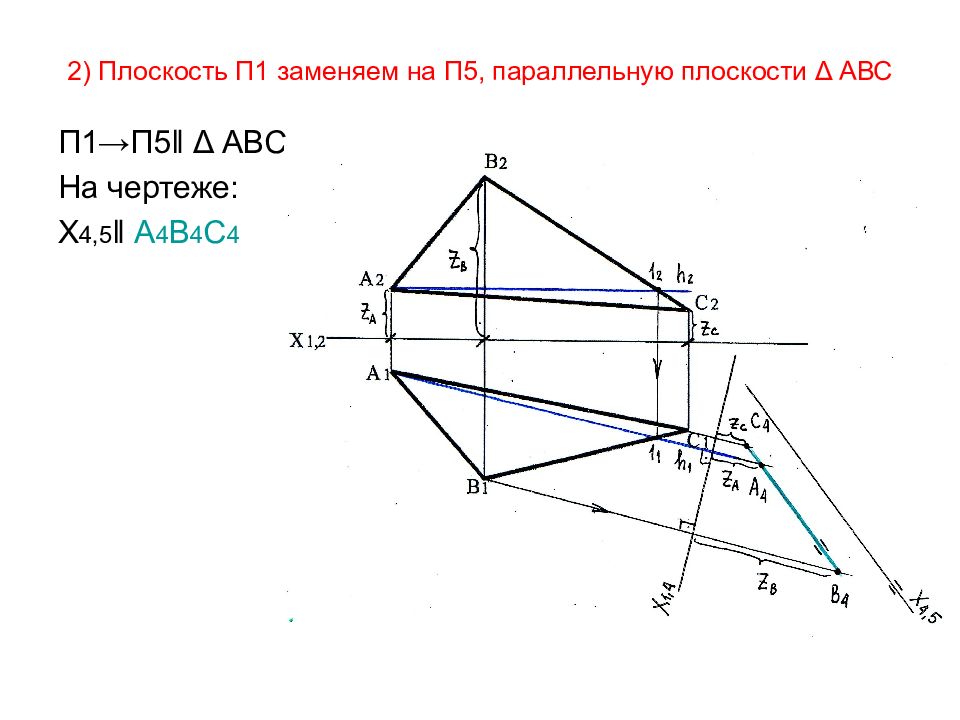
Слайд 54: 2) Плоскость П1 заменяем на П5, параллельную плоскости Δ АВС
П1 →П5‖ Δ АВС На чертеже: Х 4,5 ‖ А 4 В 4 С 4
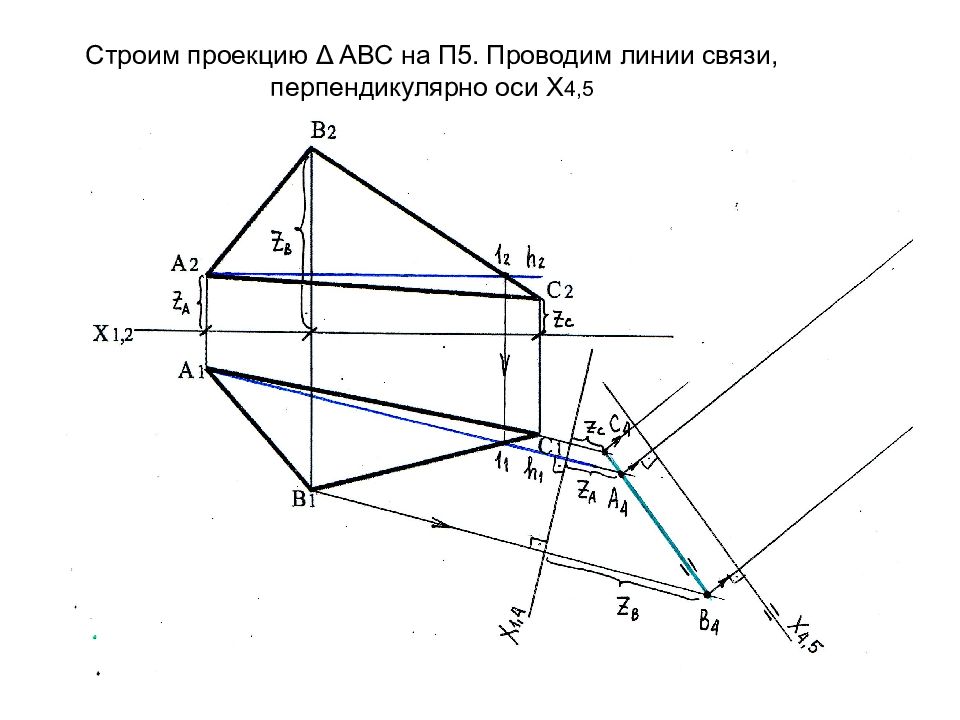
Слайд 55: Строим проекцию Δ АВС на П5. Проводим линии связи, перпендикулярно оси Х 4,5
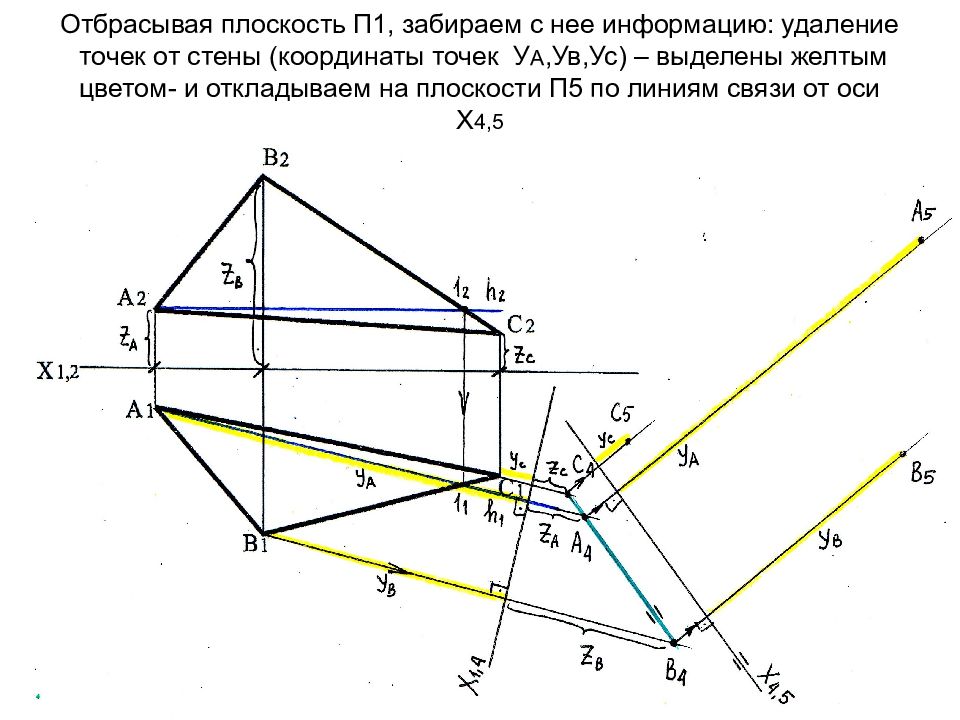
Слайд 56: Отбрасывая плоскость П1, забираем с нее информацию: удаление точек от стены (координаты точек У А,Ув,Ус) – выделены желтым цветом- и откладываем на плоскости П5 по линиям связи от оси Х 4,5
Слайд 58: Задача 6.5 стр.32
Построить проекции прямой призмы высотой 20 мм с основанием АВС
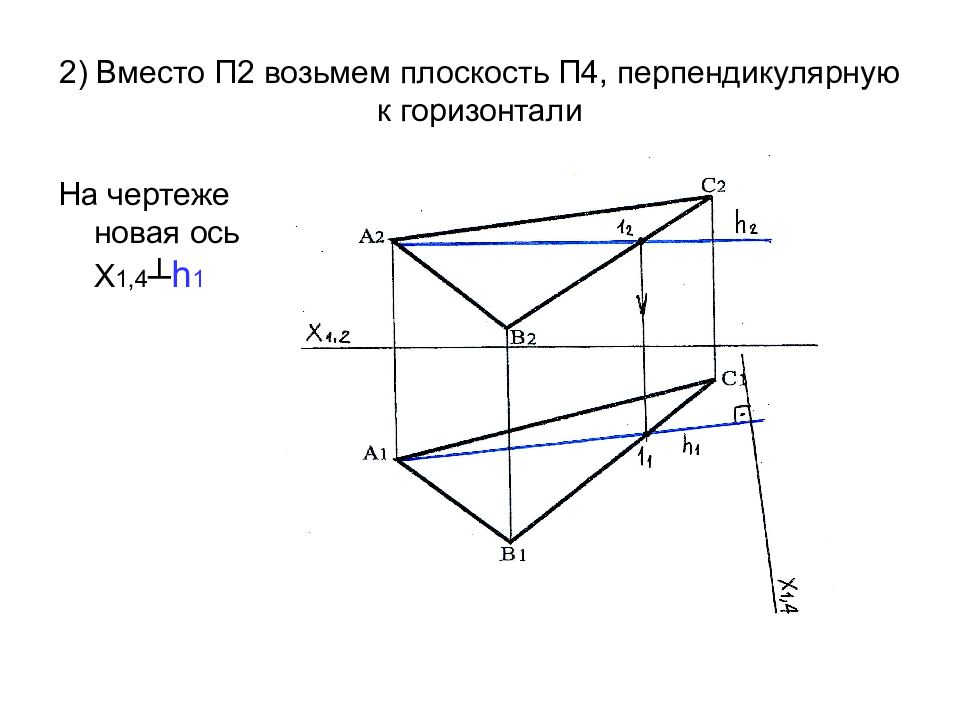
Слайд 59: Главный элемент- плоскость. Необходимо выполнить 3 типовую задачу: преобразовать плоскость общего положения в проецирующую
Решение: Зададим в плоскости линию уровня, например – горизонталь h 2 ‖ Х 1,2 → h 1 строим по признаку принадлежности прямой плоскости (как проходящую через (.)А и (.)1)
Слайд 60: 2) Вместо П2 возьмем плоскость П4, перпендикулярную к горизонтали
На чертеже новая ось Х 1,4 ┴ h 1
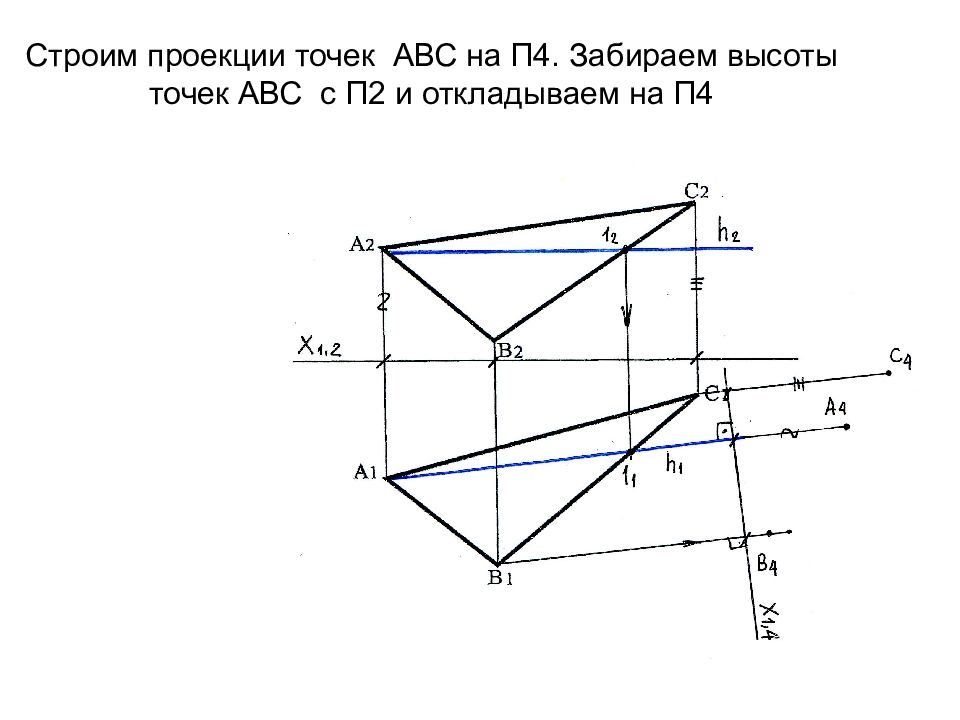
Слайд 61: Строим проекции точек АВС на П4. Забираем высоты точек АВС с П2 и откладываем на П4
Слайд 62
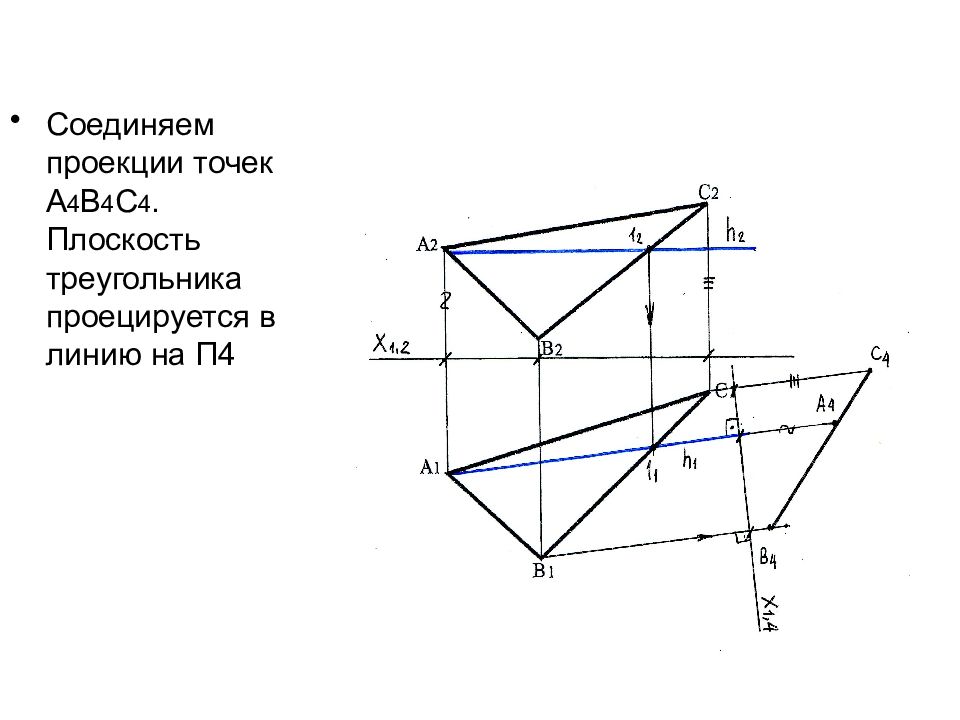
Соединяем проекции точек А 4 В 4 С 4. Плоскость треугольника проецируется в линию на П4
Слайд 63: Т.к. призма прямая, ребра располагаются перпендикулярно основанию и проецируются на П4 в натуральную величину
Отклад ываем н.в. ребер =20 мм
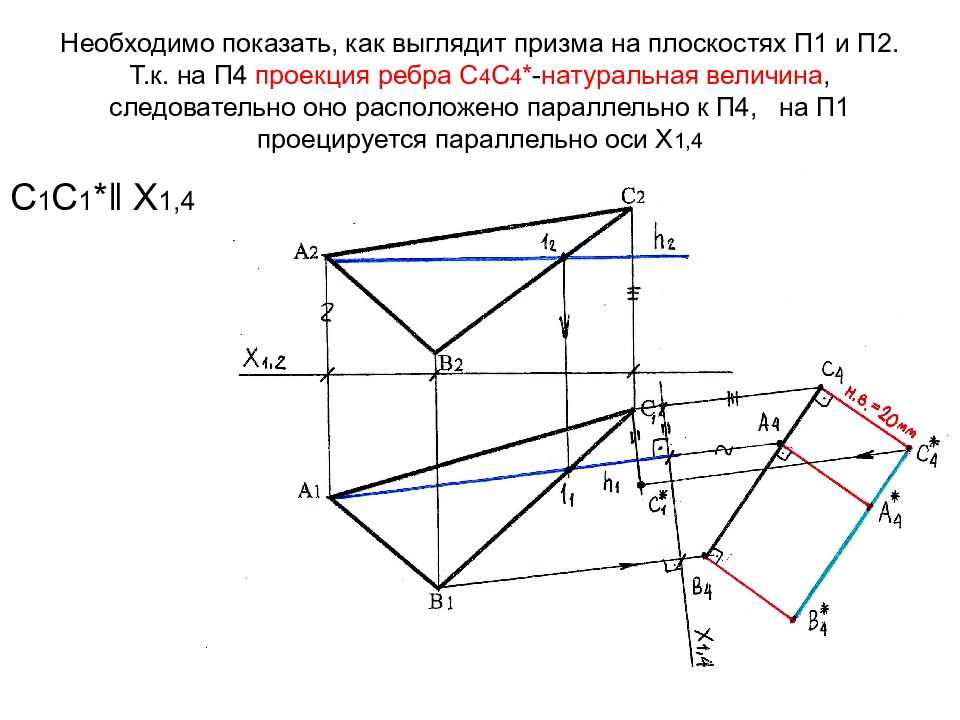
Слайд 65: Необходимо показать, как выглядит призма на плоскостях П1 и П2. Т.к. на П4 проекция ребра С 4 С 4 * - натуральная величина, следовательно оно расположено параллельно к П4, на П1 проецируется параллельно оси Х 1,4
С 1 С 1 * ‖ Х 1,4
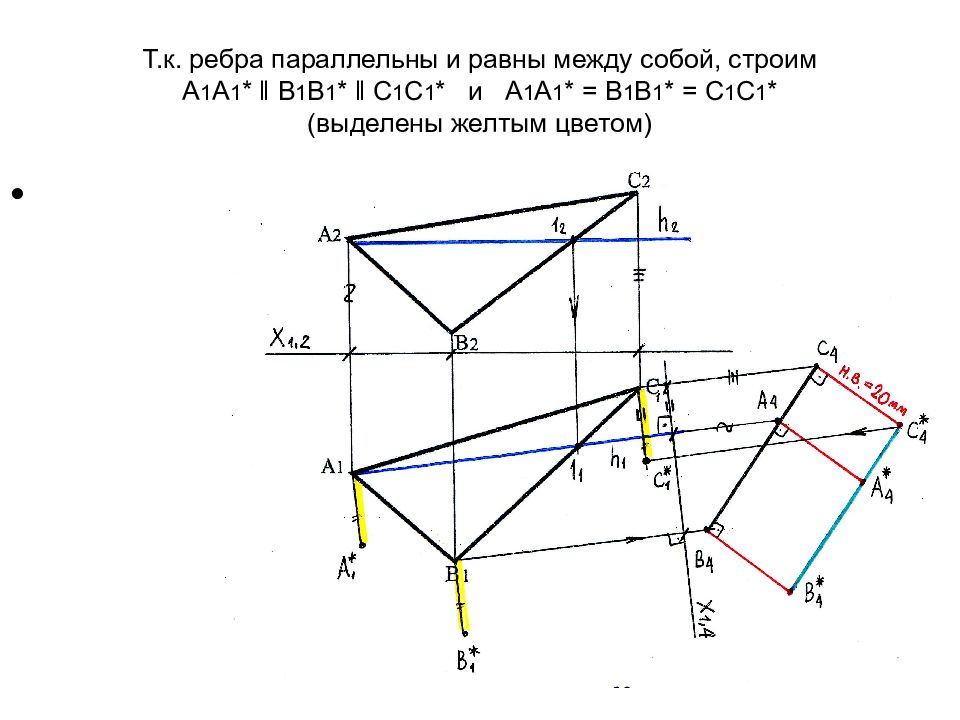
Слайд 66: Т.к. ребра параллельны и равны между собой, строим А 1 А 1 * ‖ В 1 В 1 * ‖ С 1 С 1 * и А 1 А 1 * = В 1 В 1 * = С 1 С 1 * (выделены желтым цветом)
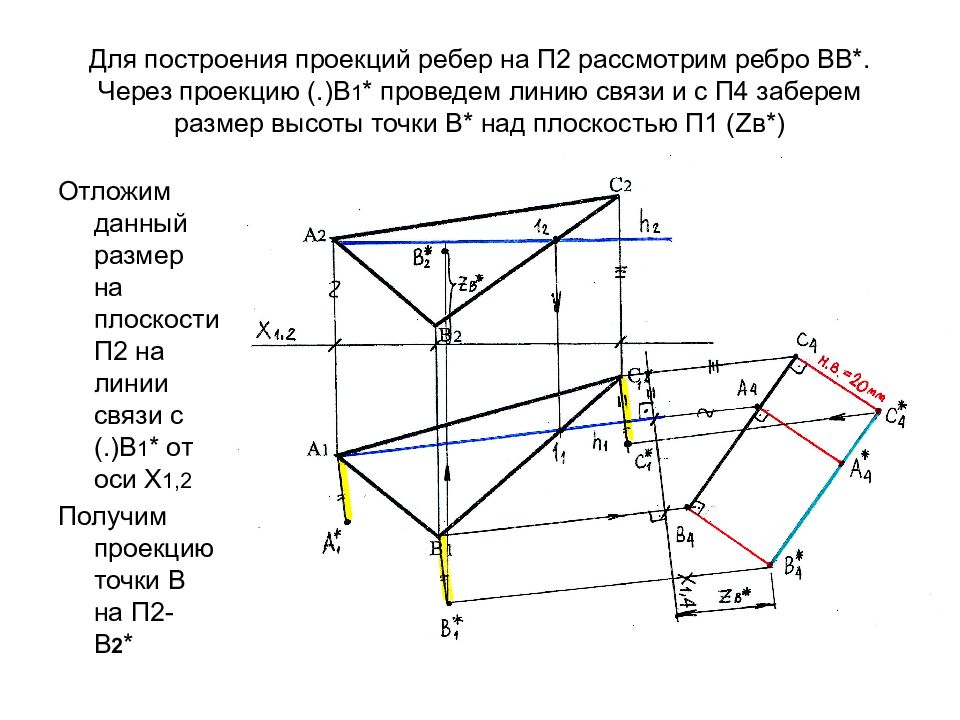
Слайд 67: Для построения проекций ребер на П2 рассмотрим ребро ВВ*. Через проекцию (.)В 1 * проведем линию связи и с П4 заберем размер высоты точки В* над плоскостью П1 ( Z в*)
Отложим данный размер на плоскости П2 на линии связи с (.)В 1 * от оси Х 1,2 Получим проекцию точки В на П2- В 2 *
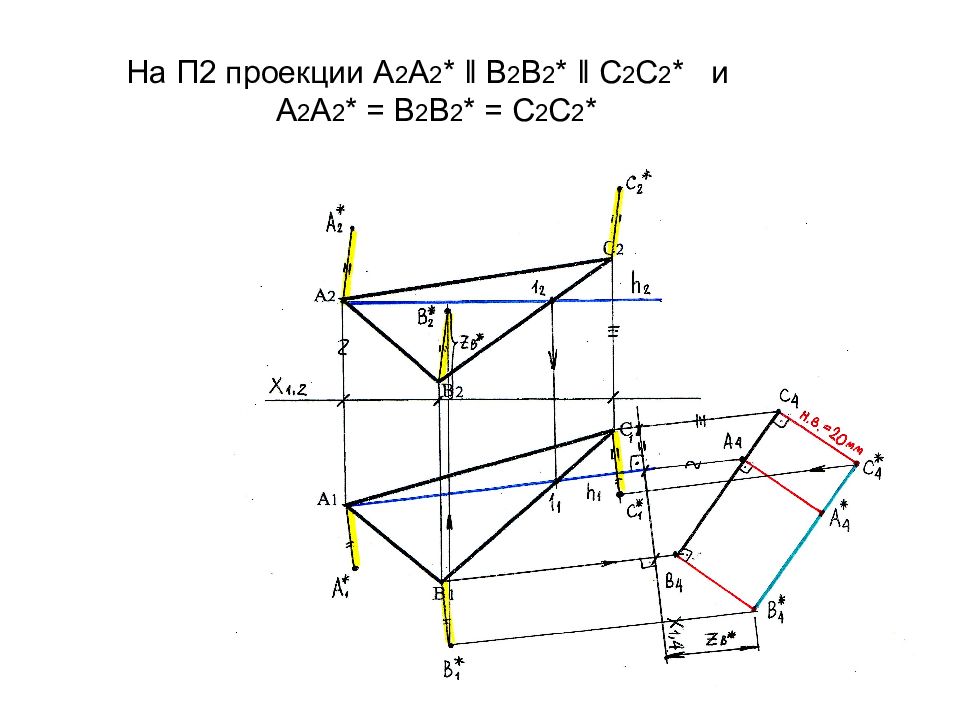
Слайд 68: На П2 проекции А 2 А 2 * ‖ В 2 В 2 * ‖ С 2 С 2 * и А 2 А 2 * = В 2 В 2 * = С 2 С 2 *
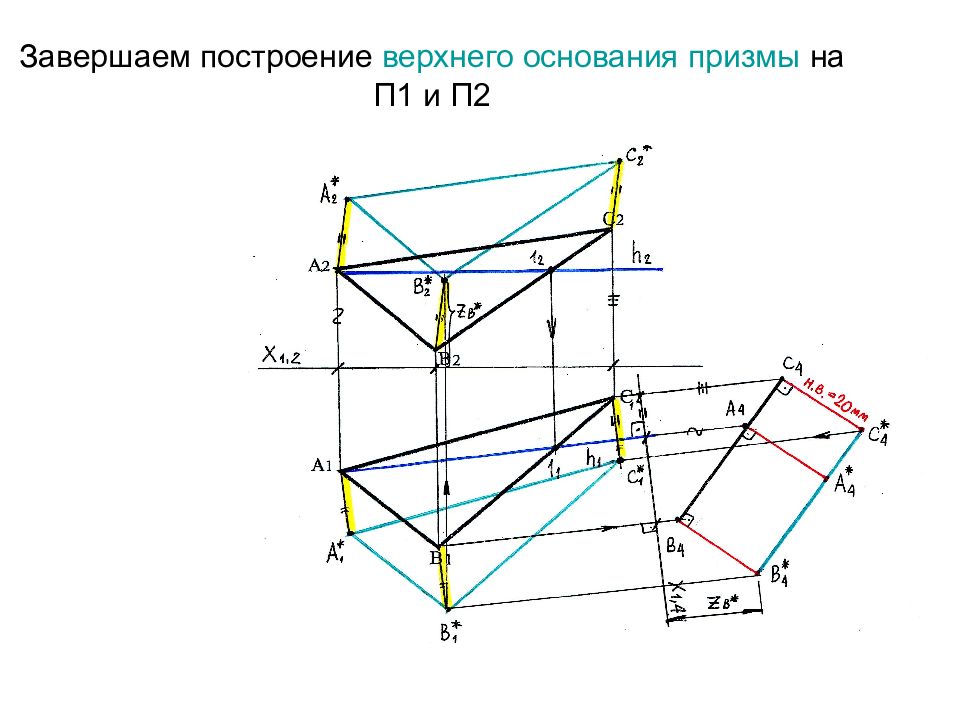
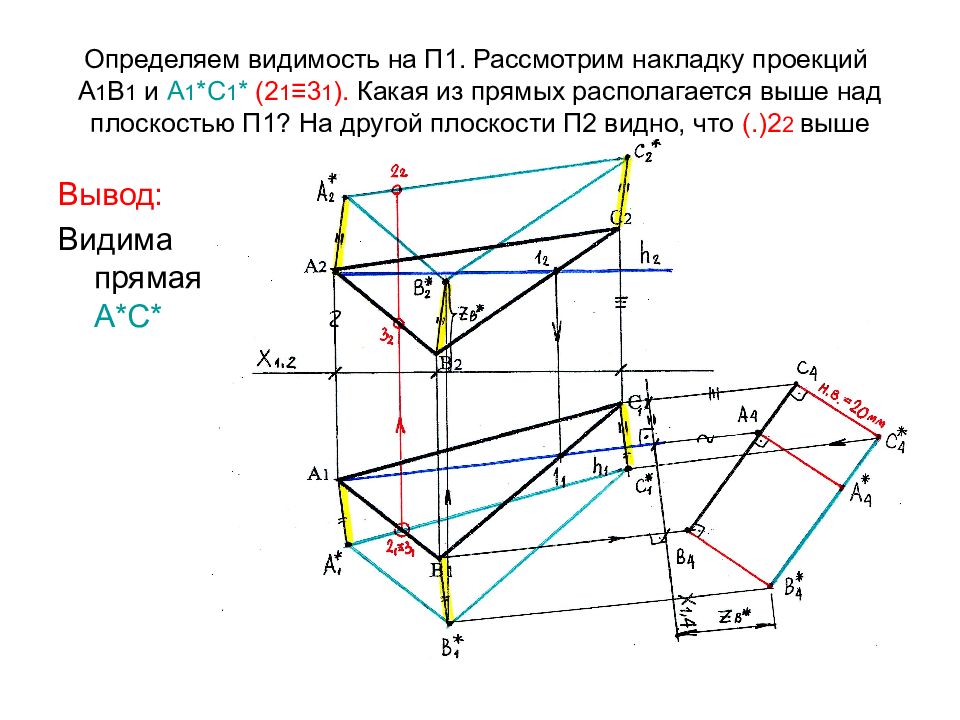
Слайд 70: Определяем видимость на П1. Рассмотрим накладку проекций А 1 В 1 и А 1 *С 1 * (2 1 ≡3 1 ). Какая из прямых располагается выше над плоскостью П1? На другой плоскости П2 видно, что (.)2 2 выше
Вывод: Видима прямая А*С*
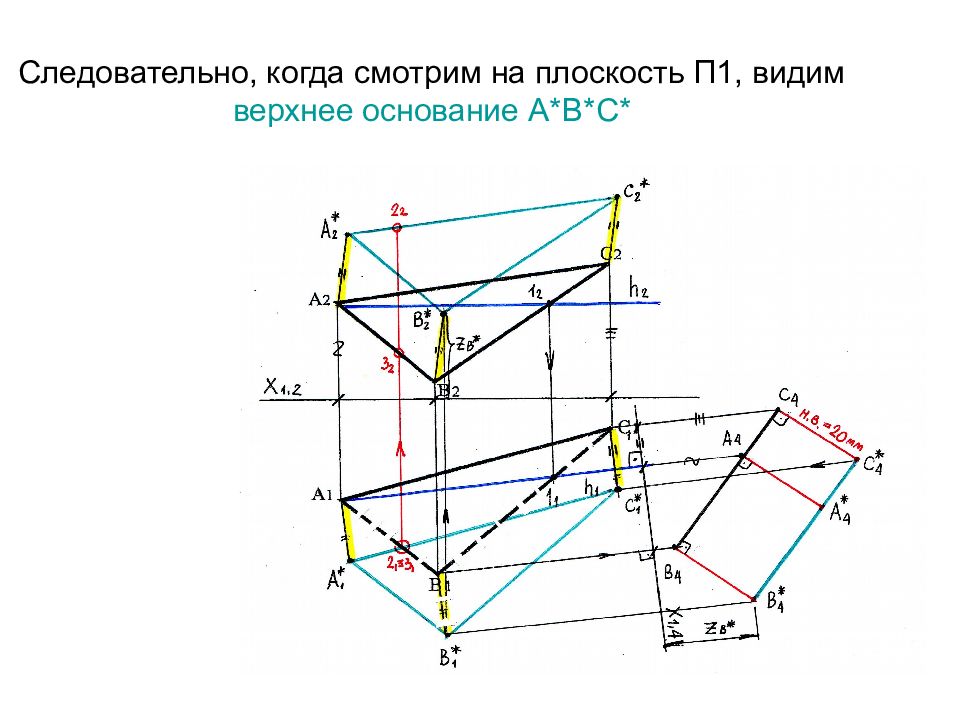
Слайд 71: Следовательно, когда смотрим на плоскость П1, видим верхнее основание А*В*С*
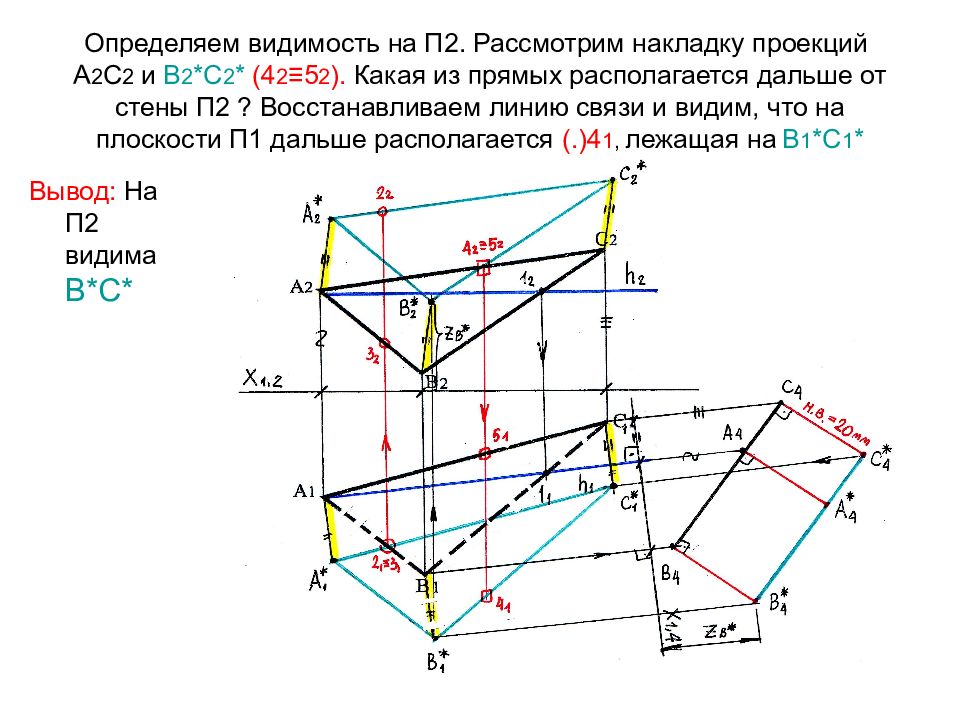
Слайд 72: Определяем видимость на П2. Рассмотрим накладку проекций А 2 С 2 и В 2 *С 2 * (4 2 ≡5 2 ). Какая из прямых располагается дальше от стены П2 ? Восстанавливаем линию связи и видим, что на плоскости П1 дальше располагается (.)4 1, лежащая на В 1 *С 1 *
Вывод: На П2 видима В*С*
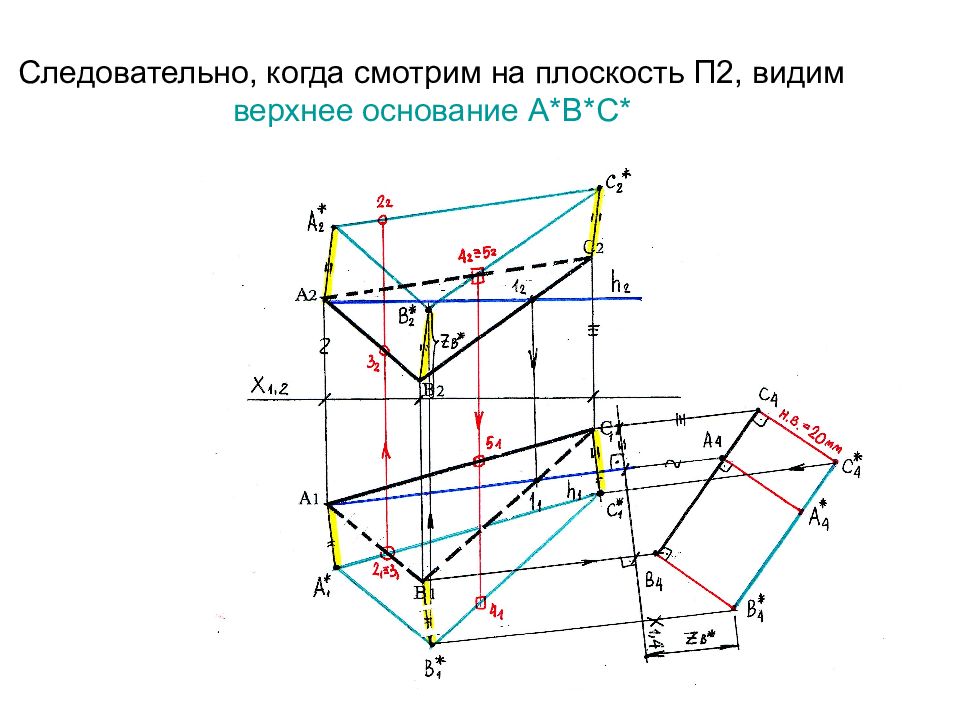
Слайд 73: Следовательно, когда смотрим на плоскость П2, видим верхнее основание А*В*С*
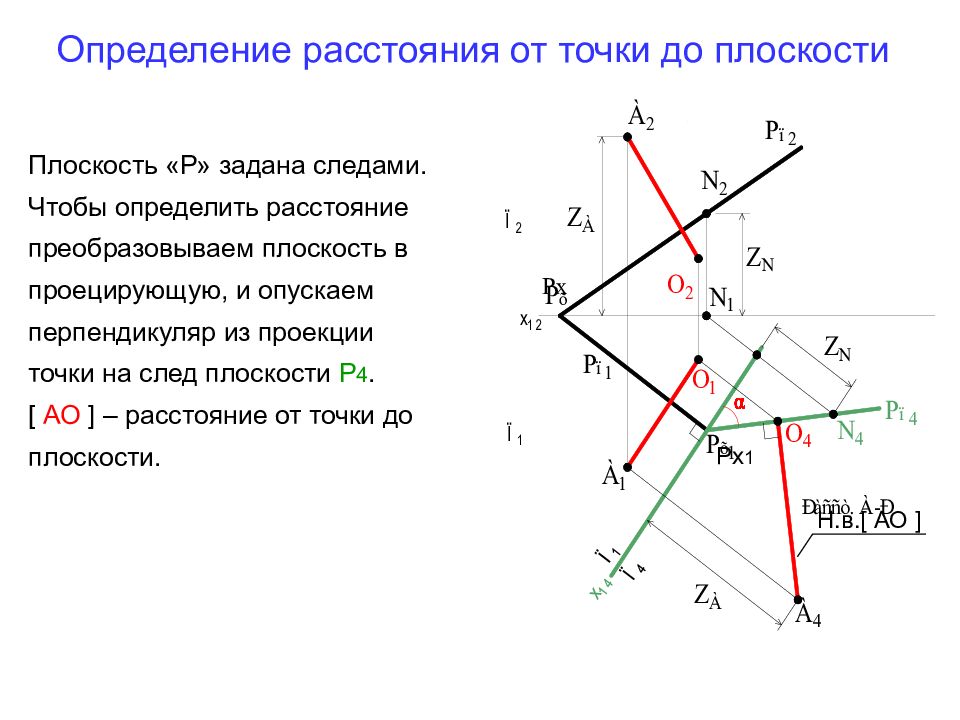
Последний слайд презентации: Лекция 4: Определение расстояния от точки до плоскости
Рх Рх 1 Н.в. [ АО ] Плоскость «Р» задана следами. Чтобы определить расстояние преобразовываем плоскость в проецирующую, и опускаем перпендикуляр из проекции точки на след плоскости Р 4. [ АО ] – расстояние от точки до плоскости.








![Лекция 4 Далее по линиям связи, перпендикулярно к оси Х1,4 определяем положение проекции О 1 и, соединив А 1 и О 1, получим [ А 1 О 1 ]](https://s0.showslide.ru/s_slide/4cd2f424201801e5049a38305eba01c5/2ab7c4b5-9766-4e2a-8a0e-005aba2b2602.jpeg)