Первый слайд презентации: СПОСОБЫ ПРЕОБРАЗОВАНИЯ
СПОСОБЫ ПОЗВОЛЯЮЩИЕ ПРЕОБРАЗОВАТЬ ДАННЫЕ ПРОЕКЦИИ ГЕОМЕТРИЧЕСКИХ ОБЪЕКТОВ В НОВЫЕ, УДОБНЫЕ ДЛЯ РЕШЕНИЯ ЗАДАЧИ СПОСОБЫ ПРЕОБРАЗОВАНИЯ ИСПОЛЬЗУЮТСЯ, В ОСНОВНОМ, ДЛЯ РЕШЕНИЯ МЕТРИЧЕСКИХ ЗАДАЧ (ОПРЕДЕЛЕНИЕ НАТУРАЛЬНОЙ ВЕЛИЧИНЫ ЗАДАННЫХ ОБЪЕКТОВ), МОГУТ БЫТЬ ИСПОЛЬЗОВАНЫ ДЛЯ РЕШЕНИЯ ПОЗИЦИОННЫХ И КОНСТРУКТИВНЫХ ЗАДАЧ
Слайд 2: ЧЕТЫРЕ ОСНОВНЫЕ ЗАДАЧИ, РЕШАЕМЫЕ СПОСОБАМИ ПРЕОБРАЗОВАНИЯ:
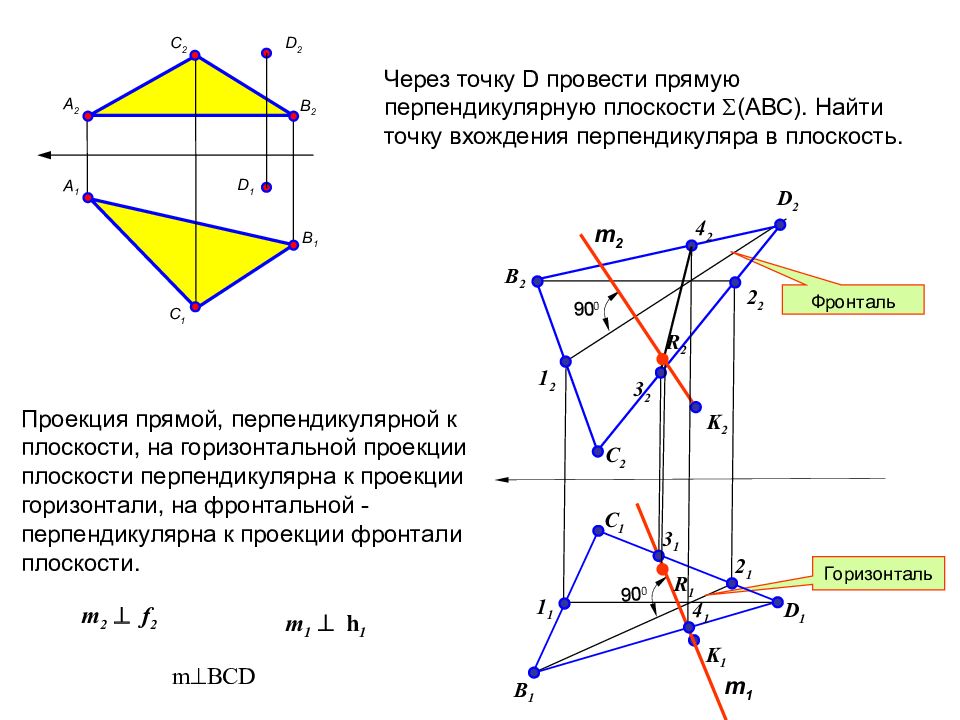
ПРЕОБРАЗОВАТЬ ПРЯМУЮ ОБЩЕГО ПОЛОЖЕНИЯ В ПРЯМУЮ УРОВНЯ (ГОРИЗОНТАЛЬ ИЛИ ФРОНТАЛЬ). ПРЕОБРАЗОВАТЬ ПРЯМУЮ УРОВНЯ В ПРЯМУЮ ПРОЕЦИРУЮЩУЮ. ПРЕОБРАЗОВАТЬ ПЛОСКОСТЬ ОБЩЕГО ПОЛОЖЕНИЯ В ПЛОСКОСТЬ ПРОЕЦИРУЮЩУЮ. 4. ПРЕОБРАЗОВАТЬ ПЛОСКОСТЬ ПРОЕЦИРУЮЩУЮ В ПЛОСКОСТЬ УРОВНЯ.
Слайд 3: ПЕРЕМЕНА ПЛОСКОСТЕЙ ПРОЕКЦИЙ
ЗАДАННЫЙ ГЕОМЕТРИЧЕСКИЙ ОБЪЕКТ НЕПОДВИЖЕН ВВОДЯТСЯ НОВЫЕ ПЛОСКОСТИ ПРОЕКЦИЙ ПАРАЛЛЕЛЬНЫЕ ИЛИ ПЕРПЕНДИКУЛЯРНЫЕ ЗАДАННОМУ ГЕОМЕТРИЧЕСКОМУ ОБЪЕКТУ
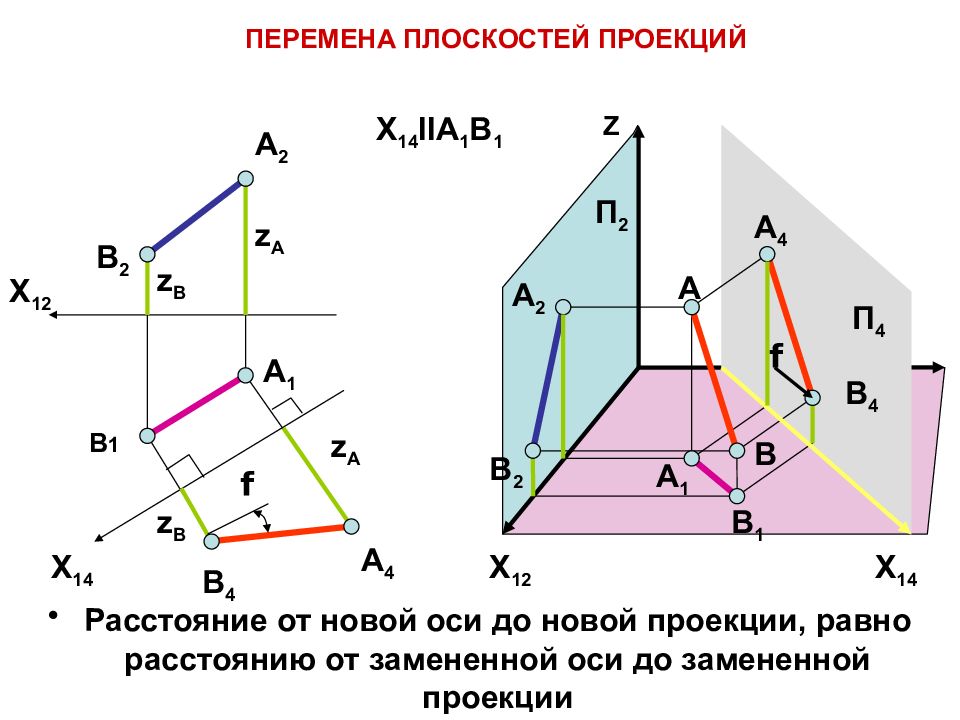
Слайд 4: ПЕРЕМЕНА ПЛОСКОСТЕЙ ПРОЕКЦИЙ
Расстояние от новой оси до новой проекции, равно расстоянию от замененной оси до замененной проекции Y X 1 2 Z А В А 1 В 1 А 2 В 2 В 4 А 4 X 1 4 П 4 П 1 П 2 ПЕРЕМЕНА ПЛОСКОСТЕЙ ПРОЕКЦИЙ П 4 ┴ П 1 П 4 II АВ X 14 IIA 1 B 1
Слайд 5: ПЕРЕМЕНА ПЛОСКОСТЕЙ ПРОЕКЦИЙ
А 1 В 1 А 2 В 2 В 4 А 4 X 12 Z А В А 1 В 1 А 2 В 2 В 4 А 4 X 14 П 4 П 2 X 12 X 14 Расстояние от новой оси до новой проекции, равно расстоянию от замененной оси до замененной проекции f z B z B z А z А f X 14 IIA 1 B 1
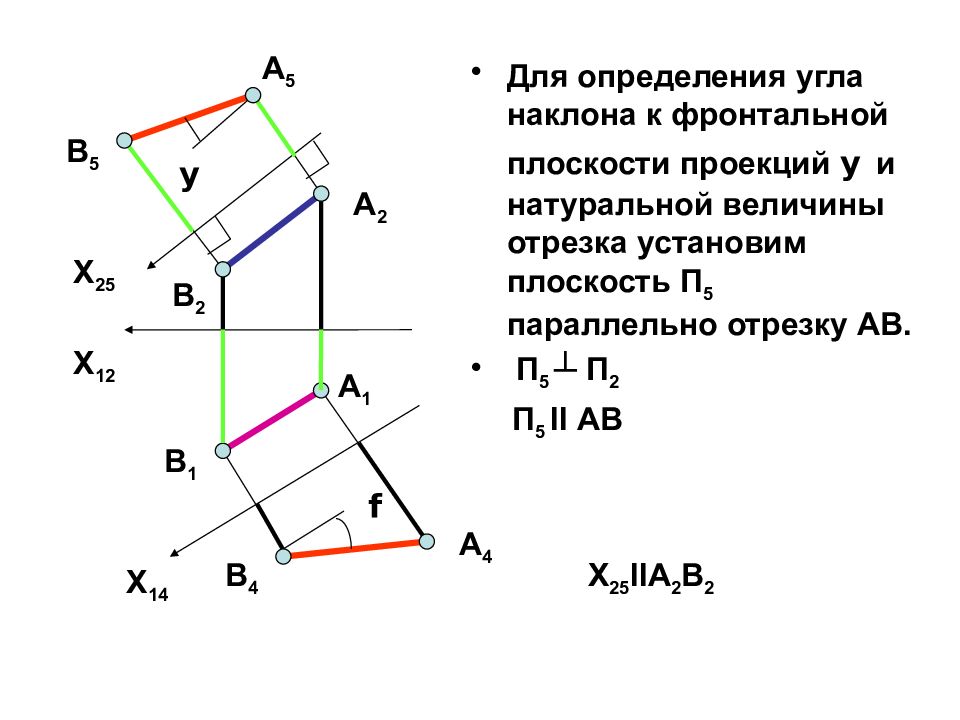
Слайд 6
Для определения угла наклона к фронтальной плоскости проекций y и натуральной величины отрезка установим плоскость П 5 параллельно отрезку АВ. П 5 ┴ П 2 П 5 II АВ А 1 В 1 А 2 В 2 В 4 А 4 X 12 X 14 f А 5 X 25 В 5 y X 25 IIA 2 B 2
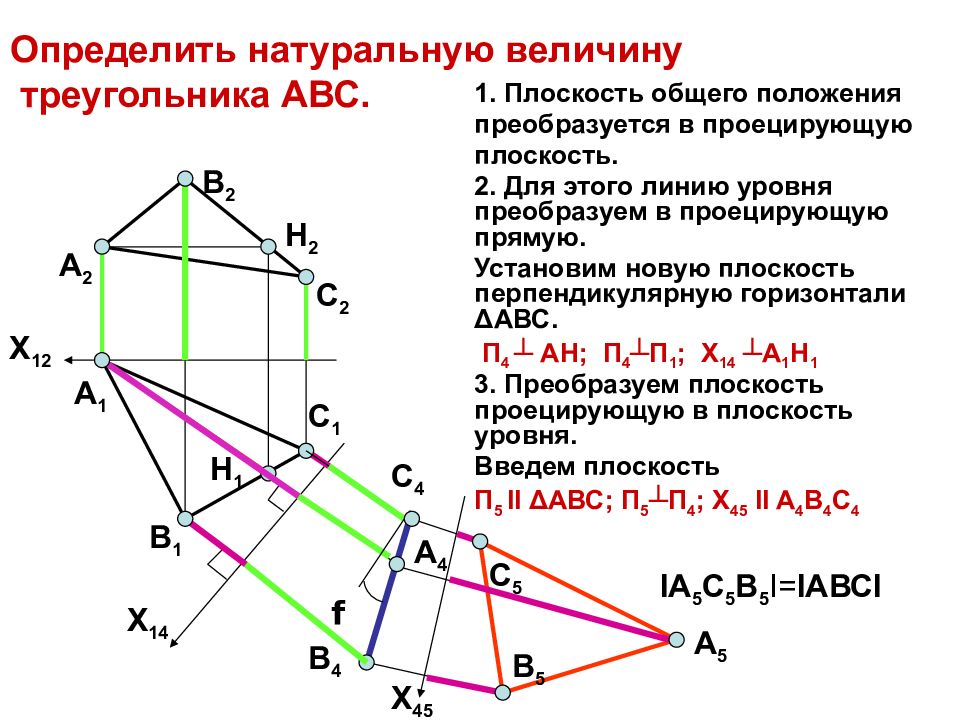
Слайд 7: Определить натуральную величину треугольника АВС
1. Плоскость общего положения преобразуется в проецирующую плоскость. 2. Для этого линию уровня преобразуем в проецирующую прямую. Установим новую плоскость перпендикулярную горизонтали Δ АВС. П 4 ┴ А H; П 4 ┴П 1 ; X 14 ┴ A 1 H 1 3. Преобразуем плоскость проецирующую в плоскость уровня. Введем плоскость П 5 ІІ Δ АВС ; П 5 ┴П 4 ; X 45 II A 4 B 4 C 4 X 12 A 1 B 2 B 1 C 1 C 2 A 2 H 2 H 1 X 14 A 4 B 4 C 4 X 45 В 5 С 5 А 5 І А 5 С 5 В 5 І= ІАВСІ f
Слайд 8: Плоскопараллельное перемещение
ЗАДАННЫЙ ГЕОМЕТРИЧЕСКИЙ ОБЪЕКТ СОВЕРШАЕТ ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ, ПРИ КОТОРОМ ВСЕ ЕГО ТОЧКИ ДВИЖУТСЯ ПАРАЛЛЕЛЬНО НЕКОТОРОЙ ПЛОСКОСТИ ДО ПОЛОЖЕНИЯ ПАРАЛЛЕЛЬНОГО ИЛИ ПЕРПЕНДИКУЛЯРНОГО ПЛОСКОСТИ ПРОЕКЦИЙ. ЛИНИИ, ПО КОТОРЫМ ПРОИСХОДИТ ПЕРЕМЕЩЕНИЕ ВСЕХ ТОЧЕК ОБЪЕКТА, НАХОДЯТСЯ В ПЛОСКОСТЯХ УРОВНЯ.
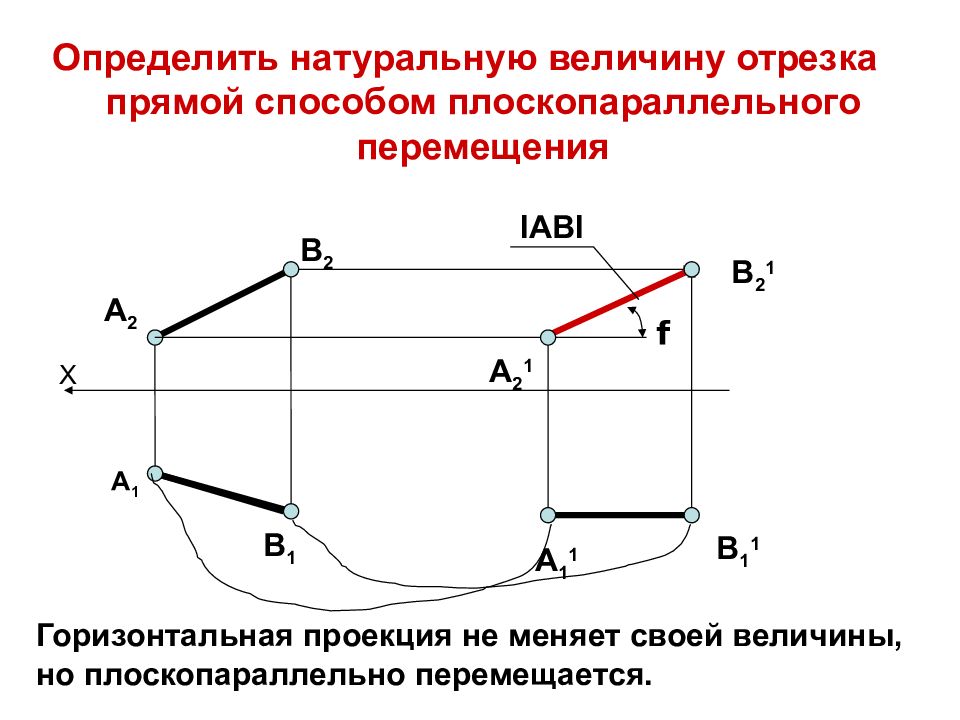
Слайд 9
Определить натуральную величину отрезка прямой способом плоскопараллельного перемещения X A 2 B 1 A 1 B 2 A 1 1 B 1 1 A 2 1 B 2 1 f I АВ I Горизонтальная проекция не меняет своей величины, но плоскопараллельно перемещается.
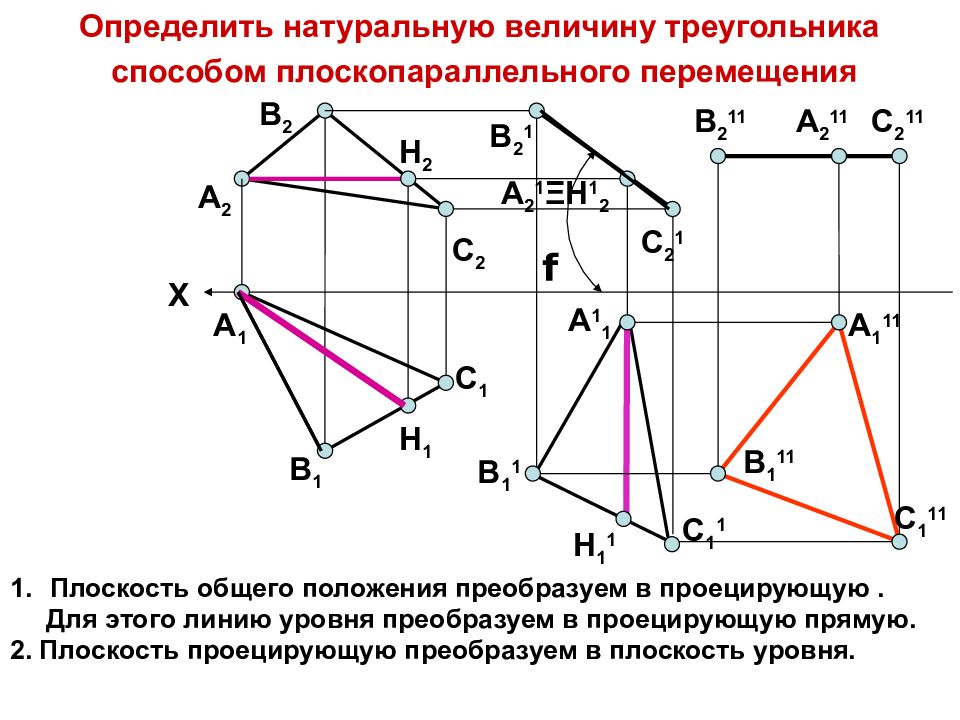
Слайд 10
Плоскость общего положения преобразуем в проецирующую. Для этого линию уровня преобразуем в проецирующую прямую. 2. Плоскость проецирующую преобразуем в плоскость уровня. Определить натуральную величину треугольника способом плоскопараллельного перемещения X A 1 B 1 C 1 C 2 B 2 A 2 A 1 1 C 1 1 B 1 1 C 2 1 B 2 1 A 2 1 Ξ H 1 2 B 2 11 A 2 11 C 2 11 B 1 11 A 1 11 C 1 11 H 1 H 2 H 1 1 f
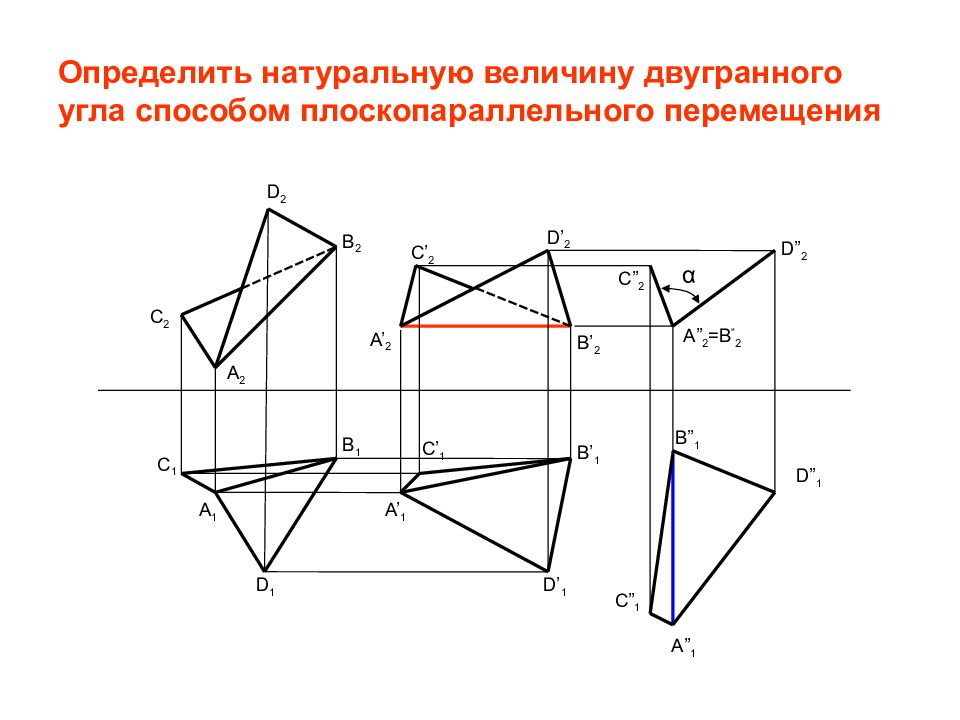
A 2 B 2 D 2 C 2 A 1 B 1 D 1 A’ 2 B’ 2 D’ 2 C’ 2 A’ 1 B’ 1 D’ 1 C’ 1 C” 1 A” 1 B” 1 D” 1 A” 2 =B ” 2 C” 2 D” 2 С 1 α
Слайд 12: ВРАЩЕНИЕ ВОКРУГ ПРЯМЫХ ПЕРПЕНДИКУЛЯРНЫХ ПЛОСКОСТЯМ ПРОЕКЦИЙ
Заданный геометрический объект вращается вокруг проецирующей оси до положения параллельного или перпендикулярного какой-либо плоскости проекций. Все точки объекта движутся по окружностям, которые располагаются в плоскостях уровня, перпендикулярных оси вращения.
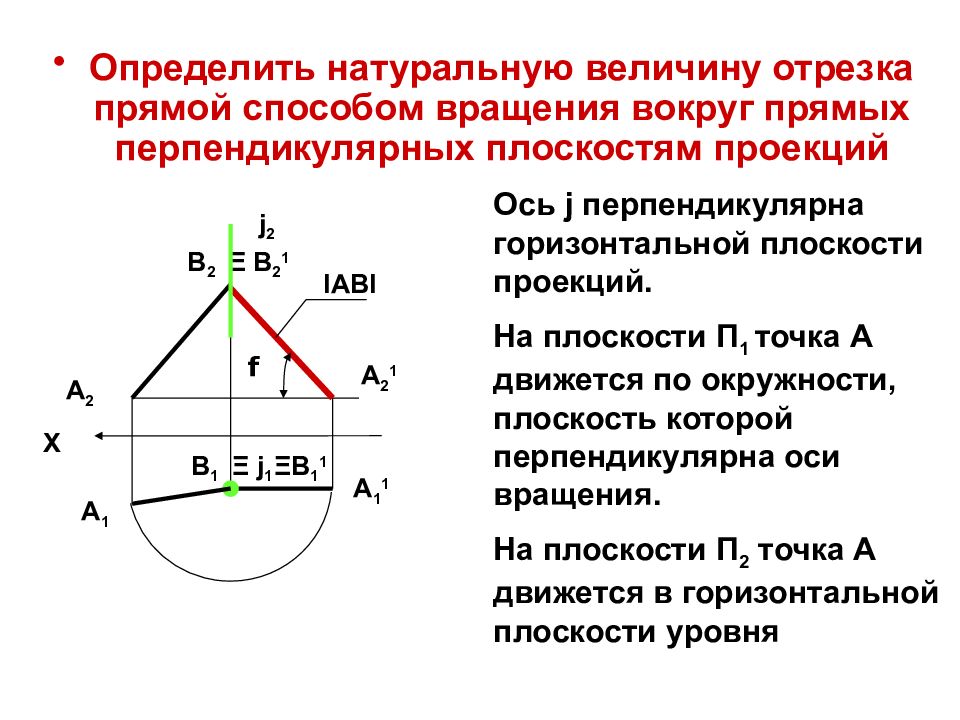
Слайд 13
Определить натуральную величину отрезка прямой способом вращения вокруг прямых перпендикулярных плоскостям проекций A 2 B 1 A 1 B 2 j 2 Ξ j 1 X A 1 1 A 2 1 I AB I Ось j перпендикулярна горизонтальной плоскости проекций. На плоскости П 1 точка А движется по окружности, плоскость которой перпендикулярна оси вращения. На плоскости П 2 точка А движется в горизонтальной плоскости уровня f Ξ B 2 1 Ξ B 1 1
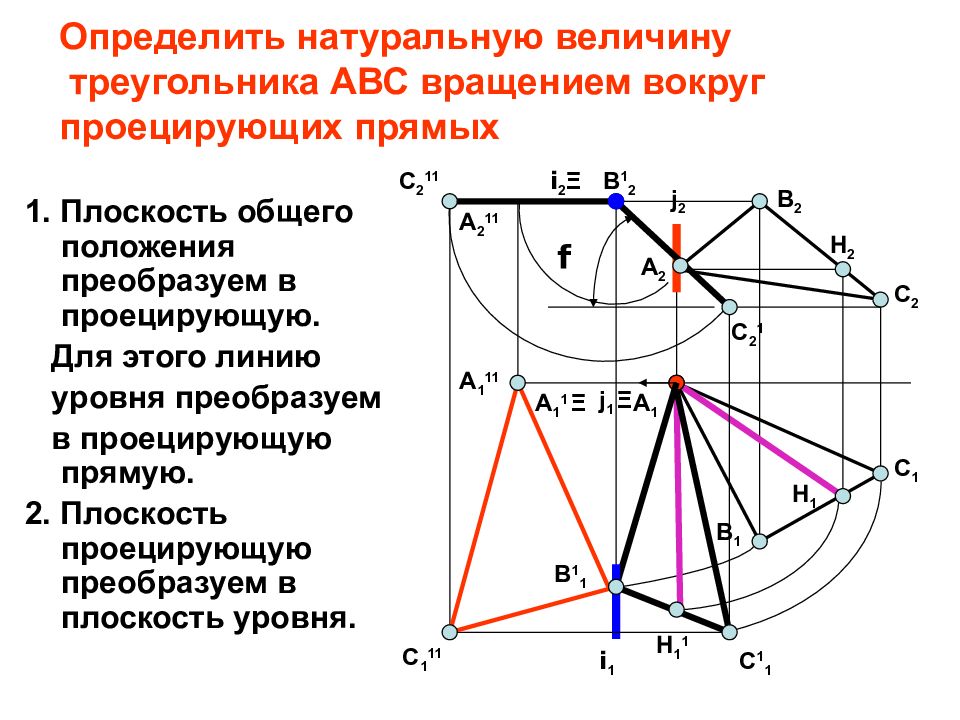
Слайд 14: Определить натуральную величину треугольника АВС вращением вокруг проецирующих прямых
1. Плоскость общего положения преобразуем в проецирующую. Для этого линию уровня преобразуем в проецирующую прямую. 2. Плоскость проецирующую преобразуем в плоскость уровня. Определить натуральную величину треугольника АВС вращением вокруг проецирующих прямых A 1 B 2 A 2 H 1 C 1 C 2 B 1 H 2 j 2 j 1 Ξ H 1 1 C 1 1 B 1 1 C 2 1 В 1 2 i 1 i 2 Ξ f C 2 11 A 2 11 C 1 11 A 1 11 А 1 1 Ξ
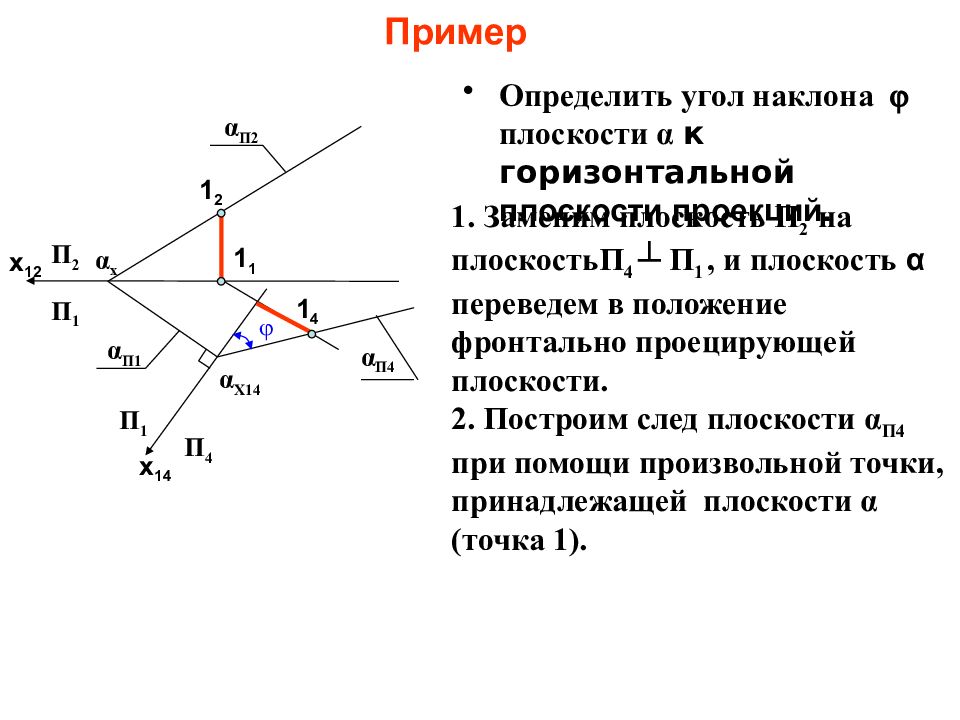
Слайд 15: Пример
Определить угол наклона плоскости α к горизонтальной плоскости проекций. x 12 x 14 α П2 α П 1 α x 1. Заменим плоскость П 2 на плоскостьП 4 ┴ П 1, и плоскость α переведем в положение фронтально проецирующей плоскости. 2. Построим след плоскости α П4 при помощи произвольной точки, принадлежащей плоскости α (точка 1). 1 2 1 1 1 4 α П4 α X 14 П 2 П 1 П 1 П 4
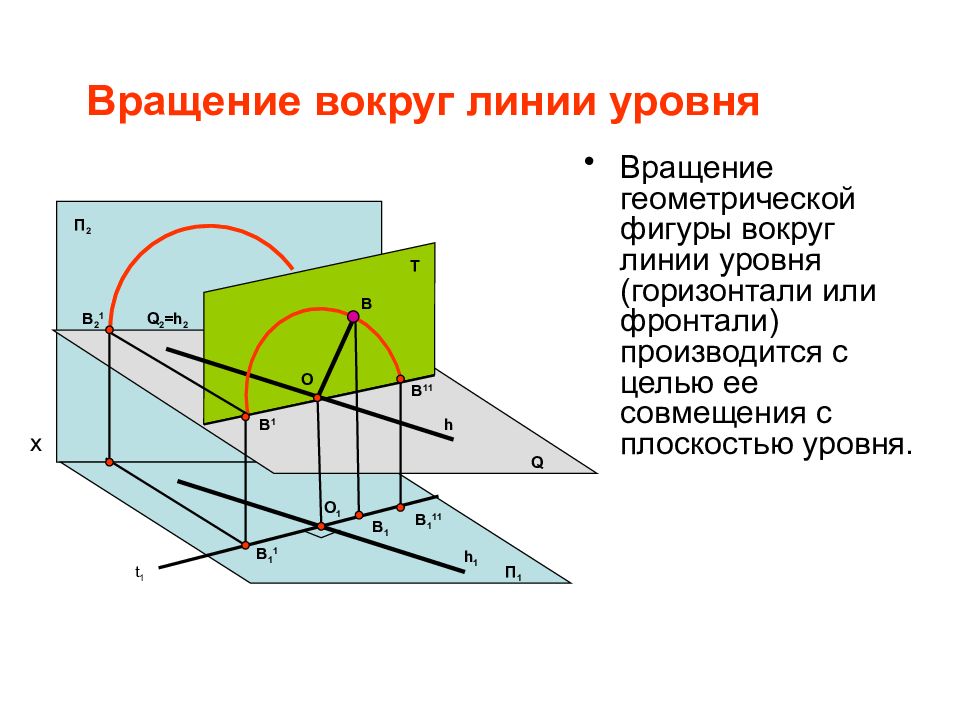
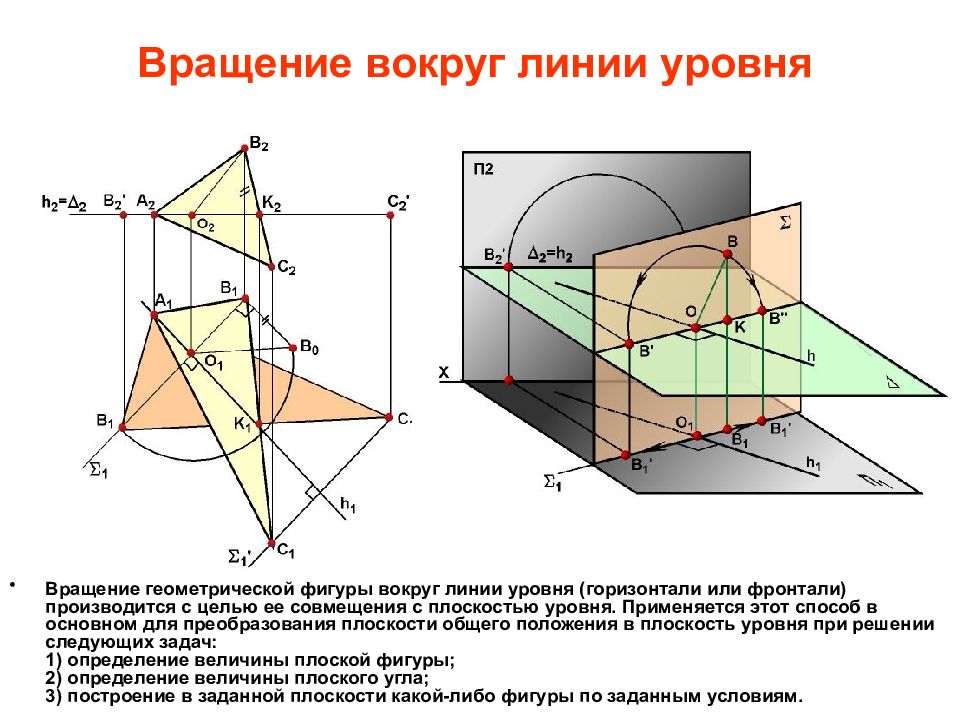
Слайд 16: Вращение вокруг линии уровня
Вращение геометрической фигуры вокруг линии уровня (горизонтали или фронтали) производится с целью ее совмещения с плоскостью уровня. B x П 2 h O B 1 П 1 h 1 O 1 T Q t 1 B 1 B 11 B 1 1 B 1 11 B 2 1 Q 2 =h 2
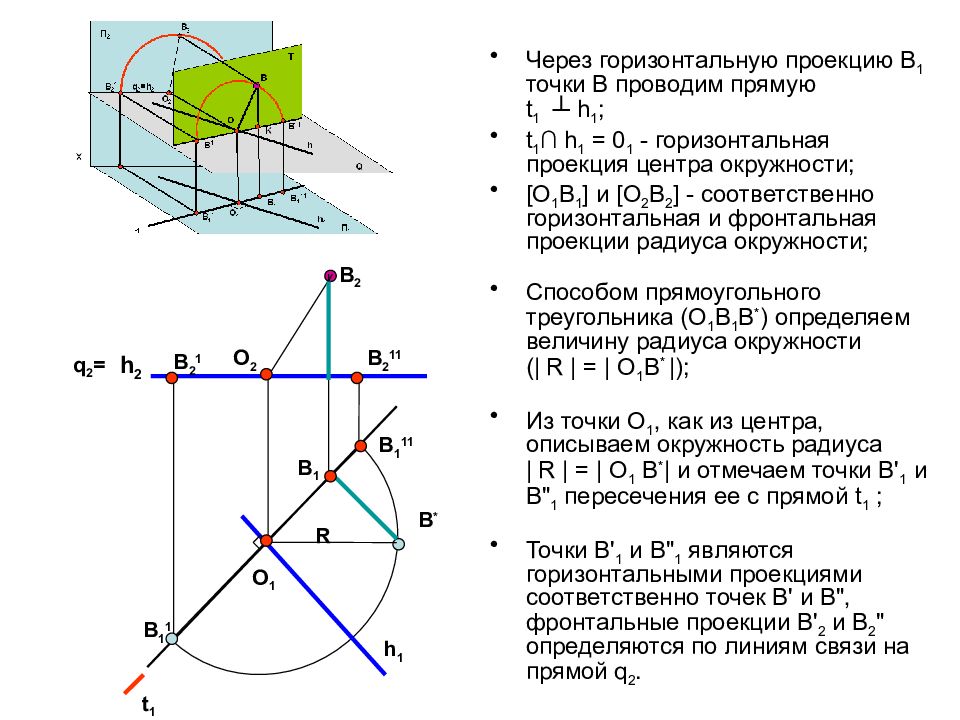
Слайд 17
Через горизонтальную проекцию В 1 точки В проводим прямую t 1 ┴ h 1 ; t 1 ∩ h 1 = 0 1 - горизонтальная проекция центра окружности; [О 1 В 1 ] и [О 2 В 2 ] - соответственно горизонтальная и фронтальная проекции радиуса окружности; Способом прямоугольного треугольника (O 1 В 1 В * ) определяем величину радиуса окружности (| R | = | О 1 B * |); Из точки О 1, как из центра, описываем окружность радиуса | R | = | О 1 В * | и отмечаем точки В' 1 и В" 1 пересечения ее с прямой t 1 ; Точки В' 1 и В" 1 являются горизонтальными проекциями соответственно точек В' и В", фронтальные проекции В' 2 и В 2 " определяются по линиям связи на прямой q 2. B 2 B 1 h 2 h 1 O 1 O 2 R B * B 1 11 B 1 1 B 2 1 B 2 11 t 1 q 2 =
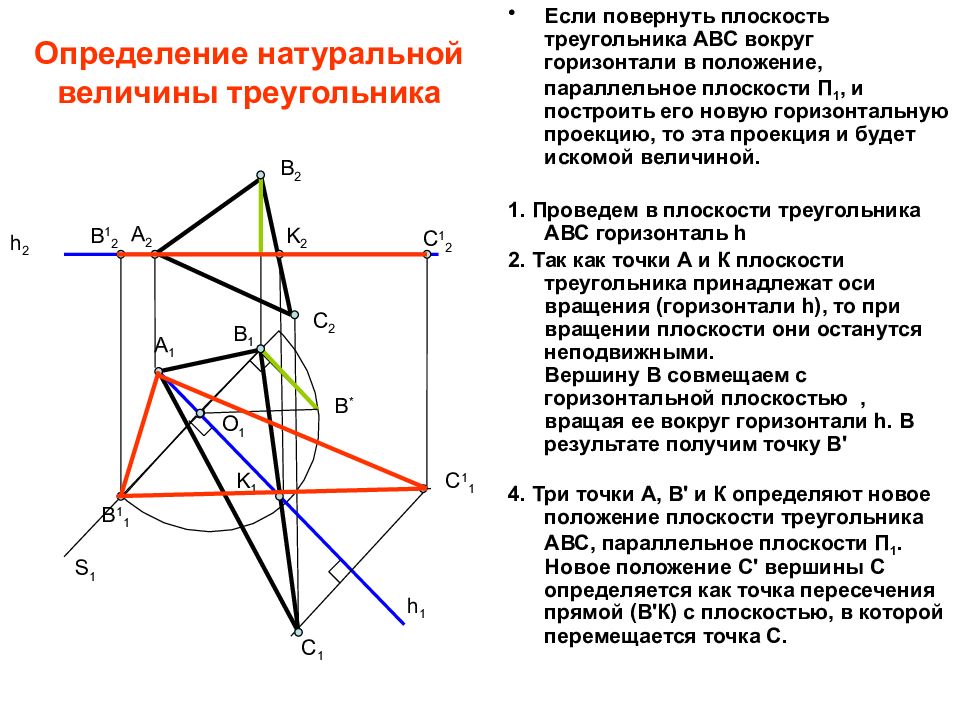
Слайд 18: Определение натуральной величины треугольника
Если повернуть плоскость треугольника АВС вокруг горизонтали в положение, параллельное плоскости П 1, и построить его новую горизонтальную проекцию, то эта проекция и будет искомой величиной. 1. Проведем в плоскости треугольника АВС горизонталь h 2. Так как точки А и К плоскости треугольника принадлежат оси вращения (горизонтали h), то при вращении плоскости они останутся неподвижными. Вершину В совмещаем с горизонтальной плоскостью, вращая ее вокруг горизонтали h. В результате получим точку В' 4. Три точки А, В' и К определяют новое положение плоскости треугольника АВС, параллельное плоскости П 1. Новое положение С' вершины С определяется как точка пересечения прямой (В'К) с плоскостью, в которой перемещается точка С. В 2 A 2 C 2 C 1 В 1 A 1 h 2 K 2 K 1 h 1 S 1 C 1 1 В * O 1 В 1 1 C 1 2 B 1 2
Последний слайд презентации: СПОСОБЫ ПРЕОБРАЗОВАНИЯ: Вращение вокруг линии уровня
Вращение геометрической фигуры вокруг линии уровня (горизонтали или фронтали) производится с целью ее совмещения с плоскостью уровня. Применяется этот способ в основном для преобразования плоскости общего положения в плоскость уровня при решении следующих задач: 1) определение величины плоской фигуры; 2) определение величины плоского угла; 3) построение в заданной плоскости какой-либо фигуры по заданным условиям.