Первый слайд презентации: Лекция 10
Алгоритм решения задач по определению линии пересечения поверхностей (линии перехода) Взаимное пересечение многогранников Пересечение кривых поверхностей.
Слайд 2: Взаимное пересечение многогранников
Линия пересечения двух многогранников представляет собой одну или две замкнутые ломаные линии. Отрезки ломаной линии являются линиями пересечения граней, а точки излома –точками пересечения ребер одного многогранника с гранями другого и ребер второго с гранями первого
Слайд 3
Если один многогранник частично пересекается другим, то линия пересечения будет представлять собой одну замкнутую ломаную линию. Такое пересечение называется неполным. Если один многогранник полностью пересекается другим, то пересечение называют полным. Линия пересечения в этом случае состоит из двух замкнутых ломаных линий.
Слайд 4
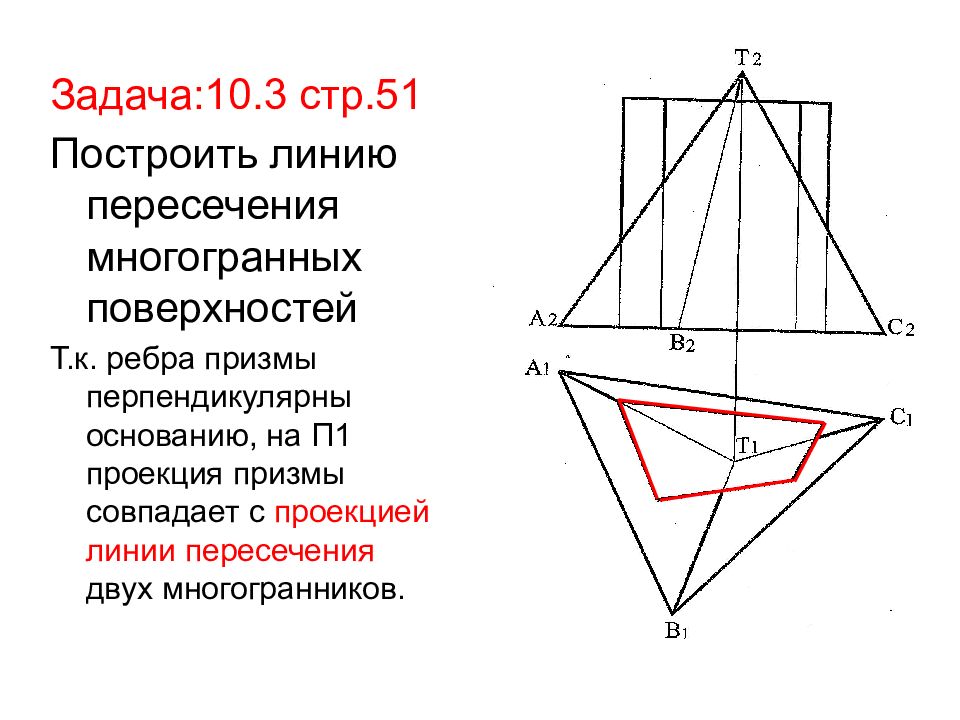
Задача:10.3 стр.51 Построить линию пересечения многогранных поверхностей Т.к. ребра призмы перпендикулярны основанию, на П1 проекция призмы совпадает с проекцией линии пересечения двух многогранников.
Слайд 5
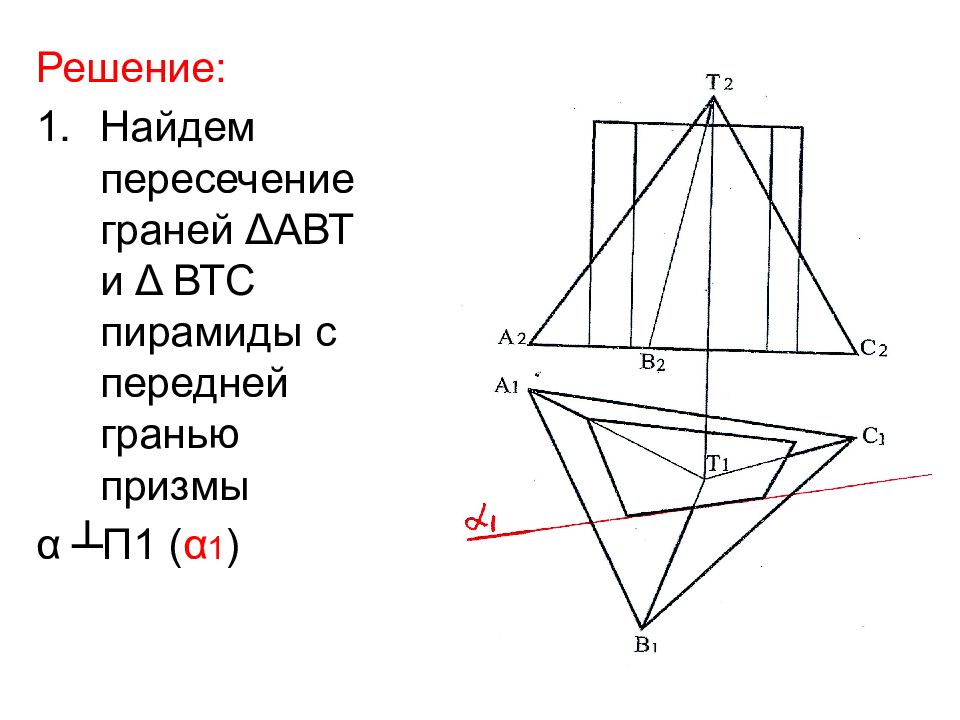
Решение: Найдем пересечение граней Δ АВТ и Δ ВТС пирамиды с передней гранью призмы α ┴П1 ( α 1 )
Слайд 6
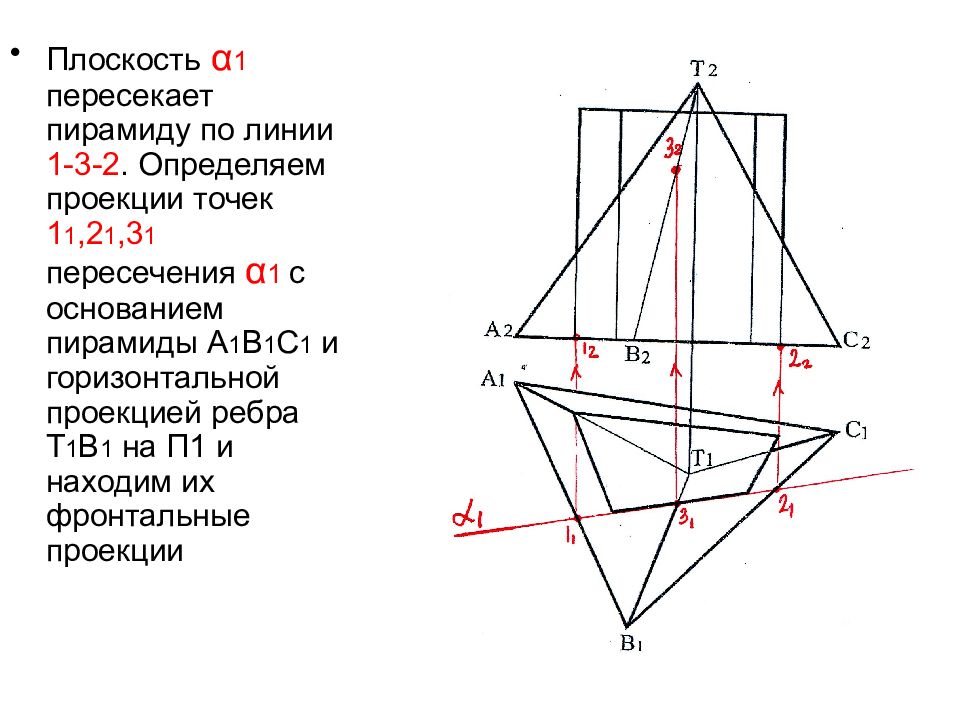
Плоскость α 1 пересекает пирамиду по линии 1-3-2. Определяем проекции точек 1 1,2 1,3 1 пересечения α 1 с основанием пирамиды А 1 В 1 С 1 и горизонтальной проекцией ребра Т 1 В 1 на П1 и находим их фронтальные проекции
Слайд 7
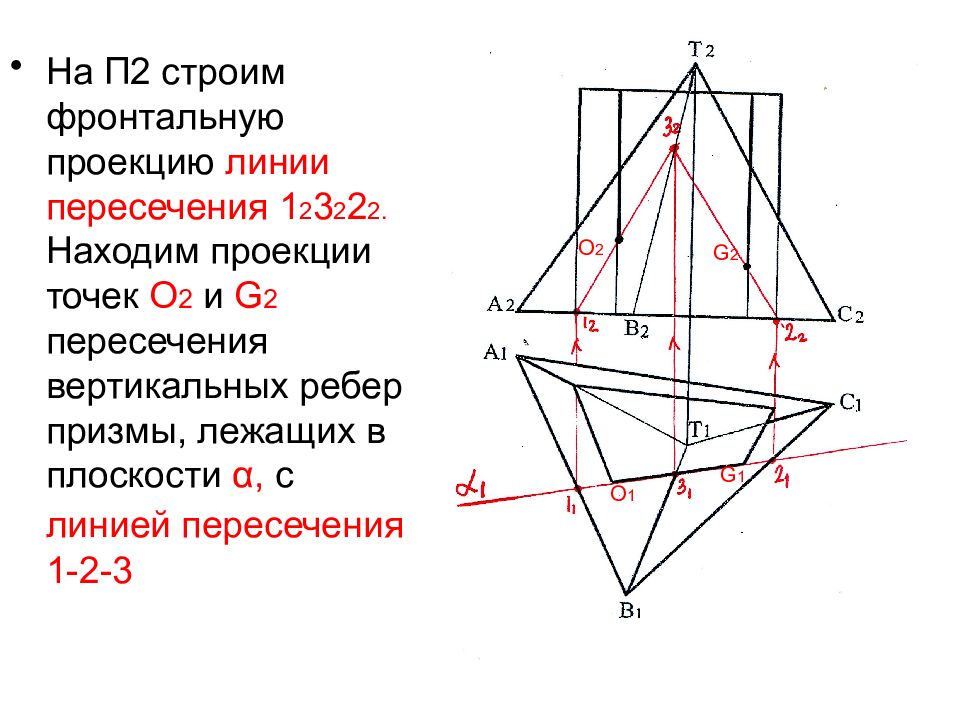
На П2 строим фронтальную проекцию линии пересечения 1 2 3 2 2 2. Находим проекции точек O 2 и G 2 пересечения вертикальных ребер призмы, лежащих в плоскости α, с линией пересечения 1-2-3 О 2 G 2 O 1 G 1
Слайд 8
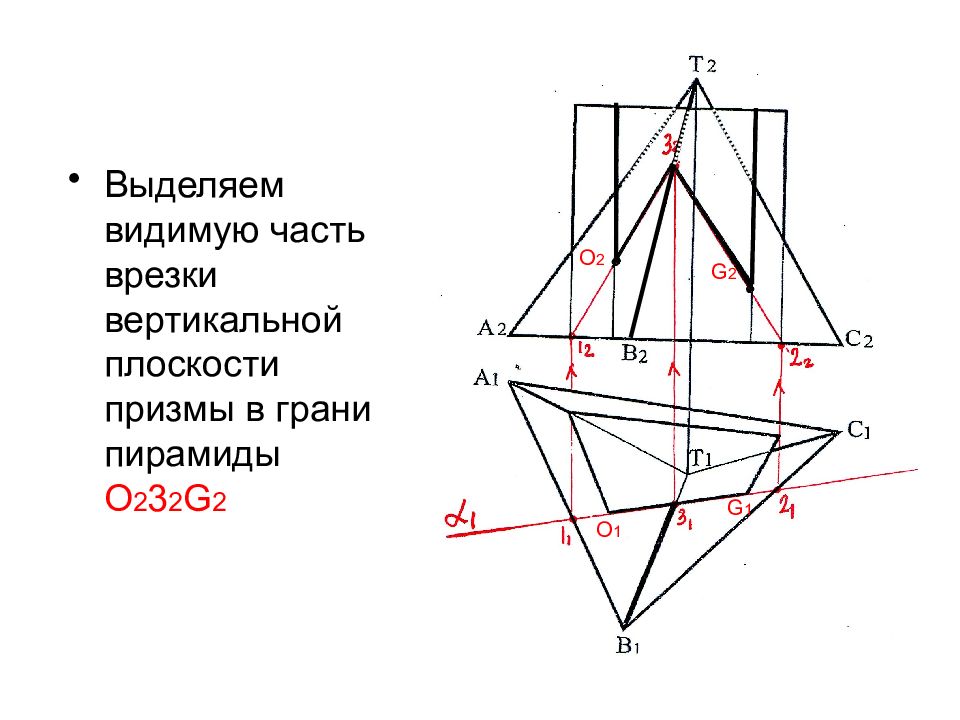
Выделяем видимую часть врезки вертикальной плоскости призмы в грани пирамиды О 2 3 2 G 2 O 2 G 2 G 1 O 1
Слайд 9
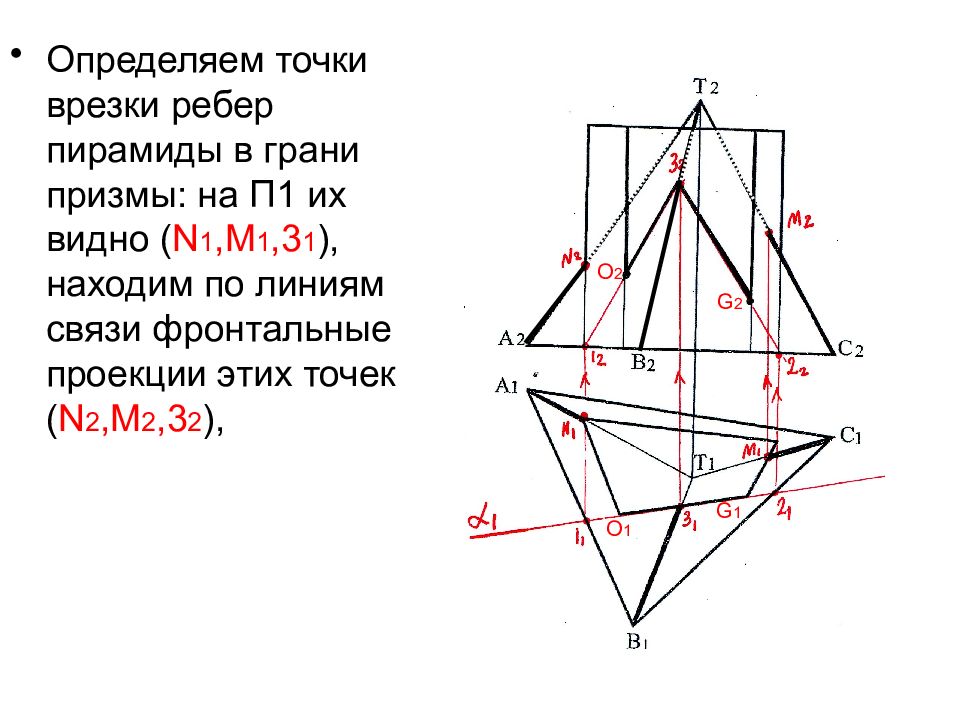
Определяем точки врезки ребер пирамиды в грани призмы: на П1 их видно ( N 1, M 1,3 1 ), находим по линиям связи фронтальные проекции этих точек ( N 2, M 2,3 2 ), O 1 O 2 G 2 G 1
Слайд 10
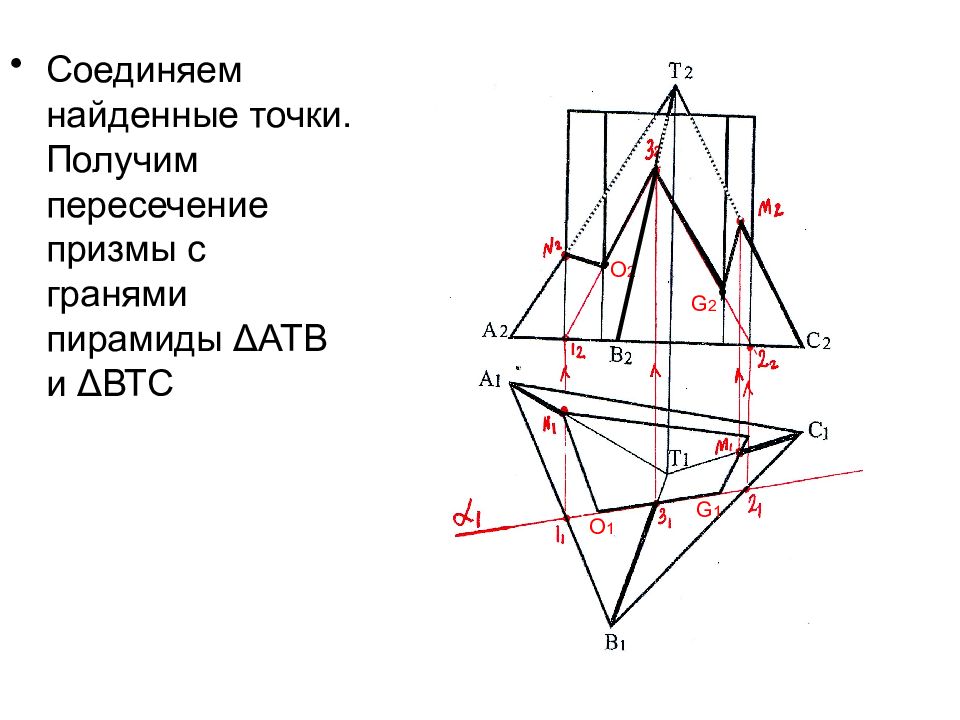
Соединяем найденные точки. Получим пересечение призмы с гранями пирамиды Δ АТВ и Δ ВТС O 2 G 2 O 1 G 1
Слайд 11
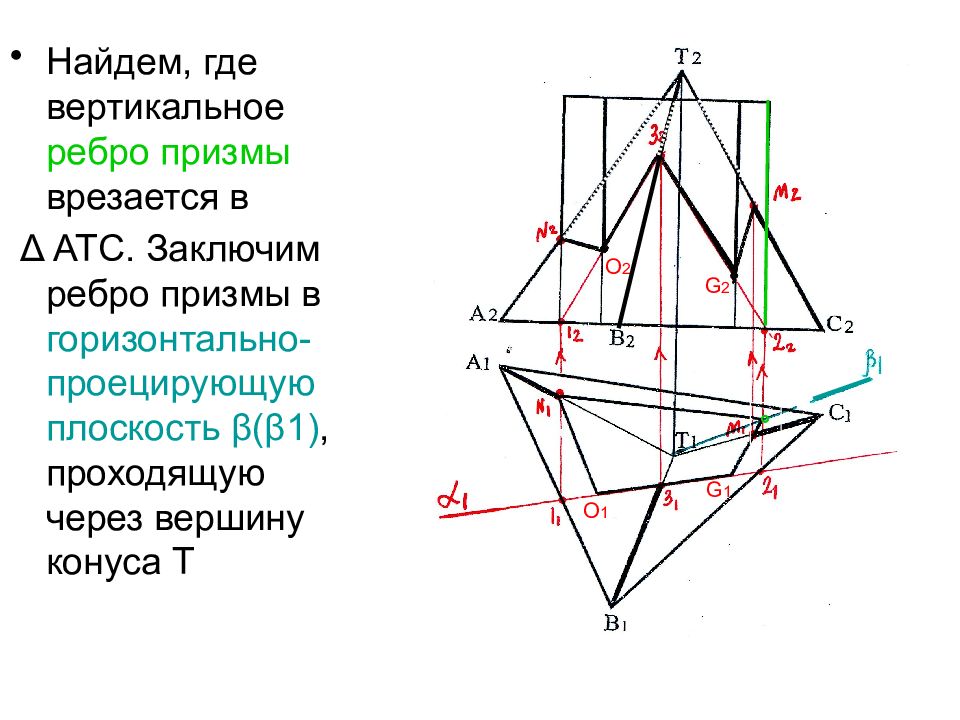
Найдем, где вертикальное ребро призмы врезается в Δ АТС. Заключим ребро призмы в горизонтально- проецирующую плоскость β ( β 1), проходящую через вершину конуса Т O 2 O 1 G 1 G 2 °
Слайд 12
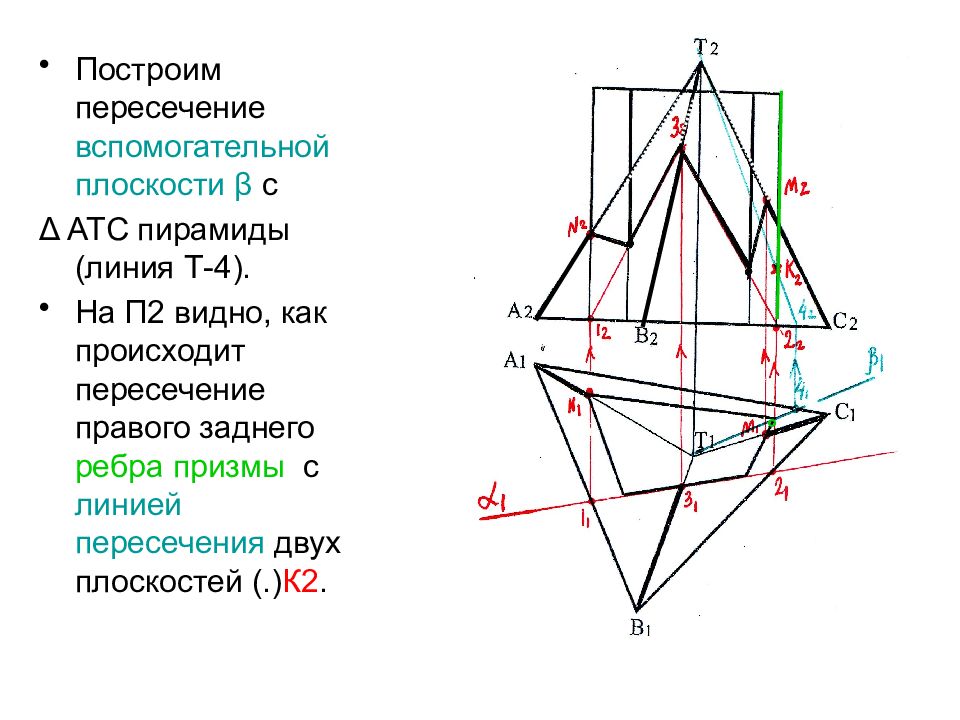
Построим пересечение вспомогательной плоскости β с Δ АТС пирамиды (линия Т-4). На П2 видно, как происходит пересечение правого заднего ребра призмы с линией пересечения двух плоскостей (.) К2. °
Слайд 13
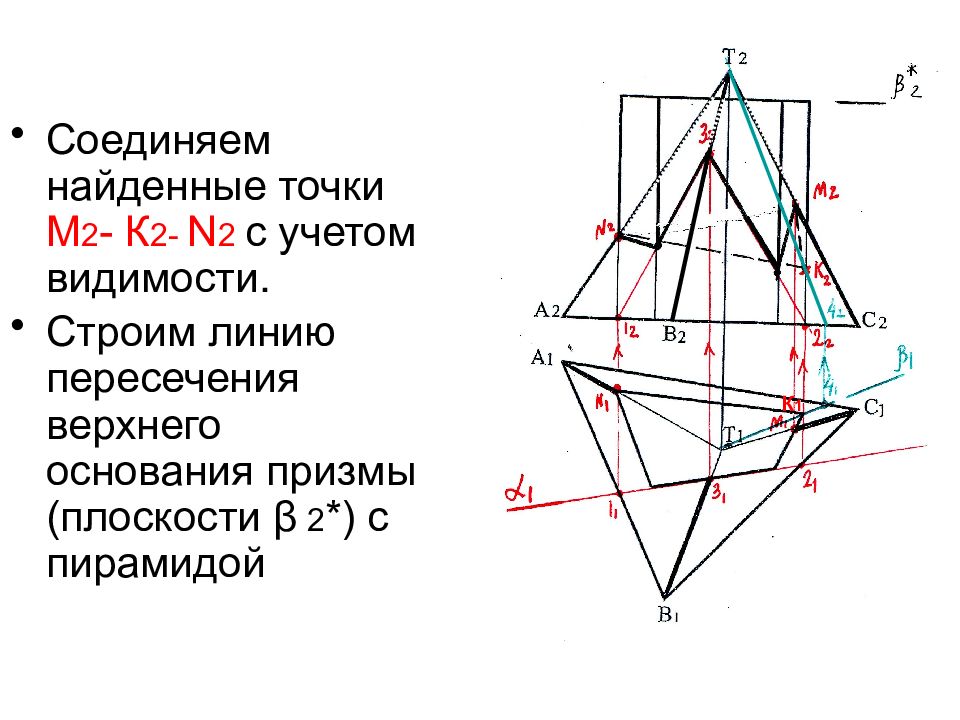
Соединяем найденные точки М 2 - К 2- N 2 c учетом видимости. Строим линию пересечения верхнего основания призмы (плоскости β 2 * ) с пирамидой К 1
Слайд 14
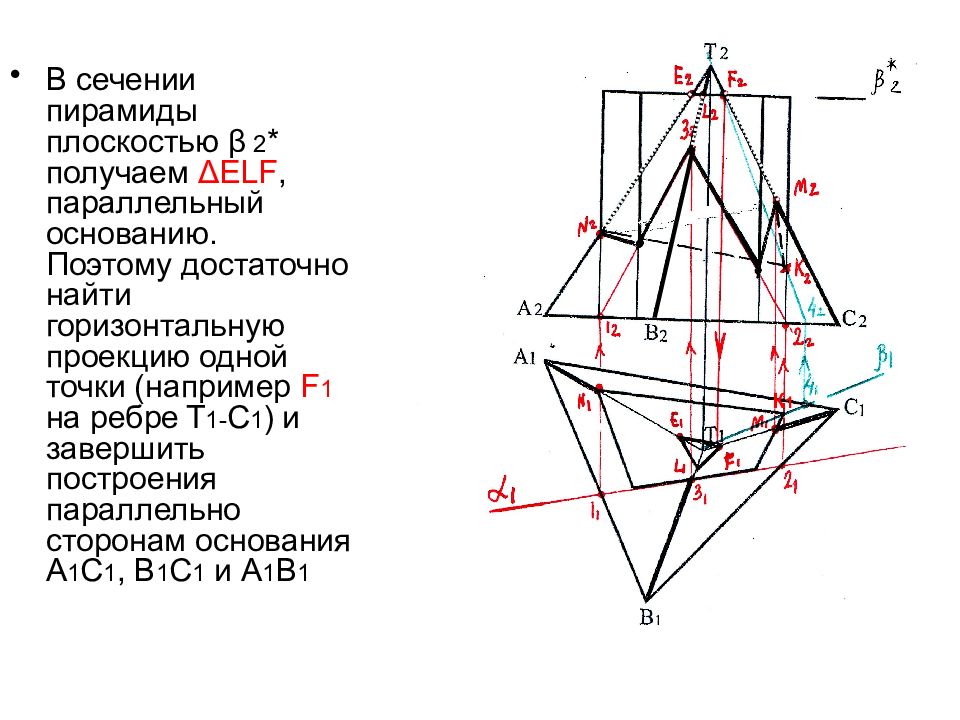
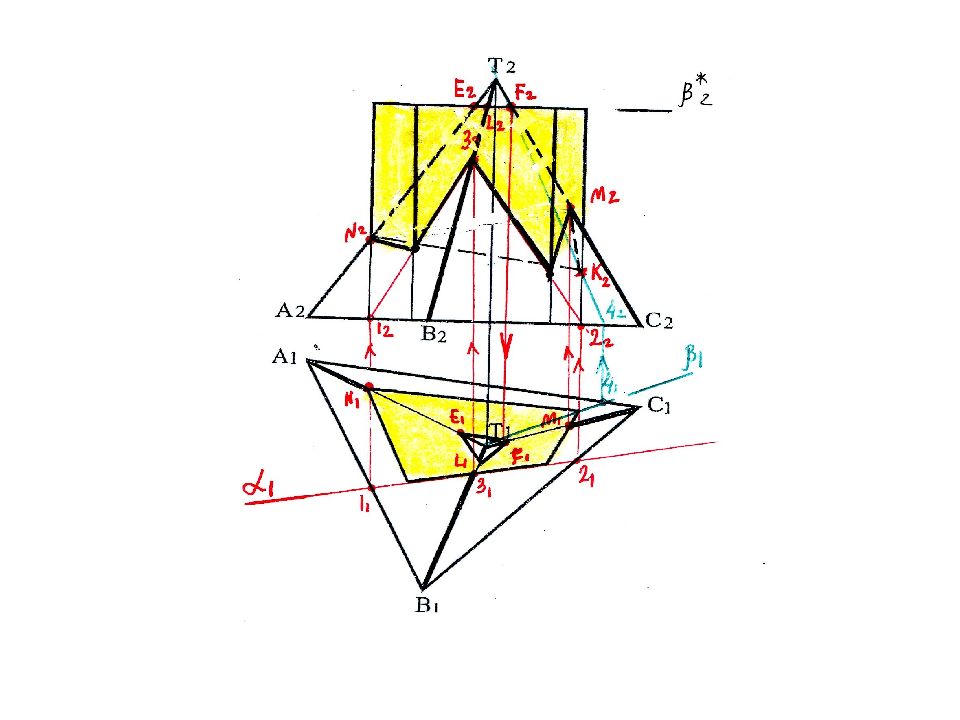
В сечении пирамиды плоскостью β 2 * получаем Δ Е LF, параллельный основанию. Поэтому достаточно найти горизонтальную проекцию одной точки (например F 1 на ребре Т 1- С 1 ) и завершить построения параллельно сторонам основания А 1 С 1, В 1 С 1 и А 1 В 1 К 1
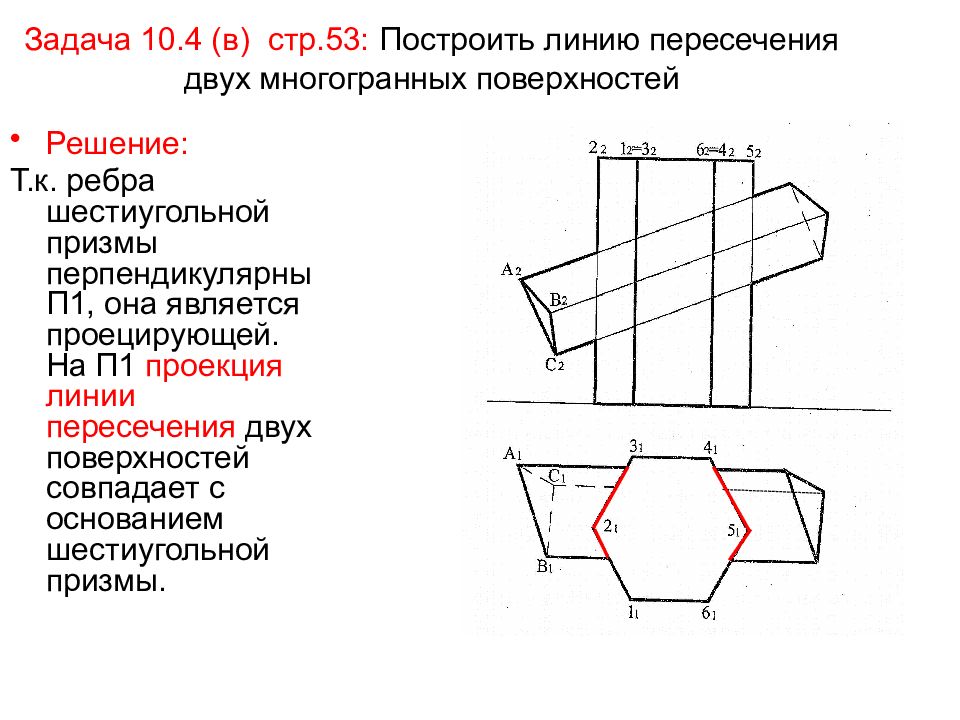
Слайд 16: Задача 10.4 (в) стр.53: Построить линию пересечения двух многогранных поверхностей
Решение: Т.к. ребра шестиугольной призмы перпендикулярны П1, она является проецирующей. На П1 проекция линии пересечения двух поверхностей совпадает с основанием шестиугольной призмы.
Слайд 17
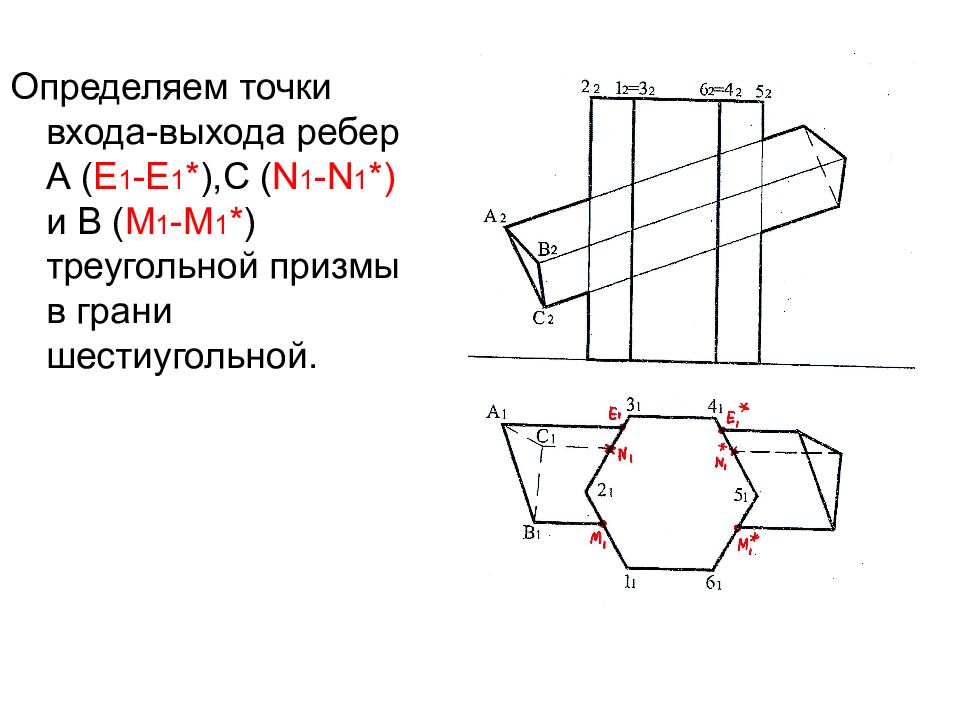
Определяем точки входа-выхода ребер А ( Е 1 -Е 1 * ),С ( N 1 - N 1 *) и В ( M 1 - M 1 * ) треугольной призмы в грани шестиугольной.
Слайд 18
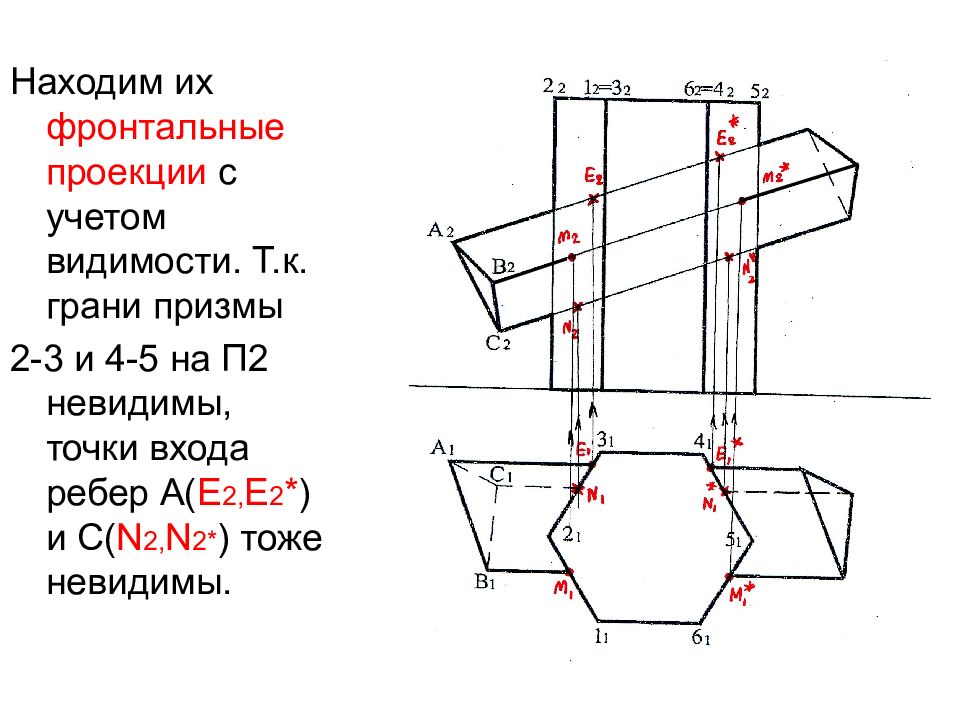
Находим их фронтальные проекции с учетом видимости. Т.к. грани призмы 2-3 и 4-5 на П2 невидимы, точки входа ребер А( Е 2, Е 2 * ) и С( N 2, N 2* ) тоже невидимы.
Слайд 19
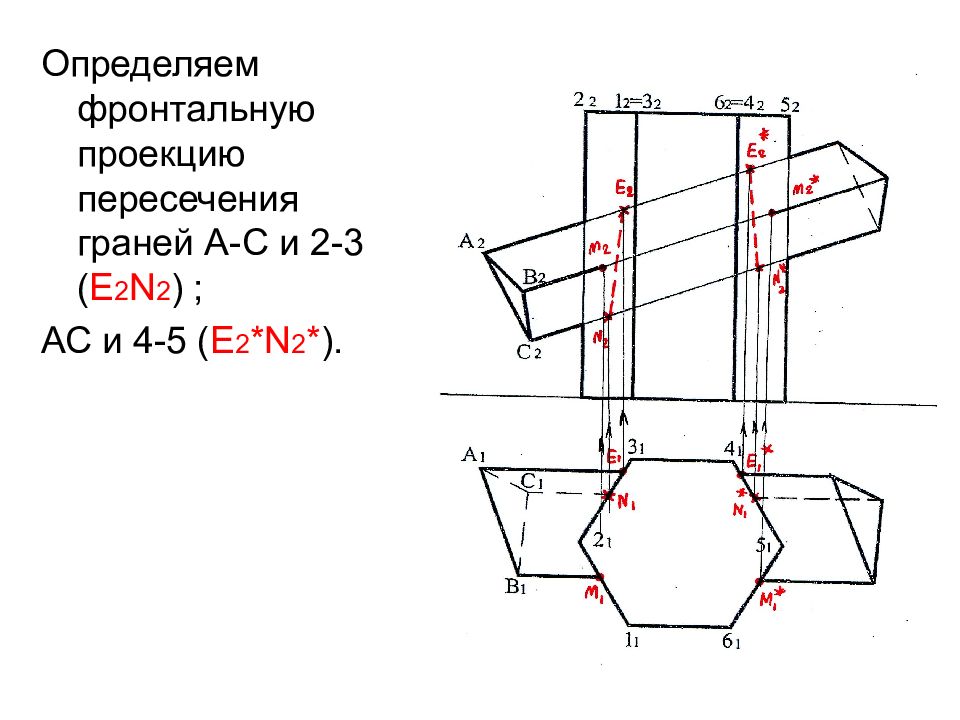
Определяем фронтальную проекцию пересечения граней А-С и 2-3 ( Е 2 N 2 ) ; АС и 4-5 ( Е 2 * N 2 * ).
Слайд 20
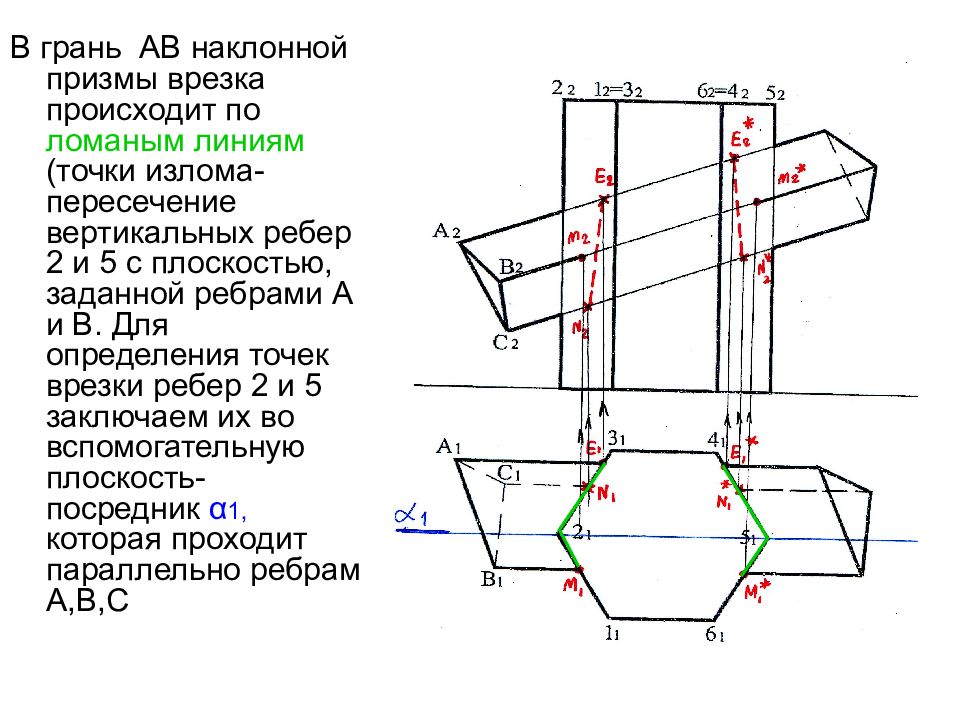
В грань АВ наклонной призмы врезка происходит по ломаным линиям (точки излома- пересечение вертикальных ребер 2 и 5 с плоскостью, заданной ребрами А и В. Для определения точек врезки ребер 2 и 5 заключаем их во вспомогательную плоскость- посредник α 1, которая проходит параллельно ребрам А,В,С
Слайд 21
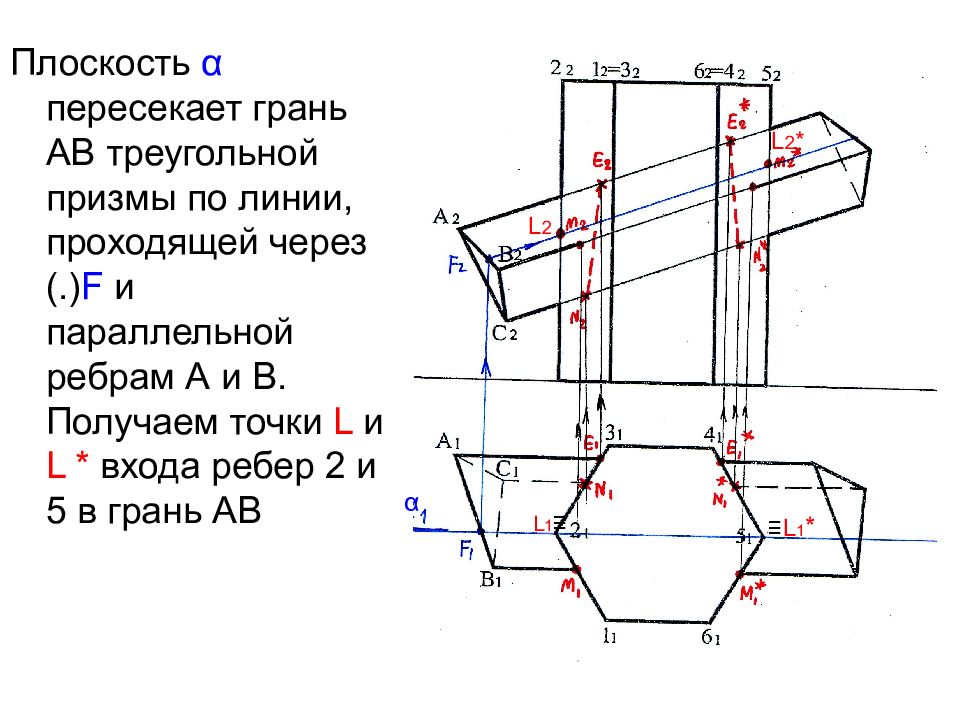
Плоскость α пересекает грань АВ треугольной призмы по линии, проходящей через (.) F и параллельной ребрам А и В. Получаем точки L и L * входа ребер 2 и 5 в грань АВ ≡ L 1 * L 1 ≡ L 2 L 2 * α
Слайд 22
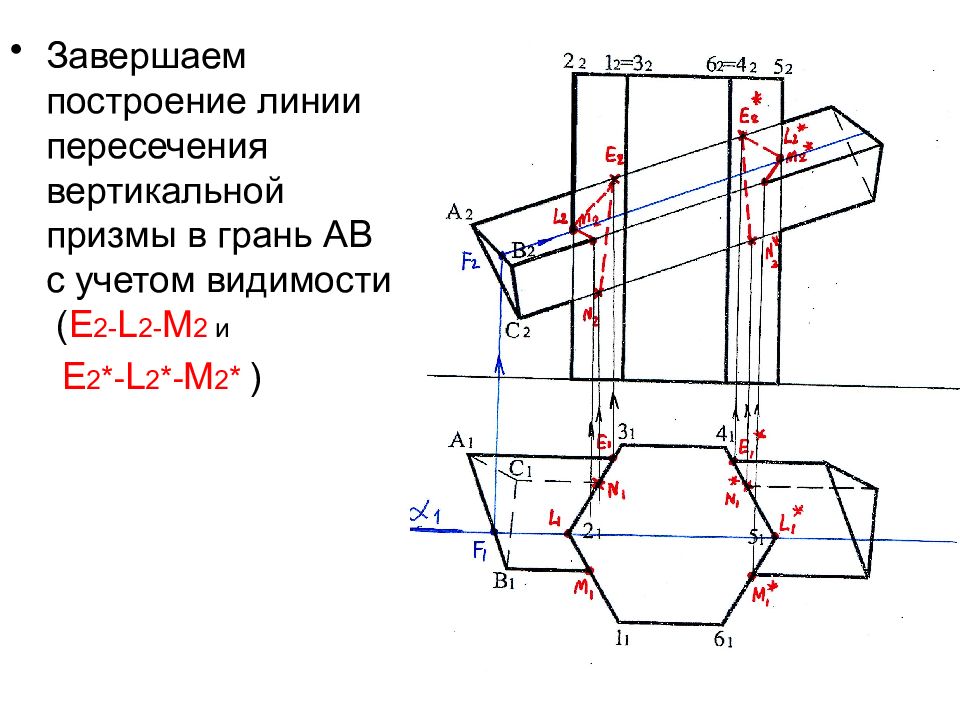
Завершаем построение линии пересечения вертикальной призмы в грань АВ с учетом видимости ( Е 2- L 2 - M 2 и Е 2 *- L 2 *- M 2 * )
Слайд 23
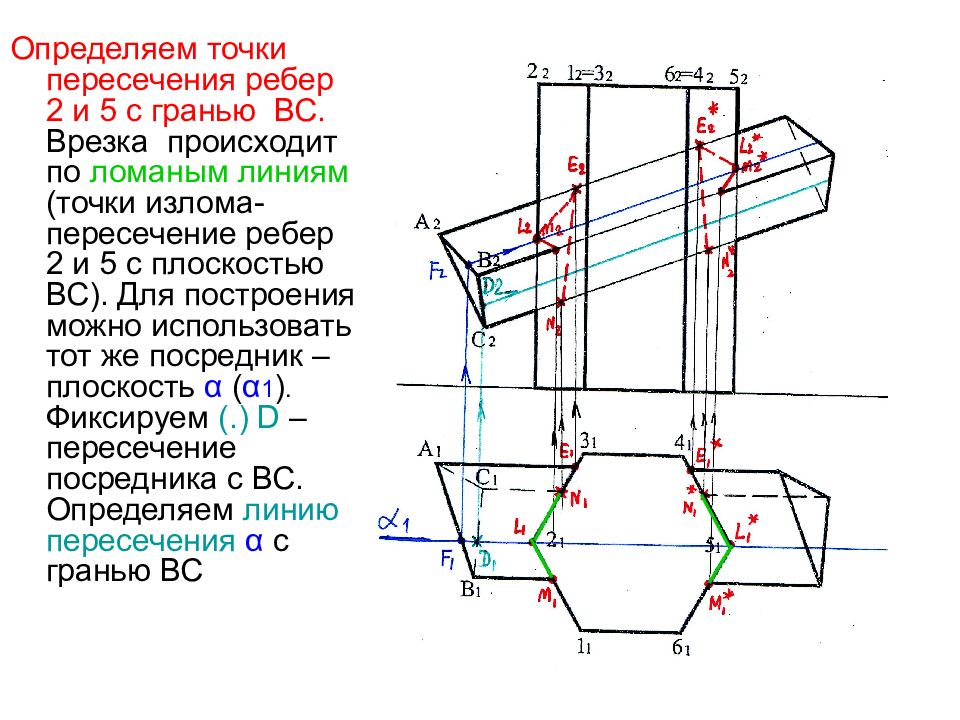
Определяем точки пересечения ребер 2 и 5 с гранью ВС. Врезка происходит по ломаным линиям (точки излома- пересечение ребер 2 и 5 с плоскостью ВС). Для построения можно использовать тот же посредник – плоскость α ( α 1 ). Фиксируем (.) D –пересечение посредника с ВС. Определяем линию пересечения α с гранью ВС
Слайд 24
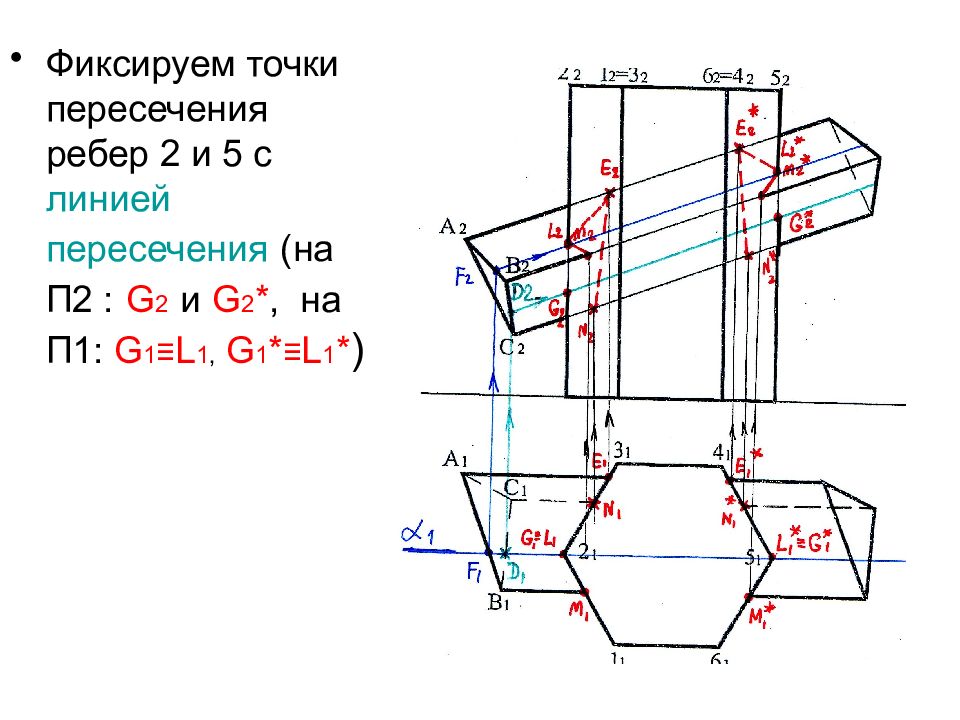
Фиксируем точки пересечения ребер 2 и 5 с линией пересечения (на П2 : G 2 и G 2 *, на П1: G 1 ≡ L 1, G 1 * ≡ L 1 * )
Слайд 25
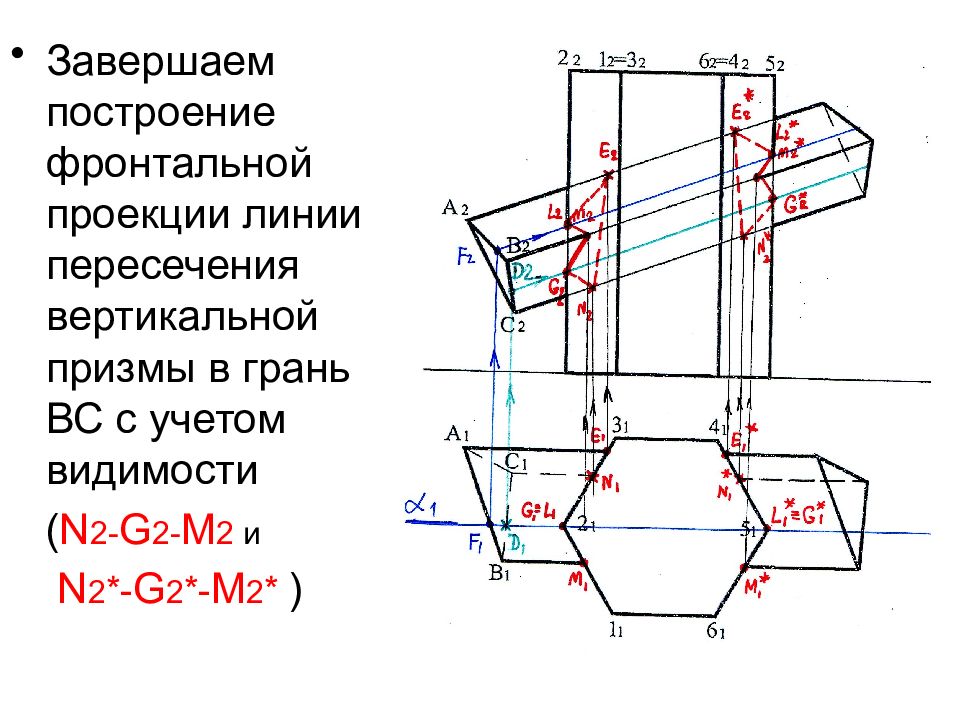
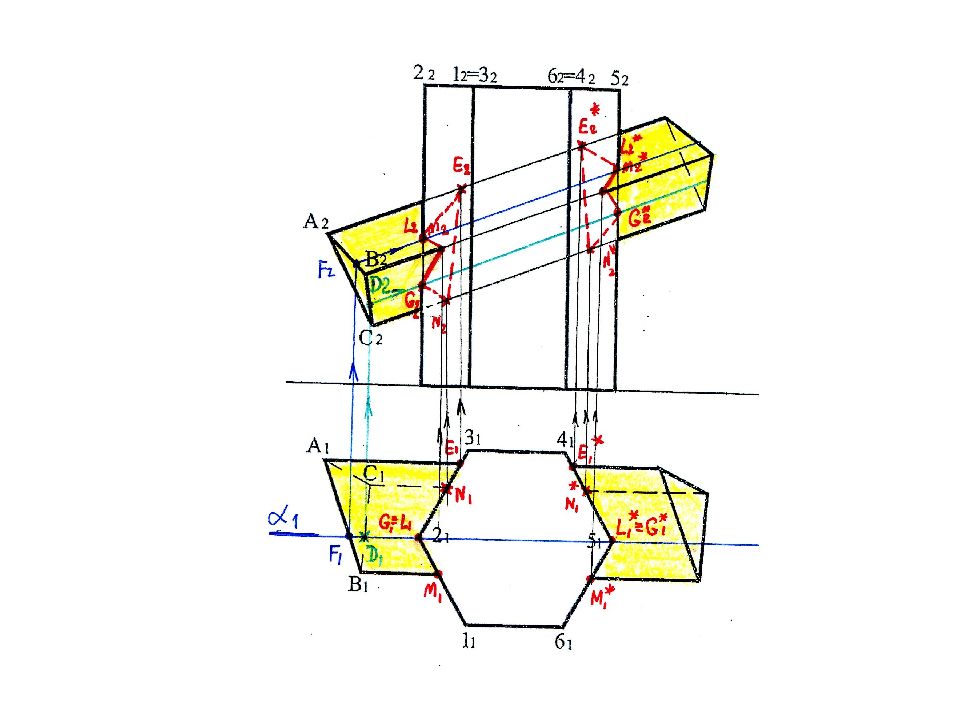
Завершаем построение фронтальной проекции линии пересечения вертикальной призмы в грань ВС с учетом видимости ( N 2- G 2 - M 2 и N 2 *- G 2 *- M 2 * )
Слайд 27
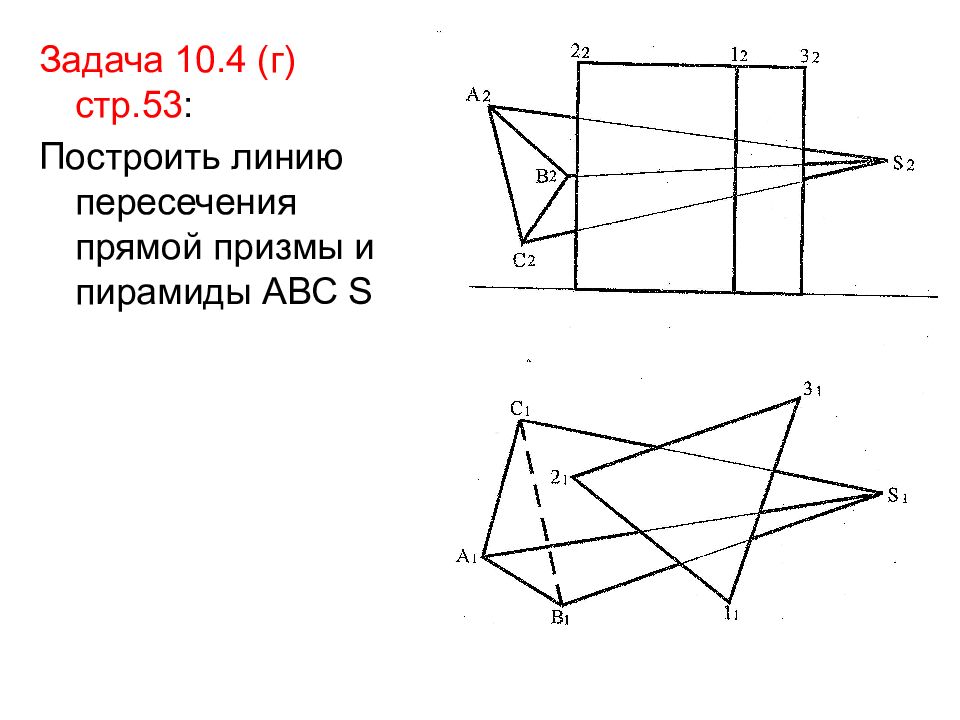
Задача 10.4 (г) стр.53 : Построить линию пересечения прямой призмы и пирамиды АВС S
Слайд 28
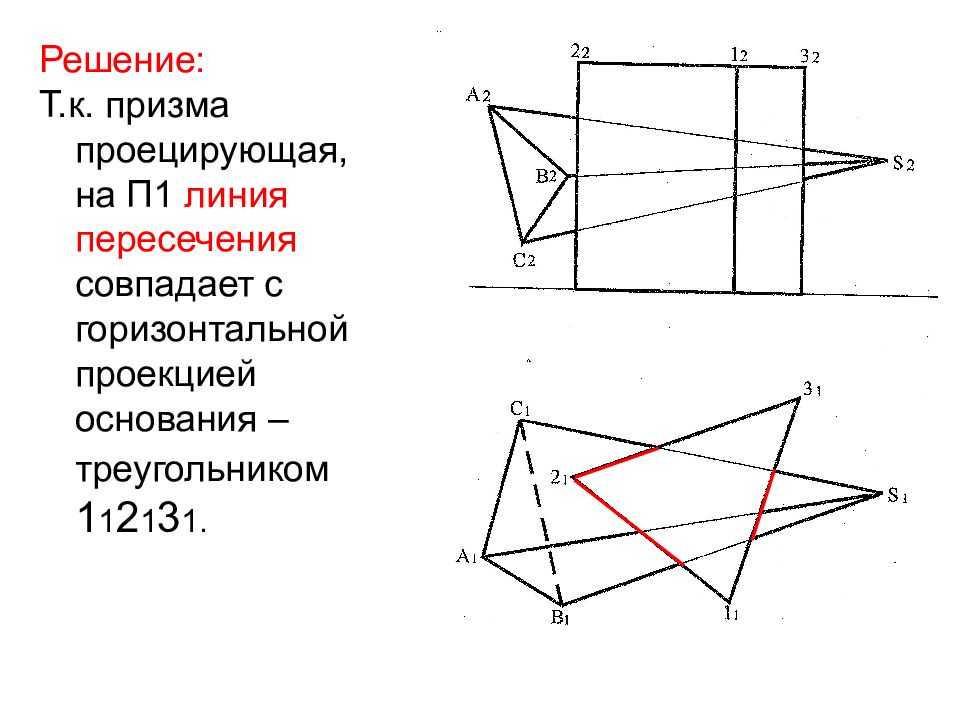
Решение: Т.к. призма проецирующая, на П1 линия пересечения совпадает с горизонтальной проекцией основания – треугольником 1 1 2 1 3 1.
Слайд 29
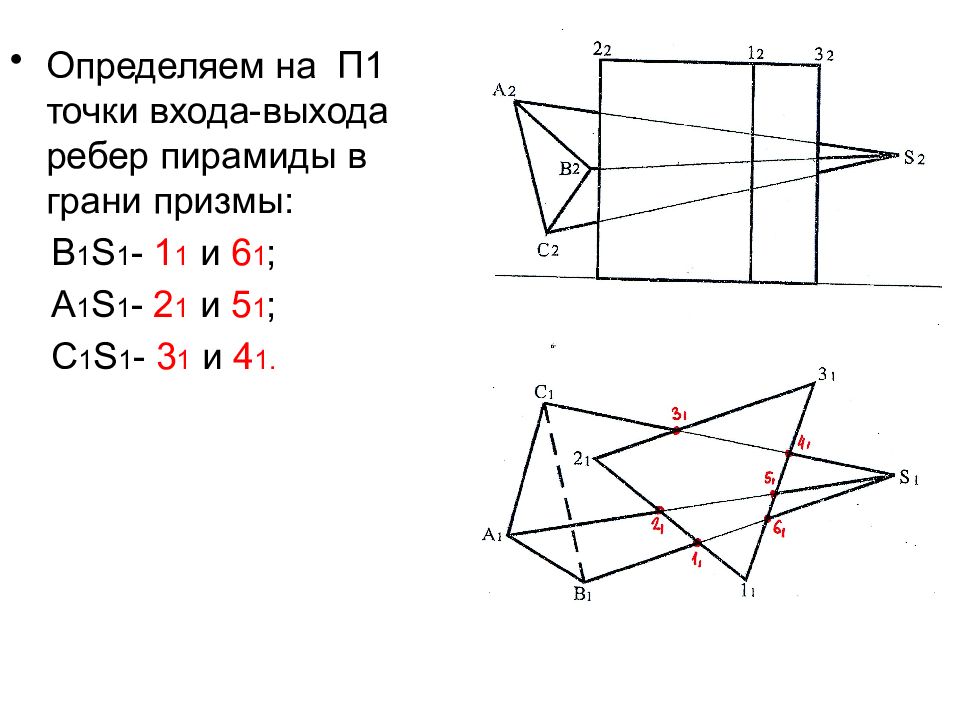
Определяем на П1 точки входа-выхода ребер пирамиды в грани призмы: В 1 S 1 - 1 1 и 6 1 ; А 1 S 1 - 2 1 и 5 1 ; С 1 S 1 - 3 1 и 4 1.
Слайд 30
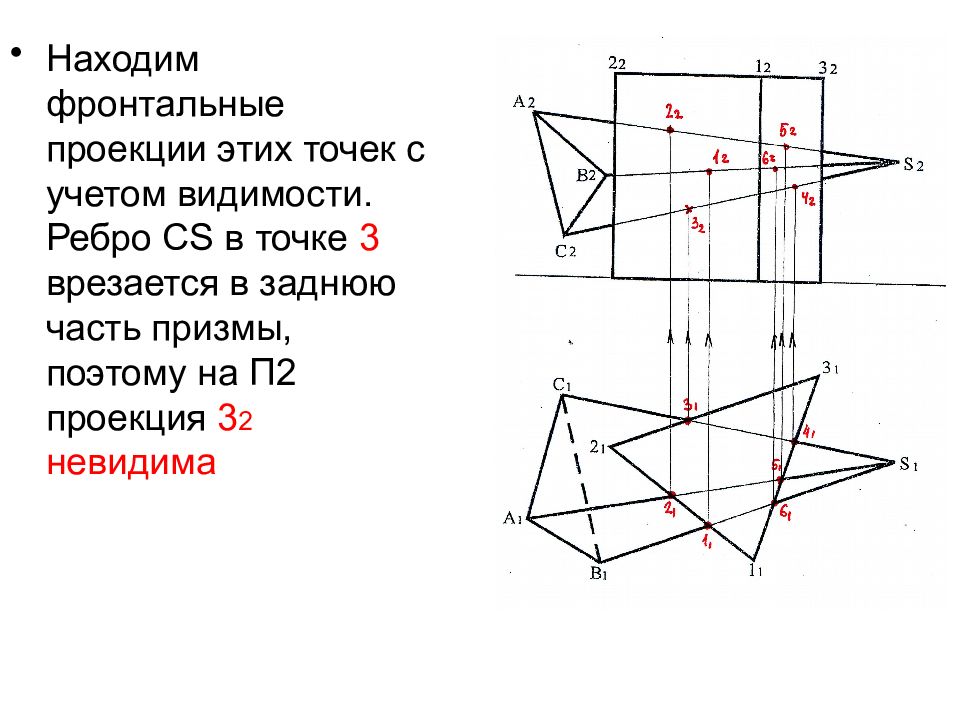
Находим фронтальные проекции этих точек с учетом видимости. Ребро С S в точке 3 врезается в заднюю часть призмы, поэтому на П2 проекция 3 2 невидима
Слайд 31
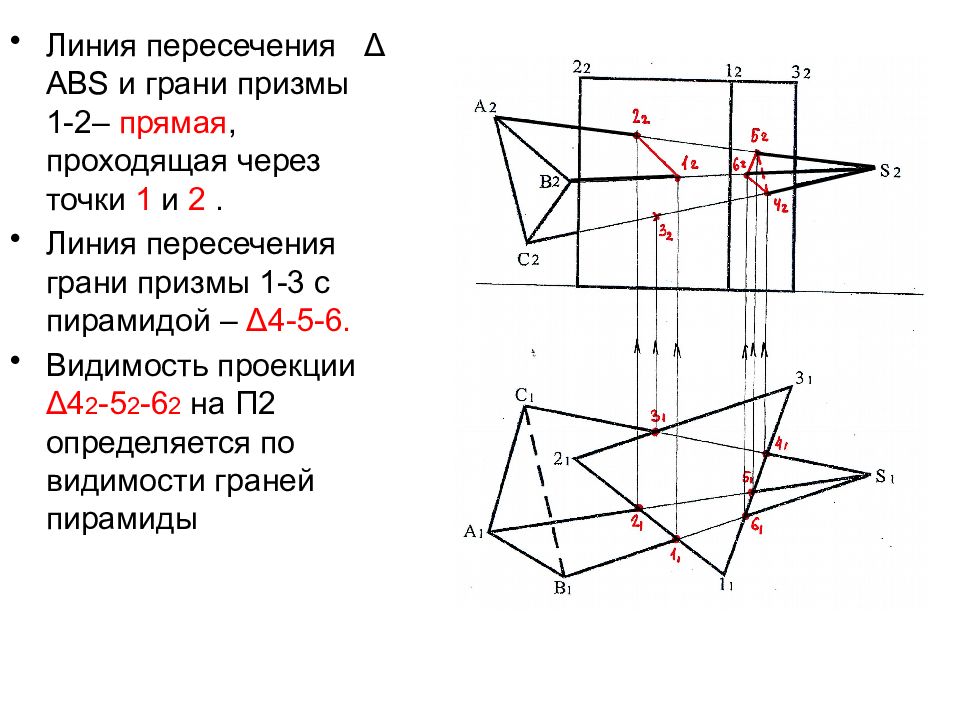
Линия пересечения Δ АВ S и грани призмы 1-2– прямая, проходящая через точки 1 и 2. Линия пересечения грани призмы 1-3 с пирамидой – Δ 4-5-6. Видимость проекции Δ 4 2 -5 2 -6 2 на П2 определяется по видимости граней пирамиды
Слайд 32
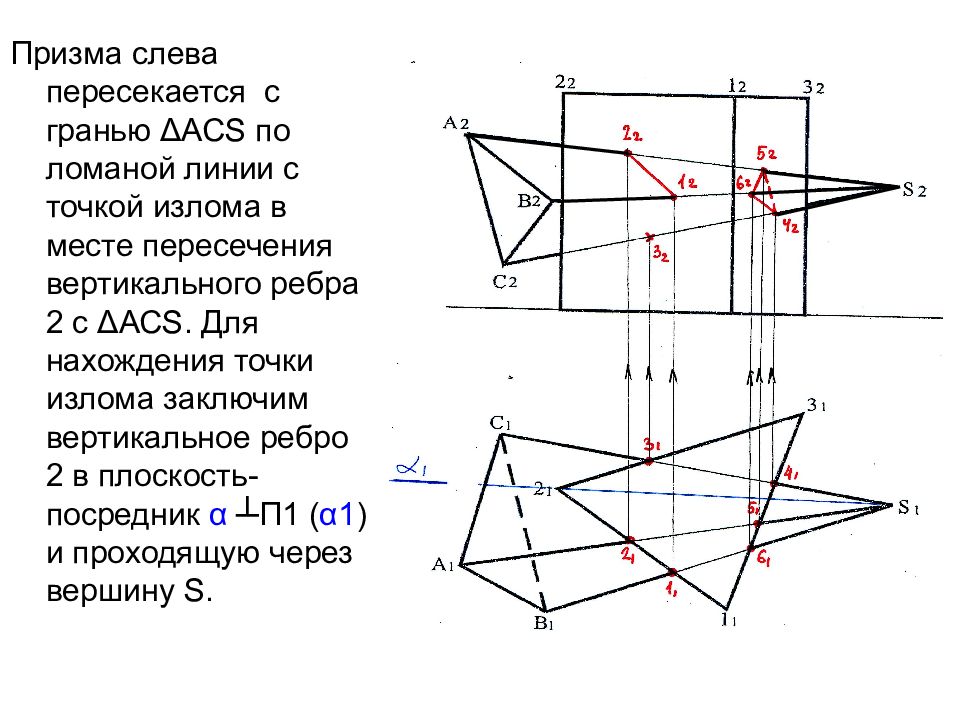
Призма слева пересекается с гранью Δ АС S по ломаной линии с точкой излома в месте пересечения вертикального ребра 2 с Δ АС S. Для нахождения точки излома заключим вертикальное ребро 2 в плоскость-посредник α ┴П1 ( α 1 ) и проходящую через вершину S.
Слайд 33
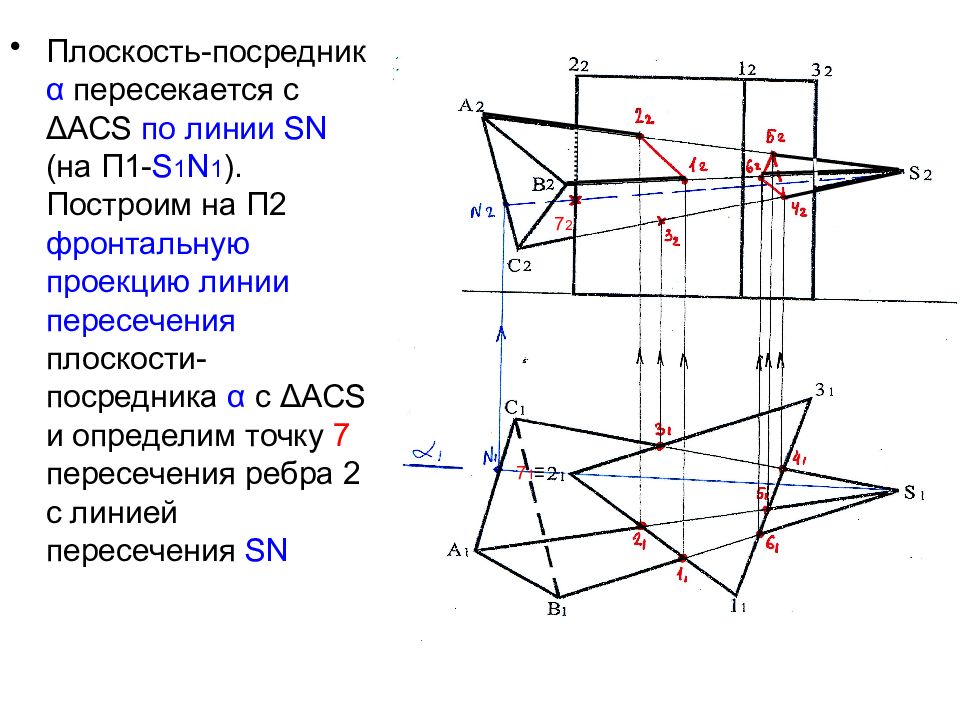
Плоскость-посредник α пересекается с Δ АС S по линии SN (на П1- S 1 N 1 ). Построим на П2 фронтальную проекцию линии пересечения плоскости-посредника α с Δ АС S и определим точку 7 пересечения ребра 2 с линией пересечения SN 7 2 7 1 ≡
Слайд 34
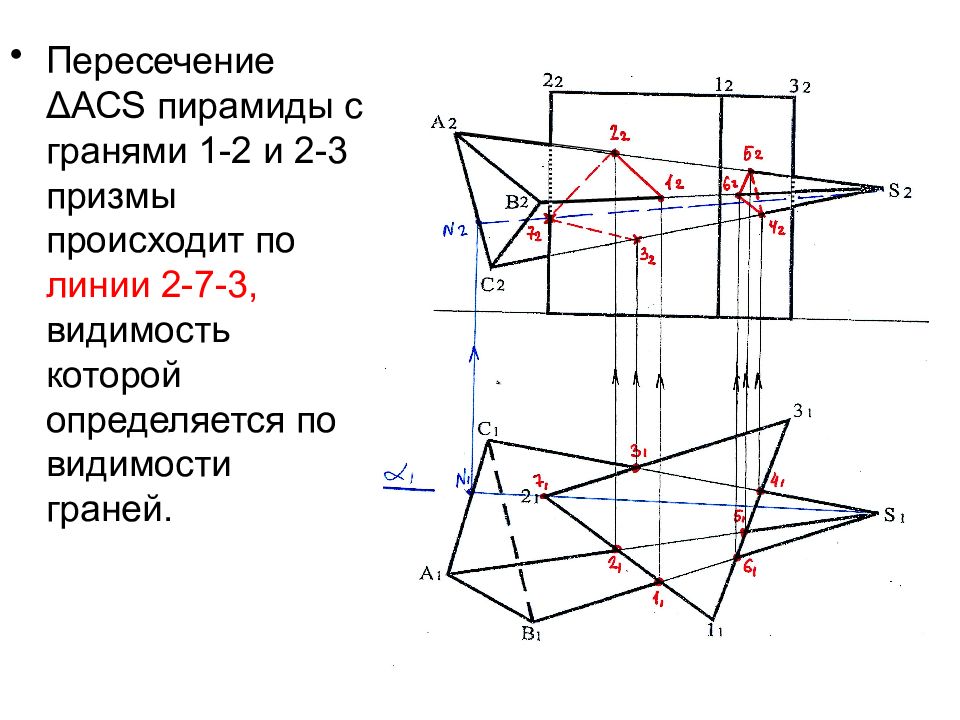
Пересечение Δ АС S пирамиды с гранями 1-2 и 2-3 призмы происходит по линии 2-7-3, видимость которой определяется по видимости граней.
Слайд 35
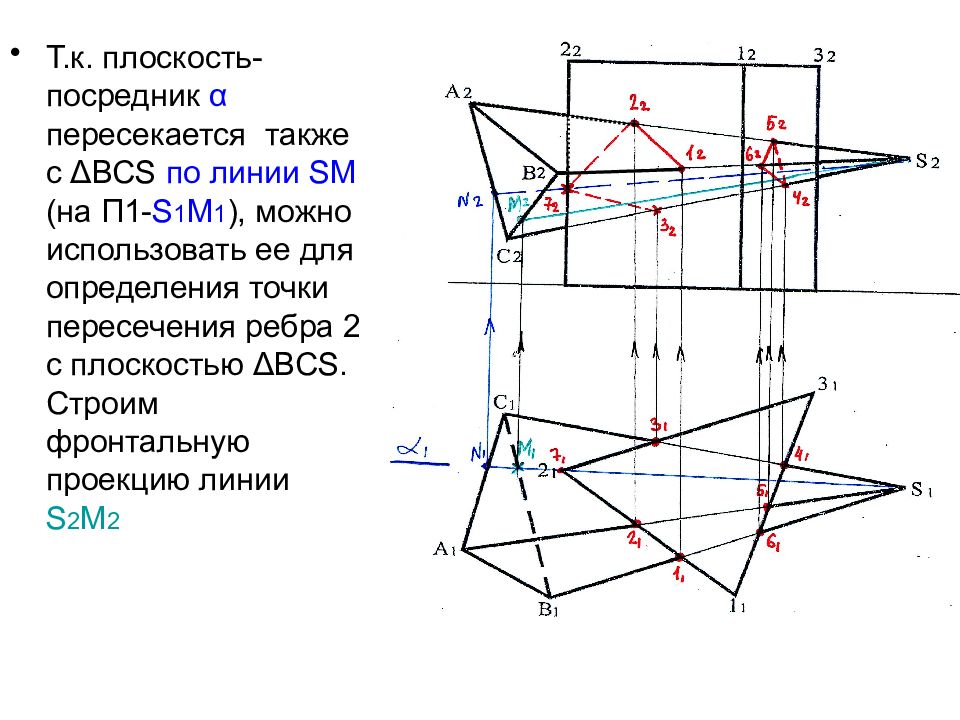
Т.к. плоскость- посредник α пересекается также с Δ ВС S по линии S М (на П1- S 1 М 1 ), можно использовать ее для определения точки пересечения ребра 2 с плоскостью Δ ВС S. Строим фронтальную проекцию линии S 2 М 2
Слайд 36
Определяем точку 8 пересечения линии S М с ребром 2 ( S 2 М 2 ∩ 2 2 = 8 2 )
Слайд 37
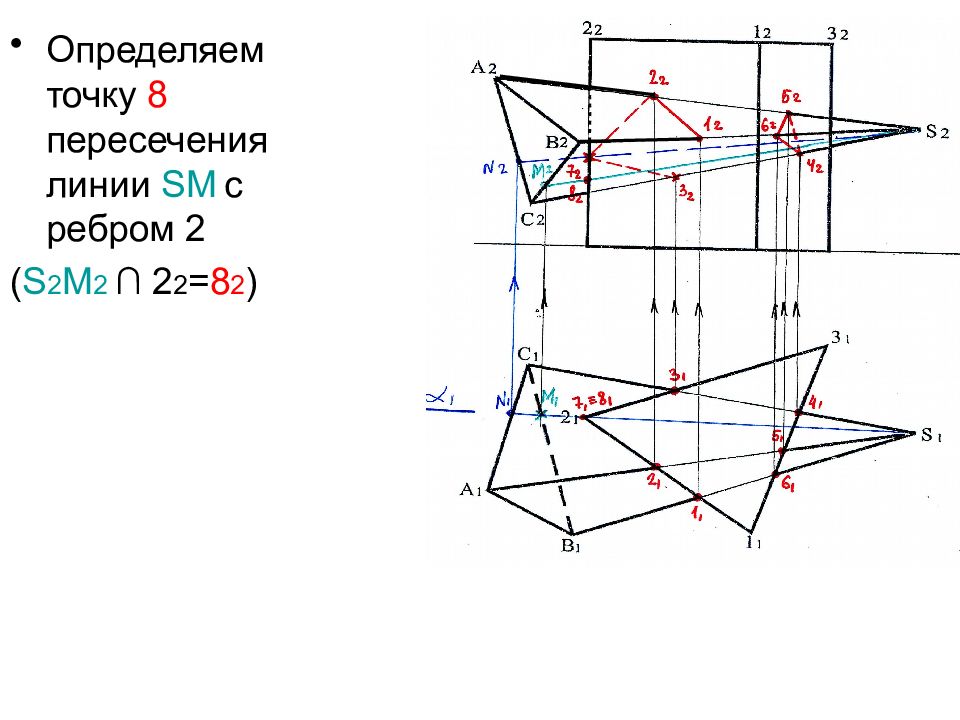
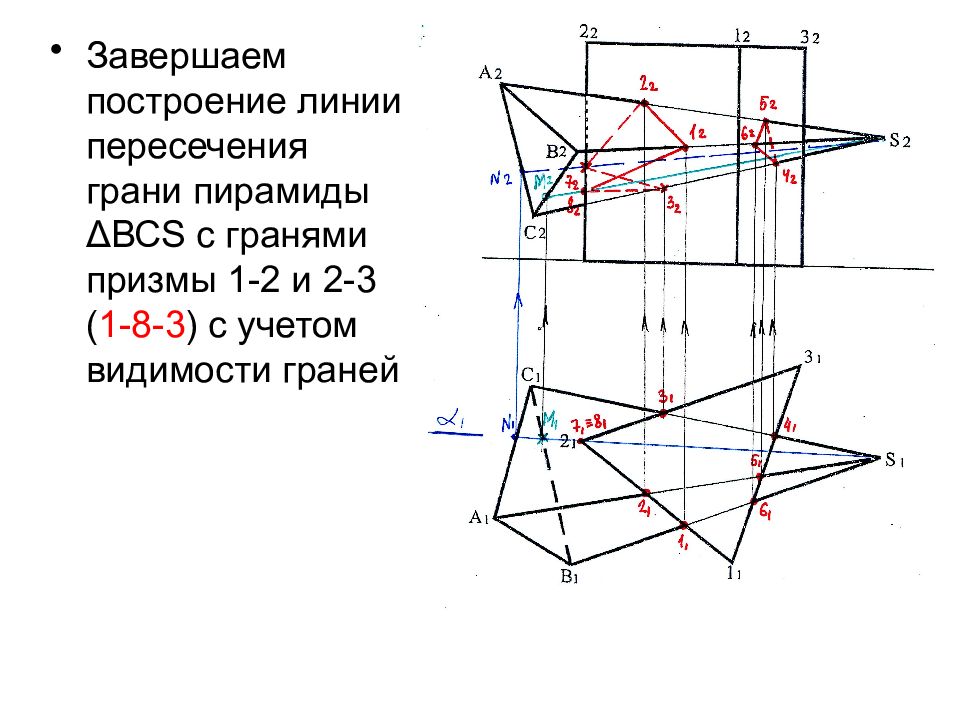
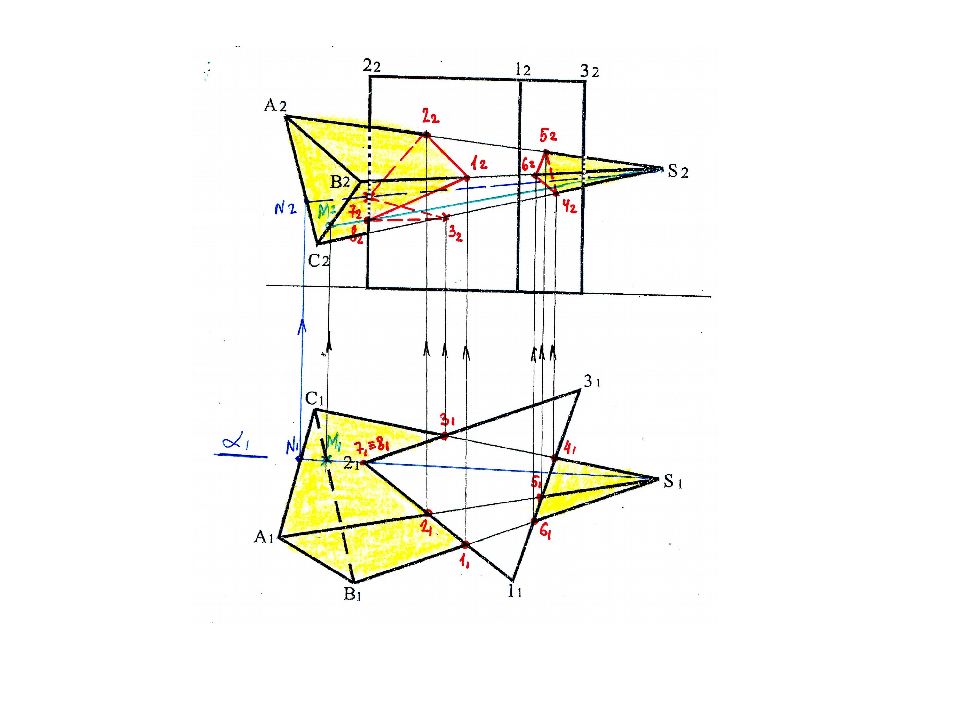
Завершаем построение линии пересечения грани пирамиды Δ ВС S с гранями призмы 1-2 и 2-3 ( 1-8-3 ) с учетом видимости граней
Многогранные поверхности широко применяются в архитектуре и строительстве. По своей общей форме большинство зданий и сооружений, а также их конструктивные элементы, представляют собой многогранники – призмы, параллелепипеды и их сочетания. Покрытия зданий в виде скатной кровли и более сложные складчатые и сетчатые пространственные покрытия представляют собой многогранные поверхности различного вида.
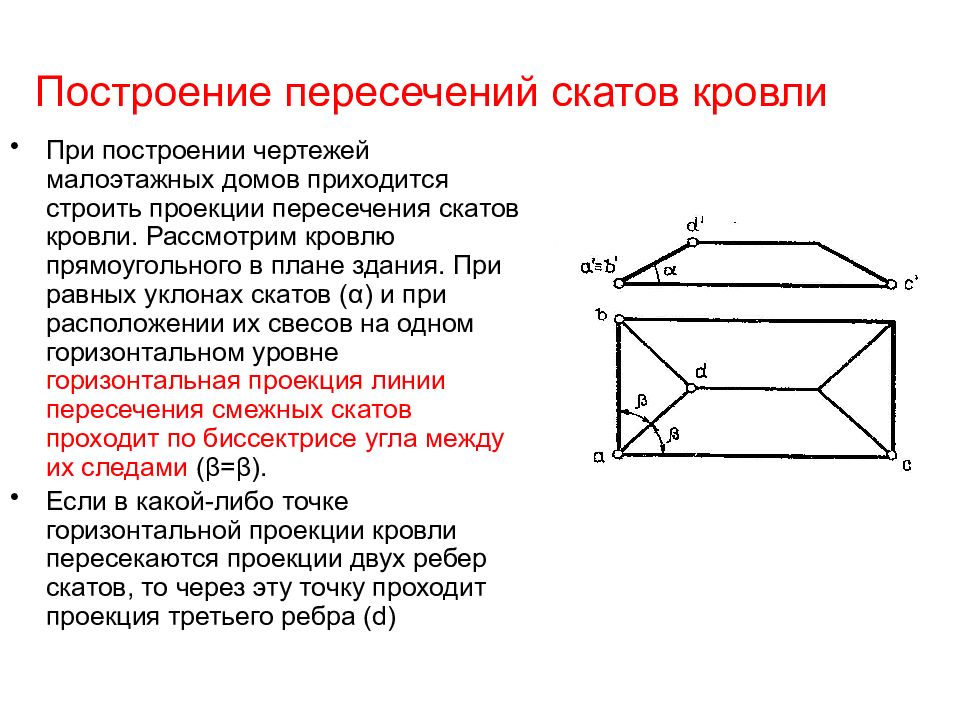
Слайд 40: Построение пересечений скатов кровли
При построении чертежей малоэтажных домов приходится строить проекции пересечения скатов кровли. Рассмотрим кровлю прямоугольного в плане здания. При равных уклонах скатов ( α ) и при расположении их свесов на одном горизонтальном уровне горизонтальная проекция линии пересечения смежных скатов проходит по биссектрисе угла между их следами ( β = β ). Если в какой-либо точке горизонтальной проекции кровли пересекаются проекции двух ребер скатов, то через эту точку проходит проекция третьего ребра ( d )
Слайд 41
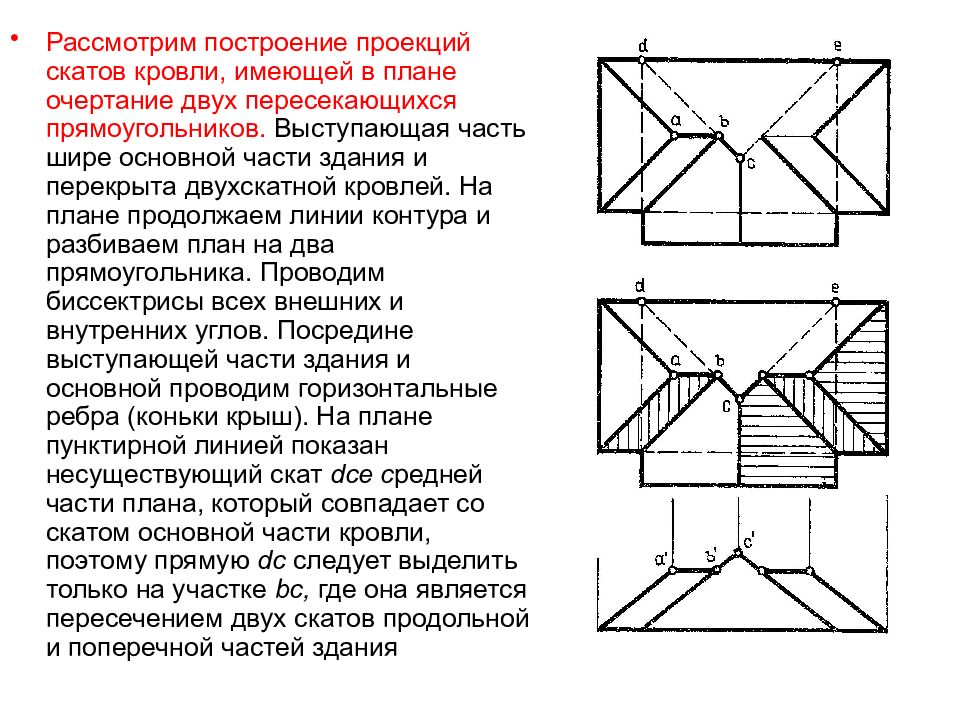
Рассмотрим построение проекций скатов кровли, имеющей в плане очертание двух пересекающихся прямоугольников. Выступающая часть шире основной части здания и перекрыта двухскатной кровлей. На плане продолжаем линии контура и разбиваем план на два прямоугольника. Проводим биссектрисы всех внешних и внутренних углов. Посредине выступающей части здания и основной проводим горизонтальные ребра (коньки крыш). На плане пунктирной линией показан несуществующий скат dce с редней части плана, который совпадает со скатом основной части кровли, поэтому прямую dc следует выделить только на участке bc, где она является пересечением двух скатов продольной и поперечной частей здания
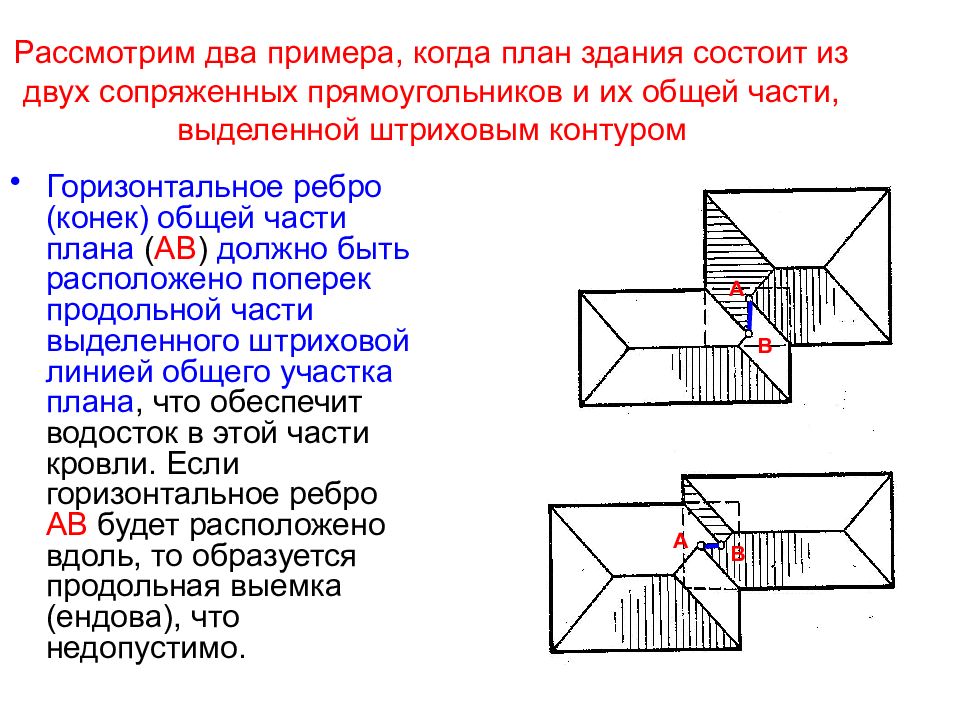
Слайд 42: Рассмотрим два примера, когда план здания состоит из двух сопряженных прямоугольников и их общей части, выделенной штриховым контуром
Горизонтальное ребро (конек) общей части плана ( АВ ) должно быть расположено поперек продольной части выделенного штриховой линией общего участка плана, что обеспечит водосток в этой части кровли. Если горизонтальное ребро АВ будет расположено вдоль, то образуется продольная выемка (ендова), что недопустимо. А В А В
Слайд 43
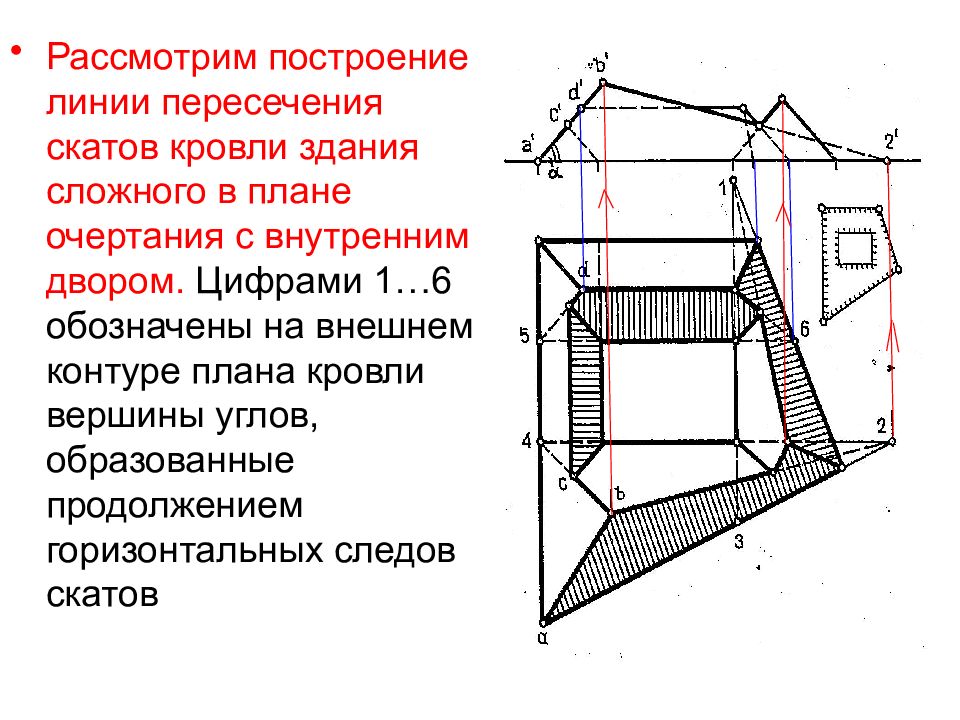
Рассмотрим построение линии пересечения скатов кровли здания сложного в плане очертания с внутренним двором. Цифрами 1…6 обозначены на внешнем контуре плана кровли вершины углов, образованные продолжением горизонтальных следов скатов
Слайд 44
При проектировании и строительстве большепролетных зданий с применением индустриальных способов монтажа большое значение имеет применение минимального количества типоразмеров сборных элементов. Наилучшее решение – использование поверхностей некоторых правильных многогранников, грани которых одинаковы по форме и размерам.
Слайд 45
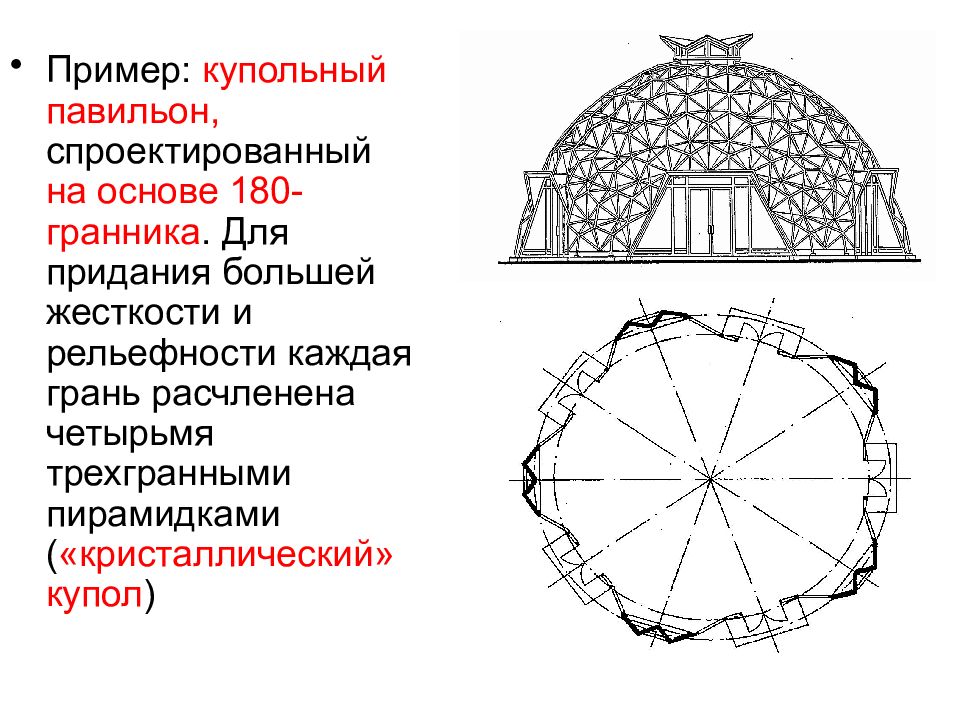
Пример: купольный павильон, спроектированный на основе 180-гранника. Для придания большей жесткости и рельефности каждая грань расчленена четырьмя трехгранными пирамидками ( «кристаллический» купол )
Слайд 46
Пример: покрытие помещения, выполненное в складках кристаллического типа
Слайд 47
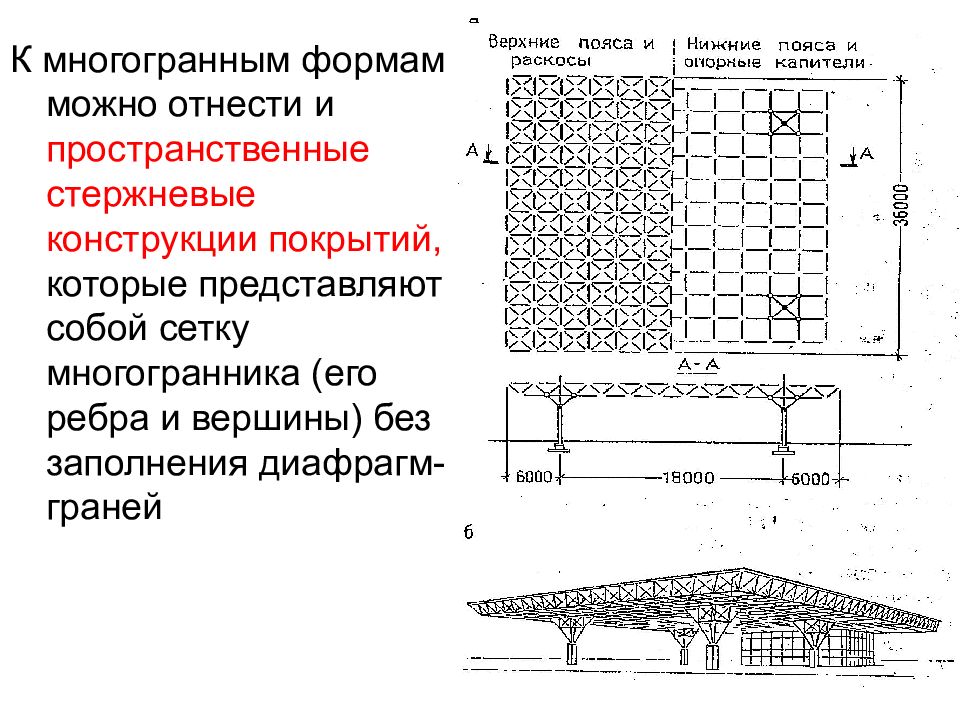
К многогранным формам можно отнести и пространственные стержневые конструкции покрытий, которые представляют собой сетку многогранника (его ребра и вершины) без заполнения диафрагм- граней
Слайд 48
Архитектурные сооружения и здания, различные фрагменты и детали являются сочетанием геометрических форм- призм, параллелепипедов, пирамид, поверхностей вращения и более сложных кривых поверхностей, пересекающихся между собой. Основной способ построения линии пересечения поверхностей- способ вспомогательных секущих поверхностей (плоскостей).
Слайд 49
Для построения линии пересечения (линии перехода) двух поверхностей необходимо построить ряд точек, принадлежащих обеим пересекающимся поверхностям. Положение вспомогательных плоскостей выбирают так, чтобы они пересекали заданные поверхности по графически простым линиям – прямым или окружностям
Слайд 50: Пересечение кривых поверхностей
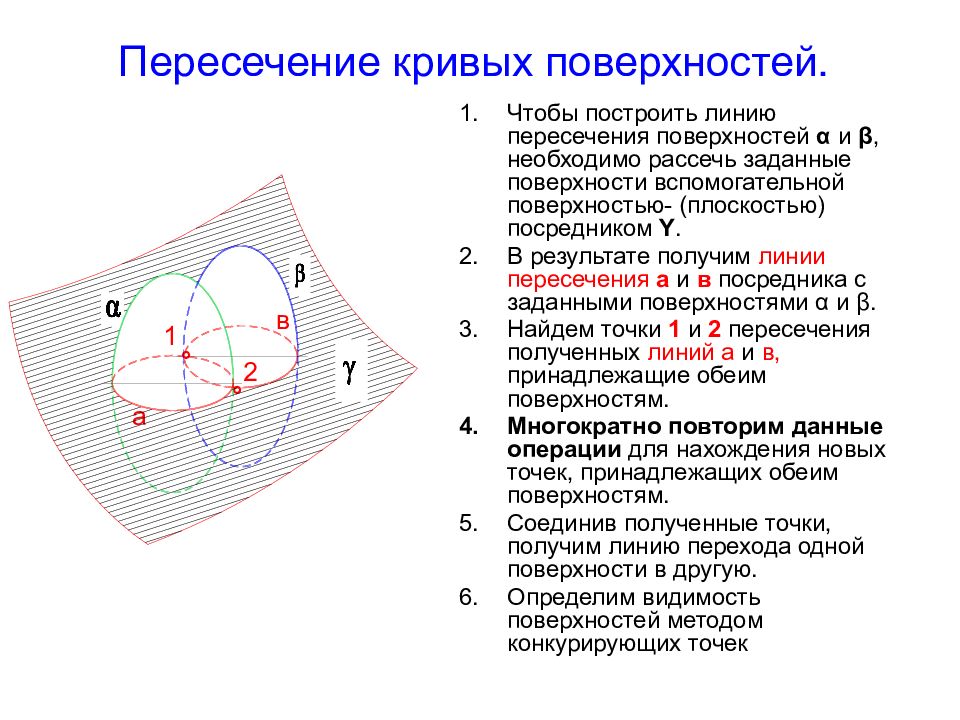
Чтобы построить линию пересечения поверхностей α и β, необходимо рассечь заданные поверхности вспомогательной поверхностью- (плоскостью) посредником Y. В результате получим линии пересечения а и в посредника с заданными поверхностями α и β. Найдем точки 1 и 2 пересечения полученных линий а и в, принадлежащие обеим поверхностям. Многократно повторим данные операции для нахождения новых точек, принадлежащих обеим поверхностям. Соединив полученные точки, получим линию перехода одной поверхности в другую. Определим видимость поверхностей методом конкурирующих точек 2 1 в а ° °
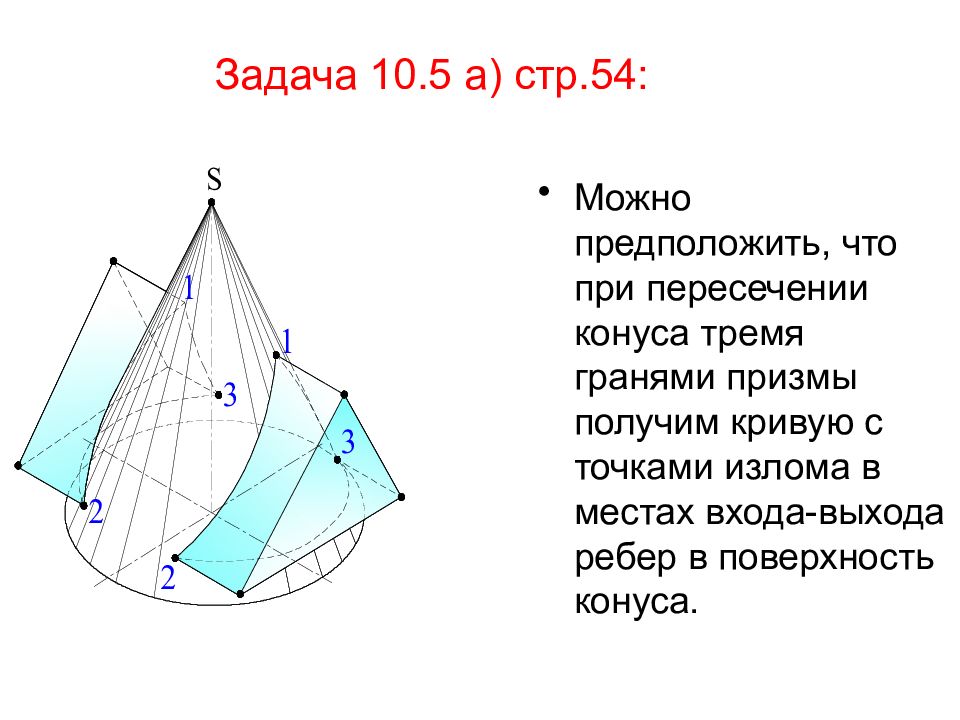
Слайд 51: Задача 10.5 а) стр.54:
Можно предположить, что при пересечении конуса тремя гранями призмы получим кривую с точками излома в местах входа-выхода ребер в поверхность конуса.
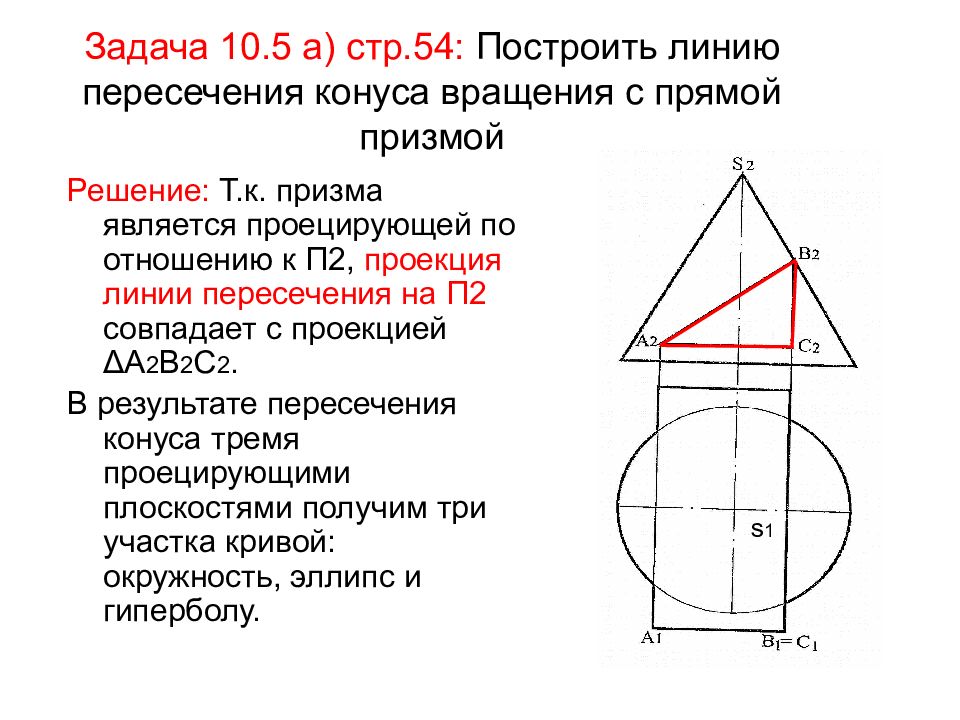
Слайд 52: Задача 10.5 а) стр.54: Построить линию пересечения конуса вращения с прямой призмой
Решение: Т.к. призма является проецирующей по отношению к П2, проекция линии пересечения на П2 совпадает с проекцией Δ А 2 В 2 С 2. В результате пересечения конуса тремя проецирующими плоскостями получим три участка кривой: окружность, эллипс и гиперболу. s 1
Слайд 53
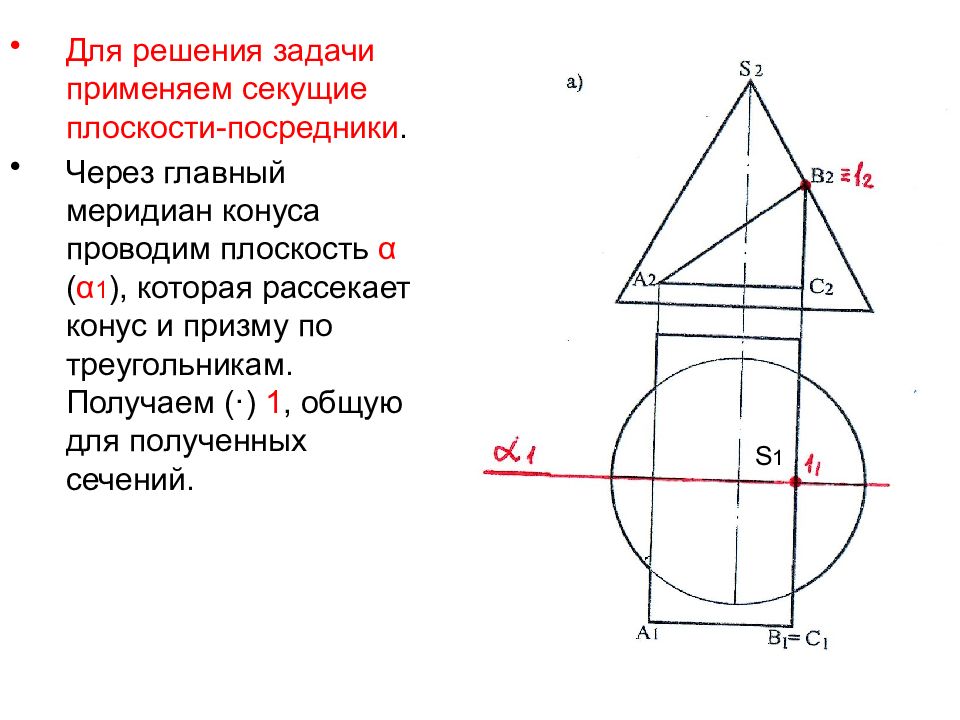
Для решения задачи применяем секущие плоскости-посредники. Через главный меридиан конуса проводим плоскость α ( α 1 ), которая рассекает конус и призму по треугольникам. Получаем ( · ) 1, общую для полученных сечений. S 1
Слайд 54
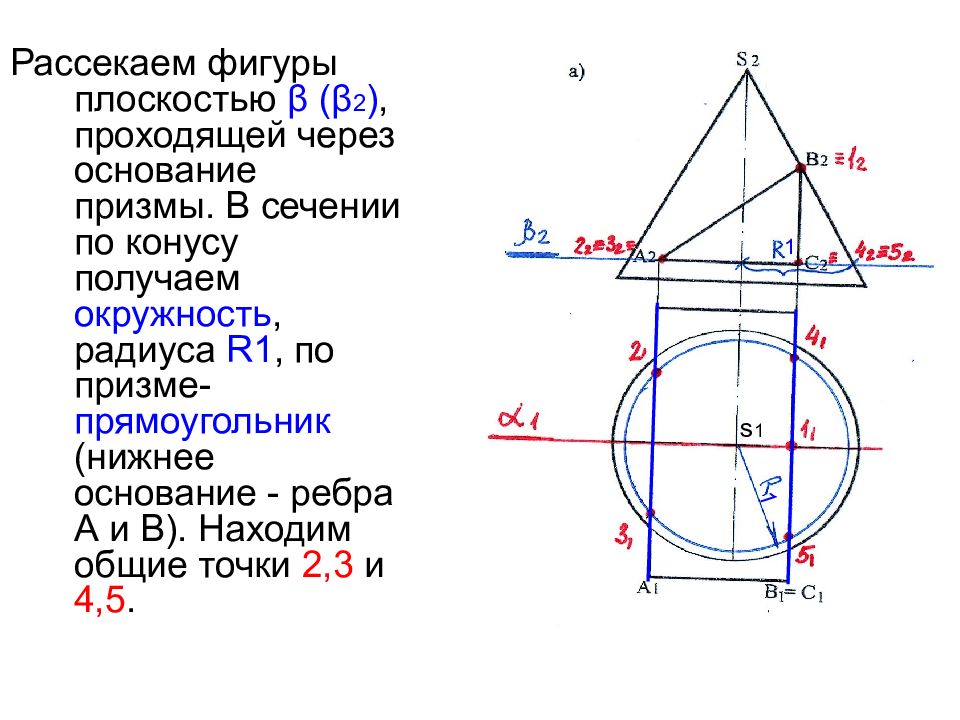
Рассекаем фигуры плоскостью β ( β 2 ), проходящей через основание призмы. В сечении по конусу получаем окружность, радиуса R 1, по призме- прямоугольник (нижнее основание - ребра А и В). Находим общие точки 2,3 и 4,5. s 1 1 1
Слайд 55
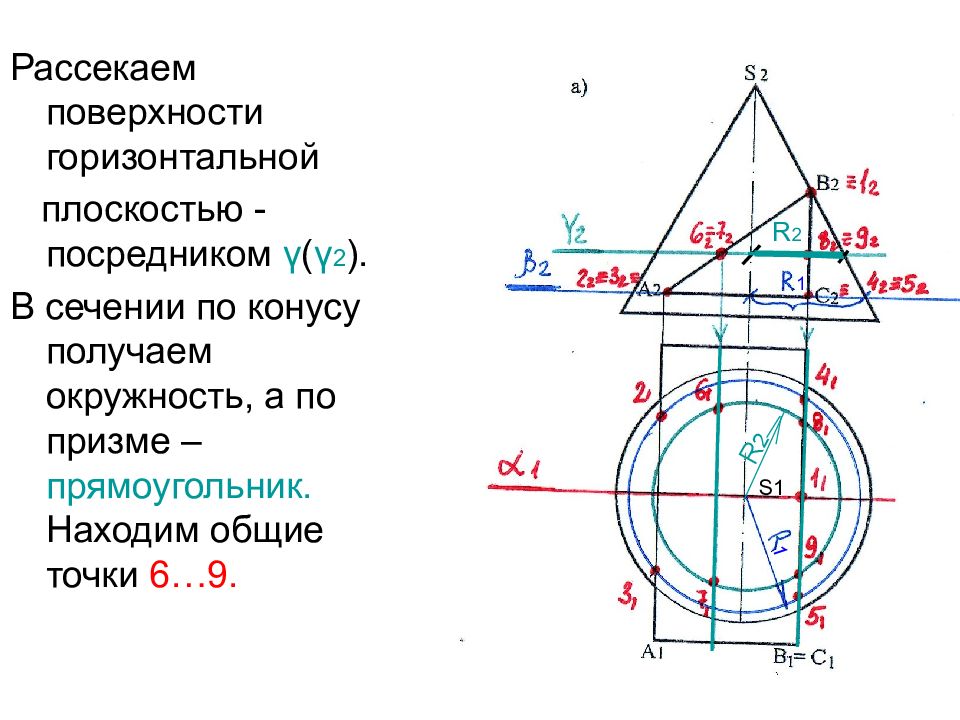
Рассекаем поверхности горизонтальной плоскостью -посредником γ ( γ 2 ). В сечении по конусу получаем окружность, а по призме – прямоугольник. Находим общие точки 6…9. R 2 R 2 1 1 S1
Слайд 56
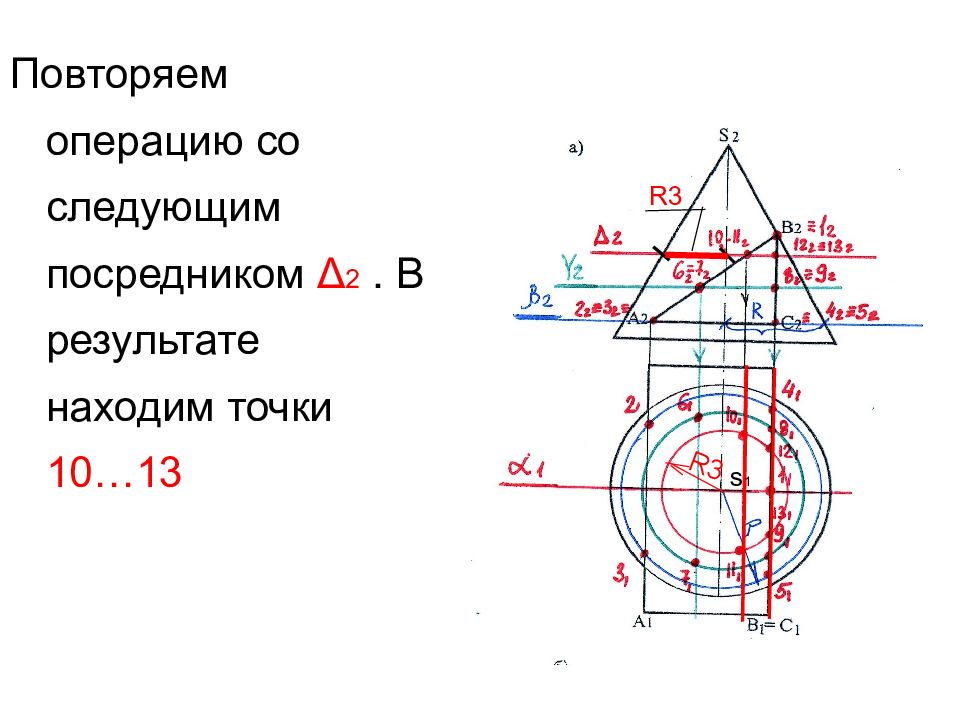
Повторяем операцию со следующим посредником Δ 2. В результате находим точки 10…13 R3 R3 s 1
Слайд 57
На плоскости проекций П1 соединяем все построенные точки между собой – получаем линию пересечения поверхностей. s 1
Слайд 58
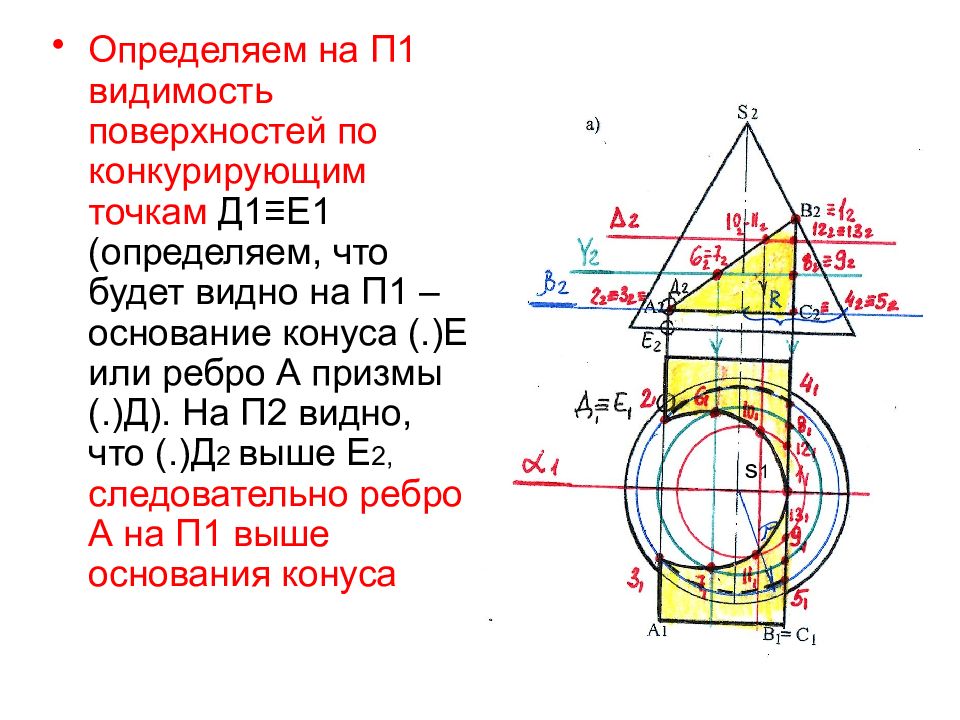
Определяем на П1 видимость поверхностей по конкурирующим точкам Д1≡Е1 (определяем, что будет видно на П1 – основание конуса (.)Е или ребро А призмы (.)Д). На П2 видно, что (.)Д 2 выше Е 2, следовательно ребро А на П1 выше основания конуса s 1
Слайд 59
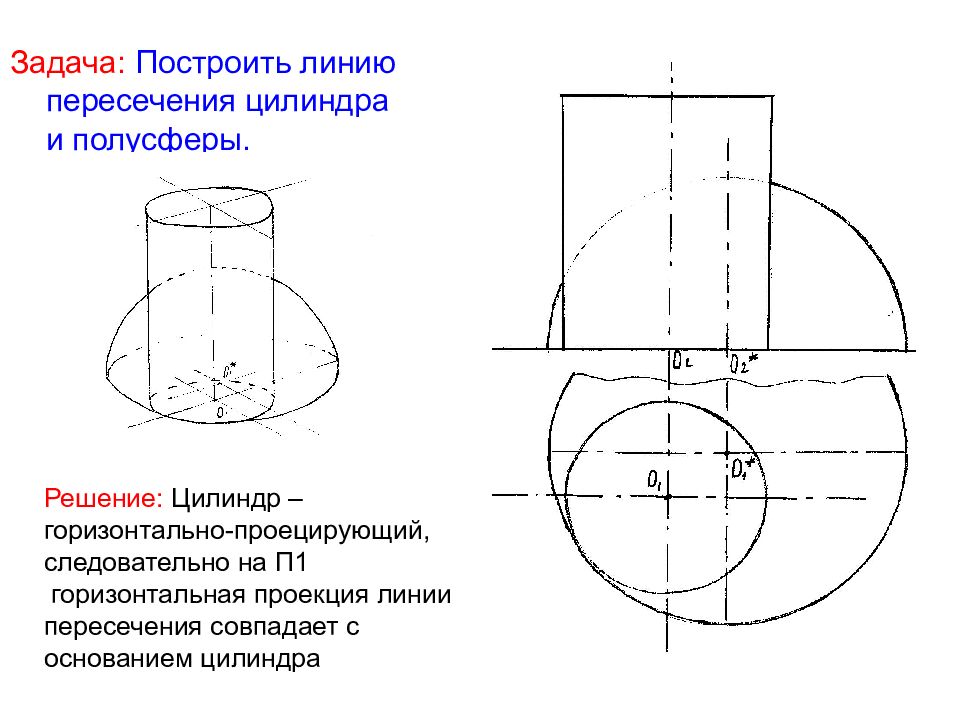
Задача: Построить линию пересечения цилиндра и полусферы. Решение: Цилиндр – горизонтально-проецирующий, следовательно на П1 горизонтальная проекция линии пересечения совпадает с основанием цилиндра
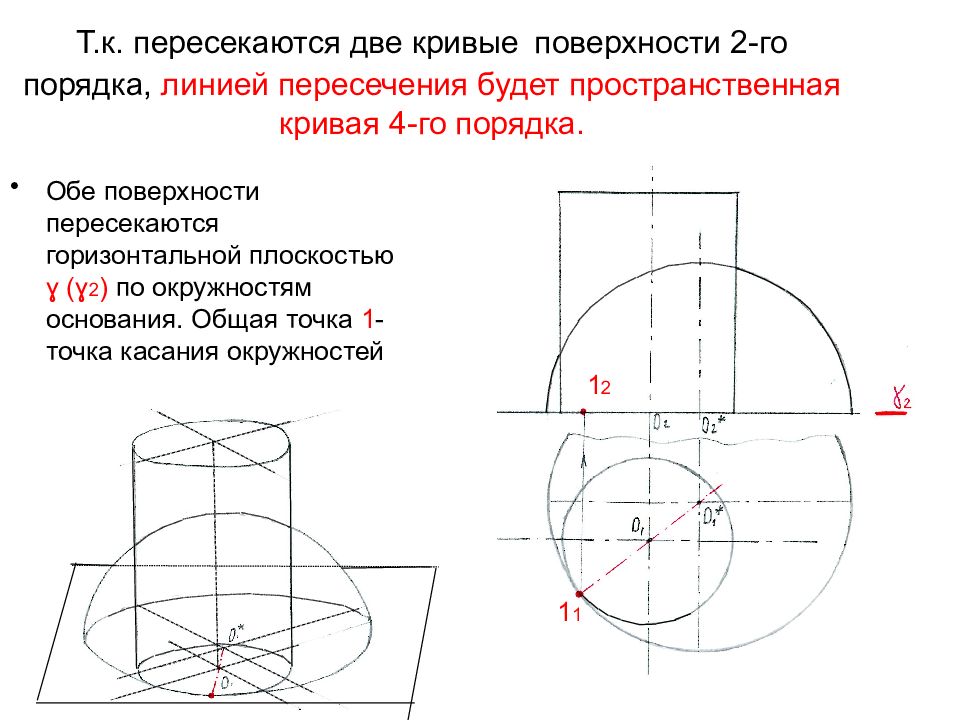
Слайд 60: Т.к. пересекаются две кривые поверхности 2-го порядка, линией пересечения будет пространственная кривая 4-го порядка
Обе поверхности пересекаются горизонтальной плоскостью ɣ (ɣ 2 ) по окружностям основания. Общая точка 1 -точка касания окружностей 1 1 1 2
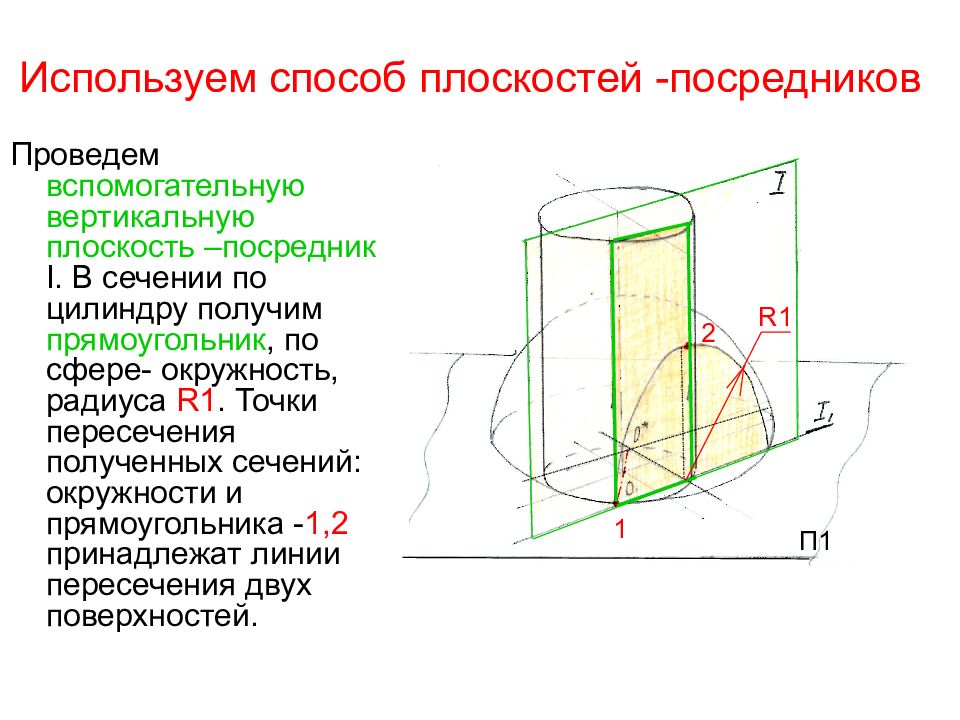
Слайд 61: Используем способ плоскостей -посредников
Проведем вспомогательную вертикальную плоскость –посредник I. В сечении по цилиндру получим прямоугольник, по сфере- окружность, радиуса R1. Точки пересечения полученных сечений: окружности и прямоугольника - 1,2 принадлежат линии пересечения двух поверхностей. R1 1 2 П1
Слайд 62
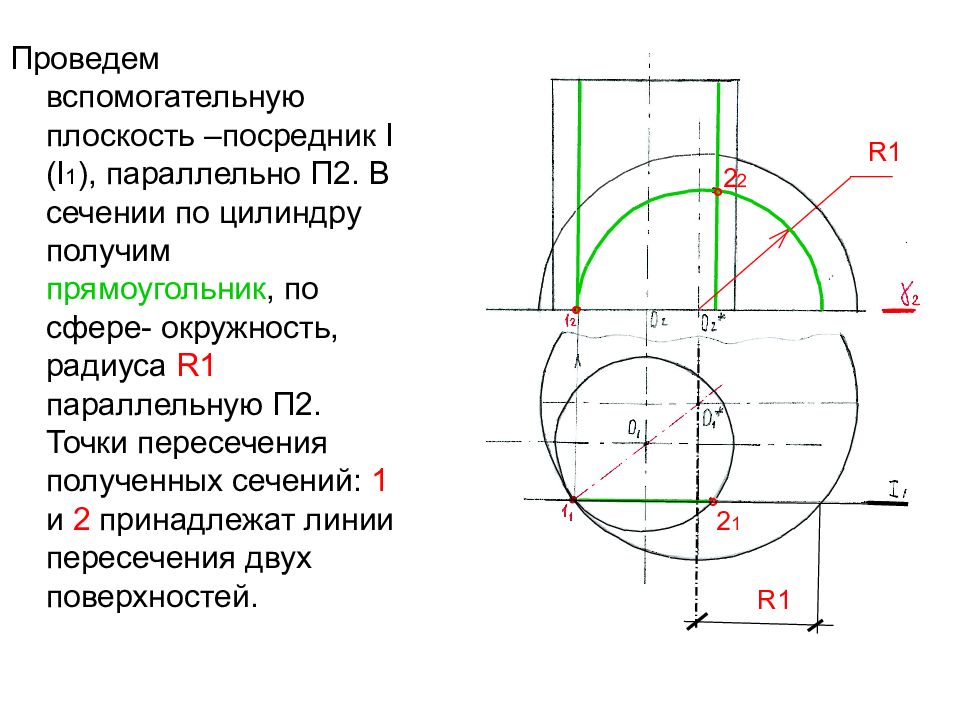
Проведем вспомогательную плоскость –посредник I (I 1 ), параллельно П2. В сечении по цилиндру получим прямоугольник, по сфере- окружность, радиуса R 1 параллельную П2. Точки пересечения полученных сечений: 1 и 2 принадлежат линии пересечения двух поверхностей. R1 R1 2 2 2 1 ° ° °
Слайд 63
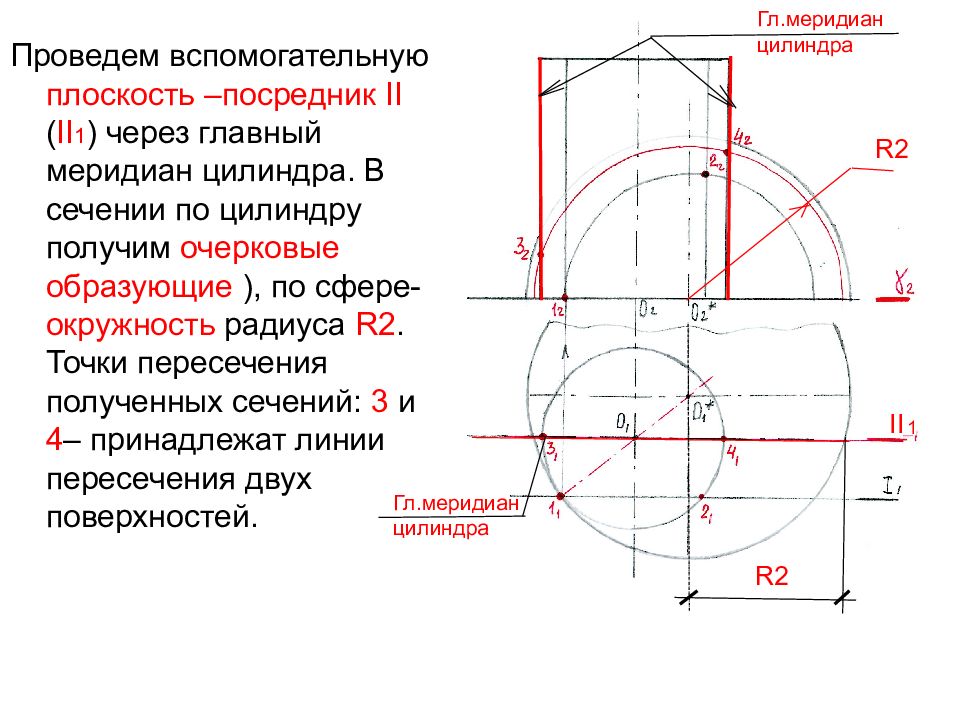
Проведем вспомогательную плоскость –посредник II ( II 1 ) через главный меридиан цилиндра. В сечении по цилиндру получим очерковые образующие ), по сфере- окружность радиуса R2. Точки пересечения полученных сечений: 3 и 4 – принадлежат линии пересечения двух поверхностей. 1 II R2 Гл.меридиан цилиндра Гл.меридиан цилиндра R2
Слайд 64
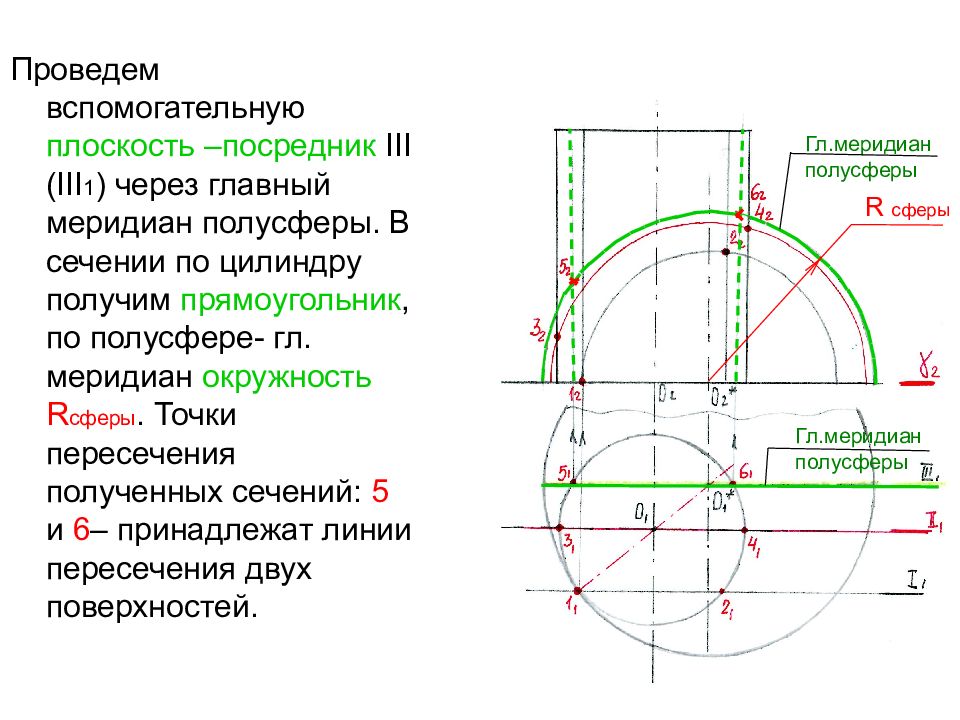
Проведем вспомогательную плоскость –посредник III (III 1 ) через главный меридиан полусферы. В сечении по цилиндру получим прямоугольник, по полусфере- гл. меридиан окружность R сферы. Точки пересечения полученных сечений: 5 и 6 – принадлежат линии пересечения двух поверхностей. R сферы Гл.меридиан полусферы Гл.меридиан полусферы
Слайд 65
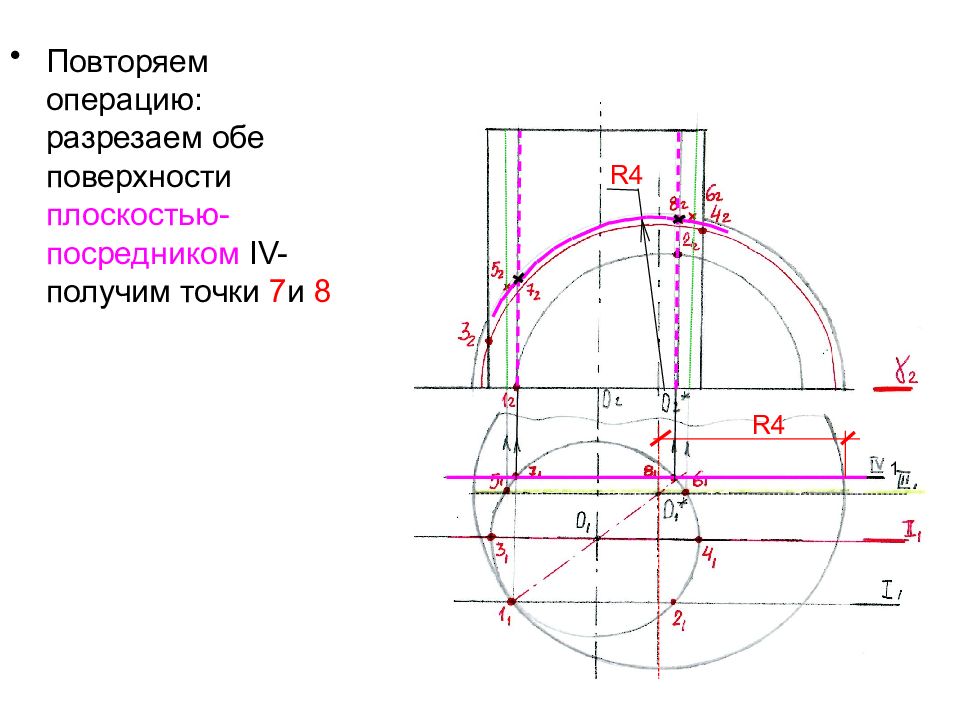
Повторяем операцию: разрезаем обе поверхности плоскостью-посредником IV- получим точки 7 и 8 1 R 4 R 4
Слайд 66
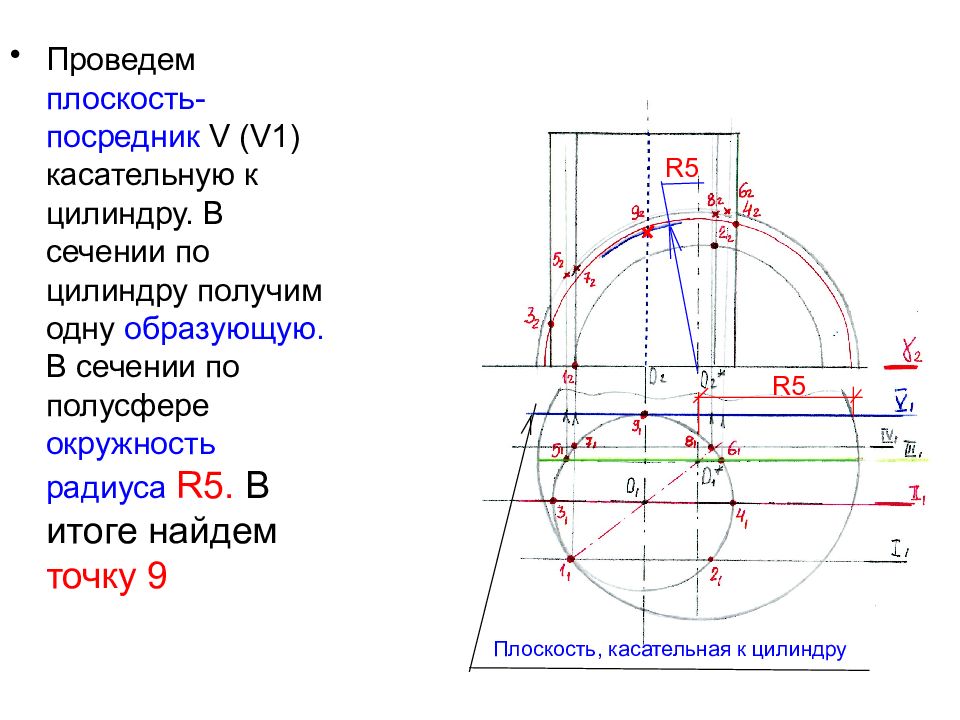
Проведем плоскость-посредник V (V1 ) касательную к цилиндру. В сечении по цилиндру получим одну образующую. В сечении по полусфере окружность радиуса R 5. В итоге найдем точку 9 R 5 R 5 Плоскость, касательная к цилиндру
Слайд 67
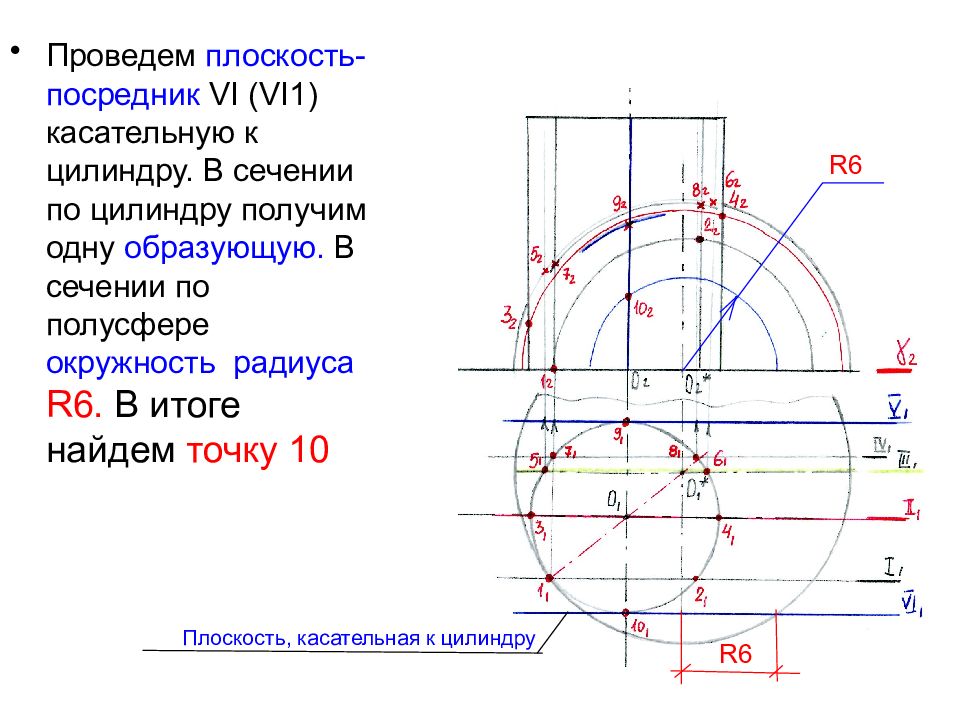
Проведем плоскость-посредник VI (VI1 ) касательную к цилиндру. В сечении по цилиндру получим одну образующую. В сечении по полусфере окружность радиуса R6. В итоге найдем точку 10 R6 R6 Плоскость, касательная к цилиндру
Слайд 68
Соединяем найденные точки 1-10 с учетом видимости. Получим линию перехода цилиндра и полусферы. Плоскость, касательная к цилиндру
Слайд 69
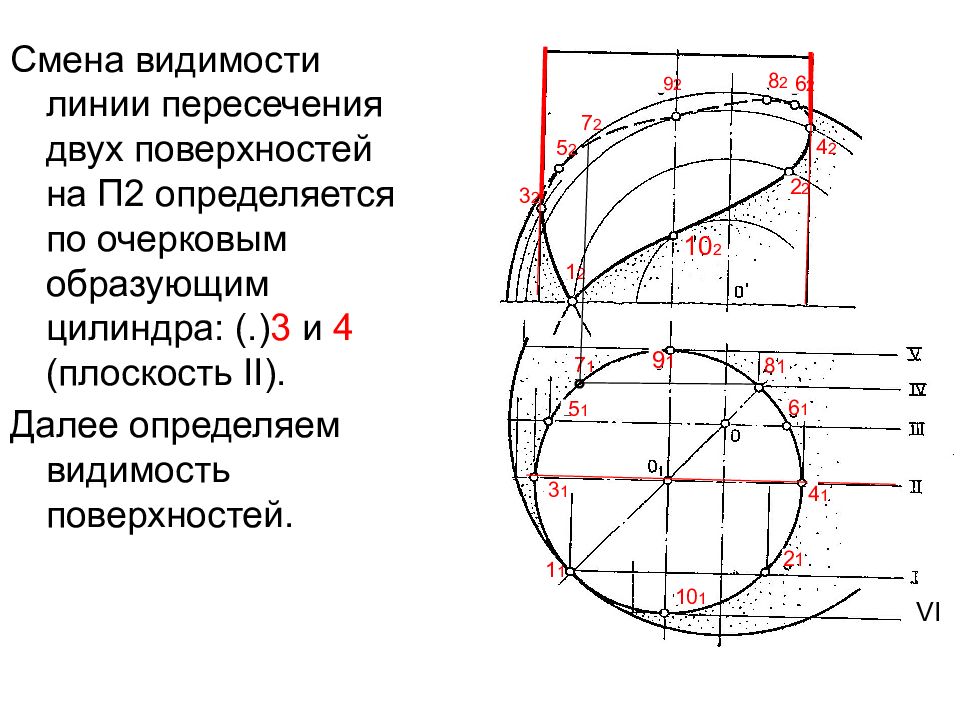
Смена видимости линии пересечения двух поверхностей на П2 определяется по очерковым образующим цилиндра: (.) 3 и 4 (плоскость II ). Далее определяем видимость поверхностей. 2 1 10 1 1 1 3 1 4 1 5 1 6 1 7 1 8 1 9 1 ° VI 9 2 2 2 10 2 1 2 3 2 4 2 5 2 6 2 7 2 8 2
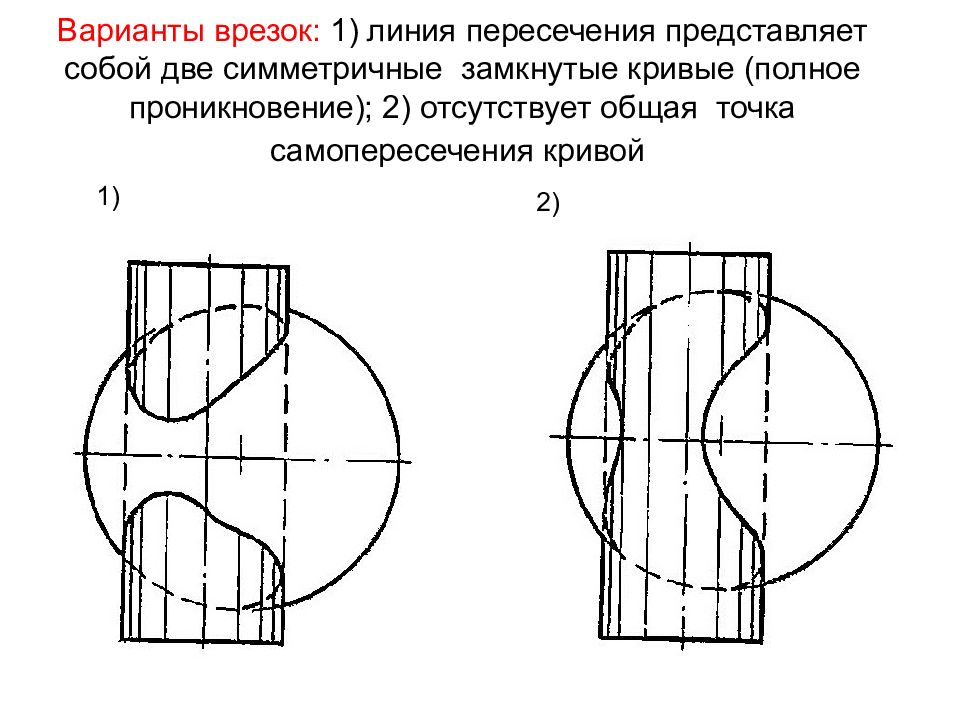
1) 2)
Слайд 71
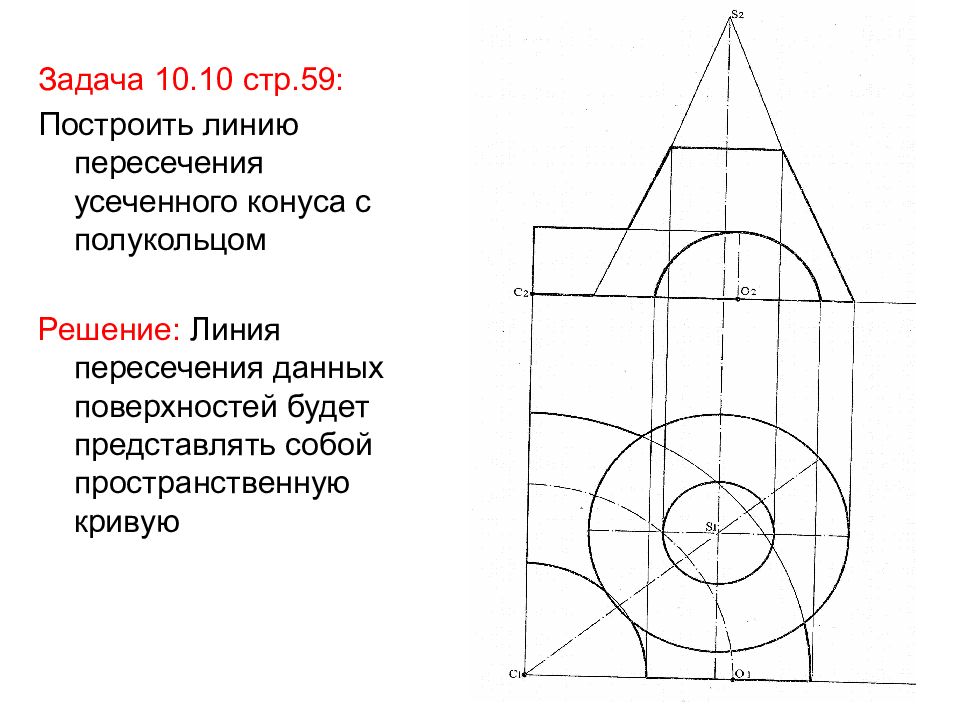
Задача 10.10 стр.59: Построить линию пересечения усеченного конуса с полукольцом Решение: Линия пересечения данных поверхностей будет представлять собой пространственную кривую
Слайд 72
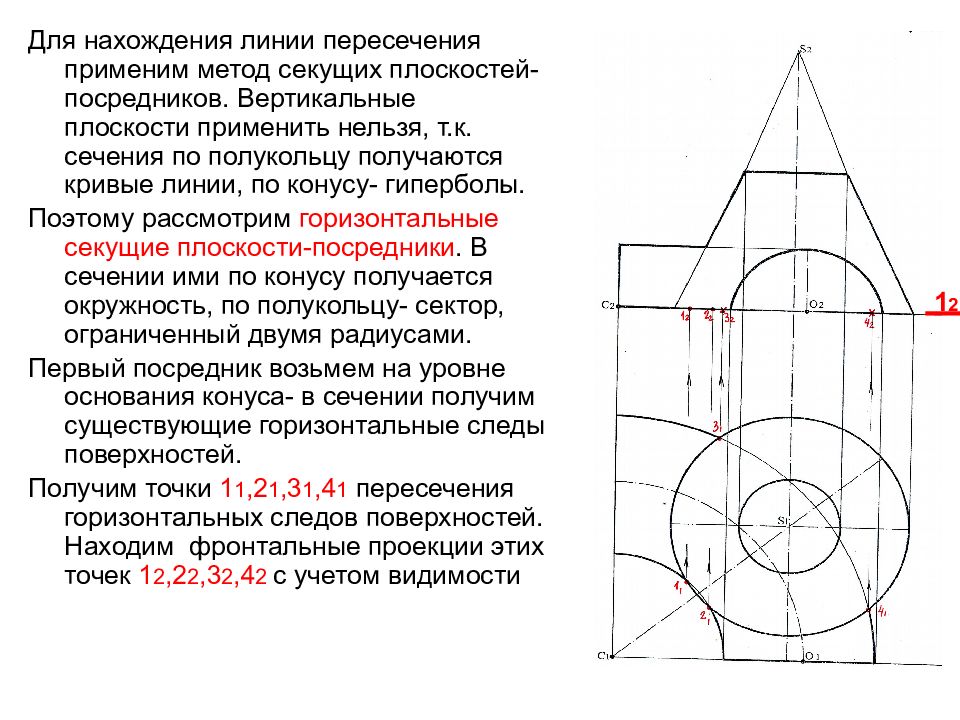
Для нахождения линии пересечения применим метод секущих плоскостей-посредников. Вертикальные плоскости применить нельзя, т.к. сечения по полукольцу получаются кривые линии, по конусу- гиперболы. Поэтому рассмотрим горизонтальные секущие плоскости-посредники. В сечении ими по конусу получается окружность, по полукольцу- сектор, ограниченный двумя радиусами. Первый посредник возьмем на уровне основания конуса- в сечении получим существующие горизонтальные следы поверхностей. Получим точки 1 1,2 1,3 1,4 1 пересечения горизонтальных следов поверхностей. Находим фронтальные проекции этих точек 1 2,2 2,3 2,4 2 с учетом видимости 1 2
Слайд 73
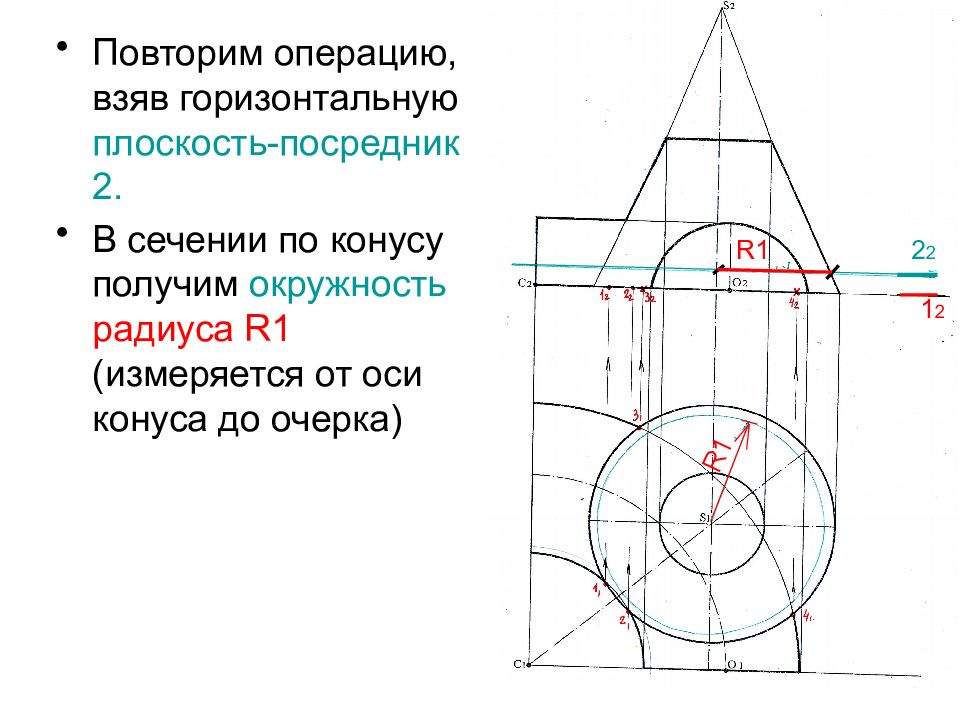
Повторим операцию, взяв горизонтальную плоскость-посредник 2. В сечении по конусу получим окружность радиуса R1 (измеряется от оси конуса до очерка) 2 2 1 2 R1 R1
Слайд 74
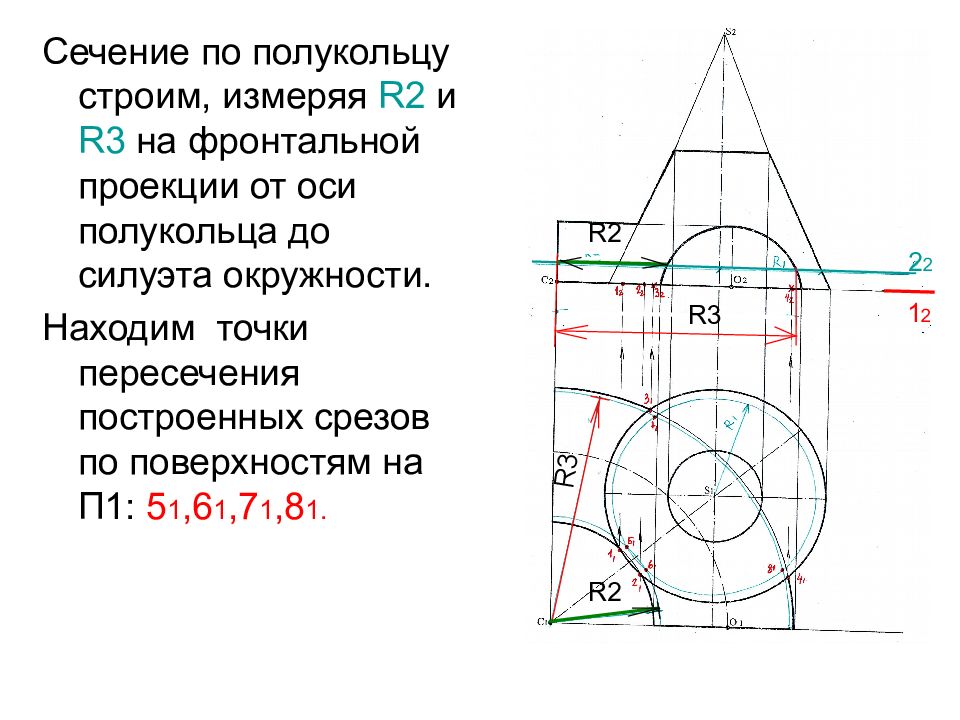
Сечение по полукольцу строим, измеряя R 2 и R 3 на фронтальной проекции от оси полукольца до силуэта окружности. Находим точки пересечения построенных срезов по поверхностям на П1: 5 1,6 1,7 1,8 1. 2 2 R3 R2 R3 R2 1 2
Слайд 75
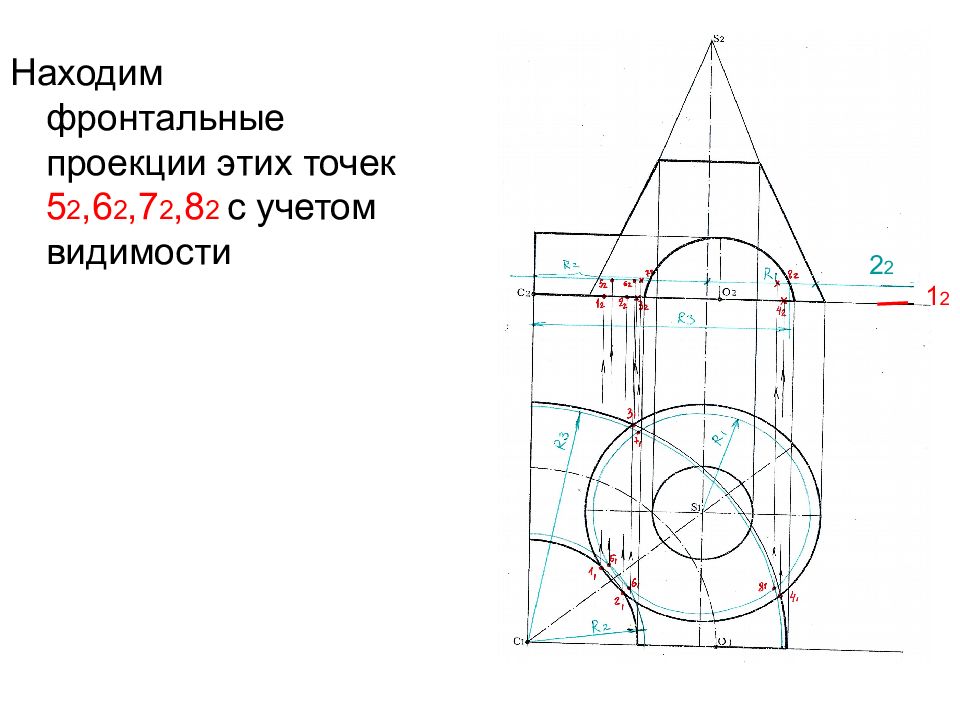
Находим фронтальные проекции этих точек 5 2,6 2,7 2,8 2 с учетом видимости 1 2 2 2
Слайд 76
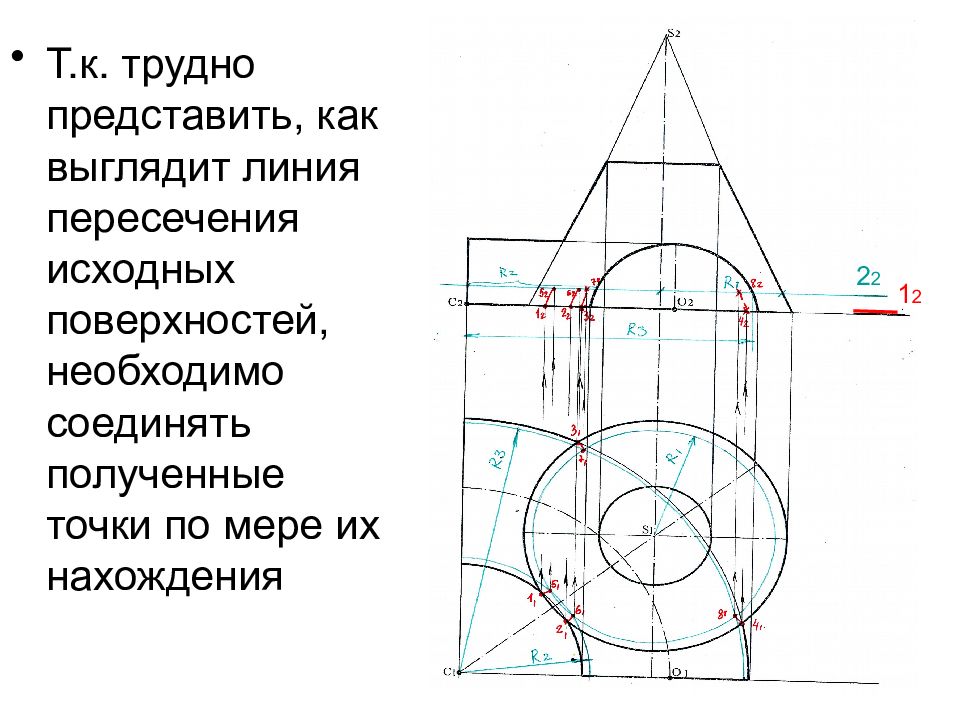
Т.к. трудно представить, как выглядит линия пересечения исходных поверхностей, необходимо соединять полученные точки по мере их нахождения 1 2 2 2
Слайд 77
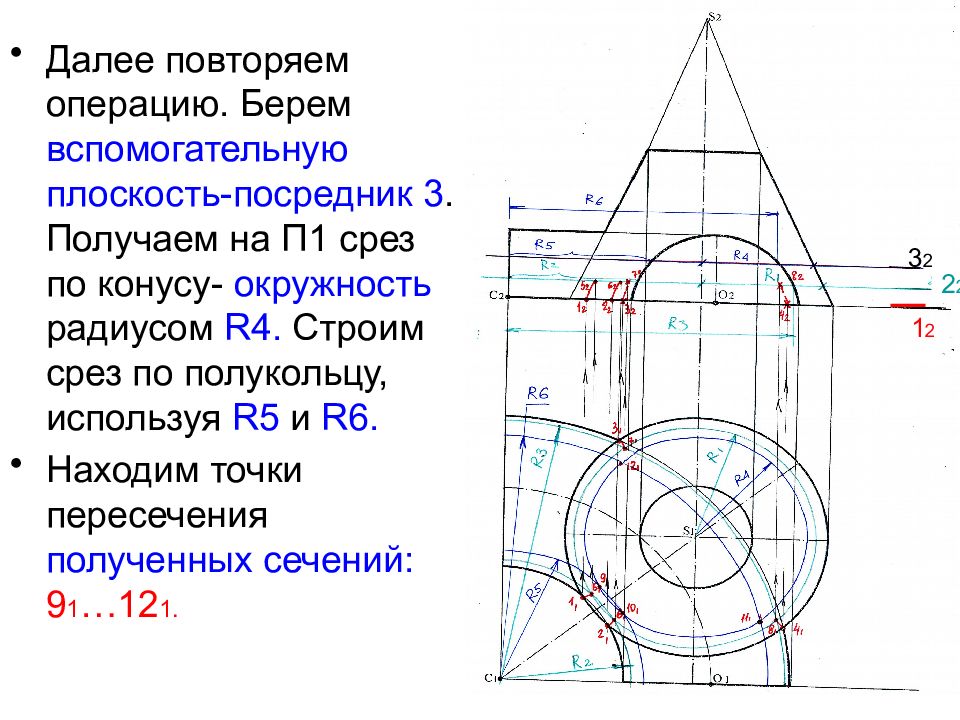
Далее повторяем операцию. Берем вспомогательную плоскость-посредник 3. Получаем на П1 срез по конусу- окружность радиусом R4. Строим срез по полукольцу, используя R 5 и R 6. Находим точки пересечения полученных сечений: 9 1 …12 1. 2 2 3 2 1 2
Слайд 78
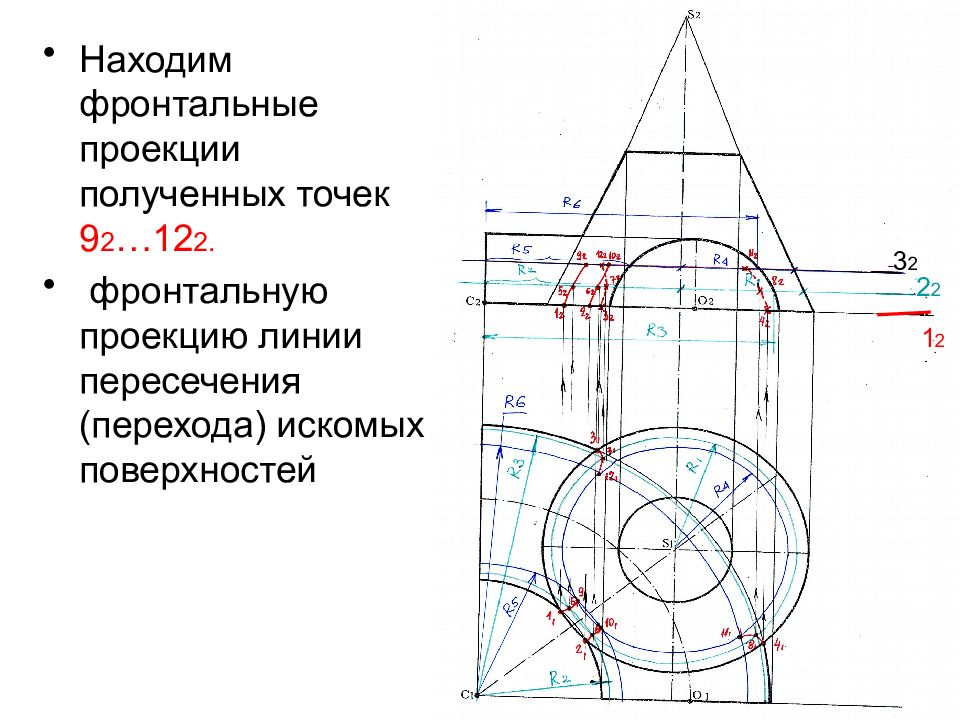
Находим фронтальные проекции полученных точек 9 2 …12 2. фронтальную проекцию линии пересечения (перехода) искомых поверхностей 3 2 2 2 1 2
Слайд 79
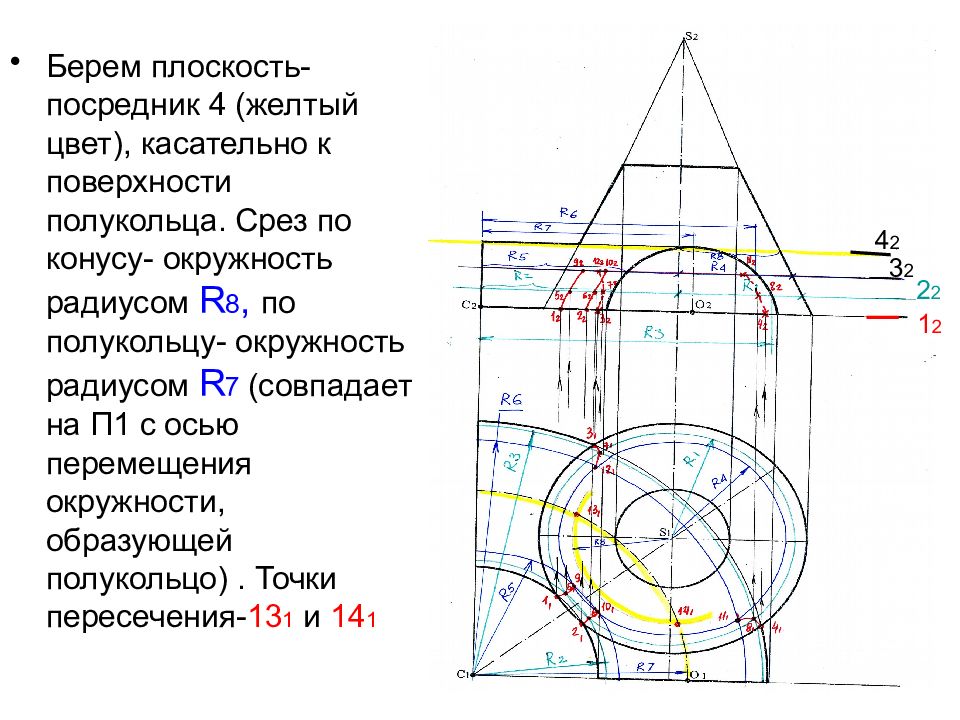
Берем плоскость-посредник 4 (желтый цвет), касательно к поверхности полукольца. Срез по конусу- окружность радиусом R 8, по полукольцу- окружность радиусом R 7 (совпадает на П1 с осью перемещения окружности, образующей полукольцо). Точки пересечения- 13 1 и 14 1 4 2 3 2 2 2 1 2
Слайд 80
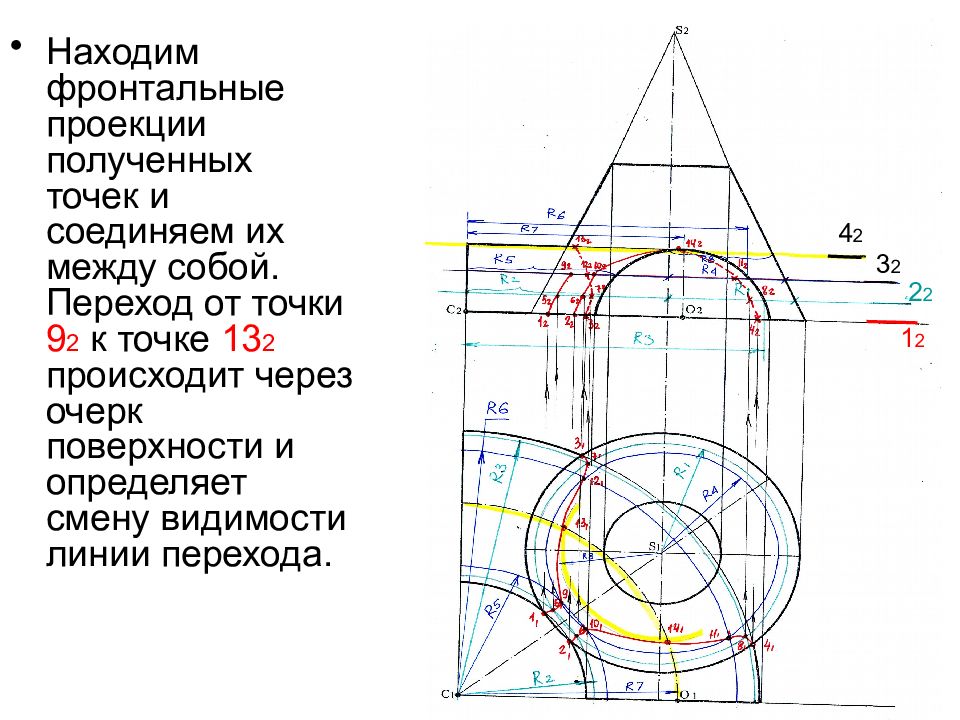
Находим фронтальные проекции полученных точек и соединяем их между собой. Переход от точки 9 2 к точке 13 2 происходит через очерк поверхности и определяет смену видимости линии перехода. 3 2 2 2 4 2 1 2
Слайд 81
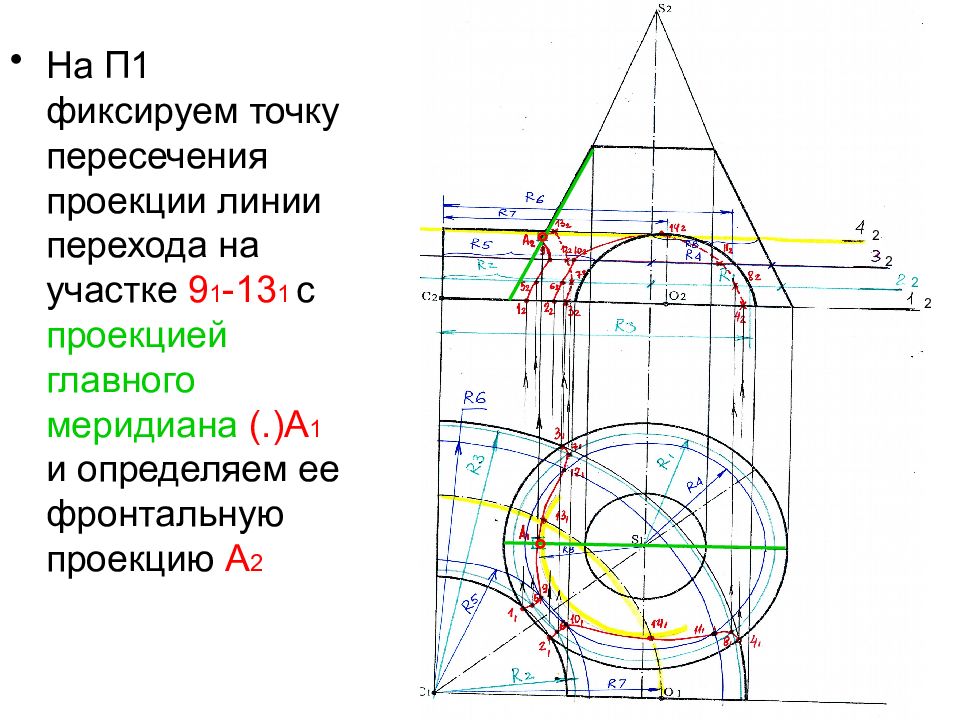
На П1 фиксируем точку пересечения проекции линии перехода на участке 9 1 -13 1 с проекцией главного меридиана (.)А 1 и определяем ее фронтальную проекцию А 2 ° ° 2 2 2 2