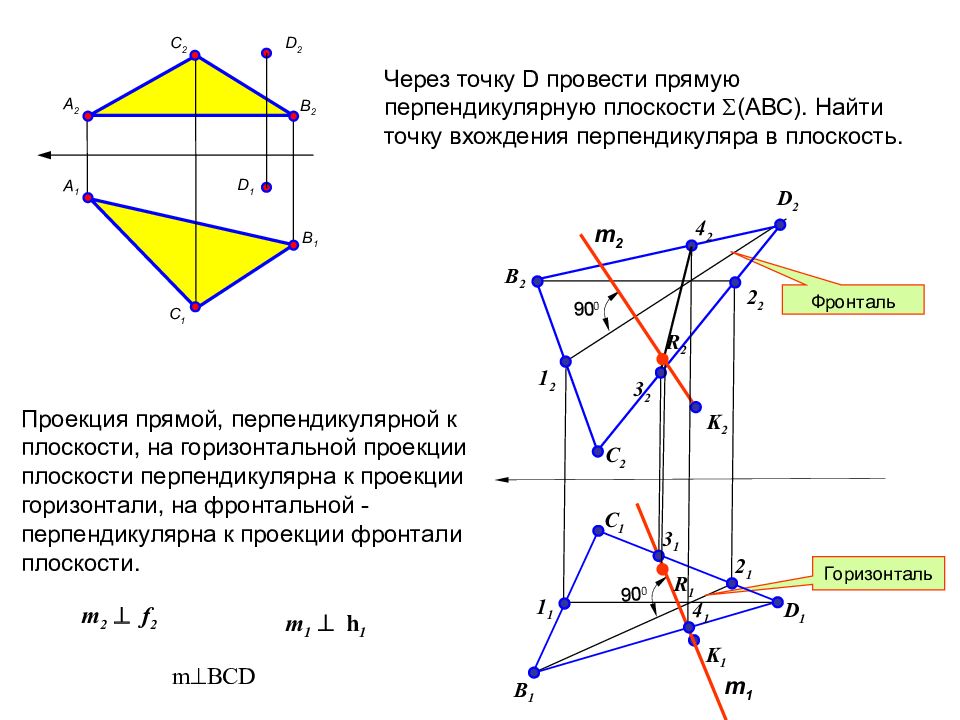
Первый слайд презентации: Курс лекций « Начертательная геометрия »
1 Курс лекций « Начертательная геометрия » 2008 г. Автор: доцент кафедры Инженерная графика МИСиС Лейкова Марина Владимировна.- mvleikova@mtu-net.ru
Слайд 2: Содержание лекции №2
2 Содержание лекции №2 1.9 Проецирование точки на дополнительные пл. проекций. Способ замены пл. пр. 1.10 Определение длины отрезка прямой общего положения и углов наклона к пл оскостям пр. 1.11 Плоскость. Задание и изображение на чертеже. 1.12 Плоскости общего положения. Плоскости частного положения. а) Проецирующие плоскости. б) Плоскости уровня. 1.13 Прямая и точка в плоскости. 1.14 Линии уровня в плоскости. 1.15 Определение натуральной величины плоской фигуры. 1.16 Взаимное расположение геометрических образов а) Построение взаимно параллельных: прямой и плоскости. б) Построение взаимно параллельных плоскостей.
Слайд 3: 1.9 Проецирование точки на дополнительные пл оскости проекций. Способ замены пл оскостей пр оекций
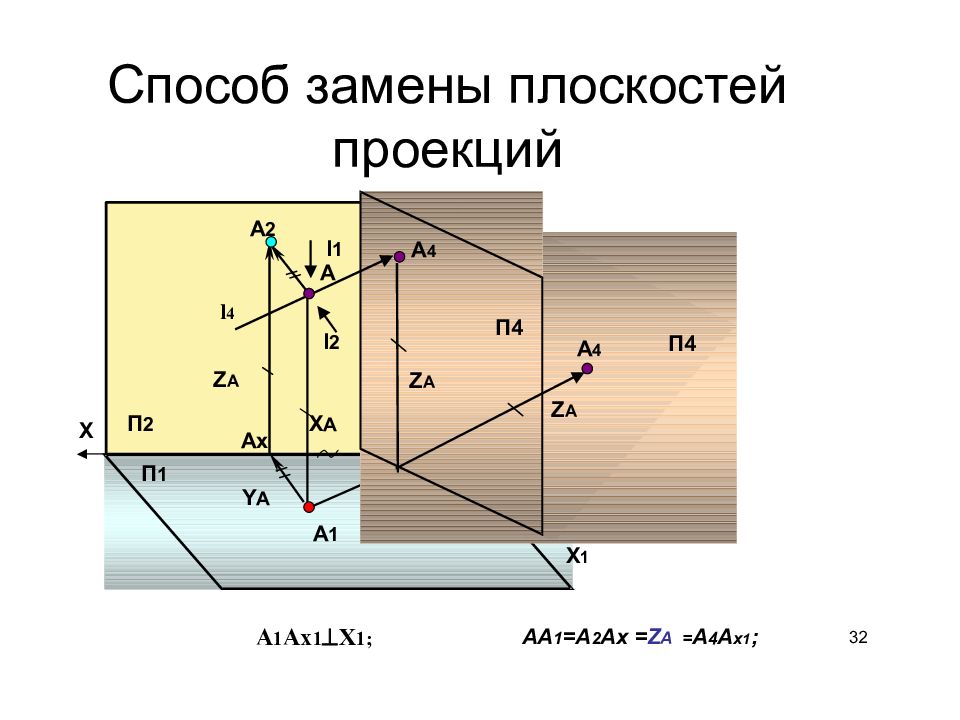
3 1.9 Проецирование точки на дополнительные пл оскости проекций. Способ замены пл оскостей пр оекций
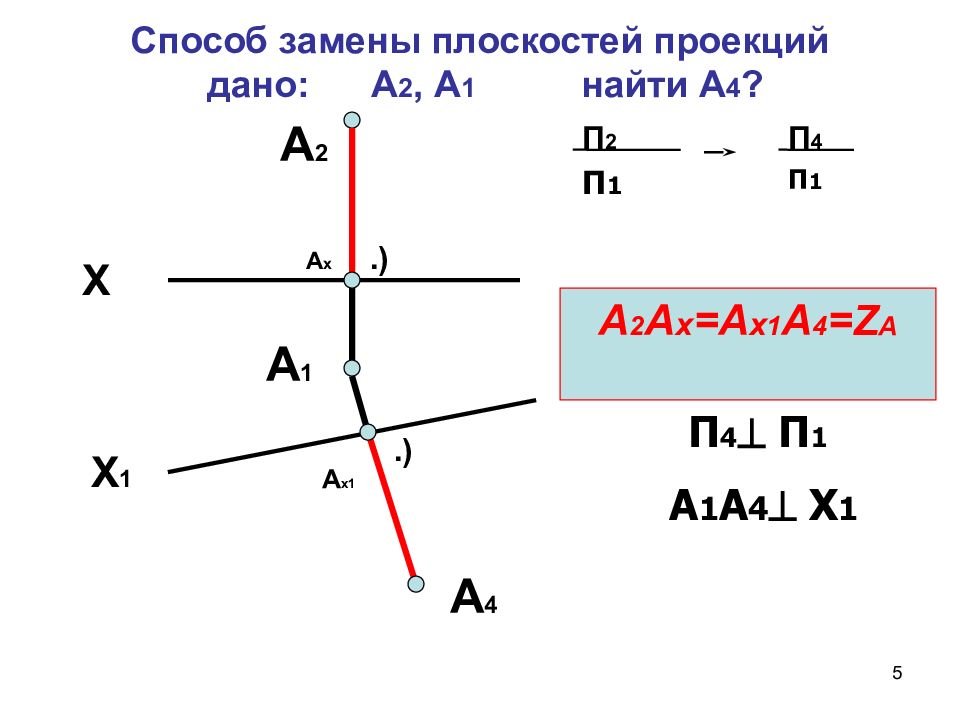
5 Способ замены плоскостей проекций дано: А 2, А 1 найти А 4 ? Х Х 1 А 2 А х А 1 А х1 А 4 .) .) А 2 А х =А х 1 А 4 = Z A П 4 П 1 А 1 А 4 Х 1 П 2 П 1 П 4 П 1
Слайд 6: Свойство неизменности расстояний:
6 Свойство неизменности расстояний: Расстояние от новой оси проекций до новой проекции точки равно такому же расстоянию в заменяемой плоскости проекций. А 2 А х =А х 1 А 4
Слайд 7: 1.10 Определение длины отрезка прямой общего положения и углов наклона к пл оскостям пр
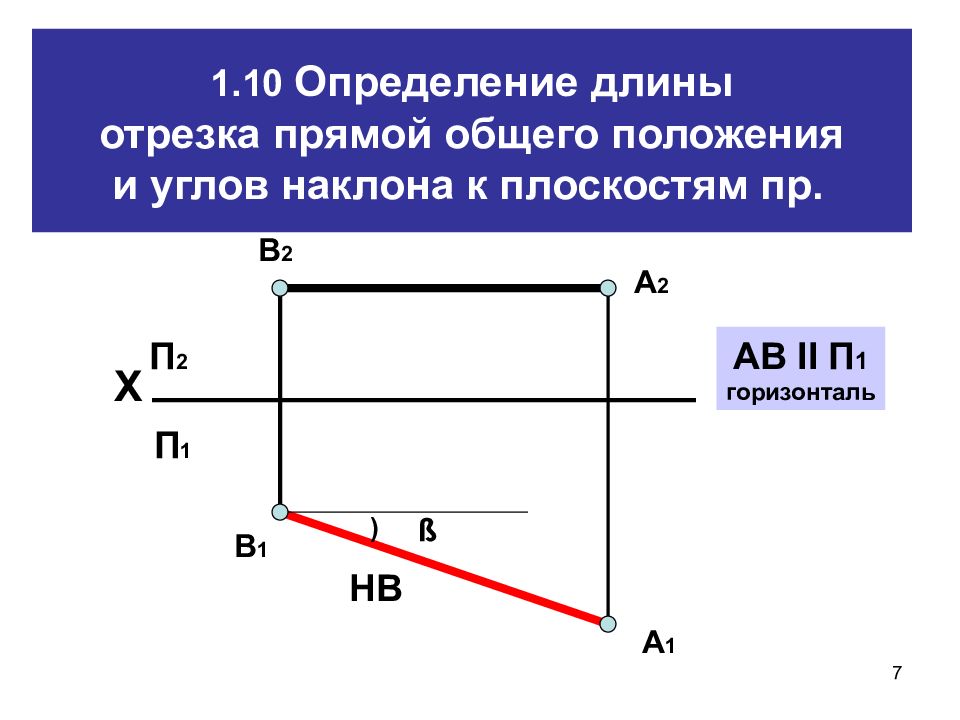
7 1.10 Определение длины отрезка прямой общего положения и углов наклона к пл оскостям пр. Х П 2 П 1 ß ) НВ А 2 А 1 В 2 В 1 АВ II П 1 горизонталь
Слайд 8: АВ – отрезок прямой общ. положения
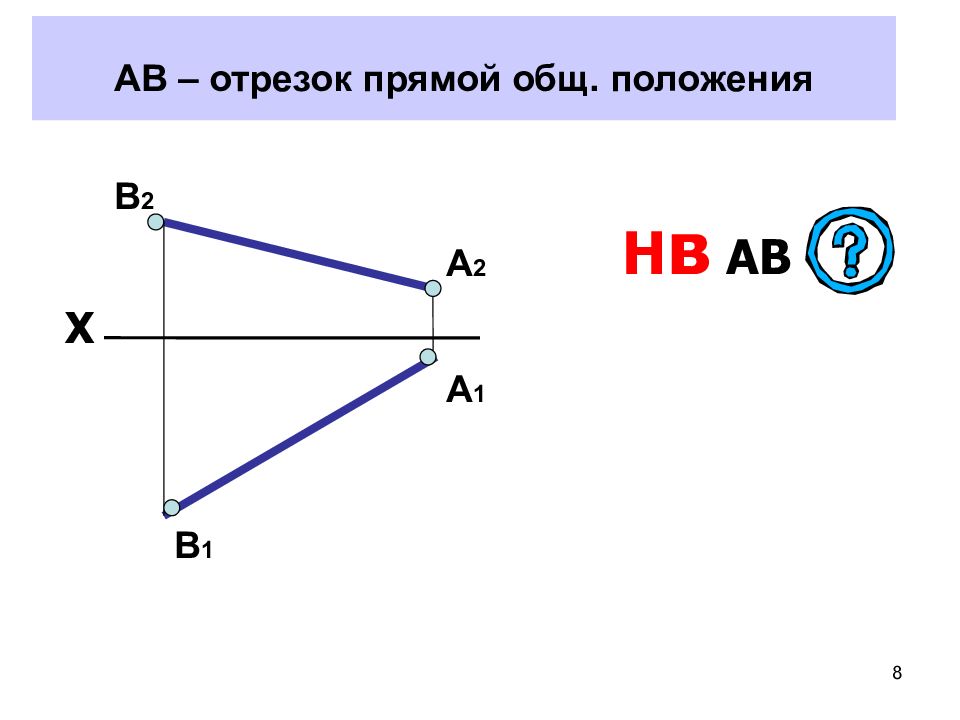
8 АВ – отрезок прямой общ. положения Х В 1 В 2 А 2 А 1 Н в АВ
Слайд 9: АВ – отрезок прямой общ. положения
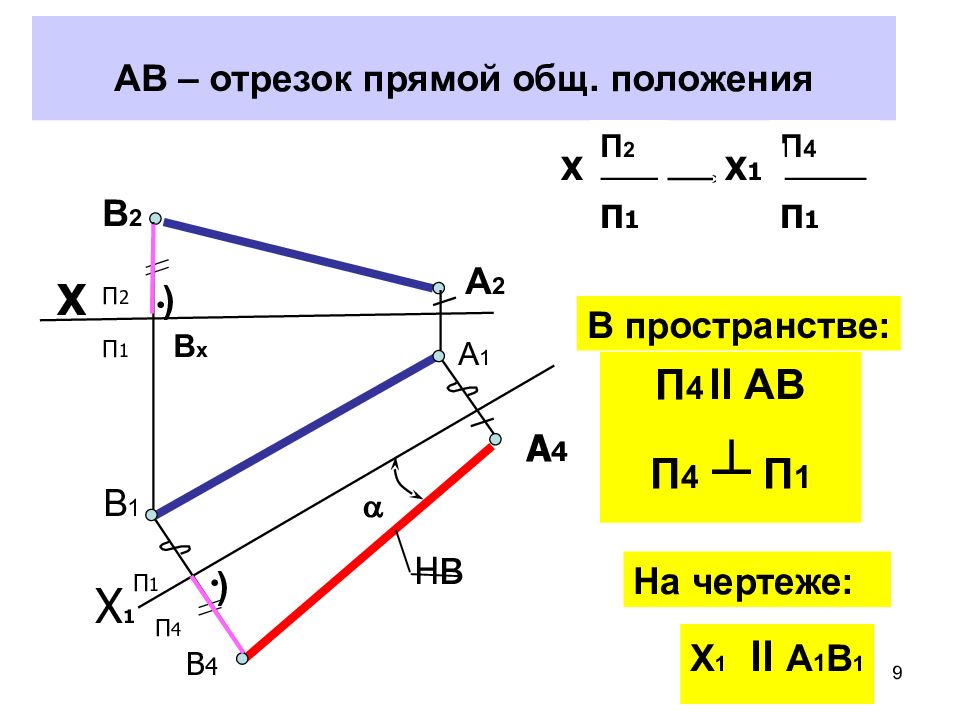
9 АВ – отрезок прямой общ. положения На чертеже: П 2 П 1 Х П 4 П 1 Х 1 Х 1 П 2 П 1 А 4 В 4 П 1 П 4 В 2 В 1 А 2 А 1 Х Н в В х В пространстве: Х 1 II А 1 В 1 • • П 4 II АВ П 4 ┴ П 1 ) )
Слайд 10: 1.11 Плоскость. Задание и изображение на чертеже
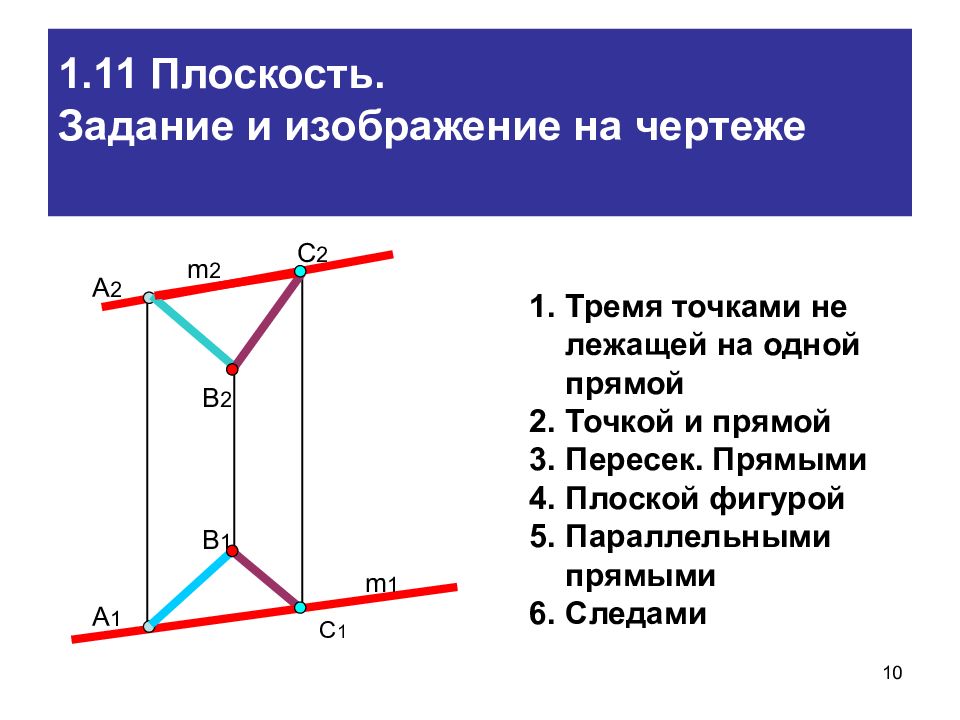
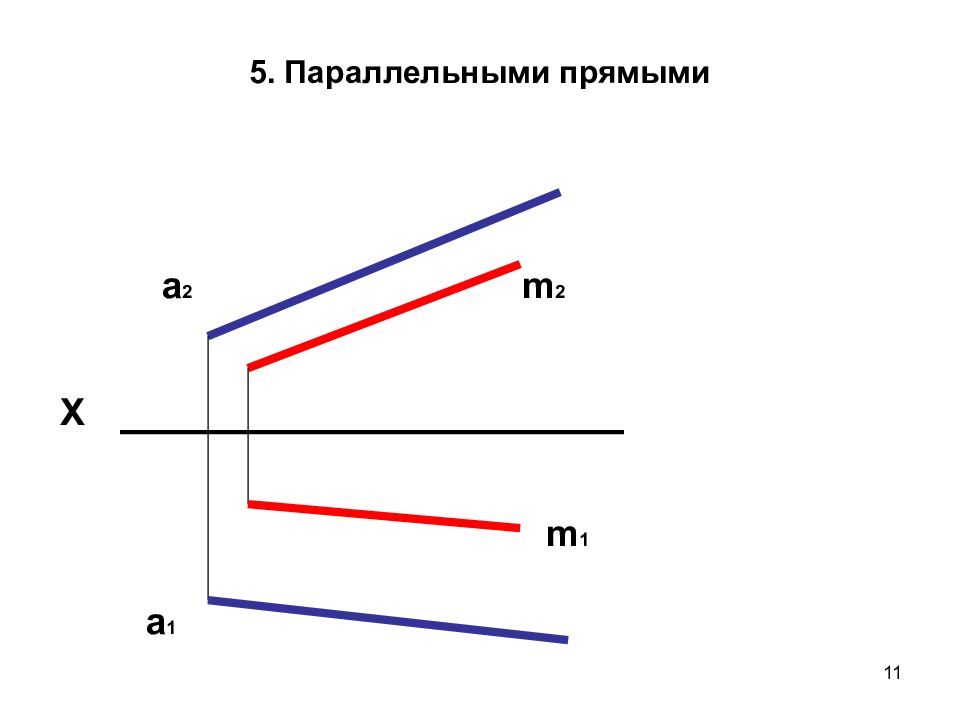
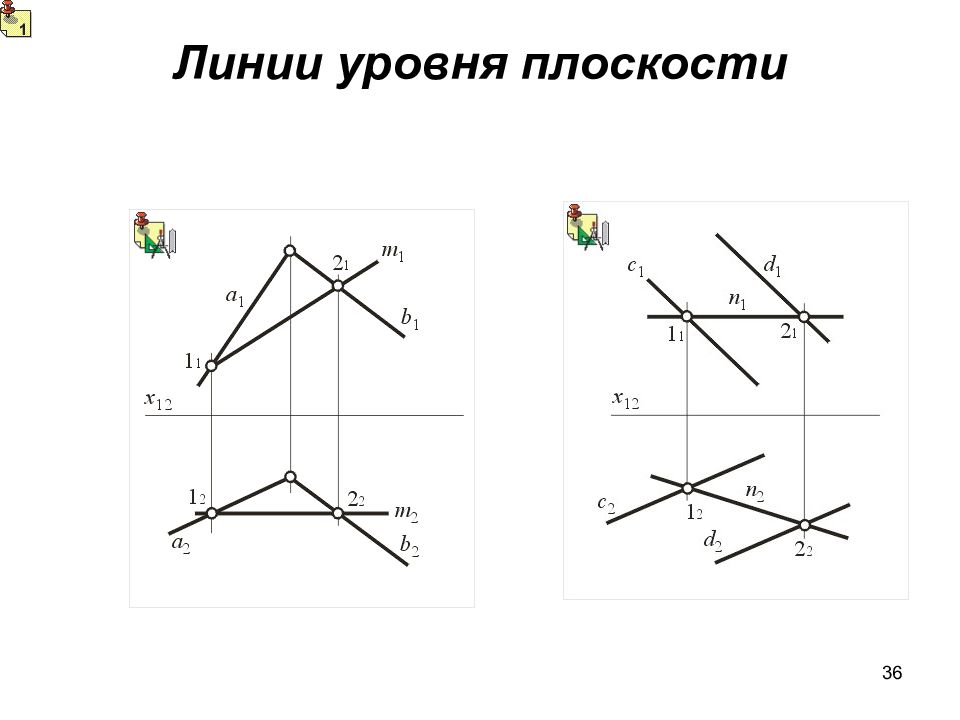
10 1.11 Плоскость. Задание и изображение на чертеже А 2 А 1 В 2 В 1 С 2 С 1 m 2 m 1 Тремя точками не лежащей на одной прямой Точкой и прямой Пересек. Прямыми Плоской фигурой Параллельными прямыми Следами
Слайд 12: 6.Следами
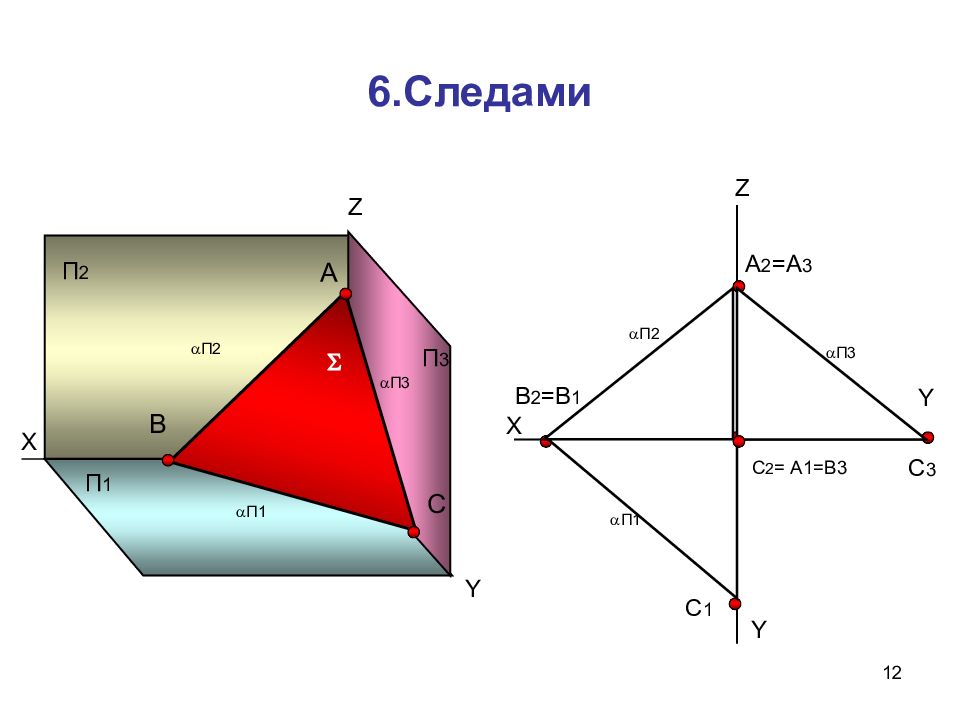
12 6.Следами Х П 1 П 2 П 3 Z Y Y X Z Y А В С А 2 =А 3 В 2 =В 1 С 1 С 3 С 2 = А1=В3 П1 П3 П2 П1 П2 П3
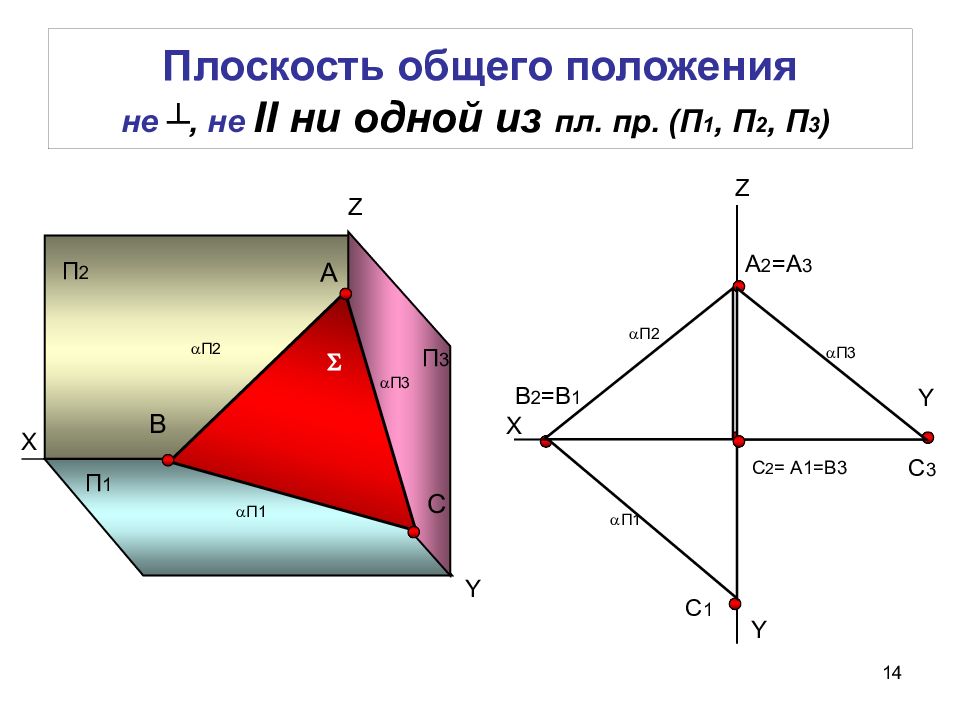
Слайд 14: Плоскость общего положения не ┴, не II ни одной из пл. пр. (П 1, П 2, П 3 )
14 Плоскость общего положения не ┴, не II ни одной из пл. пр. (П 1, П 2, П 3 ) Х П 1 П 2 П 3 Z Y Y X Z Y А В С А 2 =А 3 В 2 =В 1 С 1 С 3 С 2 = А1=В3 П1 П3 П2 П1 П2 П3
Слайд 15: Плоскости частного положения :
15 Плоскости частного положения : а) Проецирующие плоскости ( Плоскости ┴ какой-либо пл. пр. ) б) Плоскости уровня (Дважды проецирующие ┴ к 2м пл.пр. )
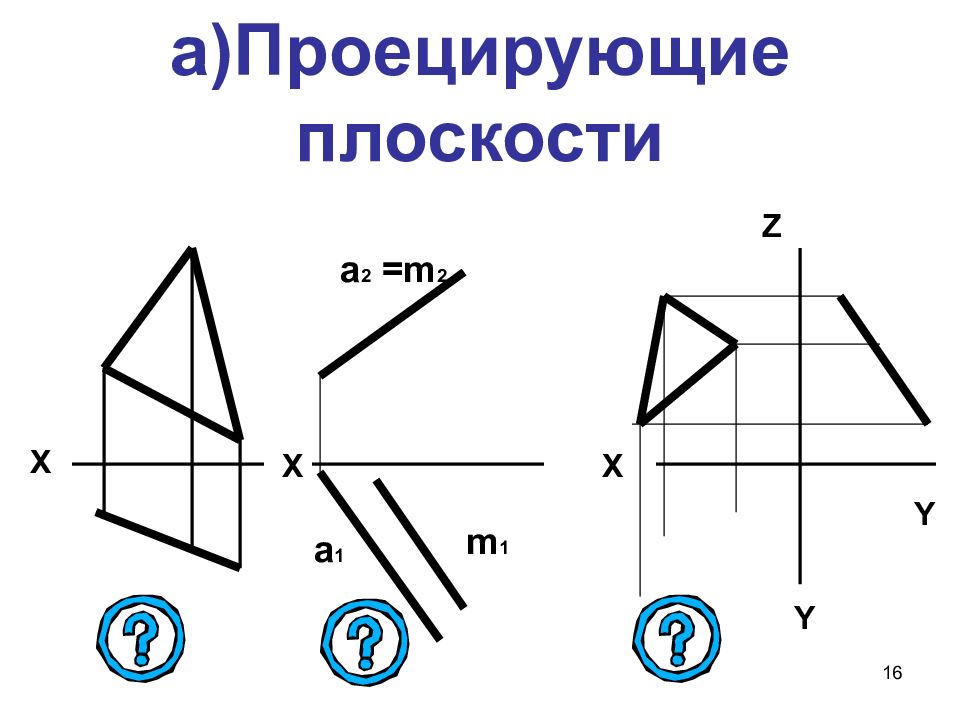
Слайд 16: а) Проецирующие плоскости
16 а) Проецирующие плоскости Х Х а 1 а 2 = m 2 m 1 Х Y Y Z
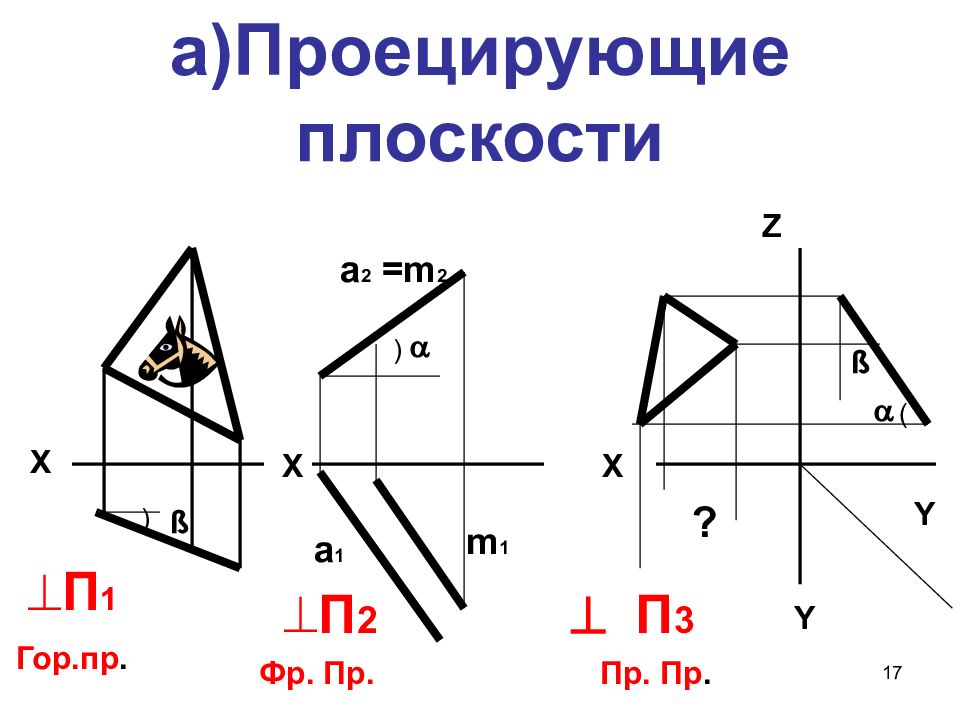
Слайд 17: а) Проецирующие плоскости
17 а) Проецирующие плоскости Х Х а 1 а 2 = m 2 m 1 Х Y Y Z П 1 Гор.пр. П 2 П 3 Фр. Пр. Пр. Пр. ? ) ( ß ) ß
Слайд 18: Собирательное свойство проецирующей плоскости:
18 Собирательное свойство проецирующей плоскости: Геометрические фигуры, принадлежащие Проецирующей пл. проецируются на ┴ю плоскость проекций в прямую, совпадающую с проекцией самой плоскости.
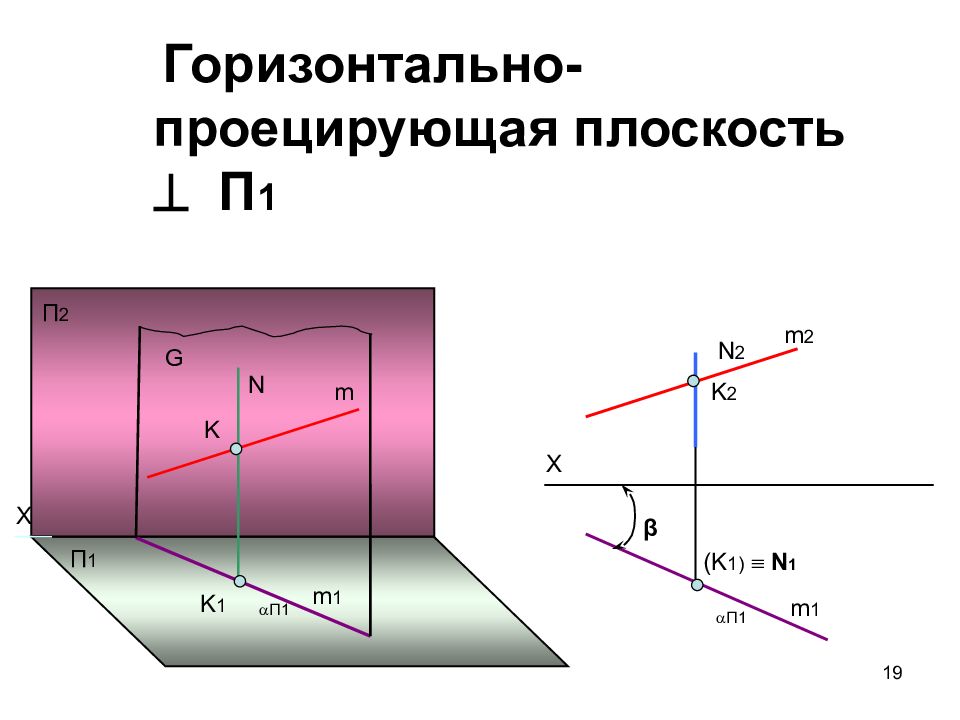
Слайд 19
19 Горизонтально-проецирующая плоскость П 1 Х П 1 П 2 N m K K 1 m 1 G Х N 2 ( K 1 ) N 1 K 2 m 2 m 1 β П1 П1
Слайд 20
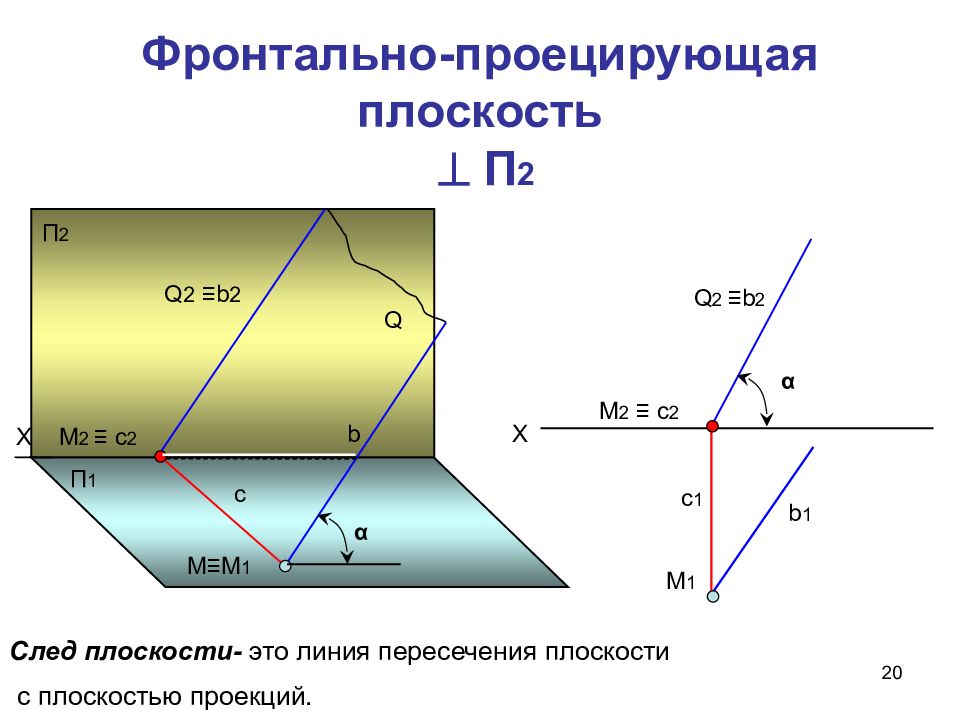
20 Х П 1 П 2 Q с b M ≡M 1 M 2 ≡ с 2 α Х Q 2 ≡b 2 M 1 c 1 b 1 M 2 ≡ с 2 α Q 2 ≡b 2 Фронтально-проецирующая плоскость П 2 След плоскости- это линия пересечения плоскости с плоскостью проекций.
Слайд 21: Профильно-проецирующая плоскость ( П 3 )
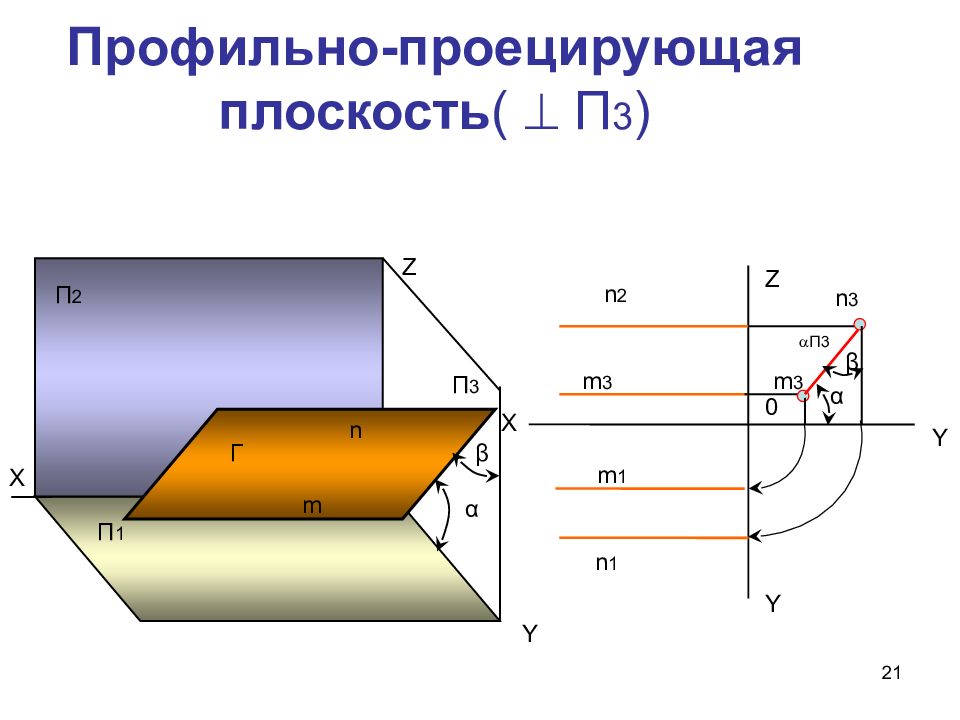
21 Профильно-проецирующая плоскость ( П 3 ) Х П 1 П 2 П 3 Y Z Г m n Х Z Y Y 0 n 2 n 3 n 1 m 3 m 3 m 1 α α β β П3
Слайд 22: б) Плоскости уровня (Дважды проецирующие ┴ к 2м пл.пр. )
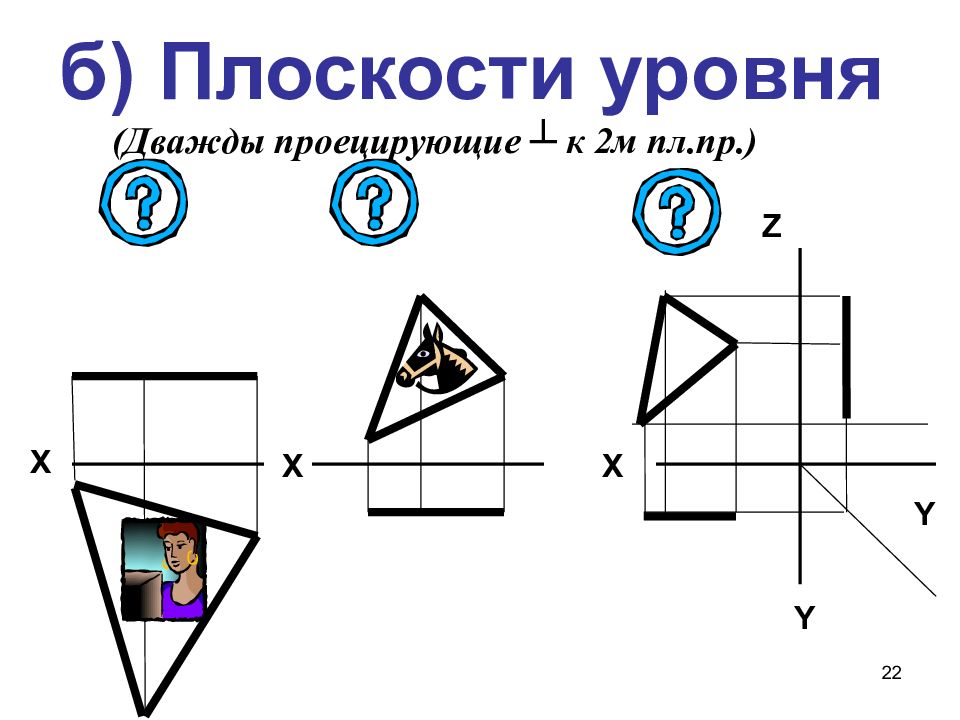
22 б) Плоскости уровня (Дважды проецирующие ┴ к 2м пл.пр. ) Х Х Х Y Y Z НВ
Слайд 23: б) Плоскости уровня (Дважды проецирующие ┴ к 2м пл.пр. )
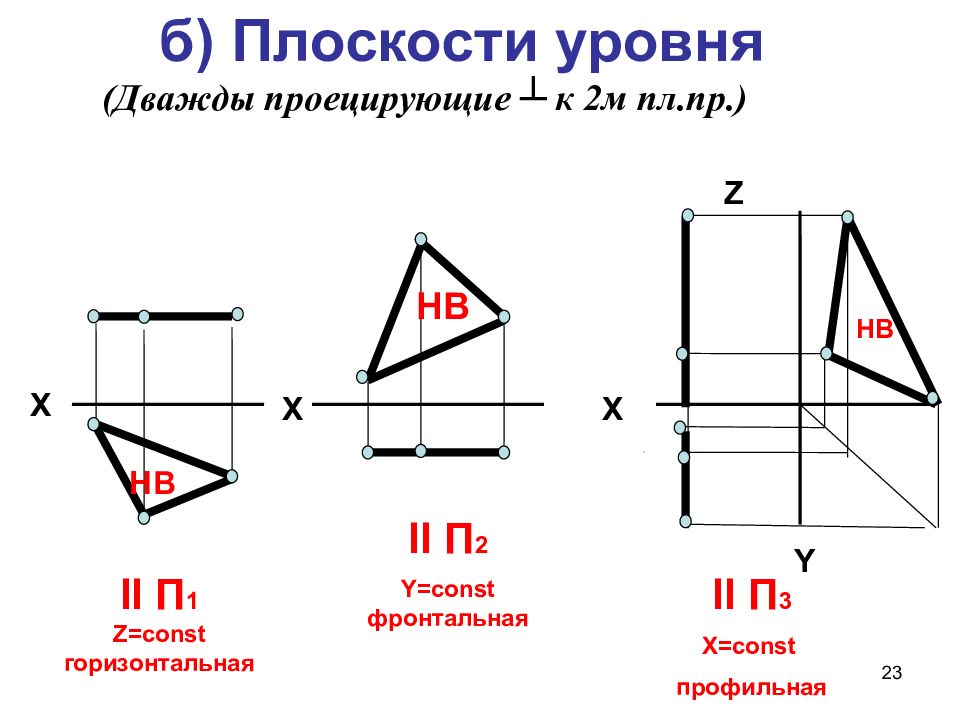
23 б) Плоскости уровня (Дважды проецирующие ┴ к 2м пл.пр. ) Х Х Х Y Z НВ НВ II П 1 Z =со nst горизонтальная II П 2 Y =со nst фронтальная II П 3 Х=со nst профильная НВ
Слайд 24: свойство плоскости уровня:
24 свойство плоскости уровня: Геометрические фигуры, принадлежащие, Пл. уровня проецируются на // пл. пр. без искажения в Н.В.
Слайд 25: Плоскости уровня
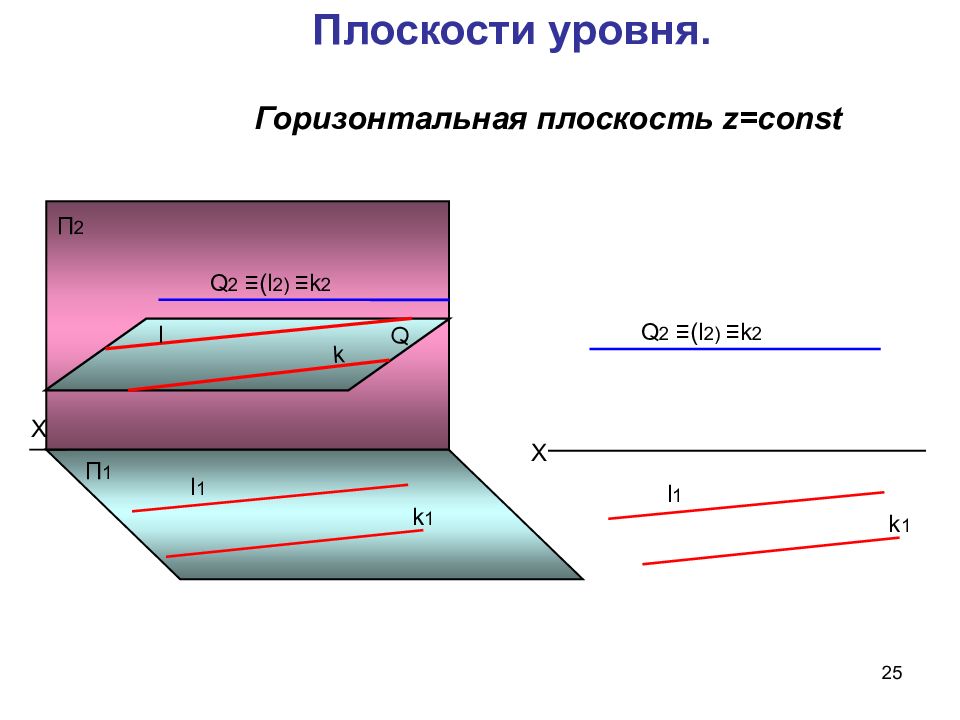
25 Плоскости уровня. Х П 1 П 2 Q 2 ≡ ( l 2 ) ≡k 2 l Q k l 1 k 1 Х Горизонтальная плоскость z=const Q 2 ≡ ( l 2 ) ≡k 2 l 1 k 1
Слайд 26: Фронтальная плоскость, ll П 2 у =const
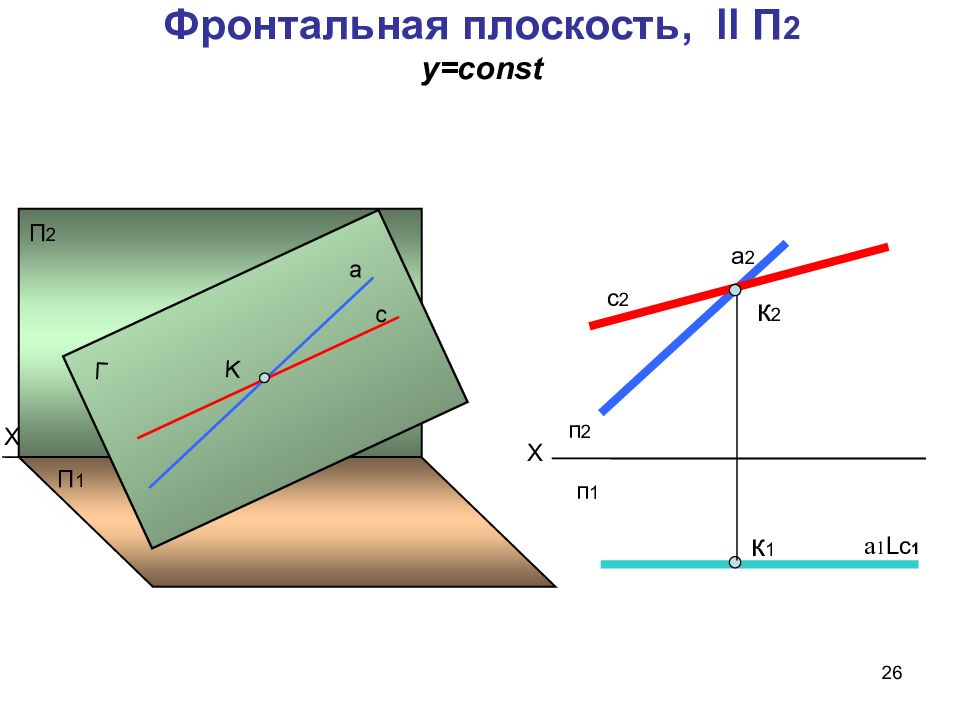
26 Фронтальная плоскость, ll П 2 у =const Х П 1 П 2 K а с Г Х к 1 а 1 L с 1 к 2 с 2 п 2 п 1 а 2
Слайд 27
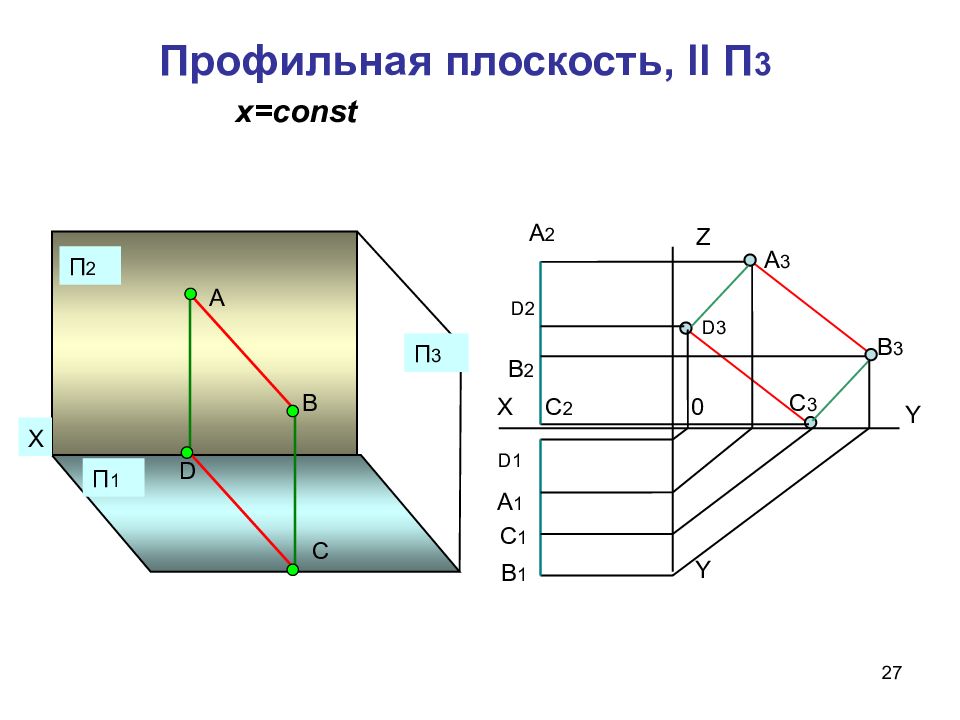
27 Профильная плоскость, ll П 3 х =const Х П 1 П 2 П 3 А В С D Z Y Х Y 0 А 3 В 3 С 3 D3 А 1 С 1 А 2 D2 В 2 С 2 D1 В 1
Слайд 28: 1.13 Прямая и точка в плоскости
28 1.13 Прямая и точка в плоскости Из планиметрии: Прямая принадлежит плоскости если: она проходит через две точки данной плоскости; если она проходит через точку, принадлежащую данной плоскости и // какой-либо прямой этой плоскости.
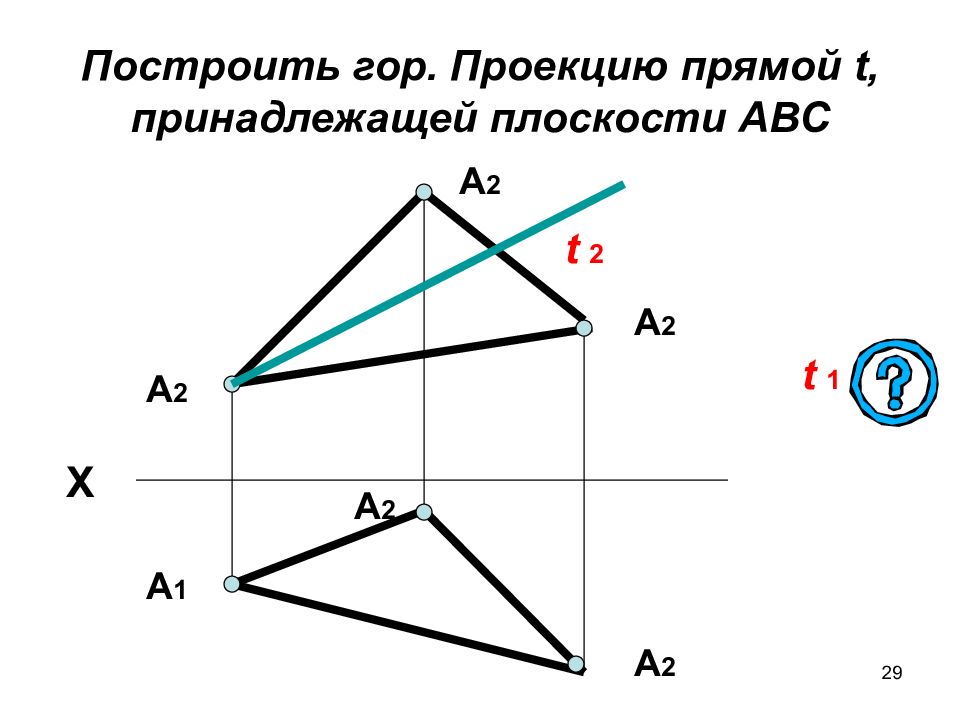
Слайд 29: Построить гор. Проекцию прямой t, принадлежащей плоскости АВС
29 Построить гор. Проекцию прямой t, принадлежащей плоскости АВС А 2 Х А 2 А 1 t 1 А 2 А 2 А 2 t 2
Слайд 30: Построить гор. Проекцию прямой t, принадлежащей плоскости АВС
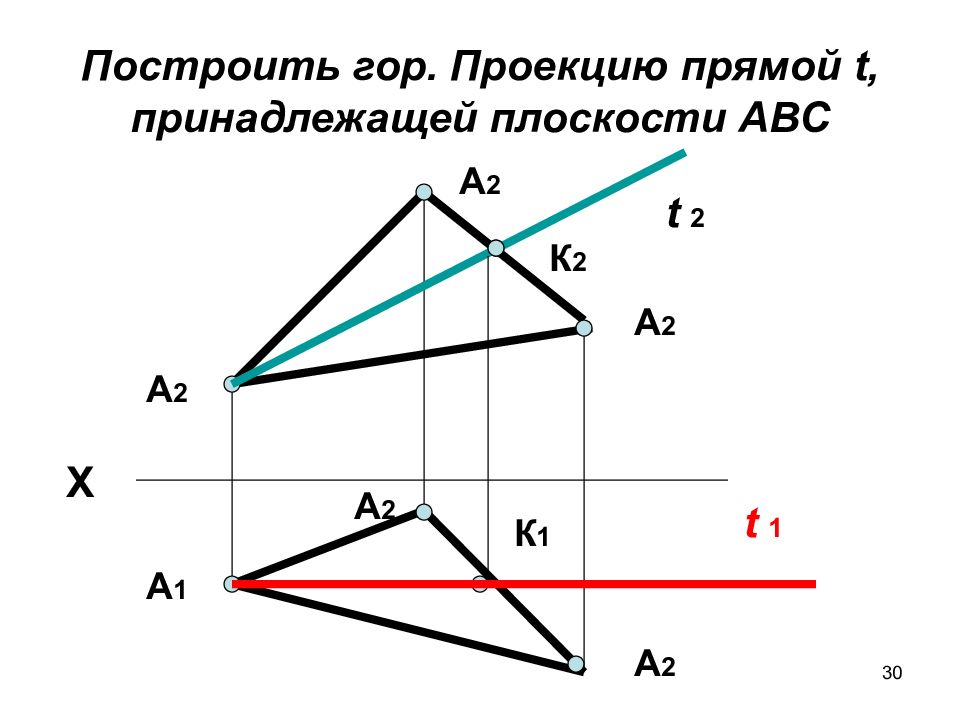
30 Построить гор. Проекцию прямой t, принадлежащей плоскости АВС А 2 Х А 2 А 1 А 2 А 2 А 2 К 2 t 2 t 1 К 1
Слайд 31: Построить гор. Проекцию прямой m, принадлежащей плоскости АВС
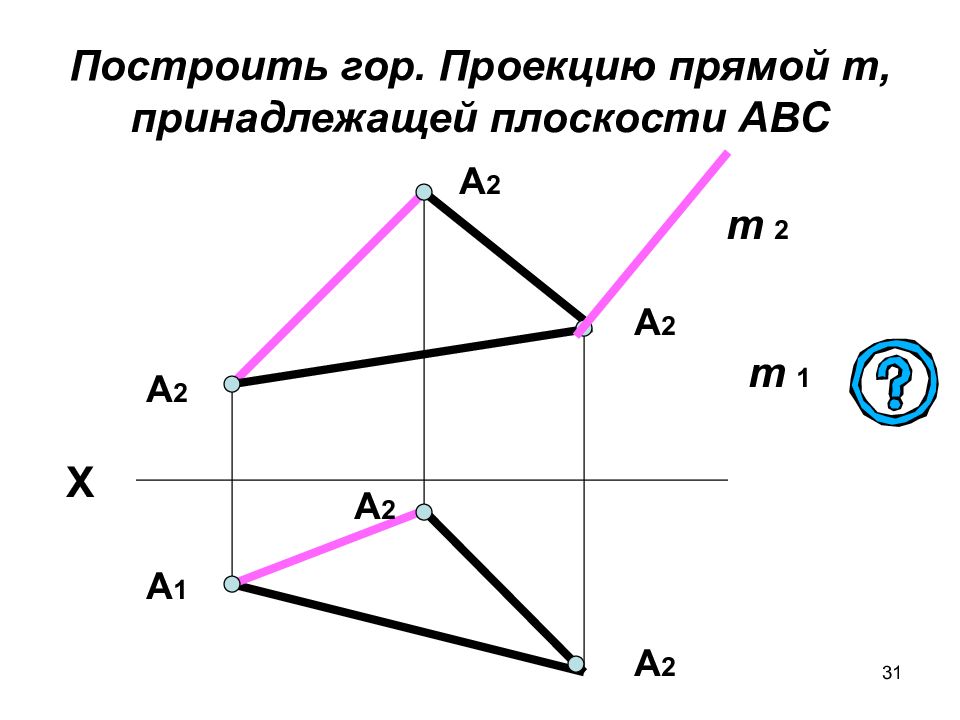
31 Построить гор. Проекцию прямой m, принадлежащей плоскости АВС А 2 Х А 2 А 1 m 1 А 2 А 2 А 2 m 2
Слайд 32: Построить гор. Проекцию прямой m, принадлежащей плоскости АВС
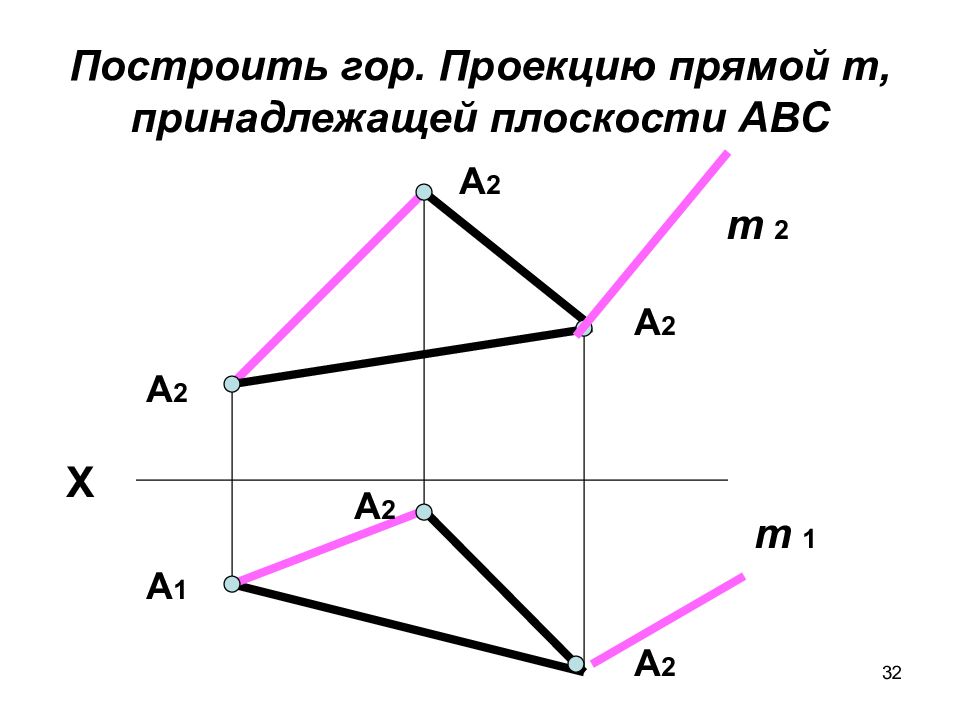
32 Построить гор. Проекцию прямой m, принадлежащей плоскости АВС А 2 Х А 2 А 1 А 2 А 2 А 2 m 2 m 1
Слайд 33: Из планиметрии:
33 Из планиметрии: Точка принадлежит пл., если она находится на прямой, принадлежащей этой плоскости.
Слайд 34: Построить гор. Проекцию точки К принадлежащей плоскости
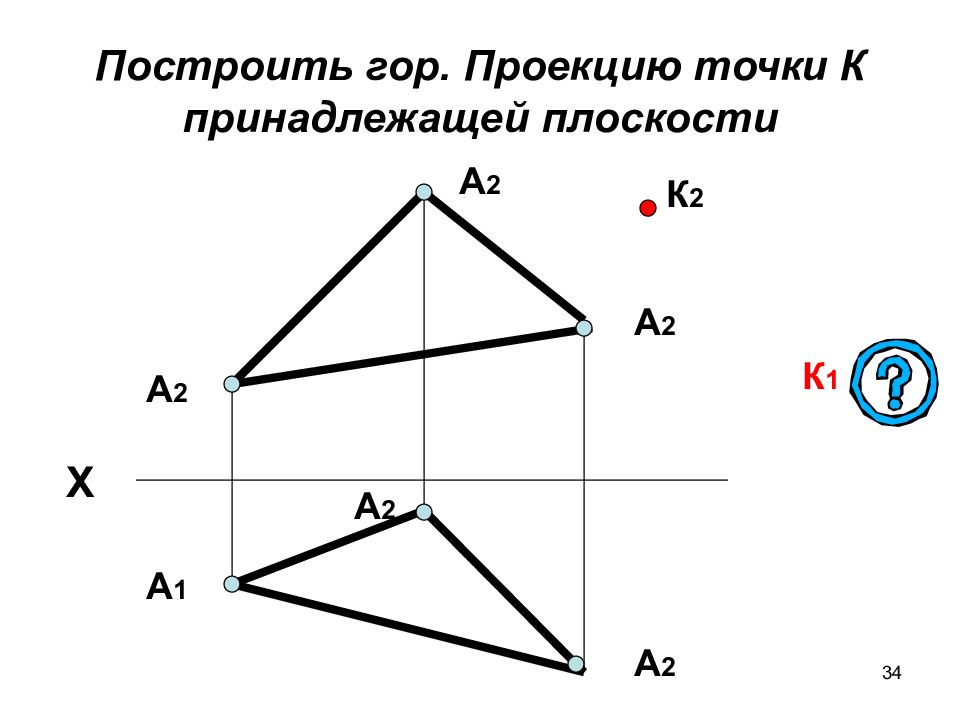
34 Построить гор. Проекцию точки К принадлежащей плоскости А 2 Х А 2 А 1 К 1 А 2 А 2 А 2 К 2
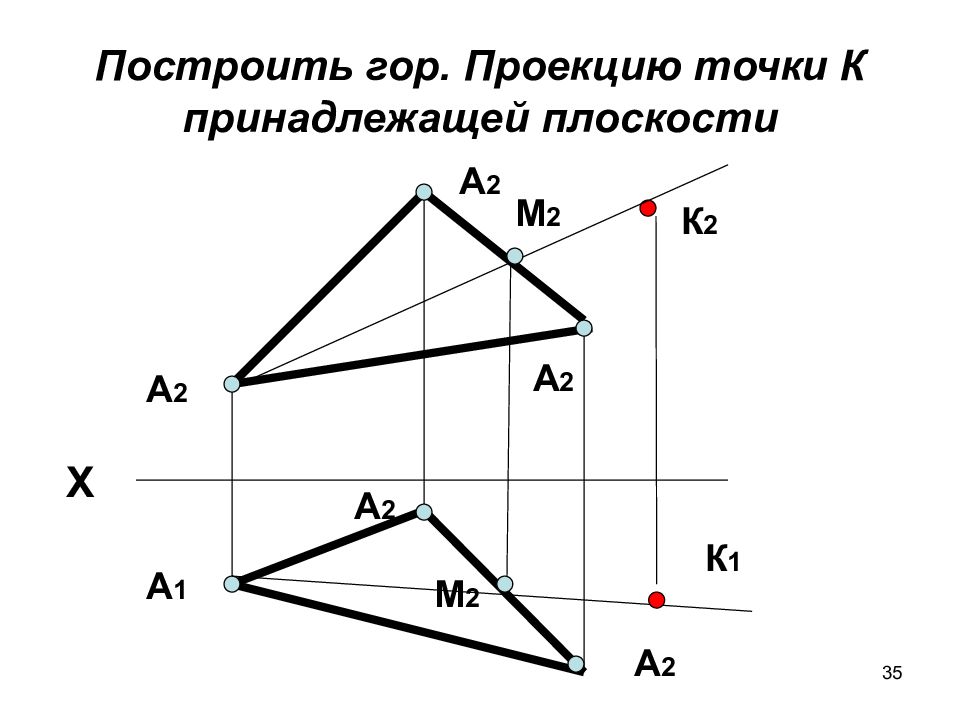
Слайд 35: Построить гор. Проекцию точки К принадлежащей плоскости
35 Построить гор. Проекцию точки К принадлежащей плоскости А 2 Х А 2 А 1 А 2 А 2 А 2 К 2 М 2 М 2 К 1
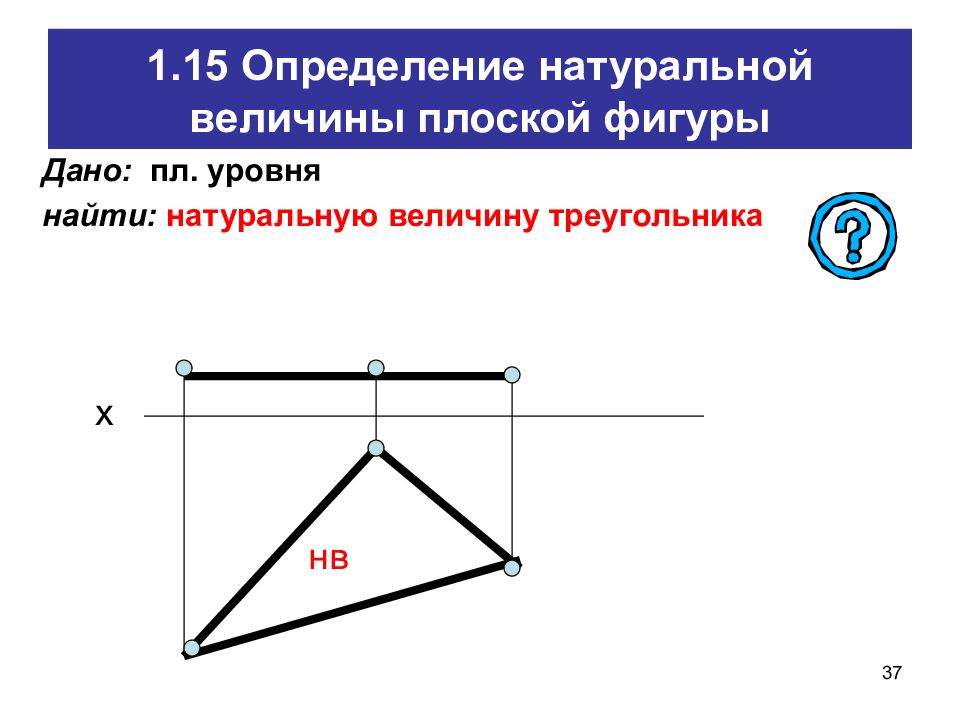
Слайд 37: 1.15 Определение натуральной величины плоской фигуры
37 1.15 Определение натуральной величины плоской фигуры Дано: пл. уровня найти: натуральную величину треугольника нв х
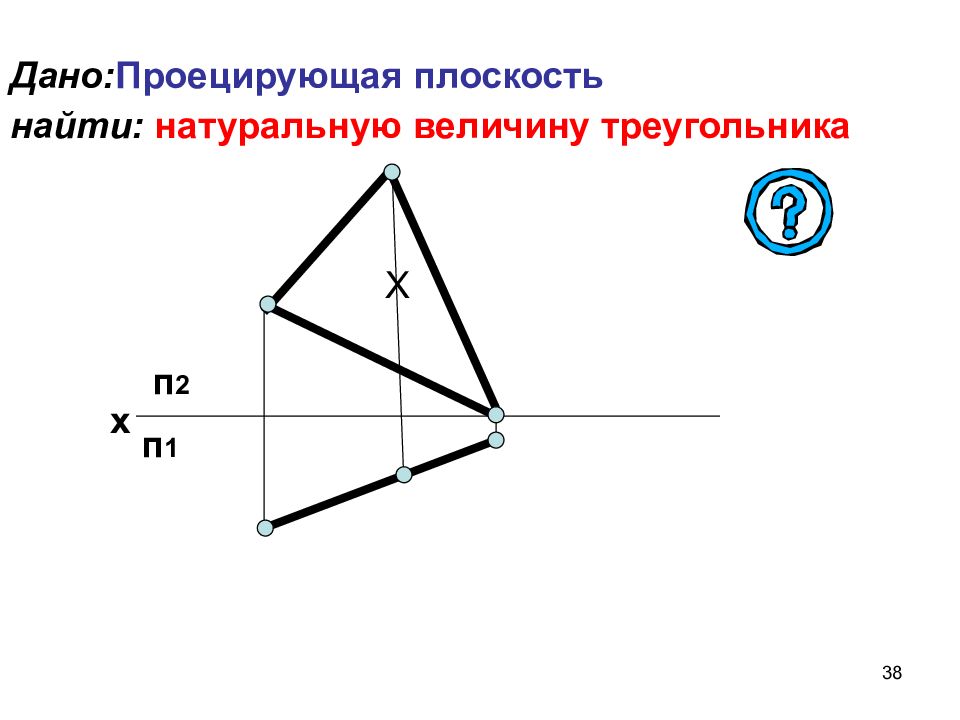
Слайд 38: Дано: Проецирующая плоскость найти: натуральную величину треугольника
38 Дано: Проецирующая плоскость найти: натуральную величину треугольника Х х п 2 п 1
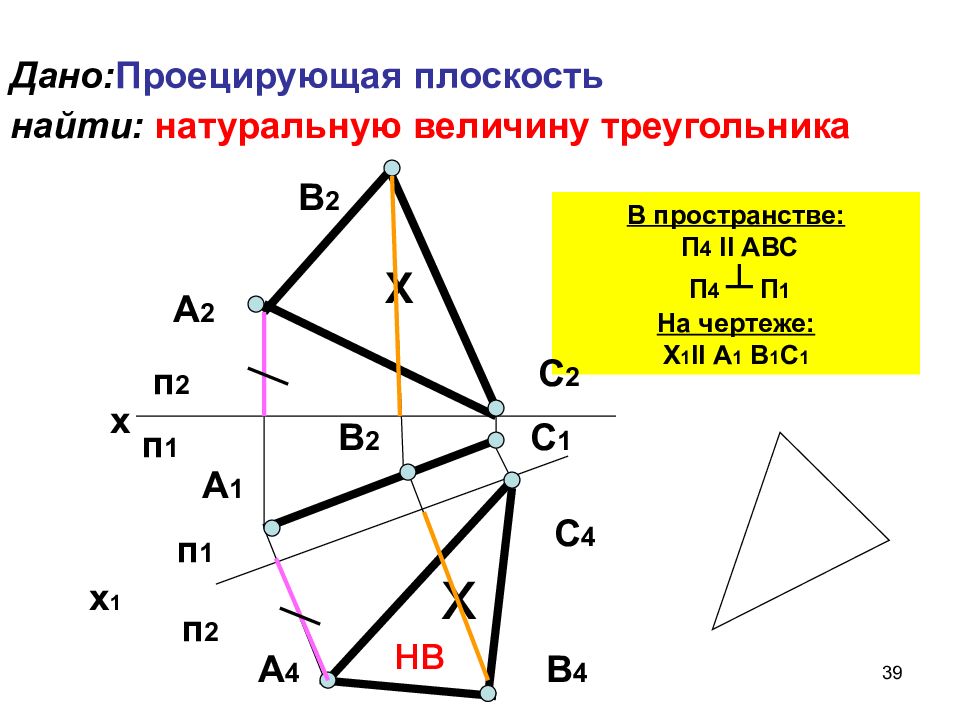
Слайд 39: Дано: Проецирующая плоскость найти: натуральную величину треугольника
39 Дано: Проецирующая плоскость найти: натуральную величину треугольника Х х х п 2 п 1 х 1 п 1 п 2 нв В пространстве: П 4 II АВС П 4 ┴ П 1 На чертеже: Х 1 II А 1 В 1 С 1 А 2 А 1 В 2 В 2 В 4 А 4 С 2 С 1 С 4
Слайд 40: 1.16 Взаимное расположение геометрических образов
40 1.16 Взаимное расположение геометрических образов а) Построение взаимно параллельных прямой и плоскости. Прямая II плоскости, если она II какой-либо прямой в этой плоскости б) Построение взаимно параллельных плоскостей Плоскости II, если 2 пересекающиеся прямые одной плоскости II двум пересекающимся прямым другой плоскости
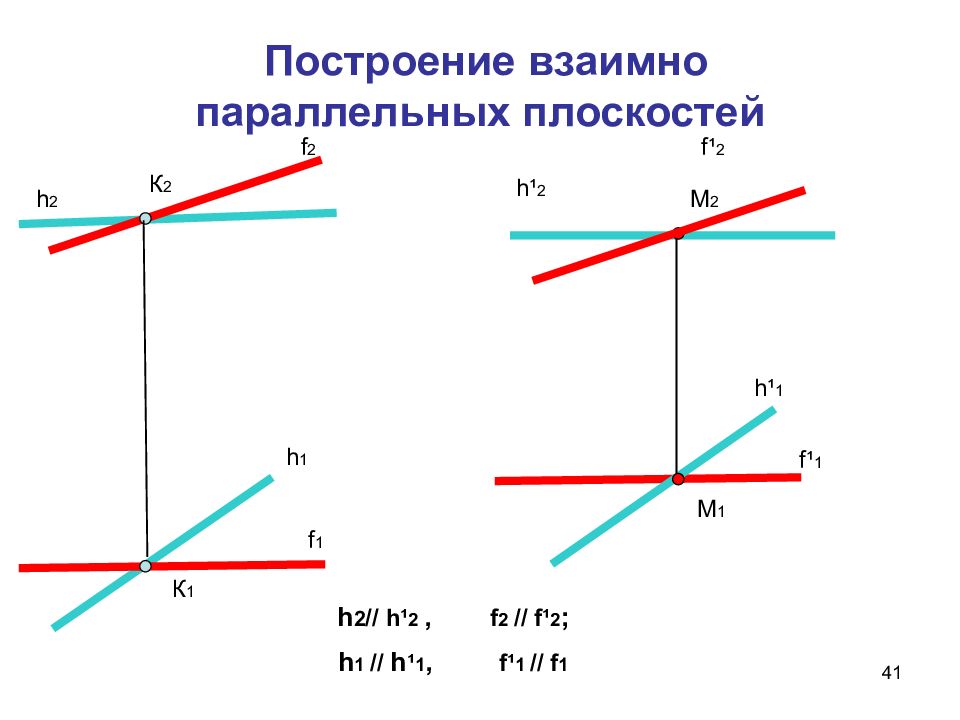
Слайд 41: Построение взаимно параллельных плоскостей
41 Построение взаимно параллельных плоскостей К 2 К 1 h 2 h 1 f 2 f 1 M 2 M 1 h¹ 2 h¹ 1 f ¹ 1 f ¹ 2 h 2 // h ¹ 2, f 2 // f¹ 2 ; h 1 // h ¹ 1, f¹ 1 // f 1
Слайд 43: Дано: плоскость общего положения найти: натуральную величину треугольника
43 Дано: плоскость общего положения найти: натуральную величину треугольника
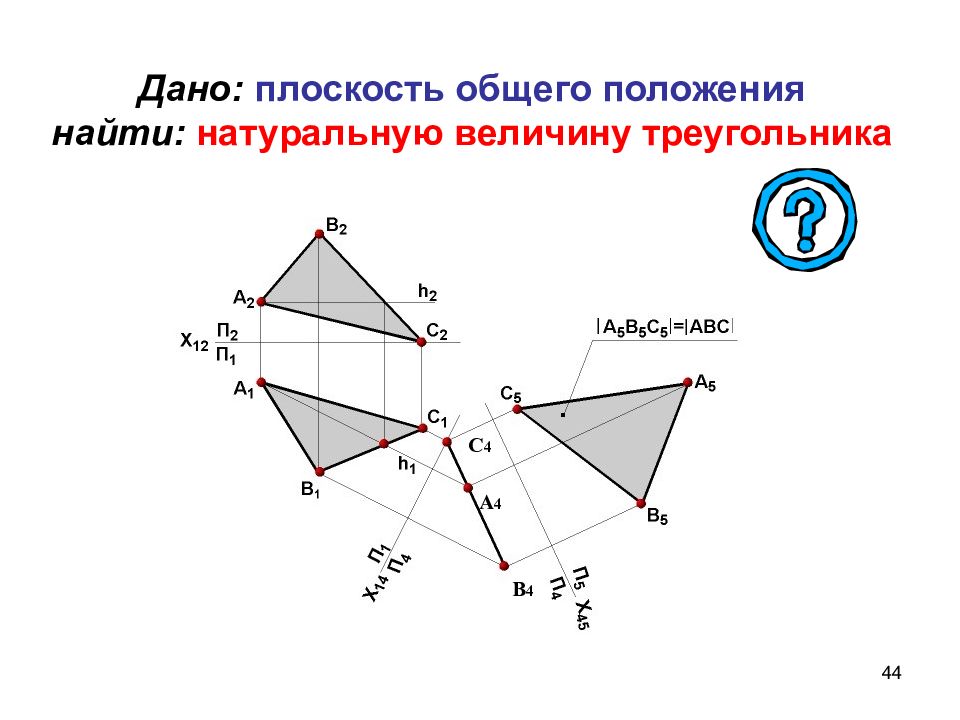
Слайд 44: Дано: плоскость общего положения найти: натуральную величину треугольника
44 Дано: плоскость общего положения найти: натуральную величину треугольника С 4 А 4 В 4
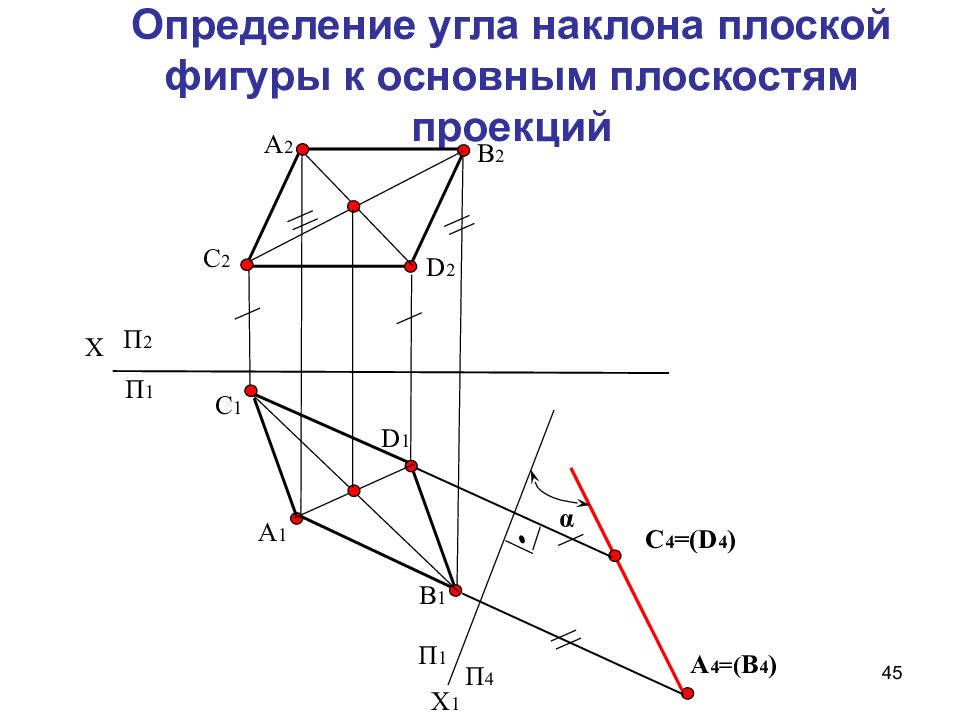
Слайд 45: Определение угла наклона плоской фигуры к основным плоскостям проекций
45 Определение угла наклона плоской фигуры к основным плоскостям проекций α Х П 2 П 1 А 2 В 2 С 2 D 2 С 1 D 1 В 1 А 1 С 4 =( D 4 ) А 4 =( В 4 ) Х 1 П 4 П 1
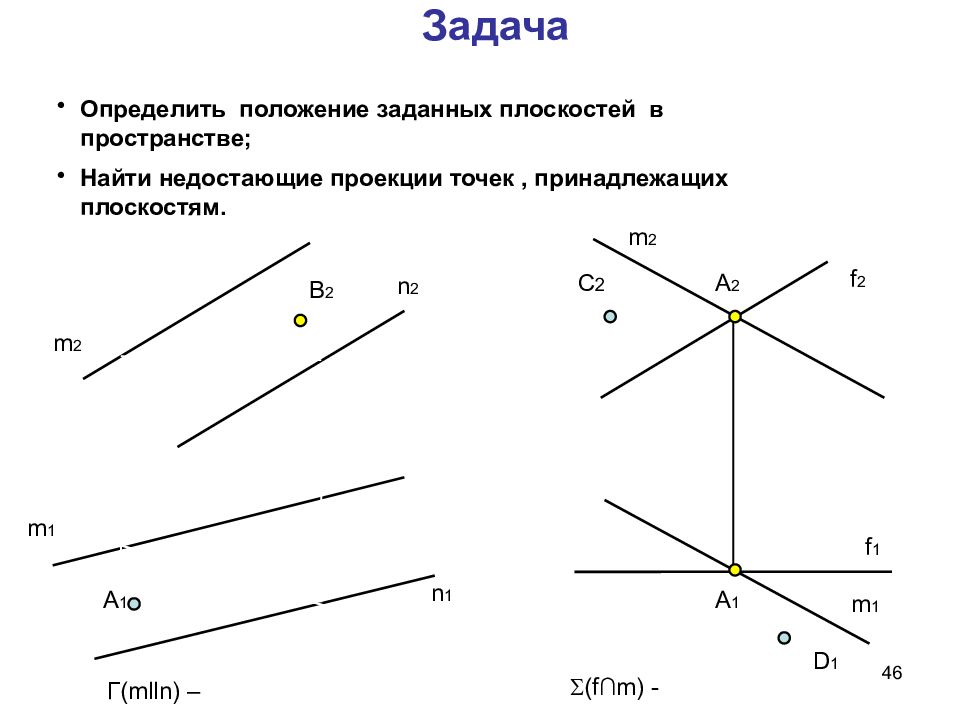
Последний слайд презентации: Курс лекций « Начертательная геометрия »: Задача
46 Задача Определить положение заданных плоскостей в пространстве; Найти недостающие проекции точек, принадлежащих плоскостям. m 2 n 2 m 1 n 1 A 1 B 2 m 2 f 2 A 2 A 1 m 1 f 1 C 2 D 1 Г( m lln) – (f ∩m) - 1 2 1 1 2 2 2 1