Первый слайд презентации: Лекция 7. Аксонометрические проекции
Аксонометрические изображения. Теорема Польке. Классификация аксонометрических проекций. Прямоугольные изометрия и диметрия. Последовательность построения модели. 1
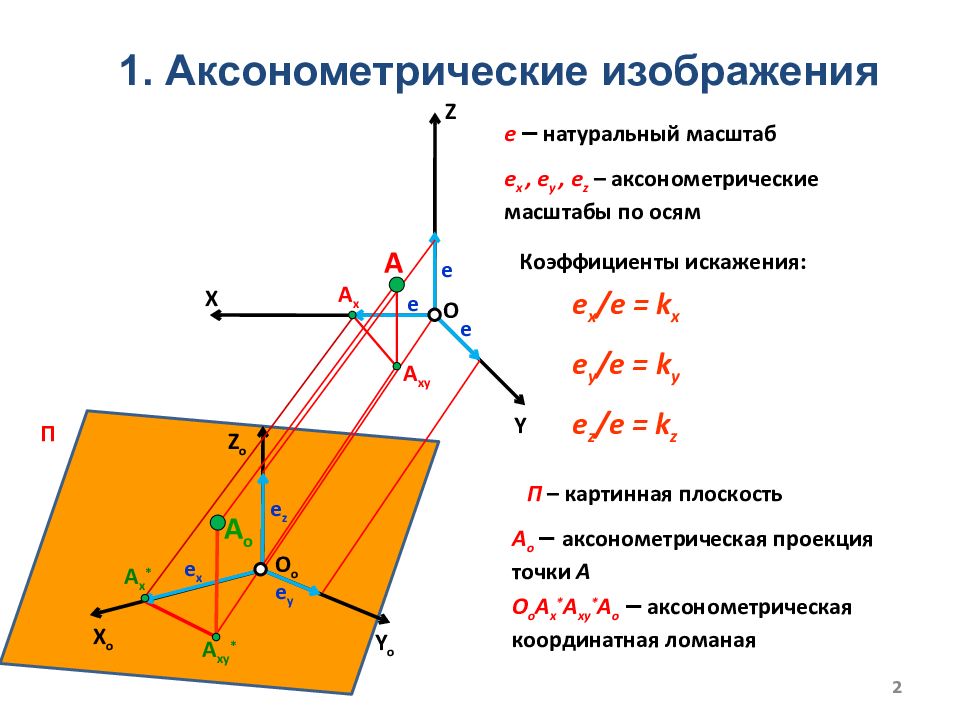
Слайд 2: 1. Аксонометрические изображения
е х /e = k x е y /e = k y е z / е = k z Коэффициенты искажения: е – натуральный масштаб е х, е y, е z – аксонометрические масштабы по осям O о A х * A xy * A о – аксонометрическая координатная ломаная A о – аксонометрическая проекция точки А 2 Z Y X о Z о X Y о e e e A А xy O о e x e z e y А x А x * A xy * A о П O П – картинная плоскость
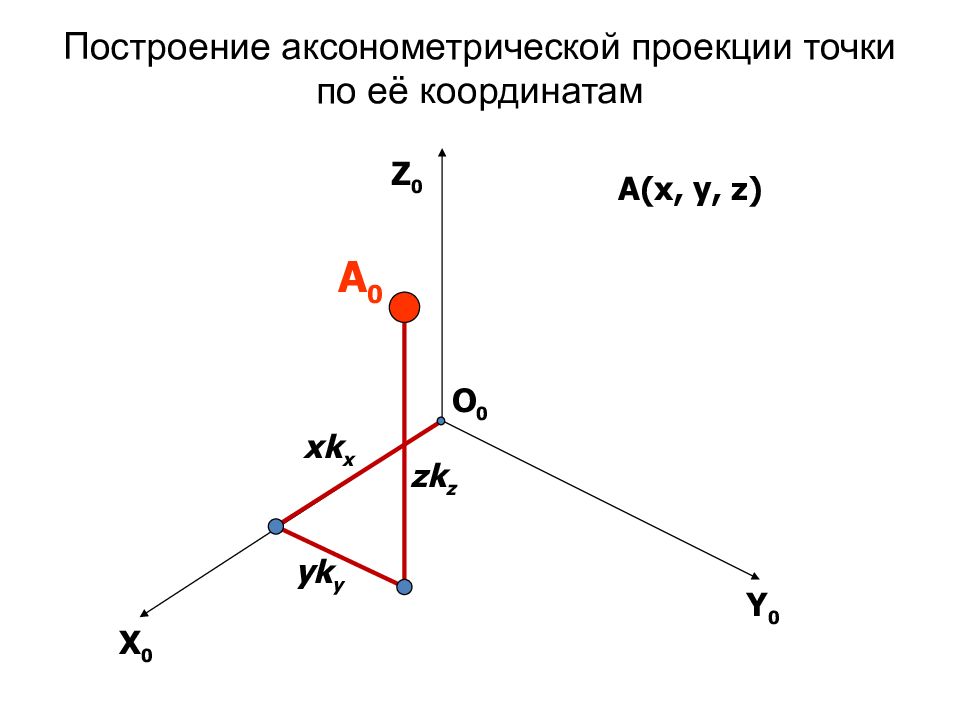
xk x yk y zk z X 0 Y 0 Z 0 А 0 О 0 А( x, y, z )
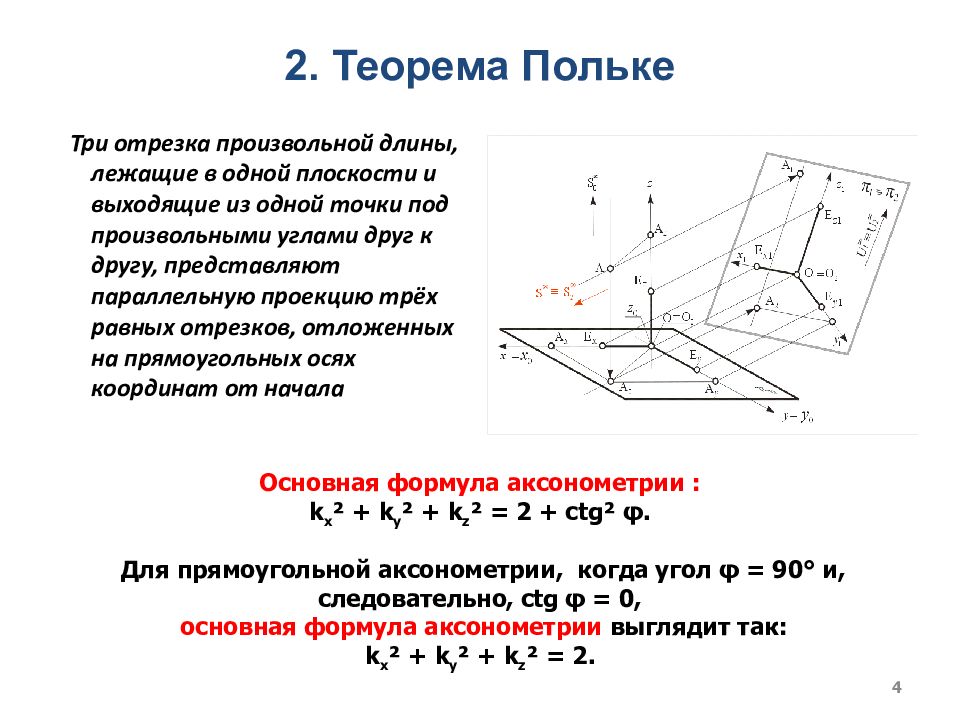
Слайд 4: 2. Теорема Польке
Три отрезка произвольной длины, лежащие в одной плоскости и выходящие из одной точки под произвольными углами друг к другу, представляют параллельную проекцию трёх равных отрезков, отложенных на прямоугольных осях координат от начала Основная формула аксонометрии : k x ² + k y ² + k z ² = 2 + ctg² φ. 4 Для прямоугольной аксонометрии, когда угол φ = 90° и, следовательно, ctg φ = 0, основная формула аксонометрии выглядит так: k x ² + k y ² + k z ² = 2.
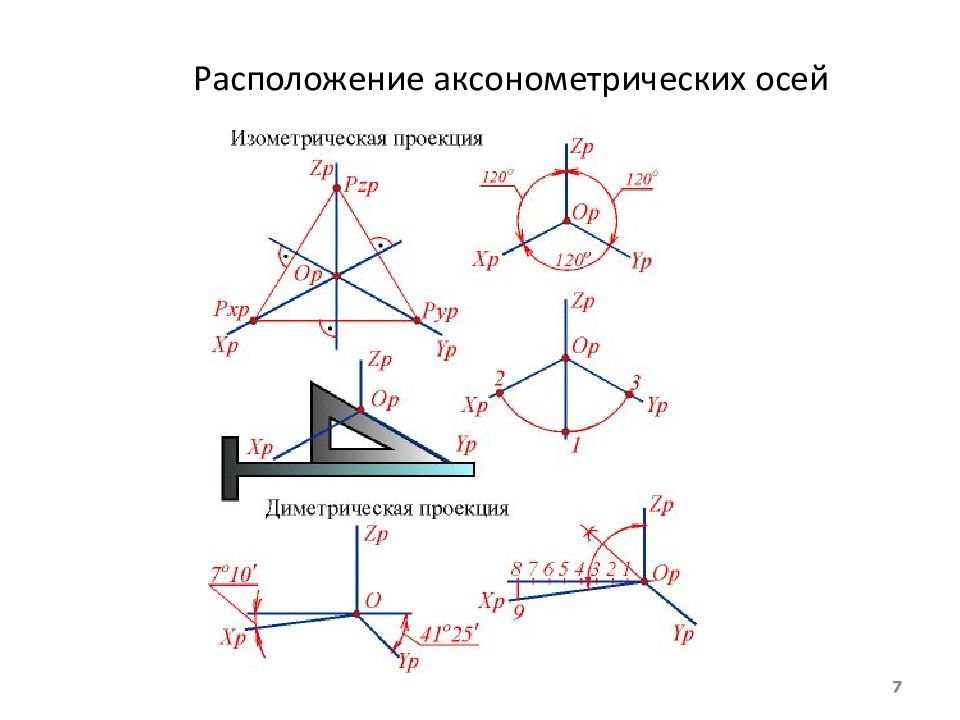
1. По направлению проецирующих лучей косоугольные (при произвольном направлении проецирующих лучей) прямоугольные (при направлении проецирования, перпендикулярном к плоскости проекций) 2. По коэффициентам искажения изометрическая, когда коэффициенты искажения по всем трём осям одинаковы ( k x = k y = k z ) диметрическая, когда коэффициенты искажения одинаковы только по двум осям ( k x = k y k z или k x = k z k y, или k z = k y k x ) триметрическая, когда коэффициенты искажения по всем трём осям различны ( k x k y k z ) 5
Слайд 6: 4. Прямоугольные изометрия и диметрия
Коэффициенты искажения Изометрия k x = k y = k z Из основной формулы аксонометрии: k x = k y = k z ≈ 0,82. Считаем, что k x = k y = k z = 1 Диметрия k x = k z, k y = 0,5 k x Из основной формулы аксонометрии: k x = k z ≈ 0,94. k y ≈ 0,47. Считаем, что k x = k z = 1, k y = 0,5 6
Слайд 8
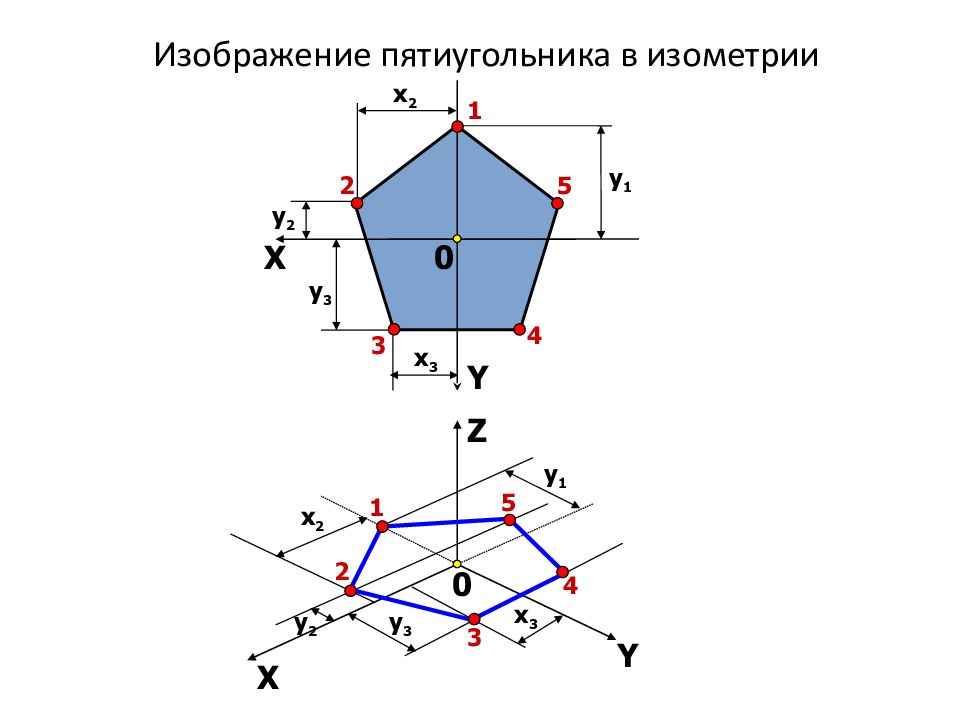
Х Y X Y Z 1 2 3 4 5 y 1 1 y 1 x 2 y 2 x 2 y 2 2 x 3 y 3 x 3 y 3 3 4 5 0 0 Изображение пятиугольника в изометрии
Слайд 9
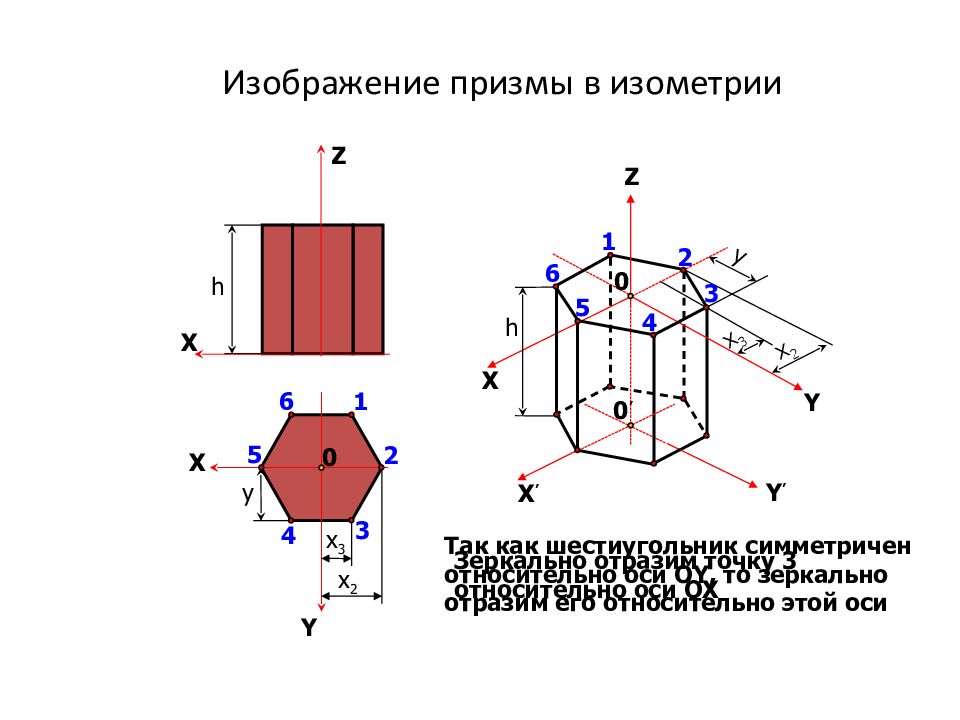
Z 0 X Y y x 3 x 2 Z X Y x 2 y h 0 Зеркально отразим точку 3 относительно оси OX 1 2 3 4 5 6 3 2 1 Так как шестиугольник симметричен относительно оси OY, то зеркально отразим его относительно этой оси x 3 h 4 5 6 X ’ Y ’ 0 ’ X Изображение призмы в изометрии
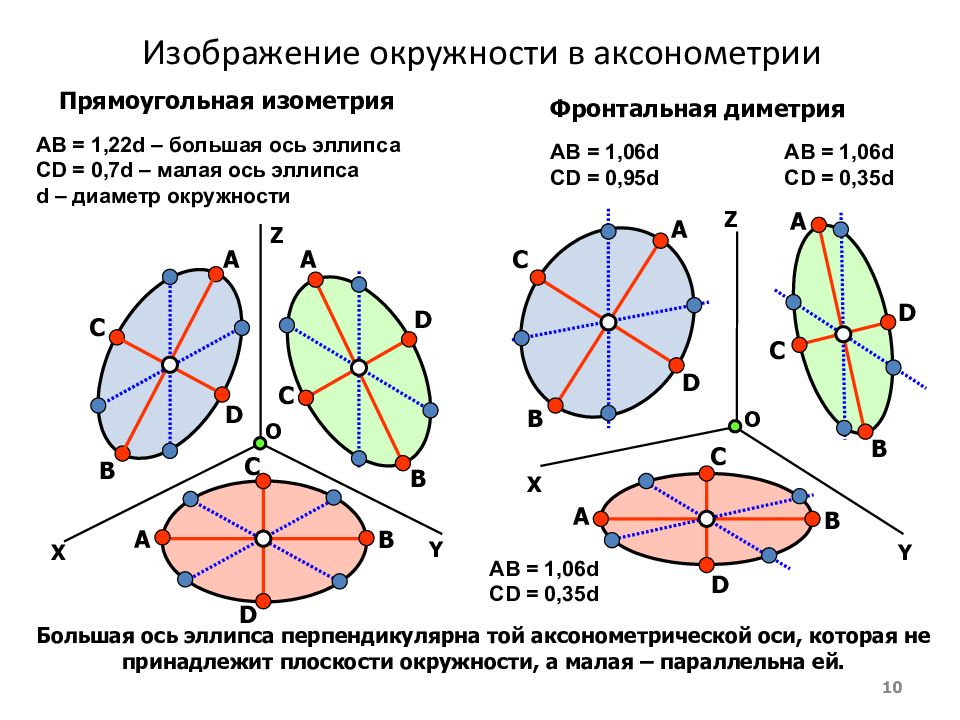
Слайд 10: Изображение окружности в аксонометрии
10 Прямоугольная изометрия А В С D Y Z X AB = 1,22d – большая ось эллипса CD = 0,7d – малая ось эллипса d – диаметр окружности О AB = 1, 06 d CD = 0, 95 d AB = 1, 06 d CD = 0, 35 d AB = 1, 06 d CD = 0, 35 d Фронтальная диметрия Большая ось эллипса перпендикулярна той аксонометрической оси, которая не принадлежит плоскости окружности, а малая – параллельна ей. А В С D А В С D А В С D А В С D А В С D Y Z X О
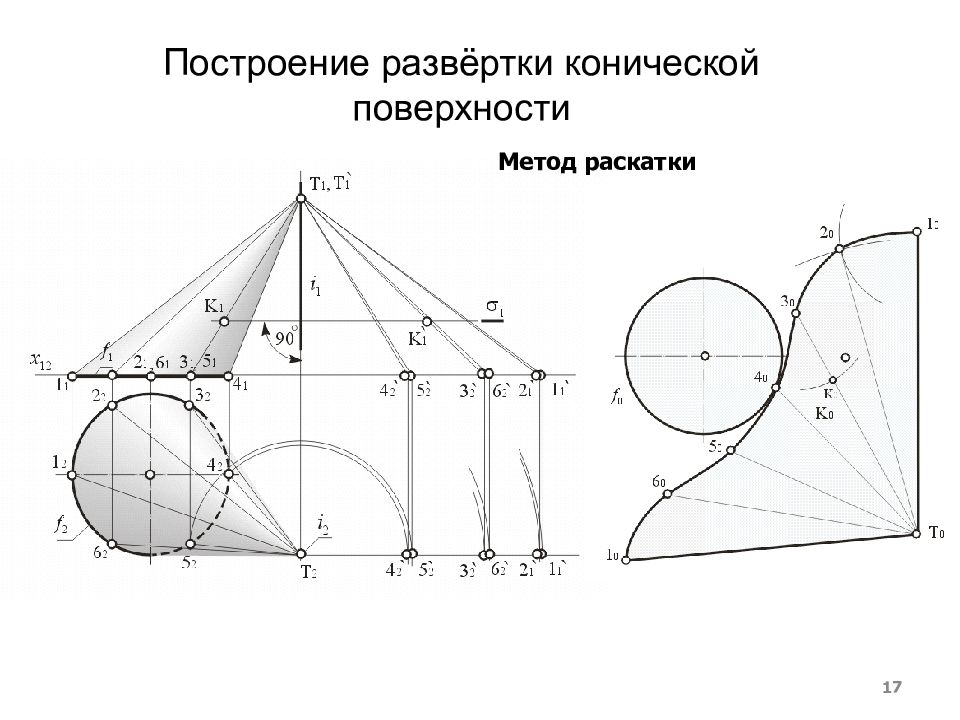
Слайд 14: Построение развёрток геометрических фигур
Преобразование поверхности геометрической фигуры, при котором поверхность совмещается с некоторой плоскостью 0 без складок и разрывов, называется построением развёртки заданной поверхности. Поверхности, допускающие такое преобразование, называются развертывающимися, а фигура, совмещённая с плоскостью 0, в которую преобразуется поверхность, называется развёрткой поверхности. 14
Слайд 15
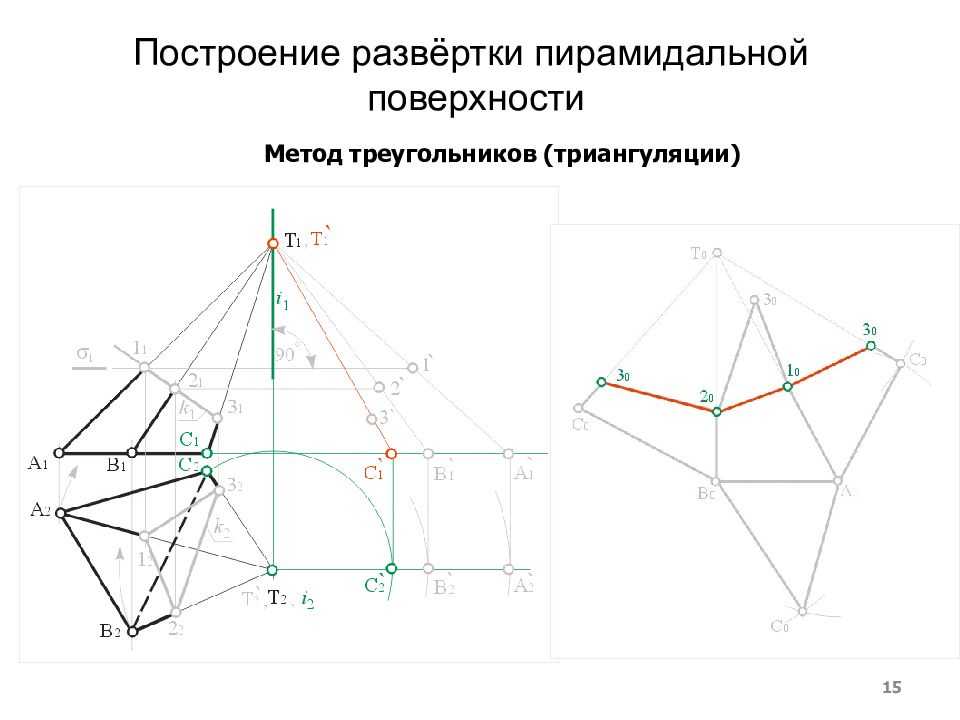
Построение развёртки пирамидальной поверхности 15 Метод треугольников (триангуляции)
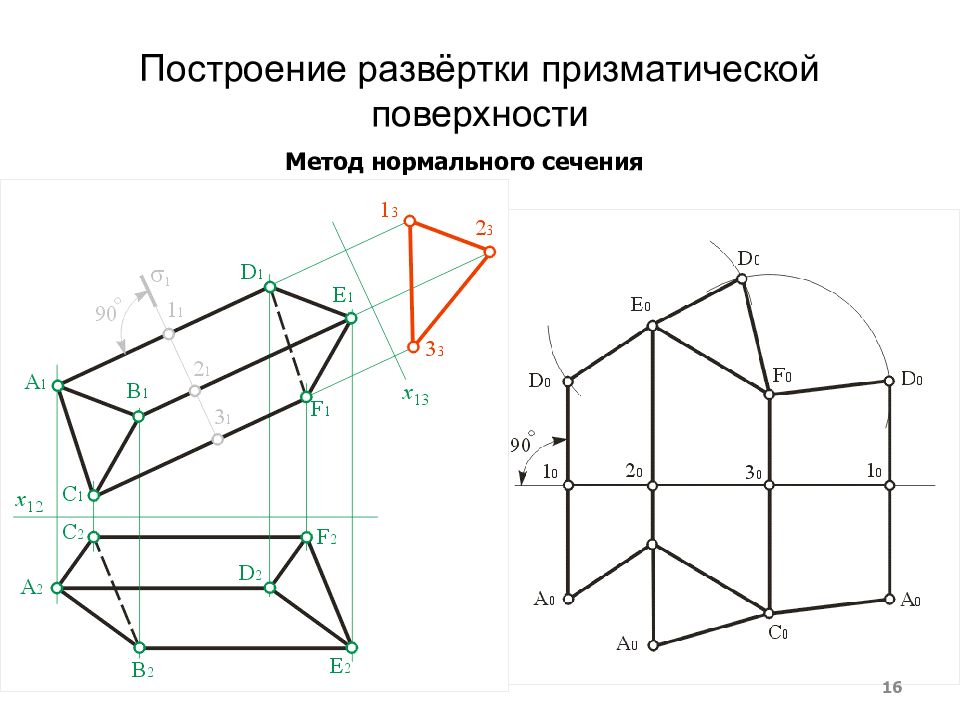
Слайд 16: Построение развёртки призматической поверхности
16 Метод нормального сечения