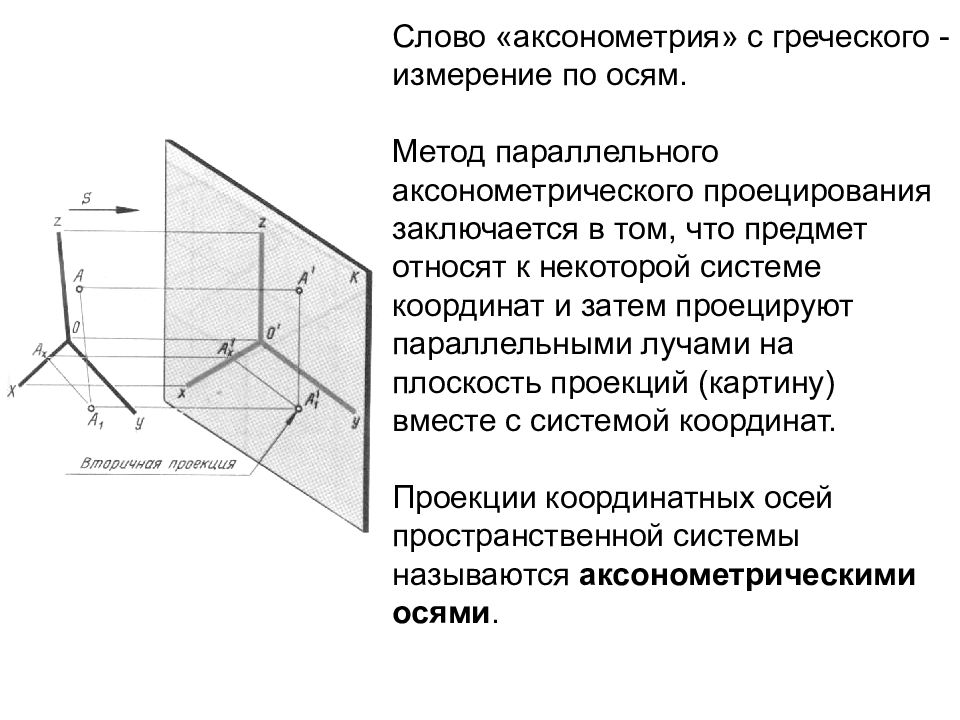
Первый слайд презентации: АКСОНОМЕТРИЧЕСКИЕ ПРОЕКЦИИ гОСТ 2.317 – 69
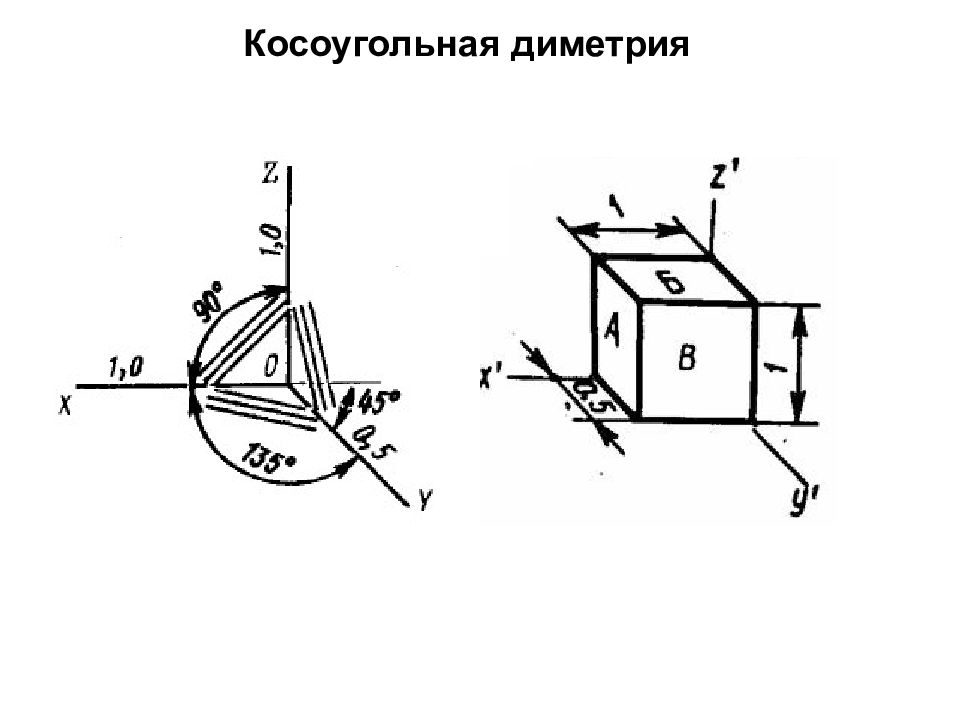
Слайд 5: В зависимости от угла наклона проецирующих лучей к картине различают: 1. Прямоугольные аксонометрические проекции 2. Косоугольные аксонометрические проекции
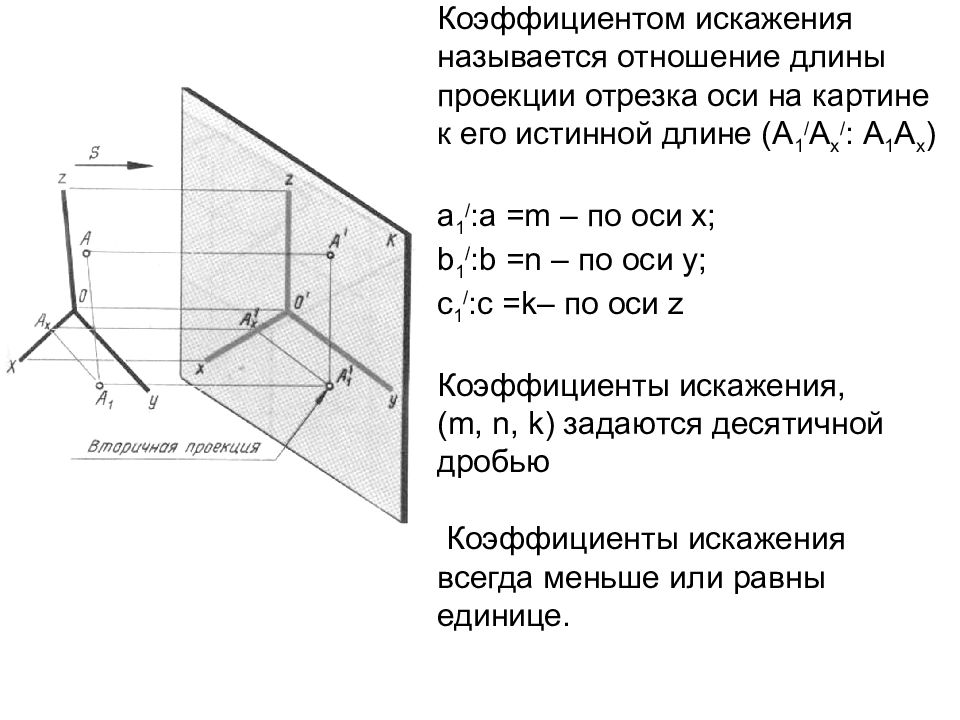
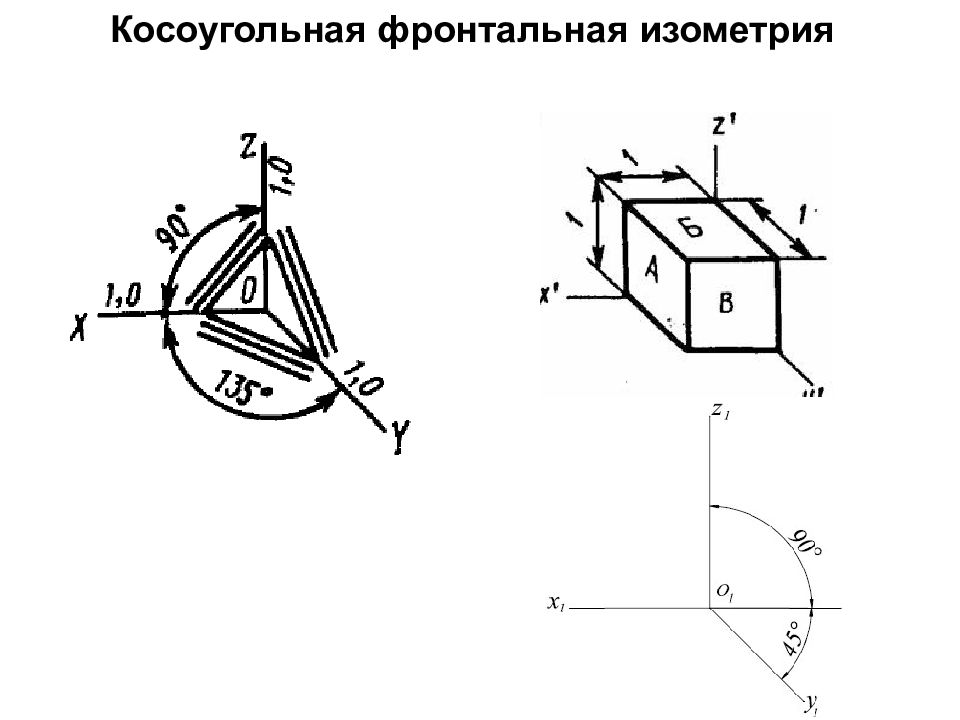
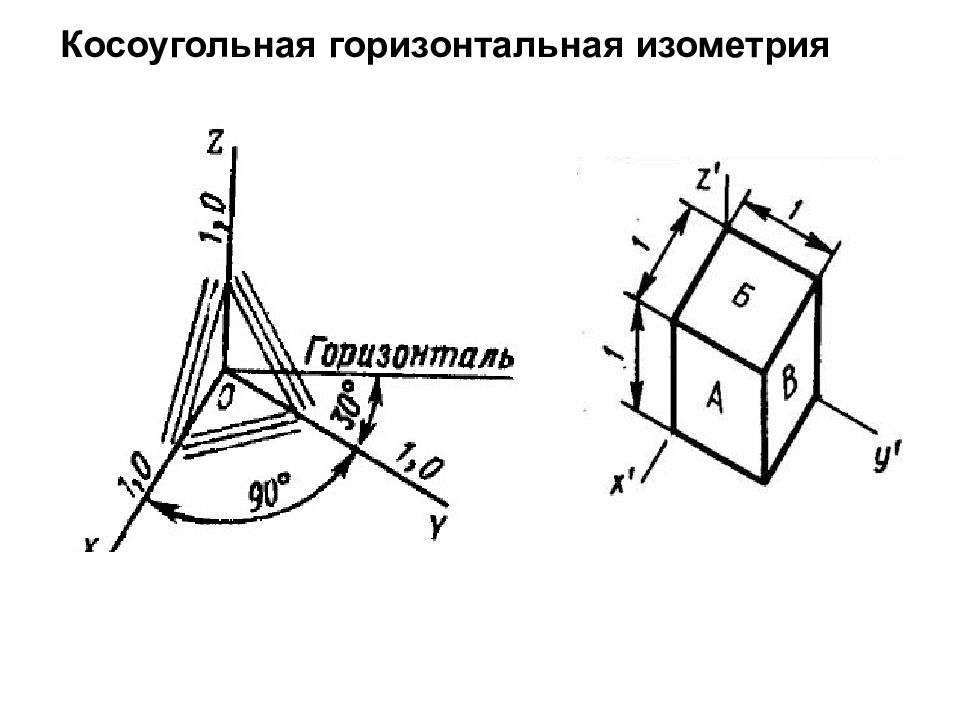
Слайд 6: В зависимости от коэффициентов искажения, аксонометрические проекции могут быть: 1. изометрическими, если коэффициенты искажения по всем трем осям равны между собой m = n = k ; 2. диметрическими, если коэффициенты искажения по двум осям равны между собой, а по третьей – отличается от первых двух m = k ≠ n ; 3. триметрическими, если все три коэффициента искажения по осям различны, m ≠ n ≠ k
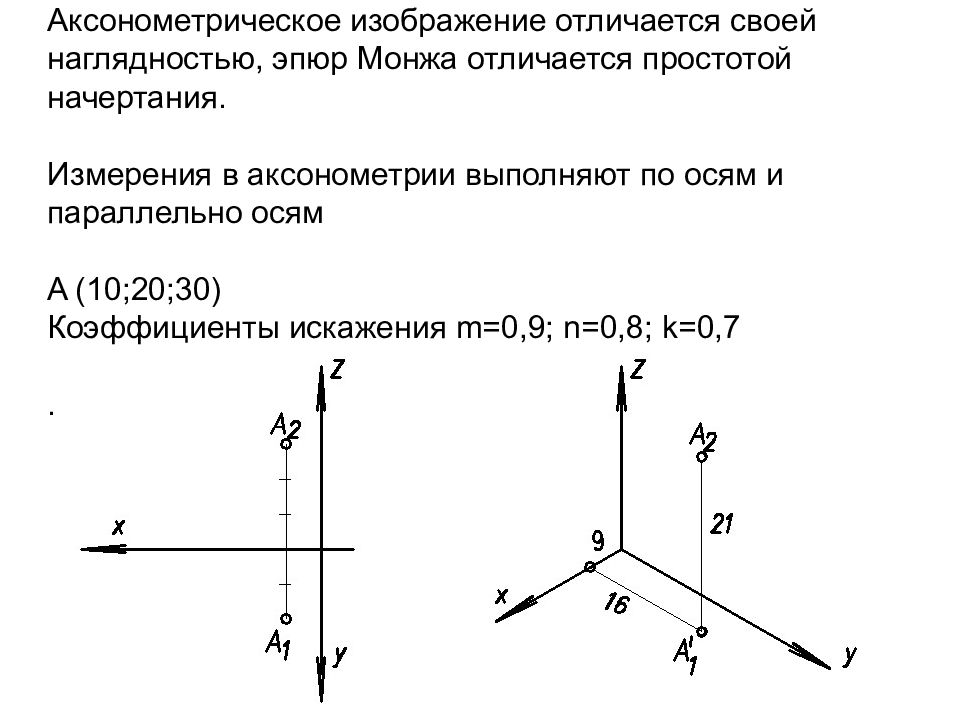
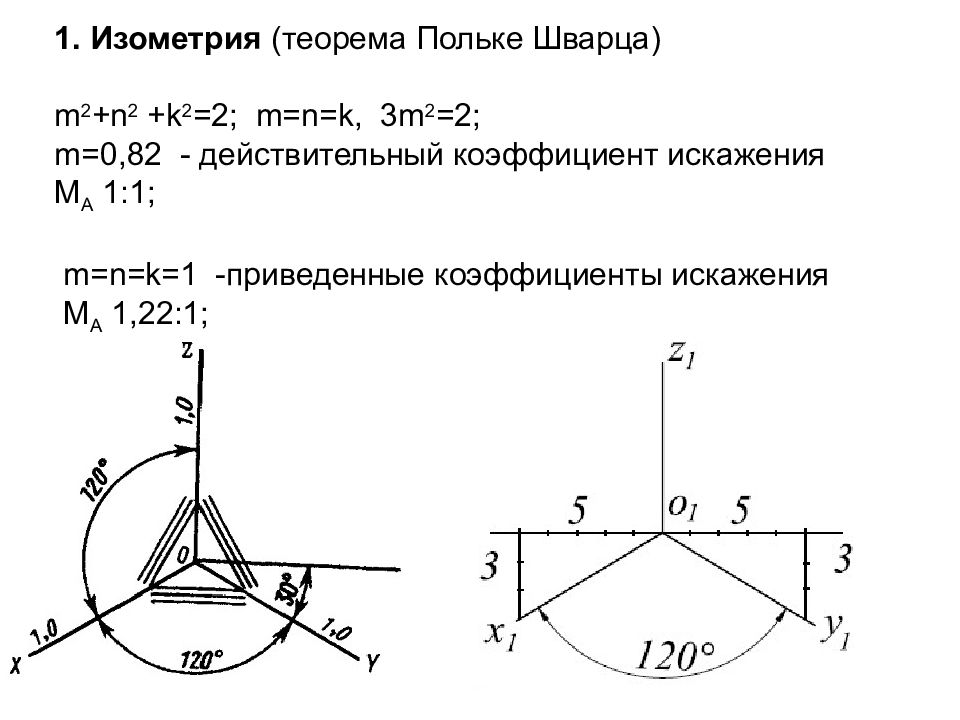
Слайд 7: 1. Изометрия (теорема Польке Шварца) m 2 +n 2 +k 2 =2 ; m = n = k, 3 m 2 =2 ; m=0,82 - действительный коэффициент искажения М А 1:1; m = n = k =1 -приведенные коэффициенты искажения М А 1,22:1;
Слайд 8
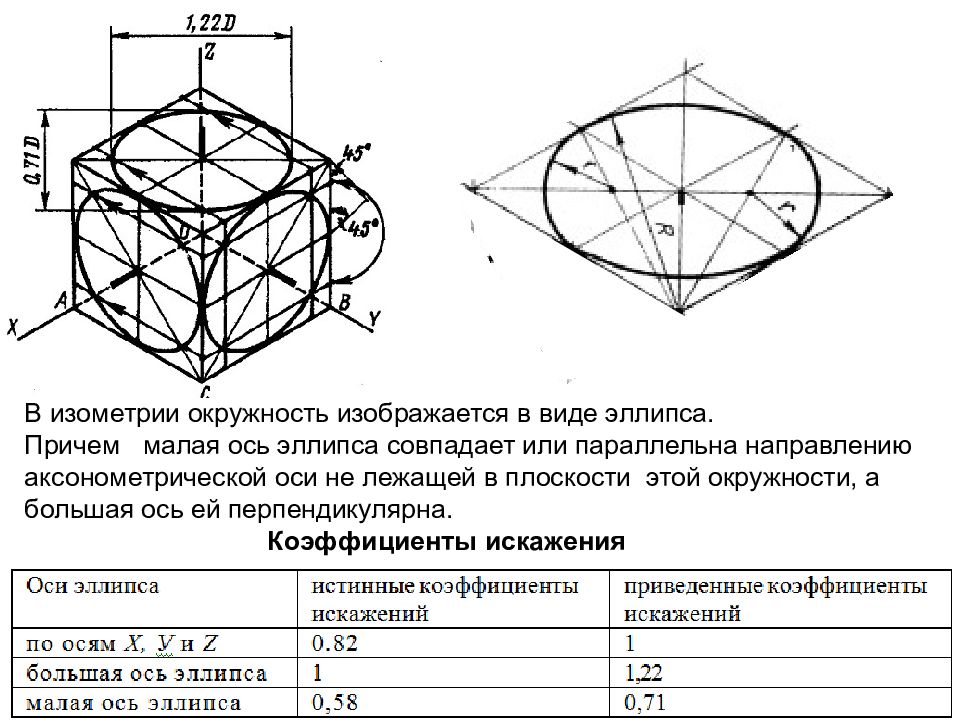
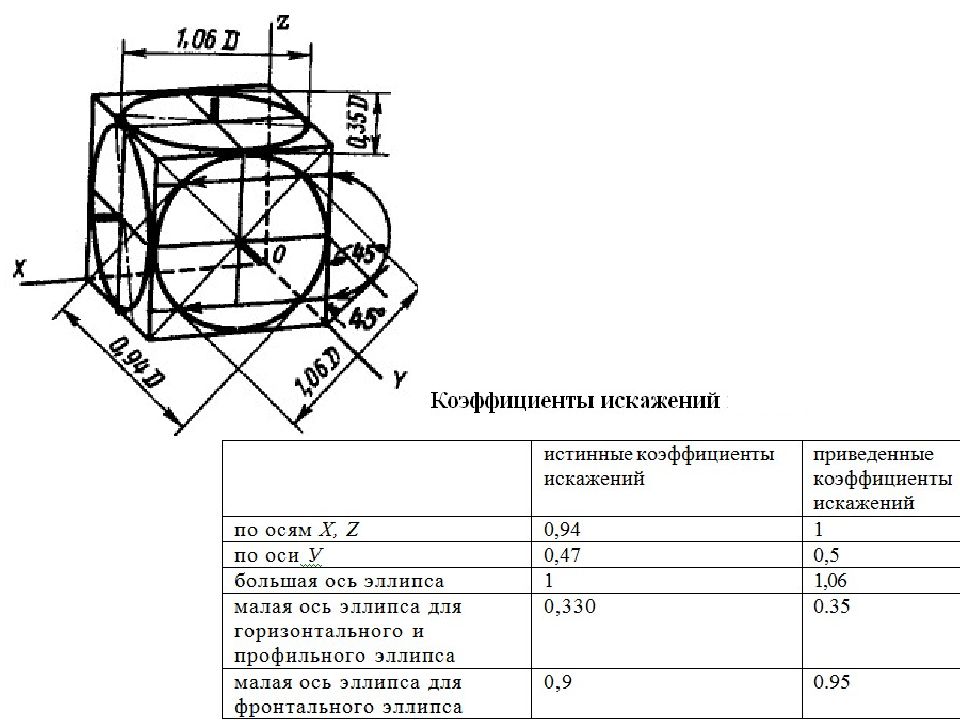
В изометрии окружность изображается в виде эллипса. Причем малая ось эллипса совпадает или параллельна направлению аксонометрической оси не лежащей в плоскости этой окружности, а большая ось ей перпендикулярна. Коэффициенты искажения
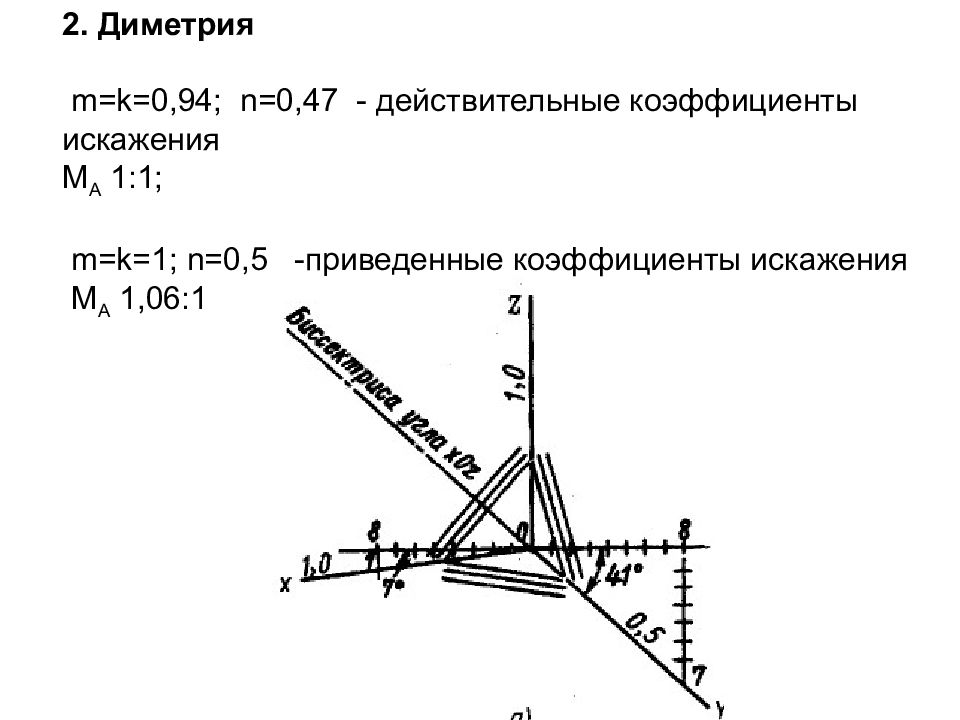
Слайд 10: 2. Диметрия m = k= 0,94; n =0,47 - действительные коэффициенты искажения М А 1:1; m = k =1; n =0,5 -приведенные коэффициенты искажения М А 1,06:1
Слайд 16: Прямая линия Прямая в пространстве бесконечна и непрерывна. Ограниченная часть прямой называется отрезком
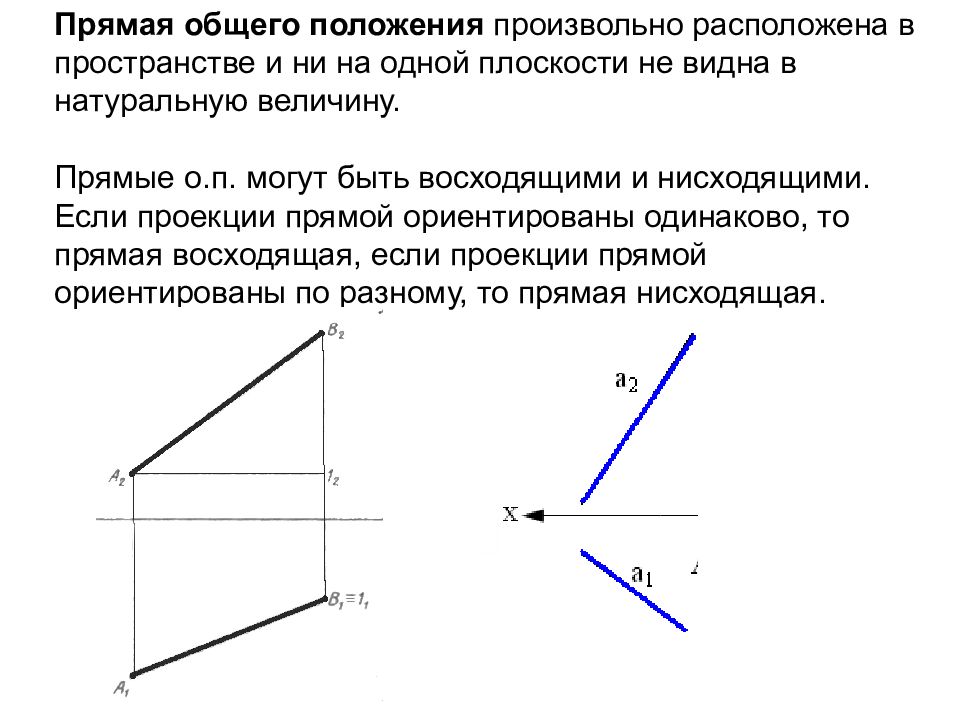
Слайд 17: Прямая общего положения произвольно расположена в пространстве и ни на одной плоскости не видна в натуральную величину. Прямые о.п. могут быть восходящими и нисходящими. Если проекции прямой ориентированы одинаково, то прямая восходящая, если проекции прямой ориентированы по разному, то прямая нисходящая
Слайд 18: Прямые частного положения это прямые, параллельные или перпендикулярные плоскости проекций 1.Прямые уровня 1.1 Горизонтальная прямая уровня 1.2 Фронтальная прямая уровня 1.3 Профильная прямая уровня 2. Проецирующие прямые (дважды прямые уровня) 2.1 Горизонтально проецирующаяся прямая 2.2 Фронтально проецирующаяся прямая 2.3 Профильно проецирующаяся прямая
Слайд 19: 1.1 Горизонтальная прямая уровня - h h // П 1, а к П 2 и П 3 расположена под углом. h [АВ] // П 1 h 2 [А 2 В 2 ] // ox h 1 [А 1 В 1 ] = н.в. h
Слайд 20: 1. 2 Фронтальная прямая уровня - f f // П 2, а к П 1 и П 3 расположена под углом. f [CD] // П 2 f 1 [C 1 D 1 ] // ox f 2 [C 2 D 2 ] = н.в. f
Слайд 21: 1.3 Профильная прямая уровня - р p // П 3, а к П 1 и П 2 расположена под углом. p [Е F] // П 3 p 2 [Е 2 F 2 ] // oz p 3 [Е 3 F 3 ] = н.в. p
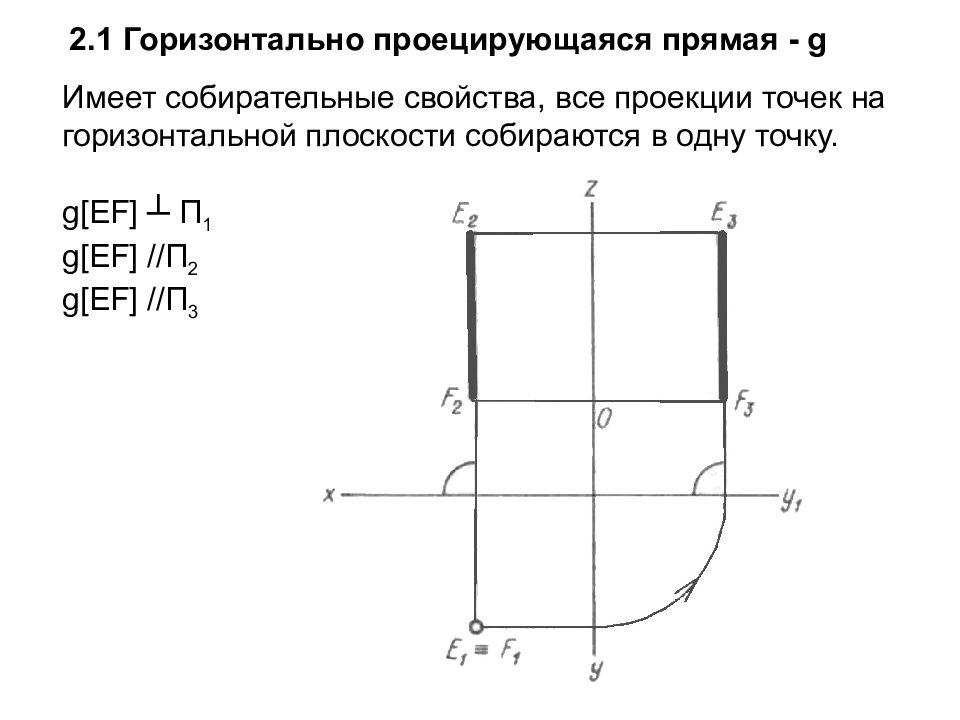
Слайд 22: 2.1 Горизонтально проецирующаяся прямая - g
Имеет c обирательные свойства, все проекции точек на горизонтальной плоскости собираются в одну точку. g [ EF ] ┴ П 1 g [ EF ] //П 2 g [ EF ] //П 3
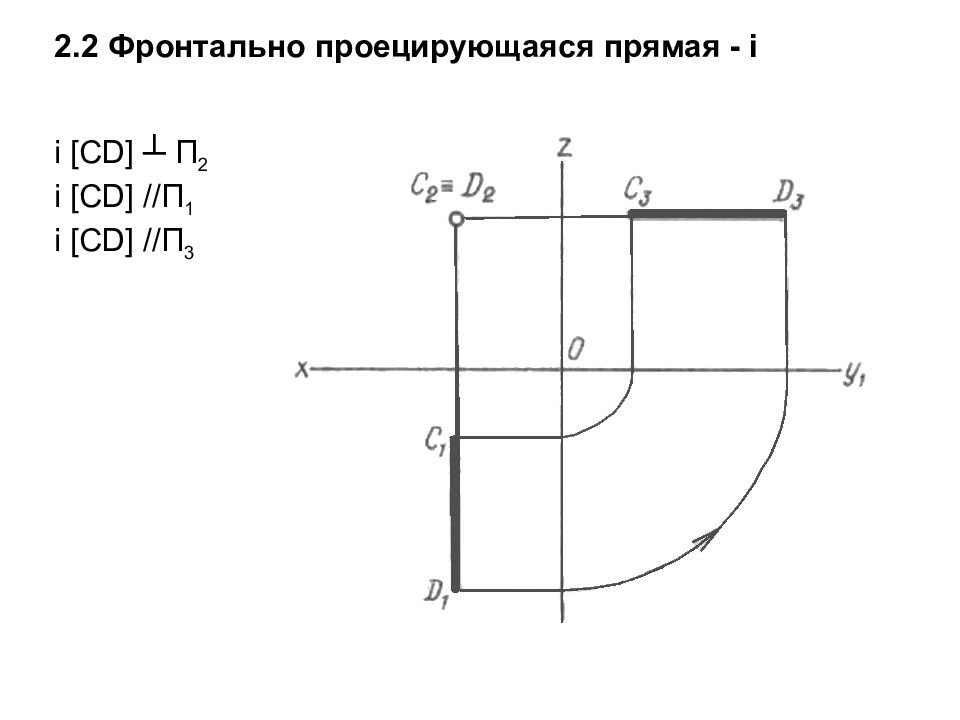
Слайд 23: 2. 2 Фронтально проецирующаяся прямая - i
i [ CD ] ┴ П 2 i [ CD ] //П 1 i [ CD ] //П 3
Слайд 24
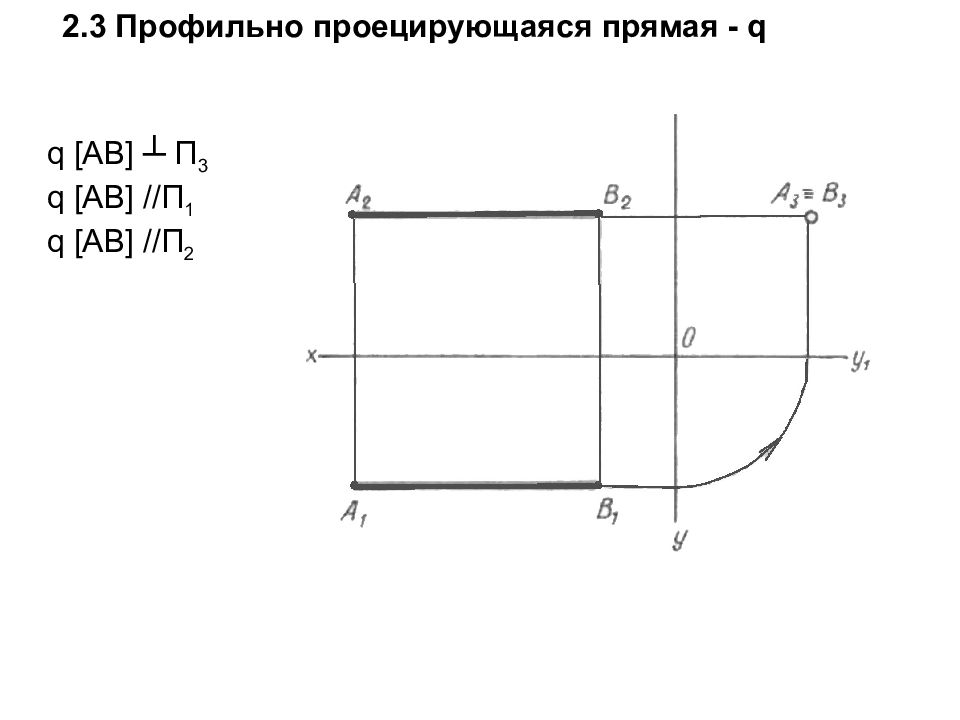
2. 3 Профильно проецирующаяся прямая - q q [ AB ] ┴ П 3 q [ AB ] //П 1 q [ AB ] //П 2
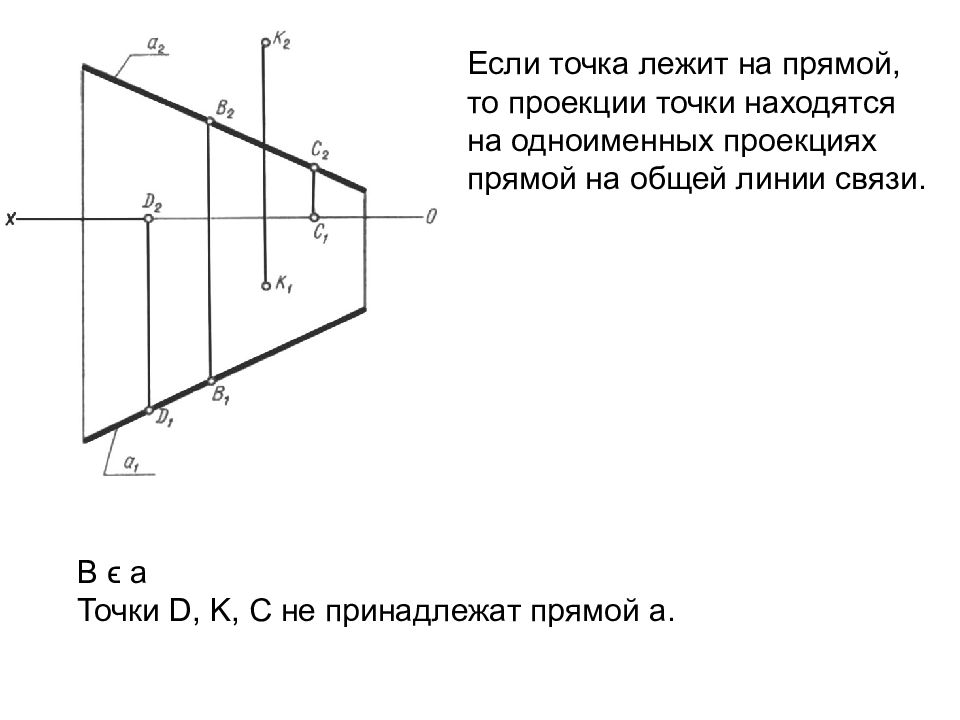
Слайд 25: В ϵ а Точки D, K, C не принадлежат прямой а
Если точка лежит на прямой, то проекции точки находятся на одноименных проекциях прямой на общей линии связи.
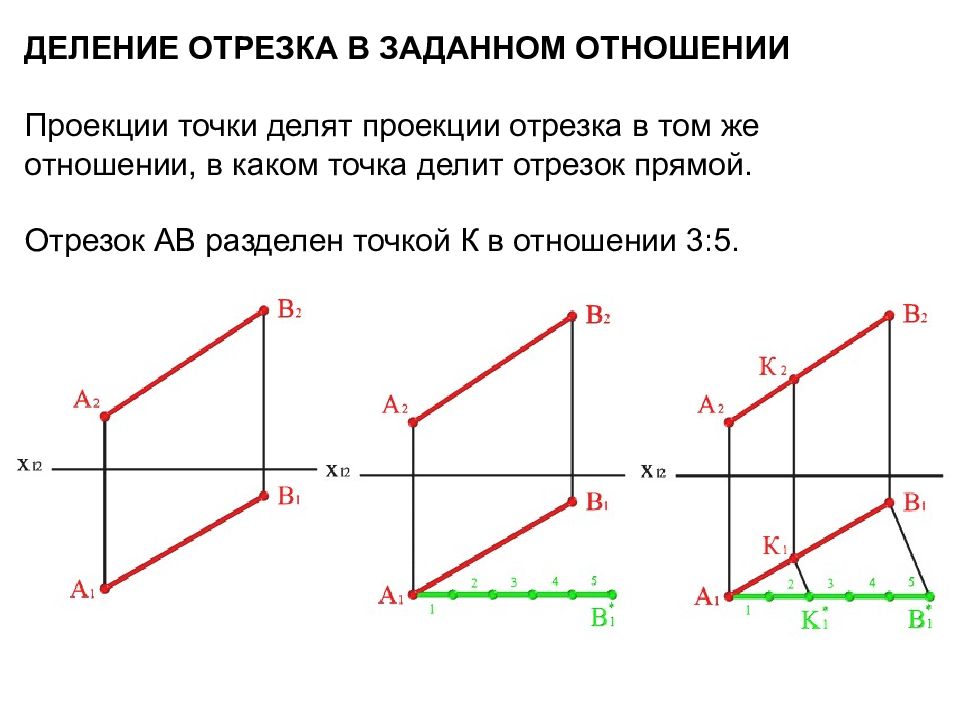
Слайд 26: ДЕЛЕНИЕ ОТРЕЗКА В ЗАДАННОМ ОТНОШЕНИИ Проекции точки делят проекции отрезка в том же отношении, в каком точка делит отрезок прямой. Отрезок АВ разделен точкой К в отношении 3:5
Слайд 27
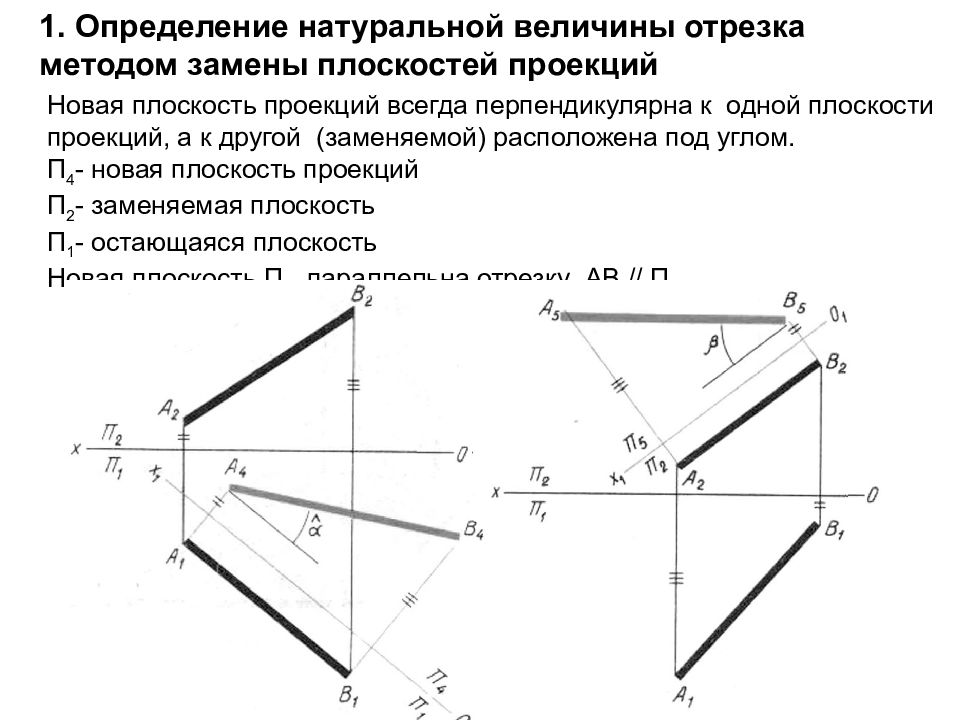
1. Определение натуральной величины отрезка методом замены плоскостей проекций Новая плоскость проекций всегда перпендикулярна к одной плоскости проекций, а к другой (заменяемой) расположена под углом. П 4 - новая плоскость проекций П 2 - заменяемая плоскость П 1 - остающаяся плоскость Новая плоскость П 4 параллельна отрезку АВ // П 4
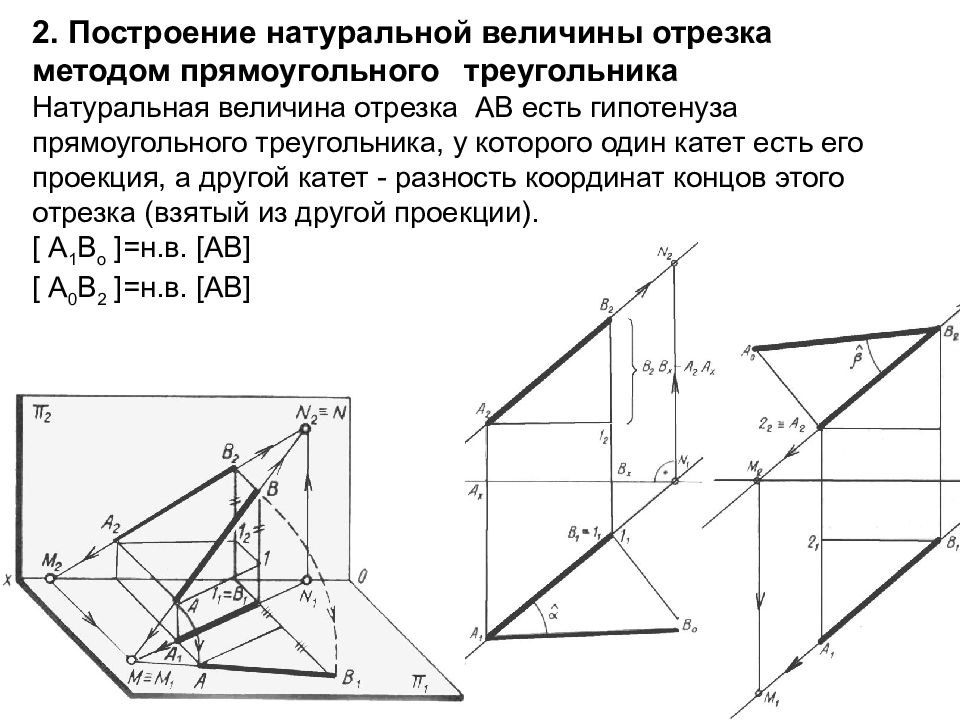
Слайд 28: 2. Построение натуральной величины отрезка методом прямоугольного треугольника
Натуральная величина отрезка АВ есть гипотенуза прямоугольного треугольника, у которого один катет есть его проекция, а другой катет - разность координат концов этого отрезка (взятый из другой проекции). [ А 1 В о ]=н.в. [АВ] [ А 0 В 2 ]=н.в. [АВ]
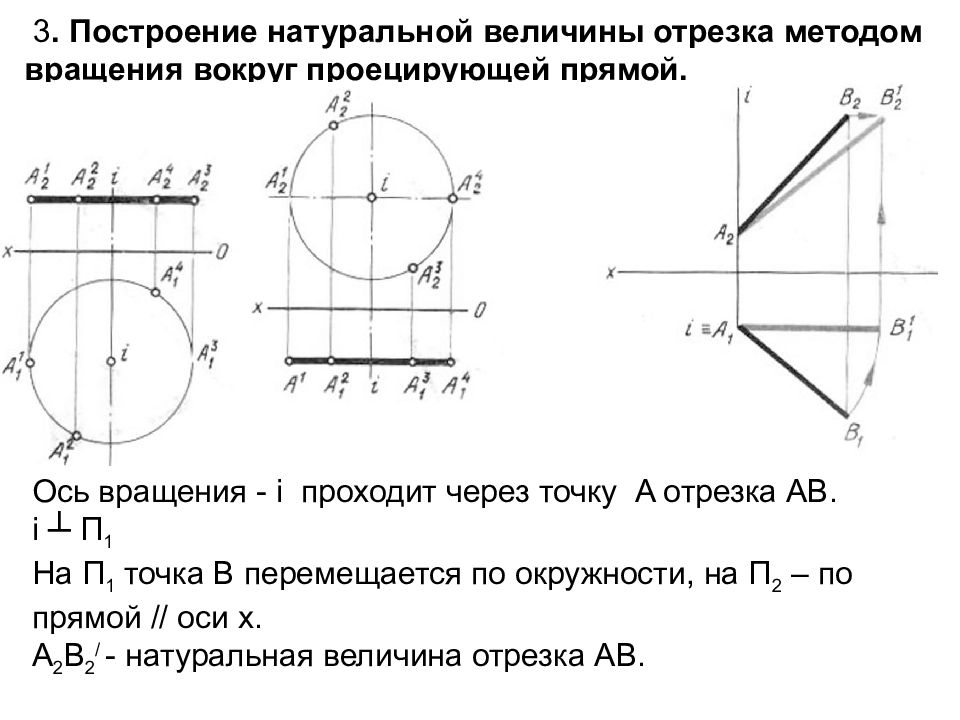
Слайд 29: 3. Построение натуральной величины отрезка методом вращения вокруг проецирующей прямой
Ось вращения - i проходит через точку A отрезка AB. i ┴ П 1 На П 1 точка В перемещается по окружности, на П 2 – по прямой // оси х. A 2 B 2 / - натуральная величина отрезка АВ.
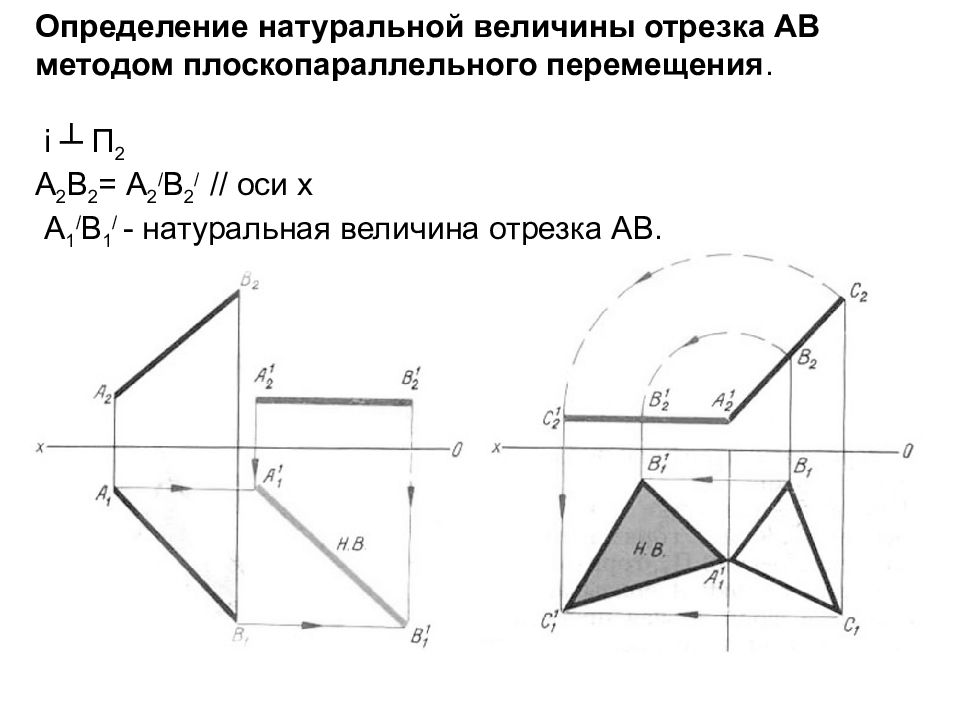
Слайд 30: Определение натуральной величины отрезка АВ методом плоскопараллельного перемещения. i ┴ П 2 А 2 В 2 = А 2 / В 2 / // оси х А 1 / В 1 / - натуральная величина отрезка АВ
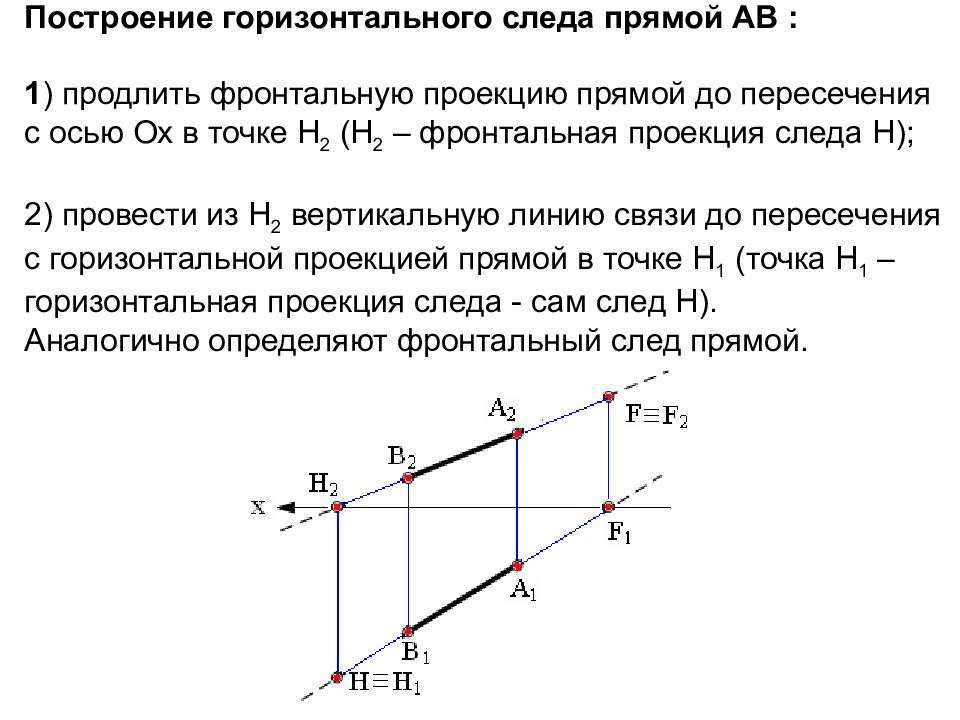
Слайд 31: Следом прямой линии называется точка, в которой прямая пересекается с плоскостью проекций. Прямая общего положения имеет: горизонтальный, ф ронтальный, профильный след
Следы прямой линии
Слайд 32: Построение горизонтального следа прямой АВ : 1 ) продлить фронтальную проекцию прямой до пересечения с осью Ох в точке Н 2 (Н 2 – фронтальная проекция следа Н); 2) провести из Н 2 вертикальную линию связи до пересечения с горизонтальной проекцией прямой в точке Н 1 (точка Н 1 – горизонтальная проекция следа - сам след Н). Аналогично определяют фронтальный след прямой
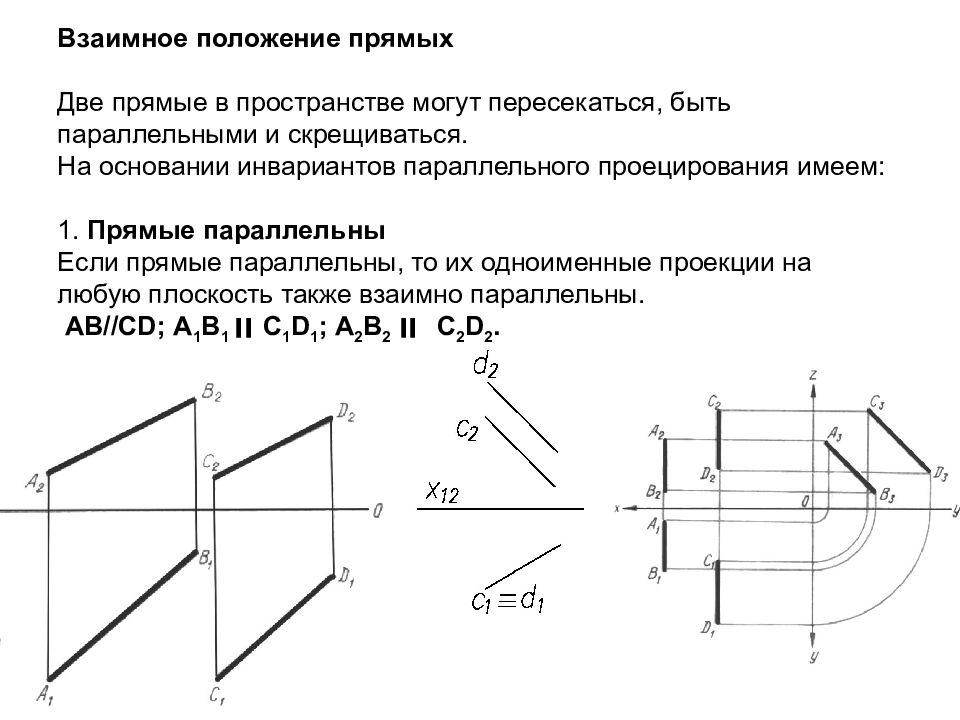
Слайд 33: Взаимное положение прямых Две прямые в пространстве могут пересекаться, быть параллельными и скрещиваться. На основании инвариантов параллельного проецирования имеем: 1. Прямые параллельны Если прямые параллельны, то их одноименные проекции на любую плоскость также взаимно параллельны. АВ// CD ; А 1 В 1 ׀׀ С 1 D 1 ; А 2 В 2 ׀׀ С 2 D 2
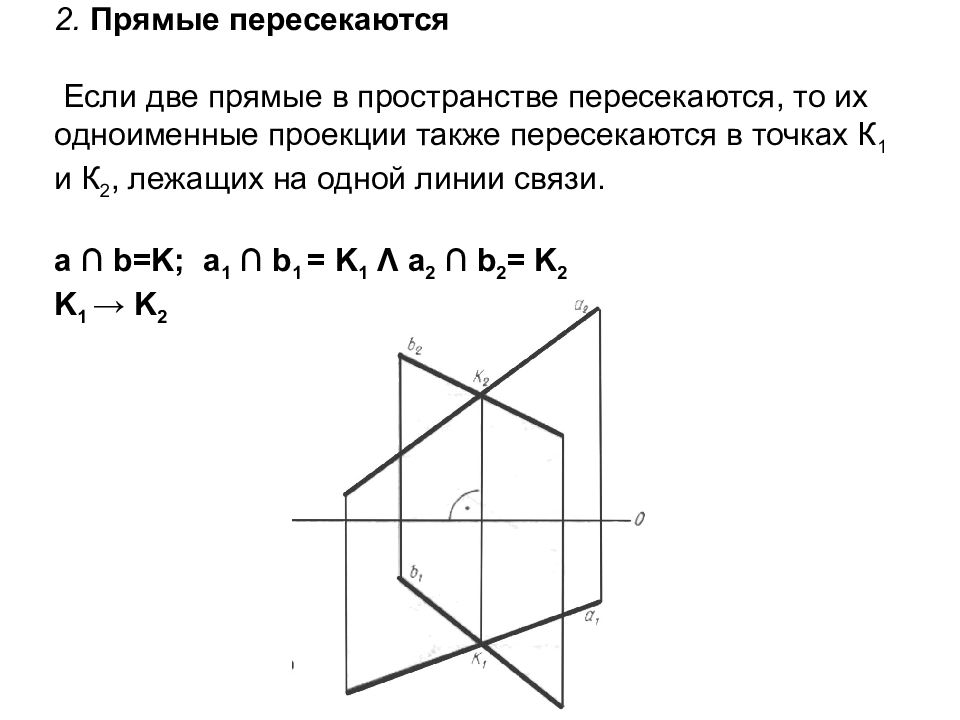
Слайд 34: 2. Прямые пересекаются Если две прямые в пространстве пересекаются, то их одноименные проекции также пересекаются в точках К 1 и К 2, лежащих на одной линии связи. a ∩ b=K ; a 1 ∩ b 1 = K 1 Λ a 2 ∩ b 2 = K 2 K 1 → K 2
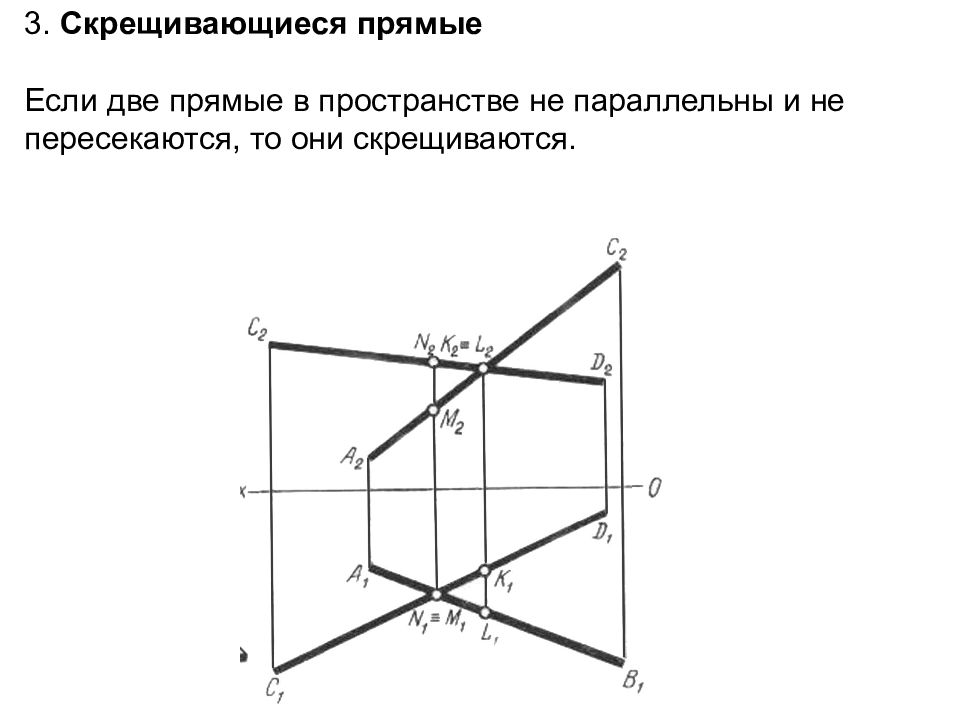
Слайд 35: 3. Скрещивающиеся прямые Если две прямые в пространстве не параллельны и не пересекаются, то они скрещиваются
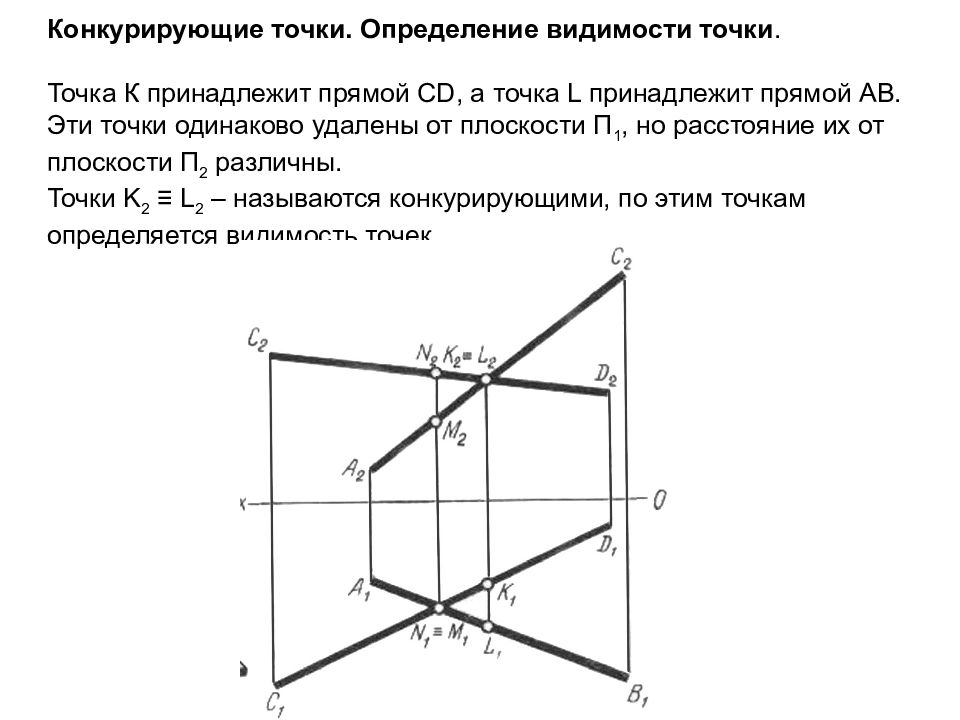
Слайд 36: Конкурирующие точки. Определение видимости точки. Точка К принадлежит прямой CD, а точка L принадлежит прямой AB. Эти точки одинаково удалены от плоскости П 1, но расстояние их от плоскости П 2 различны. Точки K 2 ≡ L 2 – называются конкурирующими, по этим точкам определяется видимость точек
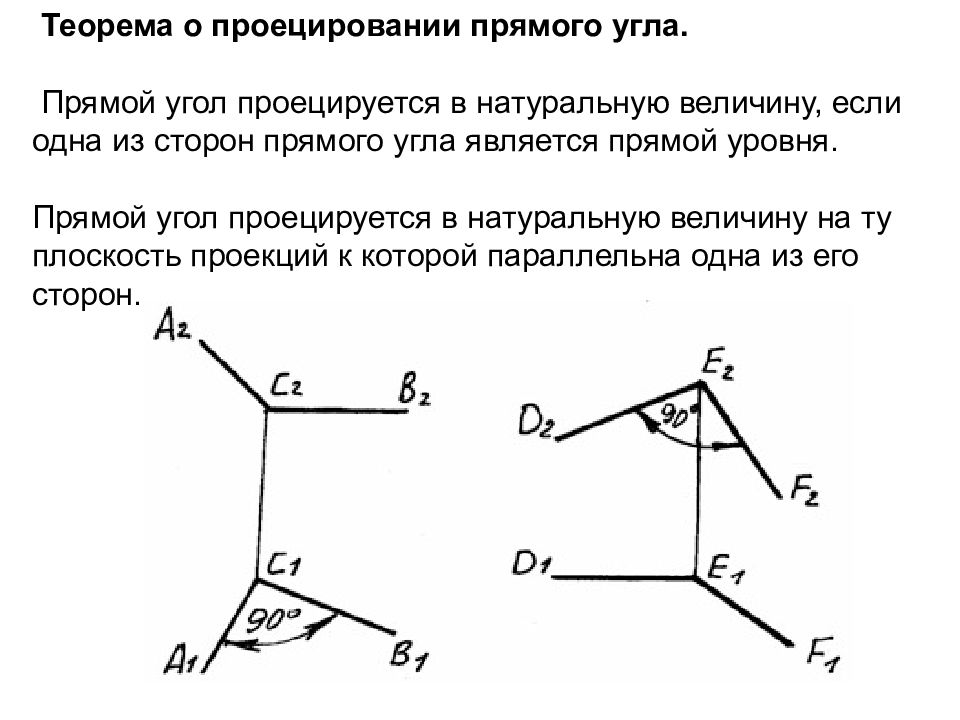
Слайд 37: Теорема о проецировании прямого угла. Прямой угол проецируется в натуральную величину, если одна из сторон прямого угла является прямой уровня. Прямой угол проецируется в натуральную величину на ту плоскость проекций к которой параллельна одна из его сторон
Слайд 38: Определение расстояния от точки до проецирующей прямой Дано: g┴ П 1 А(А 1 ;А 2 ) [А; g ] Решение: 1) А 1 ϵ n 1 n 1 ∩ g 1 =K 1 2) А 2 ϵ n 2 ┴ g 2 n 2 ∩ g 2 =K 2 3) н.в. [А; g ]= [А 1 ;К 1 ]
Слайд 39: Определение расстояния от точки до прямой уровня Дано: h(h 1 ; h 2 ) А(А 1 ;А 2 ) [А; h ] Решение: 1) П 1 /П 2 =>П 4 /П 1 ; П 4┴ h Х 14 ┴ h 1 2 ) [А 4 1 4 ] н.в. [А; h ]
Слайд 40: Определение расстояния от точки до прямой общего положения Дано: [ ВС ] - о.п. А(А 1 ;А 2 ) [А;[ВС] Чтобы определить расстояние от прямой до точки необходимо выполнить два преобразования
Ввести новую плоскость П 4, сделать прямую ВС прямой уровня П 4 // [В 2 С 2 ]. 2) Преобразовать прямую уровня в проецирующую прямую П 5 ┴ [В 4 С 4 ]. Решение: 1) П 1 /П 2 => П 4 /П 2 ; П 4 // [ВС]; Х 24 // [В 2 С 2 ] 2) П 4 /П 2 => П 4 /П 5 ; П 5 ┴ [ВС]; 3) Х 45 ┴ [В 4 С 4 ] ; [А 5 В 5 ] – н.в. расстояния от точки А до [ВС]
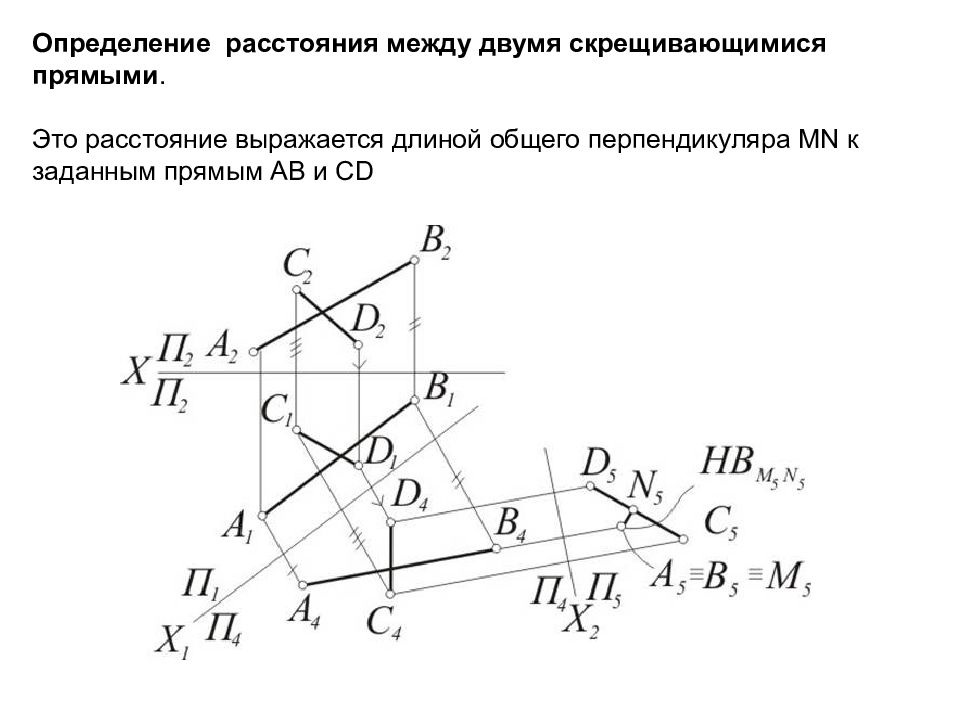
Слайд 41: Определение расстояния между двумя скрещивающимися прямыми. Это расстояние выражается длиной общего перпендикуляра MN к заданным прямым АВ и С D
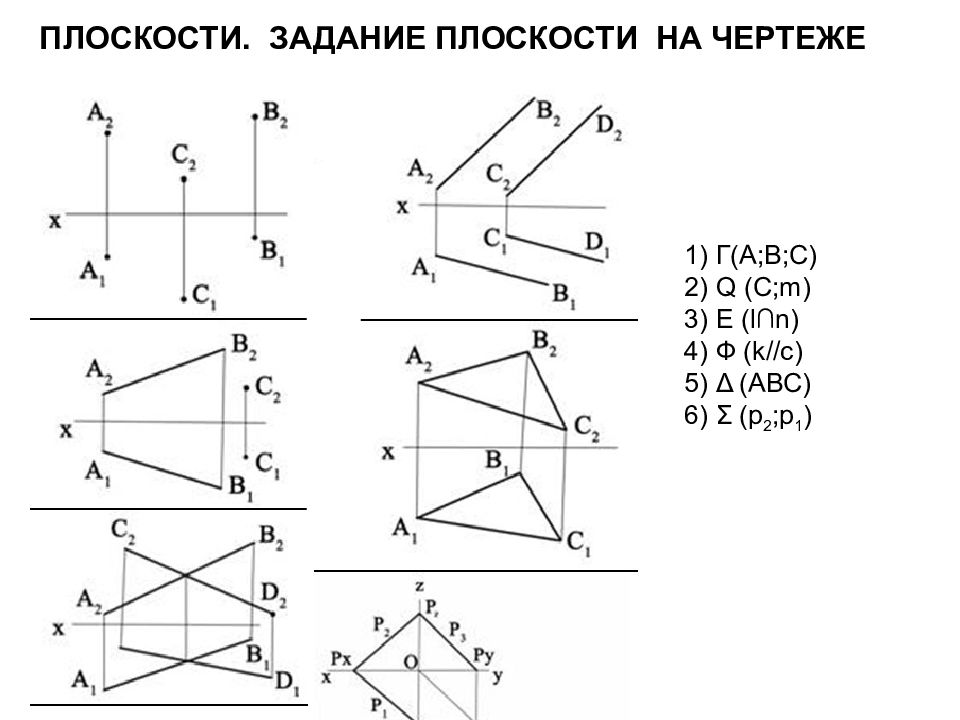
Слайд 42: Плоскости. задание плоскости НА ЧЕРТЕЖЕ
1) Г(А;В;С) 2) Q ( С; m) 3) Е ( l∩n ) 4) Ф ( k//c) 5) Δ ( АВС) 6) Σ (р 2 ;р 1 )
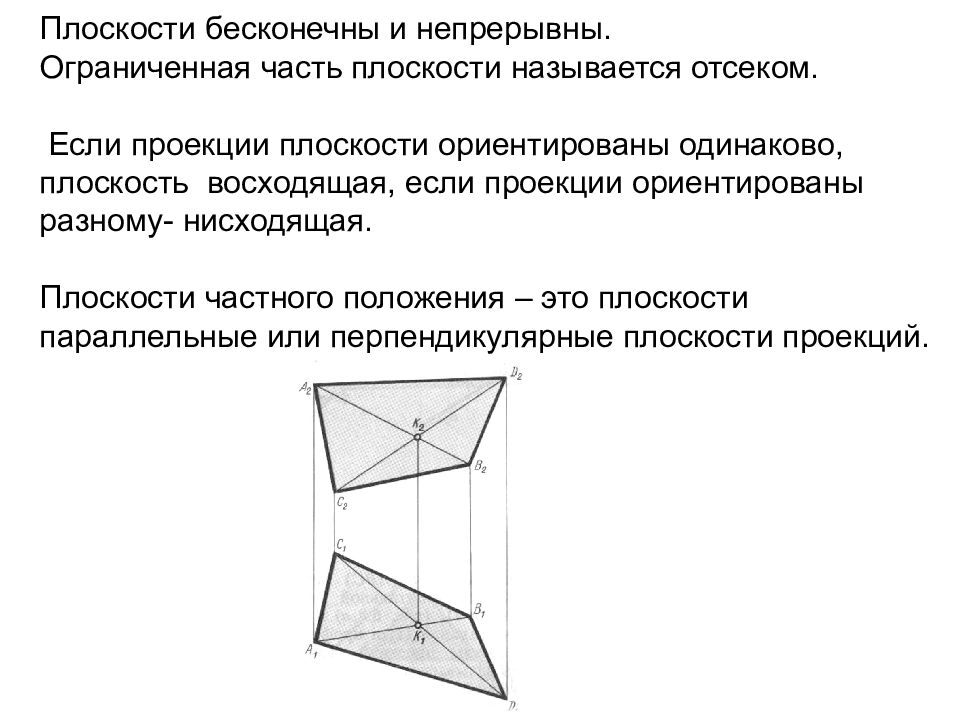
Слайд 43: Плоскости бесконечны и непрерывны. Ограниченная часть плоскости называется отсеком. Если проекции плоскости ориентированы одинаково, плоскость восходящая, если проекции ориентированы разному- нисходящая. Плоскости частного положения – это плоскости параллельные или перпендикулярные плоскости проекций
Слайд 44
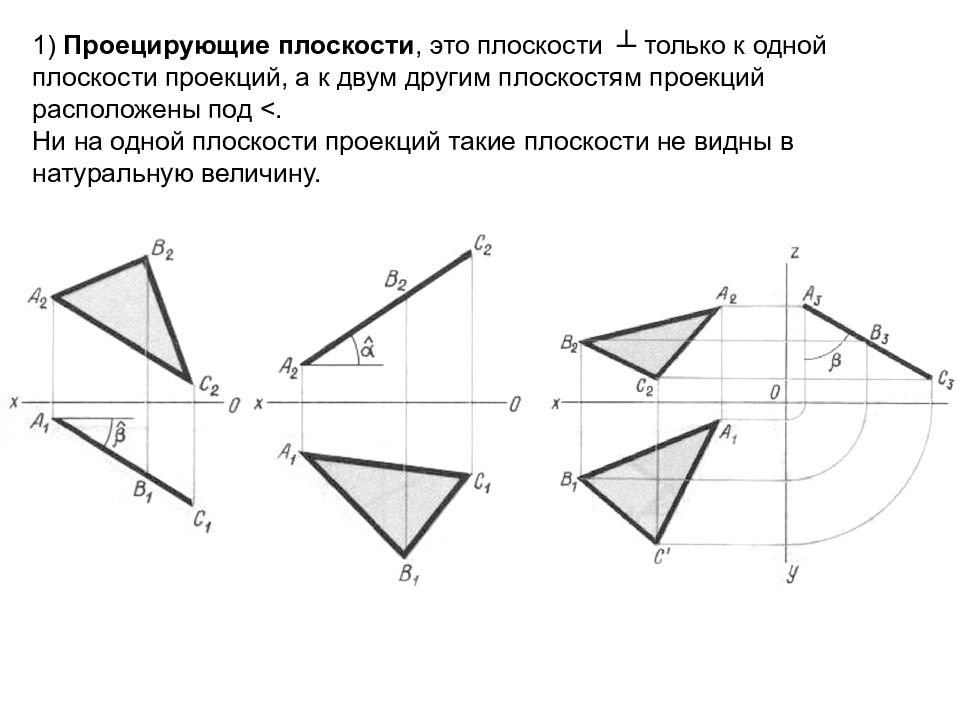
1) Проецирующие плоскости, это плоскости ┴ только к одной плоскости проекций, а к двум другим плоскостям проекций расположены под <. Ни на одной плоскости проекций такие плоскости не видны в натуральную величину.
Слайд 45
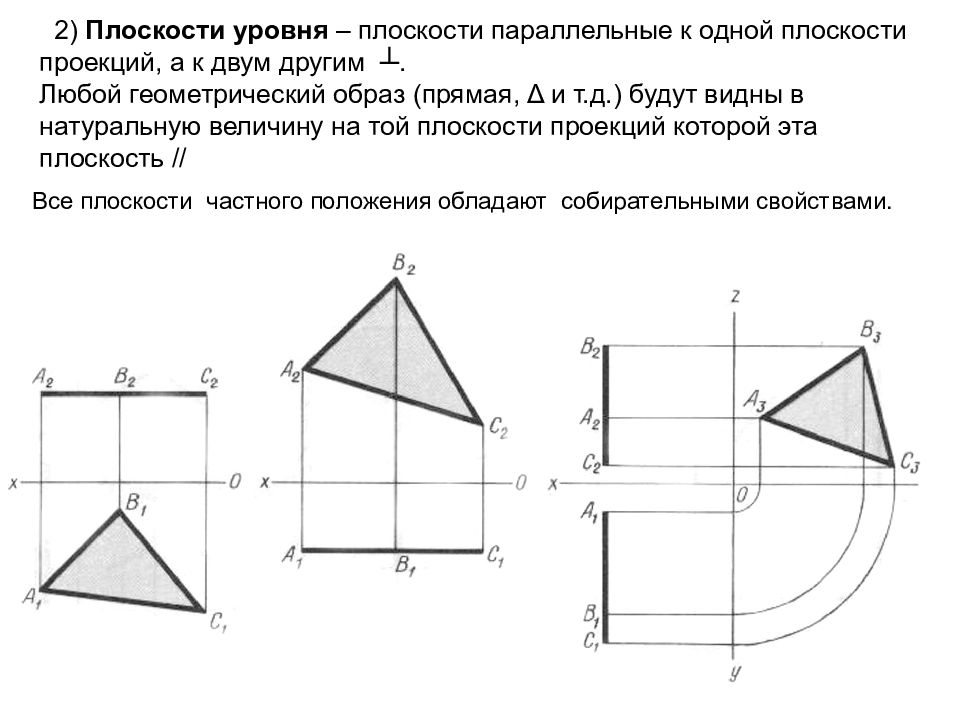
2) Плоскости уровня – плоскости параллельные к одной плоскости проекций, а к двум другим ┴. Любой геометрический образ (прямая, Δ и т.д.) будут видны в натуральную величину на той плоскости проекций которой эта плоскость // Все плоскости частного положения обладают собирательными свойствами.
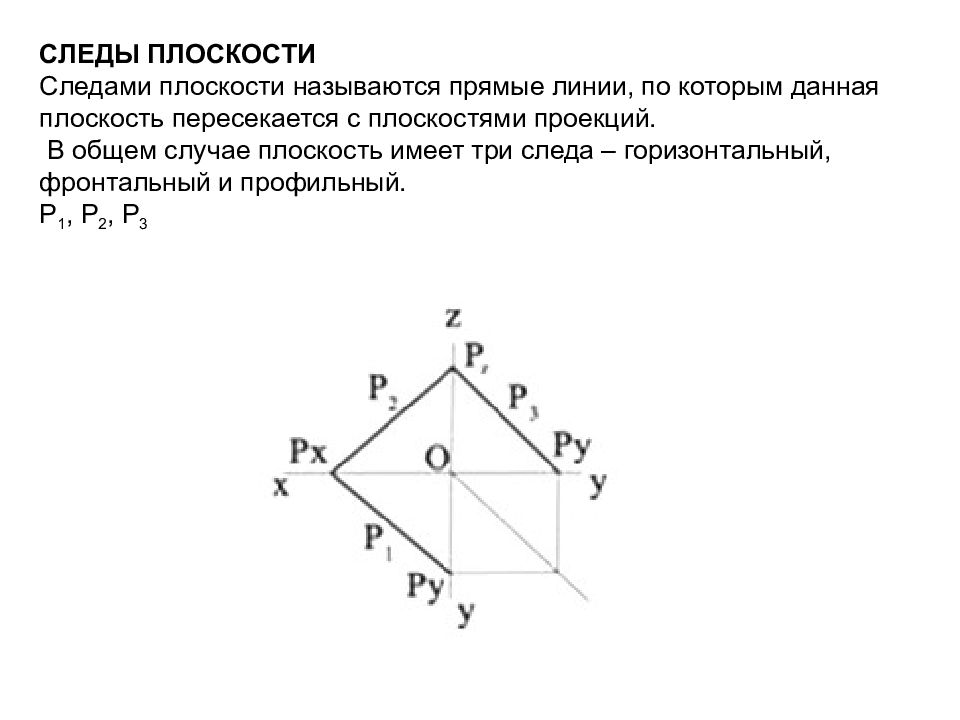
Слайд 46: Следы плоскости Следами плоскости называются прямые линии, по которым данная плоскость пересекается с плоскостями проекций. В общем случае плоскость имеет три следа – горизонтальный, фронтальный и профильный. P 1, P 2, P 3
Слайд 47
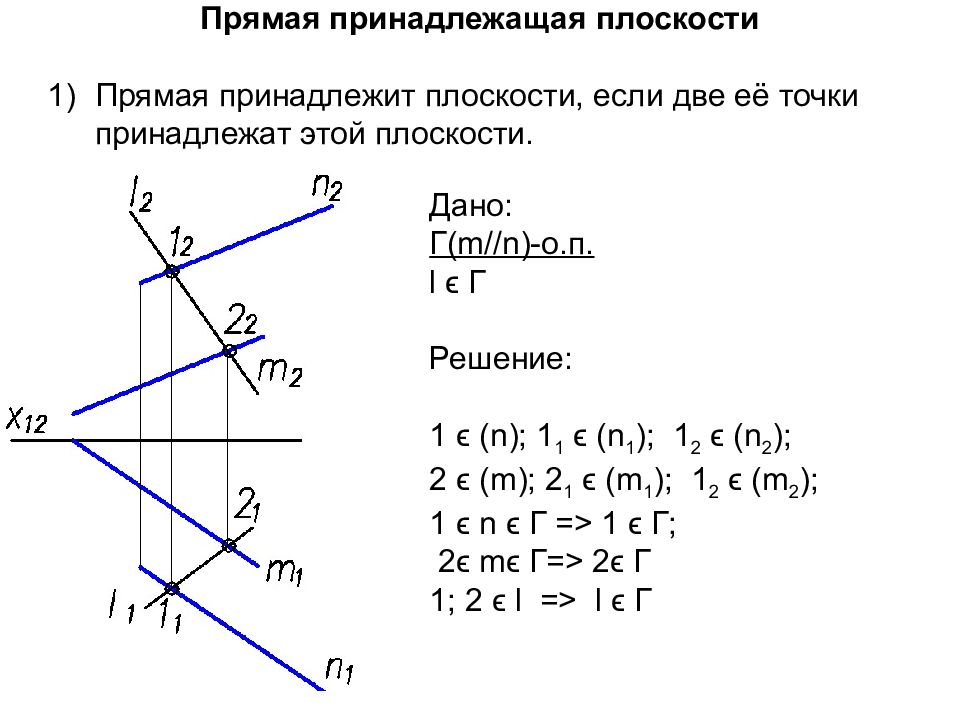
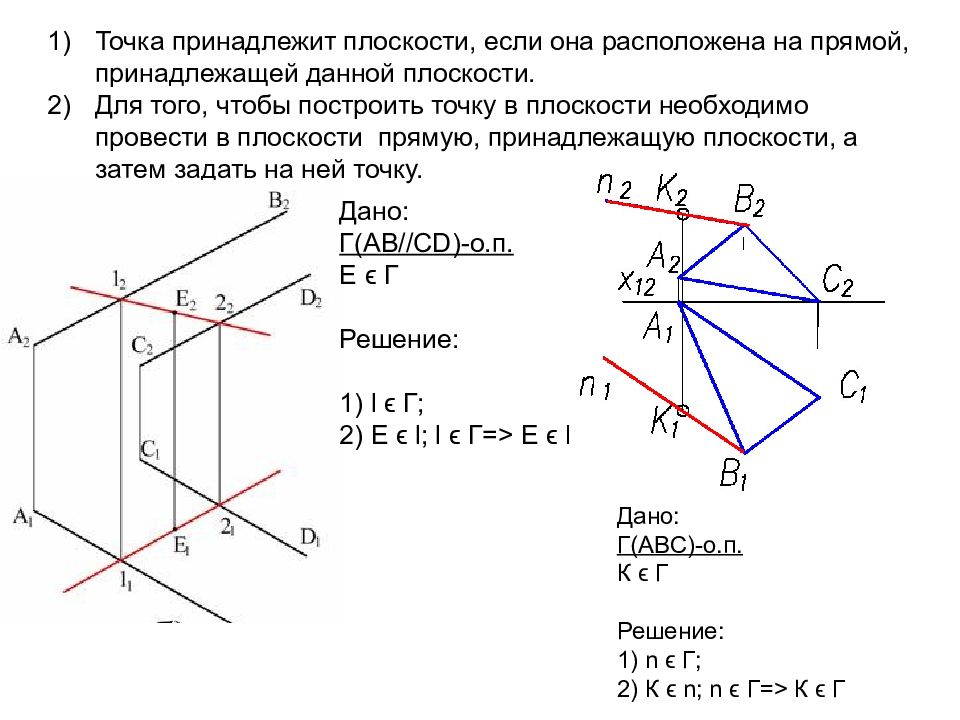
Прямая принадлежащая плоскости Прямая принадлежит плоскости, если две её точки принадлежат этой плоскости. Дано: Г( m//n)- о.п. l ϵ Г Решение: 1 ϵ (n ); 1 1 ϵ (n 1 ); 1 2 ϵ (n 2 ); 2 ϵ (m ); 2 1 ϵ (m 1 ); 1 2 ϵ (m 2 ); 1 ϵ n ϵ Г => 1 ϵ Г; 2 ϵ m ϵ Г=> 2 ϵ Г 1 ; 2 ϵ l => l ϵ Г
Слайд 48
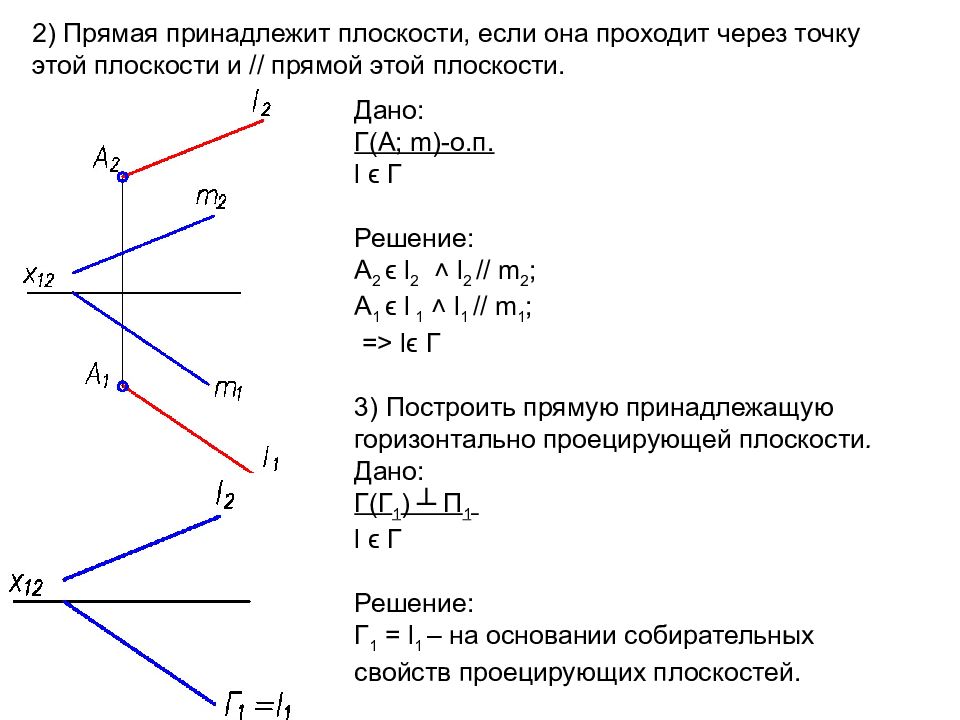
2) Прямая принадлежит плоскости, если она проходит через точку этой плоскости и // прямой этой плоскости. . Дано: Г( A ; m)- о.п. l ϵ Г Решение: А 2 ϵ l 2 ˄ l 2 // m 2 ; А 1 ϵ l 1 ˄ l 1 // m 1 ; => l ϵ Г 3) Построить прямую принадлежащую горизонтально проецирующей плоскости. Дано: Г(Г 1 ) ┴ П 1 l ϵ Г Решение: Г 1 = l 1 – на основании собирательных свойств проецирующих плоскостей.
Слайд 49
Прямая Принадлежащая плоскости Точка принадлежит плоскости, если она расположена на прямой, принадлежащей данной плоскости. Для того, чтобы построить точку в плоскости необходимо провести в плоскости прямую, принадлежащую плоскости, а затем задать на ней точку. Дано: Г( AB//CD)- о.п. E ϵ Г Решение: 1) l ϵ Г; 2) E ϵ l ; l ϵ Г=> E ϵ Г Дано: Г( AB С )- о.п. К ϵ Г Решение: 1) n ϵ Г; 2) К ϵ n ; n ϵ Г=> К ϵ Г
Слайд 50
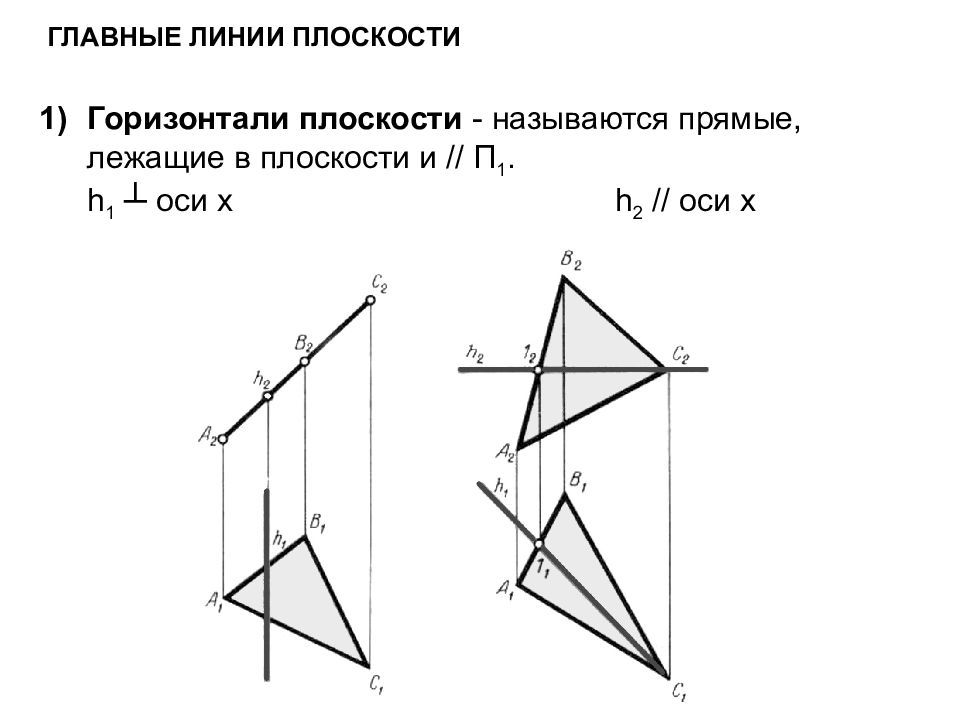
Главные линии плоскости Горизонтали плоскости - называются прямые, лежащие в плоскости и // П 1. h 1 ┴ оси х h 2 // оси х
Слайд 51
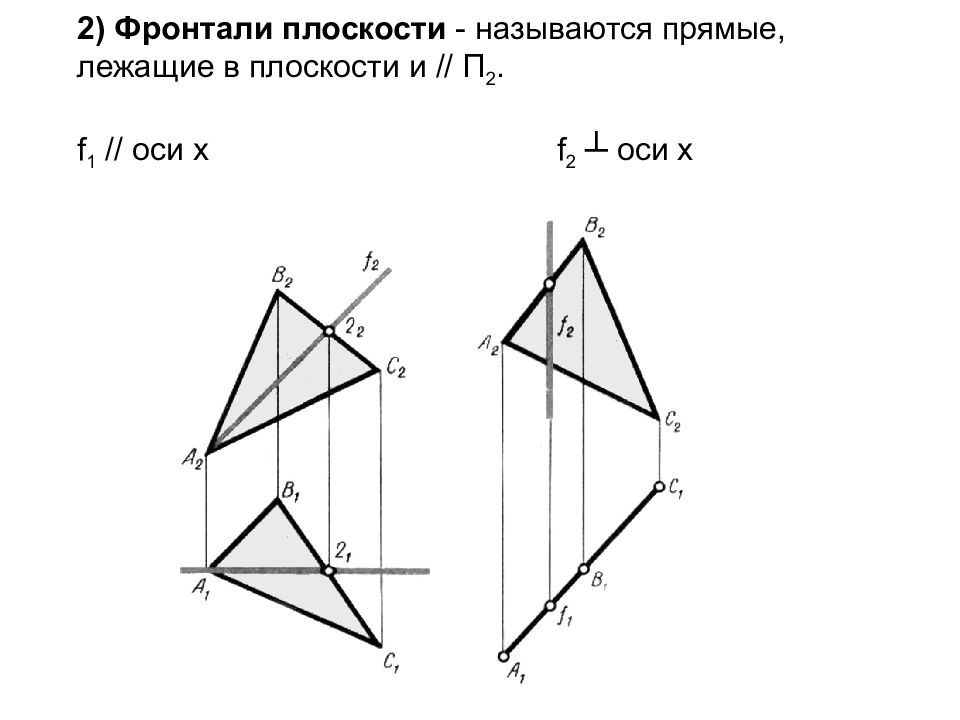
2) Фронтали плоскости - называются прямые, лежащие в плоскости и // П 2. f 1 // оси х f 2 ┴ оси х
Слайд 52
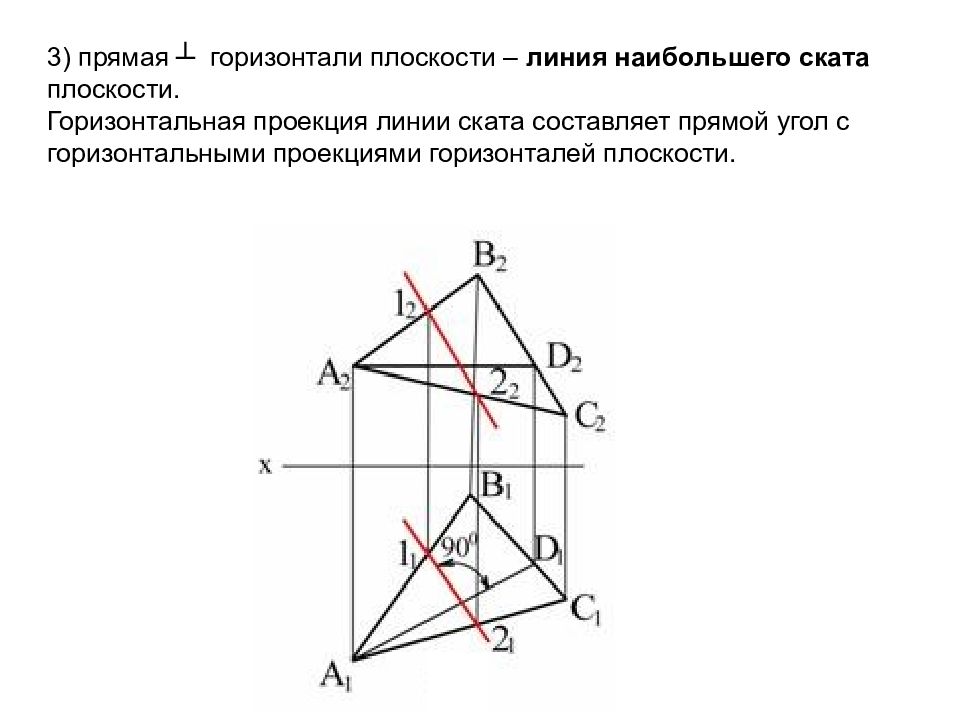
3) прямая ┴ горизонтали плоскости – линия наибольшего ската плоскости. Горизонтальная проекция линии ската составляет прямой угол с горизонтальными проекциями горизонталей плоскости.
Слайд 53
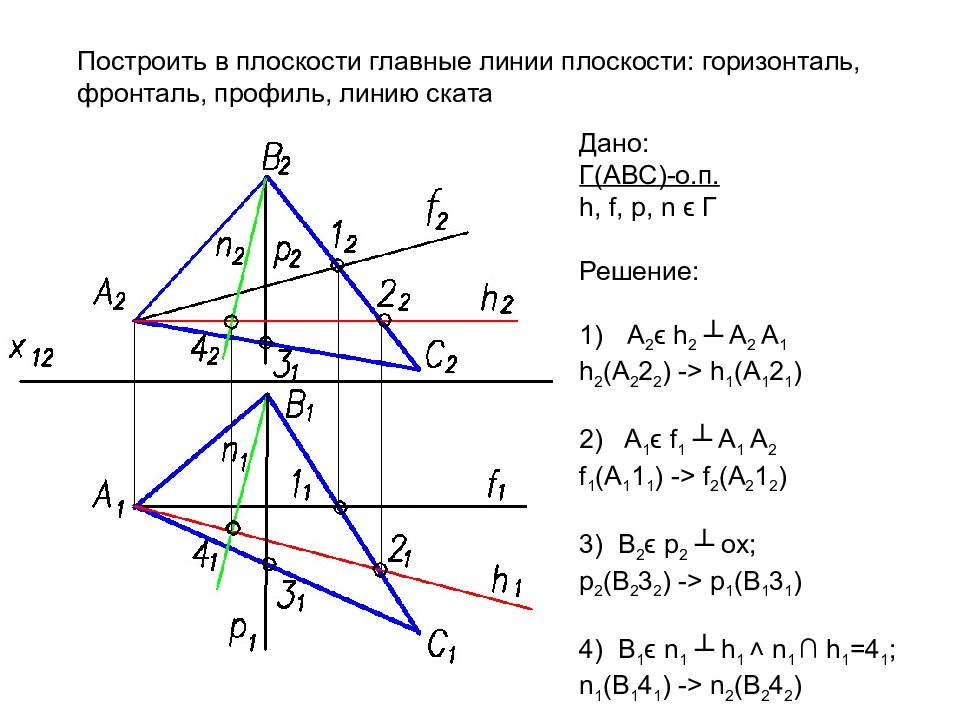
Построить в плоскости главные линии плоскости: горизонталь, фронталь, профиль, линию ската Дано: Г( ABC)- о.п. h, f, p, n ϵ Г Решение: A 2 ϵ h 2 ┴ A 2 A 1 h 2 (A 2 2 2 ) -> h 1 (A 1 2 1 ) 2) A 1 ϵ f 1 ┴ A 1 A 2 f 1 (A 1 1 1 ) -> f 2 (A 2 1 2 ) 3) B 2 ϵ p 2 ┴ ox ; p 2 (B 2 3 2 ) -> p 1 (B 1 3 1 ) 4) B 1 ϵ n 1 ┴ h 1 ˄ n 1 ∩ h 1 =4 1 ; n 1 (B 1 4 1 ) -> n 2 (B 2 4 2 )
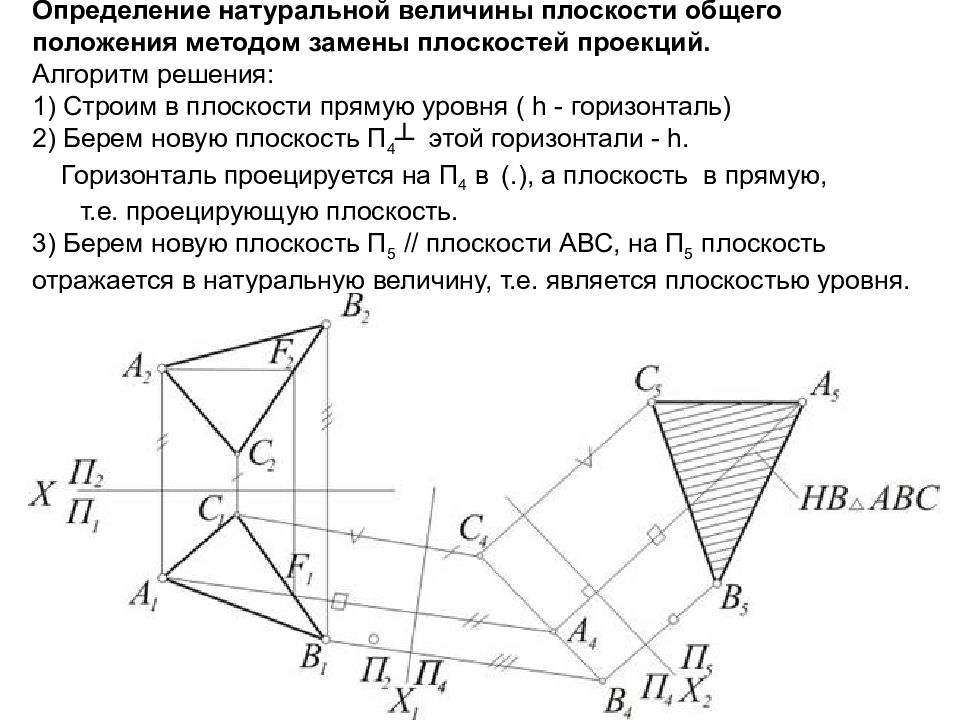
Слайд 54: Определение натуральной величины плоскости общего положения методом замены плоскостей проекций. Алгоритм решения: 1) Строим в плоскости прямую уровня ( h - горизонталь) 2) Берем новую плоскость П 4 ┴ этой горизонтали - h. Горизонталь проецируется на П 4 в (.), а плоскость в прямую, т.е. проецирующую плоскость. 3) Берем новую плоскость П 5 // плоскости АВС, на П 5 плоскость отражается в натуральную величину, т.е. является плоскостью уровня
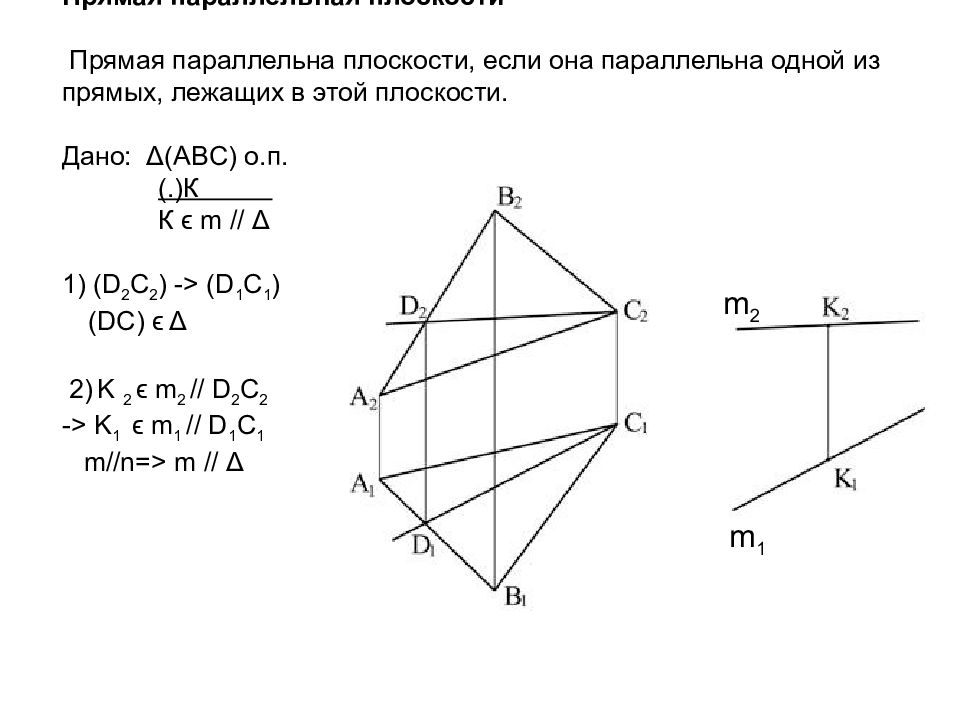
Слайд 55: Прямая параллельная плоскости Прямая параллельна плоскости, если она параллельна одной из прямых, лежащих в этой плоскости. Дано: Δ ( A В C ) о.п. (.)К К ϵ m // Δ 1) (D 2 C 2 ) -> (D 1 C 1 ) (DC) ϵ Δ 2) K 2 ϵ m 2 // D 2 C 2 -> K 1 ϵ m 1 // D 1 C 1 m//n=> m // Δ
m 2 m 1
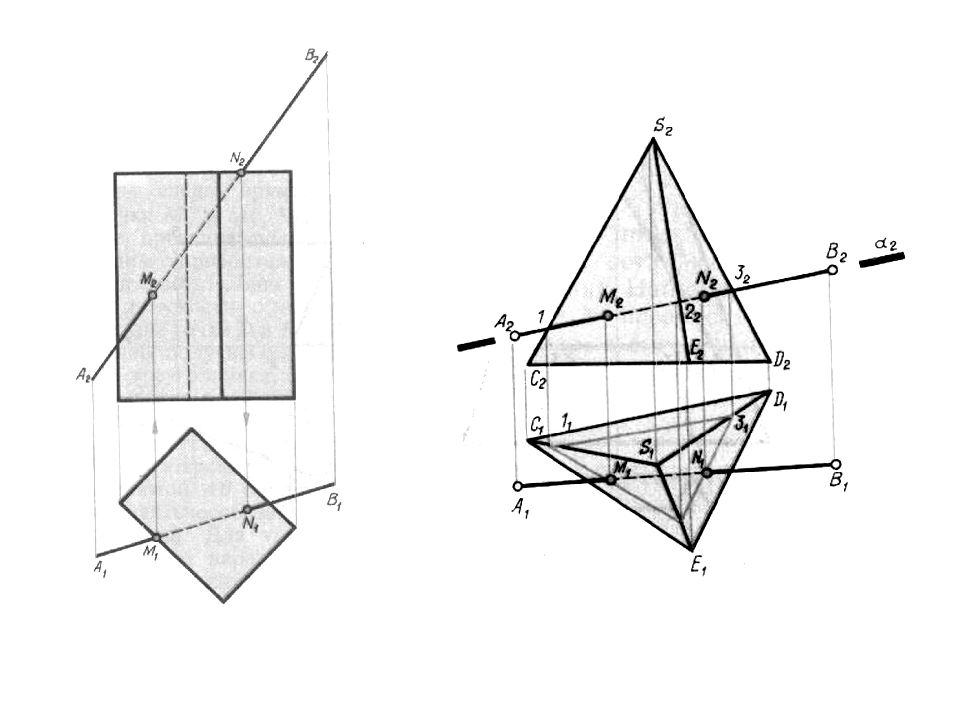
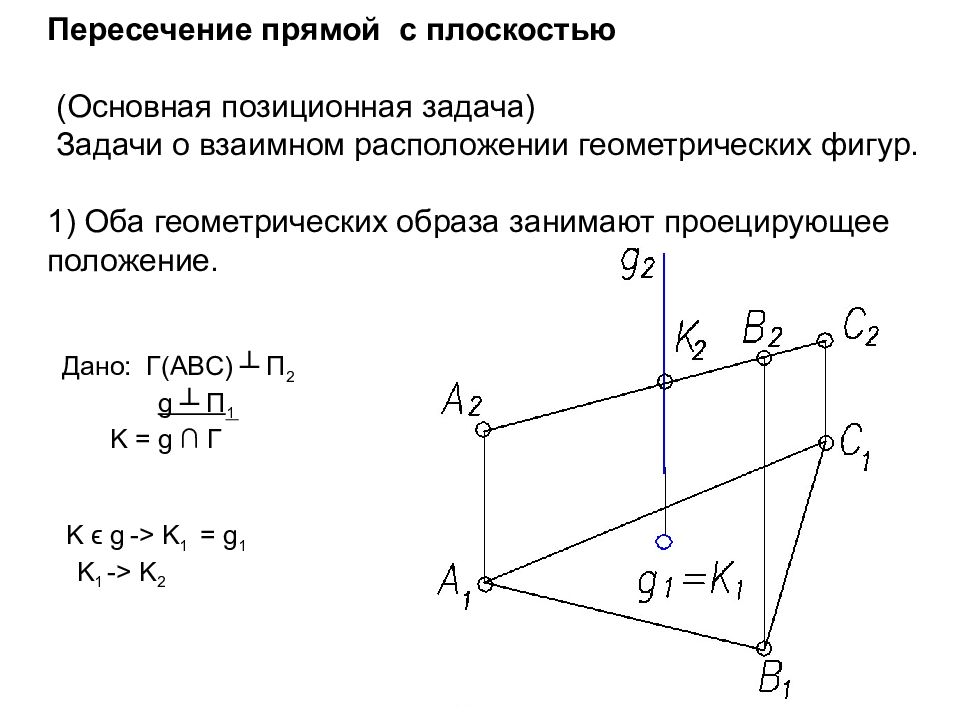
Слайд 56: Пересечение прямой с плоскостью (Основная позиционная задача) Задачи о взаимном расположении геометрических фигур. 1) Оба геометрических образа занимают проецирующее положение
Дано: Г(АВС) ┴ П 2 g ┴ П 1 K = g ∩ Г K ϵ g -> K 1 = g 1 K 1 -> K 2
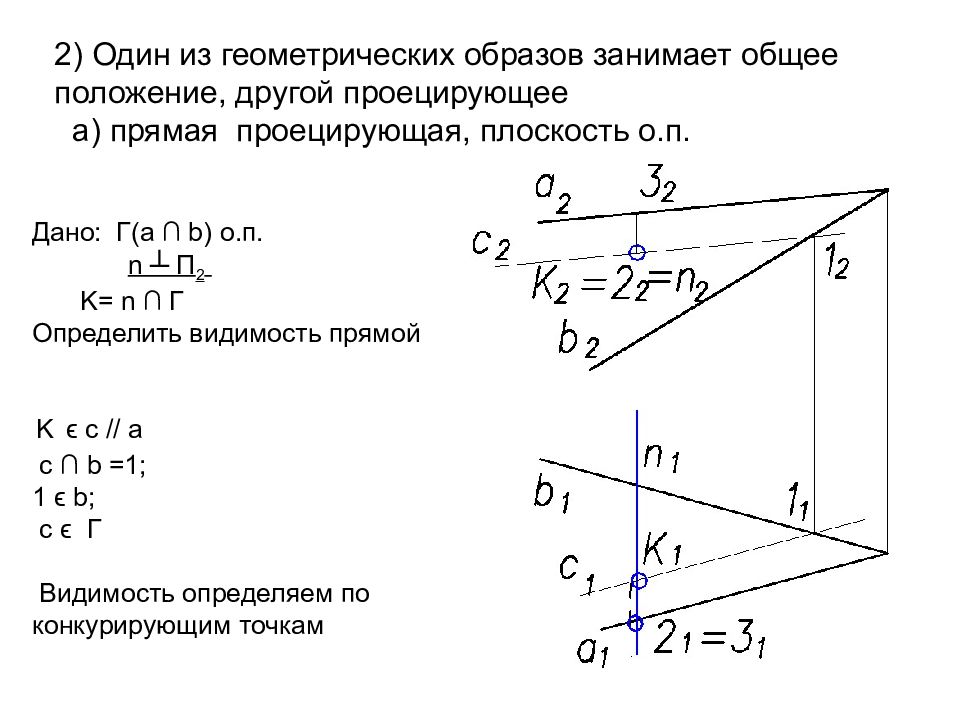
Слайд 57: 2) Один из геометрических образов занимает общее положение, другой проецирующее а) прямая проецирующая, плоскость о.п
Дано: Г(а ∩ b ) о.п. n ┴ П 2 K= n ∩ Г Определить видимость прямой K ϵ с // а с ∩ b =1; 1 ϵ b ; с ϵ Г Видимость определяем по конкурирующим точкам
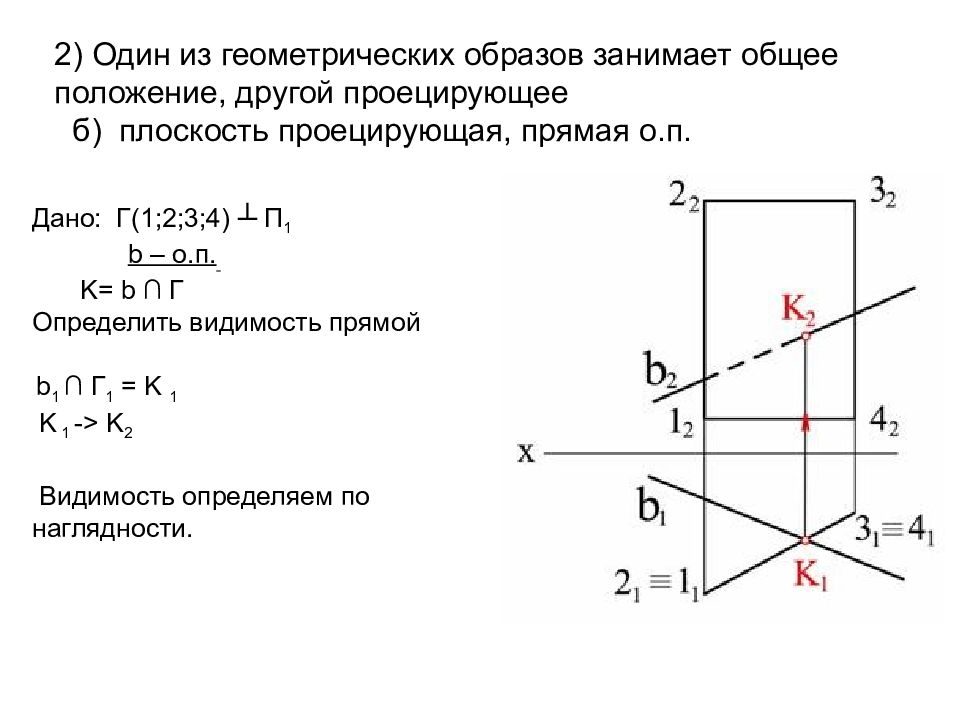
Слайд 58: 2) Один из геометрических образов занимает общее положение, другой проецирующее б) плоскость проецирующая, прямая о.п
Дано: Г( 1 ; 2 ; 3 ; 4 ) ┴ П 1 b – о.п. K= b ∩ Г Определить видимость прямой b 1 ∩ Г 1 = K 1 K 1 -> K 2 Видимость определяем по наглядности.
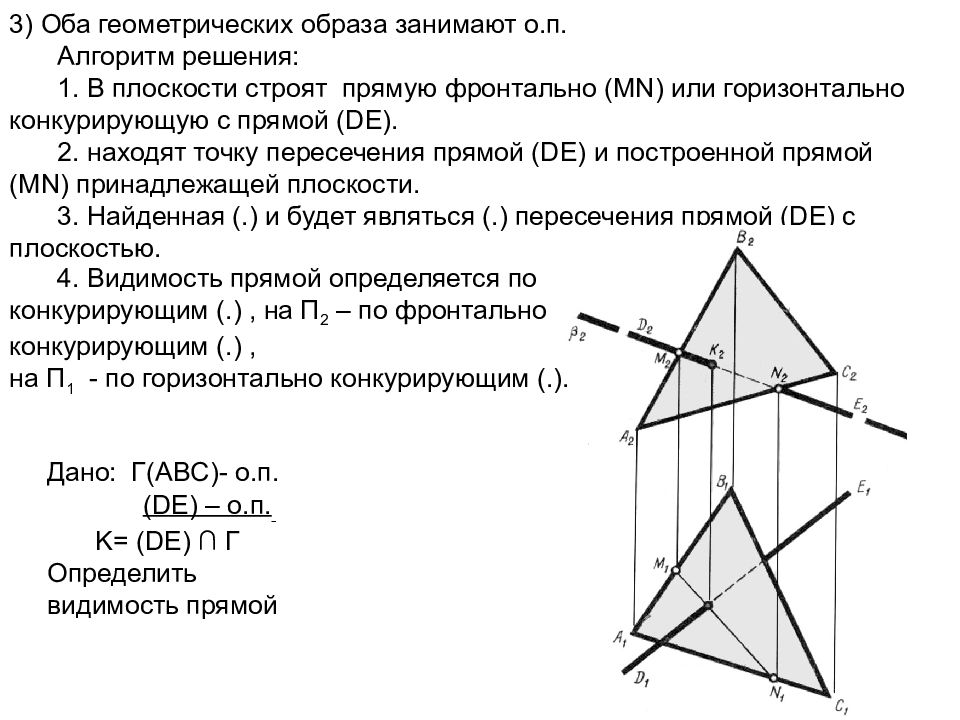
Слайд 59: 3) Оба геометрических образа занимают о.п. Алгоритм решения: 1. В плоскости c троят прямую фронтально (MN ) или горизонтально конкурирующую с прямой ( DE ). 2. находят точку пересечения прямой ( DE ) и построенной прямой (MN ) принадлежащей плоскости. 3. Найденная (.) и будет являться (.) пересечения прямой ( DE ) с плоскостью
Дано: Г( ABC )- о.п. (DE) – о.п. K= (DE) ∩ Г Определить видимость прямой 4. Видимость прямой определяется по конкурирующим (.), на П 2 – по фронтально конкурирующим (.), на П 1 - по горизонтально конкурирующим (.).
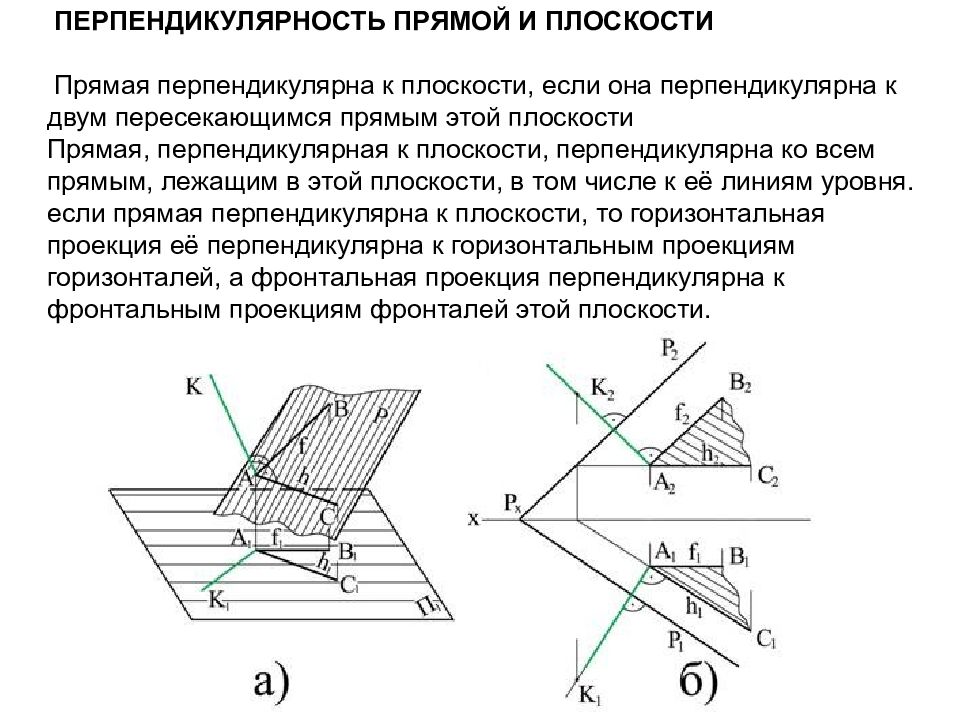
Слайд 60: Перпендикулярность прямой и плоскости Прямая перпендикулярна к плоскости, если она перпендикулярна к двум пересекающимся прямым этой плоскости Прямая, перпендикулярная к плоскости, перпендикулярна ко всем прямым, лежащим в этой плоскости, в том числе к её линиям уровня. если прямая перпендикулярна к плоскости, то горизонтальная проекция её перпендикулярна к горизонтальным проекциям горизонталей, а фронтальная проекция перпендикулярна к фронтальным проекциям фронталей этой плоскости
Слайд 61: Дано: Г( h∩f ) о.п. А(А 1 ; А 2 ) [ А;Г ] Алгоритм решения: 1) А ϵ n ┴ Г( h∩f ) А 2 ϵ n 2 ┴ f 2 А 1 ϵ n 1 ┴ h 1 2) В= n ∩ Г m ϵ Г и m 2 =n 2 m 2 (1 2 ; 2 2 ) -> m 1 (1 1 ; 2 1) m 1 ∩ n 1 = В 1 -> В 2 Находим натуральную величину [АВ] методом прямоугольного треугольника – [А 1 / В 1 ]
Слайд 62
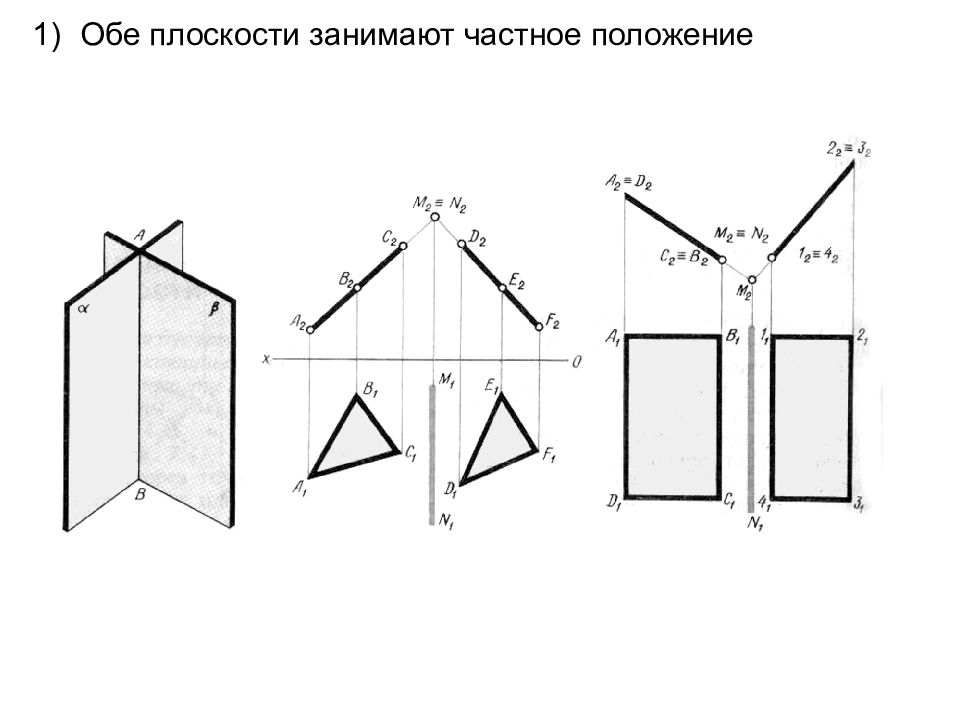
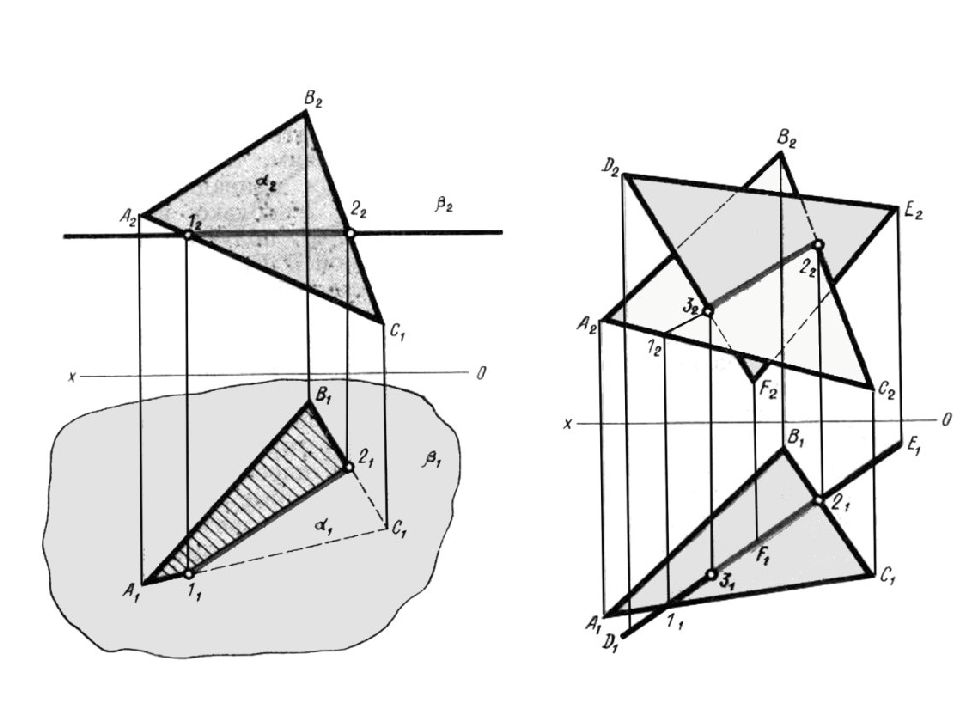
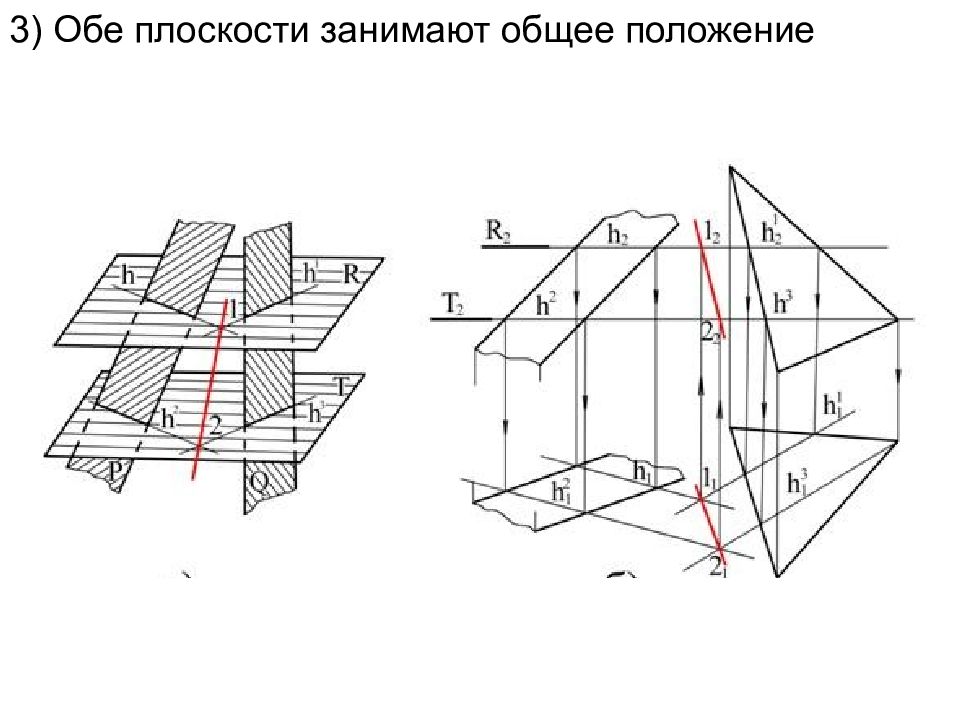
пересечение двух плоскостей Обе плоскости занимают частное положение Одна плоскость занимает частное положение, другая общее положение Обе плоскости занимают общее положение
Слайд 64
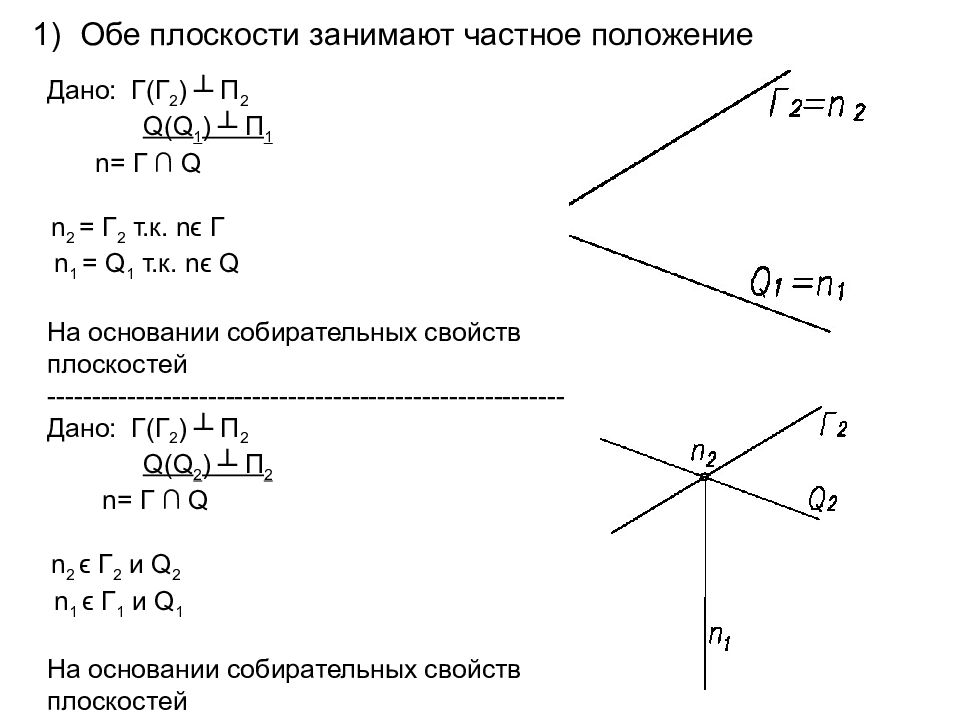
Обе плоскости занимают частное положение Дано: Г(Г 2 ) ┴ П 2 Q ( Q 1 ) ┴ П 1 n= Г ∩ Q n 2 = Г 2 т.к. n ϵ Г n 1 = Q 1 т.к. n ϵ Q На основании собирательных свойств плоскостей ---------------------------------------------------------- Дано: Г(Г 2 ) ┴ П 2 Q ( Q 2 ) ┴ П 2 n= Г ∩ Q n 2 ϵ Г 2 и Q 2 n 1 ϵ Г 1 и Q 1 На основании собирательных свойств плоскостей
Слайд 67
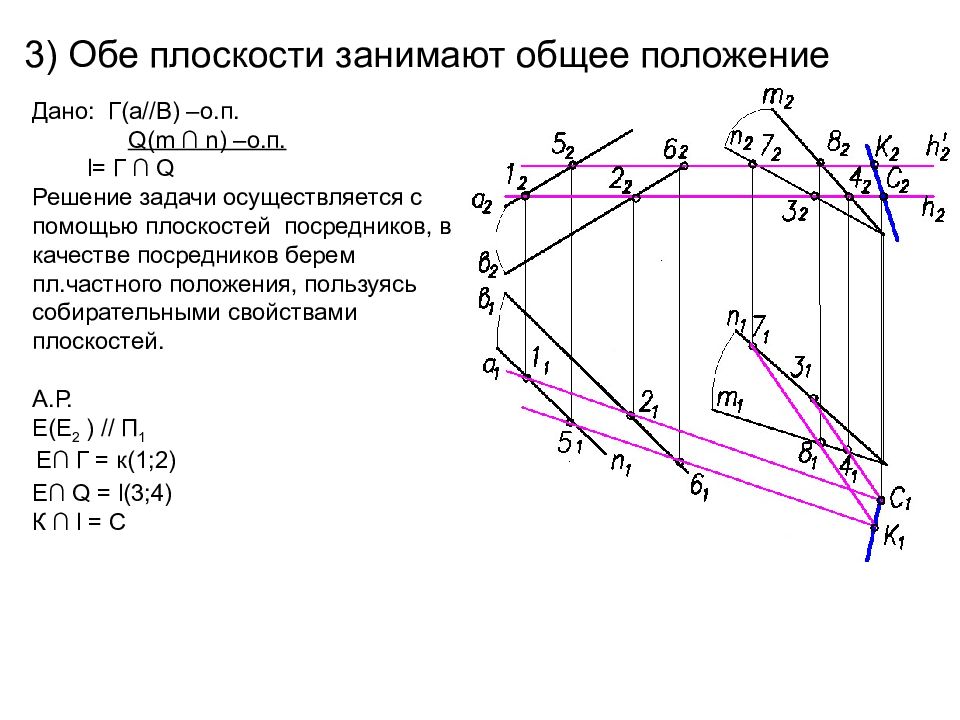
3) Обе плоскости занимают общее положение Дано: Г( a//B ) – о.п. Q ( m ∩ n ) –о.п. l= Г ∩ Q Решение задачи осуществляется с помощью плоскостей посредников, в качестве посредников берем пл.частного положения, пользуясь собирательными свойствами плоскостей. А.Р. Е(Е 2 ) // П 1 Е∩ Г = к(1;2) Е∩ Q = l ( 3 ; 4 ) К ∩ l = C
Слайд 68
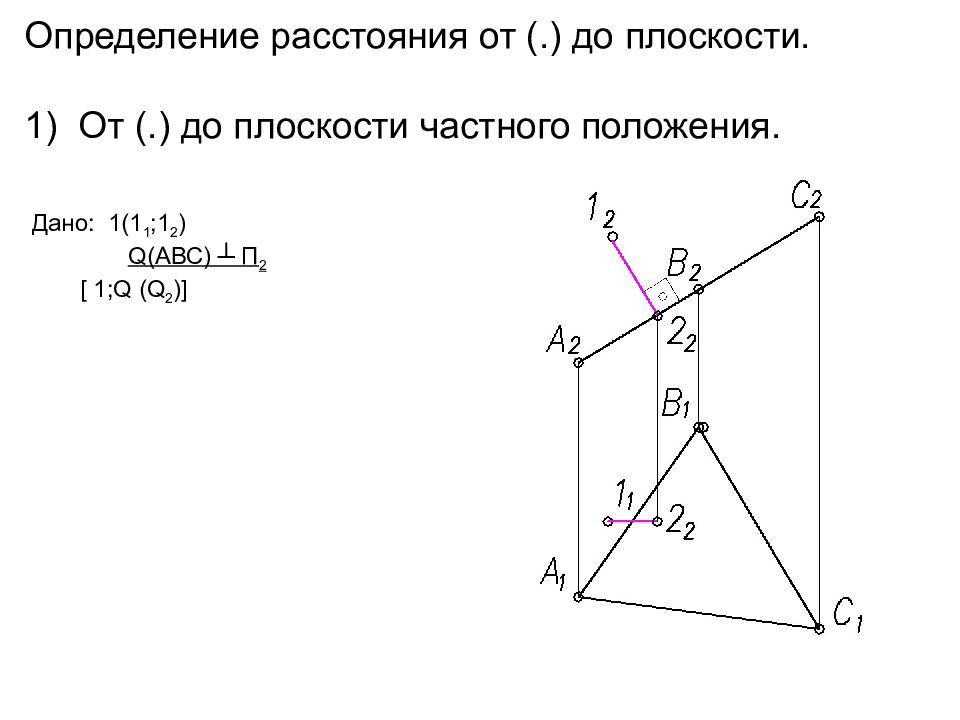
Определение расстояния от (. ) до плоскости. От (.) до плоскости частного положения. Дано: 1(1 1 ;1 2 ) Q (АВС) ┴ П 2 [ 1; Q (Q 2 )]
Слайд 69
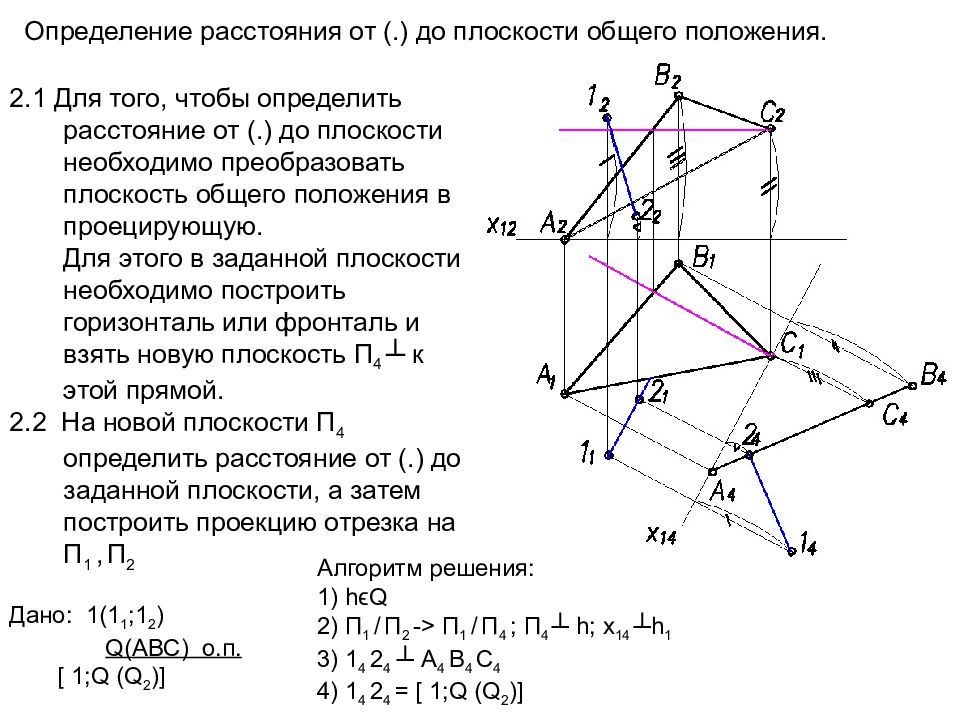
Определение расстояния от (. ) до плоскости общего положения. Дано: 1(1 1 ;1 2 ) Q (АВС) о.п. [ 1; Q (Q 2 )] 2.1 Для того, чтобы определить расстояние от (.) до плоскости необходимо преобразовать плоскость общего положения в проецирующую. Для этого в заданной плоскости необходимо построить горизонталь или фронталь и взять новую плоскость П 4 ┴ к этой прямой. 2.2 На новой плоскости П 4 определить расстояние от (.) до заданной плоскости, а затем построить проекцию отрезка на П 1, П 2 Алгоритм решения: 1) h ϵ Q 2) П 1 / П 2 -> П 1 / П 4 ; П 4 ┴ h ; х 14 ┴h 1 3) 1 4 2 4 ┴ А 4 В 4 С 4 4 ) 1 4 2 4 = [ 1; Q (Q 2 )]
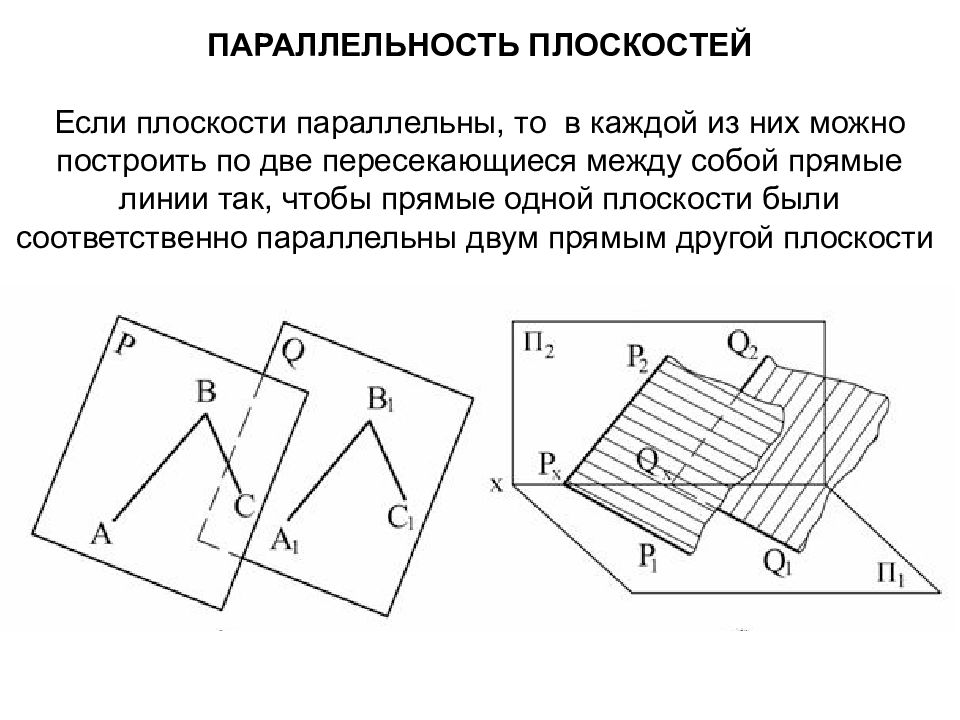
Слайд 70: Параллельность плоскостей Если плоскости параллельны, то в каждой из них можно построить по две пересекающиеся между собой прямые линии так, чтобы прямые одной плоскости были соответственно параллельны двум прямым другой плоскости
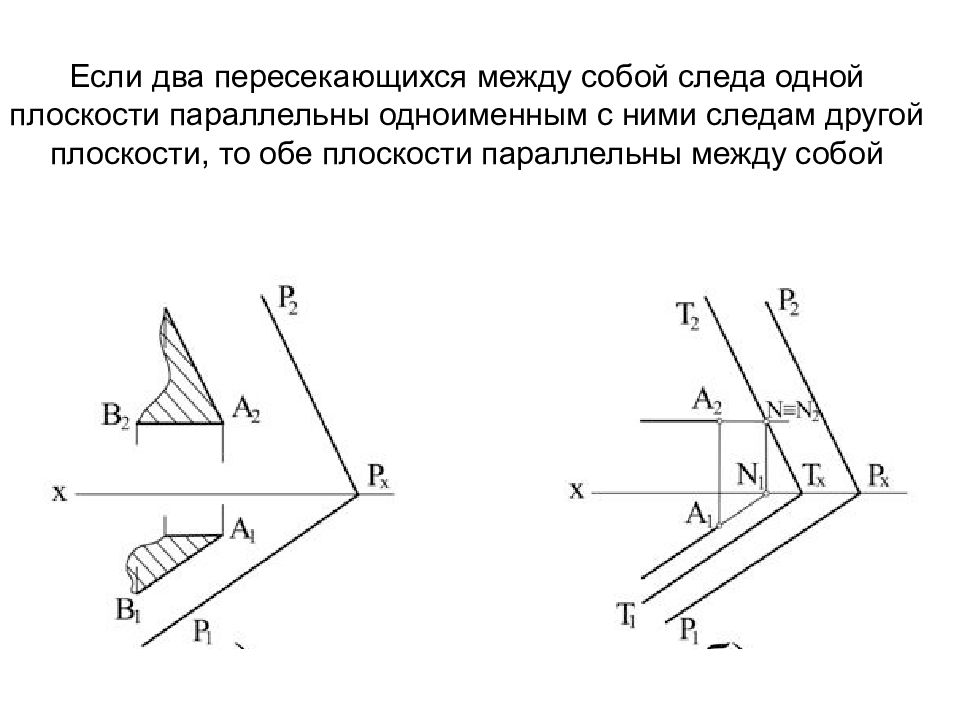
Слайд 71: Если два пересекающихся между собой следа одной плоскости параллельны одноименным с ними следам другой плоскости, то обе плоскости параллельны между собой
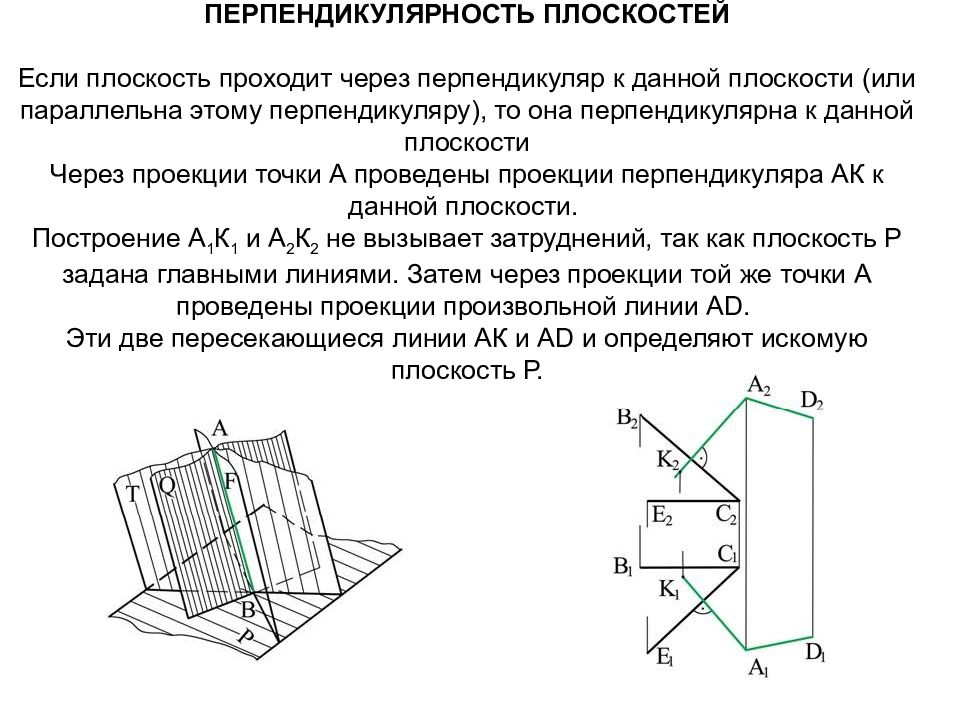
Слайд 72: Перпендикулярность плоскостей Если плоскость проходит через перпендикуляр к данной плоскости (или параллельна этому перпендикуляру), то она перпендикулярна к данной плоскости Через проекции точки А проведены проекции перпендикуляра АК к данной плоскости. Построение А 1 К 1 и А 2 К 2 не вызывает затруднений, так как плоскость Р задана главными линиями. Затем через проекции той же точки А проведены проекции произвольной линии А D. Эти две пересекающиеся линии АК и А D и определяют искомую плоскость Р
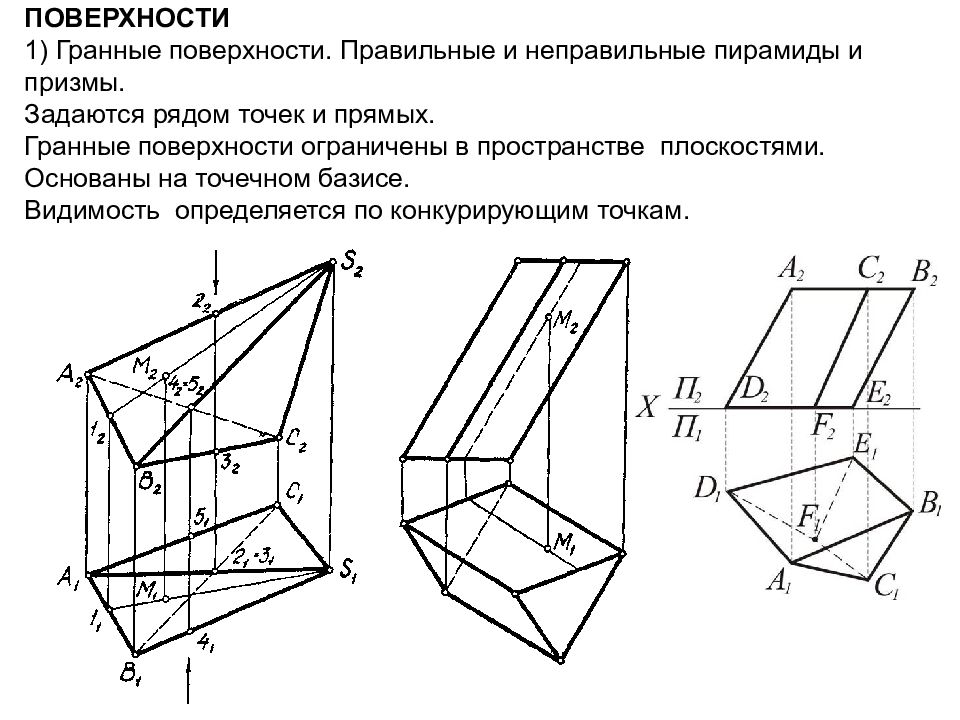
Слайд 73: поверхности 1) Гранные поверхности. Правильные и неправильные пирамиды и призмы. Задаются рядом точек и прямых. Гранные поверхности ограничены в пространстве плоскостями. Основаны на точечном базисе. Видимость определяется по конкурирующим точкам
Слайд 74
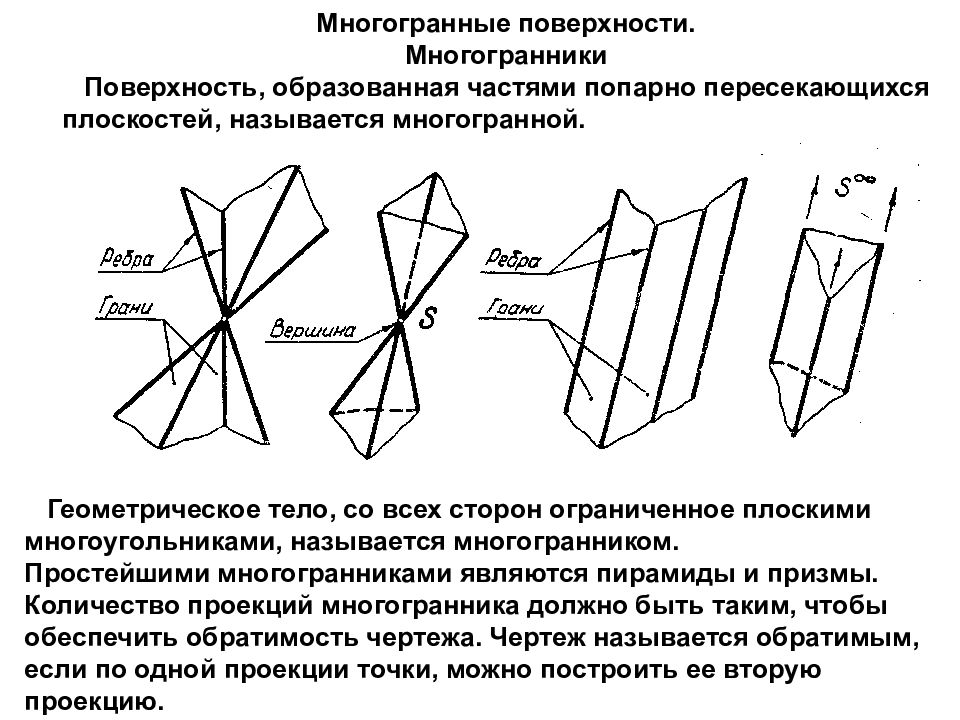
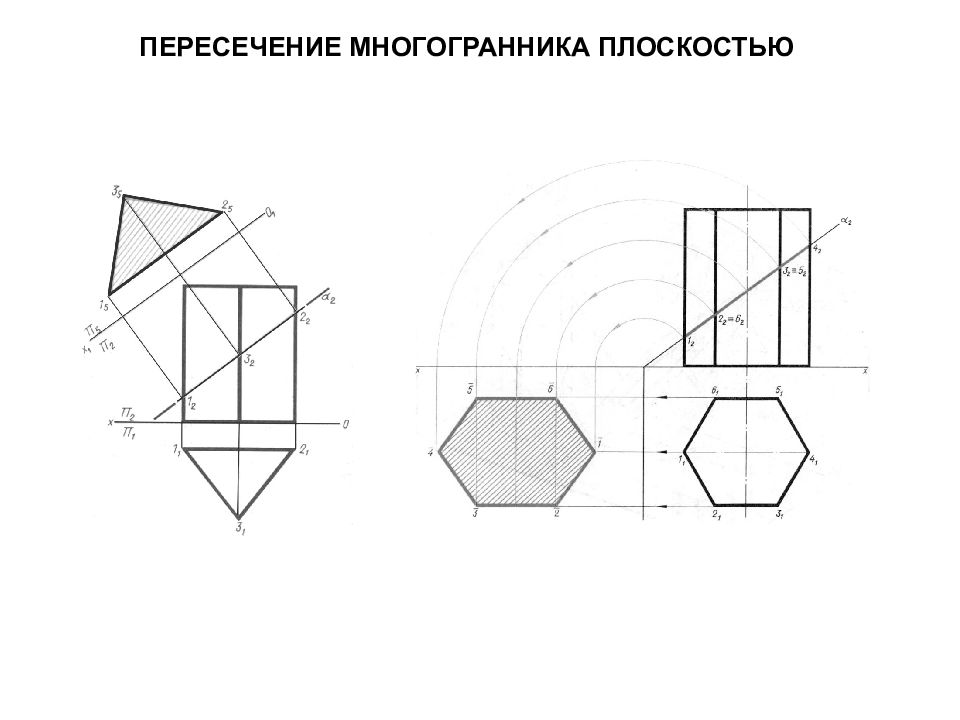
Многогранные поверхности. Многогранники Поверхность, образованная частями попарно пересекающихся плоскостей, называется многогранной. Геометрическое тело, со всех сторон ограниченное плоскими многоугольниками, называется многогранником. Простейшими многогранниками являются пирамиды и призмы. Количество проекций многогранника должно быть таким, чтобы обеспечить обратимость чертежа. Чертеж называется обратимым, если по одной проекции точки, можно построить ее вторую проекцию.
Слайд 75
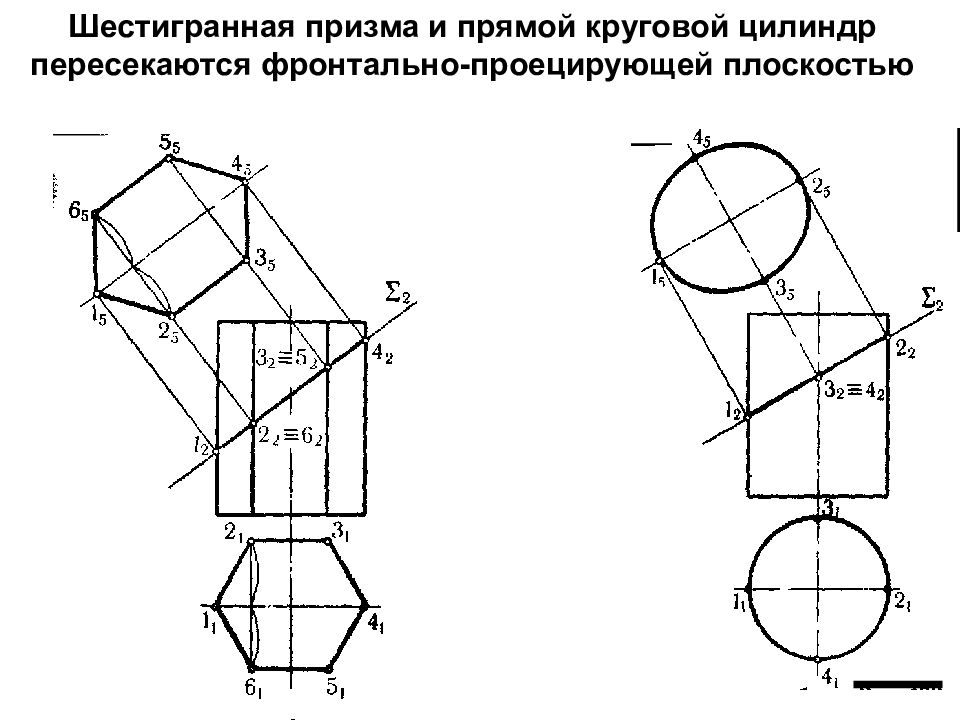
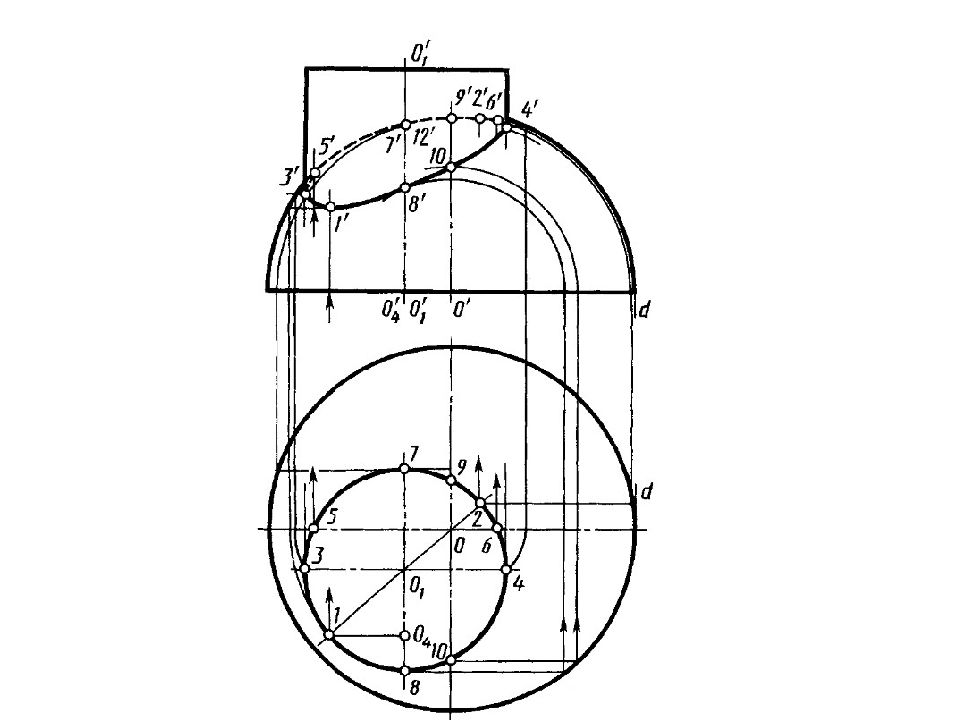
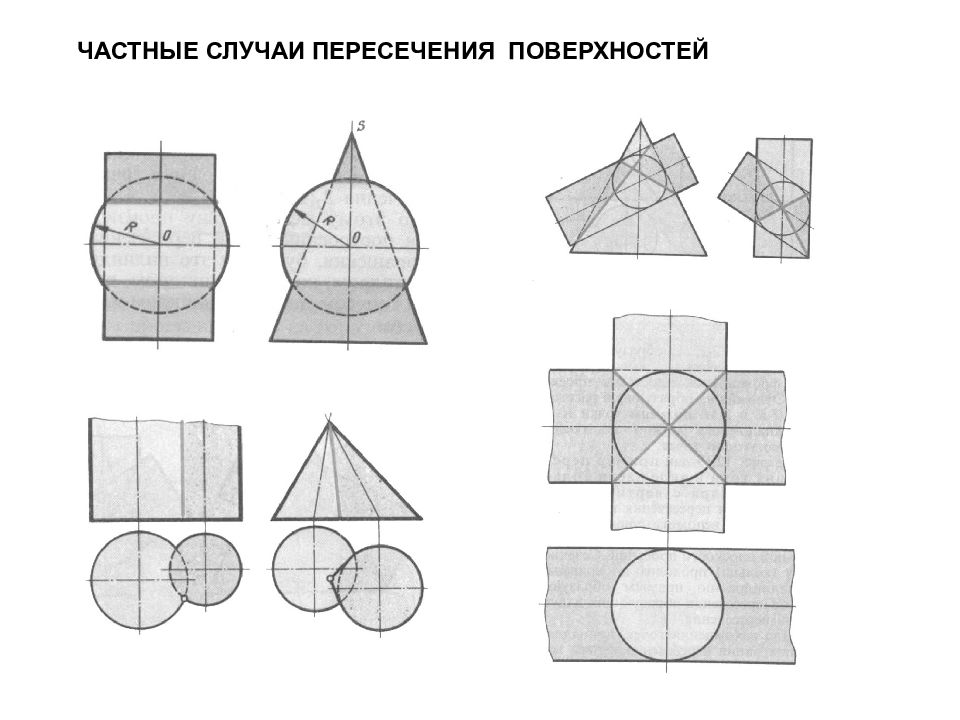
Шестигранная призма и прямой круговой цилиндр пересекаются фронтально-проецирующей плоскостью
Слайд 78
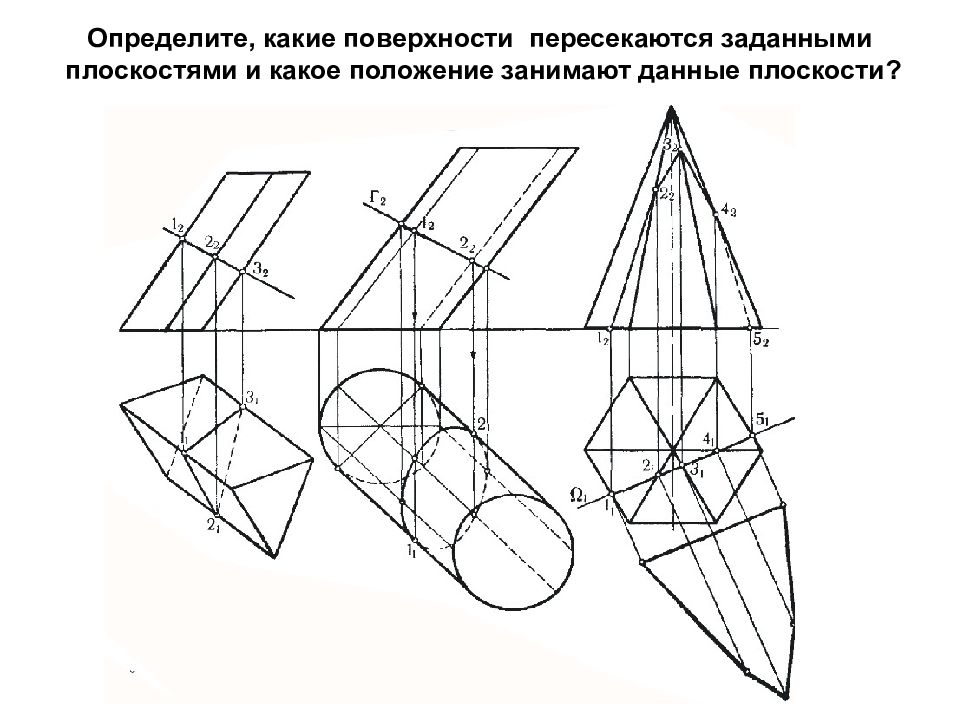
Определите, какие поверхности пересекаются заданными плоскостями и какое положение занимают данные плоскости ?
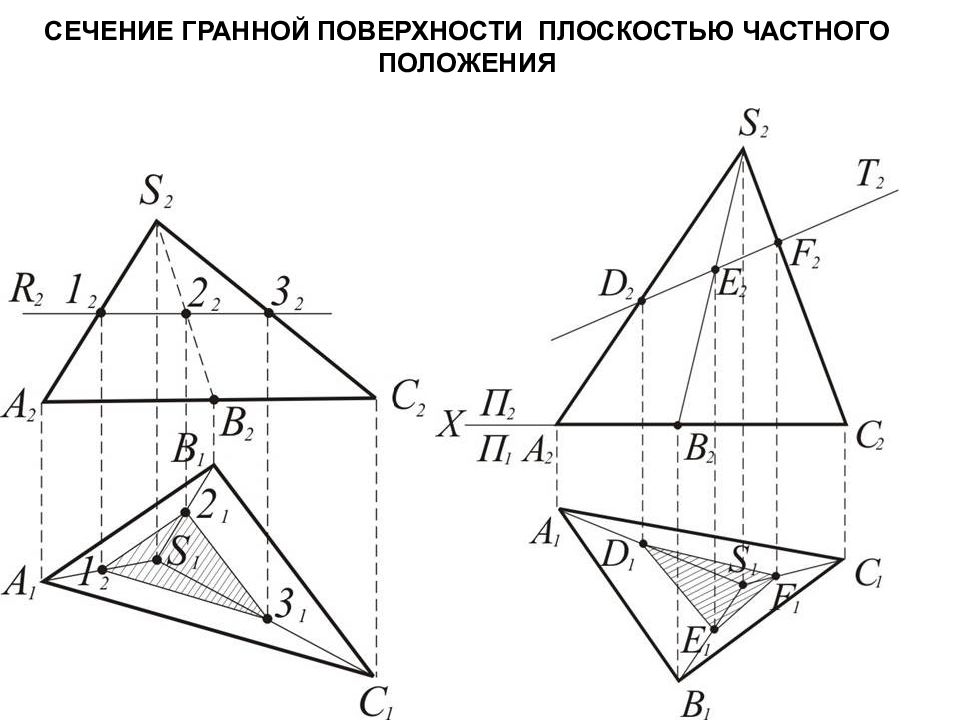
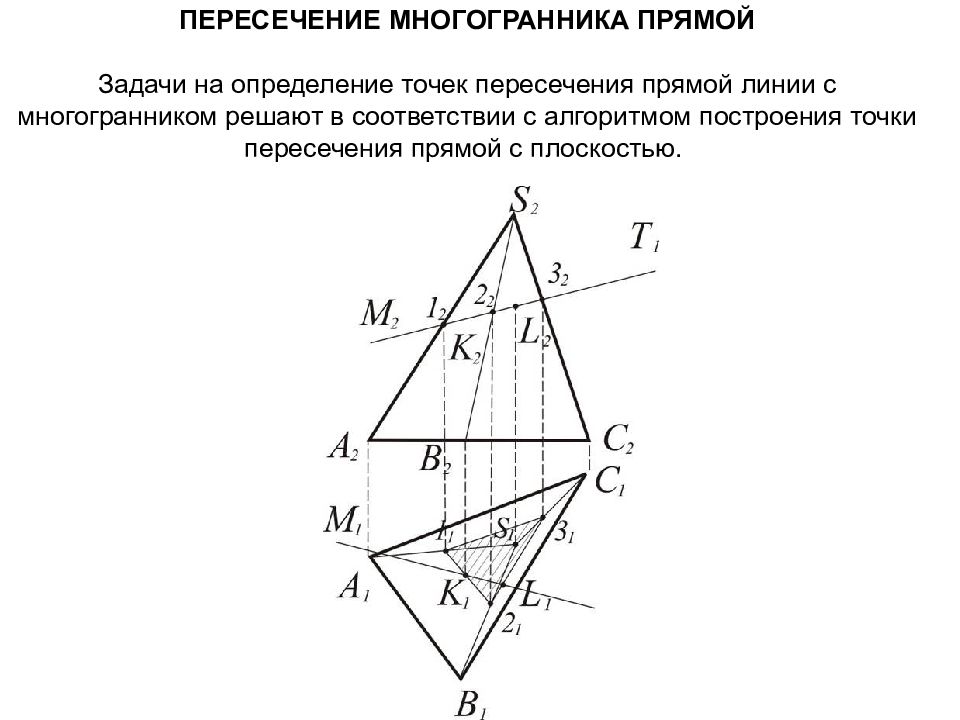
Слайд 79: Пересечение многогранника прямой Задачи на определение точек пересечения прямой линии с многогранником решают в соответствии с алгоритмом построения точки пересечения прямой с плоскостью
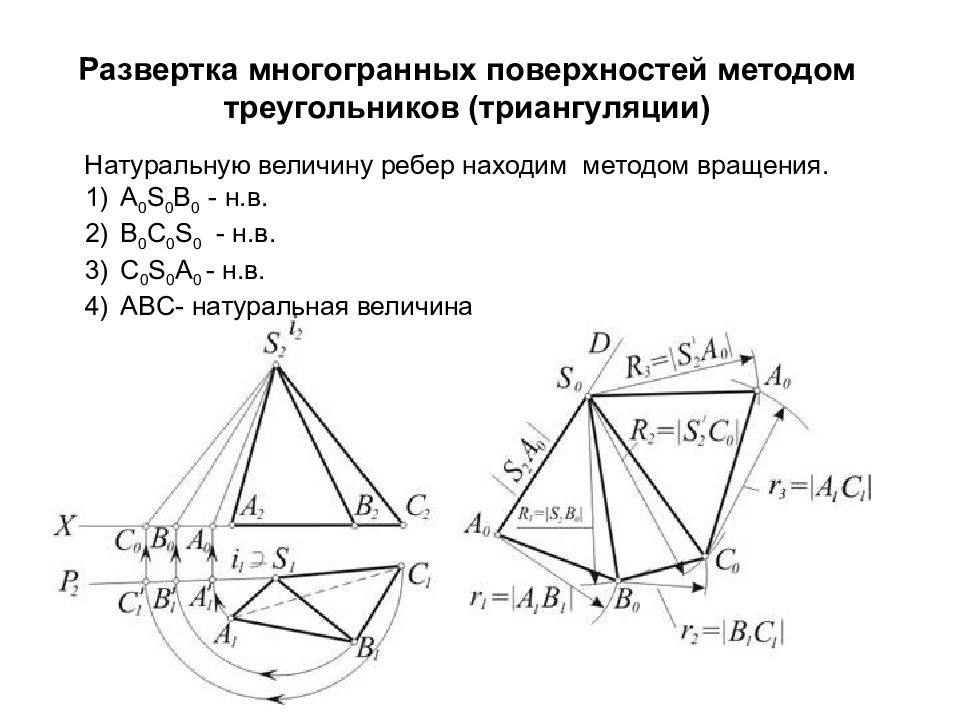
Слайд 80: Развертка многогранных поверхностей методом треугольников (триангуляции)
Натуральную величину ребер находим методом вращения. А 0 S 0 B 0 - н.в. B 0 C 0 S 0 - н.в. C 0 S 0 A 0 - н.в. ABC- натуральная величина
Слайд 81
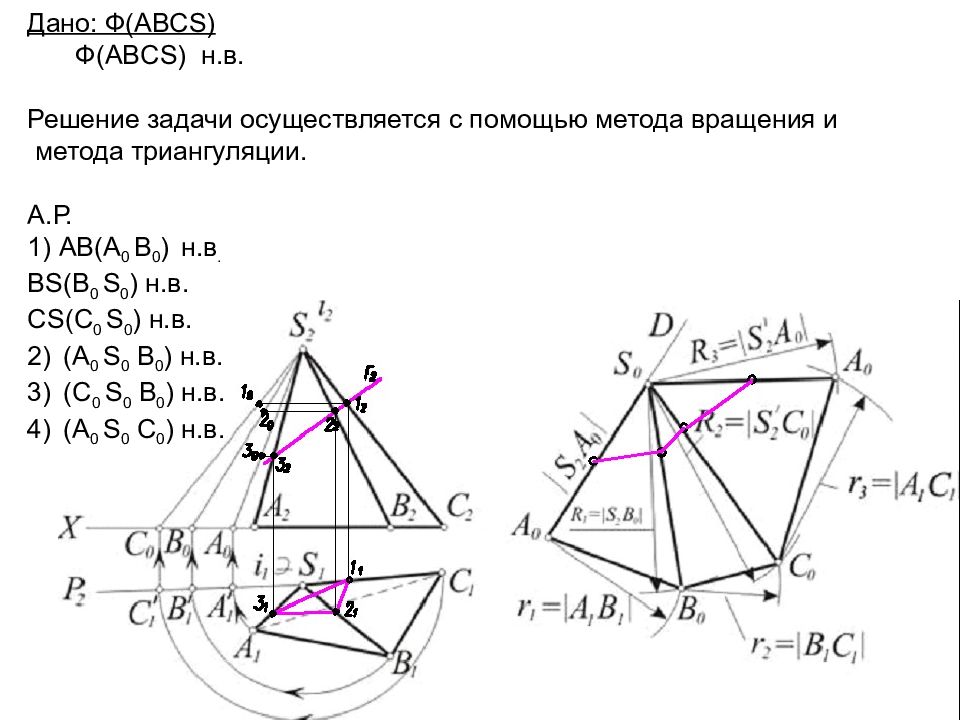
Дано: Ф( ABCS) Ф( ABCS) н.в. Решение задачи осуществляется с помощью метода вращения и метода триангуляции. А.Р. 1) АВ(А 0 В 0 ) н.в. BS ( B 0 S 0 ) н.в. CS ( C 0 S 0 ) н.в. (A 0 S 0 B 0 ) н.в. (C 0 S 0 B 0 ) н.в. (A 0 S 0 C 0 ) н.в.
Слайд 82
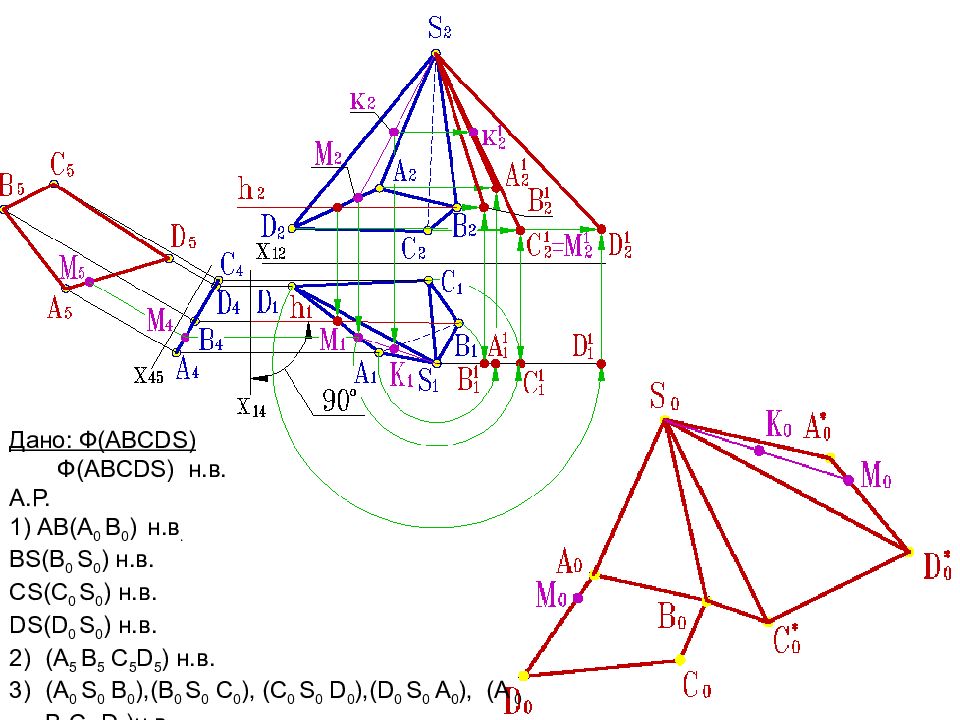
Дано: Ф( ABCDS) Ф( ABCDS) н.в. А.Р. 1) АВ(А 0 В 0 ) н.в. BS ( B 0 S 0 ) н.в. CS ( C 0 S 0 ) н.в. DS ( D 0 S 0 ) н.в. (A 5 B 5 C 5 D 5 ) н.в. (A 0 S 0 B 0 ),(B 0 S 0 C 0 ), (C 0 S 0 D 0 ),(D 0 S 0 A 0 ), (A 0 B 0 C 0 D 0 ) н.в.
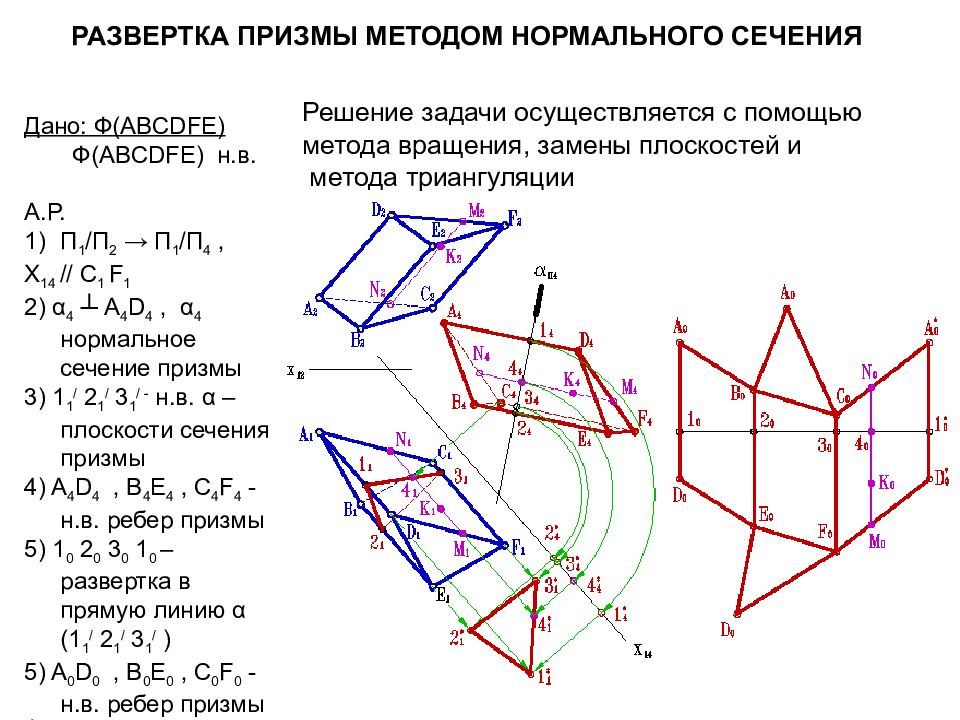
Слайд 83: Развертка призмы методом нормального сечения
Дано: Ф( ABCDFE) Ф( ABCDFE) н.в. А.Р. П 1 /П 2 → П 1 /П 4, Х 14 // С 1 F 1 2) α 4 ┴ A 4 D 4, α 4 нормальное сечение призмы 3 ) 1 1 / 2 1 / 3 1 / - н.в. α – плоскости сечения призмы 4) A 4 D 4, В 4 Е 4, С 4 F 4 - н.в. ребер призмы 5) 1 0 2 0 3 0 1 0 – развертка в прямую линию α (1 1 / 2 1 / 3 1 / ) 5) A 0 D 0, В 0 Е 0, С 0 F 0 - н.в. ребер призмы ┴ 1 0 2 0 3 0 1 0 Решение задачи осуществляется с помощью метода вращения, замены плоскостей и метода триангуляции
Слайд 84
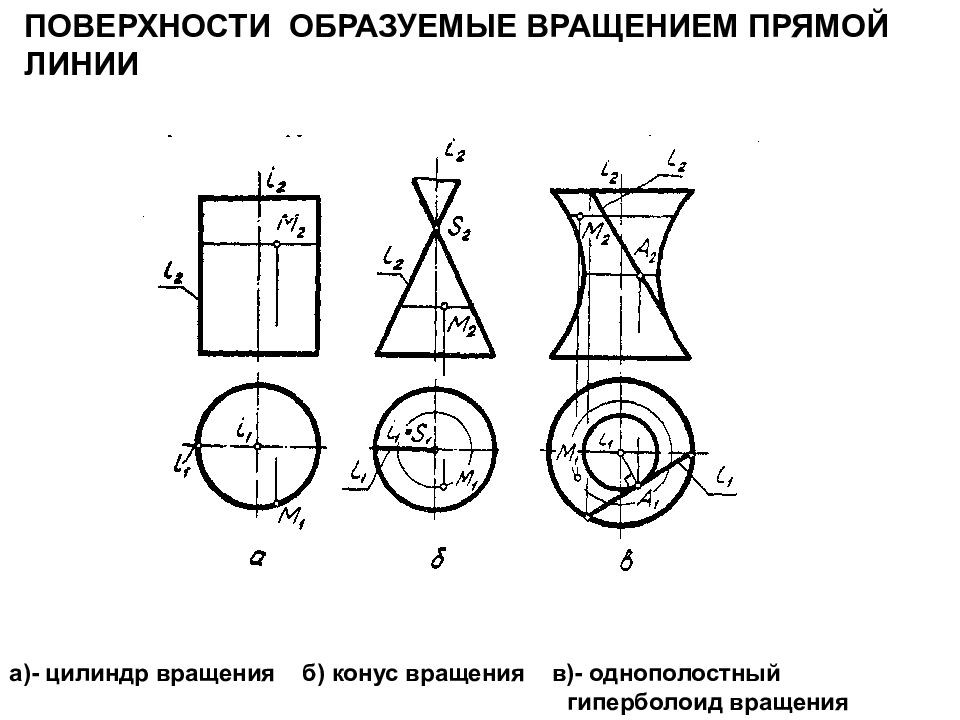
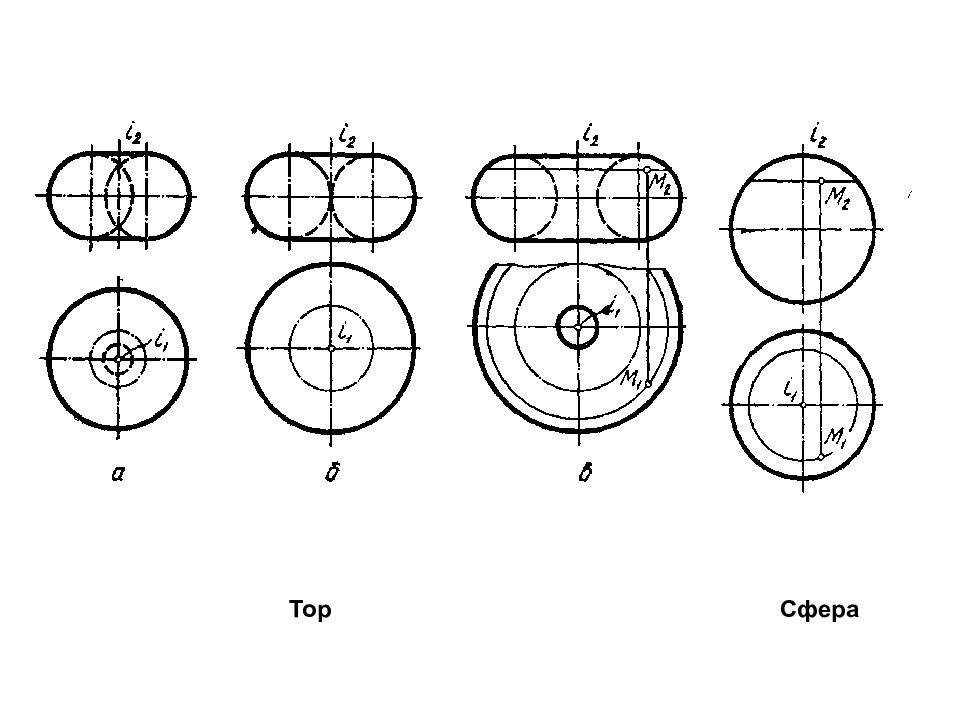
Кривые поверхности Кривые поверхности делятся на линейчатые и нелинейчатые, т.е. криволинейные. Линейчатые поверхности- у которых образующая прямая. Поверхности вращения – образуется вращением образующей вокруг оси. Цилиндрические : i //L ( образующая); Конические : L ∩ i ; Однополосный гиперболоид : L ﭞ I Особое место среди поверхностей вращения занимают сферические поверхности (шар, открытый тор (кольцо), закрытый тор, эллипсоид вращения, гиперболоид вращения, параболоид вращения). Эти поверхности называются алгебраическими поверхностями, т.к. их можно задать формулой. Эти поверхности задаются проекциями – очерками.
Слайд 85
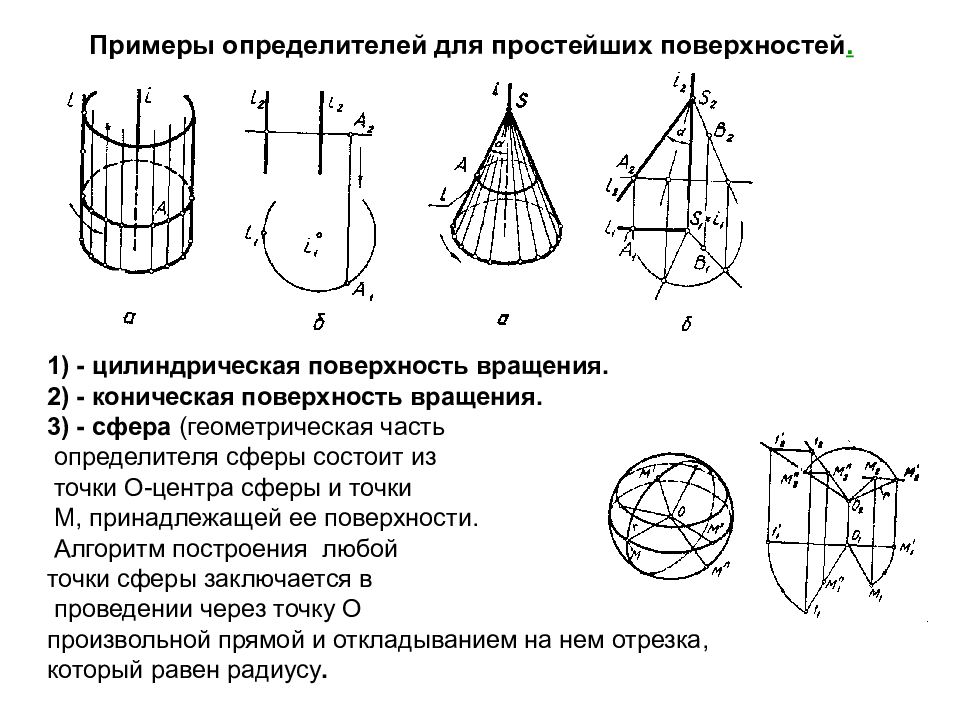
1) - цилиндрическая поверхность вращения. 2) - коническая поверхность вращения. 3) - сфера (геометрическая часть определителя сферы состоит из точки О-центра сферы и точки М, принадлежащей ее поверхности. Алгоритм построения любой точки сферы заключается в проведении через точку О произвольной прямой и откладыванием на нем отрезка, который равен радиусу. Примеры определителей для простейших поверхностей.
Слайд 86
Очерк поверхности Для придания чертежу поверхности большей наглядности прибегают к построению очерков ее проекций или проекций достаточно плотного каркаса ее образующих (в случаях, когда проекции поверхности не имеют определенного очерка) на основании алгоритмической части ее определителя. Очерк проекции поверхности является проекцией соответствующей линии видимого контура. Линия видимого контура поверхности разделяет ее на части- видимую, обращенную к наблюдателю, и невидимую.
Слайд 87
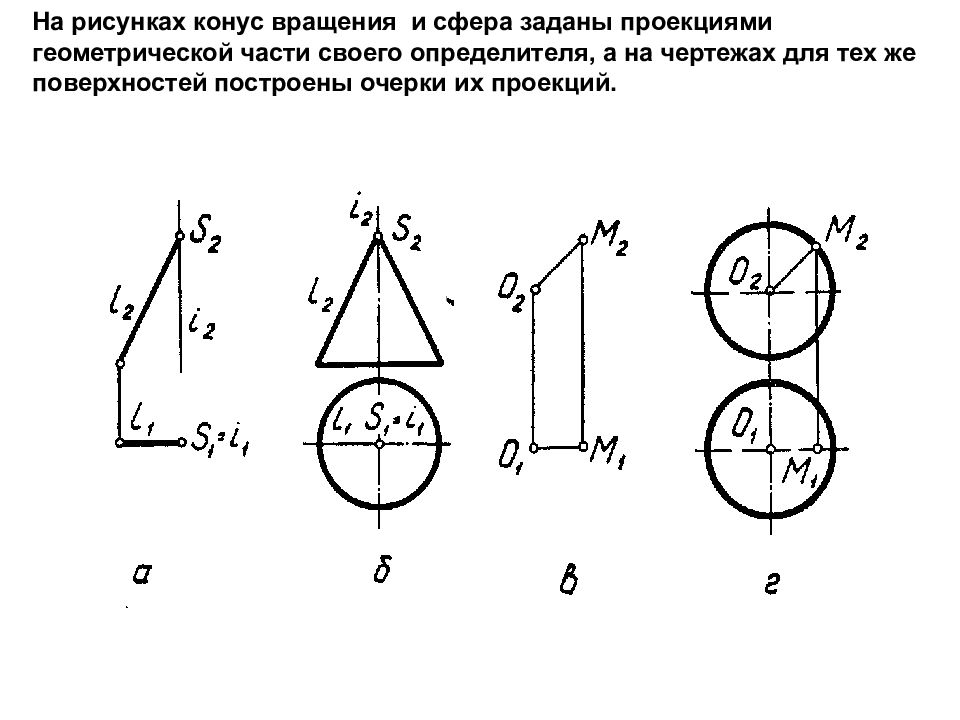
На рисунках конус вращения и сфера заданы проекциями геометрической части своего определителя, а на чертежах для тех же поверхностей построены очерки их проекций.
Слайд 88
а)- цилиндр вращения б) конус вращения в)- однополостный гиперболоид вращения поверхности ОБРАЗУЕМЫЕ ВРАЩЕНИЕМ ПРЯМОЙ ЛИНИИ
Слайд 89
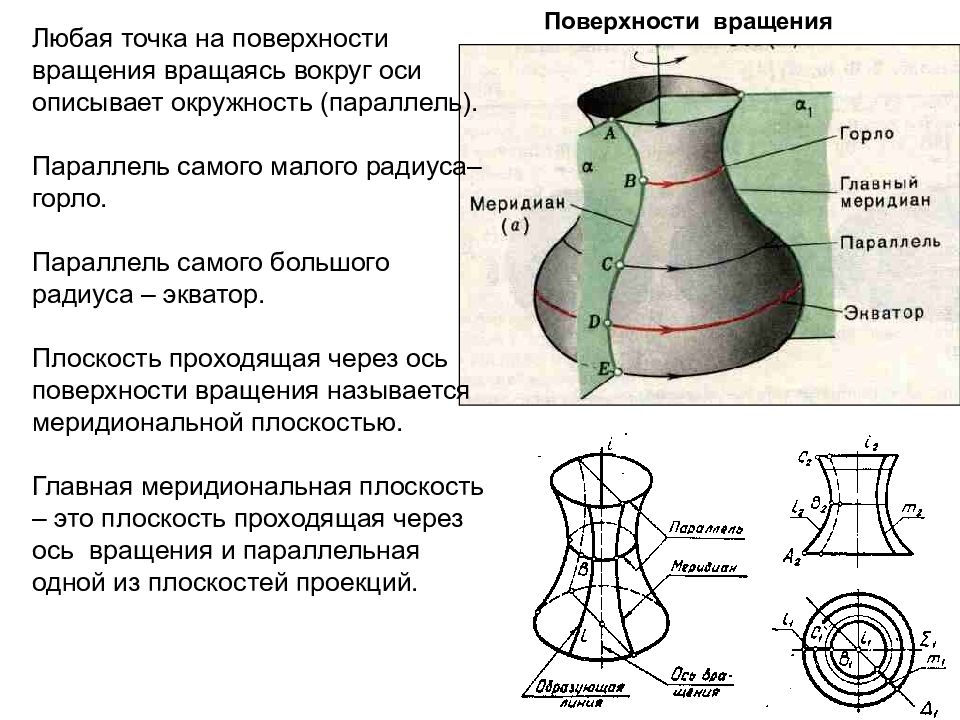
Поверхности вращения Любая точка на поверхности вращения вращаясь вокруг оси описывает окружность (параллель). Параллель самого малого радиуса– горло. Параллель самого большого радиуса – экватор. Плоскость проходящая через ось поверхности вращения называется меридиональной плоскостью. Главная меридиональная плоскость – это плоскость проходящая через ось вращения и параллельная одной из плоскостей проекций.
Слайд 90
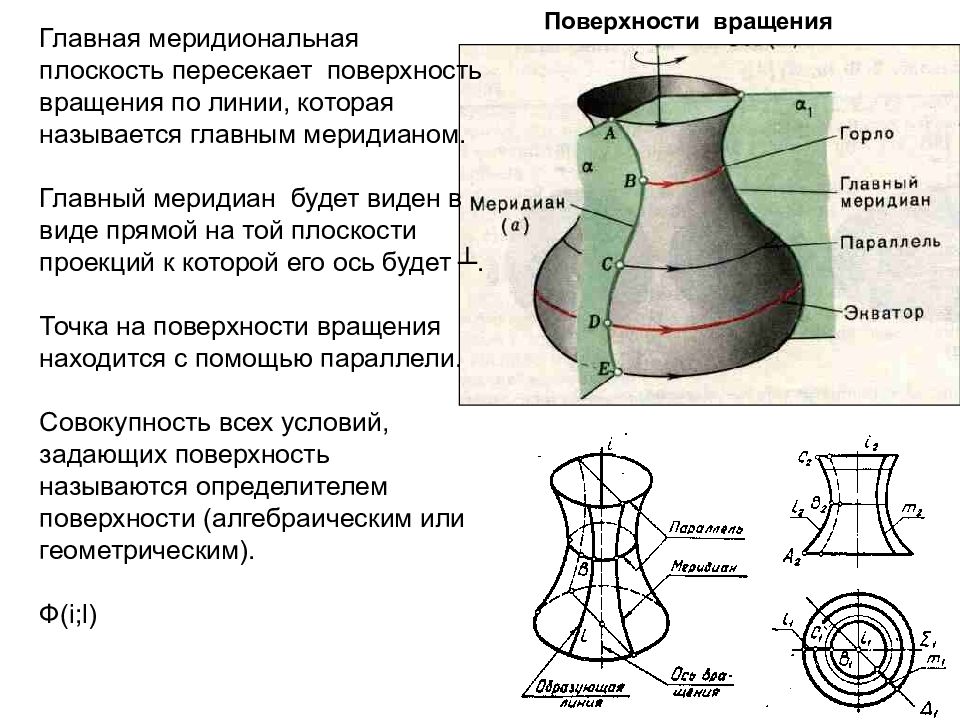
Поверхности вращения Главная меридиональная плоскость пересекает поверхность вращения по линии, которая называется главным меридианом. Главный меридиан будет виден в виде прямой на той плоскости проекций к которой его ось будет ┴. Точка на поверхности вращения находится с помощью параллели. Совокупность всех условий, задающих поверхность называются определителем поверхности (алгебраическим или геометрическим). Ф( i ; l)
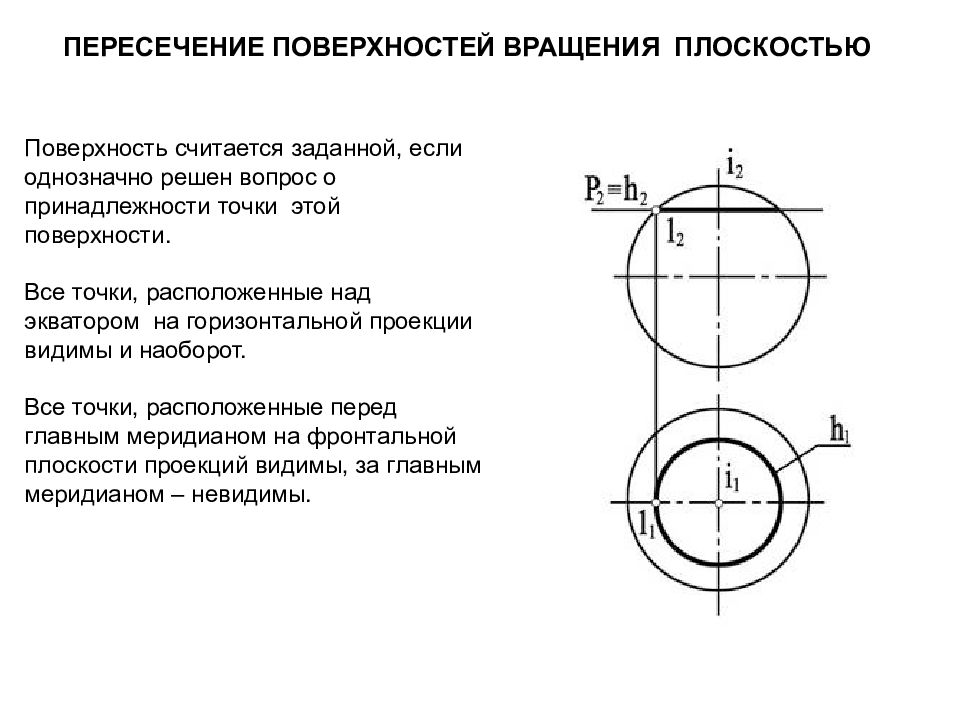
Слайд 92: Пересечение поверхностей вращения плоскостью
Поверхность считается заданной, если однозначно решен вопрос о принадлежности точки этой поверхности. Все точки, расположенные над экватором на горизонтальной проекции видимы и наоборот. Все точки, расположенные перед главным меридианом на фронтальной плоскости проекций видимы, за главным меридианом – невидимы.
Слайд 93
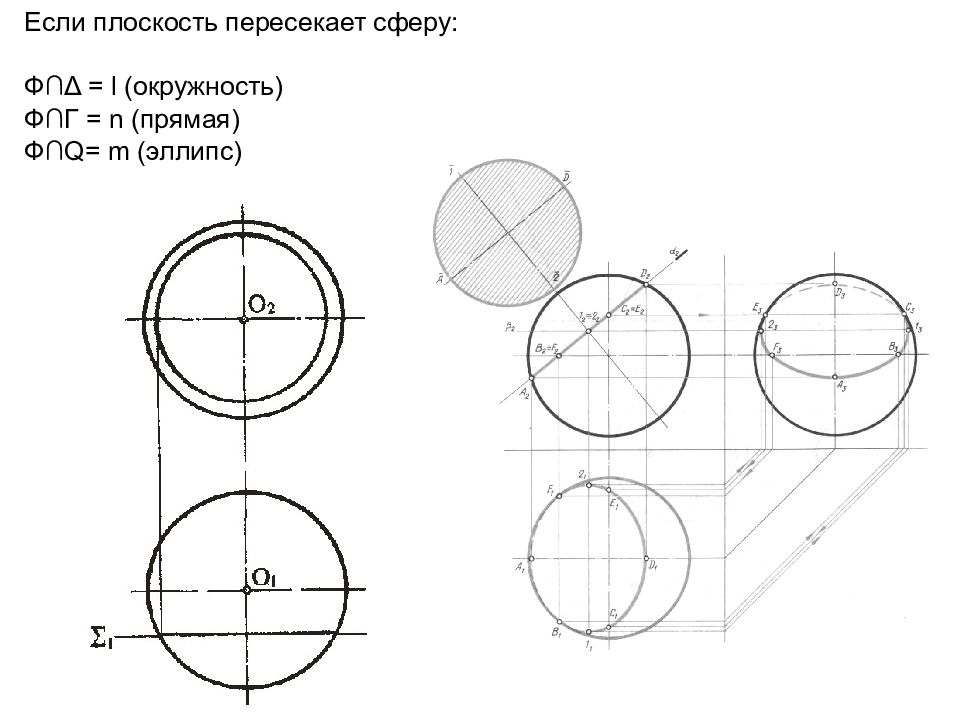
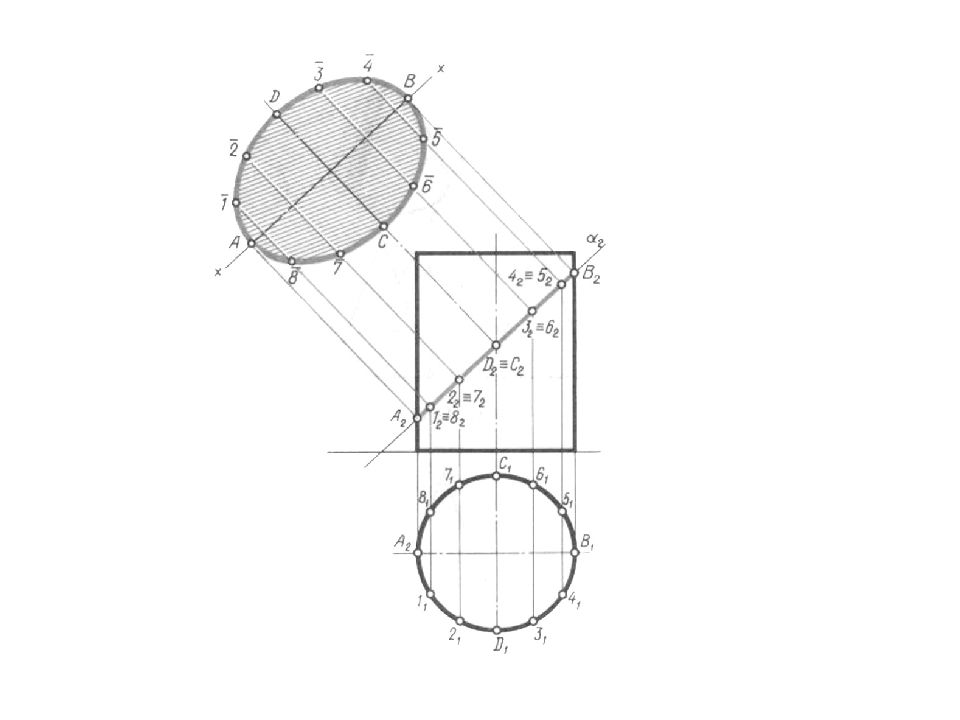
Если плоскость пересекает сферу: Ф∩ Δ = l (окружность) Ф∩Г = n (прямая) Ф∩ Q = m (эллипс)
Слайд 94
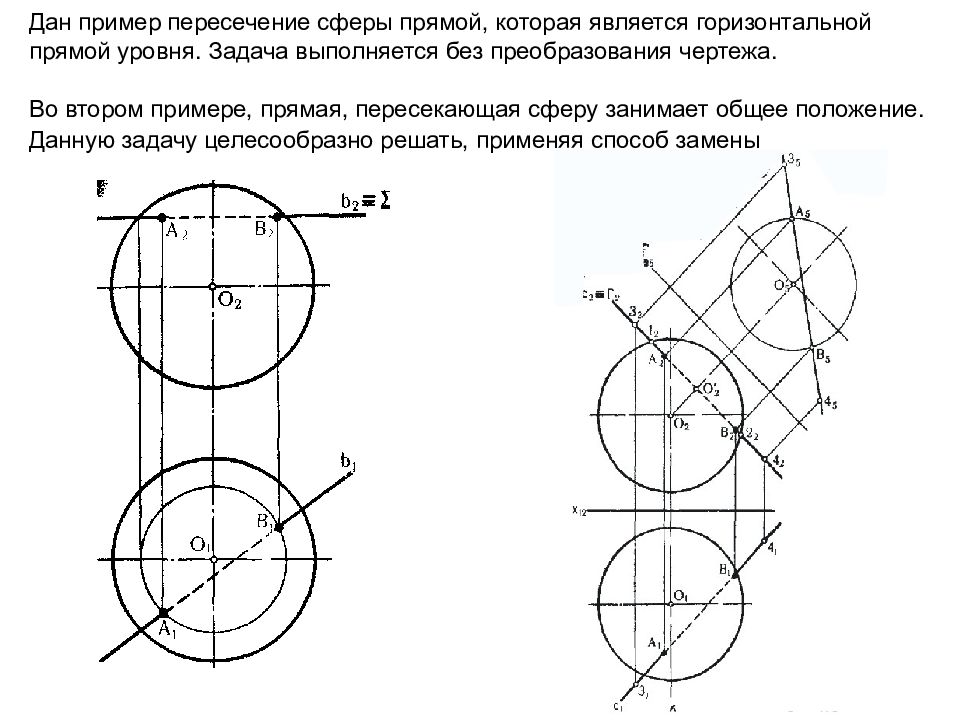
Дан пример пересечение сферы прямой, которая является горизонтальной прямой уровня. Задача выполняется без преобразования чертежа. Во втором примере, прямая, пересекающая сферу занимает общее положение. Данную задачу целесообразно решать, применяя способ замены.
Слайд 95
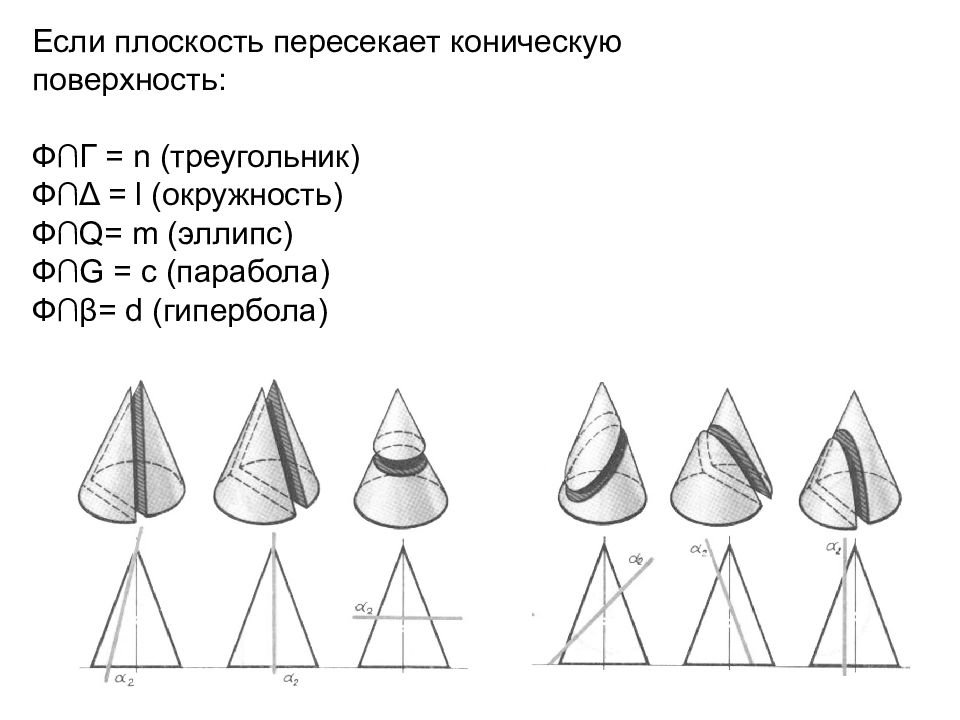
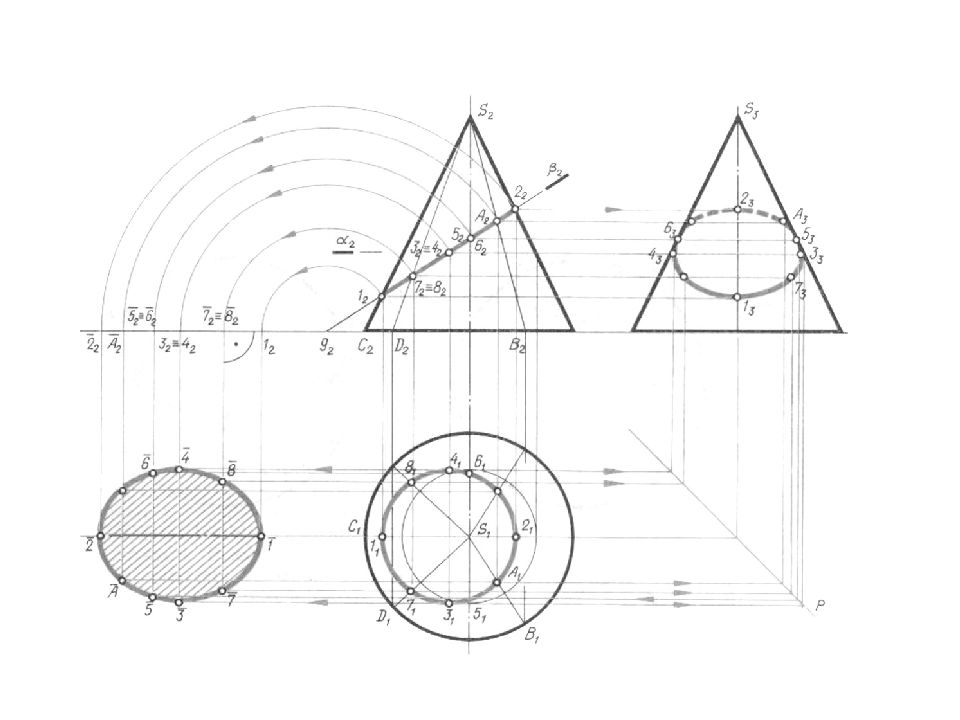
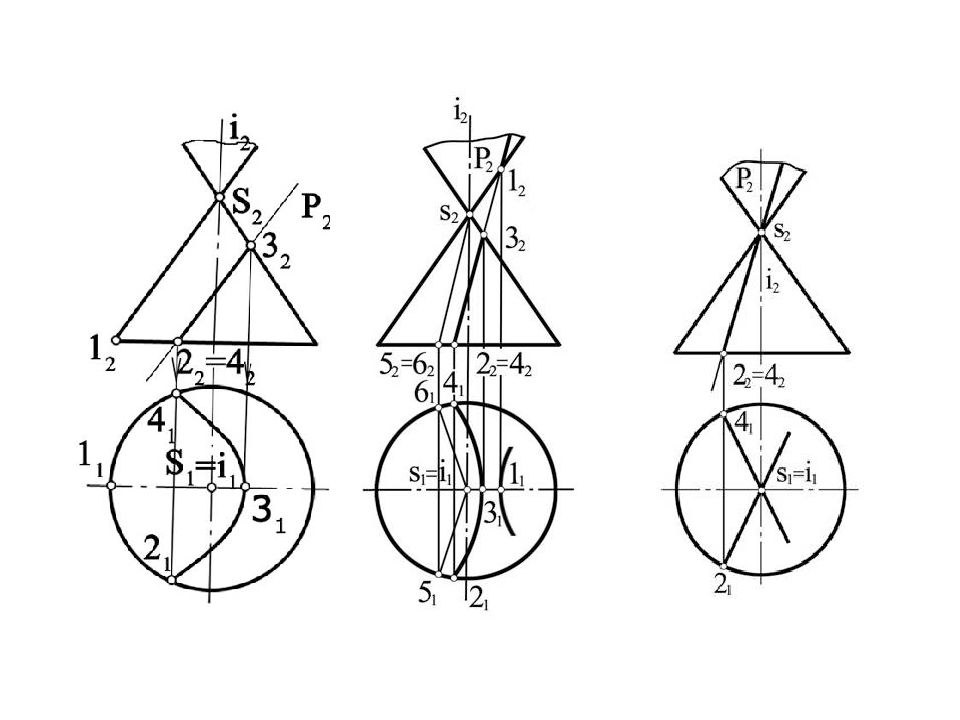
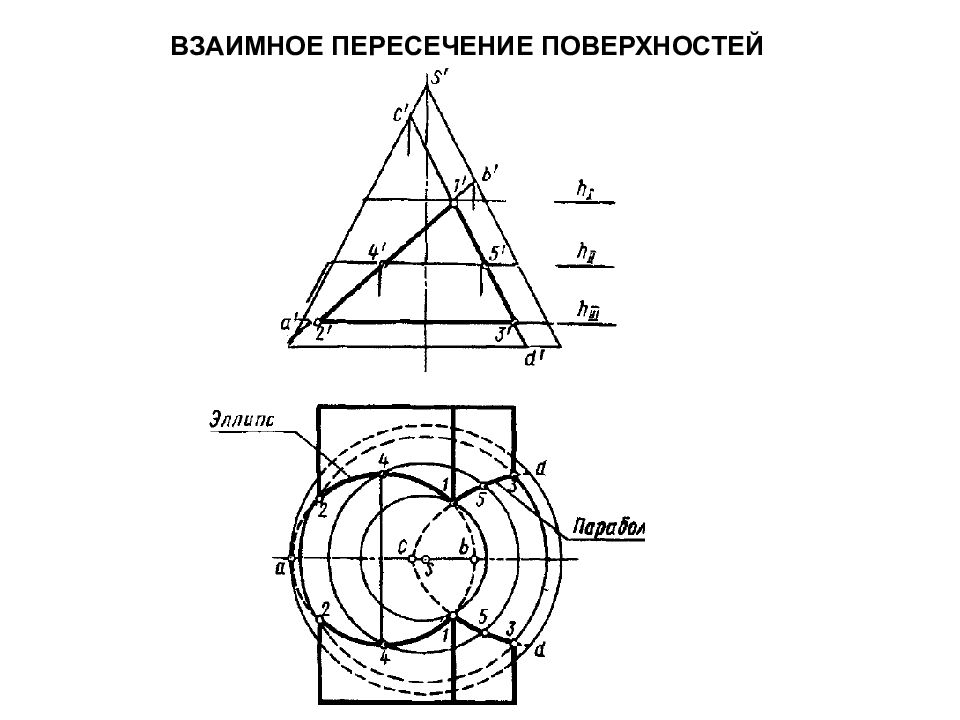
Если плоскость пересекает коническую поверхность: Ф∩Г = n (треугольник) Ф∩ Δ = l (окружность) Ф∩ Q = m (эллипс) Ф∩ G = c (парабола) Ф∩ β = d (гипербола)
Слайд 99
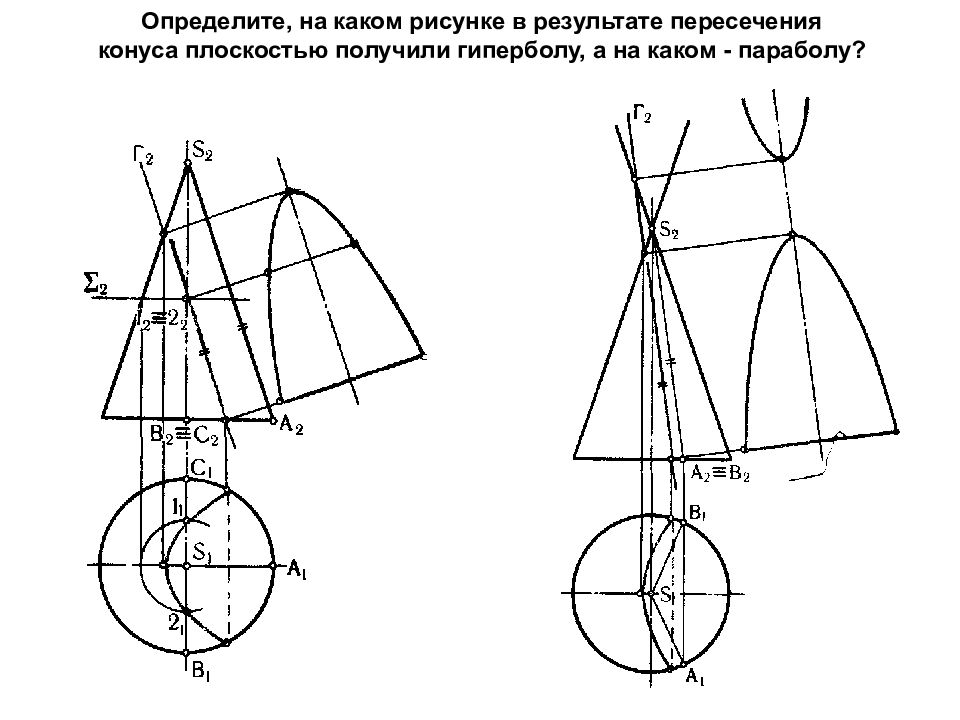
Определите, на каком рисунке в результате пересечения конуса плоскостью получили гиперболу, а на каком - параболу ?
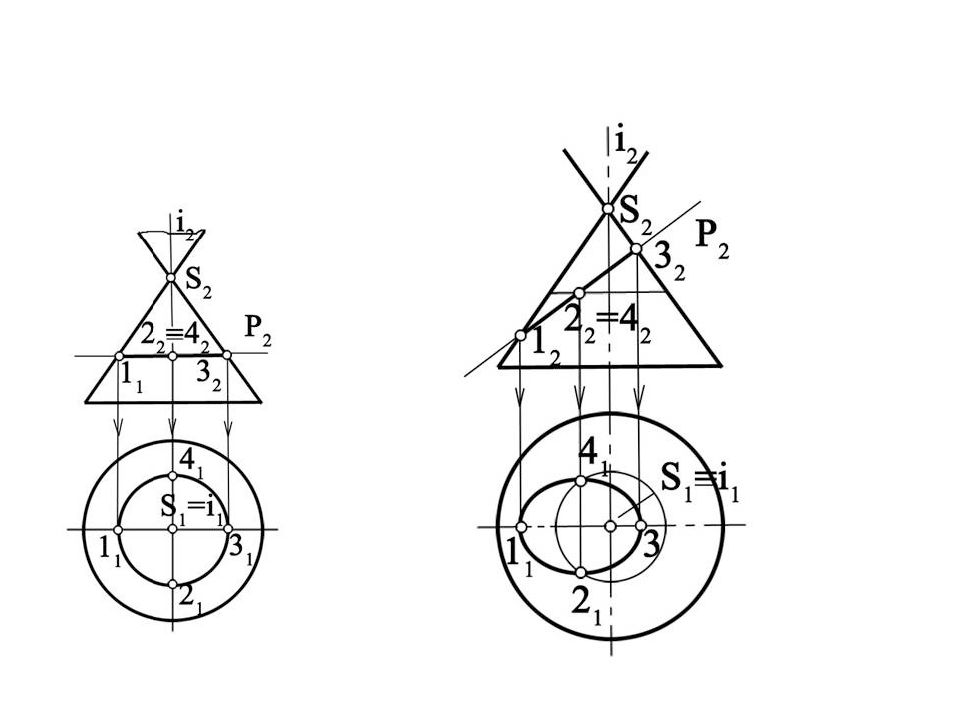
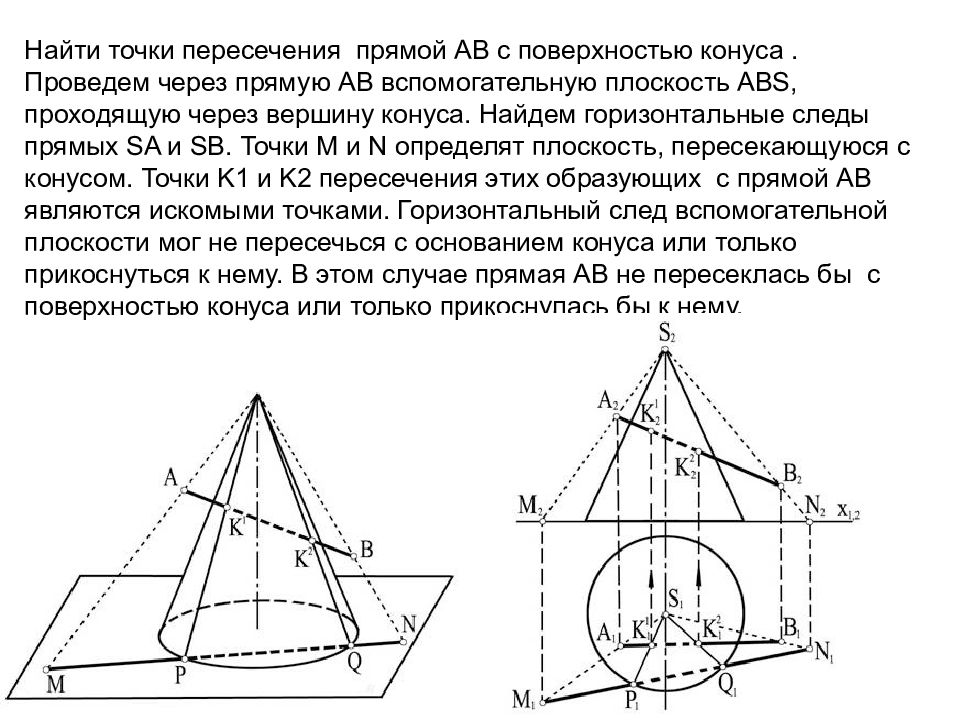
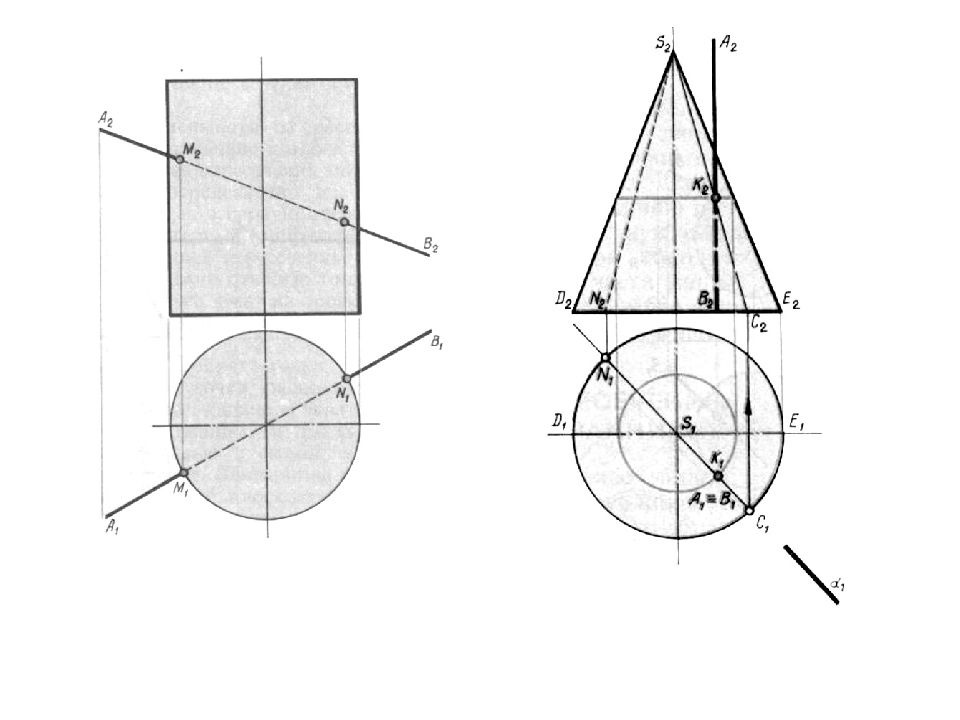
Слайд 100: Найти точки пересечения прямой АВ с поверхностью конуса. Проведем через прямую АВ вспомогательную плоскость ABS, проходящую через вершину конуса. Найдем горизонтальные следы прямых SA и SB. Точки M и N определят плоскость, пересекающуюся с конусом. Точки K 1 и K 2 пересечения этих образующих с прямой АВ являются искомыми точками. Горизонтальный след вспомогательной плоскости мог не пересечься с основанием конуса или только прикоснуться к нему. В этом случае прямая АВ не пересеклась бы с поверхностью конуса или только прикоснулась бы к нему
Слайд 102
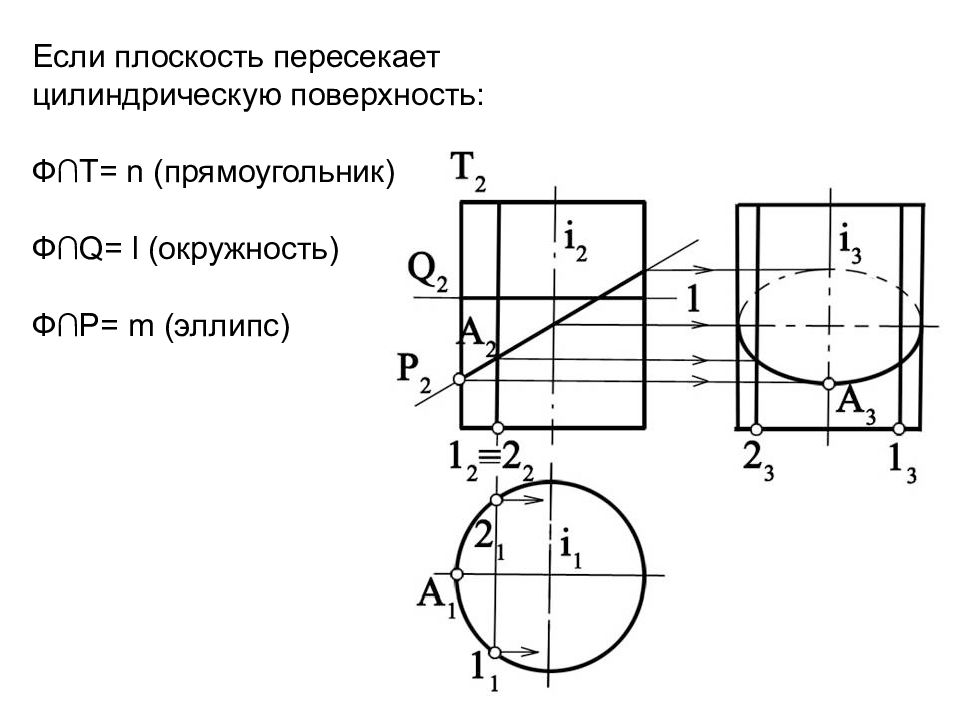
Если плоскость пересекает цилиндрическую поверхность: Ф∩Т= n (прямоугольник) Ф∩ Q = l (окружность) Ф∩ P = m (эллипс)
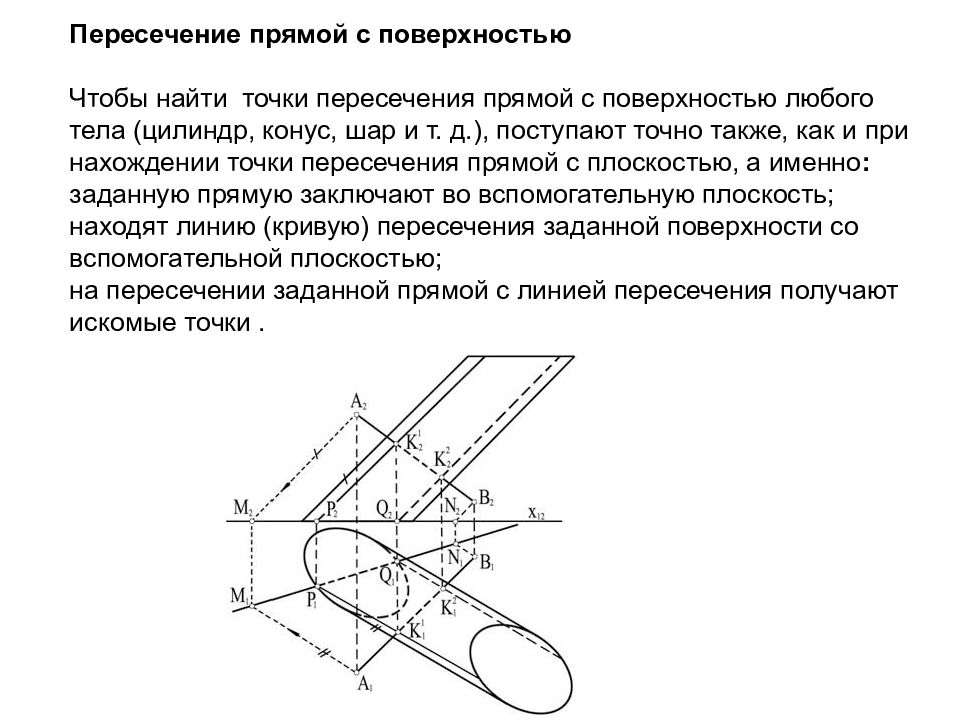
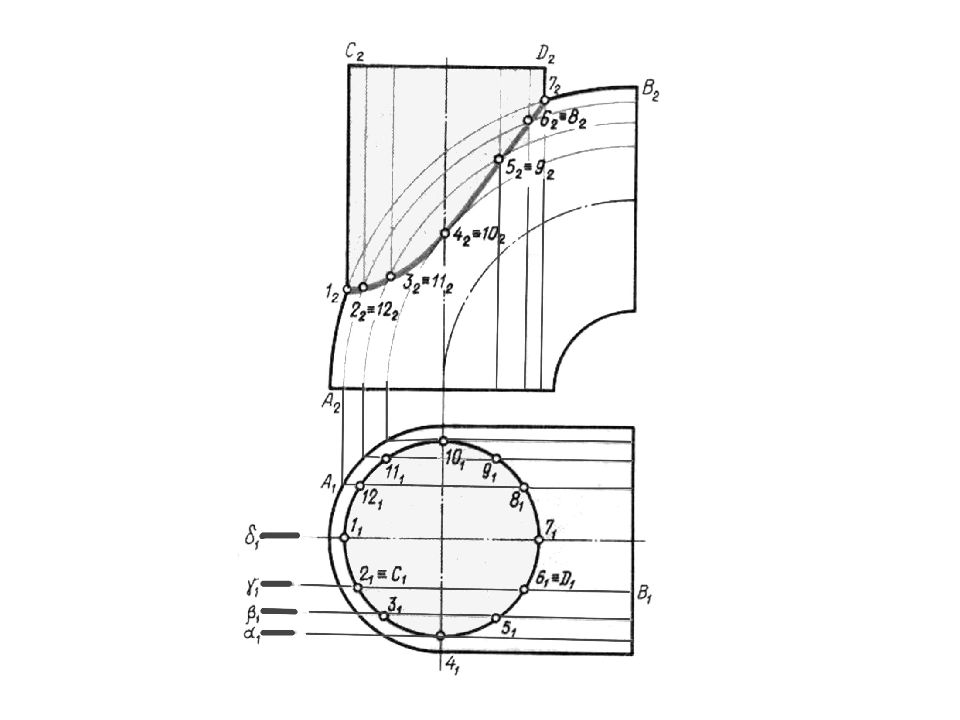
Слайд 104: Пересечение прямой с поверхностью Чтобы найти точки пересечения прямой с поверхностью любого тела (цилиндр, конус, шар и т. д.), поступают точно также, как и при нахождении точки пересечения прямой с плоскостью, а именно : заданную прямую заключают во вспомогательную плоскость; находят линию (кривую) пересечения заданной поверхности со вспомогательной плоскостью; на пересечении заданной прямой с линией пересечения получают искомые точки
Слайд 110
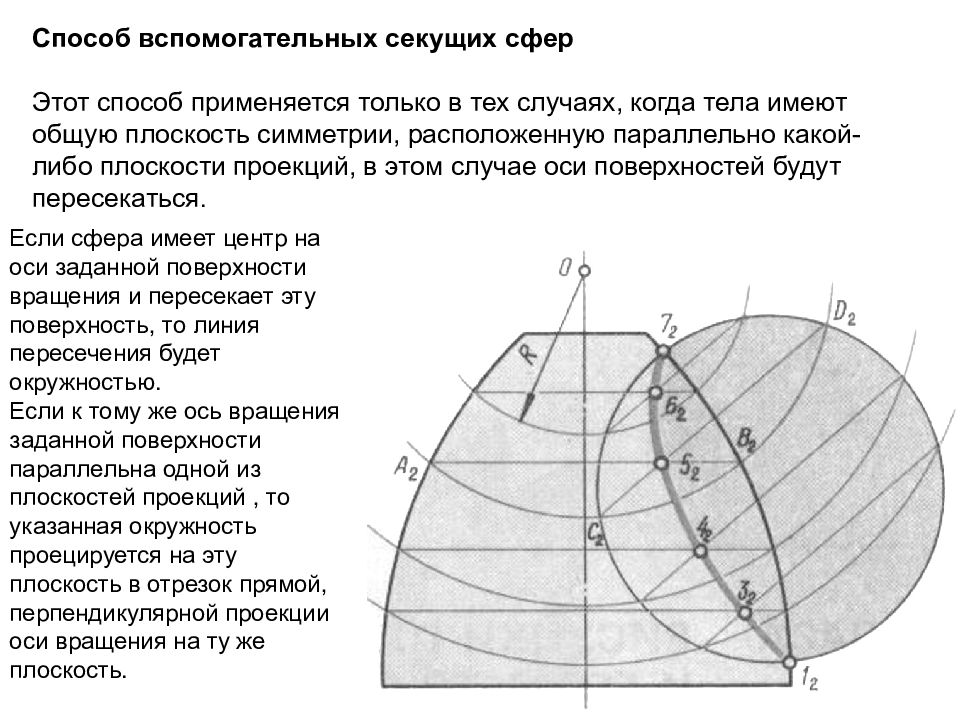
Способ вспомогательных секущих сфер Этот способ применяется только в тех случаях, когда тела имеют общую плоскость симметрии, расположенную параллельно какой-либо плоскости проекций, в этом случае оси поверхностей будут пересекаться. Если сфера имеет центр на оси заданной поверхности вращения и пересекает эту поверхность, то линия пересечения будет окружностью. Если к тому же ось вращения заданной поверхности параллельна одной из плоскостей проекций, то указанная окружность проецируется на эту плоскость в отрезок прямой, перпендикулярной проекции оси вращения на ту же плоскость.
Слайд 111
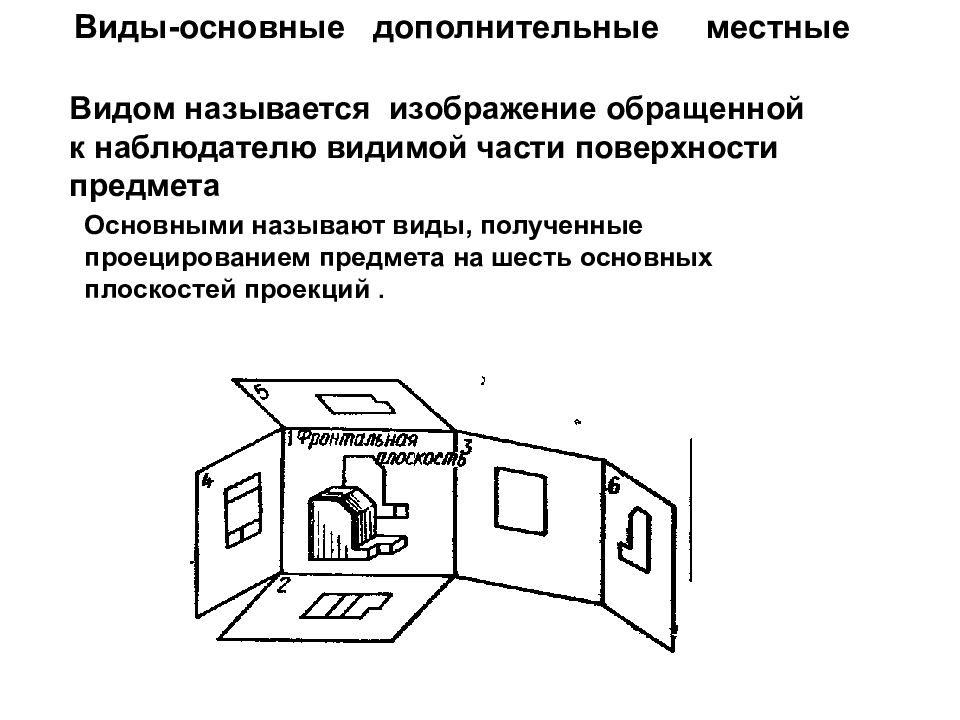
Видом называется изображение обращенной к наблюдателю видимой части поверхности предмета Виды-основные дополнительные местные Основными называют виды, полученные проецированием предмета на шесть основных плоскостей проекций.
Слайд 112
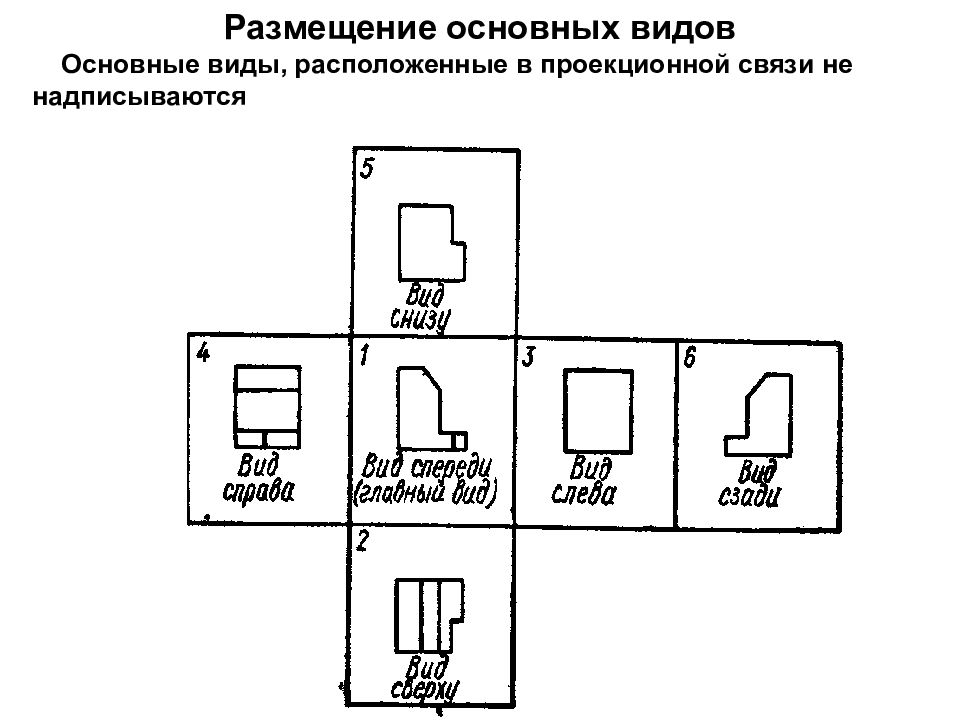
Размещение основных видов Основные виды, расположенные в проекционной связи не надписываются
Слайд 113
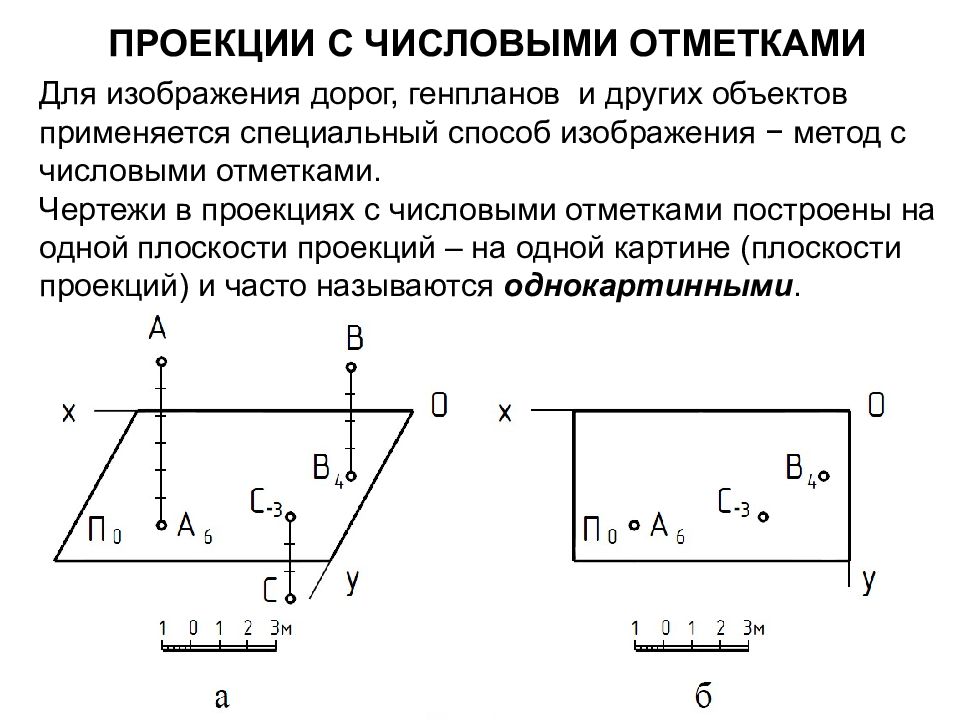
Проекции с числовыми отметками Для изображения дорог, генпланов и других объектов применяется специальный способ изображения − метод с числовыми отметками. Чертежи в проекциях с числовыми отметками построены на одной плоскости проекций – на одной картине (плоскости проекций) и часто называются однокартинными.
Слайд 114
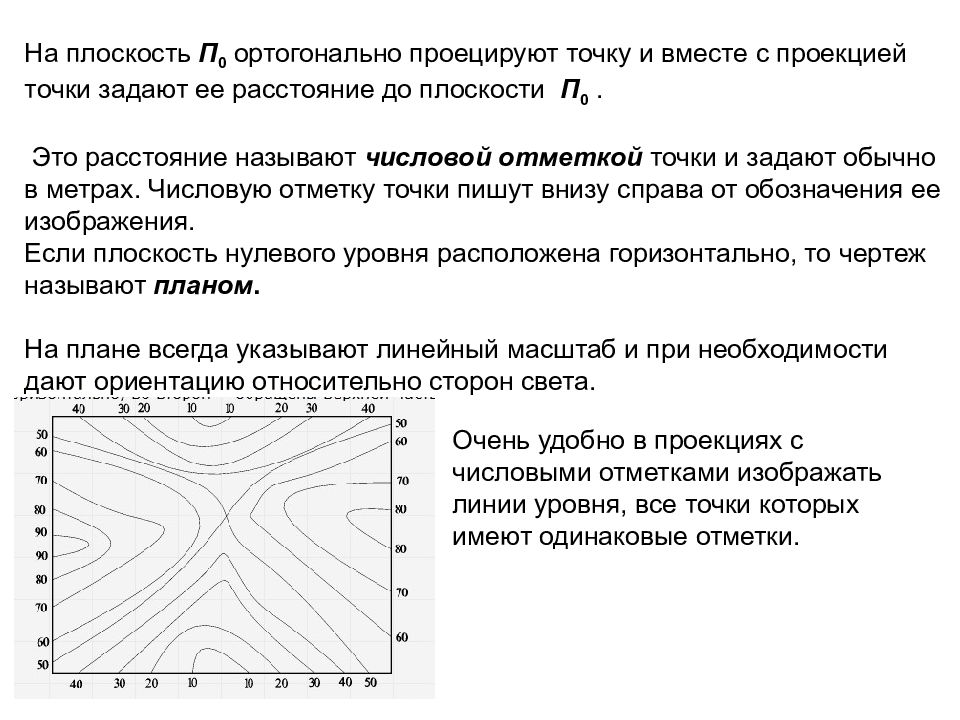
На плоскость П 0 ортогонально проецируют точку и вместе с проекцией точки задают ее расстояние до плоскости П 0. Это расстояние называют числовой отметкой точки и задают обычно в метрах. Числовую отметку точки пишут внизу справа от обозначения ее изображения. Если плоскость нулевого уровня расположена горизонтально, то чертеж называют планом. На плане всегда указывают линейный масштаб и при необходимости дают ориентацию относительно сторон света. Очень удобно в проекциях с числовыми отметками изображать линии уровня, все точки которых имеют одинаковые отметки.
Слайд 115
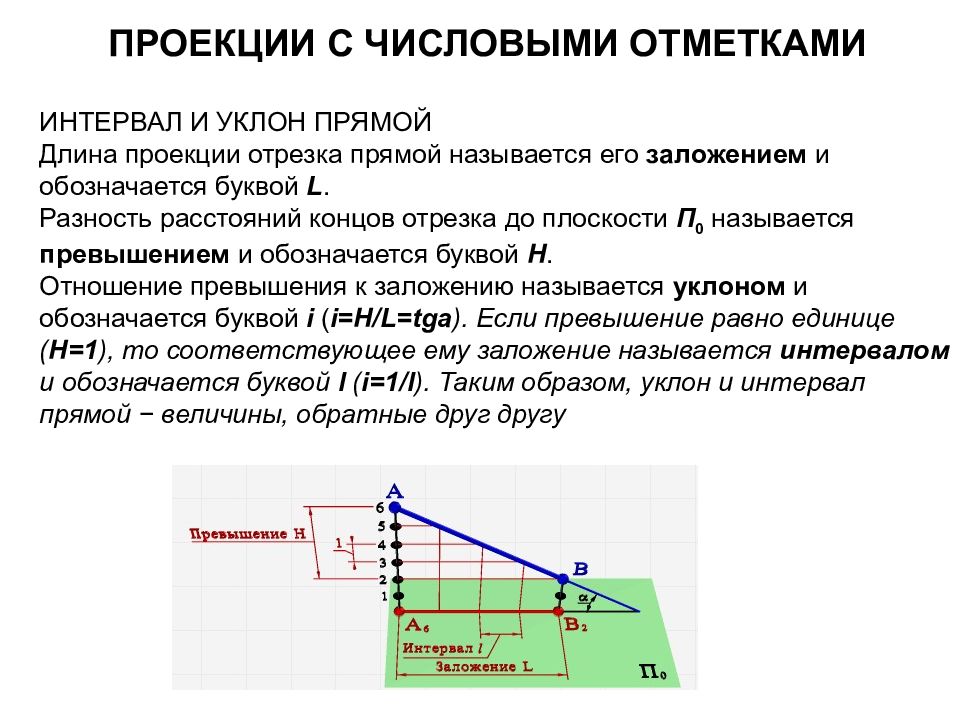
Проекции с числовыми отметками ИНТЕРВАЛ И УКЛОН ПРЯМОЙ Длина проекции отрезка прямой называется его заложением и обозначается буквой L. Разность расстояний концов отрезка до плоскости П 0 называется превышением и обозначается буквой Н. Отношение превышения к заложению называется уклоном и обозначается буквой i ( i=H / L=tga ). Если превышение равно единице ( Н=1 ), то соответствующее ему заложение называется интервалом и обозначается буквой l ( i=1/ l ). Таким образом, уклон и интервал прямой − величины, обратные друг другу
Слайд 116
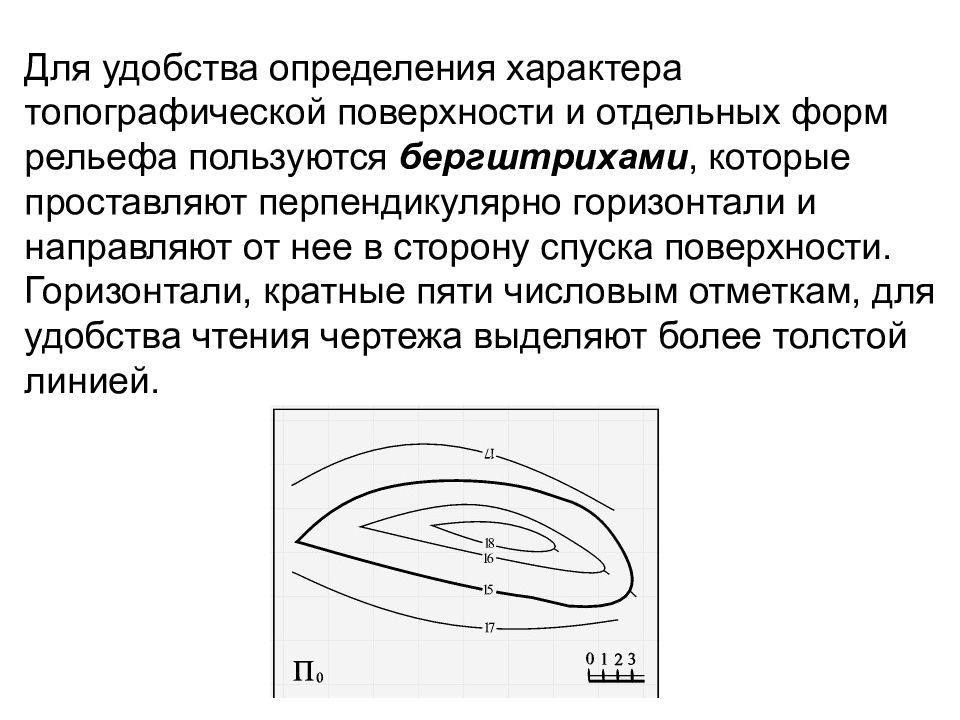
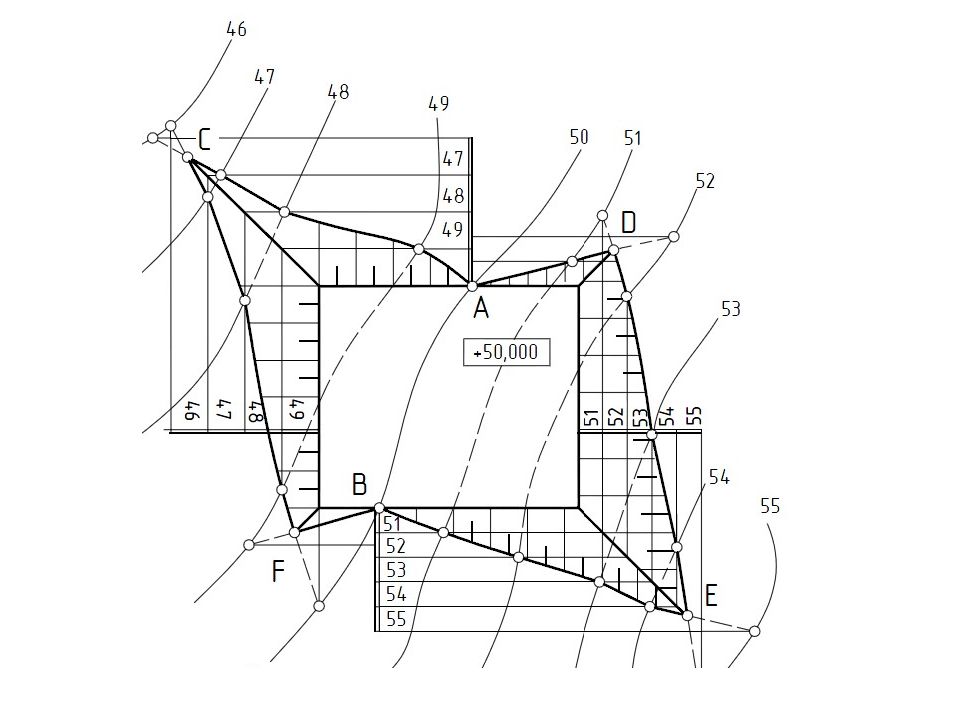
Для удобства определения характера топографической поверхности и отдельных форм рельефа пользуются бергштрихами, которые проставляют перпендикулярно горизонтали и направляют от нее в сторону спуска поверхности. Горизонтали, кратные пяти числовым отметкам, для удобства чтения чертежа выделяют более толстой линией.
Слайд 117
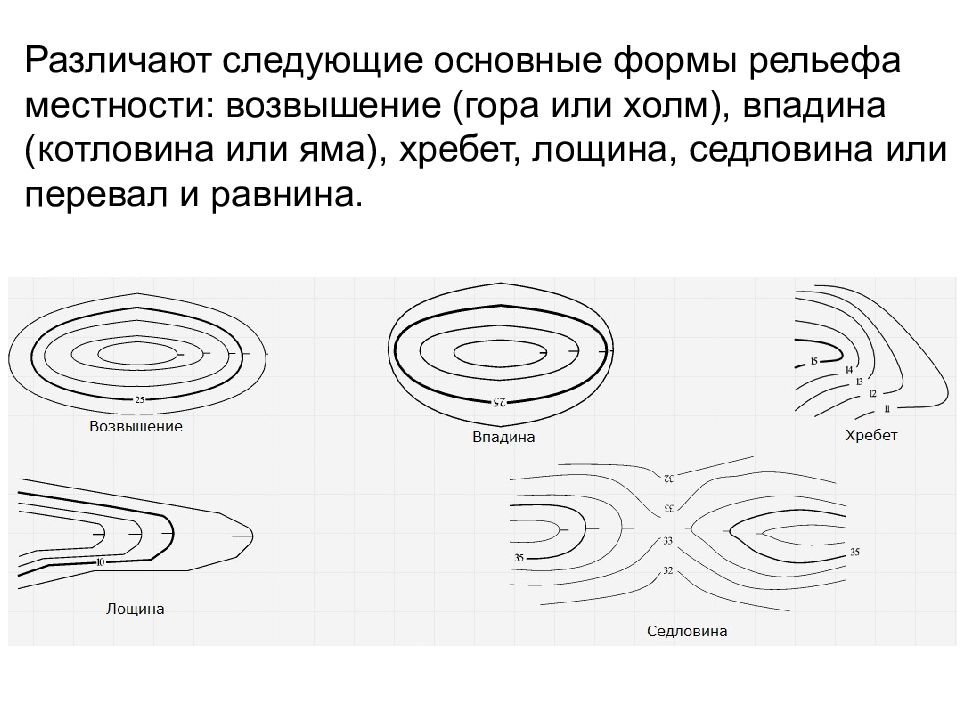
Различают следующие основные формы рельефа местности: возвышение (гора или холм), впадина (котловина или яма), хребет, лощина, седловина или перевал и равнина.
Слайд 118
Поверхность равного уклона Поверхность, все прямолинейные образующие которой составляют с горизонтальной плоскостью постоянный угол, называется поверхностью равного уклона. Такая поверхность может быть образована движением прямого кругового конуса с вертикальной осью вдоль некоторой направляющей кривой. При этом уклон конуса остается постоянным, а размеры могут меняться. Поверхности откосов, насыпей и выемок на криволинейных участках дорог являются поверхностями равного уклона
Слайд 119
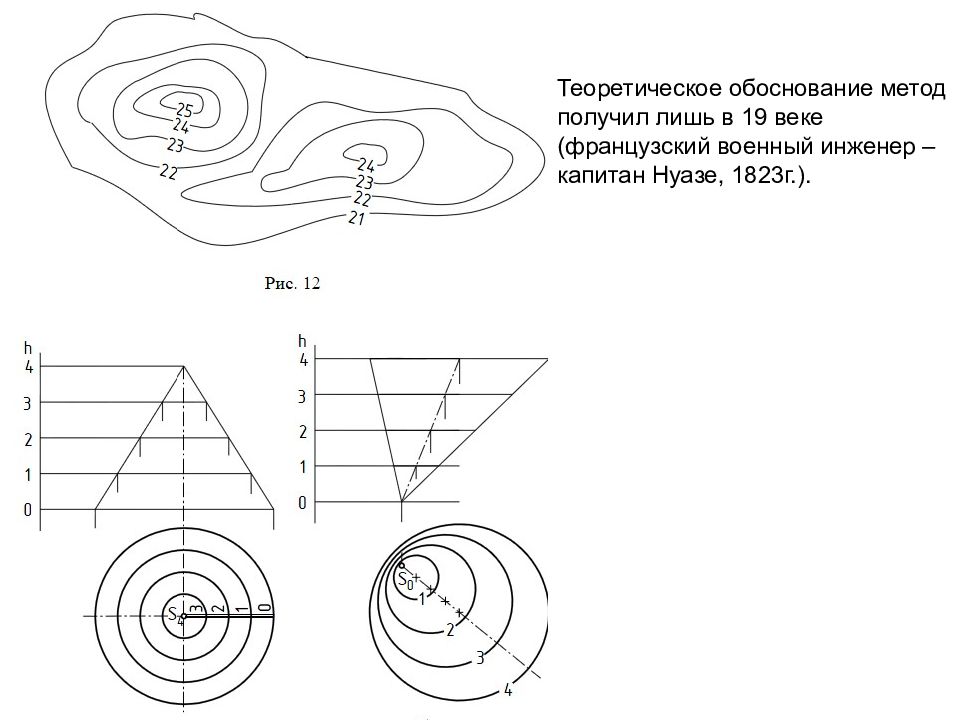
Теоретическое обоснование метод получил лишь в 19 веке (французский военный инженер – капитан Нуазе, 1823г.).
Слайд 123
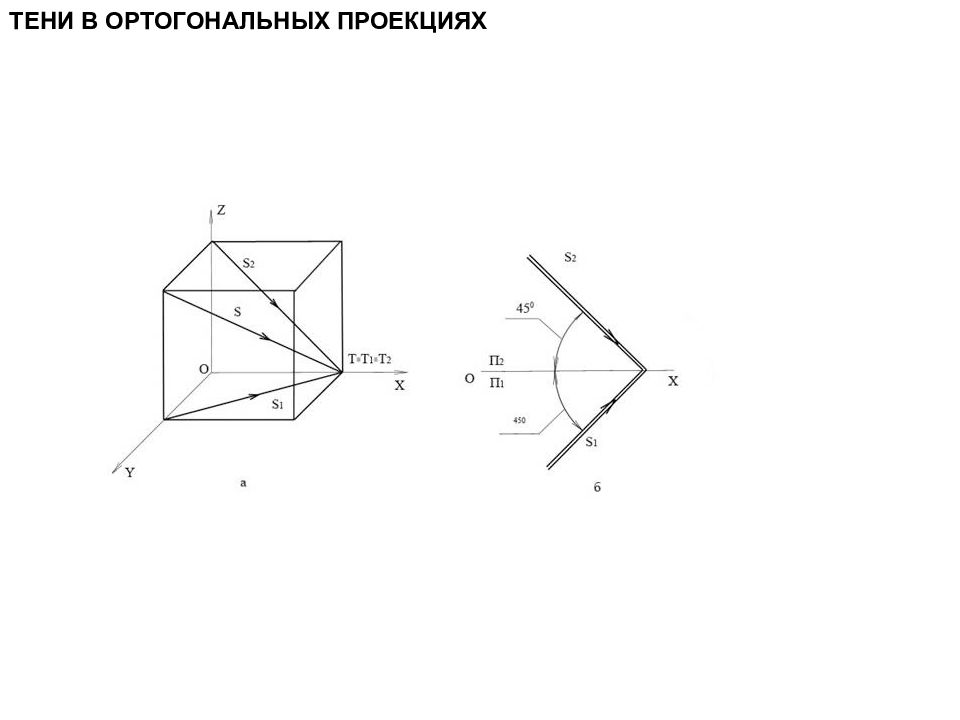
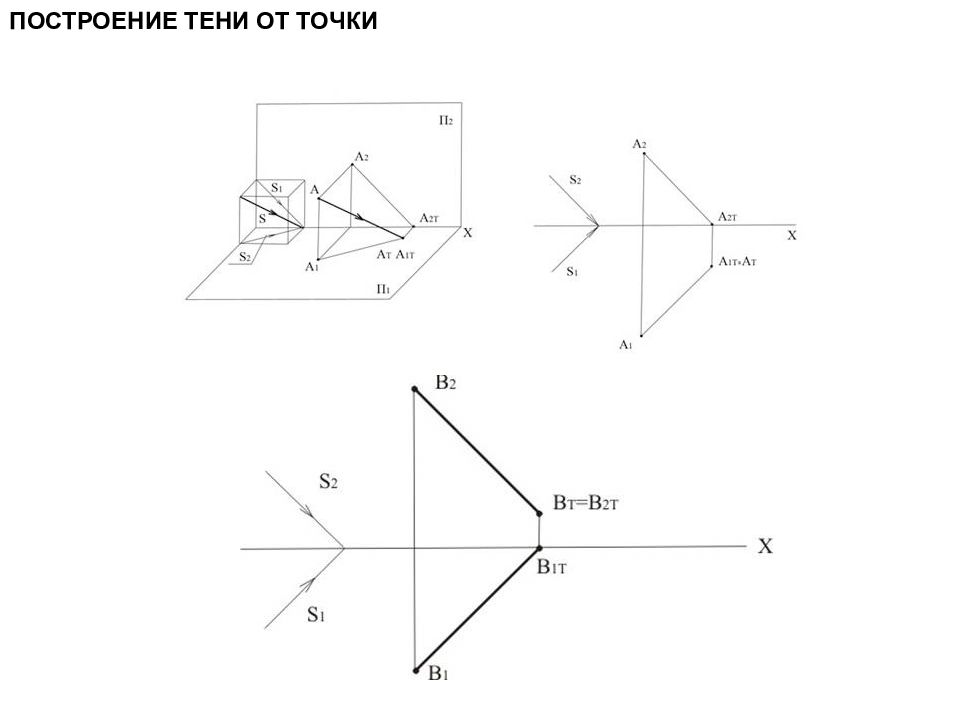
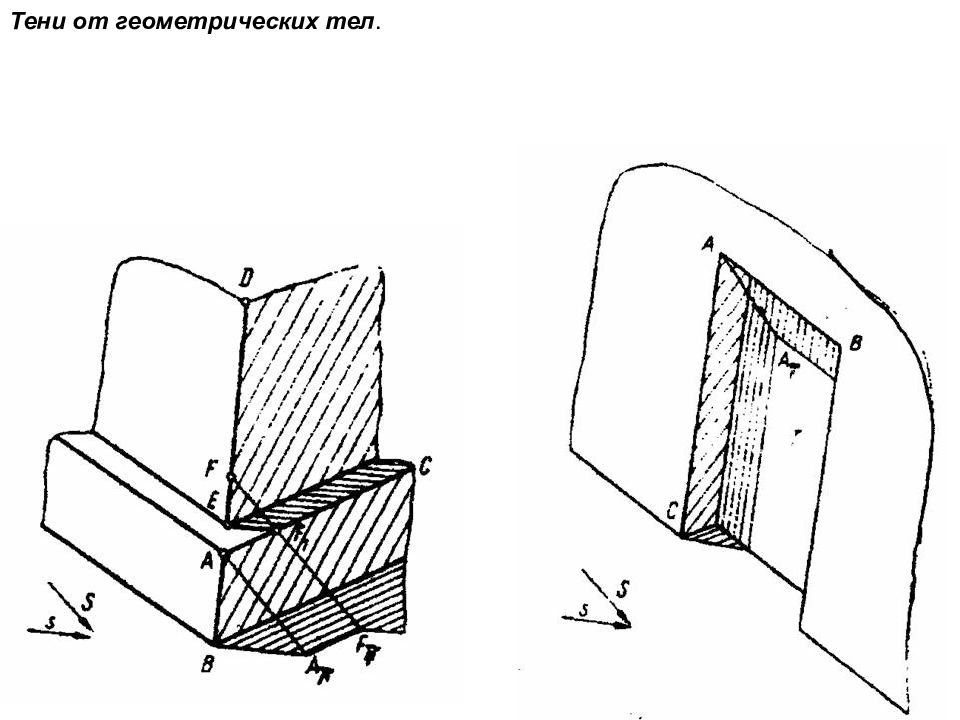
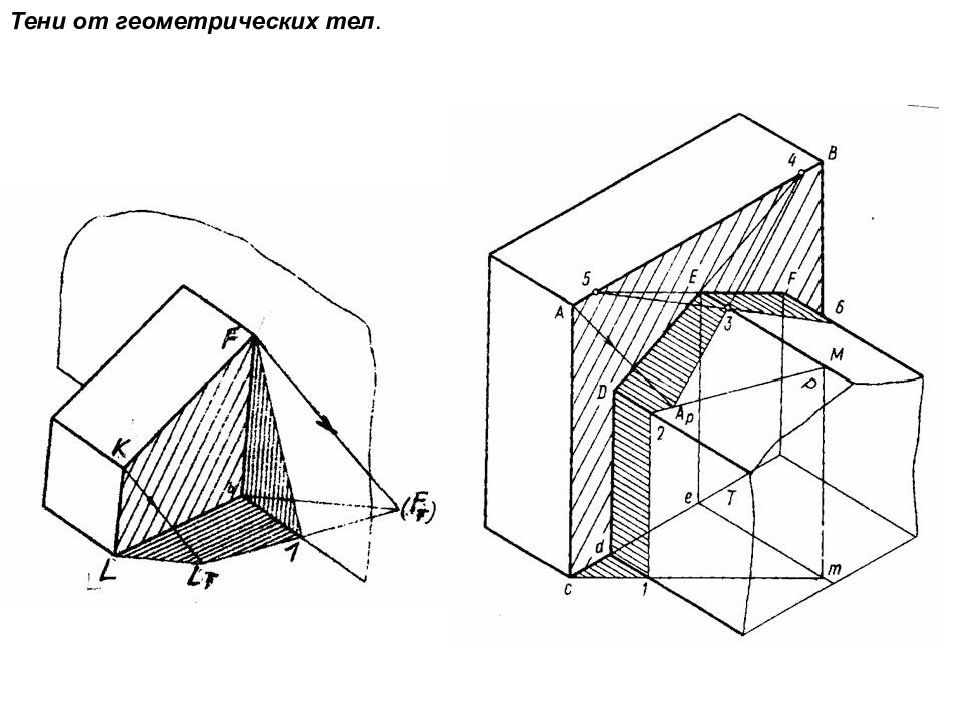
ТЕНИ В ОРТОГОНАЛЬНЫХ ПРОЕКЦИЯХ При оформлении чертежей фасадов зданий или других архитектурных сооружений возникает необходимость придать изображаемому объекту объемность, рельефность форм, подчеркнуть соотношение пропорций отдельных частей, т.е. придать чертежу наглядность, выразительность. С этой целью на чертежах наносят контуры теней, т.е. границы между освещенными и неосвещенными поверхностями предмета. Все предметы в действительности освещены лучами солнца или любым источником света. Световые лучи, распространяясь прямолинейно, падают на поверхность предмета и освещают ее. Те части поверхности предмета, на которые не падают лучи света, находятся в тени. Различают собственные и падающие тени. Собственной тенью 1 называют неосвещенную часть поверхности самого предмета. Падающей называют тень 2, отбрасываемую предметом на плоскость или на другую поверхность. Контуром собственной тени называется граница 3 между освещенной и неосвещенной поверхностью предмета
Слайд 127
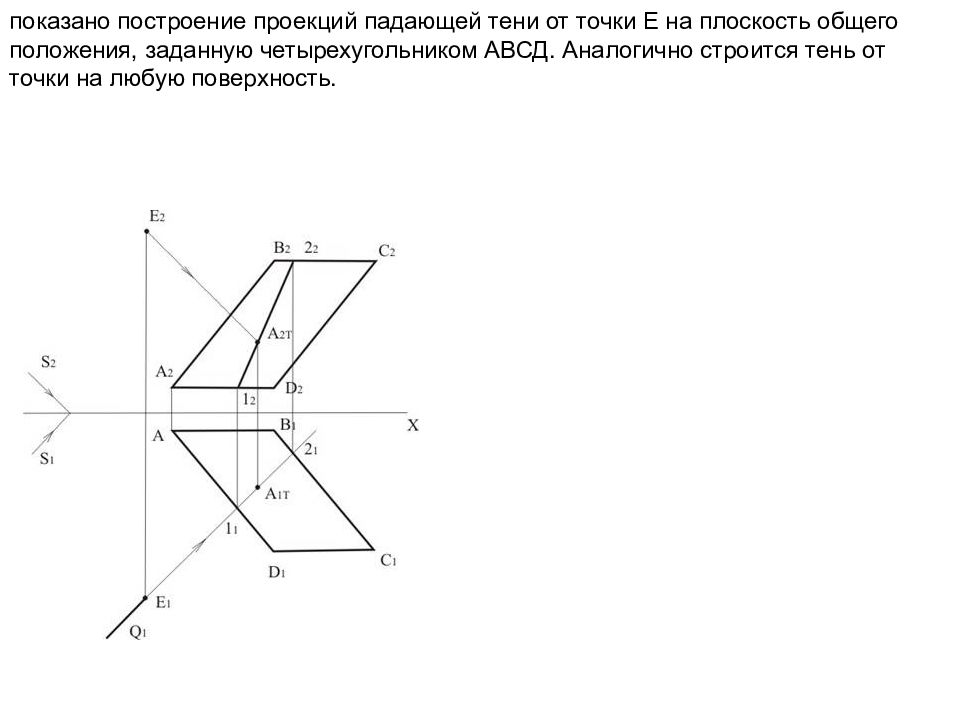
показано построение проекций падающей тени от точки Е на плоскость общего положения, заданную четырехугольником АВСД. Аналогично строится тень от точки на любую поверхность.
Слайд 130
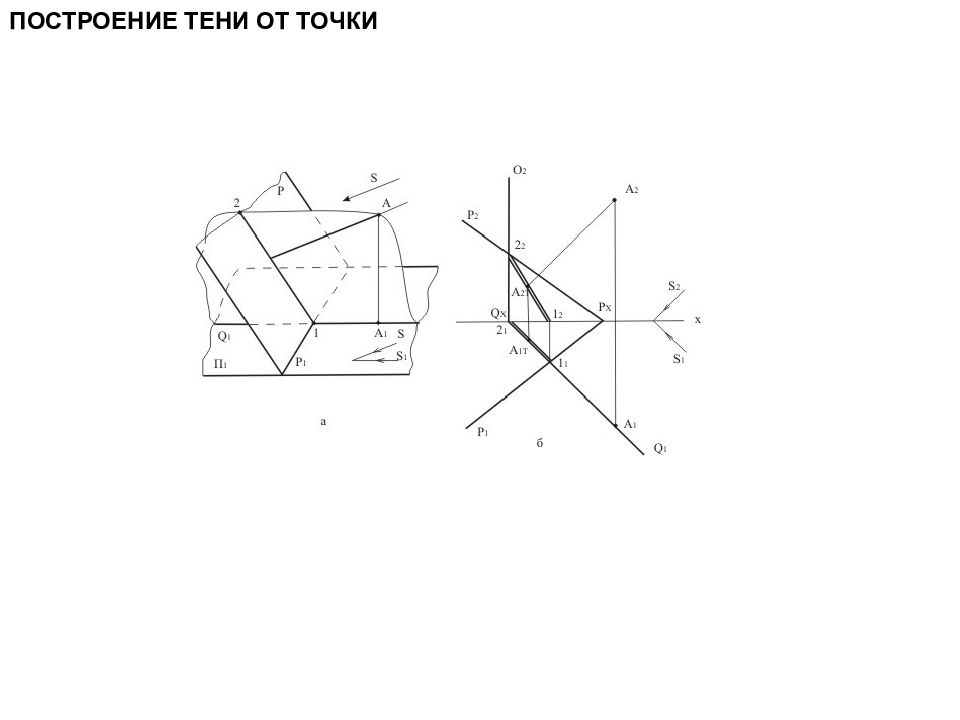
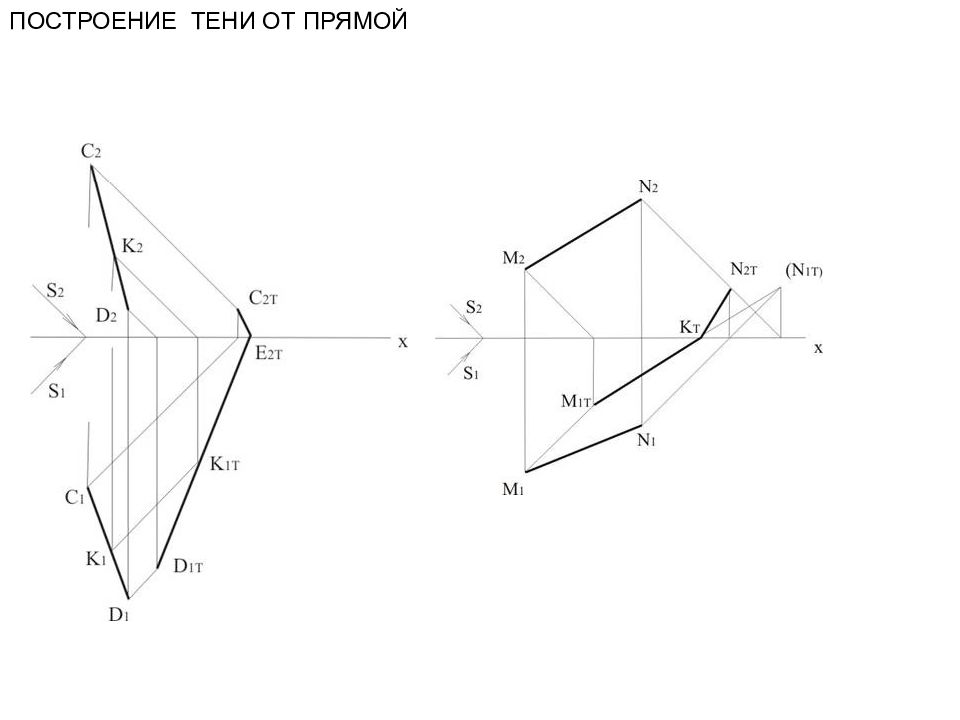
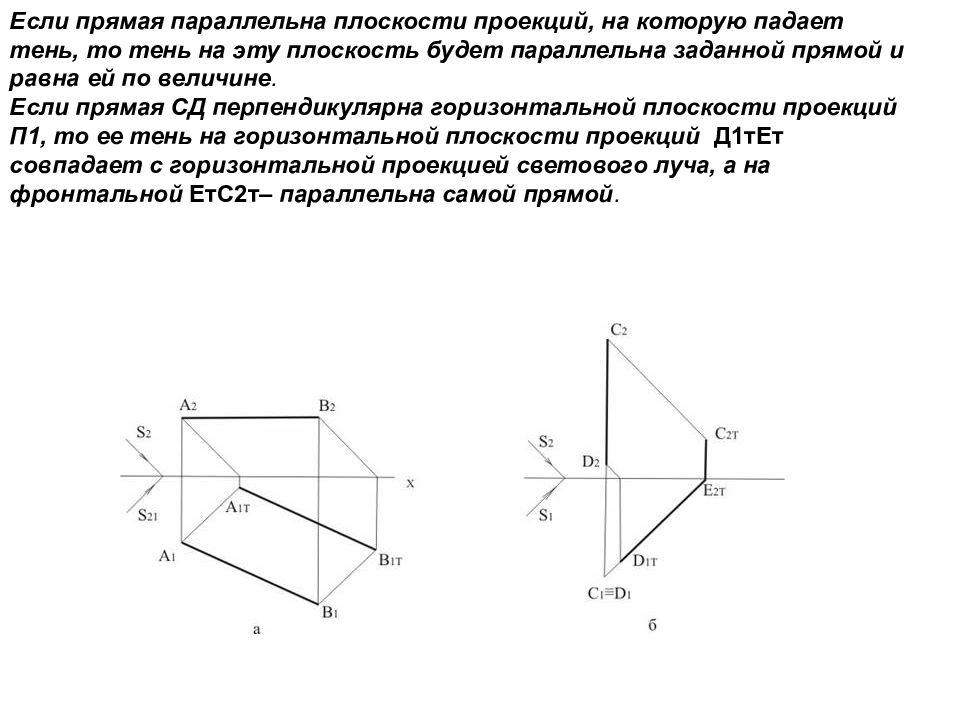
Если прямая параллельна плоскости проекций, на которую падает тень, то тень на эту плоскость будет параллельна заданной прямой и равна ей по величине. Если прямая СД перпендикулярна горизонтальной плоскости проекций П1, то ее тень на горизонтальной плоскости проекций Д1тЕт совпадает с горизонтальной проекцией светового луча, а на фронтальной ЕтС2т – параллельна самой прямой.
Слайд 131
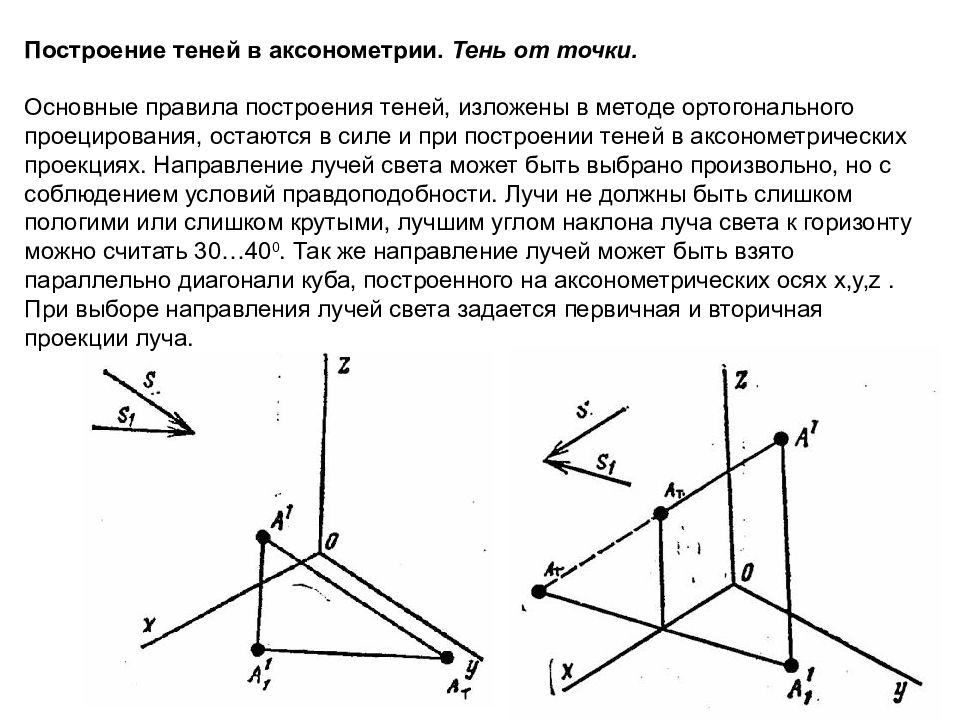
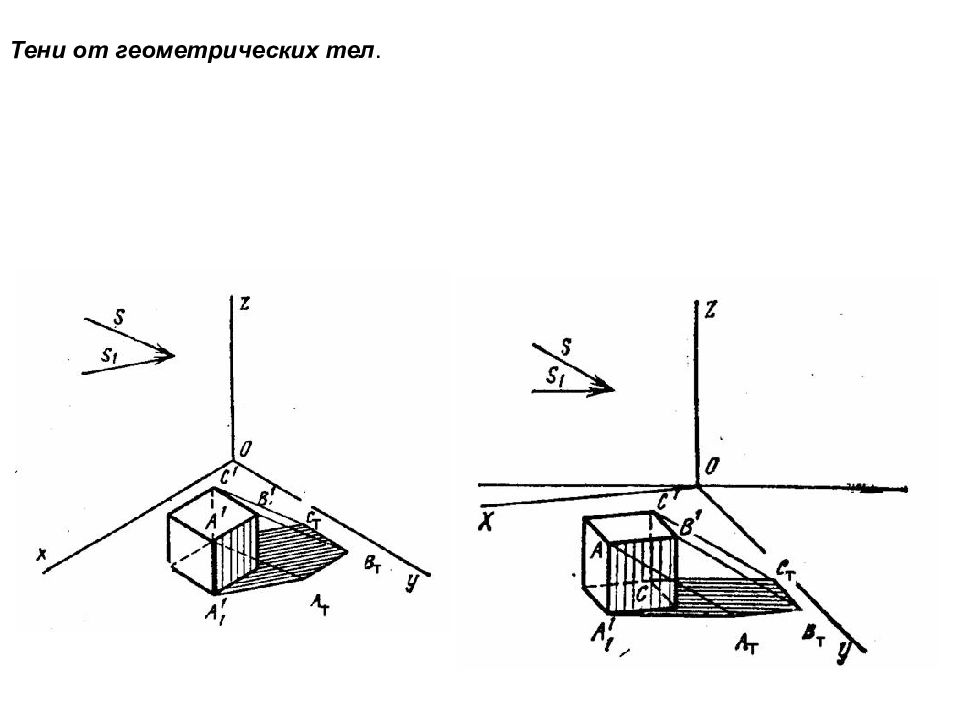
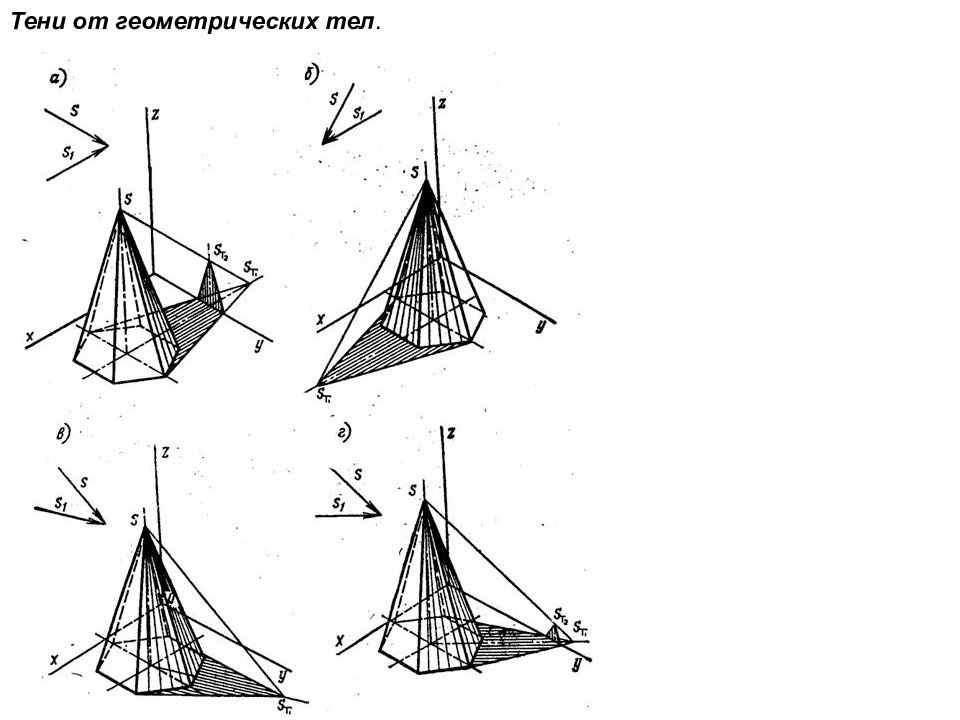
Построение теней в аксонометрии. Тень от точки. Основные правила построения теней, изложены в методе ортогонального проецирования, остаются в силе и при построении теней в аксонометрических проекциях. Направление лучей света может быть выбрано произвольно, но с соблюдением условий правдоподобности. Лучи не должны быть слишком пологими или слишком крутыми, лучшим углом наклона луча света к горизонту можно считать 30…40 0. Так же направление лучей может быть взято параллельно диагонали куба, построенного на аксонометрических осях x, y, z. При выборе направления лучей света задается первичная и вторичная проекции луча.
Слайд 132
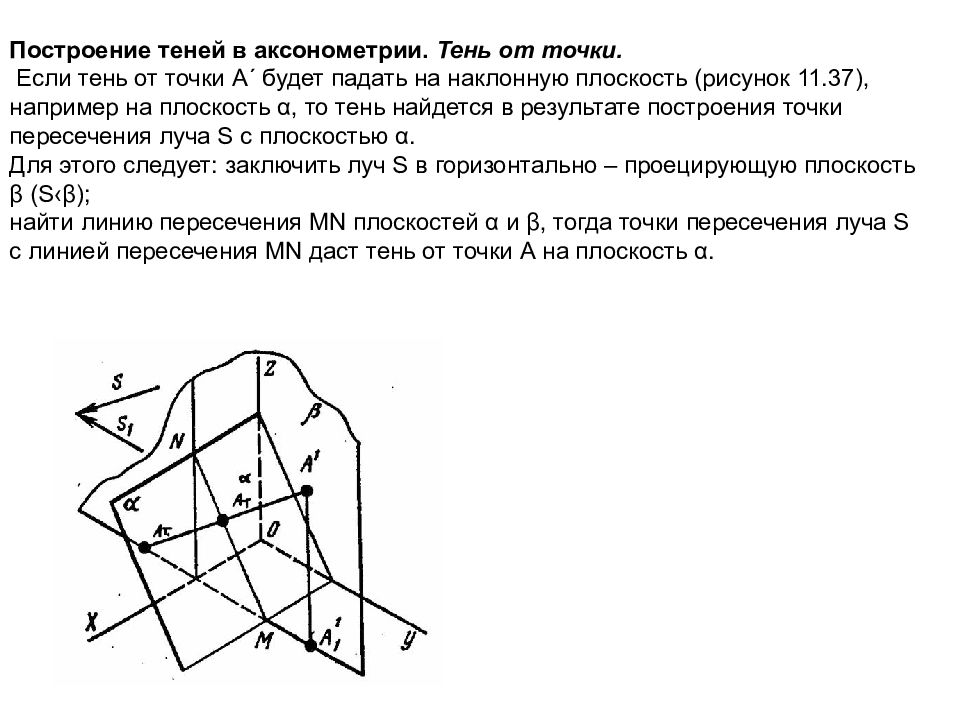
Построение теней в аксонометрии. Тень от точки. Если тень от точки А´ будет падать на наклонную плоскость (рисунок 11.37), например на плоскость α, то тень найдется в результате построения точки пересечения луча S с плоскостью α. Для этого следует: заключить луч S в горизонтально – проецирующую плоскость β (S‹β); найти линию пересечения МN плоскостей α и β, тогда точки пересечения луча S с линией пересечения МN даст тень от точки А на плоскость α.
Слайд 133
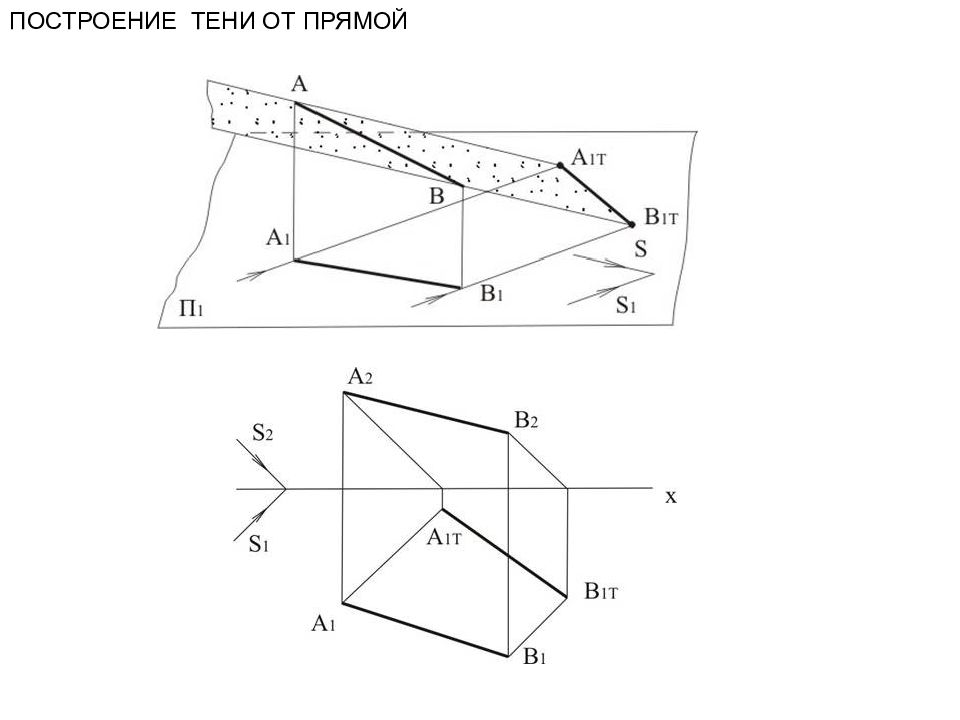
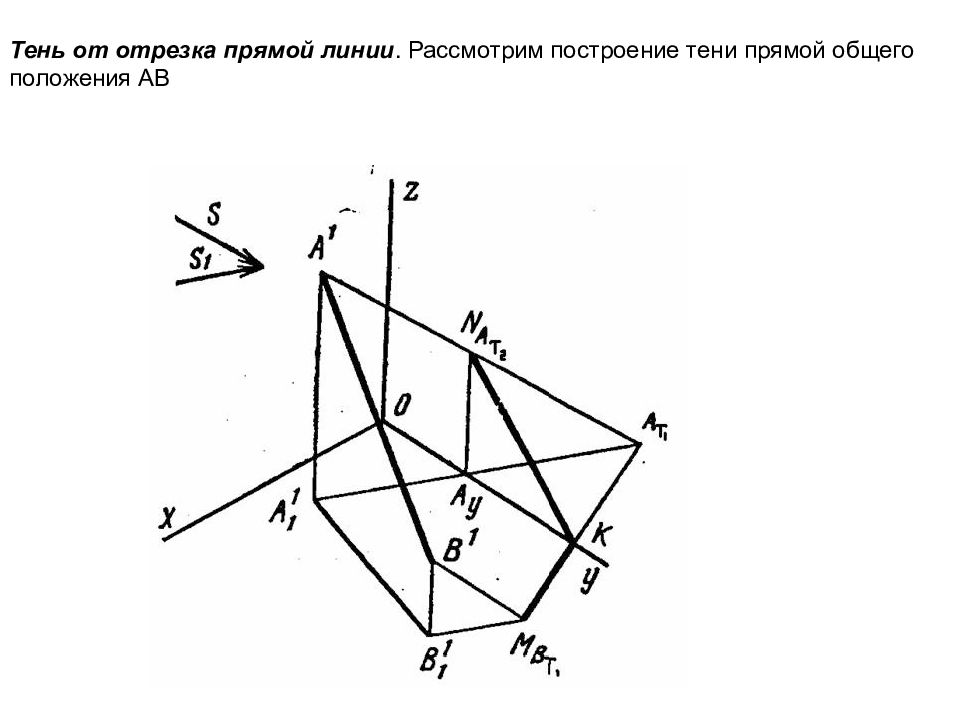
Тень от отрезка прямой линии. Рассмотрим построение тени прямой общего положения АВ





![АКСОНОМЕТРИЧЕСКИЕ ПРОЕКЦИИ гОСТ 2.317 – 69 1.1 Горизонтальная прямая уровня - h h // П 1, а к П 2 и П 3 расположена под углом. h [АВ] // П 1 h 2 [А 2 В 2 ] // ox h 1 [А 1 В 1 ] = н.в. h](https://s1.showslide.ru/s_slide/0629d24ce5bf4092348d9236ceca3bc0/918f3f76-2ea7-4dbc-9357-4bfd75b2c65f.jpeg)
![АКСОНОМЕТРИЧЕСКИЕ ПРОЕКЦИИ гОСТ 2.317 – 69 1. 2 Фронтальная прямая уровня - f f // П 2, а к П 1 и П 3 расположена под углом. f [CD] // П 2 f 1 [C 1 D 1 ] // ox f 2 [C 2 D 2 ] = н.в. f](https://s1.showslide.ru/s_slide/f29b70c0fcf7413afde8e22cfb4f49e7/da01e44b-fedc-492c-845d-4932b910ecf0.jpeg)
![АКСОНОМЕТРИЧЕСКИЕ ПРОЕКЦИИ гОСТ 2.317 – 69 1.3 Профильная прямая уровня - р p // П 3, а к П 1 и П 2 расположена под углом. p [Е F] // П 3 p 2 [Е 2 F 2 ] // oz p 3 [Е 3 F 3 ] = н.в. p](https://s1.showslide.ru/s_slide/ee7c79792cc63601dae99ae7f19de778/960f3f2e-af9e-4c2c-b8ca-a7f7b31ce104.jpeg)

![АКСОНОМЕТРИЧЕСКИЕ ПРОЕКЦИИ гОСТ 2.317 – 69 Определение расстояния от точки до проецирующей прямой Дано: g┴ П 1 А(А 1 ;А 2 ) [А; g ] Решение: 1) А 1 ϵ n 1 n 1 ∩ g 1 =K 1 2) А 2 ϵ n 2 ┴ g 2 n 2 ∩ g 2 =K 2](https://s1.showslide.ru/s_slide/f196fe7effe07be16fb354676918f71f/4d691d27-7f16-459b-ac50-c78bfd8b03dd.jpeg)
![АКСОНОМЕТРИЧЕСКИЕ ПРОЕКЦИИ гОСТ 2.317 – 69 Определение расстояния от точки до прямой уровня Дано: h(h 1 ; h 2 ) А(А 1 ;А 2 ) [А; h ] Решение: 1) П 1 /П 2 =>П 4 /П 1 ; П 4┴ h Х 14 ┴ h 1 2 ) [А 4 1 4 ]](https://s1.showslide.ru/s_slide/692275f69b75357fb3fce1f89fdf516f/25403509-24ae-4aad-98f0-1006472f908b.jpeg)
![АКСОНОМЕТРИЧЕСКИЕ ПРОЕКЦИИ гОСТ 2.317 – 69 Определение расстояния от точки до прямой общего положения Дано: [ ВС ] - о.п. А(А 1 ;А 2 ) [А;[ВС] Чтобы определить расстояние от прямой до точки необходимо](https://s1.showslide.ru/s_slide/b7cd1070e9e94a86649ed0b896de3e2b/a620b9c9-30c8-403b-9a73-f951cd3e0a07.jpeg)
![АКСОНОМЕТРИЧЕСКИЕ ПРОЕКЦИИ гОСТ 2.317 – 69 Дано: Г( h∩f ) о.п. А(А 1 ; А 2 ) [ А;Г ] Алгоритм решения: 1) А ϵ n ┴ Г( h∩f ) А 2 ϵ n 2 ┴ f 2 А 1 ϵ n 1 ┴ h 1 2) В= n ∩ Г m ϵ Г и m 2 =n 2 m 2 (1 2 ; 2 2 )](https://s1.showslide.ru/s_slide/dfc7382f0d6ccc922dd71440e2b703a7/d31ccf11-aa2e-4b40-9dfa-01f6c9ffee8f.jpeg)